Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60697,7 pages
10.4236/jmp.2015.613193
Physical Mathematical Evaluation of the Cardiac Dynamic Applying the Zipf-Mandelbrot Law
Javier Oswaldo Rodríguez1,2, Signed Esperanza Prieto1,2, Sandra Catalina Correa1,2, Fernán Mendoza3,4, Giora Weiz5, María Yolanda Soracipa1,2, Nelly Velásquez4, Juan Mauricio Pardo6, Miguel Martínez7, Freddy Barrios4
1Insight Research Group, Bogotá, Colombia
2Clínica del Country Research Center, Bogotá, Colombia
3Fundación Clínica Abood Shaio, Bogotá, Colombia
4Universidad el Bosque, Bogotá, Colombia
5Columbia University Medical Center, Cardiology Shaare Zedek Medical Center, Jerusalem, Israel
6Hospital Universitario Mayor Méderi, Bogotá, Colombia
7Physiology, Medicine Faculty, Universidad Nacional de Colombia, Bogotá, Colombia
Email: grupoinsight2025@yahoo.es
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 June 2015; accepted 24 October 2015; published 29 October 2015
ABSTRACT
Introduction: The law of Zipf-Mandelbrot is a power law, which has been observed in natural languages. A mathematical diagnosis of fetal cardiac dynamics has been developed with this law. Objective: To develop a methodology for diagnostic aid to assess the degree of complexity of adult cardiac dynamics by Zipf-Mandelbrot law. Methodology: A mathematical induction was done for this; two groups of Holter recordings were selected: 11 with normal diagnosis and 11 with acute disease of each group, one Holter of each group was chosen for the induction, the law of Zipf- Mandelbrot was applied to evaluate the degree of complexity of each Holter, searching similarities or differences between the dynamics. A blind study was done with 20 Holters calculating sensitivity, specificity and the coefficient kappa. Results: The complexity grade of a normal cardiac dynamics varied between 0.9483 and 0.7046, and for an acute dynamic between 0.6707 and 0.4228. Conclusions: A new physical mathematical methodology for diagnostic aid was developed; it showed that the degree of complexity of normal cardiac dynamics was higher than those with acute disease, showing quantitatively how cardiac dynamics can evolve to acute state.
Keywords:
Heart Rate, Cardiovascular Diseases, Zipf-Mandelbrot Law, Complexity Grade

1. Introduction
Since the first half of twentieth century, linguistics has an empirical law which quantifies the relationship between the range and frequency of words in a text, called Zipf law [1] , for this, the frequencies of occurrence of words are arranged from the highest to the lowest, and each of this frequencies is assigned to a range from 1 and the range is going to rise as the frequency decreases, creating a hyperbolic behavior between these two variables. Later Mandelbrot developed a linearization and defined the degree of complexity of de system, which was mea- sured by statistical fractal dimension [2] -[4] .
This law has been the foundation of new methodologies to interpret the information in different areas [5] -[7] , it has been applied to characterize the complexity of specific T cell repertoire in the immune response [8] [9] , it has also been established differences in the complexity degree of the repertoire T cells specifics against the poa P9 allergen in an allergic patient in the presence and absence of interferon α, and in the clones Th cells [10] , showing an analogy between phenomena of language [1] -[4] and the distributions of T cell clones against the allergen poa P9. The Zipf-Mandelbrot law was applied for developing a new diagnosis of clinical application to assess fetal monitoring, from the analysis of the Components Dynamic System (CDS) in the monitoring, from four prototypical records and its comparison with other monitoring [11] . This diagnostic method consists in a simplification of clinical parameters for the evaluation of fetal monitoring, because it requires few criteria, defined from objective and reproducible measurements, compared with traditional clinical methodology that requires five evaluation parameters, adding explanatory subparameters, which requires additional exams to determine the clinical diagnosis, it allows anticipating for adverse situations, this methodology was refined and presented at the XVIII Figo World Congress of Gynecology and Obstetrics [12] .
Cardio Vascular Diseases (CVD), according to reports from the World Health Organization, are the leading cause of death worldwide. In Colombia, DANE (Departamento Administrativo Nacional de Estadística) reported for 2009 that the CVD were one of the five principal causes of mortality, among them was ischemic heart disease with 28,650 cases and cerebrovascular disease with 14,555 cases [13] , which were considered as two of the leading causes of death in the country.
Classically, in cardiac physiology, periodic normal behaviors that characterize a system were searched, so the analysis of heart rate variability (HRV) has been widely studied [14] . Decreased HRV has been used as a prognostic value of patients with acute cardiac dynamics [15] , associating with a considerable number of cardiovascular diseases. However, recent investigations have shown the non-linearity of the cardiovascular system; its dynamic shows chaotic behavior [14] , which can be described from the fractal geometry, this geometry studies irregular objects such as structures of the human body [16] -[18] .
Pioneering work done from this perspective, like that done by Goldberger et al, allowed observing spectral abrupt changes and oscillations sustained of low frequency in patients with high risk of sudden cardiac death; the loss of complexity was associated with reduced dynamic response before sudden cardiac death and aging [19] [20] . To evaluate the complexity of cardiovascular dynamics, Pincus [21] used the entropy approximated, a technique that was improved by Richman et al. [22] and called sample entropy, which reduced bias of the original method.
It has been developed new methodologies based on theoretical physics and mathematics, which have allowed assessing cardiac dynamic system. These diagnostic methods characterize normal and diseased cardiac dynamics, achieving to foresee states that evolve to the intensification. These new mathematical and physic diagnoses are based on theories and concepts like the probability theory [23] , dynamical system and entropy [24] . The application of an exponential mathematical law [25] has allowed distinguishing objectively acute cardiac dynamic of chronic and normal dynamic, from the evaluation of Holter recordings. The clinical applicability of these methodologies has been confirmed in subsequent studies in patients of Intensive Care Units [26] , in pacemaker implant cardiac dynamic [27] and the evaluation of cardiac arrhythmias [28] . With the application of the exponential mathematical law, recently a new diagnosis was developed, which characterized the neonatal cardiac dynamics before the clinical manifestations of sepsis from the spatial occupation of cardiac chaotic attractors [29] . In the case of fetal cardiac dynamics, a mathematical diagnosis from probability and S/k relations of entropy was developed [30] , it has also been developed a diagnostic methodology based on the application of Zipf- Mandelbrot law [11] [12] to the fetal monitoring, differentiating normality of acute fetal distress, allowing overcoming inter and intra observer [31] problems of conventional clinical interpretation.
The purpose of this work is to develop a methodology for clinical diagnostic aid application to evaluate the complexity degree of adult cardiac dynamics from Zipf’s law―Mandelbrot, differentiating the degree of complexity of normal dynamics regarding dynamics with acute myocardial infarction.
2. Methodology
Definitions:
Ranges of 15 lat/min: heart rate (HR) ranges, which includes all HR within a range of 15 beats/min.
Zipf-Mandelbrot statistical fractal dimension: It is obtained through of logarithmic linearization, in this case, of occurrence frequencies distribution of ranges of 15 beats/min.
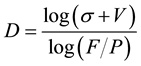
where D: is the statistical fractal dimension,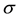 : designates the rank assumed for each range, V is defined as V = 1/N−1 where N is the frequencies number obtained in each register, P: occurrence frequency for each range and F: corresponds to a secondary factor associated to point of intersection with the vertical axis of the line obtained in linearization [2] .
: designates the rank assumed for each range, V is defined as V = 1/N−1 where N is the frequencies number obtained in each register, P: occurrence frequency for each range and F: corresponds to a secondary factor associated to point of intersection with the vertical axis of the line obtained in linearization [2] .
Procedure
22 Holter registers were selected which correspond to patients over 21 years old. Those come from the Insight database, whose Holter registers were assessed by an experienced electrophysiologist. For the mathematical induction a Holter register was taken with a normal cardiac dynamic and one with acute myocardial infarction (AMI), the values of minimum and maximum frequency were taken during each hour of each Holder test. Subsequently, for the application of Zipf-Mandelbrot law, the distribution number heart rates are in ranges of 15 beats/min was found, as well as the frequency of occurrence for each range. These values were organized in order from highest to lowest, associating to each frequency appearance a hierarchical range from one to the highest value, and increasing as the frequency of occurrence values were decreasing.
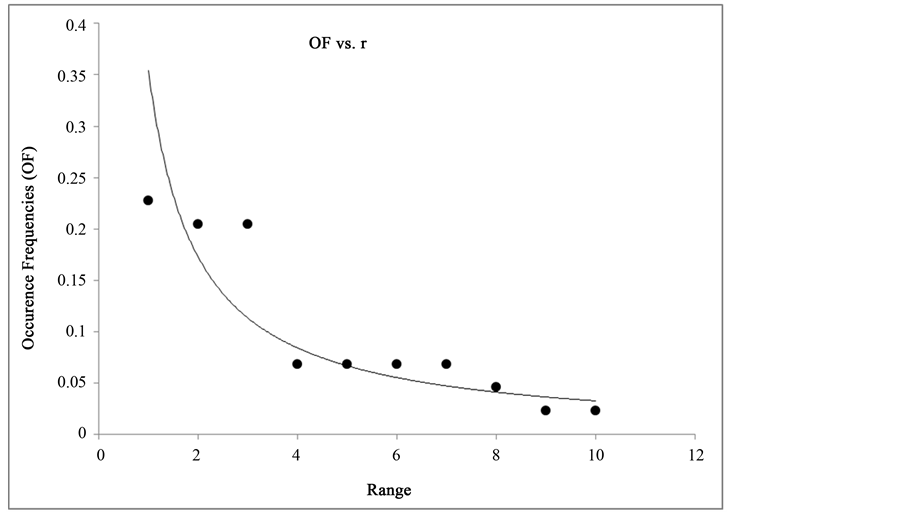
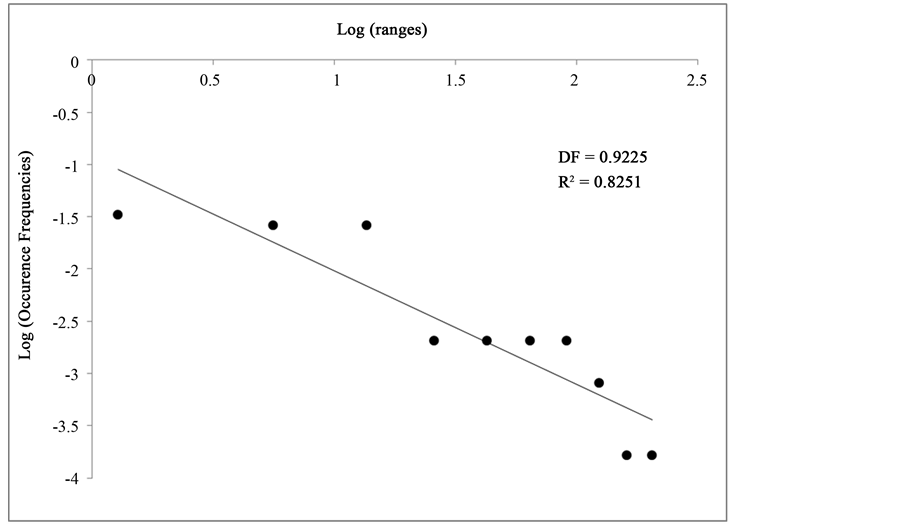
These values, the frequency of appearance associated to hierarchical ranks, are brought to a graph, seeking a hyperbolic behavior (Figure 1) as it is necessary for the law application. Once this behavior was got, a linearization was done (Figure 2), in order to find the fractal statistical dimension, seeking mathematical differences among the cardiac dynamics.
For statistical analysis, a blind study was conducted with 20 Holters, which included 10 normal Holter registers and 10 with acute heart disease. The clinical findings of Holter registers and the diagnosis made by clinical
Figure 1. Graphic of hyperbolic behavior for the normal prototype, OF: Occurrence frequency, r: range assigned by Zipf-Mandelbrot law.
Figure 2. Log (OF) vs. Log (r):Graphic of logarithmic linearization for the normal prototype. OF: Occurrence frequency, r: range assigned by Zipf-Mandelbrot law.
parameters were assumed as Gold standard. To do this the specificity and sensivity was calculated through a binary classification, where true positives (TP) corresponding to the number of abnormal patients according to the Gold-Standard and are within the mathematical values corresponding to abnormality, false positives (FP) are those which mathematically have been diagnosed as normal but whose clinical values correspond to abnormal patients, and finally true negative (TN) defined as the number of heart registers clinically diagnosed as normal and whose mathematical values also correspond to the normal.
The correlation between the physical mathematical values and the conventional clinical diagnosis was calculated through Kappa coefficient using the following formula [32] :
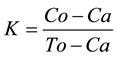
where: Co: number of concordances observed, that is, the number of patients with the same diagnosis according to the new methodology proposed and the Gold- Standard. To: All the observations, that is, all normal and disease cases. Ca: random concordances, which are calculated according to the following formula:
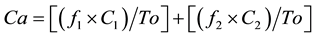
where f1 is the number of patients with mathematical values within normal limits, C1 is the number of patients clinically diagnosed within normality; f2 is the number of patients showing abnormalities associated to mathematical values, C2 is the number of patients clinically diagnosed with any kind of pathology and To is the total number of normal and abnormal cases.
3. Results
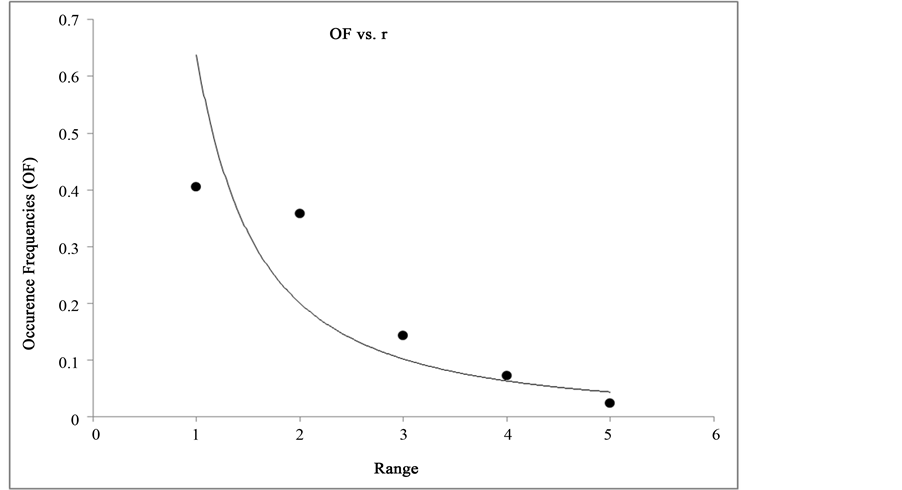
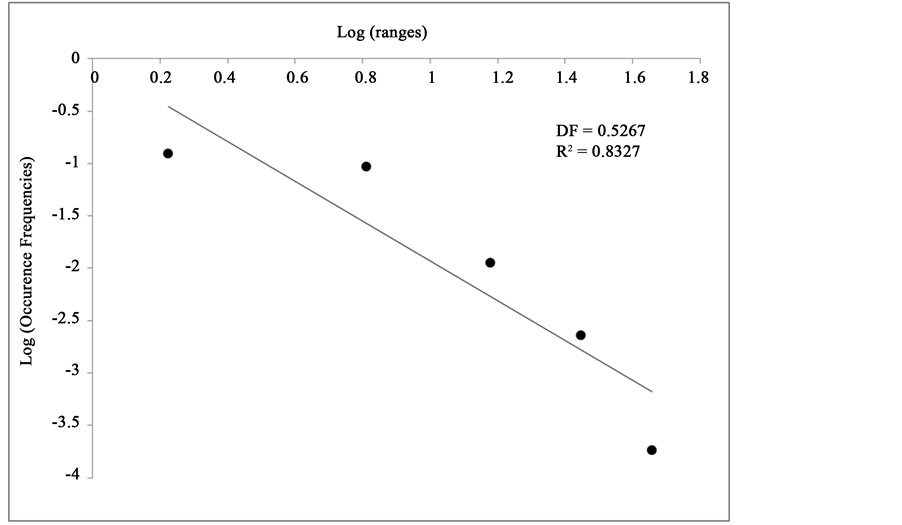
Once the fractal dimensions of the two Holter statistics records used in the induction had been realized, it was found that for normal Holter, this value was 0.9225 (Figure 1 and Figure 2), and for the cardiac dynamics with acute disease was 0.5267 (Figure 3 and Figure 4). Subsequently, when the blind study was performed with 20 Holter records, it was found that the values ranged between 0.7046 and 0.9483 for normality, and between 0.4228 and 0.6707 for acute dynamics (see Table 1). When the found fractal dimensions are compared it is observed that the normal dynamics revealed values even double compare with the dynamics of acute myocardial
Figure 3. Graphic of hyperbolic behavior for the AMI prototype. OF: Occurrence frequency, r: range assigned by Zipf-Mandelbrot law.
Figure 4. Log (OF) vs. Log (r):Graphic of logarithmic linearization for the AMI prototype. OF: Occurrence frequency, r: range assigned by Zipf-Mandelbrot law.
infarction, which evinced the optimal quantification of the differentiation between this type of dynamics.
Hyperbolic behavior between the frequencies of appearance of the ranges 15 beats/min and ranges partners in the implementation of Zipf’s law was evident-Mandelbrot, and likewise succeeded in establishing the linearization for all the dynamics, which can be seen is the R2 that were found, which ranged between 0.5924 and 0.9016 (see Table 2). The statistical analysis was performed, finding a sensitivity and specificity of 100% and a Kappa coefficient of 1.
Table 1. Values of statistical fractal dimension for the 20 records Holter, 10 normal and 10 with acute dynamic, P: Prototype of the induction.
Table 2. R2 values for the 20 Holter records, 10 normal and 10 with acute dynamic, P: Prototype of the induction.
4. Discussion
This is the first work in which a diagnostic aid methodology was developed from application of the Zipf-Man- delbrot law into cardiac dynamics, by analyzing hierarchical ordering of the maximum and minimum heart rates in each hour, in which was found a hyperbolic behavior for heart rates that were in ranges of 15 beats/min, showing a self-organization statistic fractal of the dynamic. It was evidenced that the complexity degree of normal cardiac dynamics was higher than the dynamic with acute pathologies for all Holters, showing quantitatively how the cardiac dynamics can be sharpen. This new methodology constitutes a new way to assess the complexity degree of cardiac dynamics, which simplify other methods of assessment [33] [34] .
This work is based on the theoretical physics method [35] , in which from inductions with few cases, a simplification of the phenomenon studied is achieved and general principles that characterize the phenomenon are found, for subsequently establishing a general methodology for all cases of universe. In medicine, diagnostic evaluation even includes a qualitative component, which makes that some of these evaluations show inter and intra observer [31] problems, by this reason, the development of mathematical, objective and reproducible methodologies, like as developed in this work, is vital to improve conventional diagnostic evaluations. Mathematical understanding of the phenomenon was given in this work, can not only find differentiations of normal-disease, but also opens the possibility of evaluating the evolution of cardiac dynamics, which in clinical practice is very useful in making decisions.
For example, the first work developed in the context of the theory of dynamical systems and fractal geometry contradicted the principle of homeostasis. Goldberger et al. [19] found that the disease was associated to highly regular or irregular states, while normality was established in middle of these two extremes. On the other hand, Huikuri et al. [36] characterize cardiac dynamics by applying fractal geometry, allowed them to characterize cardiac dynamics, by applying fractal geometry in post-infarcted patients and EF below 35%, finding predictors of mortality rates that exceed conventional. To assess the implications of the application of the methodology developed, for the analysis of HRV associated with a specific disease, a study was performed, which clarified that the clinical application of many of these methodologies [32] was still in discussion [37] . In this study, it establishes a mathematical order that allows evaluating other cases independently, without that the methodology being affected by causal factors and populations.
Other works based on this investigation line have resulted in a new clinical diagnosis and practices predictions in cardiology, as already described; likewise predictions have been established in other fields like immunology [38] , in predicting malaria outbreaks in Colombia with success rate 99% [39] and predicting CD4 T lymphocytes from blood count [40] [41] . Also, new diagnostics for evaluation of cervical cells from euclidian and fractal geometry [42] [43] has been performed, allowing to evaluate the total possible paths of development of illness, between normality and cervical carcinoma [44] . From this same perspective it has been developed methodologies for assessing fractal structures like coronary arteries in an experimental model of restenosis [16] . These new perspectives that provide solutions applicable to all medical fields make that medicine is positioned at the predictive field like the theoretical physics.
Acknowledgements
We thank the Universidad el Bosque, especially the Investigations Division of the Universidad el Bosque, for their support. This work is part of the products made in the PIC-2013-369 project approved by the Research Division of the Universidad el Bosque. We thank the Research Center Clinic Country, especially Dr. Tito Tulio Roa, Director of Medical Education; Dr. Jorge Ospina, Medical Director; Dr. Alfonso Correa, Director of Research Center; also Dr. Adriana Lizbeth Ortiz, epidemiologist, and Silvia Ortiz, head nurse; nurse Sandra Rodríguez and Juan Camilo Benítez, bacteriologist of clinical studies, for the continued support of our research group.
Cite this paper
Javier OswaldoRodríguez,Signed EsperanzaPrieto,Sandra CatalinaCorrea,FernánMendoza,GioraWeiz,María YolandaSoracipa,NellyVelásquez,Juan MauricioPardo,MiguelMartínez,FreddyBarrios, (2015) Physical Mathematical Evaluation of the Cardiac Dynamic Applying the Zipf-Mandelbrot Law. Journal of Modern Physics,06,1881-1888. doi: 10.4236/jmp.2015.613193
References
- 1. Zipf, G. (1949) Human Behaviour and the Principle of Least Effort: An Introduction to Human Ecology. Addison-Wesley, Cambridge.
- 2. Mandelbrot, B. (1972) Scaling and Power laws without Geometry. In: The Fractal Geometry of Nature, Freeman, San Francisco, 344-348.
- 3. Mandelbrot, B. (2000) Hierarchical or Classification Trees, and the Dimension. In: Fractals: Form, Chance and Dimension, Tusquets, Barcelona, 161-166.
- 4. Mandelbrot, B. (1954) Structure formelle des textes et comunication. World, 10, 1-27.
- 5. Adamic, L. and Huberman, B. (2002) Zipf’s Law and the Internet. Glottometrics, 3, 143-150.
- 6. Larsen-Freeman, D. (1997) Chaos/Complexity Science and Second Language Acquisition. Applied Linguistics, 18, 141-165.
http://dx.doi.org/10.1093/applin/18.2.141 - 7. Mandelbrot, B. and Hudson, R. (2006) Fractals and Finance. Tusquets, Barcelona.
- 8. Burgos, J. and Moreno-Tovar, P. (1996) Zipf-Scaling Behavior in the Immune System. Biosystems, 39, 227-232.
http://dx.doi.org/10.1016/0303-2647(96)01618-8 - 9. Burgos, J. (1996) Fractal representation of the immune B cell repertoire. Biosystems, 39, 19-24.
http://dx.doi.org/10.1016/0303-2647(95)01574-4 - 10. Rodríguez, J. (2005) Fractal Behavior of T Specify Repertory against Poa p9 Alergeno. Revista de la Facultad de Medicina, 53, 72-78.
- 11. Rodríguez, J., Prieto, S., Ortiz, L., Bautista, A., Bernal, P. and Avilán, N. (2006) Zipf-Mandelbrot Law and Mathematical Approach in Fetal Cardiac Monitoring Diagnosis. Revista Facultad de Medicina—Universidad Nacional de Colombia, 54, 96-107.
- 12. Rodríguez, J. (2006) Dynamical Systems Theory and ZIPF—Mandelbrot Law Applied to the Development of a Fetal Monitoring Diagnostic Methodology. Proceedings of the 18th FIGO World Congress of Gynecology and Obstetrics, Kuala Lumpur, 5-10 November 2006.
- 13. Robledo, R. and Escobar, F.A. (2010) Chronic Non-Communicable Diseases in Colombia. Bulletin of the Health Observatory, 3, 1-9.
- 14. Gallo, J., Farbiarz, J. and Alvarez, D. (1999) Spectral Analysis of Heart Rate Variability. IATREIA, 12, 61-71.
- 15. Harris, P., Stein, P.K., Fung, G.L. and Drew, B.J. (2014) Heart Rate Variability Measured Early in Patients with Evolving Acute Coronary Syndrome and 1-Year Outcomes of Rehospitalization and Mortality. Journal of Vascular Health and Risk Management, 10, 451- 464.
http://dx.doi.org/10.2147/VHRM.S57524 - 16. Rodríguez, J., Prieto, S., Correa, C., Bernal, P., Puerta, G., Vitery, S., et al. (2010) Theoretical Generalization of Normal and Sick Coronary Arteries with Fractal Dimensions and the Arterial Intrinsic Mathematical Harmony. BMC Medical Physics, 10, 1-6.
http://dx.doi.org/10.1186/1756-6649-10-1 - 17. Rodríguez, J., Prieto, S., Correa, C., Bernal, P., álvarez, L., Forero, G., et al. (2012) Fractal Diagnosis of Left Heart Ventriculograms Fractal Geometry of Ventriculogram during Cardiac Dynamics. Revista Colombiana de Cardiología, 19, 18-24.
- 18. Goldberger, A., Rigney, D.R. and West, B. (1990) Science in Pictures: Chaos and Fractals in Human Physiology. Scientific American, 262, 42-49.
http://dx.doi.org/10.1038/scientificamerican0290-42 - 19. Goldberger, A.L. and West, B.J. (1987) Applications of Nonlinear Dynamics to Clinical Cardiology. Annals of the New York Academy of Sciences, 504, 195-213.
http://dx.doi.org/10.1111/j.1749-6632.1987.tb48733.x - 20. Goldberger, A.L., Rigney, D.R., Mietus, J., Antman, E.M. and Greenwald, S. (1988) Nonlinear Dynamics in Sudden Cardiac Death Syndrome: Heartrate Oscillations and Bifurcations. Experientia, 44, 983-987.
http://dx.doi.org/10.1007/BF01939894 - 21. Pincus, S.M. (1991) Approximate Entropy as a Measure of System Complexity. Proceedings of the National Academy of Sciences of the United States of America, 88, 2297-2301.
http://dx.doi.org/10.1073/pnas.88.6.2297 - 22. Richman, J.S. and Moorman, J.R. (2000) Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. American Journal of Physiology—Heart and Circulatory Physiology, 278, H2039-H2049.
- 23. Rodríguez, J., Correa, C., Ortiz, L., Prieto, S., Bernal, P. and Ayala, J. (2009) Evaluación matemática de la dinámica cardiaca con la teoría de la probabilidad. Revista Mexicana de Cardiología, 20, 183-189.
- 24. Rodríguez, J. (2010) Proportional Entropy of the Cardiac Dynamic Systems. Physical and Mathematical Predictions of the Cardiac Dynamic for Clinical Application..Revista Colombiana de Cardiología, 17, 115-129.
- 25. Rodríguez, J. (2011) Mathematical Law of Chaotic Cardiac Dynamic: Predictions of Clinic Application. Journal of Medicine and Medical Sciences, 2, 1050-1059.
- 26. Rodríguez, J. (2012) Proportional Entropy Applied to the Evolution of Cardiac Dynamics. Predictions of Clinical Application. Comunidad del Pensamiento Complejo, Argentina.
- 27. Rodríguez, J., Prieto, S., Correa, C., Bernal, P., Vitery, S., álvarez, L., Aristizabal, N. and Reynolds, J. (2012) Cardiac Diagnosis Based on Probability Applied to Patients with Pacemakers. Acta Médica Colombiana, 37, 183-191.
- 28. Rodríguez, J., Narváez, R., Prieto, S., Correa, C., Bernal, P., Aguirre, G., Soracipa, Y. and Mora, J. (2013) The mathematical Law of Chaotic Dynamics Applied to Cardiac Arrhythmias. Journal of Medicine and Medical Sciences, 4, 291-300.
- 29. Rodríguez, J., Prieto, S., Flórez, M., Alarcón, C., López, R., Aguirre, G., Morales, L., Lima, L. and Méndez, L. (2014) Physical-Mathematical Diagnosis of Cardiac Dynamic on Neonatal Sepsis: Predictions of Clinical Application.. Journal of Medicine and Medical Sciences, 5, 102-108.
- 30. Rodríguez, J. (2012) New Physical and Mathematical Diagnosis of Fetal Monitoring: Clinical Application Prediction. Momento Revista de Física, 44, 49-65.
- 31. Borgatta, L., Shrout, P.E. and Divon, M.Y. (1988) Reliability and Reproducibility of Nonstress Test Readings. American Journal of Obstetrics & Gynecology, 159, 554-558.
http://dx.doi.org/10.1016/S0002-9378(88)80006-1 - 32. Cohen, J. (1960) A Coefficient of Agreement for Nominal Scales. Educational and Psychological Measurement, 20, 37-46.
http://dx.doi.org/10.1177/001316446002000104 - 33. Ksela, J., Avbelj, V. and Kalisnik, J.M. (2015) Multifractality in Heartbeat Dynamics in Patients Undergoing Beating-Heart Myocardial Revascularization. Computers in Biology and Medicine, 60, 66-73.
http://dx.doi.org/10.1016/j.compbiomed.2015.02.012 - 34. Chang, M.C., Peng, C.K. and Stanley, H.E. (2014) Emergence of Dynamical Complexity Related to Human Heart Rate Variability. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics, 90, Article ID: 062806.
http://dx.doi.org/10.1103/PhysRevE.90.062806 - 35. Einstein, A. (1934) On the Method of Theoretical Physics. Philosophy of Science, 1, 163-169.
http://dx.doi.org/10.1086/286316 - 36. Huikuri, H.V., Mökikallio, T., Peng, C.K., Goldberger, A.L., Hintze, U., Mogens Møller, M., et al. (2000) Fractal Correlation Properties of R-R Interval Dynamics and Mortality in Patients with Depressed Left Ventricular Function after an Acute Myocardial Infarction. Circulation, 101, 47-53.
http://dx.doi.org/10.1161/01.CIR.101.1.47 - 37. Voss, A., Schulz, S., Schroeder, R., Baumert, M. and Caminal, P. (2009) Methods Derived from Nonlinear Dynamics for Analysing Heart Rate Variability. Philosophical Transactions of the Royal Society A, 367, 277-296.
http://dx.doi.org/10.1098/rsta.2008.0232 - 38. Rodríguez, J. (2008) Binding to Class II HLA Theory: Probability, Combinatory and Entropy Applied to Peptide Sequences. Inmunología, 27, 151-166.
http://dx.doi.org/10.1016/S0213-9626(08)70064-7 - 39. Rodríguez, J. (2010) A Method for Forecasting the Seasonal Dynamic of Malaria in the Municipalities of Colombia.. Revista Panamericana de Salud Pública, 27, 211-218.
- 40. Rodríguez, J., Prieto, S., Correa, C., Forero, M., Pérez, C., Soracipa, Y., Mora, J., Rojas, N., Pineda, D. and López, F. (2013) Set Theory Applied to White Cell and Lymphocyte Counts: Prediction of CD4 T Lymphocytes in Patients with Human Immunodeficiency Virus/Aids. Inmunología, 32, 50-56.
http://dx.doi.org/10.1016/j.inmuno.2013.01.003 - 41. Rodríguez, J., Prieto, S., Correa, C., Pérez, C., Mora, J., Bravo, J., Soracipa, Y. and álvarez, L. (2013) Predictions of CD4 Lymphocytes’ Count in HIV Patients from Complete Blood Count. BMC Medical Physics, 13, 3.
http://dx.doi.org/10.1186/1756-6649-13-3 - 42. Rodríguez, J. (2011) New Diagnosis Aid Method with Fractal Geometry for Pre-Neoplasic Cervical Epithelial Cells.. Revista U.D.C.A Actualidad & Divulgación Científica, 14, 15-22.
- 43. Prieto, S., Rodríguez, J., Correa, C. and Soracipa, Y. (2014) Diagnosis of Cervical Cells Based on Fractal and Euclidian Geometrical Measurements: Intrinsic Geometric Cellular Organization. BMC Medical Physics, 14, 1-9.
- 44. Rodríguez, J., Prieto, S., Catalina, C., Dominguez, D., Cardona, D.M. and Melo, M. (2015) Geometrical Nuclear Diagnosis and Total Paths of Cervical Cell Evolution from Normality to Cancer. Journal of Cancer Research and Therapeutics, 11, 98-104.