Received 13 February 2015; accepted 20 April 2015; published 23 April 2015

ABSTRACT

A new approach to the problem of nuclear force nature is considered. It is shown that an attraction in the proton-neutron pair can occur due to the exchange of relativistic electron. The estimation of this exchange energy is in agreement with the experimental values of the binding energy of some light nuclei. At that, neutron is regarded as a composite corpuscule consisting of proton and relativistic electron that allows predicting the neutron magnetic moment, its mass and the energy of its decay.

Keywords:

Proton, Neutron, Magnetic Moment, Bohr Atom, Relativistic Electron, Deuteron

1. Introduction

The hydrogen atom is one of the simplest quantum systems. This is the only system for the description of which an exact solution of the Schrodinger equation can be found 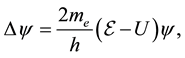[1] :

(1)

where 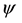is the electron wave function, 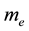is mass of electron, 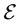and U are the full energy and the potential energy of electron.

If we neglect the motion of the nucleus, according to the solution of the Schrodinger equation, the electron in the ground state of the hydrogen atom has energy:

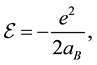(2)

where

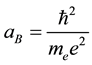(3)

is the Bohr radius.

Due to the fact that the motion of the electron in the s-shell is nonrelativistic, the characteristic parameters of the stationary state of the hydrogen atom can be obtained from a simple condition of equilibrium of forces acting on the electron in this shell. Assuming that s-shell has a radius r and the potential energy of the electron in this shell in the Coulomb field of a proton

(4)

Taking into account the Bohr postulate

(5)

(where 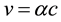is the electron velocity on the first Bohr orbit) as the result of simple substitutions we find that the radius of the s-orbit is equal to the Bohr radius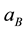, and total energy of the electron is given by the Equation (2).

2. Neutron

2.1. Magnetic Moments of the Proton and Neutron

The main physical properties of proton and neutron were scrutinized. There are measuring of their mass, charge, spin, etc. Of particular interest are their magnetic moments which are measured with very high accuracy.

In units of the nuclear magneton they are [2]

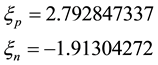(6)

2.2. The Electromagnetic Model of Neutron

For the first time after the discovery of the neutron, physicists were discussing whether or not to consider it as an elementary particle. Experimental data, which could help to solve this problem, did not exist then. And soon the opinion was formed that the neutron is an elementary particle alike proton [3] . However, the fact that the neutron is unstable and decays into a proton and an electron (+antineutrino) gives a reason to consider it as a nonelementary composite particle.

Is it possible to now on the basis of experimentally studied properties of the neutron to conclude that it is elementary particle or it is not?

Let’s consider the composite corpuscle, in which around a proton with speed 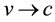spinning electron with mass 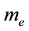and charge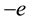. The presence of the intrinsic magnetic moment of the rotating particle does not matter because of the particularities of the resulting solutions (22).

Between the positively charged proton and negatively charged electron there must be a force Coulomb attraction:

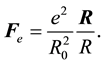(7)

It is caused by existing of the Coulomb interaction energy:

(8)

where is the radius of an orbit of the rotating particle.

The magnetic field generated by the electron orbital motion creates a force which is opposing to the Coulomb force and tends to break the orbit.

According to the Biot-Savart law an element of orbit with the current J creates at a distance R the magnetic field:

(9)

The force acting on an element coil and tending to rend the coil is

(10)

The entire coil will rupture by the force

(11)

The action of this force at balances the Coulomb attraction.

Integrating (10), we find that the element coil acquires the energy

(12)

At thus as it follows from Equation (12), the energy of ring tearing at will tend to

(13)

that together with the Coulomb energy (8) will provide the steady-state of the current ring.

As the result, the Coulomb force and the magnetic force will be compensated. Only the Lorentz’s force arising from the interaction of a moving charged electron and magnetic moment of the proton remains uncompensated.

An observer moving in a magnetic field “sees” in his reference system an electric field ([4] , §24, (24.2)):

(14)

where.

The Lorentz force conforming to this field is:

(15)

If the rotation is in the plane of the “equator” of the proton, the magnetic field is:

(16)

In equilibrium, the Lorentz force is balanced by the centrifugal force:

(17)

That allows us to determine the radius of the electron equilibrium orbit (at):

(18)

where is the fine structure constant, is the anomalous moment of proton, and

are masses of electron and proton (in the rest).

2.3. Spin of the Current Ring

The angular momentum (spin) of the current ring

(19)

is created by the generalized momentum of electron

(20)

and depends on the magnetic moment of the proton

(21)

After the substitution of value of the vector-potential A from Equation (21) and the value of radius of current ring from Equation (18) to Equation (20), at we obtain and respectively

(22)

At zero spin of the electron ring there is no preferred direction along which would be oriented own spin of the electron. Therefore, own magnetic moment of the electron does not manifest itself in establishing equilibrium in the system.

2.4. Accounting for the Effect of the Precession of the Orbit

The rotation of the electron must be characterized by two integrals of motion.

At this moving, the energy of rotating particle W and its moment of rotation K must be kept constant. If

, one can write

(23)

and

(24)

where we take the proton as the origin of the polar coordinate system (r and),

and

(25)

If to remove and t from these equations, we obtain:

(26)

where is the Compton radius.

After replacing of variable

(27)

and taking the derivative, we obtain

(28)

There we take into account that the derivative is the angular velocity of the particle rotation and we indicate.

The solution of the equation

(29)

is the ellipse

(30)

The Equation (28) describes the “almost” elliptical trajectory, which precesses around the proton: per revolution of the electron, the orbit rotates on.

Thus, this precession of the ellipse with the frequency is superimposed on the rotation of the particle on the elliptical orbit with the frequency:

(31)

To take into account the effect of this precession, instead of Equation (18), we introduce the effective radius. Due to the fact that this radius is determined by the ratio of universal constants only, it can be calculated with a very high accuracy:

(32)

2.5. The Magnetic Moment of the Neutron

Attempts to calculate the magnetic moment of the neutron have been made before [5] [6] .

In the frame of the constructed electromagnetic model, the neutron magnetic moment can be calculated with very high accuracy.

The current J in a ring with radius creates a magnetic moment that is proportional to the square of the ring:

(33)

We can rewrite it in units of nuclear Bohr magneton (, where is neutron mass). In these

units the magnetic moment of the ring is equil

(34)

The resulting magnetic moment of the neutron is equal to the sum of the proton magnetic moment and the magnetic moment of the ring:

(35)

that very well agrees with the measured value of the magnetic moment of the neutron (6):

(36)

2.6. The Energy of Neutron Decay

The depending on the relativistic factor terms of energy of the current ring form the integral of

motion Equation (23). At substituting in Equation (23) of the obtained value of the equilibrium orbit radius, we can easily see that at equilibrium the relativistic terms of energy balance each other and.

At the same time the Coulomb energy of the ring (Equation (8)) and its magnetic energy (Equation (20)) are

independent on the relativistic coefficient. Their sum is not equal to zero:

(37)

At the decay of a neutron, this energy must go into the kinetic energy of the emitted electron (and antineutrinos). That is in quite satisfactory agreement with the experimentally determined boundary of the spectrum of the decay electrons, equal to 782 keV.

2.7. Discussion

This consent of estimates and measured data indicates that the neutron is not an elementary particle. It should be seen as a relativistic analog of the Bohr hydrogen atom. With the difference: a non-relativistic electron in the Bohr atom forms a shell by means of Coulomb forces and in a neutron the relativistic electron is held by the magnetic interaction [7] .

This must change our approach to the problem of nucleon-nucleon scattering. The nuclear part of an amplitude of the nucleon-nucleon scattering should be the same at all cases, because in fact it is always proton-proton scattering (the only difference is the presence or absence of the Coulomb scattering). It creates the justification for hypothesis of charge independence of the nucleon-nucleon interaction.

According to the principle which was developed by W. Gilbert and G. Galileo more than 400 years ago, a theoretical construct can be attributed to reliably established if it is confirmed by experimental data. This principle is the basis of modern physics and therefore the measurement confirmation for the discussed above electromagnetic model of neutron is the most important, required and completely sufficient argument of its credibility. Nevertheless, it is important for the understanding of the model to use the standard theoretical apparatus at its construction. It should be noted that for the scientists who are accustomed to the language of relativistic quantum physics, the methodology used for the above estimates does not contribute to the perception of the results at a superficial glance. It is commonly thought that for the reliability, a consideration of an affection of relativism on the electron behavior in the Coulomb field should be carried out within the Dirac theory. However that is not necessary in the case of calculating of the magnetic moment of the neutron and its decay energy. In this case, spin of the electron in this state is equal to zero and all relativistic effects described by the terms with

coefficients compensate each other and completely fall out. The neutron considered in our model

is the quantum object. Its radius is proportional to the Planck constant. But it can not be considered as

relativistic particle, because coefficient is not included in the definition of. In the particular

case of the calculation of the magnetic moment of the neutron and the energy of its decay, it allows to find an equilibrium of the system from the balance of forces, as it can be made in the case of non-relativistic objects. Another case exits at the evaluation of the neutron lifetime. The relativism affects on this parameter apparently and one can not obtain even a correct estimation of the order of its value.

3. The One-Electron Bond between Two Protons

Let us consider a quantum system consisting of two protons and one electron. If protons are separated by a large distance, this system consists of a hydrogen atom and the proton. If the hydrogen atom is at the origin, then the operator of energy and wave function of the ground state have the form:

(38)

If hydrogen is at point R, then respectively

(39)

In the assumption of fixed protons, the Hamiltonian of the total system has the form:

(40)

At that if one proton removed on infinity, then the energy of the system is equal to the energy of the ground state, and the wave function satisfies the stationary Schrodinger equation:

(41)

We seek a zero-approximation solution in the form of a linear combination of basis functions:

(42)

where coefficients and are functions of time, and the desired function satisfies to the energy- dependent Schrodinger equation:

(43)

where is the Coulomb energy of the system in one of two cases.

Hence, using the standard procedure of transformation, we obtain the system of equations

(44)

where we have introduced the notation of the overlap integral of the wave functions

(45)

and notations of matrix elements

(46)

Given the symmetry

(47)

after the adding and the subtracting of equations of the system (44), we obtain the system of equations

(48)

where

(49)

As a result, we get two solutions

(50)

where

(51)

From here

(52)

and

(53)

As

(54)

with the initial conditions

(55)

and

(56)

or

(57)

we obtain the oscillating probability of placing of electron near one or other proton:

(58)

Thus, electron jumps into degenerate system (hydrogen + proton) with frequency from one proton to another.

In terms of energy, the frequency corresponds to the energy of the tunnel splitting arising due to electron jumping (Figure 1).

As a result, due to the electron exchange, the mutual attraction arises between protons. It decreases their energy on

(59)

The arising attraction between protons is a purely quantum effect, it does not exist in classical physics.

The tunnel splitting (and the energy of mutual attraction between protons) depends on two parameters:

(60)

where is energy of the unperturbed state of the system (i.e., the electron energy at its association with one of proton, when the second proton removed on infinity), and function of the mutual distance between the protons.

This dependence according to Equation (54) has the form:

(61)

The graphic estimation of the exchange splitting indicates that this effect decreases exponentially with

increasing a distance between the protons in full compliance with the laws of the particles passing through the tunnel barrier.

4. The Molecular Hydrogen Ion

The quantum-mechanical model of simplest molecule―the molecular hydrogen ion―was first formulated and solved by Walter Heitler and Fritz London in 1927 [8] -[10] .

At that, they calculate the Coulomb integral (Equation (46)):

(62)

the integral of exchange (Equation (46))

(63)

and the overlap integral (Equation (45))

(64)

where is the dimensionless distance between the protons.

The potential energy of hydrogen atom

(65)

and with taking into account Equation (62)-Equation (64)

(66)

At varying the function we find that the energy of the system has a minimum at where. As a result of permutations of these values we find that in this minimum energy the mutual attraction of protons reaches a maximum value

(67)

This result agrees with measurements of only the order of magnitude. The measurements indicate that the equilibrium distance between the protons in the molecular hydrogen ion and its breaking energy on proton and hydrogen atom is close to.

The remarkable manifestation of an attraction arising between the nuclei at electron exchange is showing himself in the molecular ion of helium. The molecule He₂ does not exist. But a neutral helium atom together with a singly ionized atom can form a stable structure―the molecular ion. The above obtained computational evaluation is in accordance with measurement as for both―hydrogen atom and helium atom―the radius of s-shells is equal to, the distance between the nuclei in the molecular ion of helium, as in case of the hydrogen molecular ion, must be near and its breaking energy near.

In order to achieve a better agreement between calculated results with measured data, researchers usually produce variation of the Schrodinger equation in the additional parameter―the charge of the electron cloud. At that, one can obtain the quite well consent of the calculations with experiment. But that is beyond the scope of our interest as we were needing the simple consideration of the effect.

5. Deutron

The electromagnetic model of a neutron, discussed above, gives possibility on a new look on the mechanism of the proton-neutron interaction. According to this model a neutron is a proton surrounded by a relativistic electron cloud. Therefore a deuteron consists of the same particles as the molecular ion of hydrogen. There is a difference. In the case of a deuteron, the relativistic electron cloud has the linear dimension (Equation (18)). One might think that a feature occurs at such a small size of the electron cloud. When an electron jumps from one proton to another, a spatial overlap of the wave functions will not arise and therefore the overlap integral S Equation (45) can be set equal to zero.

In accordance with the virial theorem and Equation (37), the potential energy of this system at the un- perturbed state is

(68)

The function (Equation (61)) at and taking into account Equation (63) obtains the form

(69)

(where is a dimensionless distance between the protons.)

When varying this expression we find its maximum value at.

After substituting these values, we find that at the minimum energy of the system due to exchange of relativistic electron, two protons reduce their energy on

(70)

To compare this binding energy with the measurement data, let us calculate the mass defect of deuteron

(71)

where is mass of deuteron.

This mass defect corresponds to the the binding energy

(72)

Thus the quantum mechanical estimation of the bonding energy of deuteron Equation (70), as in the case of the hydrogen molecular ion, consistent with the experimentally measured value Equation (72), although their match is not very accurate.

6. Conclusions

The good agreement between the calculated binding energy of the neutron-proton pair and the measured deuteron binding energy suggests that nuclear force has really the exchange character described above. These forces arise as a result of the quantum-mechanical exchange and have no classical explanation.

For the first time the attention on the possibility of explaining the nuclear forces based on the effect of electron exchange apparently drew I. E. Tamm [11] back in the 30s of the last century. However, later the model of the -meson exchange becomes the dominant in nuclear physics. The reason for that is clear. To explain the magnitude and range of the nuclear forces need particle with a small wavelength. Non-relativistic electrons do not fit it. However, on the other hand, the model -meson exchange was not productive: it gives not possibility to calculate the binding energy of even such a simple nucleus as deuteron.

Therefore, the simple assessment of the binding energy given above and consistent with measurements is the clear proof that the so-called strong interaction (at least in the case of the deuteron) is a manifestation of the quantum-mechanical effect of attraction between protons produced by the relativistic electron exchange.

Cite this paper

BorisV. Vasiliev, (2015) About Nature of Nuclear Forces. Journal of Modern Physics,06,648-659. doi: 10.4236/jmp.2015.65071

References