Journal of Modern Physics
Vol.05 No.18(2014), Article ID:52749,6 pages
10.4236/jmp.2014.518209
A Possible Role of the Gailitis Resonance in Muon Catalyzed Fusion
Chi Yu Hu1, David Caballero1,2
1Department of Physics and Astronomy, California State University, Long Beach, USA
2Claremont Graduate University, Claremont, USA
Email: Chiyu.hu@CSULB.Edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 October 2014; revised 26 October 2014; accepted 15 November 2014
ABSTRACT
In a previous JMP article published May 2013, a comprehensive calculation was presented for all properties of a number of long-life s-state Gailitis resonances lying just above the PS(n = 2) formation threshold in a positron-Hydrogen scattering system. The six open-channel calculation was carried out by solving a set of four hundred thousand coupled linear equations. The modified Faddeev equation was used to obtain the wave-amplitude for each of the six open channels. Details can be found in reference [1] . This note presents some qualitative properties of Gailitis resonances in the scattering systems of d + tu just above the thresholds of the opening of a new channel of the muonic atoms tu(n) or du(n), n > 2 is the principal quantum number. u is a negatively charged muon, d and t are the nuclei of the two isotopes of the Hydrogen atom with one and two neutrons in the nucleus respectively. We study the possible decay channels of some of the long-life Gailitis resonances. Of particular interest is a transition directly from a Gailitis (3-body) resonance to the bound states dtu molecular ions via a radiative emission of a photon or an external auger ejection of a nearby electron. Possible experimental evidence will be presented.
Keywords:
Faddeev, Resonance, Cross Section, 3-Body Scattering

1. Introduction
Muon catalyzed fusion has had a long and exciting history since the discovery of the Vesman resonance formation mechanism [2] . For a comprehensive review of this subject and numerous references see refs. [3] [4] .
The Vesman resonance is a six-body system. A typical process is
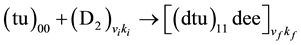 (1)
(1)
D2 is the molecule of heavy Hydrogen (deuteron atom). 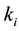 and
and 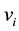 are the rovibrational quantum numbers of D2,
are the rovibrational quantum numbers of D2, 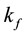 and
and 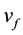 are the rovibrational quantum numbers of the complex molecule on the right hand side of Equation (1).
are the rovibrational quantum numbers of the complex molecule on the right hand side of Equation (1).
This process is accomplished after the  + d sub-system on the left hand side resonantly transfers 0.66 eV of energy to the rovibrational energy of the large complex molecule and becomes a weakly bounded small molecular ion
+ d sub-system on the left hand side resonantly transfers 0.66 eV of energy to the rovibrational energy of the large complex molecule and becomes a weakly bounded small molecular ion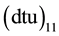 .
.
 lies only 0.66 eV below the muonic atom
lies only 0.66 eV below the muonic atom 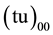 ground state.
ground state.
Subsequent radiative decays lead to the 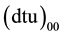 three-body ground state at 319.13 eV below
three-body ground state at 319.13 eV below 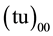 threshold. The nuclear fusion takes place at a rate ~108/s.
threshold. The nuclear fusion takes place at a rate ~108/s.
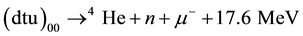 (2)
(2)
W. Beunlich et al. [5] measured the fusion time spectra in 1984. All of their measurements display a sharp transient structure with initial time peak much larger than 108/s.
This large transient fusion rate is attributed to the epithermal energy collision in Equation (1) [6] . In this note, an argument will be presented for possible Gailitis resonance contribution to this initial transient fusion phenomenon. Section 2 will review [1] some properties of the Gailitis resonance [7] . Section 3 provides upper bounds for the life-time of the Gailitis resonances just above the thresholds of the new channels involving du(n) or 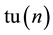 for a number of
for a number of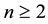 .
. 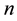 is the principal quantum number of the muonic atoms. Section 4 presents a simple model calculation to estimate the lower bound of the rate of radiative transition from a Gailitis resonance located just above the
is the principal quantum number of the muonic atoms. Section 4 presents a simple model calculation to estimate the lower bound of the rate of radiative transition from a Gailitis resonance located just above the  energy level to a bound dtu molecular ion. This calculation is needed to support the discussion in section 5. Section 5 will discuss the possibility that the Gailitis resonance may have contributed to the unique experimental phenomenon, the appearance of large initial transient fusion peaks in muon catalyzed fusion experiments [5] .
energy level to a bound dtu molecular ion. This calculation is needed to support the discussion in section 5. Section 5 will discuss the possibility that the Gailitis resonance may have contributed to the unique experimental phenomenon, the appearance of large initial transient fusion peaks in muon catalyzed fusion experiments [5] .
2. The Gailitis Resonance
The first indication of the existence of the Gailitis resonance was provided by Gailitis and Damburg in their calculation of the electron-Hydrogen scattering system [7] . The resonances become obsolescence, mainly due to a lack of interest. It was difficult to study it using conventional methods until recently [1] . They have much smaller energy widths compared to Feshbach resonances [1] and occupy much larger configuration space compared to the size of the atoms. That means the calculation must have small enough energy grids and large enough effective cut-off distances. Reference [1] provides such a calculation using the modified Faddeev equation. This calculation solved a six-open channel system from first principles without intermediate approximations of any kind.
A complete set of the properties of the resonances are calculated directly including their wave functions. As a result, it becomes possible to identify the simple physical mechanism responsible for these resonances. Namely, it is a “dynamic” Stark effect [1] [7] -[9] . While an atom with Coulomb degeneracy acquires a dipole moment in the field of colliding charged particles, this field also splits some of the Coulomb degeneracy into separate Stark energy levels. If the energy of the incoming particle matches the Stark energy split at certain distances from the target atom resonance occurs. The energy is transferred to the atom via the exchange of a photon. During the life-time of the resonance the incoming particle remains a wave packet centered at a distance 
or





wave packet in Jacobian coordinates. The atom is initially in an excited state with principal quantum number

Initially, the wave packet has a width equal to the DeBroglie wavelength of the incoming charged particle,

Thus 

The life-time of the resonances (or the wave packet) can be determined using the uncertainty principle [9] , such that

The small energy width 
Some useful information of the Gailitis resonance can be seen from Figure 1, taking from Ref. [1] , which illustrates its unique singular behavior in the resonant channels 5 and 6. Taking from the six open channel K-matrix [1] , the diagonal matrix elements of channels 5 and 6 are plotted as function of collision energies. The matrix elements and their corresponding phase-shifts cross the zero axis between adjacent singularities. They remain small and negative on the lower energy side of the resonances. But the phase-shifts moves rapidly towards 90 degree approaching the resonant energies, these repulsive behaviors [8] provide rapid deceleration forcing the incoming charged particle to deliver all of its energy to excite the Stark energy levels of the target at the speed of light via a Bremsstrahlung photon while the incoming particle wave packet remains far from the target Equation (3). The phase shift jumps from 


3. Lower Bounds of the Gailitis Resonant Energies in d + tu(n), t + du(n) Scattering with n ≥ 2
In principle, the calculation of ref. [1] for 

Figure 1. The diagonal matrix elements 






time, especially when the current interest for these systems involves 

The resonant series in Equation (3) must be truncated when 
For the purpose of estimating the lower bounds, 






In the following, a special case of 



Equation (4), gives
The wave length is in muonic Bohr radius au.
A similar table for t + du should have a difference of only ~1% from the numbers in Table 1. Please note, this table gives only the respective bounds of the Gailitis resonances. The properties of the resonance themselves can only be determined by the dynamic of the three-body systems, such as that carried out in reference [1] .
Table 1. Summarized bounds In d + tu(n).



4. Gailitis Resonances and Bound State dtu Molecular Ions
Can a photon or an auger electron carry away the excess energy between a Gailitis resonance and its bound state 3-body molecular ions, such as dtu in a d + tu scattering system?
The only satisfactory answer must be the precise solution of a time dependent multichannel 3-body quantum equation that is not possible at this time. Nevertheless, it is possible to find experimental evidence using the vast volume of experimental data on muon catalyzed fusion research [3] , and its plausible theoretical interpretation from presently available theoretical calculations [11] - [13] .
We use the perturbative formula of photon emission by a muonic atom (or one electron atom) [13] derived from the Golden Rule, the transition probability per unit time, P2, is








According to reference [11] , for the muonic atom pμ
We have:

For the purpose of providing a lower bound, we propose a very simple model for the dipole matrix element in Equation (7).






This is less than that of Equation (8), but is of the same order of magnitude.
This simple model can be used to provide a lower bound for the three body radiative decay.
Equation (7) must be modified for three-body bound state transitions:



Consider the case when the initial state is a time dependent Gailitis resonance. As qualitatively described in Section 2 from the behavior of the phase shift, it is clear the perturbative formula (11) cannot be applied near the singular point which can be excluded from the following average over the life time of the resonance

From the qualitative behavior of the Gailitis resonance described in Section 2 the major contribution to the integral must come near the end of life of the resonance. It is possible to provide a lower bound to this integral using the model provided by the two-body radiative decay, Equation (9). The 

We are interested in the principle quantum number
thus the “size” of the initial state is of the order of the resonant wavelength, the final state is one of the bound states of the dtu molecular ions. Their “size” ranges from 3 au to 10 au (from unpublished calculations).
Consider the “size” of the final state




Equation (12) becomes




This value is comparable to that of Equation (8), thus supporting the possibility of dtu molecular formation via the Gailitis resonances.
5. Discussion and Conclusions
Muon catalyzed fusion utilizing the six-body resonance Equation (1) is carried out in various mixtures of molecules of heavy Hydrogen and their nuclei, such as D2, DT and t. According to cascade models [10] [11] , when the negative muon is first introduced into such mixtures, it displaces a ground state electron from a D atom and forms an excited state muonic atom


From Table 1, the lifetime of these resonances is of the order of 10−9 sec. It is stable against all other pro- cesses [1] and comparable to radiative decay of muonic atoms with 
Sakamoto et al. [12] presented direct measurements of the energy spectra of prompt X-rays from ppu and ddu fusion experiments respectively. The large peaks of



Clearly the contribution is not significant in these experiments.
A deuteron beam of appropriate range of energies that covers the energy levels of



The advantages of this approach are:
1) The experiment can be carried out in room temperature.
2) Such low energy deuteron beam can be produced easily.
3) If it becomes necessary, precision quantum three-body.
Scattering calculations for this system is possible.
In view of the long-term needs for dependable clean nuclear energy, this simple mechanism for muon catalyzed fusion must be given a chance to be tested!
References
- Hu, C.Y. and Caballero, D. (2013) Journal of Modern Physics, 4, 622-627.
- Vesman, E.A. (1967) Soviet Physics-JETP Letters, 5, 91.
- Petitjean, C. (2007) International Conference on Muon Catalyzed Fusion (uCF-07), 82-87.
- Ponomarev, L.I. (2007) International Conference on Muon Catalyzed Fusion (uCF-07), 405-410.
- Breunlich, W., et al. (1984) Physical Review Letters, 53, 1137. http://dx.doi.org/10.1103/PhysRevLett.53.1137
- Faifman, M.P. and Ponomerev, L.I. (1991) Physics Letters, B265, 201-206. http://dx.doi.org/10.1016/0370-2693(91)90041-N
- Gailitis, M. and Damburg, R. (1963) Soviet Physics-JETP, 17, 1107.
- Shiff, L.I. (1949) Quantum Mechanics. Landau and Lifshitz, Quantum Mechanics, Non-Relative Theory.
- Gailitis, M. and Damburg, R. (1963) Proceedings of the Physical Society, 82, 192. http://dx.doi.org/10.1088/0370-1328/82/2/305
- Cohen, J.S. and Leon, M. (1985) Physical Review Letters, 55, 52. http://dx.doi.org/10.1103/PhysRevLett.55.52
- Markushin, V.E. (1994) Physical Review A, 50, 1137. http://dx.doi.org/10.1103/PhysRevA.50.1137
- Sakamoto, S., Ishia, K., Matsuzaki, T. and Nagamine, K. (1999) Hyperfine Interaction, 119, 115-120. http://dx.doi.org/10.1023/A:1012618905252
- Merzbacher, E. (1970) Quantum Mechanics. 2nd Edition, John Wiley & Son, Inc., New York, 563.















