Received 29 July 2014; revised 23 August 2014; accepted 16 September 2014

ABSTRACT

The equation of state (EOS) of symmetric nuclear and pure neutron matter has been investigated extensively by adopting the non-relativistic Brueckner-Hartree-Fock (BHF). For more comparison, the extended BHF approaches using the self-consistent Green’s function approach or by including a three-body force will be done. The EOS will be studied for different approaches at zero temperature. We can calculate the total mass and radius of neutron stars using various equations of state. A comparison with relativistic BHF calculations will be done. Relativistic effects are known to be important at high densities, giving an increased repulsion. This leads to a stiffer EOS compared to the EOS derived with a non-relativistic approach.

Keywords:

Symmetric Nuclear Matter, Equation of State, Three-Body Force, Pressure, Incompressibility, Neutron Star Properties

1. Introduction

The properties of neutron stars depend on the equation of state (EOS) at densities up to an order of magnitude higher than those observed in ordinary nuclei. The EOS determines properties such as the mass range, the mass-radius relationship, the crust thickness and the cooling rate [1] -[3] . Data on the EOS can be obtained from many sources, such as studies of the monopole resonance in finite nuclei, high energy nuclear collisions, supernovae, and neutron stars. Supernovae simulations seem to require an EOS which is too soft to support some observed masses of neutron stars, whereas analyses of high energy nuclear collisions indicate a rather stiff EOS, predicting neutron star masses which are too large. Thus, no definite statements can be made about the EOS at high densities, except that it should probably be moderately stiff in order to support maximum neutron star masses in a range of approximately 1.4 M_סּ to 1.9 M_סּ, where M_סּ is the solar mass [4] .

Several theoretical approaches to calculations of the EOS have been considered. The hypothesis that strange quark matter may be the absolute ground state of the strong interaction [5] , has been used by Rosenhauer et al. [6] in the investigation of the possibility of interpreting pulsars as rotating strange stars. Other approaches introduce exotic states of nuclear matter, such as kaon [7] or pion condensation [8] .

The scope of this work is to derive the EOS from the underlying many-body theory, derived from realistic nucleon-nucleon (NN) interactions such as CD-Bonn potential [9] . The many-body approaches that be used are self-consistent Green’s function (SCGF) approach [10] -[14] and the Brueckner-Hartree-Fock (BHF) approach [15] supplemented by three-body force [16] or contact-term interaction to give more repulsive EOS [17] . From this EOS we will study neutron star observables such as the mass-radius relationship. Baldo et al. [18] have shown that any realistic EOS must satisfy several requirements to be used in studding neutron star properties: 1) It must display the correct saturation point for symmetric nuclear matter (SNM); 2) It must give a symmetry energy consistent with nuclear phenomenology and well behaved at high densities; 3) The nuclear incompressibility for SNM at saturation must be compatible with the values extracted from phenomenology (210 ± 30 MeV [19] ); 4) The speed of sound remains smaller than the speed of light, (causality condition), for all densities relevant in neutron stars, i.e., where P is the pressure and 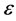is the energy density. The latter condition is automatically satisfied only in fully relativistic theory.

In the self-consistent Green’s function approach, the binding energy as well as all single-particle observables in the nuclear matter are calculated from the exact in-medium single-particle propagator. The latter is obtained from the Dyson equation, where medium effects are taken into account by the irreducible self-energy that is obtained from an expansion in terms of the effective interaction obtained from the sum of all ladder diagrams. One important feature of the SCGF approach is that particles and holes are treated on an equal footing, whereas in BHF only intermediate particle states are included in the ladder diagrams. This feature assures that the thermodynamic consistency is satisfied in the SCGF approach, e.g., the Fermi energy or chemical potential of the nucleons equals the binding energy at saturation (i.e., the Hugenholz-van Hove theorem) [20] . In the low- density limit, the BHF approach and the SCGF approach coincide. As the density increases, the phase space for hole-hole propagation is no longer negligible, and this leads to an important repulsive effect on the total energy. Since particle-particle (pp) and hole-hole (hh) ladders are treated in a completely symmetrical way in the SCGF approach, the Green’s function scheme is also suited for calculations at higher densities [12] -[14] . Furthermore, the SCGF generates realistic spectral functions, which can be used to evaluate the effective interaction and corresponding nucleon self-energy [10] [11] .

The paper is organized as follows. In the next section we will describe the formalisms within the non-relati- vistic approaches we have employed. Results for the EOS and pressure of symmetric and pure neutron matter using suggested models, together with neutron star matter observables will be presented in Section 3. A short summary and some conclusions will be given in Section 4.

2. The Theoretical Model

2.1. BHF Approximation

Starting from realistic nucleon-nucleon (NN) interaction, we have to use more advanced many-body approximations like the BHF which have the capability to account for the effects of correlations, which are due to the strong tensor and short-range components of such realistic NN interaction. The single-particle energy of a particle in the BHF approximation corresponds to the Hartree-Fock expression using the G-matrix for the effective interaction. This means that the self-energy of a nucleon in nuclear matter with momentum k, isospin 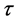and energy 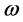in asymmetric nuclear matter is given by [1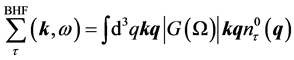1]

(1)

with the occupation probability of a free Fermi gas of protons and neutrons 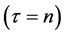with a Fermi momentum

(2)

This means for asymmetric nuclear matter with a total density 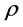and asymmetry parameter α that

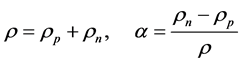(3)

With Fermi momenta for protons 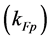and neutrons 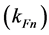which are related to the corresponding densities by

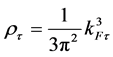(4)

The matrix elements in Equation (1) denote antisymmetrized matrix elements of the Brueckner G-matrix that are determined by solving the Bethe-Goldstone equation for a given realistic NN interaction V

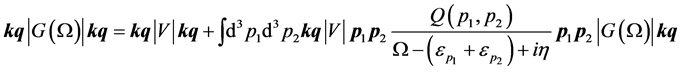(5)

The single-particle energies of the intermediate states should be the corresponding BHF single-particle energies which are defined in terms of the real part of the BHF self-energy of Equation (1) by

(6)

with a starting energy parameter in the Bethe-Goldstone Equation (5).

The Pauli operator restricts the intermediate states to particle states with momenta p₁, p₂, which are above the corresponding Fermi momentum. However, the single-particle spectrum is often parameterized in the form of an effective mass

(7)

so that a so-called angle-averaged propagator can be defined, which reduces the Bethe-Goldstone equation to an integral equation in one dimension. The exact Pauli operator has been treated in [21] .

2.2. Self-Consistent Green’s Function

One of the drawbacks of the BHF approximation is the fact that it does not provide results for the equation of state, which are consistent from the point of view of thermodynamics. As an example we mention that BHF results do not fulfill, e.g., the Hugenholtz-Van Hove theorem [22] . This is due to the fact that the BHF approximation does not consider the propagation of particle and hole states on equal footing. An extension of the BHF approximation, which obeys this symmetry, is the self-consistent Green’s function (SCGF) method using the so-called T-matrix approximation. During the last years techniques have been developed, which allow to evaluate the solution of the SCGF equations for microscopic NN interactions [23] -[25] . Those calculations demonstrate that for the case of realistic NN interactions, the contribution of particle-particle ladders dominates the contribution of corresponding hole-hole propagation terms. This justifies the use of the BHF approximation and a procedure, which goes beyond BHF and accounts for hole-hole terms in a perturbative way [26] . This leads to a modification of the self-energy in the BHF approximation by adding a hole-hole term of the form [26]

(8)

The quasi-particle energy for the extended self-energy can be defined as

(9)

The spectral functions for hole and particle strength, and, are obtained from the real and imaginary part of the self-energy

(10)

where the plus and minus sign on the left-hand side of this equation refers to the case of hole and particle states, respectively. The hole strength represents the probability that a nucleon with isospin i, momentum k, and energy can be removed from the ground state of the nuclear system with the removal energy, whereas the particle strength denotes the probability that such a nucleon can be added to the ground state of the system with A nucleons resulting in a state of the A + 1 particle system which has an energy of relative to the ground state of the A particle system.

Integrating the spectral distribution of the hole states yields the occupation probability

(11)

In the case of two body interactions, the hole spectral function gives access, through the Koltun sum-rule [27] , to the binding energy per particle,

(12)

with deg denoting the degeneracy of the single-particle level, which is 4 for nuclear matter. The kinetic energy per nucleon,

(13)

and the potential energy per particle has the form. Introducing the removal energy,

(14)

One can express the total binding energy per nucleon as

. (15)

In Brueckner-Hartree-Fock, , i.e. it coincides with the quasi-particle energy, and denotes the step function, , therefore [28]

. (16)

2.3. Tolman-Oppenheimer-Volkov

Neutron stars are very interesting physical systems and their properties, such as masses and radii as function of the central density, can be derived from the equation of state (EOS) of the β-stable matter contained in them. The EOS is microscopically calculated from the sections a and b. After that, briefly we outline the derivation of neutron-star properties from its EOS. One starts from the Tolman-Oppenheimer-Volkov (TOV) equations for the total pressure P and the enclosed mass m [29] [30] ,

(17)

(18)

where is the pressure at radius r, is the gravitational mass inside r, and G is the gravitational constant.

From the EOS pure neutron matter, we calculate the nuclear contribution to the total pressure of stellar matter using the relation

(19)

Then the total pressure and the total mass density are given by

(20)

(21)

Being and the lepton contribution to the total pressure and energy density, m_N is the nucleon mass and c is the speed of light in vacuum. Starting with a central mass density, we integrate out until the pressure on the surface equals the one corresponding to the density of iron. This gives the stellar radius R and the gravitational mass is then

(22)

For the outer part of the neutron star we have used the equations of state by Baym et al. [31] , and for the middle density region (0.001 fm⁻³ < ρ < 0.08 fm⁻³) we have used the results of Negele et al. [32] . In the high-density part of neutron star, (ρ > 0.08 fm⁻³), the present EOS will be used.

3. Results and Discussion

3.1. EOS, Pressure and Incompressibility of Nuclear Matter

All results of calculations, which refer to realistic NN interactions, have been obtained using the CD-Bonn interaction [9] . This includes all BHF and SCGF calculations. The effects which are related to the use of various NN interactions, which all fit the NN phase shifts, have been discussed before for BHF approach only [15] .

In Figure 1, the binding energy per particle of symmetric nuclear is plotted versus the density. The BHF results are indicated by a solid line, whereas the results of the full SCGF calculation, computed at zero temperature, are presented by a dashed line. In the case of symmetric nuclear matter, Figure 1, the empirical saturation point is given by the big square. Comparing the BHF and the SCGF results, the hole-hole contributions to the nucleon self-energy, which are included in the SCGF approach, yield a repulsive contribution to the energy per nucleon. One should keep in mind that this repulsion increases with increasing nuclear density. This shifts the saturation point to a lower density and binding energy per nucleon so that also the saturation point obtained with SCGF is within the Coester band [33] . Due to this effect, the saturation density in the SCGF approximation, and, is considerably smaller than the saturation density in the BHF approach that has the value, and. After all the saturation density is reduced by almost 50%; however, both values are not near the empirical one (ρ₀ = 0.16 fm⁻³; E₀ = −16 MeV). In the low-density limit, the BHF approach and the SCGF approach coincide. As the density increases, the phase space for hole-hole propagation is no longer negligible, and this leads to an important repulsive effect on the total energy. Since particle-particle and hole-hole ladders are treated in a completely symmetrical way in the SCGF approach, the Green’s function scheme is also appropriated for calculations at higher densities [12] [13] .

As we see, non-relativistic calculations, based on purely two-body interaction, fail to reproduce the correct saturation point for symmetric nuclear matter. This well-known deficiency is commonly corrected by introducing three-body force (3BF). Relevant progress has been made in the theory of nucleon 3BF, but a complete theory is not yet available. A realistic model for nuclear 3BF has been introduced by the Urbana group [34] .

There is another method used to achieve saturation properties in nuclear matter. One has to supplement the effective interaction or the self-energy of BHF and SCGF calculations by a simple contact interaction (CT), which we have chosen following the notation of the Skyrme interaction to be of the form

(14)

where is the matter density, t₀, t₃ and are parameters. The parameter t₀ and t₃ represent the zero range and 3-body strength while the exponent determines the high density behavior. The Hamiltonian density of the contact term, which is used in the last equation, has no isospin dependence. More parameters used in [35] [36] to give a more quantitative estimate of the needed correction to the BHF results.

Now the nuclear many-body approach plus the above contact term is fit to reproduce the saturation point ρ₀ = 0.16 fm⁻³ and E₀ = −16.0 MeV at fixed (typically). The results for these fitting parameters are listed in Table 1, whereas the corresponding EOS versus density curves are displayed in Figure 1 using dotted line for BHF + CT and double dash-dotted line for SCGF + CT. Also, the EOS’s using all discussed approaches are listen in Table 2 For all cases, the fit yields an attractive two-body contact interaction and a repulsive t₃ term. Comparing the suggested approaches with the relativistic Brueckner-Hartree-Fock (RBHF) approach [37] , we find that RBHF approach leads to the stiffer EOS around the saturation density as well as at higher densities than the others. The SCGF and the RBHF calculations yield rather similar results after the contact terms are included up to density equals to 2.5ρ₀, but the difference increases at high densities, which are a little bit softer than the BHF + CT results.

We will extend the analysis to pure neutron matter EOS, which is more suitable for neutron star studies, at densities up to about five times the saturation one. Moreover, we consider the calculations for two nucleon- nucleon potential, i.e., CD-Bonn interaction likes symmetric nuclear matter EOS. The results for the EOS of the pure neutron matter, obtained by including only two-body force, is reported (solid line for BHF and dashed line for SCGF approaches) in Figure 2. The results of both BHF and SCGF approaches plus a simple contact interaction, with the same parameters defined in Table 1, are illustrated by dotted and double dash-dotted curves, respectively. As for symmetric nuclear matter, all present EOS’s for neutron matter are compared with the RBHF calculations introduced by Müther et al. [37] . Comparing the BHF and the SCGF results without the contact term, it gets clear that the inclusion of hh excitations makes EOS of neutron matter more repulsive especially at high density. When the contact term is added to the BHF and the SCGF approaches, the results for EOS are more comparable stiffness. Also, these observations are shown in Table 3. As one can see that, the SCGF and the RBHF calculations yield rather similar results after the contact terms are introduced up to density greater than twice of saturation density. Furthermore the relative differences between two approaches are smaller.

The pressure of nuclear matter is defined in terms of the energy per nucleon as in Equation (16). In Figure 3

and Figure 4, we show the pressure from the BHF + CT and SCGF + CT approaches based on EOS for symmetric matter and neutron matter. These values of the pressure are compared with RBHF results by Müther et al. [37] . The area within the double dash-dotted lines indicates EOS consistent with the elliptic flow measurements reported in Ref. [38] of symmetric nuclear matter. For the case of neutron matter, two different parameterizations for the symmetry energy, , are assumed in the analysis. The two pressure contours appear in Figure 4 correspond to the weakest (lower contour with double dot-dashed line) and the strongest (higher contour with double dash-dotted line) density dependence for suggested by Prakash et al. [39] . It is fair to say that SCGF + CT predictions produce a reasonable amount of repulsion like RBHF calculations, whose generate too much pressure, while the EOS compared to that BHF + CT predictions are less repulsive.

There is another important characteristic of the EOS and it enters in the discussion of a variety of phenomena such as supernovae explosions or heavy ion collisions, that it is the incompressibility K. It measures the stiffness of the EOS, usually defined as a slope of the pressure at saturation point:

(28)

The experimental value of the incompressibility of symmetric nuclear matter at its saturation density ρ₀ has been determined to be 210 ± 30 MeV [19] . At the saturation density, the values of the incompressibility and the binding energy per nucleon obtained for symmetric nuclear matter are summarized in Table 4. In the case of RBHF, although the EOS of nuclear matter is characterized by a relatively low value of K, the behavior with increasing density is fairly stiff. This is reflected in the relatively large values of the pressure in the region (2 - 5) ρ₀ as one sees from Figure 3.

3.2. Neutron Star Properties

Using the methods just described we obtain for each model the EOS for cold pure neutron matter. The TOV general relativistic equations for a spherically symmetric (non-rotating) neutron star are solved, then the gravitational mass of the star M_G is obtained as a function of both the stellar radius R and a central density. The dependence of the neutron star masses on the stellar radius R for three models is shown in Figure 5. Results with the RBHF by Müther et al. [37] are included for comparison. The maximum masses for the three models as function of are illustrated in Figure 6. From Figure 5 and Figure 6 we find a maximum mass of neutron star is M_max ≈ 1.98 M_סּ, in the case of BHF + CT calculation, at a central density of ρ_c = 2.82 × 10¹⁵ gm/cm³ with

a radius R ≈ 10.05 km. This value is consistent with the recent observation of a (1.97 ± 0.04) M_סּ neutron star (Demorest et al. [40] ). Also, it was reported that a new massive NS, PSR J0348 + 0432 with (2.01 ± 0.04) M_סּ, was observed very recently by Antoniadis et al. [41] . Whereas a maximum mass of M_max ≈ 1.98 M_סּ at a central density of ρ_c = 2.52 × 10¹⁵ gm/cm³ with a radius R ≈ 10.5 km for SCGF+CT model. The present non-relativistic calculations are compared with RBHF results [37] where a maximum mass of M_max ≈ 2.5 M_סּ at a central density of ρ_c = 1.995 × 10¹⁵ gm/cm³ with a radius R ≈ 11.58 km.

One can see that the results from our non-relativistic equation of state may look more reasonable than those from the relativistic one. The present results are more compatible with recent microscopic calculations of neutron matter based on nuclear interactions derived from chiral effective field theory [42] . They have constructed three representative EOSs (soft, intermediate, and stiff), consistent with the constraints from nuclear physics and observation. Generally, simple construction of neutron stars from the EOS of pure neutron matter is not enough for a consistency check between the theoretical neutron star maximum mass and the observed neutron star masses. If it is possible to duly deduce the information on the EOS of nuclear matter by ignoring other constituents than nucleons, it would be reasonable to focus on low mass neutron stars (see, e.g., Sotani et al. [43] ).

4. Conclusions

Comparing the non-relativistic approaches from realistic interaction among themselves, we find that the effect of the hole-hole interaction has been found to be important; it significantly accounts for more repulsion at large densities. Also, it enhances the nuclear matter E/A and at the same time reduces the saturation density ρ₀, as compared with the BHF results. If we do not consider the contact term these characteristics lead to better values for the saturation point. In general, microscopic BHF or SCGF calculations cannot simultaneously reproduce nuclear matter E/A and ρ₀. To improve the situation, one may either extend to three-body force to the effective interaction or include relativistic corrections RBHF, then the EOS of pure neutron matter can be used to determine the structure of neutron stars.

Using the present EOS’s of pure neutron matter at absolute zero, the TOV equation of general relativity, from which the gross properties of neutron stars follow, e.g., mass and radius can be solved numerically. It turns out that both maximum stable masses and radii depend crucially on the stiffness of the suggested EOS. Neutron stars including realistic EOS give the following general results: star model calculated with a stiff EOS have a lower central density, a larger radius than do stars of the same mass computed from a soft EOS. There is another important consequence; NS parameters such as the total mass and radius, are sensitive to microscopic model calculations. Also, the results from non-relativistic equation of state may look more reasonable than those from the relativistic one.

Acknowledgements

The present research support from Taif University, Kingdom of Saudi Arabia under Project No. 1-434-2667 is acknowledged.

References