Journal of Modern Physics Vol.05 No.15(2014), Article ID:50242,5
pages
10.4236/jmp.2014.515155
The Bowing Parameters of
 Ternary Alloys
Ternary Alloys
Sinem Erden Gulebaglan1, Emel Kilit Dogan2, Murat Aycibin2, Mehmet Nurullah Secuk2, Bahattin Erdinc2, Harun Akkus2
1Department of Electric Program, Vacational School of Van, Yuzuncu Yıl University, Van, Turkey
2Physics Department, Faculty of Sciences, Yüzüncü Yıl University, Van, Turkey
Email: sinemerden@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 8 May 2014; revised 4 June 2014; accepted 2 July 2014

ABSTRACT
On the basis of first principles calculations using density functional theory, we
explore the struc- tural and electronic properties of two binaries: CaO and MgO
in rock salt structures. Structural properties of the semiconductor
 alloys are derived from total-energy minimization within the General Gradient Approximation.
The band gap bowing parameters dependence is very powerful Calcium composition.
The results offer that an average bowing parameter of
alloys are derived from total-energy minimization within the General Gradient Approximation.
The band gap bowing parameters dependence is very powerful Calcium composition.
The results offer that an average bowing parameter of
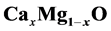 alloys is b = ~0.583$ eV. We analyzed the volume deformation, charge transfer and
structural relaxation effects of the
alloys is b = ~0.583$ eV. We analyzed the volume deformation, charge transfer and
structural relaxation effects of the
 alloys.
alloys.
Keywords:
Density Functional Theory, Ternary Alloys, Band-Gap Bowing Parameter

1. Introduction
Recently, the binary compounds such as TlAs, AlAs, ScN, GaN and their mixtures such
as TlAlAs, ScGaN have been studied theoretically [1] -[3] , because the wide range
of the band gap is important for microelectronics devices. Generally, monoxide compounds
are known as rock salt structures (B1) at room temperature and under pressure. Y.
Duan et al. [4] have been handled the electronic properties of XO (X = Be, Mg, Ca,
Sr, Ba, Zn and Cd) for wrutzite, zincblende and rock salt structure. Ponce et al.
[5] have analyzed theoreticaly and experimentaly electronic and optic properties
of CaS nad CaO. Albuquerque and Vasconcelos [6] are reported structual, electronic
and optical properties of CaO. Karki et al. [7] [8] have inversigated structual,
dynamic and electronic properties of liquid MgO via density functional theory. Makaremi
and Nourbakhsh have declerated structual, electronic and magnetic properties of
Mgo nanolayers. Nishi et al. [9] have investigated experimentally metastable
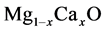 solid solutions film ZnO layers. Stolbov and Cohen [10] have studied the electronic
structure for equilibrium MgO-CaO. Miloua et al. [11] have calculated the electronic
properties of
solid solutions film ZnO layers. Stolbov and Cohen [10] have studied the electronic
structure for equilibrium MgO-CaO. Miloua et al. [11] have calculated the electronic
properties of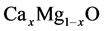 ,
theoretically. Besides, A. Srivastava et al. [12] calculated phase translations
in
,
theoretically. Besides, A. Srivastava et al. [12] calculated phase translations
in
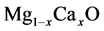 alloys.
alloys.
In this paper, we represent the bowing parameter of
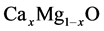 alloys by first principles density functional theory. To the best of our knowledge,
no theoretical as well as experimental work has been performed thus far for the
bowing parameter of
alloys by first principles density functional theory. To the best of our knowledge,
no theoretical as well as experimental work has been performed thus far for the
bowing parameter of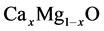 .
The aim of this paper is to understand the attitude of the bowing parameters and
contribution to the gap bowing parameters. The paper is methodized as follows: computational
methodology is given in Section 2. Results and discussion are represented in Section
3. The study is concluded in Section 4.
.
The aim of this paper is to understand the attitude of the bowing parameters and
contribution to the gap bowing parameters. The paper is methodized as follows: computational
methodology is given in Section 2. Results and discussion are represented in Section
3. The study is concluded in Section 4.
2. Computational Details
The calculations for CaO, MgO and
 in the rock salt structure were investigated within the generalized gradient approximation
(GGA) of density functional theory (DFT) using the PWSCF code [13] . In Quantum
Espresso, the examining is performed by utilizing the Kohn-Sham [14] formation established
on the DFT. Total energies have been calculated by using ultrasoft pseudopotentials
and plane-wave basis sets. The exchange- correlation potentials in the GGA [15]
is separately used in the calculations. The electronic configurations used for the
pseudo potentials were Ca(3p64s), Mg(2p63s) and O(2s22p4).
The Khon-Sham [14] orbitals were described using a plane wave basis set. The highest
kinetic energy of a plane wave in the chosen fundamental set is known the cutoff
energy. Specialize assignation of the cutoff energy is important for achieving accurate
results with available computational process. The values of cutoff energies used
in our calculations are summarized in Table 1.
in the rock salt structure were investigated within the generalized gradient approximation
(GGA) of density functional theory (DFT) using the PWSCF code [13] . In Quantum
Espresso, the examining is performed by utilizing the Kohn-Sham [14] formation established
on the DFT. Total energies have been calculated by using ultrasoft pseudopotentials
and plane-wave basis sets. The exchange- correlation potentials in the GGA [15]
is separately used in the calculations. The electronic configurations used for the
pseudo potentials were Ca(3p64s), Mg(2p63s) and O(2s22p4).
The Khon-Sham [14] orbitals were described using a plane wave basis set. The highest
kinetic energy of a plane wave in the chosen fundamental set is known the cutoff
energy. Specialize assignation of the cutoff energy is important for achieving accurate
results with available computational process. The values of cutoff energies used
in our calculations are summarized in Table 1.
The plane wave energy cut off is selected 90 Ry. Accurate Brillounin zone investigations
are carried out using the standard special k-points technique of Monkhorst and Pack
[16] . The Brillouin zone investigation was performed over a
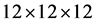 mesh points. Our calculations involve an 16 atom for
mesh points. Our calculations involve an 16 atom for
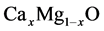 alloys in a supercell. We start at MgO cluster and finish at CaO cluster.
alloys in a supercell. We start at MgO cluster and finish at CaO cluster.
3. Results and Discussion
3.1. Structural Properties of Binary Compounds
The ternary compounds
 are bordered by two binary compounds of CaO and MgO. In order to be able to analyze
the energy band gaps and bowing parameters of
are bordered by two binary compounds of CaO and MgO. In order to be able to analyze
the energy band gaps and bowing parameters of
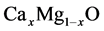 ternary alloys, it is wholesome to study the CaO and MgO binary compounds in terms
of their structural and electronic properties. By lessening the total energy with
regards to the atomic positions and lattice parameters we carried out the structural
optimization. Equilibrium lattice parameters are obtained by fitting the total energy
with the different volumes according to the Birch equation of states.
ternary alloys, it is wholesome to study the CaO and MgO binary compounds in terms
of their structural and electronic properties. By lessening the total energy with
regards to the atomic positions and lattice parameters we carried out the structural
optimization. Equilibrium lattice parameters are obtained by fitting the total energy
with the different volumes according to the Birch equation of states.
The Birch equation of states [17] can be seen in the Equation (1):
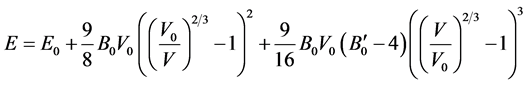 (1)
(1)
where
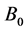 and
and


Table 1. Ground state energies for equilibrium MgO and CaO with various cutoff energies.
lated values for the equilibrium of CaO and MgO are 4.805 Å and 4.263 Å,
respectively. We represented and compered the equilibrium lattice parameter, bulk
modulus


3.2. Structural Properties of
In this paper, we examined the effectiveness of the Vegard’s law for rocksalt




where






The results also propose that the composition-dependent lattice parameter of the


The bowing parameter,

Table 2. Itemized lattice
parameter a, bulk modulus


Table 3. Itemized lattice
parameter a for the ternary alloys

composition amount

The band gap energy of ternary alloys


Here,










The combination-dependent bowing parameter function [21]


The band gap of the ternary alloys are correlated with the band gaps of the binary
compounds. The band gap bowing parameters

Finally, the total band gap bowing parameter can be written by resolving into its components as:

The effect of volume deformation causes the first term of bowing parameter,

Figure 1. Composition dependence
of the bowing parameter for

Table 4. Itemized bowing
parameter and contribution of the bowing parameter a for the ternary alloys

tional response of MgO(CaO) to hydrostatical pressure states this term via the effect
of the contribution of balanced lattice constant



A charge transfer in MgO and CaO at



The third term,


In Table 4, the values of bowing parameter,





The results also propose that the combination-dependent bowing parameter of the



















4. Conclusion
We have examined the electronic properties of the rocksalt










References
- Erden Gulebaglan, S. (2012) Modern Physics Letters B, 26, 1250199-8.
- Mazouza, H.M.A., Belabbesa, A., Zaouib, A. and Ferhat, M. (2010) Superlattices and Microstructures, 48, 560-568. http://dx.doi.org/10.1016/j.spmi.2010.09.012
- Moreno-Armenta, M.G., Mancera, L. and Takeuchi, N. (2003) Physica Status Solidi (B), 238, 127-135. http://dx.doi.org/10.1002/pssb.200301808
- Duan, Y., Qin, L., Tang, G. and Shi, L. (2008) European Physical Journal B, 66, 201-209. http://dx.doi.org/10.1140/epjb/e2008-00415-3
- Ponce, S., Bertrand, B., Smet, P.F., Poelman, D., Mikami, M. and Ganze, X. (2013) Optical Materials, 35, 1477-1480. http://dx.doi.org/10.1016/j.optmat.2013.03.001
- Albuquerque, E.L. and Vasconcelos, M.S. (2008) Journal of Physics: Conference Series, 042006, 1-4. http://dx.doi.org/10.1088/1742-6596/100/4/042006
- Karki Bijiya, B., Bhattarai, D. and Stixrude, L. (2006) Physical Review B, 73, 174208-1:7. http://dx.doi.org/10.1103/PhysRevB.73.174208
- Makaremi, N. and Nourbakhsh, Z. (2013) Journal of Superconductivity and Novel Magnetism, 26, 818-824. http://dx.doi.org/10.1007/s10948-012-1991-5
- Nishii, J., Ohtomo, A., Ikeda, M., Yamado, Y., Ohtani, K., Ohno, H. and Kawasahi, M. (2006) Applied Surface Science, 252, 2507-2511. http://dx.doi.org/10.1007/s10948-012-1991-5
- Stolbov, S.V. and Cohen, R.E. (2002) Physical Review B, 65, 092203-3. http://dx.doi.org/10.1103/PhysRevB.65.092203
- Miloua, R., Miloua, F., Kebbab, Z. and Benramdane, N. (2008) ISJAEE, 6, 91-95.
- Srivastava, A., Chauhan, M., Singh, R.K. and Padegaonker, R. (2011) Physica Status Solidi B, 248, 1901-1907. http://dx.doi.org/10.1002/pssb.201046508
- Baroni, S., Corso, A.D., de Gironcoli, S. and Giannozzi, P. http://www.pwscf.org
- Kohn, W. and Sham, L.J. (1965) Physical Review, 140, 1133-1138. http://dx.doi.org/10.1103/PhysRev.140.A1133
- Perdew, J.P., Burke, K. and Ernzerhof, M. (1996) Physical Review Letters, 77, 3865-3868. http://dx.doi.org/10.1103/PhysRevLett.77.3865
- Monkhorst, H.J. and Pack, J.D. (1976) Physical Review B, 13, 5188-5192. http://dx.doi.org/10.1103/PhysRevB.13.5188
- Mehl, M.J., Klein, B.M. and Papaconstantopoulos, D.A. (1995) Intermetallic Compounds: Principles and Practice, Vol. 1: Principles. 195-210.
- Fei, Y. (1999) American Mineralogist, 84, 272-276.
- Karki, B.B., Stixrude, L., Clark, S.J., Warren, M.C., Ancland, G.J. and Crain, J. (1997) American Mineralogist, 82, 51- 60.
- Richet, P., Mao, H.K. and Bell, P.M. (1988) Journal of Geophysical Research: Solid Earth, 93, 15279-15288. http://dx.doi.org/10.1029/JB093iB12p15279
- Drablia, S., Meradji, H., Ghemid, S., Labidi, S. and Bouhafs, B. (2009) Physica Scripta, 79, Article ID: 045002.





