Journal of Modern Physics
Vol.5 No.8(2014), Article
ID:46476,18
pages
DOI:10.4236/jmp.2014.58082
Some New Features of Photon Statistics in a Fully Quantized Parametric Amplification Process
Joseph Akeyo Omolo
Department of Physics, Maseno University, Maseno, Kenya
Email: ojakeyo04@yahoo.co.uk
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 January 2014; revised 21 February 2014; accepted 9 March 2014
ABSTRACT
An exact quantum treatment reveals that signal and idler photon number operators are not wellbehaved dynamical operators for studying photon statistics in parametric amplification/downconversion processes. Contrary to expectations, the mean signal-idler photon number difference 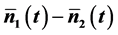 varies with time, while the corresponding signal-idler photon number cross-correlation function
varies with time, while the corresponding signal-idler photon number cross-correlation function  is complex and experiences an interference phenomenon driven by the interaction parameters. The intensity operators and related polarization operators of the polarized signal-idler photon pair in positive and negative helicity states are identified as the appropriate operators specifying a conservation law and the dynamical symmetry group (SU(1, 1)) of the parametric amplification process. The conservation of the mean positive and negative helicity photon intensity difference and the purely real positive-negative helicity intensity cross-correlation function correctly account for the simultaneous production of polarized signal and idler photons in positive and negative helicity states.
is complex and experiences an interference phenomenon driven by the interaction parameters. The intensity operators and related polarization operators of the polarized signal-idler photon pair in positive and negative helicity states are identified as the appropriate operators specifying a conservation law and the dynamical symmetry group (SU(1, 1)) of the parametric amplification process. The conservation of the mean positive and negative helicity photon intensity difference and the purely real positive-negative helicity intensity cross-correlation function correctly account for the simultaneous production of polarized signal and idler photons in positive and negative helicity states.
Keywords:Quantized Parametric Amplification, Jaynes-Cummings Interaction, Fluctuation State Vectors, Fractional Revivals, Interference, Positive-Negative Helicity Intensity/Polarization Operators, SU(1, 1) Symmetry Group

1. Introduction
The fully quantized parametric amplification process treated in this paper consists of a pump photon of angular frequency ω, annihilation operator  and creation operator
and creation operator ![]() interacting with a non-linear crystal to generate two photons, the signal and idler, of angular frequencies
interacting with a non-linear crystal to generate two photons, the signal and idler, of angular frequencies![]() ,
, 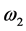 , annihilation operators
, annihilation operators ,
, ![]() and creation operators
and creation operators![]() ,
, ![]() , respectively. The model Hamiltonian for this process is obtained in the trilinear form [1] [2]
, respectively. The model Hamiltonian for this process is obtained in the trilinear form [1] [2]
 (1)
(1)
where g is a constant coupling parameter.
Transformation to the interaction frame through application of a transformation operator 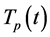 according to a general transformation law
according to a general transformation law
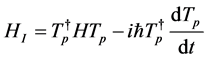 (2a)
(2a)
where the transformation operator takes the form
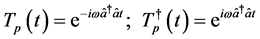 (2b)
(2b)
puts the Hamiltonian H from Equation (1) into an interaction form
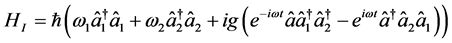 (2c)
(2c)
which specifically describes the interaction of signal ( -mode) and idler (
-mode) and idler (![]() -mode) photons coupled by a single quantized pump photon (a-mode).
-mode) photons coupled by a single quantized pump photon (a-mode).
The time evolution equations governing the dynamics of signal and idler photons are obtained through Heisenberg’s equations for the annihilation and creation operator pair (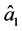 ,
,![]() ) in the form
) in the form
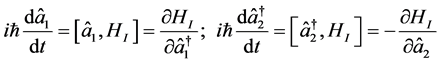 (3a)
(3a)
which on substituting  from Equation (2c) become
from Equation (2c) become
 (3b)
(3b)
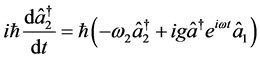 (3c)
(3c)
The general procedure for obtaining exact analytical solutions to these equations has been developed by the present author in a recent paper on fully quantized parametric oscillation/frequency-conversion process [3] . A summary of the procedure is presented in the next section to obtain exact analytical solutions for a fully quantized parametric amplification/down-conversion process.
2. The Matrix Method: Jaynes-Cummings Interaction
The coupled time evolution Equations (3b), (3c) are expressed in an appropriate matrix form by introducing a two-component signal-idler photon annihilation-creation operator column matrix 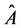 defined by
defined by
 (4a)
(4a)
to obtain
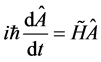 (4b)
(4b)
where  is a
is a 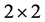 Hamiltonian matrix obtained as
Hamiltonian matrix obtained as
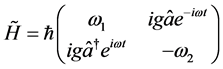 (4c)
(4c)
Introducing the 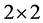 identity and the usual Pauli spin operators
identity and the usual Pauli spin operators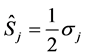 ,
,  , giving
, giving
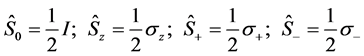 (5)
(5)
the Hamiltonian matrix in Equation (4c) is expressed in the form
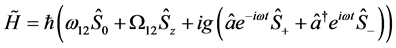 (6a)
(6a)
where the frequency difference  and sum
and sum  are defined by
are defined by
 (6b)
(6b)
An important point to note here is that, except for the factor  in the interaction term specifying the parametric interaction mechanism, the Hamiltonian H in Equation (6a) takes the form of a Jaynes-Cummings interaction Hamiltonian [4] -[10] for a 2-level atom interacting with a quantized single-mode electromagnetic field. Since the interaction term
in the interaction term specifying the parametric interaction mechanism, the Hamiltonian H in Equation (6a) takes the form of a Jaynes-Cummings interaction Hamiltonian [4] -[10] for a 2-level atom interacting with a quantized single-mode electromagnetic field. Since the interaction term  of
of 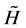 in Equation (6a) is anti-Hermitian according to
in Equation (6a) is anti-Hermitian according to
 (6c)
(6c)
it may appropriately be referred to as an anti-Jaynes-Cummings Hamiltonian.
In this respect, the Hamiltonian 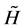 in Equation (6a) is non-Hermitian, yet it generates the internal dynamics of a non-dissipative parametric amplification process governed by the original Hermitian Hamiltonian H in Equation (1).
in Equation (6a) is non-Hermitian, yet it generates the internal dynamics of a non-dissipative parametric amplification process governed by the original Hermitian Hamiltonian H in Equation (1).
2.1. Signal-Idler Photon Polarization Operator Vector
To gain complete understanding of the 2-level Jaynes-Cummings mode of interaction in the fully quantized parametric amplification process, consider that according to Equation (4b), the Jaynes-Cummings interaction Hamiltonian  generates of the dynamics vector the signal-idler photon system by operating on the two-component operator
generates of the dynamics vector the signal-idler photon system by operating on the two-component operator  defined in Equation (4a), which is now expressed in the appropriate form
defined in Equation (4a), which is now expressed in the appropriate form
 (7a)
(7a)
after introducing the 2-dimensional Hilbert space basis vectors 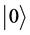 and
and  defined as usual by
defined as usual by
 (7b)
(7b)
It is clear that  takes exactly the form of a two-level atomic state vector as defined within the standard Jaynes-Cummings model in quantum optics [4] -[10] and in general quantum mechanics. In standard photon dynamics, the basis vectors
takes exactly the form of a two-level atomic state vector as defined within the standard Jaynes-Cummings model in quantum optics [4] -[10] and in general quantum mechanics. In standard photon dynamics, the basis vectors 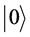 and
and  are interpreted as the basic circular polarization state vectors. In particular, using the Pauli matrix
are interpreted as the basic circular polarization state vectors. In particular, using the Pauli matrix  defined by
defined by
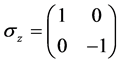 (7c)
(7c)
gives
 (7d)
(7d)
which leads to the standard interpretation that 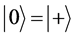 is a positive helicity state vector, while
is a positive helicity state vector, while  is a negative helicity state vector for circularly polarized photons [11] .
is a negative helicity state vector for circularly polarized photons [11] .
The two-component vector  is then specifically interpreted as a polarization operator vector for the coupled circularly polarized signal-idler photon pair. The component annihilation and creation operators
is then specifically interpreted as a polarization operator vector for the coupled circularly polarized signal-idler photon pair. The component annihilation and creation operators 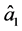 and
and ![]() are interpreted as photon intensity operator amplitudes for signal and idler photons in positive and negative helicity states
are interpreted as photon intensity operator amplitudes for signal and idler photons in positive and negative helicity states 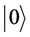 and
and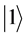 , respectively.
, respectively.
Using  from Equation (7a) and its Hermitian conjugate
from Equation (7a) and its Hermitian conjugate 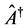 obtained as
obtained as
![]() (7e)
(7e)
the total signal-idler photon intensity operator 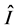 follows from the inner product according to
follows from the inner product according to
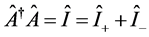 (7f)
(7f)
after introducing positive and negative helicity polarized signal-idler photon intensity operators![]() ,
, ![]() , respectively obtained as
, respectively obtained as
 (7g)
(7g)
It follows from Equations (4b), (6a) and (7a) that the underlying dynamics in a fully quantized parametric amplification process is a two-state dynamics characterized by the time evolution of circular polarization state vectors of the coupled signal-idler photon pair generated by a Jaynes-Cummings mode of interaction. This leads to the general interpretation that the coupled signal-idler photon pair constitutes a composite circularly polarized two-state system specified by the positive and negative helicity states interacting with a single-mode quantized pump field equivalent to an (anti)-Jaynes-Cummings model for a single two-level atom. A comprehensive presentation of photon polarization state dynamics in linear and nonlinear quantum optics is currently under preparation in a more elaborate paper by the present author.
2.2. General Solution
A complete picture of the Jaynes-Cummings mode of interaction is obtained by transforming Equation (4b) back to the original frame by applying the inverse operator  from Equation (2b) according to
from Equation (2b) according to
![]() (8a)
(8a)
which is used in Equation (4b) to obtain the effective time evolution equation in the original frame in the form
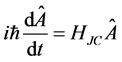 (8b)
(8b)
where the Hamiltonian 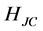 follows from the transformation in the form
follows from the transformation in the form
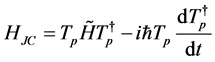 (8c)
(8c)
This essentially reverses the general transformation law in Equation (2a) as expected. Substituting  from Equation (6a) into Equation (8c) and applying standard algebraic relations gives the final form
from Equation (6a) into Equation (8c) and applying standard algebraic relations gives the final form
 (8d)
(8d)
The obvious interpretation is that  in Equation (8d) is the full (anti)-Jaynes-Cummings Hamiltonian which generates the dynamics of a fully quantized parametric amplification process through its action on the signal-idler photon polarization operator vector
in Equation (8d) is the full (anti)-Jaynes-Cummings Hamiltonian which generates the dynamics of a fully quantized parametric amplification process through its action on the signal-idler photon polarization operator vector  according to Equation (8b). The anti-Hermitian property of its interaction term
according to Equation (8b). The anti-Hermitian property of its interaction term  is responsible for the characteristic features of the amplification process. As observed earlier, the non-Hermitian nature of
is responsible for the characteristic features of the amplification process. As observed earlier, the non-Hermitian nature of  is not in any way associated with dissipation, since the (anti)-Jaynes-Cummings mode of interaction only characterizes the general dynamics generated by the original continuous variable operator Hermitian Hamiltonian H in Equation (1).
is not in any way associated with dissipation, since the (anti)-Jaynes-Cummings mode of interaction only characterizes the general dynamics generated by the original continuous variable operator Hermitian Hamiltonian H in Equation (1).
The time evolution Equation (8b) can now be solved exactly by applying the usual procedure for solving the Jaynes-Cummings problem in quantum optics [9] [10] . Adding and subtracting 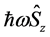 in Equation (8e) and introducing frequency detuning δ defined by
in Equation (8e) and introducing frequency detuning δ defined by
 (9a)
(9a)
puts  in the form
in the form
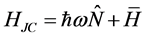 (9b)
(9b)
where the operator ![]() and interaction Hamiltonian H are defined by
and interaction Hamiltonian H are defined by
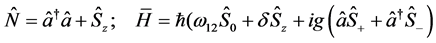 (9c)
(9c)
Using standard algebraic relations for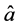 ,
, ![]() ,
, ![]() ,
, ![]() ,
, 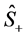 ,
, 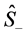 easily gives
easily gives
 (9d)
(9d)
Since both components 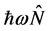 and
and  commute with
commute with , they are constants of the motion. The Hamiltonian
, they are constants of the motion. The Hamiltonian 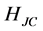 is thus time-independent, leading to a solution of the time evolution Equation (8b) through simple integration giving
is thus time-independent, leading to a solution of the time evolution Equation (8b) through simple integration giving
![]() (10a)
(10a)
where the initial polarization operator vector ![]() takes the form in Equation (7a). The general time evolution operator
takes the form in Equation (7a). The general time evolution operator  governing the dynamics under
governing the dynamics under  has been obtained as
has been obtained as
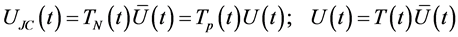 (10b)
(10b)
after applying the commutation of  and
and 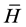 as in Equation (9d) and using
as in Equation (9d) and using
 (10c)
(10c)
 (10d)
(10d)
2.2.1. Evaluating 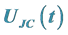
Substituting  from Equation (10d) into Equation (10b) and using
from Equation (10d) into Equation (10b) and using 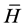 from Equation (9c) gives
from Equation (9c) gives 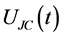 in the form
in the form
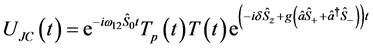 (11a)
(11a)
after considering that the identity  commutes with the rest of the operators to effect a factorization as appropriate. Expanding the exponential operator in Equation (11a) and carrying out straightforward algebraic manipulation with details presented in [3] yields the final form
commutes with the rest of the operators to effect a factorization as appropriate. Expanding the exponential operator in Equation (11a) and carrying out straightforward algebraic manipulation with details presented in [3] yields the final form
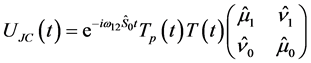 (11b)
(11b)
after introducing the time evolving pump photon interaction operators![]() ,
,  ,
,  ,
, ![]() defined by
defined by
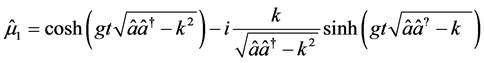 (12a)
(12a)
 (12b)
(12b)
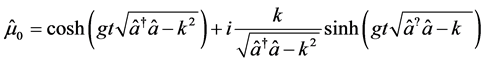 (12c)
(12c)
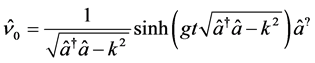 (12d)
(12d)
with Hermitian conjugates easily obtained as
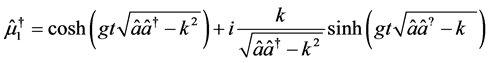 (12e)
(12e)
 (12f)
(12f)
 (12g)
(12g)
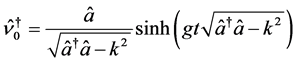 (12h)
(12h)
2.2.2. Evaluating ![]()
Substituting  from Equation (11b) into Equation (10a), using the initial
from Equation (11b) into Equation (10a), using the initial ![]() from Equation (7a), together with T(t) from Equation (10c) and applying
from Equation (7a), together with T(t) from Equation (10c) and applying
 (13a)
(13a)
 (13b)
(13b)
then reorganizing the result gives the final form
![]() (14a)
(14a)
where the general time evolving signal photon annihilation operator  and idler photon creation operator
and idler photon creation operator ![]() have been obtained in the form
have been obtained in the form
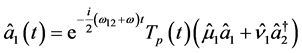 (14b)
(14b)
 (14c)
(14c)
These are the desired exact analytical solutions determined within the Heisenberg picture, where they can be used in the calculation of mean values, fluctuations and cross-correlation functions of various physical quantities which characterize the dynamics of a fully quantized parametric amplification process generated by the trilinear Hamiltonian 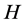 in Equation (1).
in Equation (1).
2.3. Pump Photon Operator Action on Fock State ![]()
The pump photon operators![]() ,
,  ,
, 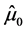 ,
, ![]() , together with their Hermitian conjugates defined in the set of Equations (12a)-(12h) act on the pump photon Fock state vector
, together with their Hermitian conjugates defined in the set of Equations (12a)-(12h) act on the pump photon Fock state vector 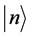 according to [3]
according to [3]
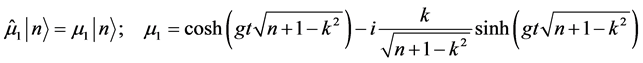 (15a)
(15a)
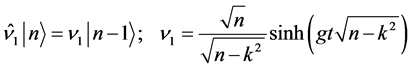 (15b)
(15b)
 (15c)
(15c)
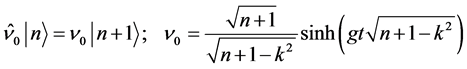 (15d)
(15d)
![]() (15e)
(15e)
which provide useful c-number variables![]() ,
, 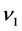 ,
,  ,
, ![]() in explicit forms to describe features of the dynamics. It is to be noted that
in explicit forms to describe features of the dynamics. It is to be noted that![]() ,
, 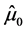 generate eigenvalue equations, while
generate eigenvalue equations, while 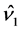 acts like an annihilation operator and
acts like an annihilation operator and ![]() acts like a creation operator. Indeed, using Equations (15b) and (15d) shows that the operator products
acts like a creation operator. Indeed, using Equations (15b) and (15d) shows that the operator products  and
and  act like photon number operators according to
act like photon number operators according to
![]() (15f)
(15f)
where
![]() (15g)
(15g)
show that 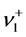 is easily obtained by setting n → n + 1 in Equation (15b), while
is easily obtained by setting n → n + 1 in Equation (15b), while 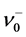 is easily obtained by setting n → n − 1 in Equation (15d). These simple operations apply to the pump photon Fock state and indeed to various forms of the pump photon initial state vectors generally expressible as superpositions of Fock state vectors.
is easily obtained by setting n → n − 1 in Equation (15d). These simple operations apply to the pump photon Fock state and indeed to various forms of the pump photon initial state vectors generally expressible as superpositions of Fock state vectors.
3. Fluctuation (Noise) State Vectors
State vectors which describe the fluctuations of various physical quantities (observables) are here referred to as fluctuation state vectors in the sense that their occupation numbers (or inner products) define the fluctuations. The interpretation of fluctuations as noise may also lead to a corresponding reference as noise state vectors. The fluctuation (noise) state vectors are generated through repeated application of annihilation (fundamental) or creation (dual) operators on the appropriate initial state vectors. The action of the annihilation or creation operators causes de-excitation or excitation, which generally produce fluctuations or noise during measurements. In general, repeated applications of annihilation and creation operators in appropriate order are equivalent to operations with corresponding observable operators formed as products of the annihilation and creation operators.
In this study, the initial state vector 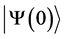 of the pump, signal and idler photons is taken as the Fock state vector defined using usual notation in the product form
of the pump, signal and idler photons is taken as the Fock state vector defined using usual notation in the product form
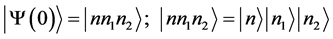 (16a)
(16a)
For an observable represented by an operator ![]() at any time t ≥ 0, the Q-fluctuation state vector is obtained as
at any time t ≥ 0, the Q-fluctuation state vector is obtained as
 (16b)
(16b)
The Q-mean value is obtained as
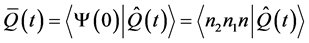 (16c)
(16c)
while the Q-second moment is obtained as the occupation number (or inner product) according to
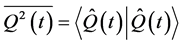 (16d)
(16d)
The Q-fluctuation is obtained using equations (16c)-(16d) in the general form
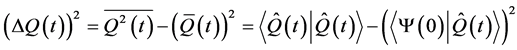 (16e)
(16e)
For two observables represented by operators![]() ,
, ![]() , where j , k are suitable labels, which can be numbers or appropriate symbols, the cross-correlation functions are obtained according to
, where j , k are suitable labels, which can be numbers or appropriate symbols, the cross-correlation functions are obtained according to
 (16f)
(16f)
while the cross-correlation fluctuations defined by
 (16g)
(16g)
are obtained according to
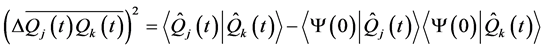 (16h)
(16h)
These results are general enough to apply to various operators and their Hermitian conjugates.
4. Signal and Idler Photon Number Fluctuation State Vectors
This section investigates the suitability of the signal and idler photon number operators ,
,  as dynamical operators for studying photon statistics in a fully quantized parametric amplification process. In this respect, the observable operator
as dynamical operators for studying photon statistics in a fully quantized parametric amplification process. In this respect, the observable operator ![]() is the photon number. For signal and idler photons,
is the photon number. For signal and idler photons, ![]() ,
, . Photon number fluctuation state vectors are defined to evaluate photon number mean values, fluctuations and cross-correlation functions. These will reveal some new, i.e., unfamiliar, features originating from the full quantum treatment of the parametric amplification process generated by the trilinear Hamiltonian
. Photon number fluctuation state vectors are defined to evaluate photon number mean values, fluctuations and cross-correlation functions. These will reveal some new, i.e., unfamiliar, features originating from the full quantum treatment of the parametric amplification process generated by the trilinear Hamiltonian 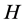 in Equation (1).
in Equation (1).
The signal and idler photon number operators  and
and  generally used in studying photon statistics in the parametric amplification process in quantum optics [1] [2] [12] -[15] are defined by
generally used in studying photon statistics in the parametric amplification process in quantum optics [1] [2] [12] -[15] are defined by
![]() (17a)
(17a)
Setting![]() ,
, 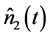 in Equation (16b), using the definitions from Equation (17a) and applying Equations (14b), (14c) and their Hermitian conjugates, together with Equations (15a)-(15e), gives the signal and idler photon number fluctuation state vectors
in Equation (16b), using the definitions from Equation (17a) and applying Equations (14b), (14c) and their Hermitian conjugates, together with Equations (15a)-(15e), gives the signal and idler photon number fluctuation state vectors  and
and , respectively in the final form
, respectively in the final form
 (17b)
(17b)
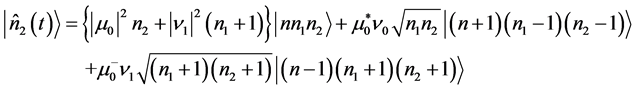 (17c)
(17c)
where
 (17d)
(17d)
The photon number fluctuation state vectors in Equations (17b), (17c) are used in the general definitions in Equations (16c) and (16e) with![]() ,
,  to obtain the mean signal and idler photon numbers
to obtain the mean signal and idler photon numbers 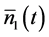 and
and 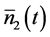 and their corresponding fluctuations in the Fock state in the final forms
and their corresponding fluctuations in the Fock state in the final forms
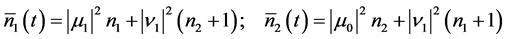 (18a)
(18a)
 (18b)
(18b)
 (18c)
(18c)
Finally, using equations (17b)-(17c) in the general definition in Equations (16f)-(16h) with ,
,  ,
, ![]() ,
, ![]() , easily gives the signal-idler photon number cross-correlation functions
, easily gives the signal-idler photon number cross-correlation functions  and the corresponding fluctuation in the Fock state in the form
and the corresponding fluctuation in the Fock state in the form
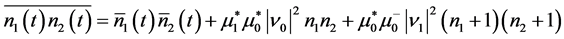 (19a)
(19a)
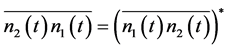 (19b)
(19b)
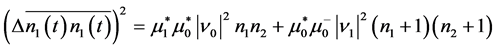 (19c)
(19c)
4.1. New Features in Signal-Idler Photon Statistics
Substituting![]() ,
,  and
and  from Equations (15a)-(15c) into Equation (18a), the mean signal and idler photon numbers are expressed in the explicit form
from Equations (15a)-(15c) into Equation (18a), the mean signal and idler photon numbers are expressed in the explicit form
 (20a)
(20a)
+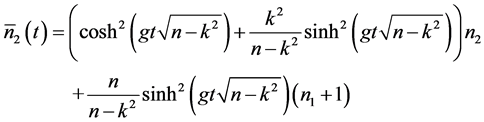 (20b)
(20b)
which display some new, i.e., unfamiliar, features of signal-idler photon statistics appearing in the dynamics of a fully quantized parametric amplification process.
According to Equation (20a), the mean signal photon number  evolves over two different time scales specified by
evolves over two different time scales specified by 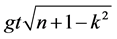 and
and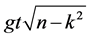 . The physical consequence is that for values
. The physical consequence is that for values 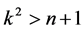 such that
such that
 (20c)
(20c)
with
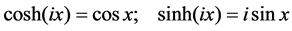 (20d)
(20d)
the time evolution becomes oscillatory and the beating of competing oscillations over the two time scales generates fractional revivals in the mean signal photon number as demonstrated in Figure 1.
On the other hand, Equation (20b) shows that the mean idler photon number  evolves over a single time scale specified only by
evolves over a single time scale specified only by 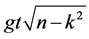 so that for values
so that for values 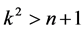 (implies
(implies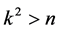 ), the time evolution of the mean idler photon number is composed of simple oscillations as demonstrated in Figure 2.
), the time evolution of the mean idler photon number is composed of simple oscillations as demonstrated in Figure 2.
These results show that signal and idler photon numbers have different modes of behavior, which may also account for the difference in number fluctuations in Equations (18b) and (18c).
The second very important feature arising as a consequence of the different time evolution patterns in Equations (20a)-(20b) is the unexpected time evolution of the mean signal-idler photon number difference 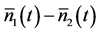 in the form
in the form
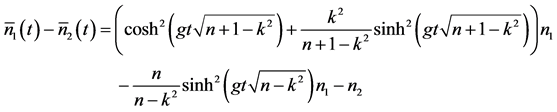 (20e)
(20e)
This result contradicts the expected conservation of the mean signal-idler photon number difference,
 , generally obtained in the parametric/semi-classical approximation and inferred through the commutation of the corresponding number difference operator
, generally obtained in the parametric/semi-classical approximation and inferred through the commutation of the corresponding number difference operator 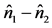 with the bilinear or trilinear Hamiltonian (
with the bilinear or trilinear Hamiltonian ( ) of the parametric amplification process [1] [2] [13] -[16] . The time variation of
) of the parametric amplification process [1] [2] [13] -[16] . The time variation of 

Figure 1. Signal number 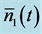 in (20a) over scaled time τ = gt, n = 3, k = 5,
in (20a) over scaled time τ = gt, n = 3, k = 5, 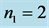 ,
,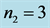 .
.

Figure 2. Idler number 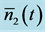 in (20b) over scaled time τ = gt, n = 3, k = 5,
in (20b) over scaled time τ = gt, n = 3, k = 5, 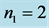 ,
,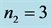 .
.
emerges here as a new feature of the dynamics of a fully quantized parametric amplification process. The immediate physical implication is that the time varying 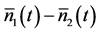 does not account for the experimentally or numerically observed simultaneous production of signal and idler photon pairs in a parametric amplification process. This observation may also be supported by the fact that the differing photon number fluctuations in Equations (18b)-(18c) mean that the measurements of signal and idler photon numbers involve different quantum noise levels, which can cause delays in the counts of either signal or idler photons. The important phenomenon of simultaneous production of signal and idler photons is addressed through photon polarization state dynamics in the next section.
does not account for the experimentally or numerically observed simultaneous production of signal and idler photon pairs in a parametric amplification process. This observation may also be supported by the fact that the differing photon number fluctuations in Equations (18b)-(18c) mean that the measurements of signal and idler photon numbers involve different quantum noise levels, which can cause delays in the counts of either signal or idler photons. The important phenomenon of simultaneous production of signal and idler photons is addressed through photon polarization state dynamics in the next section.
The third important feature follows from the results in Equations (19a)-(19b), which show that the signal-idler photon number cross-correlation functions are generally complex, with ![]() being the complex conjugate of
being the complex conjugate of![]() . According to the definitions of the c-number variables
. According to the definitions of the c-number variables![]() ,
, 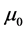 ,
,  in Equations (15a), (15c) and (17d), the complex form of the number cross-correlation functions is an off-resonance feature associated with non-zero values of the frequency detuning parameter k, i.e.,
in Equations (15a), (15c) and (17d), the complex form of the number cross-correlation functions is an off-resonance feature associated with non-zero values of the frequency detuning parameter k, i.e.,  is complex for
is complex for![]() , otherwise, the signal-idler photon number cross-correlation functions are real under the resonance condition,
, otherwise, the signal-idler photon number cross-correlation functions are real under the resonance condition,![]() . Calculations performed under the resonance condition do not reveal the complex form of the signal-idler photon number cross-correlation functions.
. Calculations performed under the resonance condition do not reveal the complex form of the signal-idler photon number cross-correlation functions.
The average signal-idler photon cross-correlation function denoted here by ![]() is obtained as
is obtained as
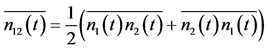 (21a)
(21a)
which on substituting Equation (19a) and its complex conjugate in accordance with Equation (19b) becomes
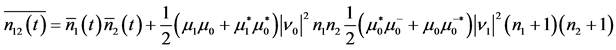 (21b)
(21b)
It is interesting to introduce the polar forms
 (22a)
(22a)
to express Equation (21b) in the convenient form
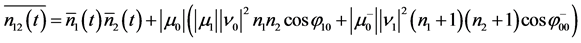 (22b)
(22b)
after introducing interaction parameter dependent phase differences  and
and 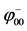 defined by
defined by
 (22c)
(22c)
The amplitudes and phase angles (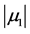 ,
, ), (
), (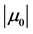 ,
,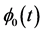 ) and (
) and (![]() ,
, ) are obtained using Equations (15a), (15c) and (17d), respectively, in the form
) are obtained using Equations (15a), (15c) and (17d), respectively, in the form
 (22d)
(22d)
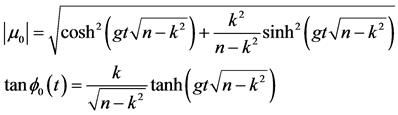 (22e)
(22e)
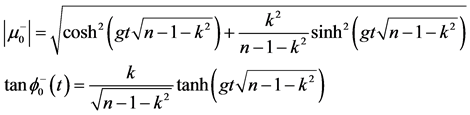 (22f)
(22f)
It is clear that the phase angles vanish under the resonance condition k = 0 and the number cross-correlation function as presented in Equations (22b)-(22c) becomes real. But, for off-resonance dynamics with![]() , Equation (22b) shows that the signal-idler photon number cross-correlation function is characterized by an interference phenomenon controlled by interaction parameters. It is an interesting interference phenomenon characterized by two generally unequal phase differences
, Equation (22b) shows that the signal-idler photon number cross-correlation function is characterized by an interference phenomenon controlled by interaction parameters. It is an interesting interference phenomenon characterized by two generally unequal phase differences  and
and . The interference phenomenon in the off-resonance signal-idler photon number dynamics may also have some constructive or destructive effect on the expected simultaneous production of signal and idler photons.
. The interference phenomenon in the off-resonance signal-idler photon number dynamics may also have some constructive or destructive effect on the expected simultaneous production of signal and idler photons.
4.2. Recalling the Parametric/Semi-Classical Approximation
An important observation is that the time variation of the mean signal-idler photon number difference 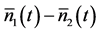 and the complex form yielding the interference phenomenon in the signal-idler photon number cross-correlation function
and the complex form yielding the interference phenomenon in the signal-idler photon number cross-correlation function ![]() are both quantum effects characterizing the dynamics of a fully quantized parametric amplification process. These effects do not appear in the parametric/semi-classical approximation.
are both quantum effects characterizing the dynamics of a fully quantized parametric amplification process. These effects do not appear in the parametric/semi-classical approximation.
In the parametric approximation or semi-classical model where the pump photon is considered to be generated by a high intensity laser field, the mean pump photon number n is obtained from a c-number field amplitude α of very large magnitude according to
![]() (22g)
(22g)
from which follows
![]() (22h)
(22h)
Using Equation (22h) in Equations (18a) and (19a) gives the mean photon numbers, number difference and cross-correlation function in the parametric approximation/semi-classical model in the familiar forms [1] [16]
![]() (22i)
(22i)
![]() (22j)
(22j)
![]() (22k)
(22k)
Using Equation (22h) in Equations (18b)-(18c) and comparing the results with Equation (22k) gives the number fluctuations in the parametric/semiclassical approximation in the form
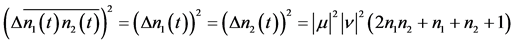 (22l)
(22l)
These results show that, in the parametric approximation or the semi-classical model, the mean signal-idler photon number difference is conserved according to Equations (22i), (22j) and the number cross-correlation function is real according to Equation (22k). The simultaneous production of signal and idler photons predicted within the parametric/semi-classical approximation is based on Equations (22j) and (22l) [1] .
The above results confirm that the complex forms and the time variation obtained in Equations (19a) and (20e), respectively, emerge entirely as quantum effects in the fully quantized parametric amplification process.
The main conclusion drawn from the investigation in this section is that the signal and idler photon number operators 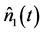 and
and 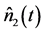 are not well-behaved and are therefore not suitable dynamical operators for studying photon statistics in a fully quantized parametric amplification process. The non-conservation of the mean number difference
are not well-behaved and are therefore not suitable dynamical operators for studying photon statistics in a fully quantized parametric amplification process. The non-conservation of the mean number difference  is inconsistent with the commutation relation
is inconsistent with the commutation relation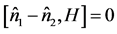 , which shows that the number operator difference
, which shows that the number operator difference 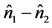 is a constant of the motion, while the number cross-correlation function
is a constant of the motion, while the number cross-correlation function ![]() is generally complex and experiences an interference phenomenon. In addition, comparing the results obtained within the full quantum treatment in Equations (19a), (20e) with the results obtained within the parametric/semi-classical approximation in Equations (22j), (22k) as appropriate reveals contradictions between number-based photon statistics determined in the fully quantized and in the parametric/semi-classical approximation models of the parametric amplification process. Polarized signal-idler photon intensity operators are identified to be the well-behaved dynamical operators for studying photon statistics in parametric amplification/ down-conversion processes in the next section.
is generally complex and experiences an interference phenomenon. In addition, comparing the results obtained within the full quantum treatment in Equations (19a), (20e) with the results obtained within the parametric/semi-classical approximation in Equations (22j), (22k) as appropriate reveals contradictions between number-based photon statistics determined in the fully quantized and in the parametric/semi-classical approximation models of the parametric amplification process. Polarized signal-idler photon intensity operators are identified to be the well-behaved dynamical operators for studying photon statistics in parametric amplification/ down-conversion processes in the next section.
5. The Polarization Operators and Symmetry Group of the Parametric Amplification Process
This section establishes that the appropriate dynamical operators which characterize the dynamics and specify the dynamical symmetry group of the parametric amplification process are the polarization operators 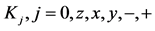 derivable from the polarization operator vector
derivable from the polarization operator vector 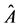 and its Hermitian conjugate
and its Hermitian conjugate 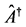 according to
according to
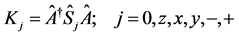 (23a)
(23a)
where
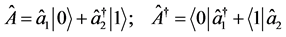 (23b)
(23b)
and ![]() are the usual Pauli spin operators defined according to
are the usual Pauli spin operators defined according to
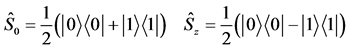 (23c)
(23c)
 (23d)
(23d)
Using Equations (23c), (23d) in Equation (23a) provides the desired polarization operators in the form
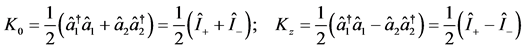 (24a)
(24a)
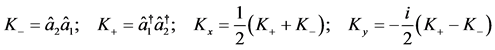 (24b)
(24b)
where 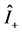 and
and  are the positive and negative helicity intensity operators defined earlier in Equation (7g).
are the positive and negative helicity intensity operators defined earlier in Equation (7g).
Application of the usual commutation relations between the annihilation and creation operators 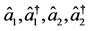 provides the algebraic relations
provides the algebraic relations
 (24c)
(24c)
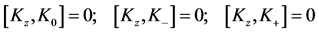 (24d)
(24d)
which constitute the Lie algebra of the 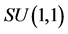 symmetry group. By Equation (24d),
symmetry group. By Equation (24d), 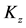 commutes with all the other operators and may be identified with the identity operator in
commutes with all the other operators and may be identified with the identity operator in 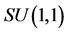 algebra. The set of polarization operators
algebra. The set of polarization operators  defined in Equations (24a), (24b) therefore constitute the continuous variable generators of the
defined in Equations (24a), (24b) therefore constitute the continuous variable generators of the 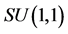 symmetry group covering the dynamics of the non-degenerate parametric amplification process. The polarization operators thus specify the Lie group
symmetry group covering the dynamics of the non-degenerate parametric amplification process. The polarization operators thus specify the Lie group  as the dynamical symmetry group of the parametric amplification/down-conversion process. The polarization states of the coupled signal-idler photon pairs are therefore appropriately specified by points on the two-sheet hyperboloid of the
as the dynamical symmetry group of the parametric amplification/down-conversion process. The polarization states of the coupled signal-idler photon pairs are therefore appropriately specified by points on the two-sheet hyperboloid of the 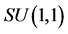 manifold.
manifold.
Using Equations (24a), (24b) in Equation (1) puts the Hamiltonian H in the form
 (24e)
(24e)
where the angular frequency difference 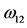 and sum
and sum  are as defined earlier in Equation (6b). An inconsequential constant term
are as defined earlier in Equation (6b). An inconsequential constant term 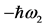 in
in ![]() has been ignored. Application of Equation (24d) gives the important result
has been ignored. Application of Equation (24d) gives the important result
 (24f)
(24f)
which leads to the conclusion that the polarization operator 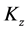 is a constant of the motion specifying a conservation law governing the dynamics of the coupled signal-idler photon pairs in the fully quantized parametric amplification process. The polarization operator
is a constant of the motion specifying a conservation law governing the dynamics of the coupled signal-idler photon pairs in the fully quantized parametric amplification process. The polarization operator  will be treated as a well-behaved dynamical operator if its mean value is conserved to maintain consistency with the result in Equation (24f). This is established below.
will be treated as a well-behaved dynamical operator if its mean value is conserved to maintain consistency with the result in Equation (24f). This is established below.
5.1. Intensity Fluctuation State Vectors
It is necessary to study the behavior of the intensity operators which constitute the polarization operators 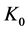 and
and 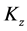 according to Equation (24a). The definitions of the time evolving positive and negative helicity intensity operators
according to Equation (24a). The definitions of the time evolving positive and negative helicity intensity operators  and
and 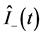 for the coupled polarized signal-idler photon pairs follow from Equation (7g) in the form
for the coupled polarized signal-idler photon pairs follow from Equation (7g) in the form
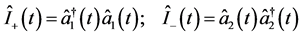 (25a)
(25a)
The time evolving positive and negative helicity intensity fluctuation state vectors  and
and , respectively are easily obtained using Equations (14b), (14c), (25a) and the general definition in Equation (16b) with
, respectively are easily obtained using Equations (14b), (14c), (25a) and the general definition in Equation (16b) with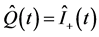 ,
, 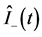 in the final form (noting
in the final form (noting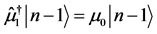 ,
, )
)
 (25b)
(25b)
 (25c)
(25c)
Using the intensity fluctuation state vectors from Equations (25b), (25c) according to the general definitions in Equations (16c) and (16e) with ,
,  , the mean values and corresponding fluctuations of the positive and negative helicity intensities
, the mean values and corresponding fluctuations of the positive and negative helicity intensities ,
, 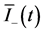 in the Fock state are obtained in the final forms
in the Fock state are obtained in the final forms
![]() (26a)
(26a)
![]() (26b)
(26b)
The positive and negative helicity intensity cross-correlation functions and cross-correlation fluctuations are obtained using Equations (25b)-(25c) and the general definitions in Equations (16f) and (16h) with![]() ,
, ![]() ,
,  ,
, 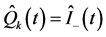 in the final form
in the final form
![]() (26c)
(26c)
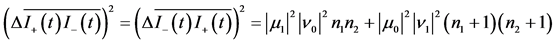 (26d)
(26d)
Comparing Equations (26b) and (26d) gives the important result
 (26e)
(26e)
Two important features characterizing the coupled signal-idler photon polarization state dynamics follow from the results in Equations (26a) and (26e). The results in Equation (26a) give the mean positive and negative helicity intensity difference as
 (27a)
(27a)
which on using  from Equations (15a)-(15d) to obtain
from Equations (15a)-(15d) to obtain
![]() (27b)
(27b)
provides the conservation law
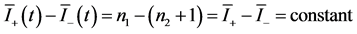 (27c)
(27c)
where ,
,  are the respective initial mean positive and negative helicity intensities. The result in Equation (26e) gives the cross-correlation coefficient
are the respective initial mean positive and negative helicity intensities. The result in Equation (26e) gives the cross-correlation coefficient
 (27d)
(27d)
The two results in Equations (27c) and (27d) show that in the fully quantized parametric amplification process, polarized signal and idler photons in the positive and negative helicity states are produced simultaneously.
5.2. Polarization Fluctuation State Vectors
Using the results and general definitions obtained above as appropriate give the polarization fluctuation state vectors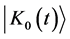 ,
, 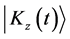 in the form
in the form
 (28a)
(28a)
where 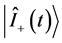 and
and  are already obtained in Equations (25b) and (25c), respectively, while the fluctuation state vectors
are already obtained in Equations (25b) and (25c), respectively, while the fluctuation state vectors 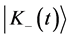 and
and  defined by
defined by
 (28b)
(28b)
take the final form (noting![]() ,
,![]() )
)
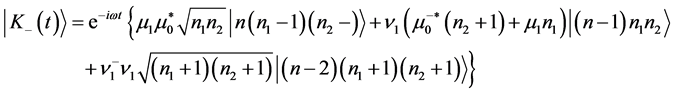 (28c)
(28c)
 (28d)
(28d)
The mean values of the time evolving polarization operators in the Fock state are easily obtained using the general definitions as
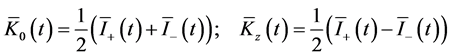 (29a)
(29a)
 (29b)
(29b)
where  and
and 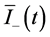 are the mean positive and negative helicity intensities obtained earlier in Equation (26a).
are the mean positive and negative helicity intensities obtained earlier in Equation (26a).
Using Equations (15a)-(15d) in Equation (26a) and substituting the results into Equation (29a) gives
 (29c)
(29c)
 (29d)
(29d)
It is clear from Equation (29c) that the mean value 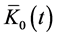 evolves in time over two different time scales specified by
evolves in time over two different time scales specified by 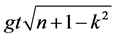 and
and , which for
, which for 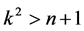 develops into an oscillatory evolution characterized by fractional revivals due to the beating of oscillations over the two time scales. This behavior takes exactly the form demonstrated in Figure 1.
develops into an oscillatory evolution characterized by fractional revivals due to the beating of oscillations over the two time scales. This behavior takes exactly the form demonstrated in Figure 1.
The result in Equation (29d) shows that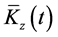 , which according to the definition in Equation (23a) for
, which according to the definition in Equation (23a) for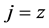 , also defines the mean intensity inversion between the positive and negative helicity states, is conserved in time. This is in complete agreement with the earlier result obtained in Equation (24f) establishing that the polarization operator
, also defines the mean intensity inversion between the positive and negative helicity states, is conserved in time. This is in complete agreement with the earlier result obtained in Equation (24f) establishing that the polarization operator  is a constant of the motion specifying a conservation law governing the dynamics of a fully quantized parametric amplification process. This consistency leads to identification of the polarization operator (or
is a constant of the motion specifying a conservation law governing the dynamics of a fully quantized parametric amplification process. This consistency leads to identification of the polarization operator (or 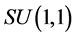 generator)
generator)  as defined in Equation (24a) as the appropriate well-behaved dynamical operator for specifying the conservation law governing the dynamics of a fully quantized parametric amplification process.
as defined in Equation (24a) as the appropriate well-behaved dynamical operator for specifying the conservation law governing the dynamics of a fully quantized parametric amplification process.
Fluctuations of the Polarization Operators
The fluctuations in  and
and  are easily obtained in the form
are easily obtained in the form
 (30a)
(30a)
 (30b)
(30b)
after applying the definitions of fluctuations in the intensities and cross-correlation functions obtained earlier. Application of Equation (26e) in Equations (30a), (30b) gives the final results
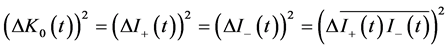 (30c)
(30c)
 (30d)
(30d)
Noting that
 (31a)
(31a)
the second moments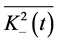 ,
,  and cross-correlation functions
and cross-correlation functions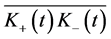 ,
,  are defined by
are defined by
 (31b)
(31b)
 (31c)
(31c)
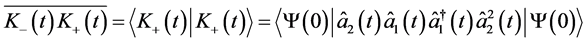 (31d)
(31d)
where Equations (31c), (31d) are noted to define some commonly calculated cross-correlation functions expressed in normal or anti-normal order [1] . Using Equations (28c), (28d) gives
 (31e)
(31e)
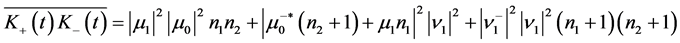 (31f)
(31f)
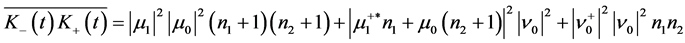 (31g)
(31g)
The fluctuations follow easily in the form
 (32a)
(32a)
 (32b)
(32b)
Finally, the definitions of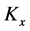 ,
, 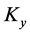 in Equation (24b) easily gives the corresponding fluctuation state vectors, mean values and fluctuations in the respective forms (recalling Equation (31a)).
in Equation (24b) easily gives the corresponding fluctuation state vectors, mean values and fluctuations in the respective forms (recalling Equation (31a)).
 (32c)
(32c)
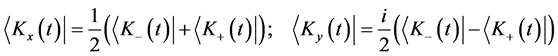 (32d)
(32d)
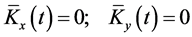 (32e)
(32e)
 (32f)
(32f)
The time evolution of the fluctuations  obtained using Equations (31f), (31g) in Equation (32f) is characterized by fractional revivals as demonstrated in Figure 3.
obtained using Equations (31f), (31g) in Equation (32f) is characterized by fractional revivals as demonstrated in Figure 3.
6. Conclusions
This paper reveals that the internal dynamics of a fully quantized parametric amplification process is characterized by an (anti)-Jaynes-Cummings mode of interaction governing the time evolution of the polarization state vectors of the coupled signal-idler photon pair. The exact analytical solutions obtained in the paper have successfully revealed some uniquely quantum mechanical effects such as the unexpected time variation (non-conservation) of the signal-idler photon number inversion ( ) and the complex form as well as the interference phenomenon characterizing the signal-idler number cross-correlation function under off-resonance dynamics. The physical implication is that the signal and idler photon number operators are not well-behaved operators for studying photon statistics in a fully quantized parametric amplification process. In particular, the time variation of the number inversion and the interference phenomenon mean that the observed simultaneous production of signal and idler photons is not specified by the signal-idler photon number cross-correlations as generally believed. It has been established here that the dynamics is characterized by the polarization states of the coupled signal-idler photon pairs. Polarized signal-idler photon intensity operators and the related polarization operators, which specify the dynamical symmetry group (
) and the complex form as well as the interference phenomenon characterizing the signal-idler number cross-correlation function under off-resonance dynamics. The physical implication is that the signal and idler photon number operators are not well-behaved operators for studying photon statistics in a fully quantized parametric amplification process. In particular, the time variation of the number inversion and the interference phenomenon mean that the observed simultaneous production of signal and idler photons is not specified by the signal-idler photon number cross-correlations as generally believed. It has been established here that the dynamics is characterized by the polarization states of the coupled signal-idler photon pairs. Polarized signal-idler photon intensity operators and the related polarization operators, which specify the dynamical symmetry group ( ) of the system, have been identified as the well-behaved operators for describing photon statistics in the fully quantized (as well as the semi-classical)
) of the system, have been identified as the well-behaved operators for describing photon statistics in the fully quantized (as well as the semi-classical)

Figure 3. Polarization fluctuations 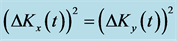 in (32d) over scaled time τ = gt, n = 3, k = 5,
in (32d) over scaled time τ = gt, n = 3, k = 5,  ,
, .
.
parametric amplification processes. The conservation of the positive-negative helicity intensity inversion and the purely real cross-correlation function directly specify the simultaneous production of positive and negative helicity polarized signal and idler photons. The dynamics of the fully quantized parametric amplification process has also been shown to be characterized by the fundamental quantum mechanical phenomenon of fractional revivals when the pump, signal and idler photons are in the initial Fock state. General collapses and revivals (not explicitly included in this paper) emerge when the pump photon is taken in an initial coherent state, as elaborated in [3] .
In general, the exact analytical expressions obtained in this paper provide opportunities for in-depth studies of the statistical properties of fully quantized parametric amplification/down-conversion processes. The concept of fluctuation state vectors, which arises from the evaluation of expectation values of time evolving operators within the Heisenberg picture, constitutes an exact quantum state engineering process [17] and the corresponding density matrices can be used to study the entanglement properties of the fully quantized parametric amplification process. The positive and negative helicity intensity operators, together with the polarization operators, are useful in the construction of intelligent state vectors on an SU(1, 1) manifold [18] . In particular, polarization operators are currently employed in characterization and tomography of photon polarization states, mostly under parametric interactions [19] -[22] . These are important for applications in the design and implementation of quantum information processing, quantum computation, quantum tomography and other quantum-based precision technologies.
Acknowledgements
I thank my colleague Dr. B. O. Ndinya for valuable support in preparation of diagrams. This work was fully supported by Maseno University.
References
- Mandel, L. (1986) Quantum Effects in Spontaneous Parametric Down Conversion of light. In: Pike, E.R. and Sarkar, S., Eds., Frontiers in Quantum Optics, Adam Hilger, Bristol and Boston, 318.
- Nation, P.D. and Blencowe, M.P. (2010) New Journal of Physics, 12, Article ID: 09013.http://dx.doi.org/10.1088/1367-2630/12/9/095013
- Omolo, J.A. (2013) Journal of Modern Optics, 60, 578. http://dx.doi.org/10.1080/09500340.2013.798039
- Jaynes, E.T. and Cummings, F.W. (1963) Proceedings of the IEEE, 51, 89.http://dx.doi.org/10.1109/PROC.1963.1664
- Knight, P.L. and Radmore, P.M. (1982) Physical Review A, 26, 676. http://dx.doi.org/10.1103/PhysRevA.26.676
- Shore, B.W. and Knight, P.L. (1993) Journal of Modern Optics, 40, 195.http://dx.doi.org/10.1080/09500349314551321
- Meystre, P. and Sargent III, M. (1991) Elements of Quantum Optics. Springer-Verlag, Berlin Heidelberg New York.http://dx.doi.org/10.1007/978-3-662-11654-8
- Averbukh, I.Sh. (1992) Physical Review A, 46, R2205. http://dx.doi.org/10.1103/PhysRevA.46.R2205
- Azuma, H. (2009) Application of Abel-Abner Formula for Collapse and Revival of Rabi Oscillations in Jaynes-Cummings Model.
- El-Orany, F.A.A. (2009) Revival-Collapse Phenomenon in the Quadrature Squeezing of the Multiphoton Intensity-Dependent Jaynes-Cummings Model.
- Glauber, R.J. (1986) Amplifiers, Attenuators, and the Quantum Theory of Measurement. In: Pike, E.R. and Sarkar, S., Eds., Frontiers in Quantum Optics, Malvern Physics Series, Adam Hilger, Bristol and Boston, 534.
- Jyotsna, I.V. and Agarwal, G.S. (1997) Journal of Modern Optics, 44, 305-312.http://dx.doi.org/10.1080/09500349708241872
- Drobny, G. and Jex, I. (1992) Physical Review A, 46, 499; (1992) Physical Review A, 45, 1816.http://dx.doi.org/10.1103/PhysRevA.45.1816
- Walls, D.F. and Barakat, R. (1970) Physical Review A, 1, 446; Walls, D.F. and Tindle, C. (1972) Physical Review A: General Physics, 5, 534. http://dx.doi.org/10.1088/0305-4470/5/4/010
- Hillery, M. (2009) Acta Physica Slovaca, 59, 1-80. http://dx.doi.org/10.2478/v10155-010-0094-8
- Omolo, J.A. (2008) PRAMANA-Journal of Physics, 71, 1311.
- Dell’Anno, F., et al. (2006) Physics Reports, 428, 53-168. http://dx.doi.org/10.1016/j.physrep.2006.01.004
- Joanis, P. (2010) Journal of Physics A: Mathematical and Theoretical, 43, Article ID: 385304.http://dx.doi.org/10.1088/1751-8113/43/38/385304
- Bjork, G., et al. (2012) Physical Review A, 85, Article ID: 053835. http://dx.doi.org/10.1103/PhysRevA.85.053835
- Soderholm, J., et al. (2012) New Journal of Physics, 14, Article ID: 115014.http://dx.doi.org/10.1088/1367-2630/14/11/115014
- Schilling, U., et al. (2010) Physical Review A, 81, Article ID: 013826. http://dx.doi.org/10.1103/PhysRevA.81.013826
- Wolf, E. (2008) Optics Letters, 33, 642. http://dx.doi.org/10.1364/OL.33.000642

