Journal of Modern Physics
Vol. 4 No. 5 (2013) , Article ID: 31935 , 25 pages DOI:10.4236/jmp.2013.45094
Discrete Symmetry in Relativistic Quantum Mechanics
1Department of Physics, Portland State University, Portland, USA
2Department of Physics, Fudan University, Shanghai, China
Email: pdx01018@pdx.edu, suqing_chen@yahoo.com, xujj@fudan.edu.cn
Copyright © 2013 Guang-jiong Ni et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 24, 2013; revised March 25, 2013; accepted April 18, 2013
Keywords: CPT Invariance; Antiparticle; Quantum Mechanics; Quantum Field Theory
ABSTRACT
EPR experiment on 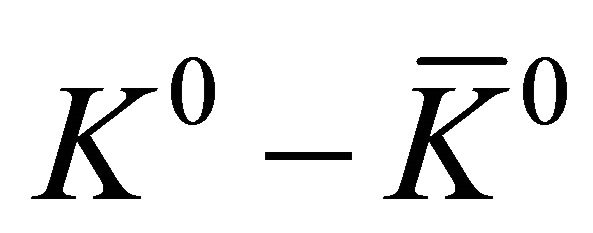 system in 1998 [1] strongly hints that one should use operators
system in 1998 [1] strongly hints that one should use operators 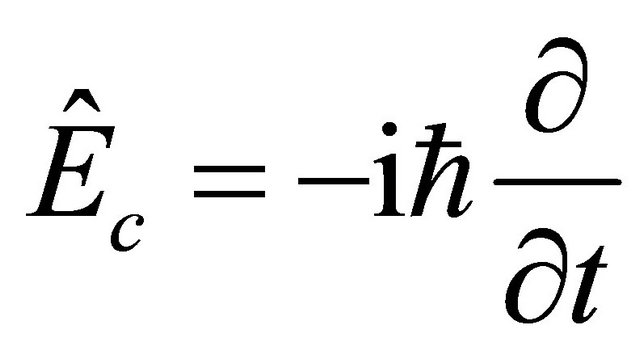 and
and 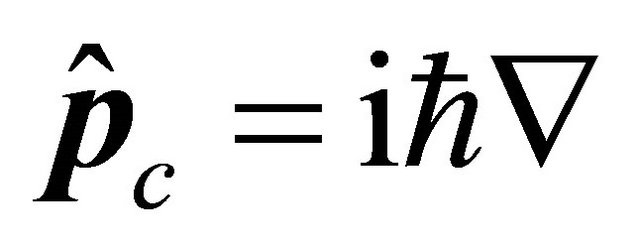 for the wavefunction (WF) of antiparticle. Further analysis on Klein-Gordon (KG) equation reveals that there is a discrete symmetry hiding in relativistic quantum mechanics (RQM) that
for the wavefunction (WF) of antiparticle. Further analysis on Klein-Gordon (KG) equation reveals that there is a discrete symmetry hiding in relativistic quantum mechanics (RQM) that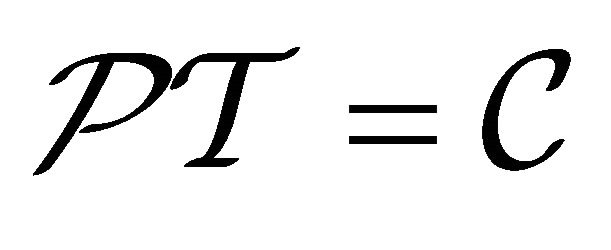 . Here
. Here ![]() means the (newly defined) combined space-time inversion (with
means the (newly defined) combined space-time inversion (with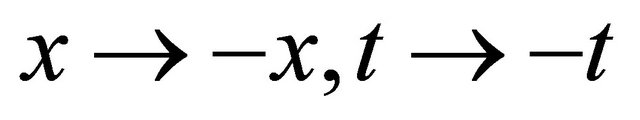 ), while
), while ![]() the transformation of WF
the transformation of WF 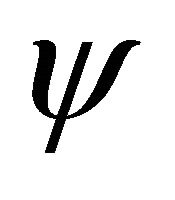 between particle and its antiparticle whose definition is just residing in the above symmetry. After combining with FeshbachVillars (FV) dissociation of KG equation
between particle and its antiparticle whose definition is just residing in the above symmetry. After combining with FeshbachVillars (FV) dissociation of KG equation 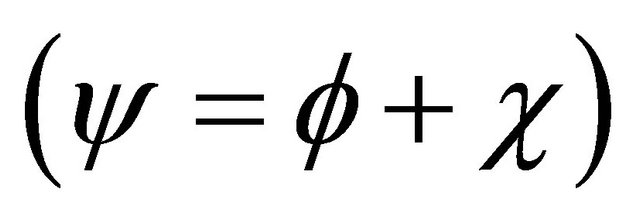 [2], this discrete symmetry can be rigorously reformulated by the invariance of coupling equation of
[2], this discrete symmetry can be rigorously reformulated by the invariance of coupling equation of  and
and 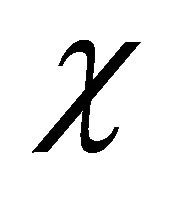 under either the combined space-time inversion
under either the combined space-time inversion ![]() or the mass inversion
or the mass inversion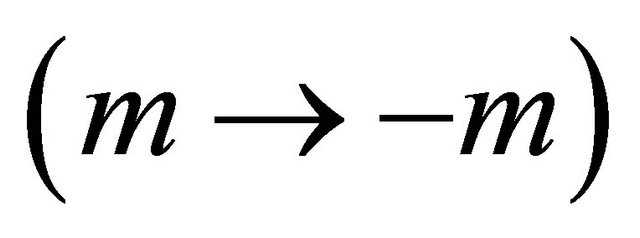 , which makes the KG equation a self-consistent theory. Dirac equation is also discussed accordingly. Various applications of this discrete symmetry are discussed, including the prediction of antigravity between matter and antimatter as well as the reason why we believe neutrinos are likely the tachyons.
, which makes the KG equation a self-consistent theory. Dirac equation is also discussed accordingly. Various applications of this discrete symmetry are discussed, including the prediction of antigravity between matter and antimatter as well as the reason why we believe neutrinos are likely the tachyons.
1. Introduction
In 1956-1957, the historical discovery of the parity violation [3-6] reveals that both P and C symmetries are violated to maximum in weak interactions. Then in 1964- 1970, both CP and T are experimentally verified to be violated in some cases (though to a tiny degree) [7,8] whereas the product symmetry CPT holds intact to this day [9]. The CPT invariance in quantum field theory (QFT) was first proved by Lüders and Pauli in 1954- 1957 [10-12] via the introduction of the “strong reflection” for proving the CPT theorem. In 1965, Lee and Wu proposed that the definition of particle 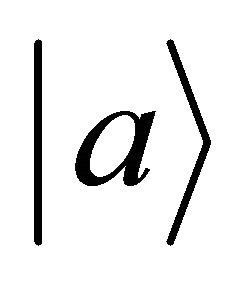 versus its antiparticle
versus its antiparticle 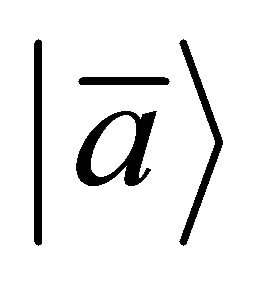 should be [13]
should be [13]
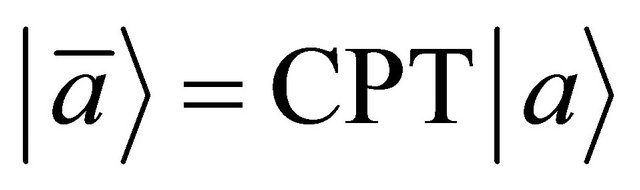 (1.1)
(1.1)
Regrettably, the counterpart of “strong reflection” at the level of RQM went nearly unnoticed in the past decades. In this paper, we are going to study the RQM thoroughly. Not only a discrete symmetry 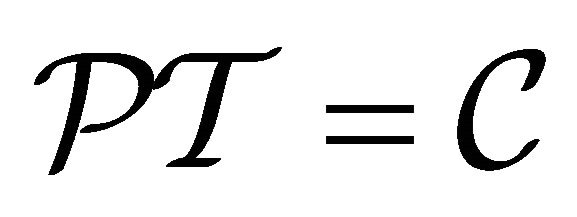 is found in RQM as the counterpart of “strong reflection” in QFT, it is also evolved into the invariance of space-time inversion
is found in RQM as the counterpart of “strong reflection” in QFT, it is also evolved into the invariance of space-time inversion 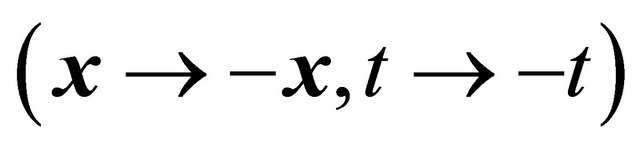 or mass inversion
or mass inversion 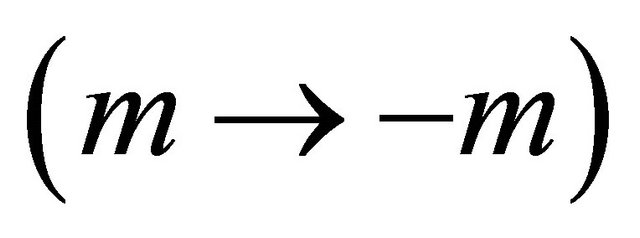 , showing that a WF in RQM is always composed of two parts in confrontation inside a particle and then RQM becomes a self-consistent theory. Furthermore, this symmetry can serve as a “theoretical tool” in searching for new applications in today’s physics.
, showing that a WF in RQM is always composed of two parts in confrontation inside a particle and then RQM becomes a self-consistent theory. Furthermore, this symmetry can serve as a “theoretical tool” in searching for new applications in today’s physics.
The organization of this paper is as follows: In section II, the EPR paradox [14] is discussed together with the 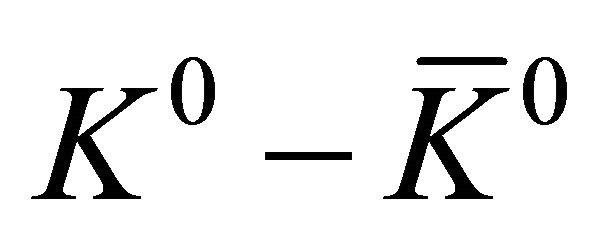 correlation experimental data [1], yielding a strong hint that the energy-momentum operators for antiparticle’s WF should be
correlation experimental data [1], yielding a strong hint that the energy-momentum operators for antiparticle’s WF should be 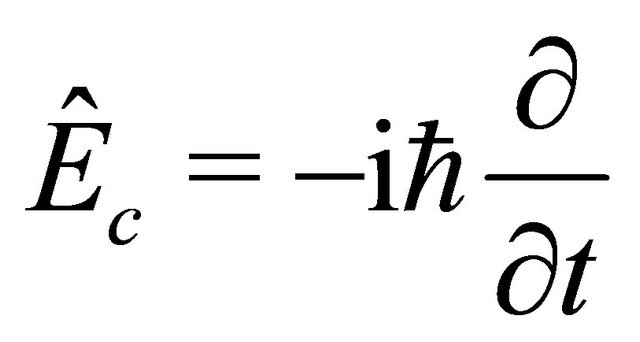 and
and 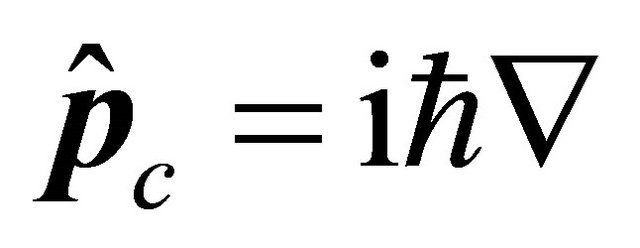 respectively. Section III is focused on a discrete symmetry
respectively. Section III is focused on a discrete symmetry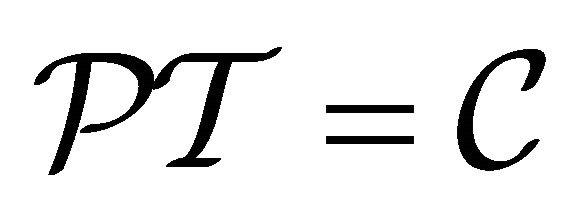 , here
, here  means the (newly defined) combined space-time inversion (with
means the (newly defined) combined space-time inversion (with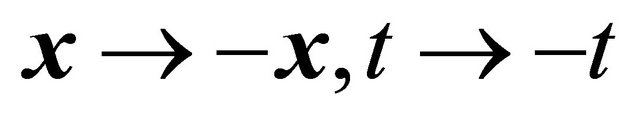 ), while
), while ![]() the transformation of WFs between particle and antiparticle, whose definition is just residing in the symmetry. Then after combining with FV dissociation of KG equation [2] in which the WF
the transformation of WFs between particle and antiparticle, whose definition is just residing in the symmetry. Then after combining with FV dissociation of KG equation [2] in which the WF 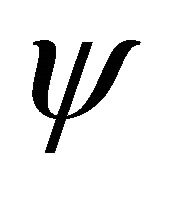 is composed of two fields:
is composed of two fields: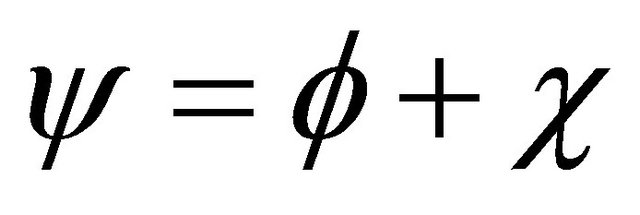 , the above symmetry can be realized in terms of
, the above symmetry can be realized in terms of  and
and 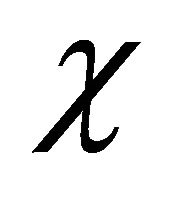 rigorously via the invariance of their coupling equation either under the spacetime inversion or a mass inversion
rigorously via the invariance of their coupling equation either under the spacetime inversion or a mass inversion 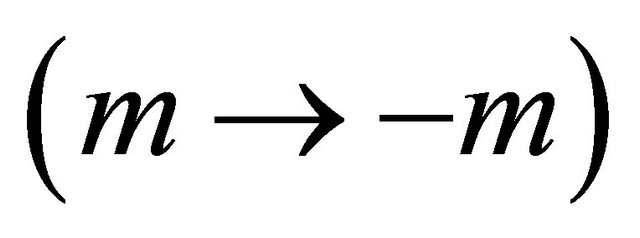 In this way, the probability density is ensured to be positive definite for WFs of either particle or antiparticle. Section IV ascribes various phenomena in the theory of special relativity (SR) to the effects of enhancement of the hidden
In this way, the probability density is ensured to be positive definite for WFs of either particle or antiparticle. Section IV ascribes various phenomena in the theory of special relativity (SR) to the effects of enhancement of the hidden 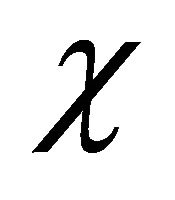 field in a moving particle. In Section V, Dirac equation is discussed accordingly with the importance of helicity being stressed. Section VI contains a brief discussion on the QFT. Sections VII, VIII and IX are devoting to seek for possible applications of the above symmetry in today’s physical problems: Why a parity violation phenomenon was overlooked since 1956-1957? Why we believe neutrinos are likely the tachyons? And the prediction of antigravity between matter and antimatter. The last Section X contains a summary. In the Appendix, the Klein paradox is solved for both KG equation and Dirac equation without resorting to the “hole theory”.
field in a moving particle. In Section V, Dirac equation is discussed accordingly with the importance of helicity being stressed. Section VI contains a brief discussion on the QFT. Sections VII, VIII and IX are devoting to seek for possible applications of the above symmetry in today’s physical problems: Why a parity violation phenomenon was overlooked since 1956-1957? Why we believe neutrinos are likely the tachyons? And the prediction of antigravity between matter and antimatter. The last Section X contains a summary. In the Appendix, the Klein paradox is solved for both KG equation and Dirac equation without resorting to the “hole theory”.
2. What the 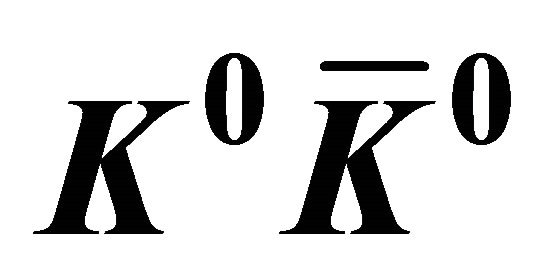 Correlation Experimental Data Are Telling?
Correlation Experimental Data Are Telling?
To our knowledge, beginning from Bohm and Bell [15,16], physicists gradually turned their research of EPR paradox [14] onto the entangled state composed of electrons, especially photons with spin and achieved fruitful results. However, as pointed out by Guan (1935-2007), EPR’s paper [14] is focused on two spinless particles and Guan found that there is a commutation relation hiding in such a system as follows [17]:
Consider two particles in one dimensional space with positions 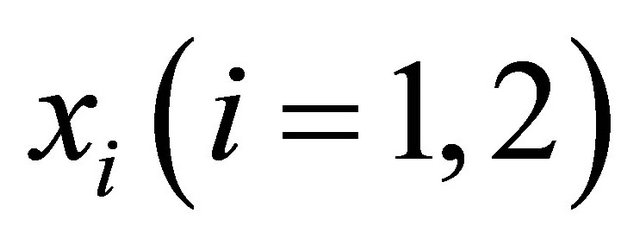 and momentum operators
and momentum operators
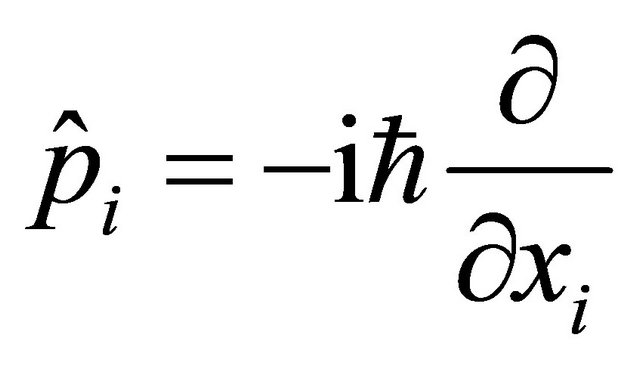 . Then a commutation relation arises as
. Then a commutation relation arises as
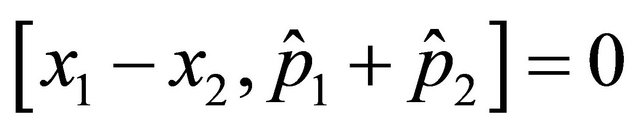 (2.1)
(2.1)
According to QM’s principle, there may be a kind of common eigenstate having eigenvalues of these two commutative (i.e., compatible)observables like:
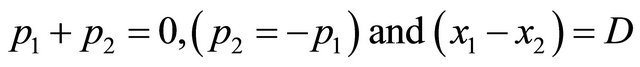 (2.2)
(2.2)
with D being their distance. The existence of such kind of eigenstate described by Equation (2.2) puzzled Guan, he asked: “How can such kind of quantum state be realized?” A discussion between Guan and one of present authors (Ni) in 1998 led to a paper [18].
Here we are going to discuss further, showing that the correlation experiment on a 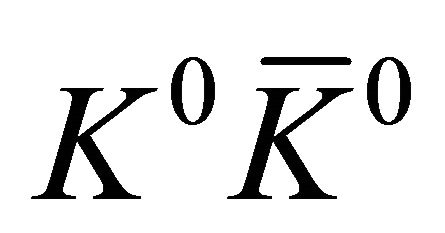 system (which just realized an entangled state composed of two spinless particles) in 1998 by CPLEAR collaboration [1] actually revealed some important features of QM and then answered the puzzle raised by EPR in a surprising way. First, besides Equation (1), let us consider another three commutation relations simultaneously:
system (which just realized an entangled state composed of two spinless particles) in 1998 by CPLEAR collaboration [1] actually revealed some important features of QM and then answered the puzzle raised by EPR in a surprising way. First, besides Equation (1), let us consider another three commutation relations simultaneously:
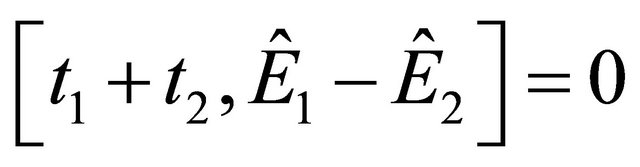 (2.3)
(2.3)
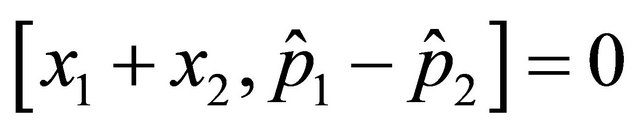 (2.4)
(2.4)
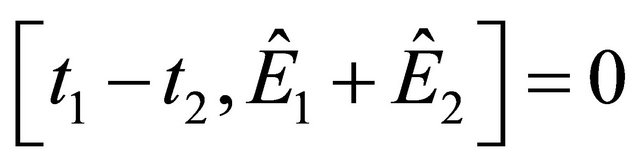 (2.5)
(2.5)
(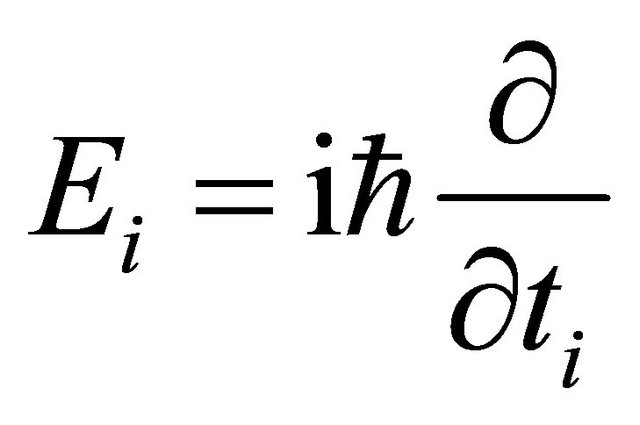 with
with 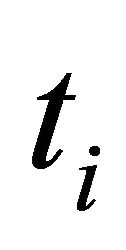 being the time during which the i-th particle is detected). In accordance with Ref. [1], we also focus on back-to-back events. The evolution of
being the time during which the i-th particle is detected). In accordance with Ref. [1], we also focus on back-to-back events. The evolution of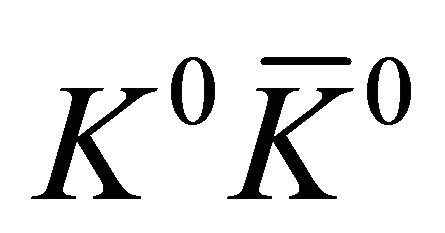 ’s wavefunction (WF) will be considered in three inertial frames: The center-of-mass system S is at rest in laboratory with its origin x = 0 located at the apparatus’ center, where the antiprotons’ beam is stopped inside a hydrogen gas target to create
’s wavefunction (WF) will be considered in three inertial frames: The center-of-mass system S is at rest in laboratory with its origin x = 0 located at the apparatus’ center, where the antiprotons’ beam is stopped inside a hydrogen gas target to create 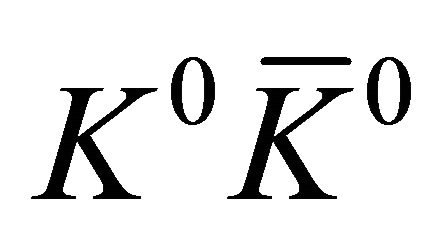 pairs by
pairs by 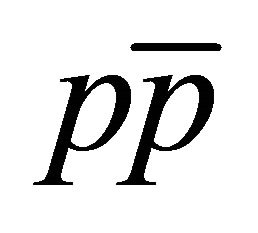 annihilation. The
annihilation. The 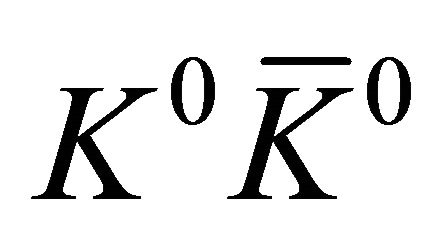 pairs are detected by a cylindrical tracking detector located inside a solenoid providing a magnetic field parallel to the antiprotons’ beam. For back-to-back events, the space-time coordinates in Equations (1)-(5) refer to particles moving to the right
pairs are detected by a cylindrical tracking detector located inside a solenoid providing a magnetic field parallel to the antiprotons’ beam. For back-to-back events, the space-time coordinates in Equations (1)-(5) refer to particles moving to the right 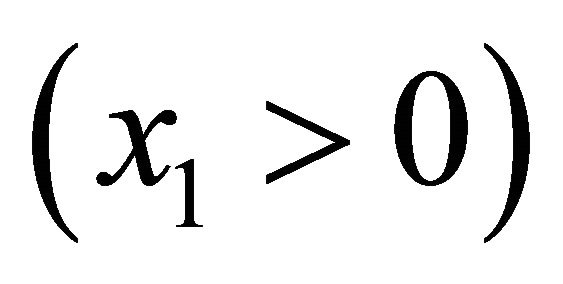 and left
and left 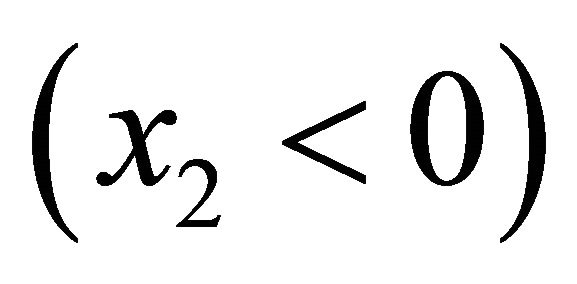 respectively. Second, we take an inertial system
respectively. Second, we take an inertial system 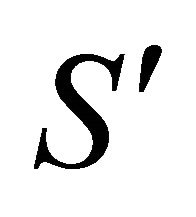 with its origin located at particle 1 (i.e.,
with its origin located at particle 1 (i.e.,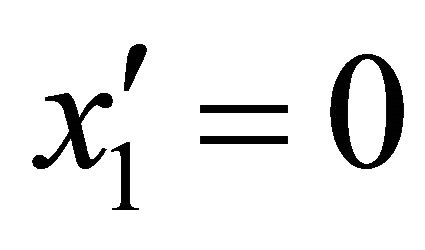 ).
). 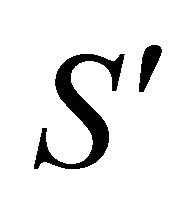 is moving in a uniform velocity
is moving in a uniform velocity ![]() with respect to
with respect to![]() . (For Kaon’s momentum of
. (For Kaon’s momentum of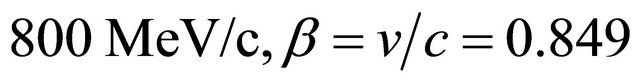 ). Another
). Another 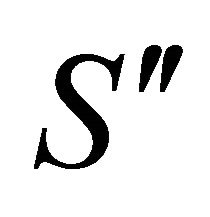 system is chosen with its origin located at particle
system is chosen with its origin located at particle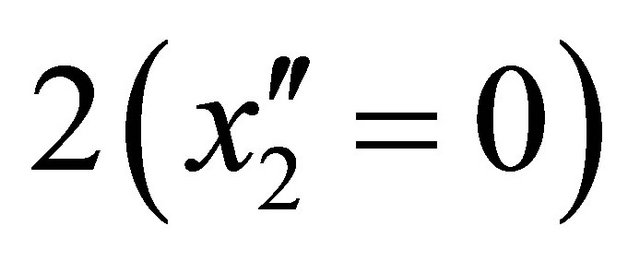 .
.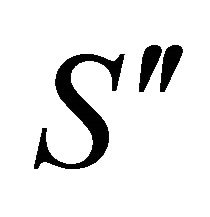 is moving in a velocity
is moving in a velocity 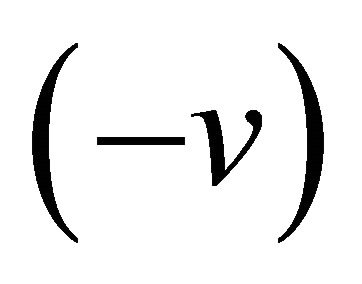 with respect to
with respect to![]() . Thus we have Lorentz transformation among the space-time coordinates being
. Thus we have Lorentz transformation among the space-time coordinates being
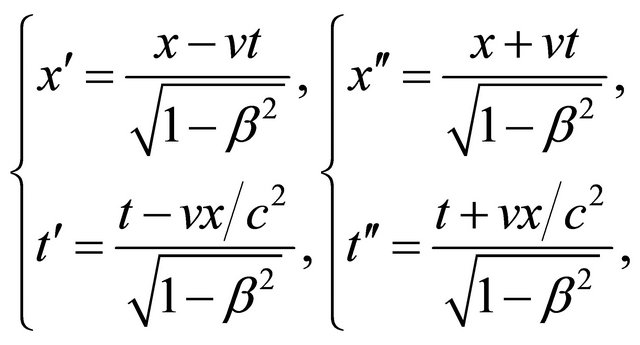 (2.6)
(2.6)
Here 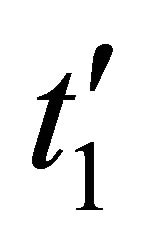 and
and ![]() correspond to the proper time
correspond to the proper time ![]() and
and ![]() in Ref.[1] respectively. The common time origin
in Ref.[1] respectively. The common time origin 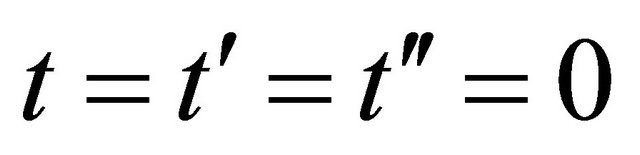 is adopted.
is adopted.
A 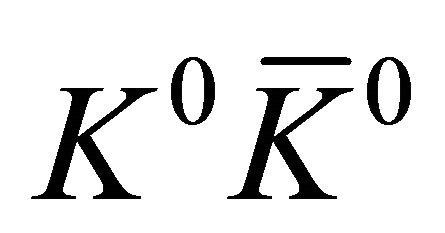 pair, created in a
pair, created in a  antisymmetric state, can be described by a two-body WF depending on time as ([1], see also [19,20])
antisymmetric state, can be described by a two-body WF depending on time as ([1], see also [19,20])
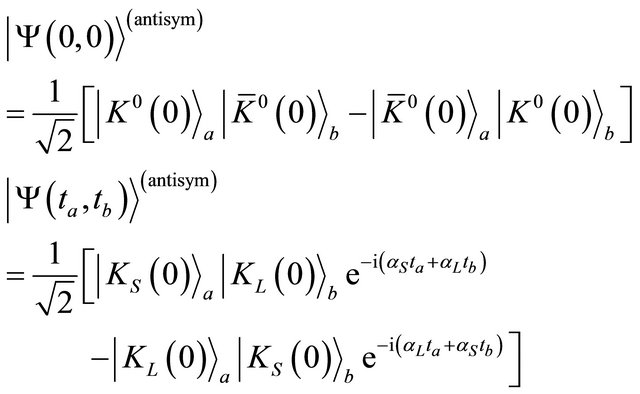 (2.7)
(2.7)
with
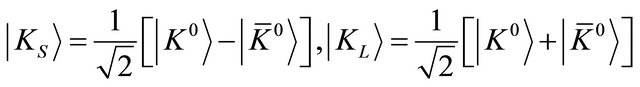 (2.8)
(2.8)
where the CP violation has been neglected and
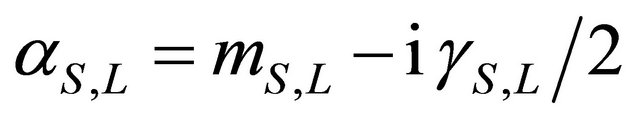 ,
, ![]() and
and 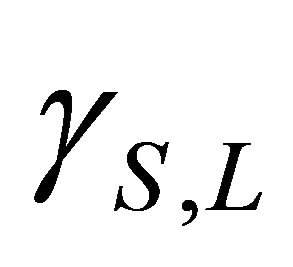 being the
being the  masses and decay widths, respectively. From Equation (7), the intensities of events with like-strangeness (
masses and decay widths, respectively. From Equation (7), the intensities of events with like-strangeness (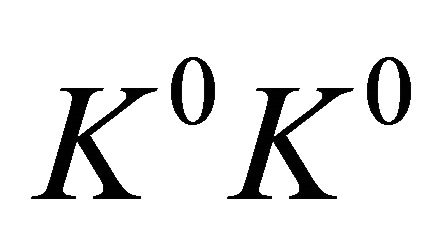 or
or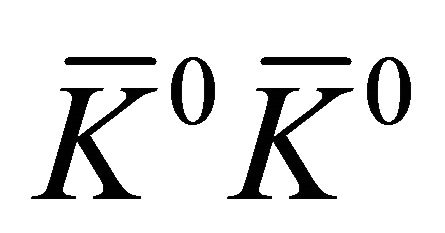 ) and unlike-strangeness (
) and unlike-strangeness (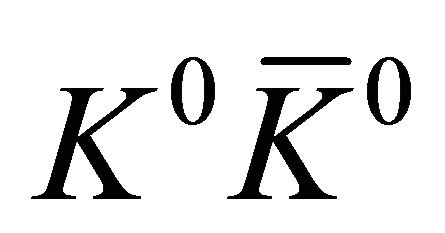 or
or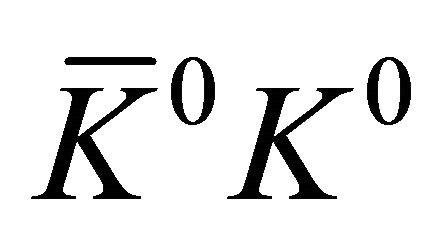 ) can be evaluated as
) can be evaluated as
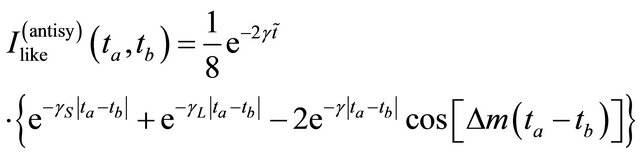 (2.9)
(2.9)
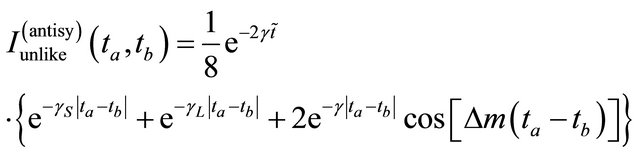 (2.10)
(2.10)
where 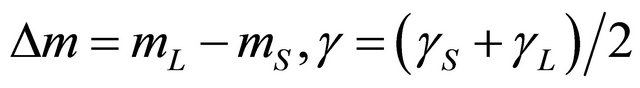 and
and
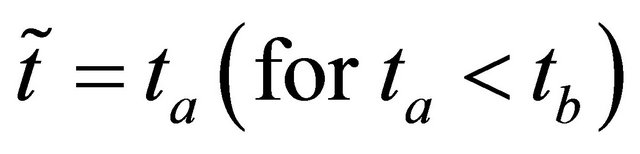 or
or .
.
Similarly, for 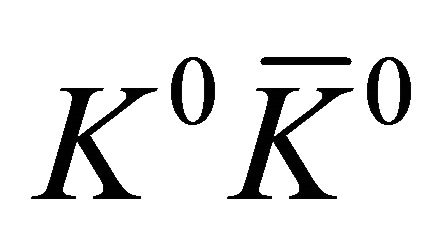 created in a
created in a  or
or  symmetric state as:
symmetric state as:
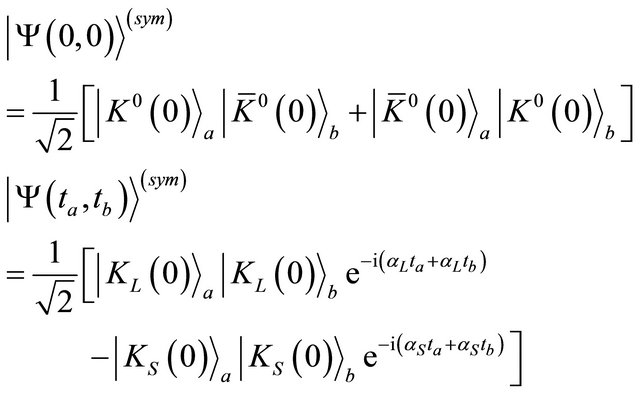 (2.11)
(2.11)
the predicted intensities read
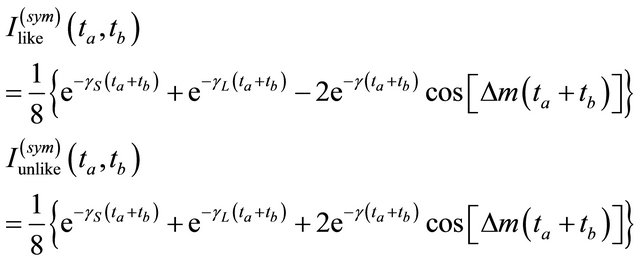
(2.12)
The experiment [1] reveals that the  pairs are mainly created in the antisymmetric state shown by Equations (2.9) and (2.10) while the contribution in a symmetric state shown by Equations (2.11) and (2.12) accounts for 7.4%.
pairs are mainly created in the antisymmetric state shown by Equations (2.9) and (2.10) while the contribution in a symmetric state shown by Equations (2.11) and (2.12) accounts for 7.4%.
What we learn from Ref. [1] in combination with Equations (2.1)-(2.5) are as follows:
(a) Because only back-to-back events are involved in the ![]() system, we denote three commutative operators as: the “distance” operator
system, we denote three commutative operators as: the “distance” operator
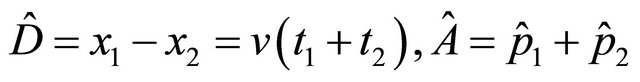 and
and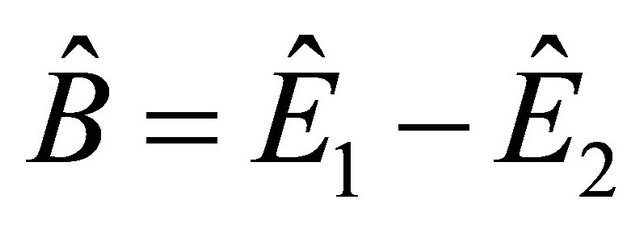 , Equations (2.1) and (2.3) read
, Equations (2.1) and (2.3) read
 (2.13)
(2.13)
So they may have a kind of common eigenstate during the measurement composed of 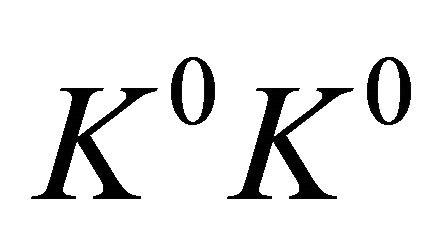 and projected from the symmetric state shown by Equation (11). It is assigned by a continuous eigenvalue
and projected from the symmetric state shown by Equation (11). It is assigned by a continuous eigenvalue  (with continuous index
(with continuous index ) of operator
) of operator 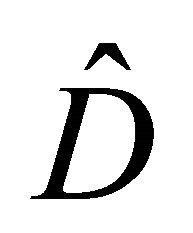 acting on the WF,
acting on the WF, 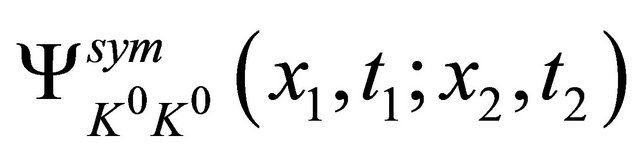 , as1
, as1
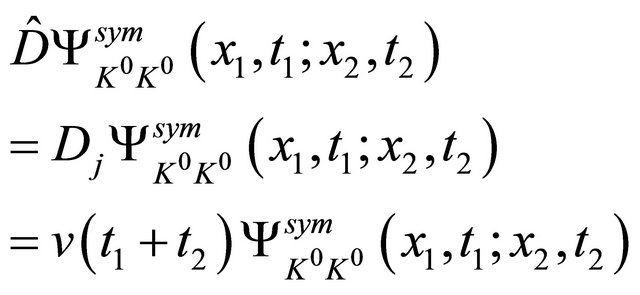 (2.14a)
(2.14a)
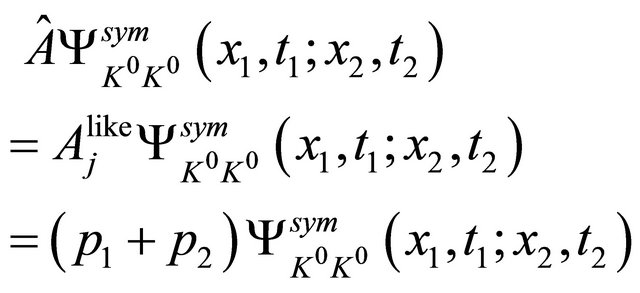 (2.15)
(2.15)
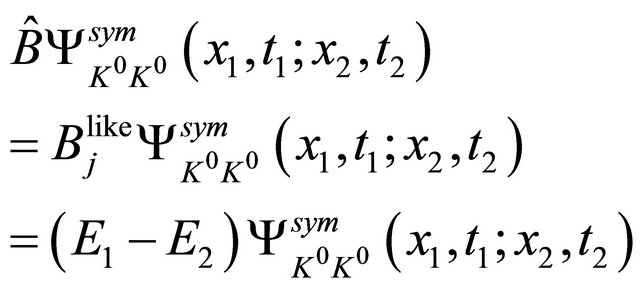 (2.16)
(2.16)
where the lowest eigenvalue of  is
is
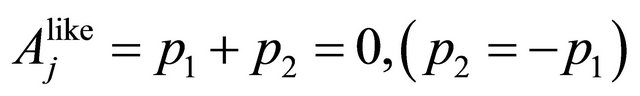 , and that of
, and that of  is
is
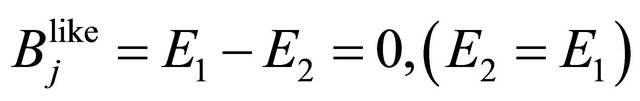 respectively. These eigenstates of like-strangeness events predicted by Equation (11) are really observed in the experiment [1] (these eigenstates of
respectively. These eigenstates of like-strangeness events predicted by Equation (11) are really observed in the experiment [1] (these eigenstates of  were overlooked in the Ref. [18]).
were overlooked in the Ref. [18]).
(b) The more interesting case occurs for 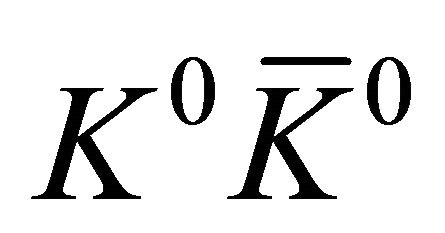 pair created in the antisymmetric state with intensity given by Equation (10) being a function of
pair created in the antisymmetric state with intensity given by Equation (10) being a function of 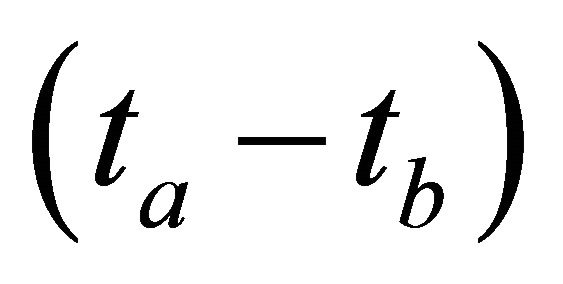 (not
(not 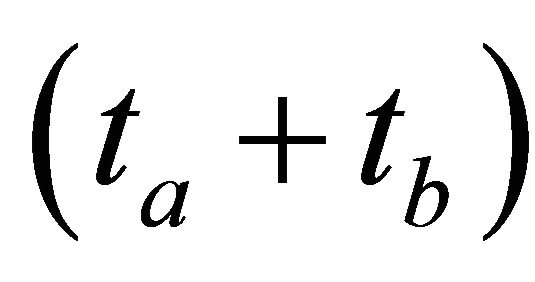 as shown by Equation (12) for symmetric states)
as shown by Equation (12) for symmetric states)
which is proportional to 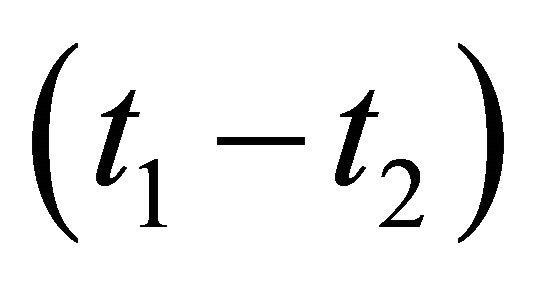 in the S system. In the EPR limit
in the S system. In the EPR limit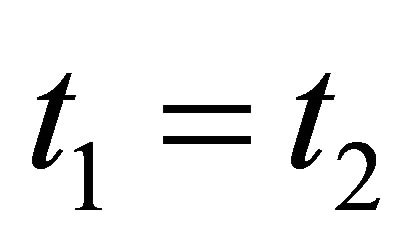 ,
, 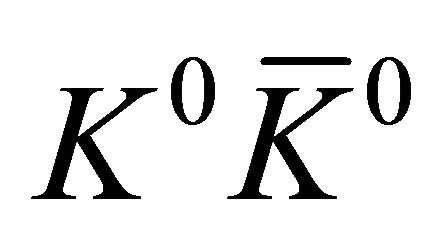 events dominate whereas likestrangeness events are strongly suppressed as shown by Equation (9) (see Figure 1 in [1]). So the experimental facts remind us of the possibility that
events dominate whereas likestrangeness events are strongly suppressed as shown by Equation (9) (see Figure 1 in [1]). So the experimental facts remind us of the possibility that 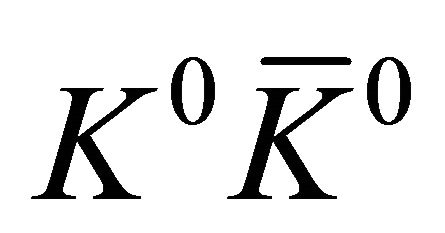 events may be related to common lowest (zero) eigenvalues of some commutative operators (just like what happened in Equations (15) and (16) for operators
events may be related to common lowest (zero) eigenvalues of some commutative operators (just like what happened in Equations (15) and (16) for operators  and
and  (which are applied to symmetric states (due to
(which are applied to symmetric states (due to
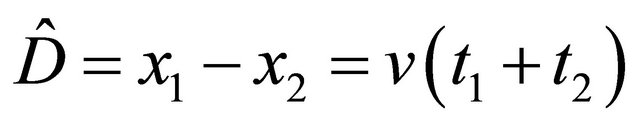 ) but are not suitable for antisymmetric states), there are another three operators shown by Equations (4) and (5) being: the operator of “flight-path difference”
) but are not suitable for antisymmetric states), there are another three operators shown by Equations (4) and (5) being: the operator of “flight-path difference” 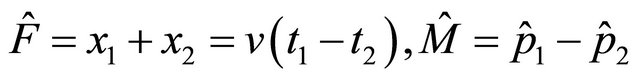 and
and
 with commutation relations as:
with commutation relations as:
 (2.17)
(2.17)
which are just suitable for antisymmetric states. For 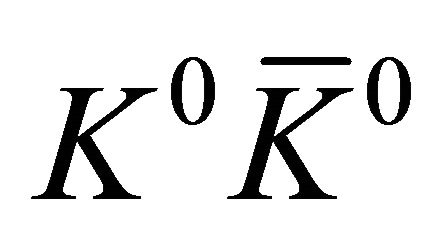 back-to-back events, assume that one of two particles, say 2, is an antiparticle with its momentum and energy operators being
back-to-back events, assume that one of two particles, say 2, is an antiparticle with its momentum and energy operators being
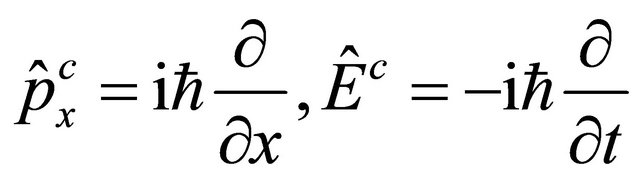 (2.18)
(2.18)
(the superscript ![]() means “antiparticle”) versus that for particle being
means “antiparticle”) versus that for particle being
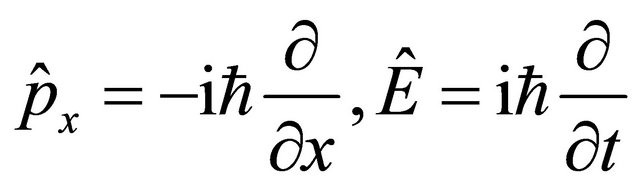 (2.19)
(2.19)
For instance, a freely moving particle’s WF reads2:
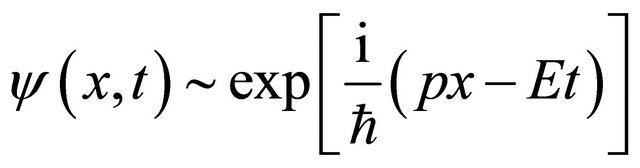 (2.20)
(2.20)
whereas
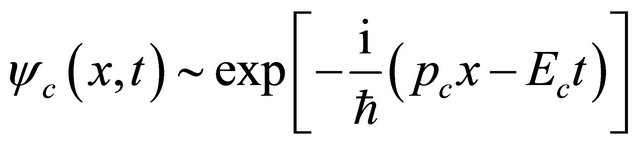 (2.21)
(2.21)
for its antiparticle with 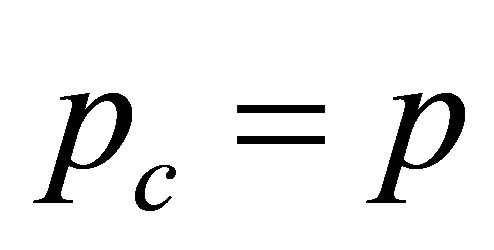 and
and 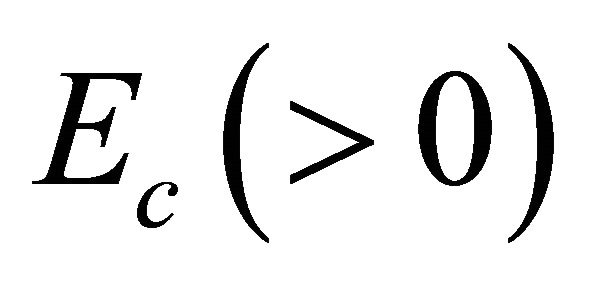 being momentum and energy of the antiparticle in accordance with Equation (2.18). If using Equations (2.18)-(2.21), we find
being momentum and energy of the antiparticle in accordance with Equation (2.18). If using Equations (2.18)-(2.21), we find
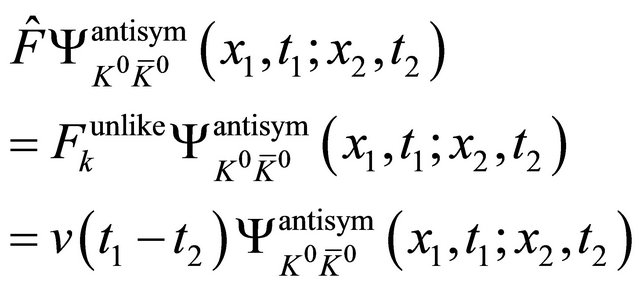 (2.22)
(2.22)
with continuous index 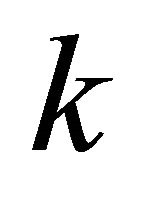 referring to continuous eigenvalues
referring to continuous eigenvalues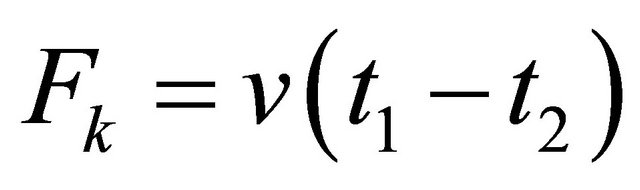 . Here, the WF in space-time of this system during measurement reads approximately:
. Here, the WF in space-time of this system during measurement reads approximately:
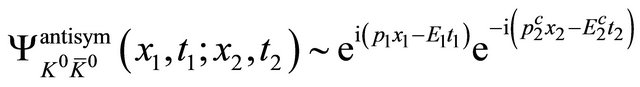 (2.23)
(2.23)
with antiparticle 2 moving opposite to particle 1 and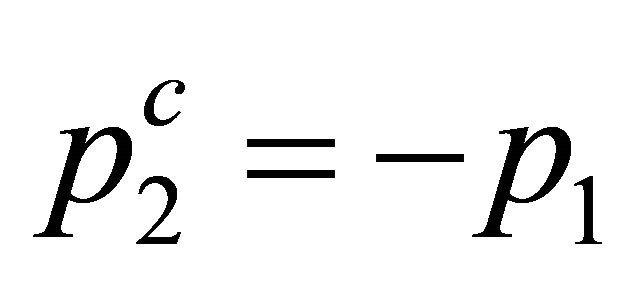 .
.
Now we use 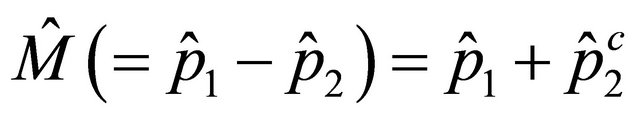 on
on 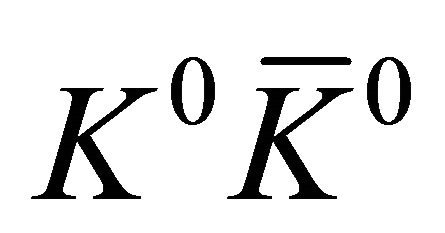 system, yielding
system, yielding
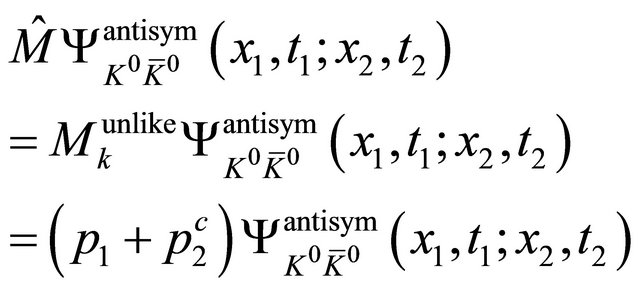 (24)
(24)
Similarly, we have 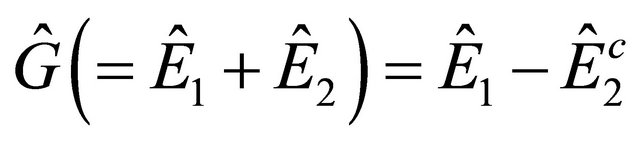 and find
and find
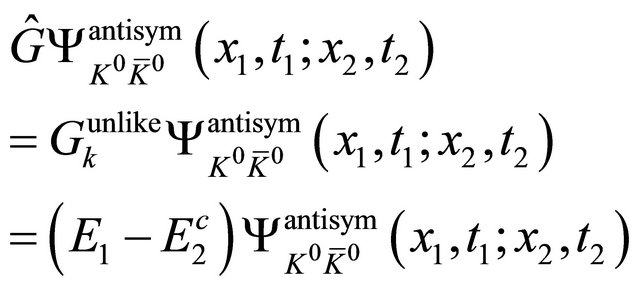 (25)
(25)
Hence we see that once Equations (2.18) and (2.21)
are accepted, the WFs 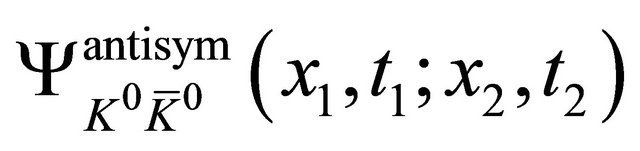 show up in experiments as the only WFs with strongest intensity at the EPR limit
show up in experiments as the only WFs with strongest intensity at the EPR limit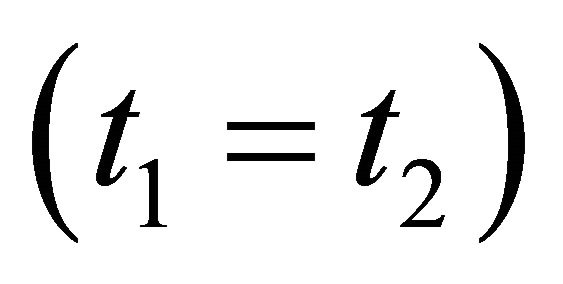 corresponding to their three eigenvalues being all zero:
corresponding to their three eigenvalues being all zero: 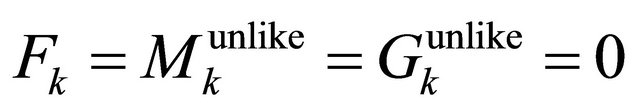 and they won’t change even when accelerator’s energies are going up.
and they won’t change even when accelerator’s energies are going up.
If using Equation (2.18), the eigenvalues of  and
and
 for the WF
for the WF 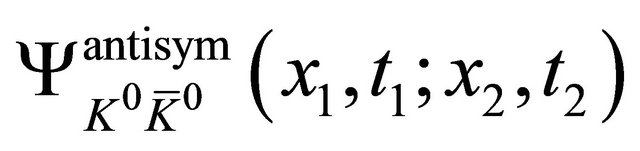 are
are
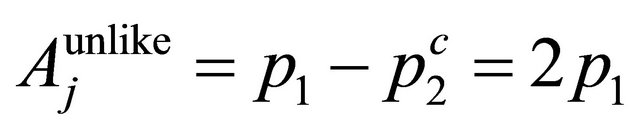 and
and 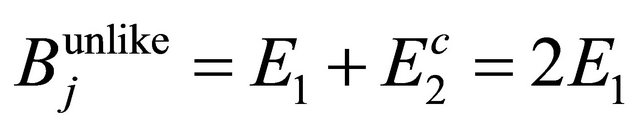 respectively, while that of
respectively, while that of  and
and 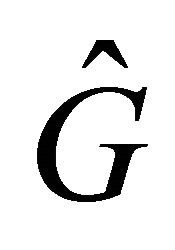 for the WF
for the WF
 are
are 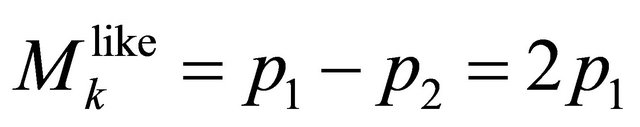 and
and
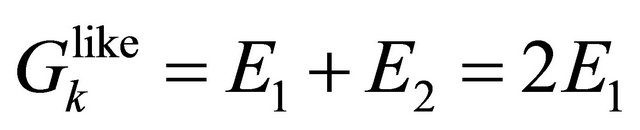 , respectively, those eigenvalues are much higher than zero and going up with the accelerator’s energy.
, respectively, those eigenvalues are much higher than zero and going up with the accelerator’s energy.
Something is very interesting here: If we deny Equation (2.18) but insist on unified operators ![]() and
and  for both particle and antiparticle, there would be no difference in eigenvalues between like-strangeness events and unlike-strangeness ones. For example, the
for both particle and antiparticle, there would be no difference in eigenvalues between like-strangeness events and unlike-strangeness ones. For example, the 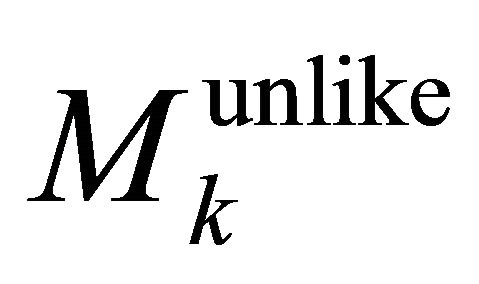 and
and 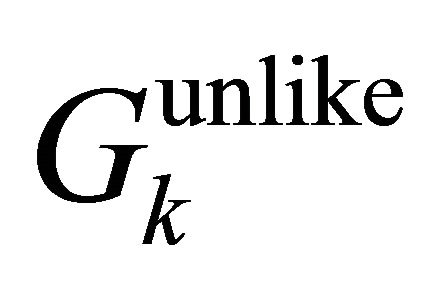 would be
would be 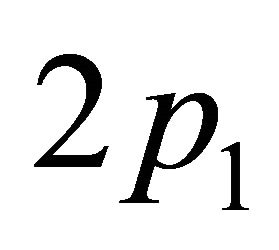 and
and 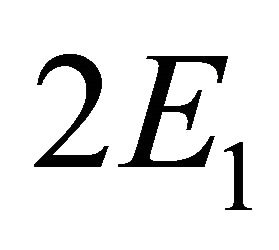 too (instead of “0” as in Equations (2.24) and (2.25)). This would mean that three commutative operators
too (instead of “0” as in Equations (2.24) and (2.25)). This would mean that three commutative operators 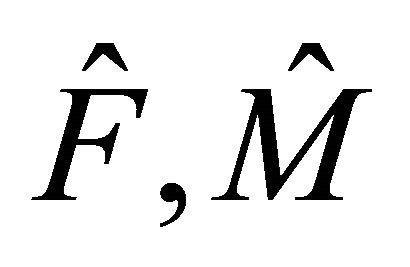 and
and 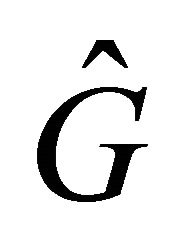 are not enough to distinguish the WF
are not enough to distinguish the WF 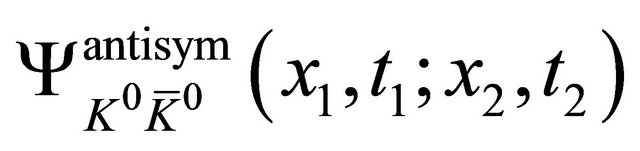 from the WF
from the WF 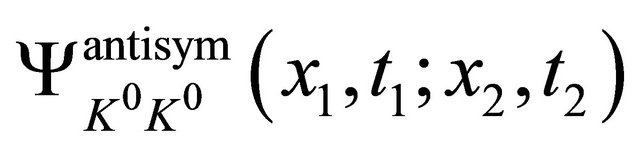 even they behave so differently as shown by Equations (9) and (10)), especially at the EPR limit
even they behave so differently as shown by Equations (9) and (10)), especially at the EPR limit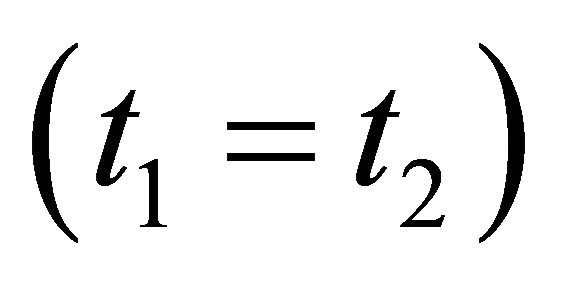 .
.
Equation (2.18) together with the identification of WF
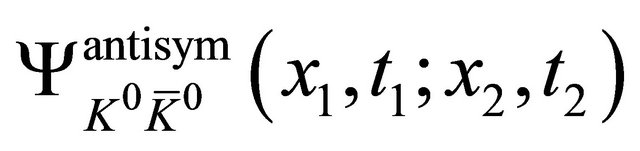 by three zero eigenvalues implies that the difference of a particle from its antiparticle is not something hiding in the “intrinsic space” like opposite charge (for electron and positron) or opposite strangeness (for
by three zero eigenvalues implies that the difference of a particle from its antiparticle is not something hiding in the “intrinsic space” like opposite charge (for electron and positron) or opposite strangeness (for 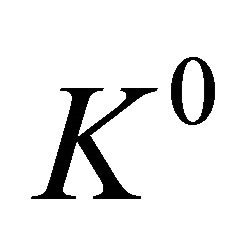 and
and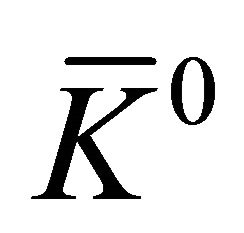 ) but can be displayed in their WFs evolving in space-time at the level of QM.
) but can be displayed in their WFs evolving in space-time at the level of QM.
In summary, instead of one set of WF with its operators (Equations (2.19) and (2.20)), two sets of WFs with operators separately (shown as Equations (2.18)- (2.21)) are strongly supported by the original EPR paradox and its “solution” provided by the 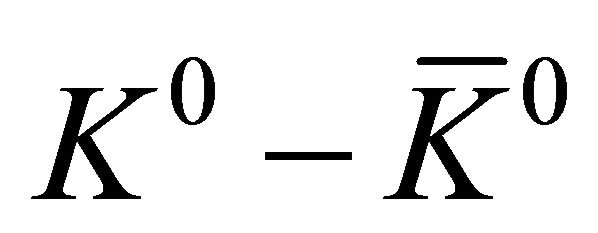 experiment.
experiment.
To our knowledge, Equation (2.18) can be found at a page note of a paper by Konopinski and Mahmaud in 1953 [21], also appears in Refs. [18,22-28].
3. How to Make Klein-Gordon Equation a Self-Consistent Theory in RQM? A Discrete Symmetry
3.1. The Negative Energy Solution and the WF of Antiparticle
Let us begin with the energy conservation law for a particle in classical mechanics:
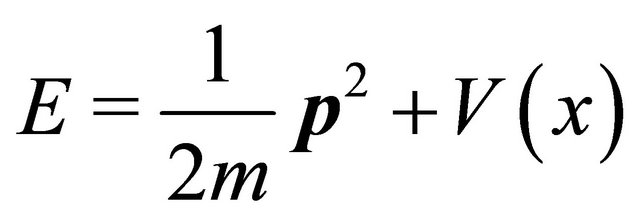 (3.1)
(3.1)
Consider the rule promoting observables into operators:
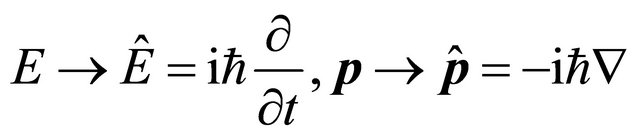 (3.2)
(3.2)
and let Equation (3.1) act on a wavefunction (WF)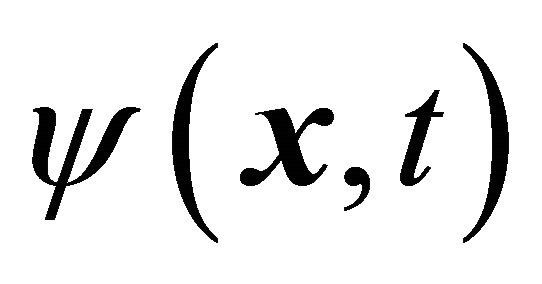 , the Schrödinger equation
, the Schrödinger equation
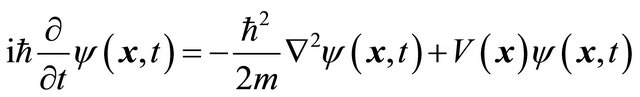 (3.3)
(3.3)
follows immediately. In mid 1920’s, considering the kinematical relation for a particle in the theory of special relativity (SR):
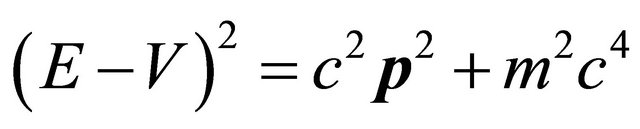 (3.4)
(3.4)
and using Equation (3.2) again, the Klein-Gordon (KG) equation was established as:
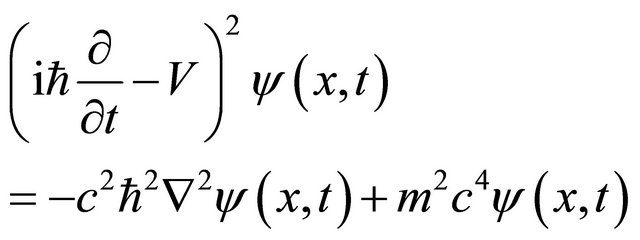 (3.5)
(3.5)
For a free KG particle, its plane-wave solution reads:
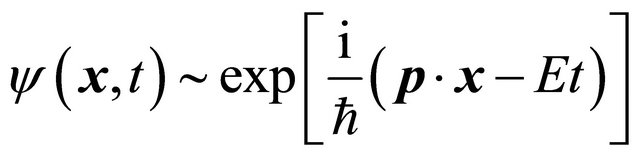 (3.6)
(3.6)
However, two difficulties arose:
(a) The energy E in Equation (6) has two eigenvalues:
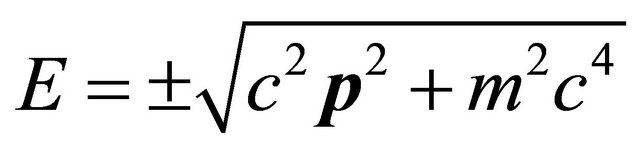 (3.7)
(3.7)
In general, 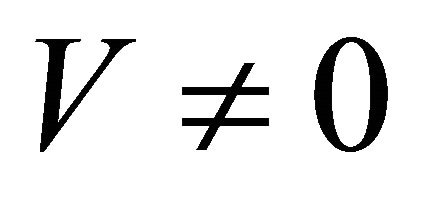 , the WFs of KG particle’s energy eigenstates can always be divided into two parts:
, the WFs of KG particle’s energy eigenstates can always be divided into two parts:
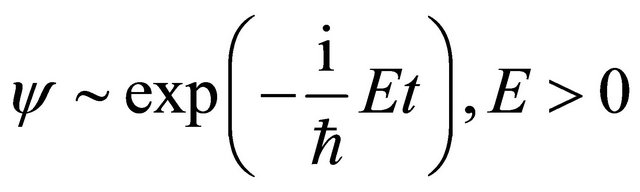 (3.8)
(3.8)
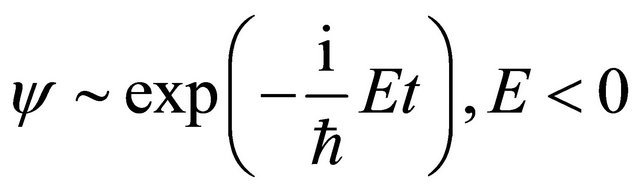 (3.9)
(3.9)
where only the original operators Equation (3.2) are used. But what the “negative energy” means?
(b) The continuity equation is derived from Equation (5) as
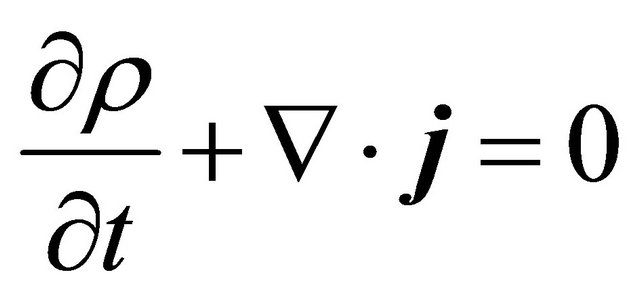 (3.10)
(3.10)
where
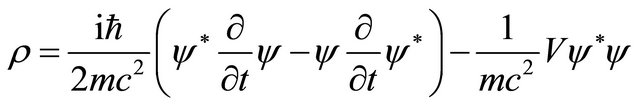 (3.11)
(3.11)
and
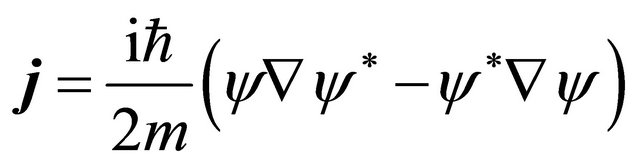 (3.12)
(3.12)
are the “probability density” and “probability current density” respectively. While the latter is the same as that derived from Equation (3.3), Equation (3.11) seems not positive definite and dramatically different from 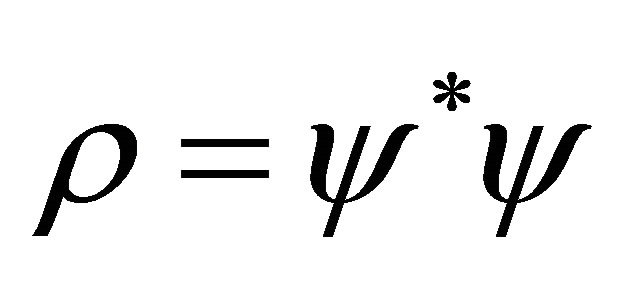 in Equation (3.3). Why?
in Equation (3.3). Why?
In hindsight, for a linear equation in RQM, either KG or Dirac equation, the emergence of WFs with both positive and negative energy  is inevitable and natural. From mathematical point of view, the set of WFs cannot be complete if without taking the negative energy solutions into account. And physicists believe that these negative-energy solutions might be relevant to antiparticles. However, we physicists admit that both a rest particle’s energy
is inevitable and natural. From mathematical point of view, the set of WFs cannot be complete if without taking the negative energy solutions into account. And physicists believe that these negative-energy solutions might be relevant to antiparticles. However, we physicists admit that both a rest particle’s energy 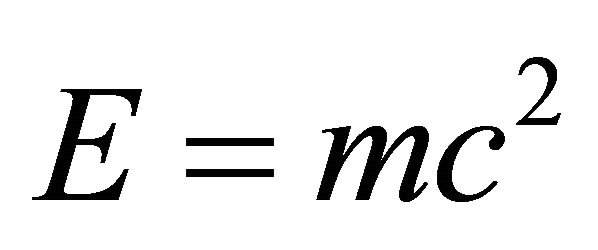 and a rest antiparticle’s energy
and a rest antiparticle’s energy 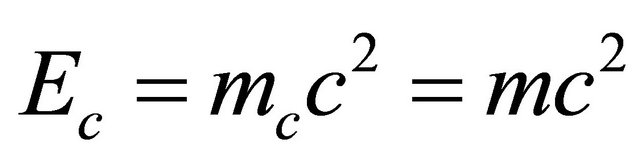 are positive, as verified by numerous experiments like that of pair-creation process
are positive, as verified by numerous experiments like that of pair-creation process 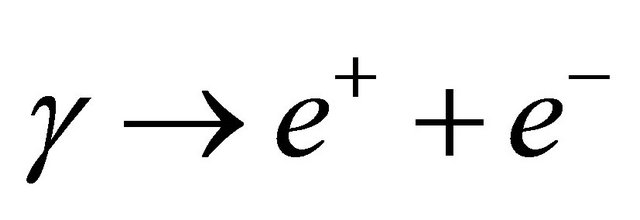 . The above contradiction constructs socalled “negative-energy paradox” in RQM. For Dirac particle, majority (not all) of physicists accept the “hole theory” to explain the “paradox”. But for KG particle, no such kind of “hole theory” can be acceptable. It was this “negative-energy paradox” as well as the four “commutation relations”, Equations (2.1)-(2.5), hidden in the two-particle system discussed by EPR [14] gradually prompted us to realize that the root cause of difficulty in RQM lies in an a priori notion—only one kind of WF with one set of operators (like Equation (3.2)) can be acceptable in QM, either for NRQM or RQM.
. The above contradiction constructs socalled “negative-energy paradox” in RQM. For Dirac particle, majority (not all) of physicists accept the “hole theory” to explain the “paradox”. But for KG particle, no such kind of “hole theory” can be acceptable. It was this “negative-energy paradox” as well as the four “commutation relations”, Equations (2.1)-(2.5), hidden in the two-particle system discussed by EPR [14] gradually prompted us to realize that the root cause of difficulty in RQM lies in an a priori notion—only one kind of WF with one set of operators (like Equation (3.2)) can be acceptable in QM, either for NRQM or RQM.
Once getting rid of the constraint in the above notion and introducing two sets of WFs and operators for particle and antiparticle respectively, we can identify the negative energy solution, Equation (3.9), with the antiparticle’s WF directly
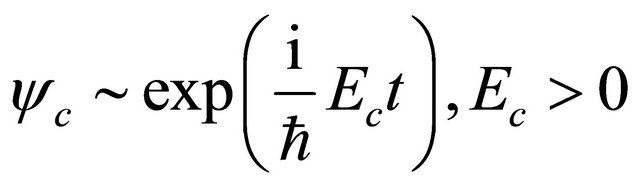 (3.13)
(3.13)
which implies an antiparticle with positive energy 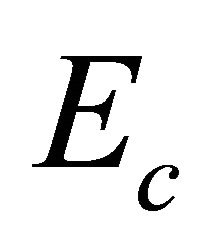 by using Equation (2.18). This claim will be proved rigorously in the next subsection.
by using Equation (2.18). This claim will be proved rigorously in the next subsection.
One may ask: When you assume the negative energy solution being the WF of antiparticle, how about the difficulty of negative probability density? Below we will see how to solve these two difficulties simultaneously and make KG equation a self-consistent theory at the level of RQM.
3.2. The Proof of a Discrete Symmetry 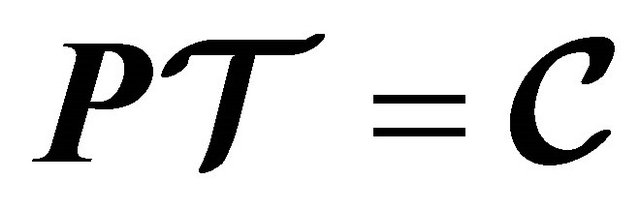 for KG Particle
for KG Particle
Let us introduce an operator of (newly defined) combined space-time inversion  for KG equation. It should change the space-time coordinates as
for KG equation. It should change the space-time coordinates as
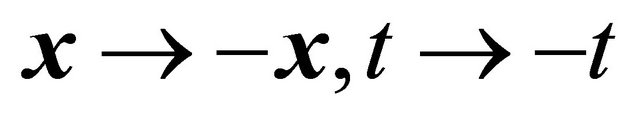 (3.14)
(3.14)
then accordingly
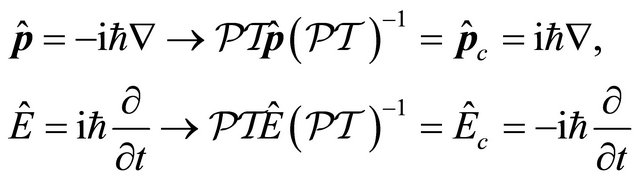 (3.15)
(3.15)
Because the antiparticle has opposite charge 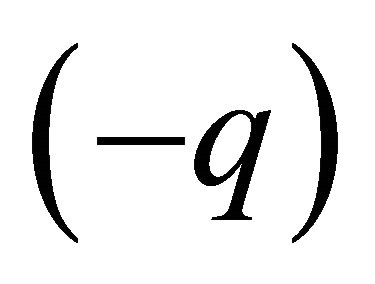 versus
versus 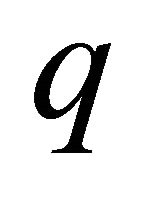 for particle, so
for particle, so
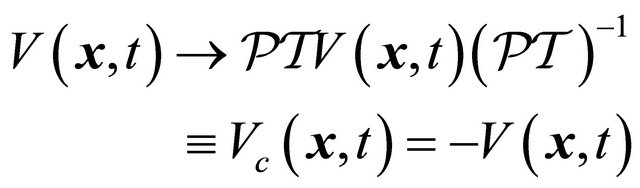 (3.16)
(3.16)
When performing  inversion on KG equation, Equation (3.5), from left to right, we meet eventually the WF and define the antiparticle’s WF as
inversion on KG equation, Equation (3.5), from left to right, we meet eventually the WF and define the antiparticle’s WF as
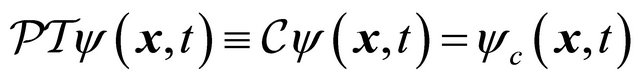 (3.17)
(3.17)
Thus KG particle’s equation, Equation (3.5), is transformed into 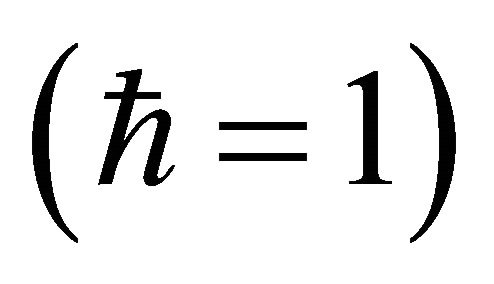
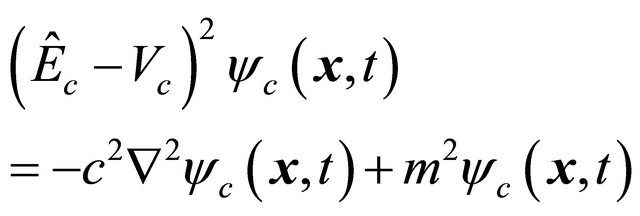 (3.18)
(3.18)
or
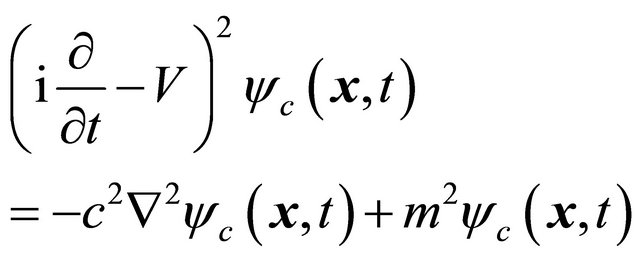 (3.19)
(3.19)
which is formally the same as Equation (3.5) though we should use 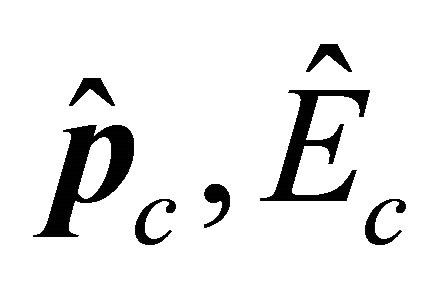 for
for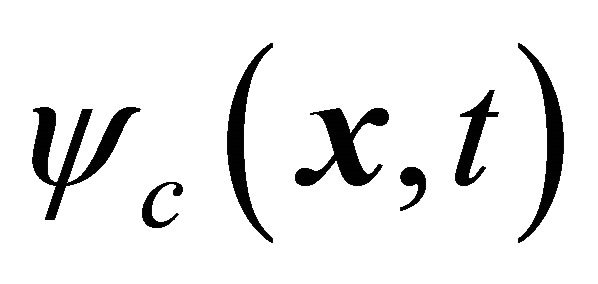 . Hence the KG equation remains invariant under the
. Hence the KG equation remains invariant under the  operation, Equations (3.14)-(3.17). Notice further that Equation (3.18) is just the “quantized” equation of the kinematical relation for an antiparticle in SR
operation, Equations (3.14)-(3.17). Notice further that Equation (3.18) is just the “quantized” equation of the kinematical relation for an antiparticle in SR
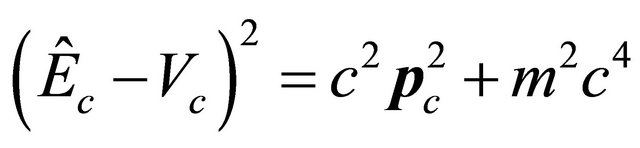 (3.20)
(3.20)
which is the counterpart of Equation (3.4) for a particle. For example, a KG particle’s scattering WF 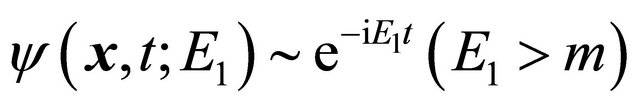 is attracted by an spherically symmetric potential
is attracted by an spherically symmetric potential 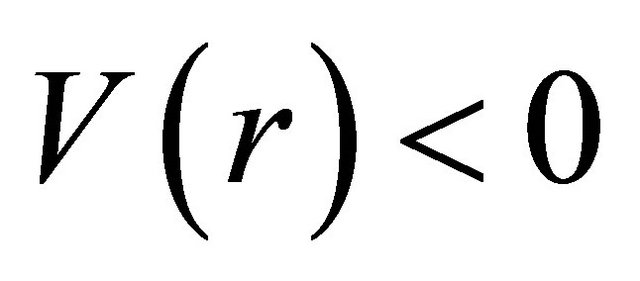 and so has a positive phase-shift
and so has a positive phase-shift 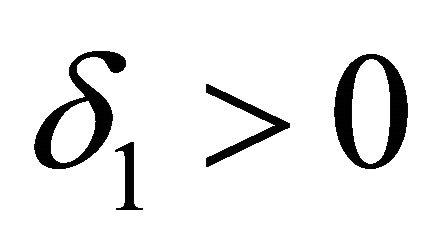 (in the, say,
(in the, say, 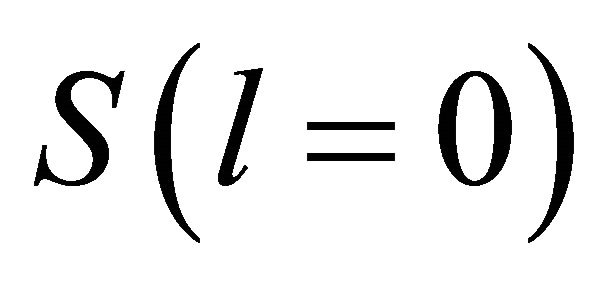 state). Then physically, its antiparticle’s WF
state). Then physically, its antiparticle’s WF
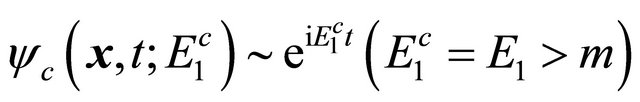 is repelled by the potential
is repelled by the potential 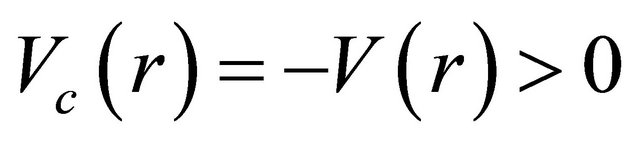 and has a negative phaseshift
and has a negative phaseshift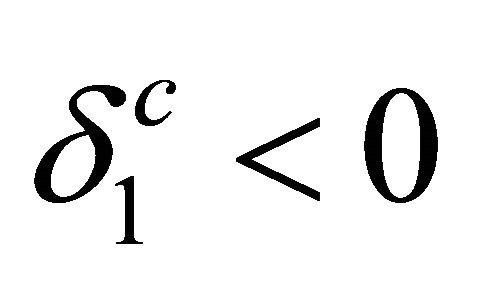 .
.
Note that, however, corresponding to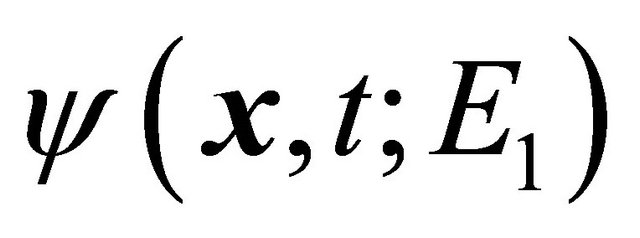 , there is another negative energy particle’s WF
, there is another negative energy particle’s WF
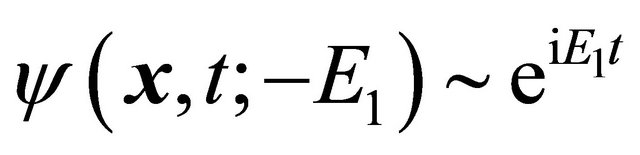 satisfying Equation (3.5)
satisfying Equation (3.5)
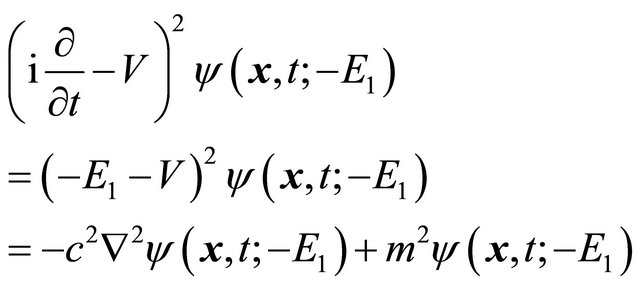 (3.21)
(3.21)
whose space-time behavior is precisely the same as the antiparticle’s WF 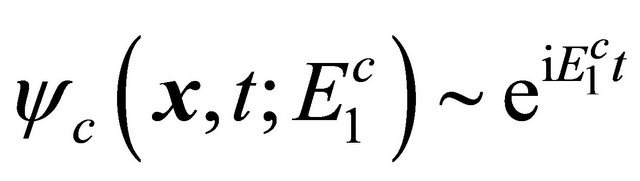 with
with 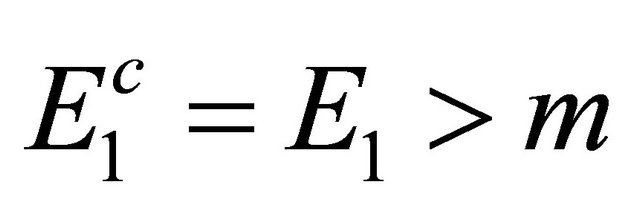
as shown by Equation (3.18) since
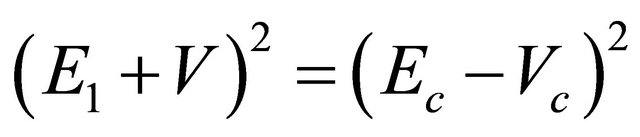 . Thus, for avoiding confusion, we have
. Thus, for avoiding confusion, we have
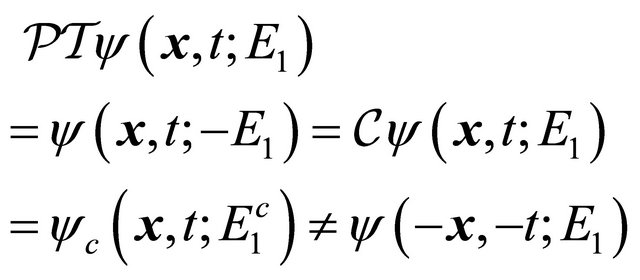 (3.22)
(3.22)
and
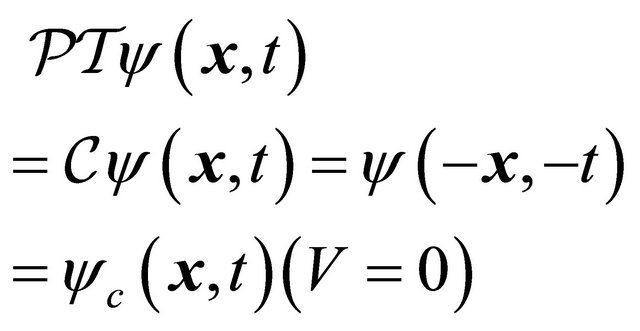 (3.23)
(3.23)
achieving the proof of the discrete symmetry 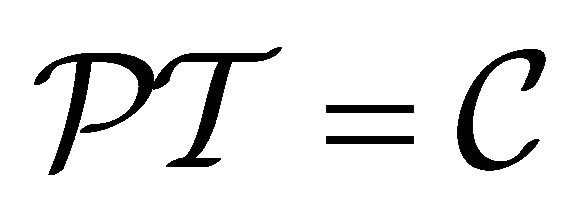 for KG particle shown by Equation (3.17). In summary, the “negative-energy paradox” for KG equation is solved in a physical way with following advantages:
for KG particle shown by Equation (3.17). In summary, the “negative-energy paradox” for KG equation is solved in a physical way with following advantages:
a) By using two sets of WFs and momentum-energy operators for particle and antiparticle respectively, both particle’s WF 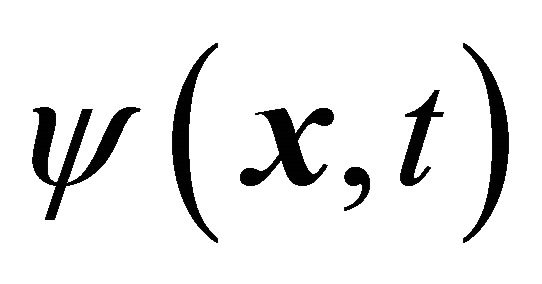 and antiparticle’s WF
and antiparticle’s WF 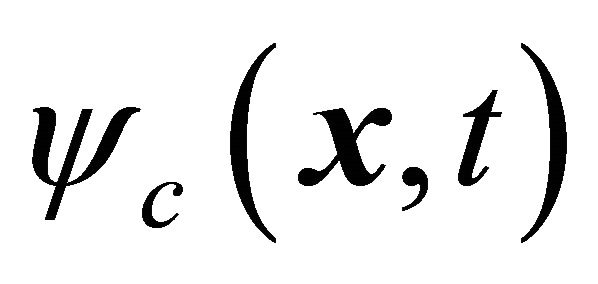 have positive energies
have positive energies 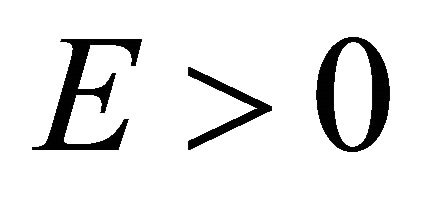 and
and 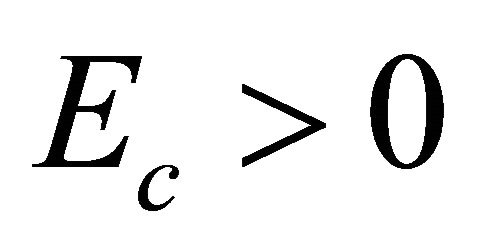 respectively.
respectively.
b) While satisfying the same KG equation with same potential 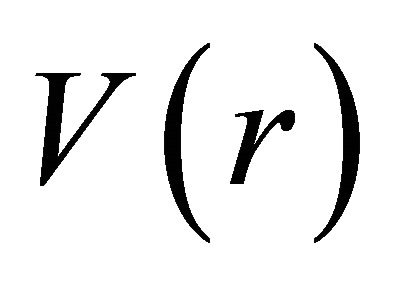 formally,
formally, 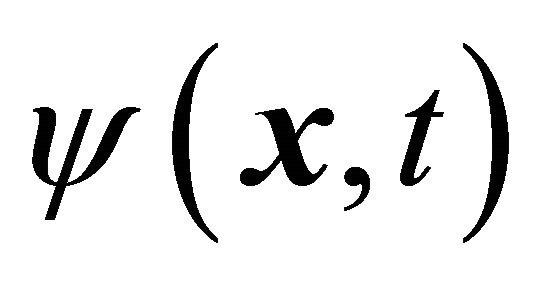 and
and 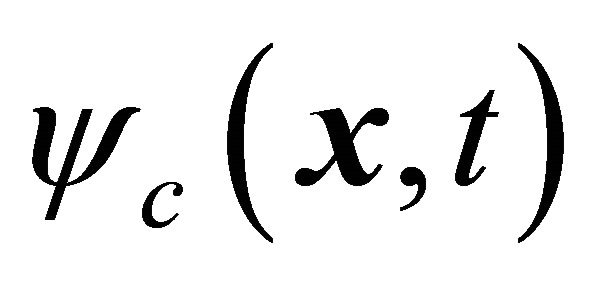 are actually subject to opposite “force” for particle and antiparticle respectively.
are actually subject to opposite “force” for particle and antiparticle respectively.
c) The space-time behavior of  can be identified with that of a negative energy particle’s WF
can be identified with that of a negative energy particle’s WF
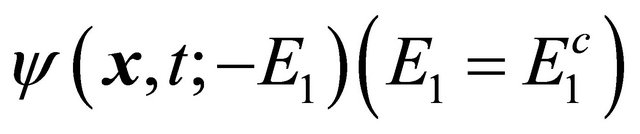 , in a one-to-one correspondence.
, in a one-to-one correspondence.
Thus from mathematical point of view, all solutions of KG equation form a complete set including both positive and negative energy values of one operator 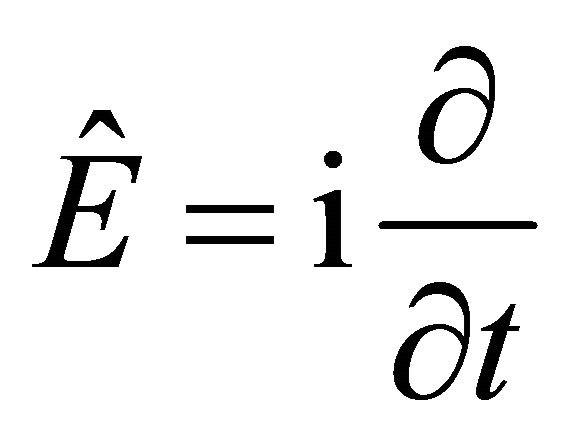
exactly.
By contrast, usually, aiming at finding an anti-particle’s WF, one performs the CPT transformation on a particle’s WF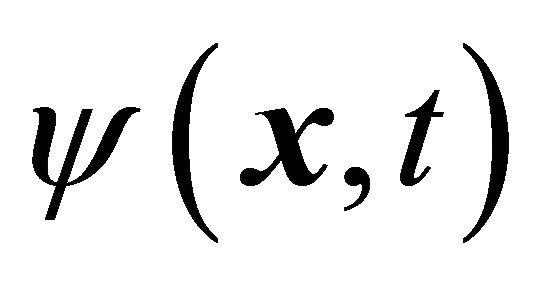 , yielding [29-32]
, yielding [29-32]
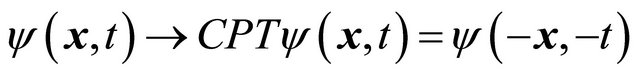 (3.24)
(3.24)
whose character can also be summed up as follows:
a’) By using one set of WF and relevant operators for both particle and antiparticle, at the LHS of Equation (3.24), 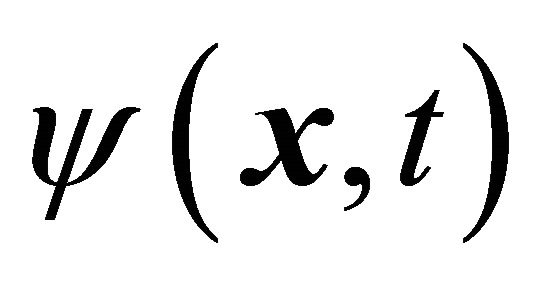 , and
, and 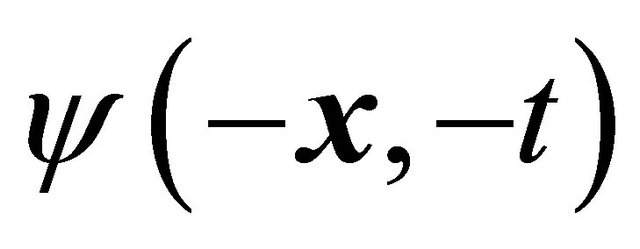 at RHS must have opposite energies inevitably.
at RHS must have opposite energies inevitably.
b’) By design in the C transformation, 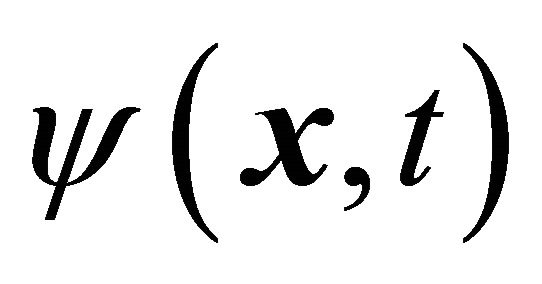 and
and 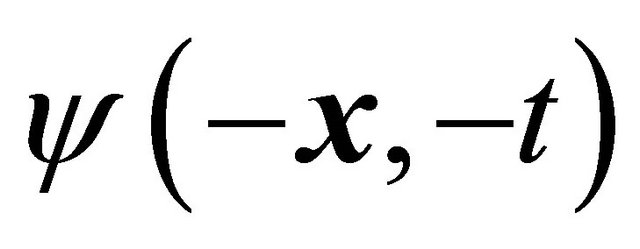 in Equation (3.24) satisfy different equations with
in Equation (3.24) satisfy different equations with  and
and 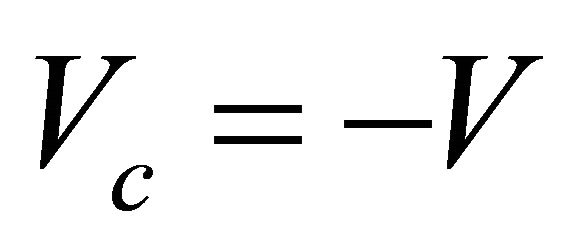 respectively. But with opposite energies, they are actually subject to the same (either attractive or repulsive) “force”. So one cannot distinguish particle from antiparticle through what their WFs “feel” after the CPT transformation.
respectively. But with opposite energies, they are actually subject to the same (either attractive or repulsive) “force”. So one cannot distinguish particle from antiparticle through what their WFs “feel” after the CPT transformation.
c’) From mathematical point of view, we should keep all negative-energy solutions for one equation. However, even facing WFs in doubled numbers, we still don’t know how to choose half of them for describing particle and its antiparticle separately in physics.
But we haven’t solve the difficulty of negative probability density in KG equation yet, awaiting for another enlightenment which was already there since 1958.
3.3. Feshbach and Villars (FV) Dissociation of KG WF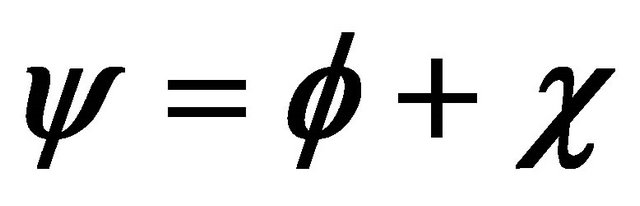 , a Reformulated Symmetry between
, a Reformulated Symmetry between ![]() and
and 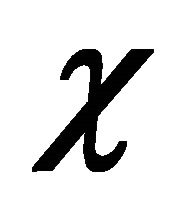 under the Space-Time (or Mass) Inversion
under the Space-Time (or Mass) Inversion
In 1958, dividing the WF into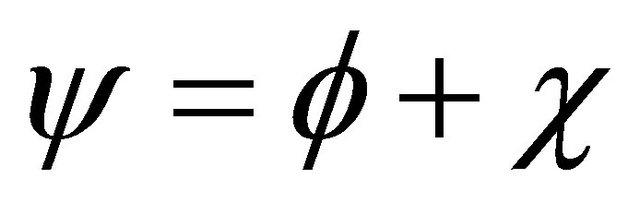 , Feshbach and Villars [2] recast Equation (5) into two coupled Schrödinger-like equations as3:
, Feshbach and Villars [2] recast Equation (5) into two coupled Schrödinger-like equations as3:
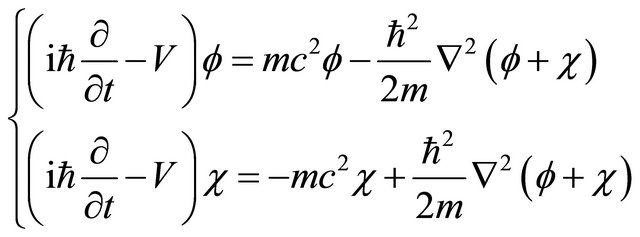 (3.25)
(3.25)
where
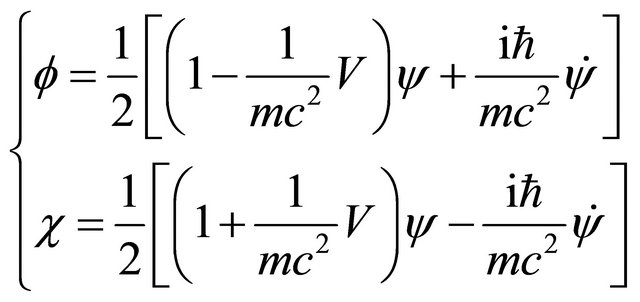 (3.26)
(3.26)
 . Interestingly, the “probability density”, Equation (3.11) can be recast into a difference between two positive-definite densities [18,20]:
. Interestingly, the “probability density”, Equation (3.11) can be recast into a difference between two positive-definite densities [18,20]:
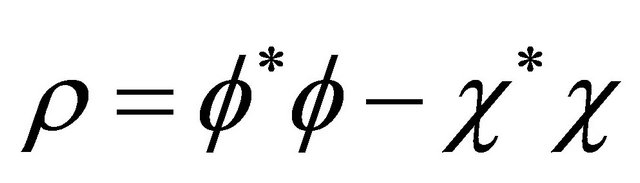 (3.27)
(3.27)
while the probability current density contains interference terms between  and
and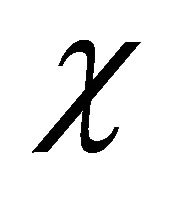 :
:
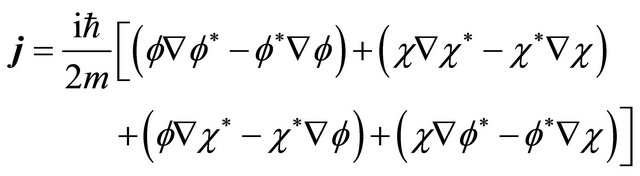 (3.28)
(3.28)
The expression of 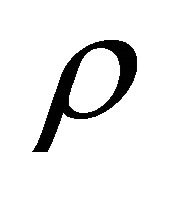 as shown by Equation (3.27) strongly hints that the
as shown by Equation (3.27) strongly hints that the 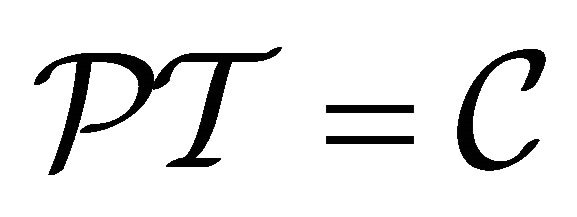 symmetry proved in the last subsection may be combined with the FV dissociation of KG equation such that the positive-definite property of
symmetry proved in the last subsection may be combined with the FV dissociation of KG equation such that the positive-definite property of 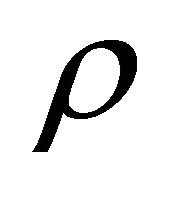 can be ensured for both particle and antiparticle.
can be ensured for both particle and antiparticle.
Indeed, after inspecting Equation (3.25) carefully, we do find a hidden symmetry in the sense that it is invariant (in its form) under the following reformulated space-time inversion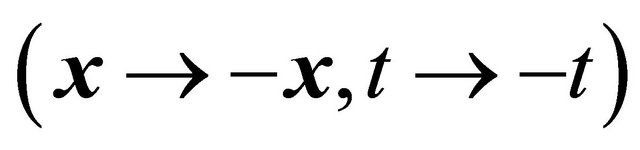 , i.e.,
, i.e., 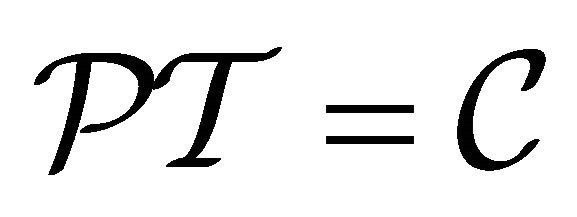 transformation:
transformation:
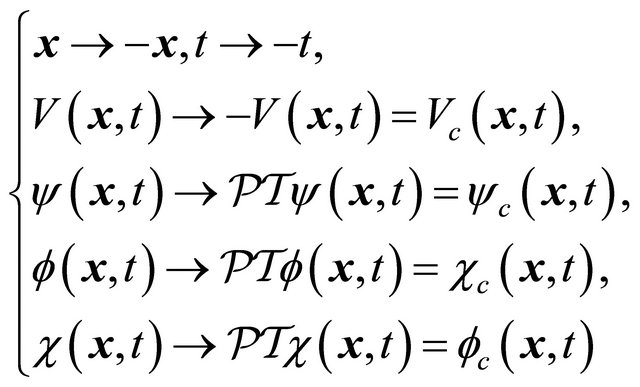 (3.29)
(3.29)
Performing transformation Equation (3.29) on Equation (3.26), we find 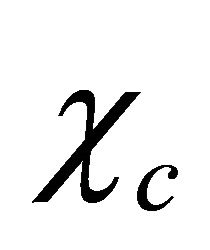 satisfying the same equation of
satisfying the same equation of 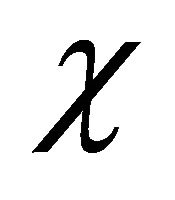 and
and 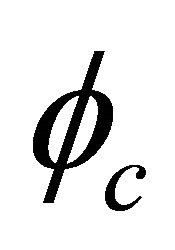 satisfying that of
satisfying that of . They read
. They read
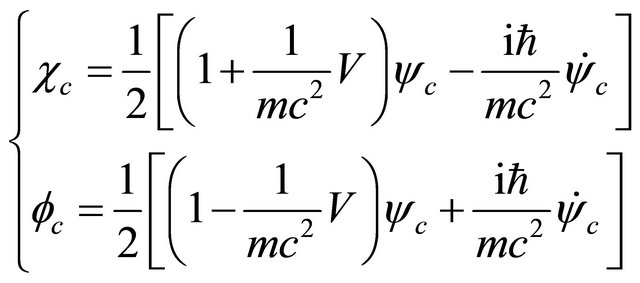 (3.30)
(3.30)
Remember, for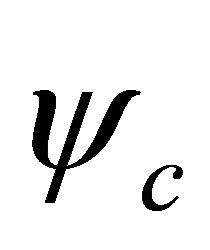 , we should use operator Equation (3.15). Accordingly, the probability density for
, we should use operator Equation (3.15). Accordingly, the probability density for 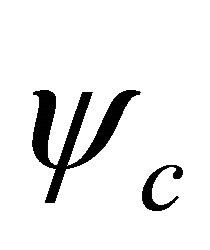 is defined as
is defined as
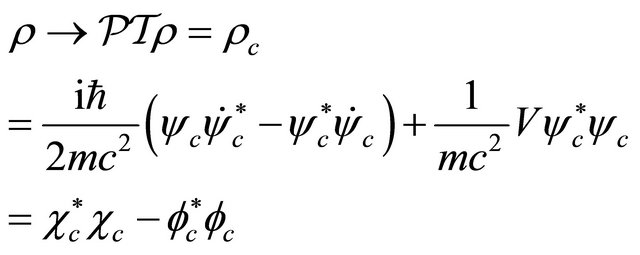 (3.31)
(3.31)
Similarly, we have 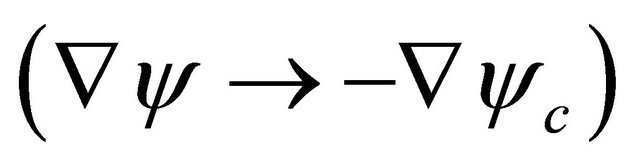
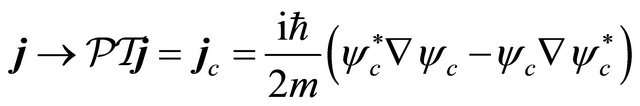 (3.32)
(3.32)
For simplicity, consider a free KG particle  with WF Equation (3.6). Then
with WF Equation (3.6). Then 
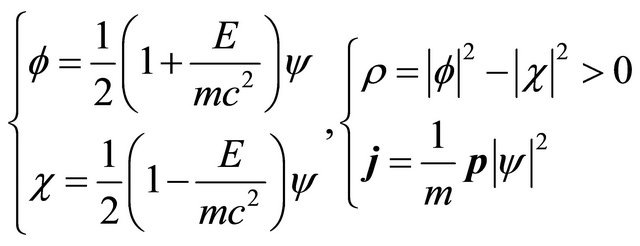 (3.33)
(3.33)
But for a free 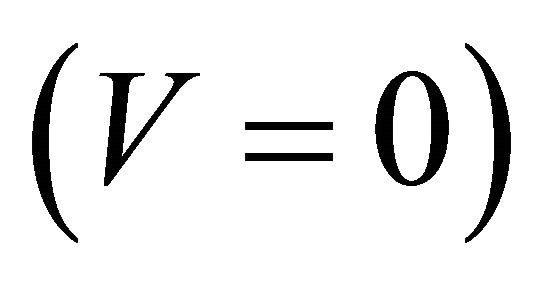 KG antiparticle with WF Equation (2.21), it has
KG antiparticle with WF Equation (2.21), it has 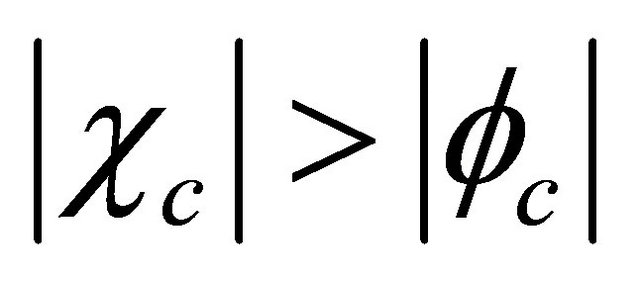
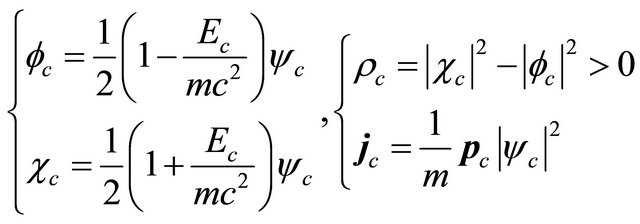 (3.34)
(3.34)
Equations (3.33) and (3.34) satisfy all physical conditions we need. If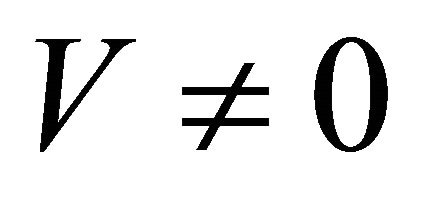 , as long as
, as long as 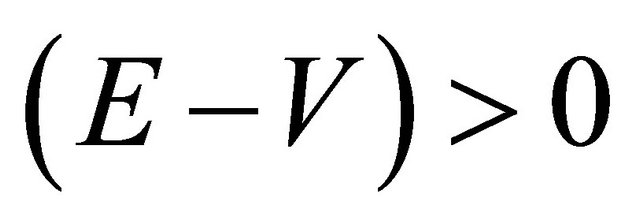 for particle or
for particle or 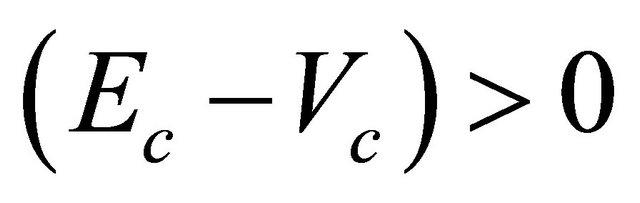 for antiparticle, the situation remains the same. However, once
for antiparticle, the situation remains the same. However, once 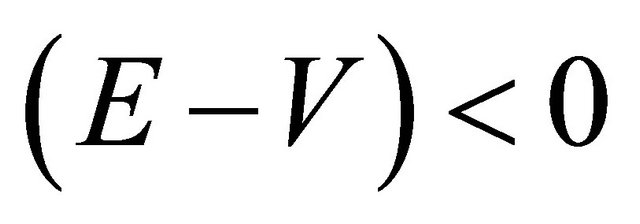 or
or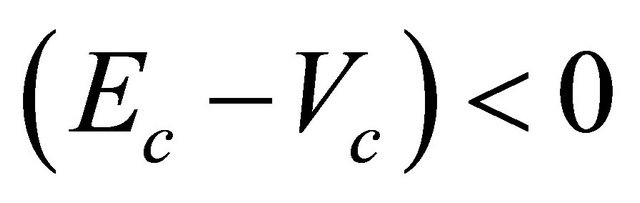 , some complications would occur. For further discussion, please see the Appendix.
, some complications would occur. For further discussion, please see the Appendix.
Therefore, we see that the reformulated space-time inversion, Equation (3.29), reflects the underlying symmetry between a particle’s WF 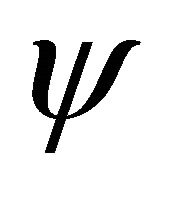 and its antiparticle’s WF
and its antiparticle’s WF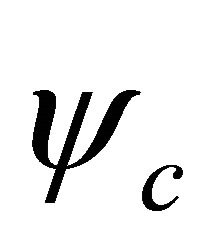 . As both
. As both  and
and  in
in 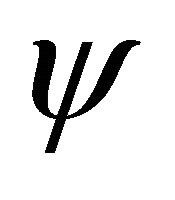 or
or 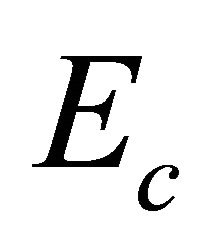 and
and 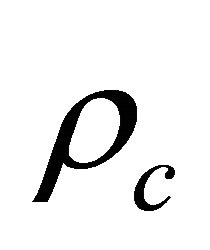 in
in 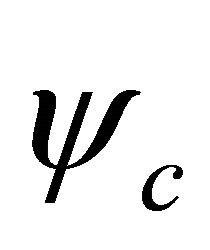 are positive definite, all difficulties in KG equation disappear and the latter becomes a self-consistent theory.
are positive definite, all difficulties in KG equation disappear and the latter becomes a self-consistent theory.
Moreover, instead of Equation (3.29), a “mass inversion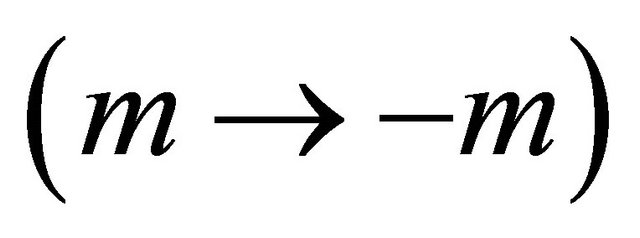 ” can realize the same symmetry, the invariance under a
” can realize the same symmetry, the invariance under a 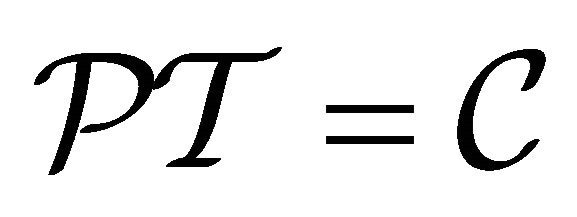 transformation, via the following operation on Equation (3.25):
transformation, via the following operation on Equation (3.25):
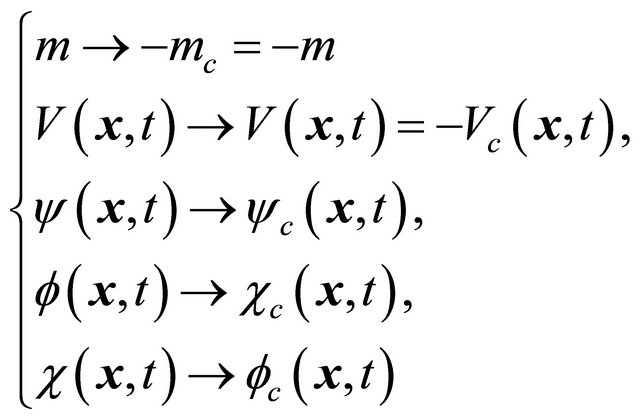 (3.35)
(3.35)
Notice that, when![]() , we have
, we have 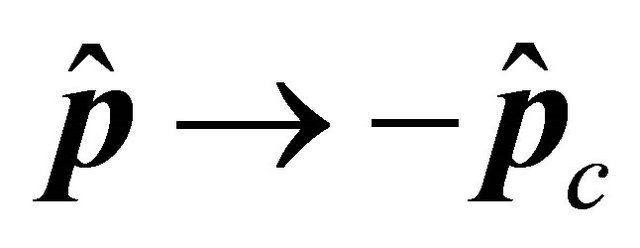 and
and
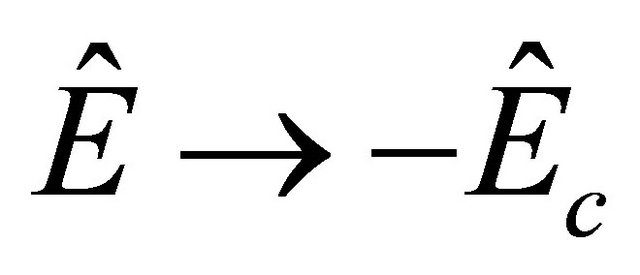 , i.e.
, i.e. ,
, 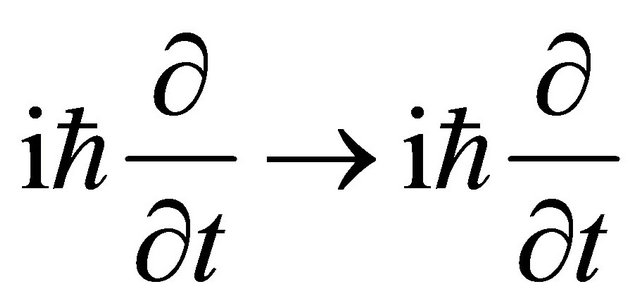 , in contrast to Equation (3.15) [1].4
, in contrast to Equation (3.15) [1].4
The reason why 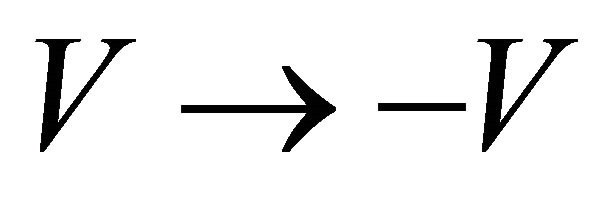 in the space-time inversion Equation (3.29) whereas
in the space-time inversion Equation (3.29) whereas  in the mass inversion Equation (3.35) can be seen from the classical equation: The Lorentz force F on a particle exerted by an external potential
in the mass inversion Equation (3.35) can be seen from the classical equation: The Lorentz force F on a particle exerted by an external potential  reads:
reads: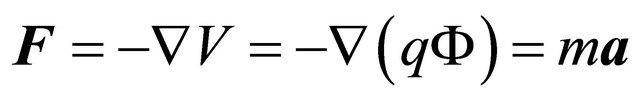 . As the acceleration
. As the acceleration ![]() of particle will change to
of particle will change to ![]() for its antiparticle, there are two alternative explanations: either due to the inversion of charge
for its antiparticle, there are two alternative explanations: either due to the inversion of charge 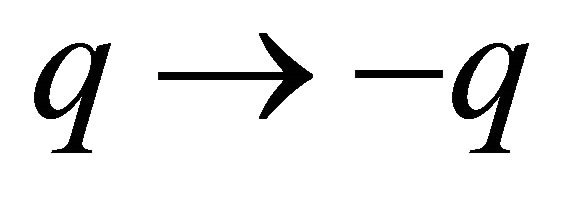 (i.e.,
(i.e., 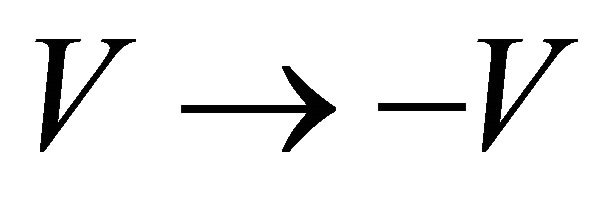 but keeping
but keeping ![]() unchanged) or due to the inversion of mass
unchanged) or due to the inversion of mass ![]() (but keeping
(but keeping 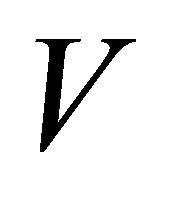 unchanged).
unchanged).
4. Reinterpretation of WF and the Relativistic Effects
The success of FV’s dissociation of KG equation should be ascribed to their deep insight that a unified WF 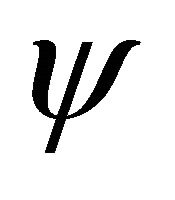 is composed of two fields
is composed of two fields  and
and 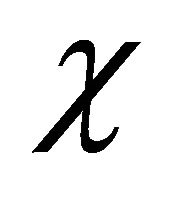 in confrontation. Note that Equation (3.25) reduces into two equations separately for a static KG particle
in confrontation. Note that Equation (3.25) reduces into two equations separately for a static KG particle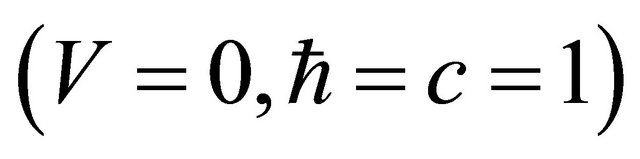 :
:
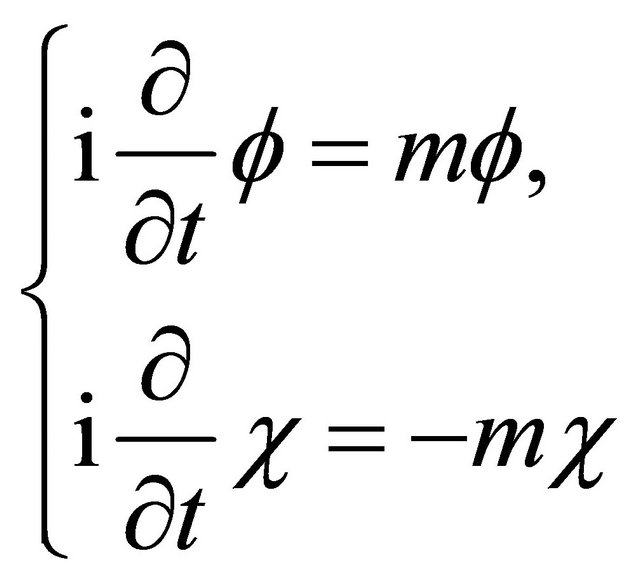 (4.1)
(4.1)
with two separated solutions being:
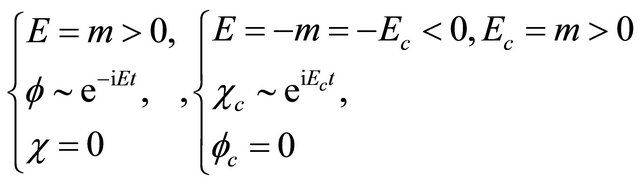 (4.2)
(4.2)
Once the particle (antiparticle) is moving with a velocity, 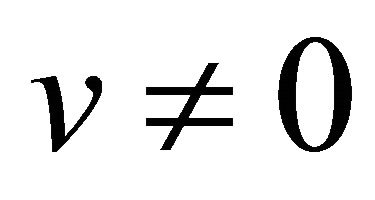 ,
,  and
and 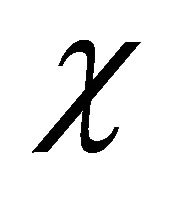 (
(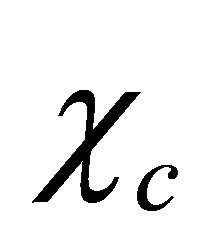 and
and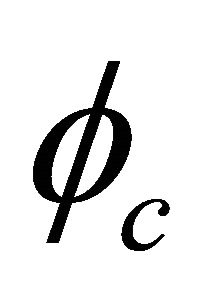 ) couple together and the WF
) couple together and the WF 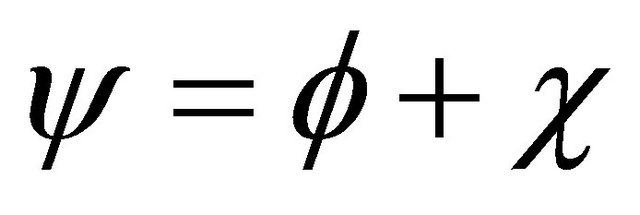
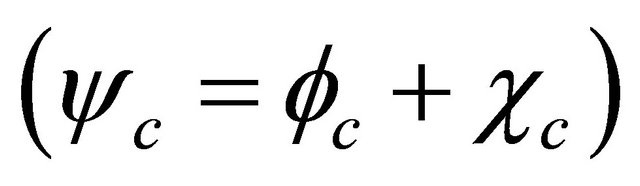 for a free particle (antiparticle) read (in one-dimensional space)
for a free particle (antiparticle) read (in one-dimensional space)
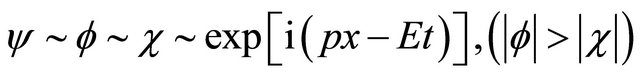 (4.3a)
(4.3a)
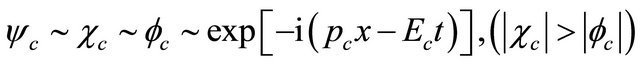 (4.3b)
(4.3b)
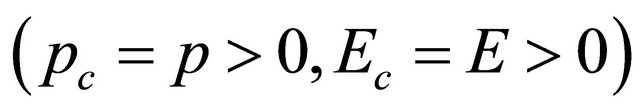 respectively. In Equation (4.3a),
respectively. In Equation (4.3a),  dominates
dominates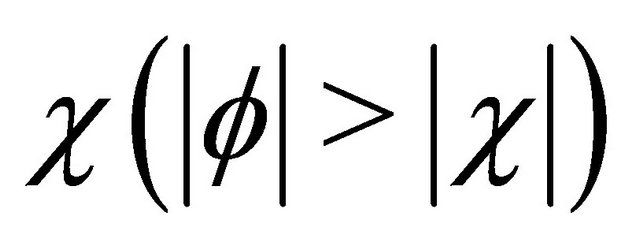 . By contrast, in Equation (4.3b) it is
. By contrast, in Equation (4.3b) it is 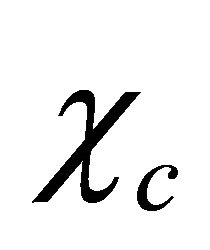 who dominates
who dominates 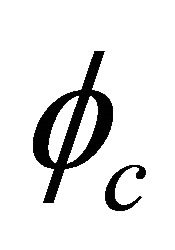 (The status remains the same for
(The status remains the same for  cases as discussed in the last section).
cases as discussed in the last section).
Despite  and
and 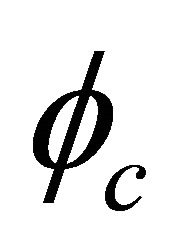 (
(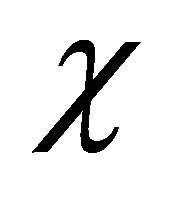 and
and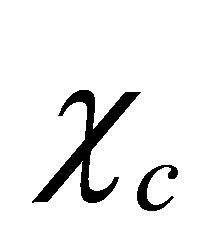 ) having the “intrinsic tendency” to evolve as
) having the “intrinsic tendency” to evolve as
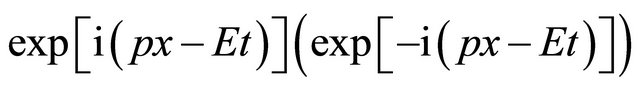 , however, in a WF of particle (antiparticle),
, however, in a WF of particle (antiparticle), 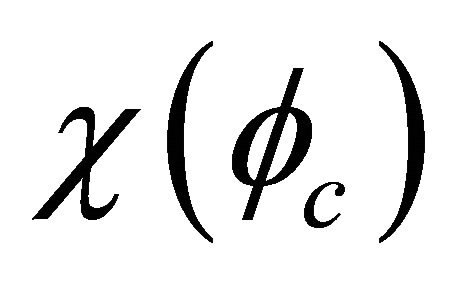 must follow
must follow 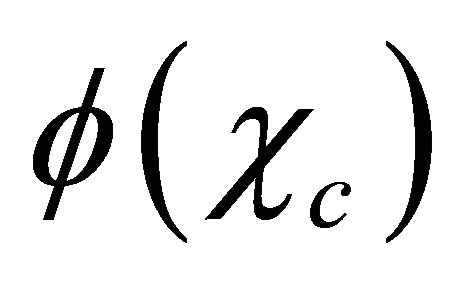 to evolve like that shown by Equation (4.3a) (Equation
to evolve like that shown by Equation (4.3a) (Equation
(4.3b)), as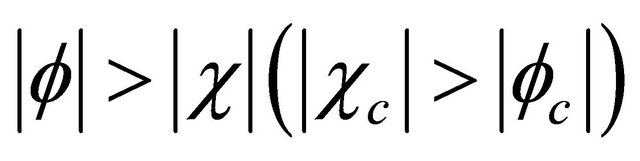 . So it seems suitable to name
. So it seems suitable to name  the “hidden particle field” inside a particle while
the “hidden particle field” inside a particle while 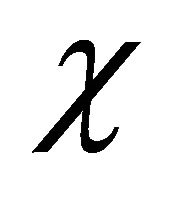 the “hidden antiparticle field” (rather than the “negative-energy component”) inside the same particle.
the “hidden antiparticle field” (rather than the “negative-energy component”) inside the same particle.
Let us try to reinterpret the phenomena displayed in the kinematics of special relativity (SR) via the enhancement of 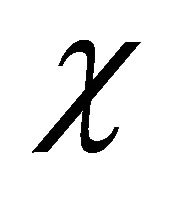 field in a particle [22-25]:
field in a particle [22-25]:
(a) Lorentz transformation Consider a particle’s WF shown by Equation (4.3a) in an inertial frame S (laboratory). Then take another 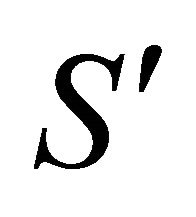 frame resting on the particle, so
frame resting on the particle, so 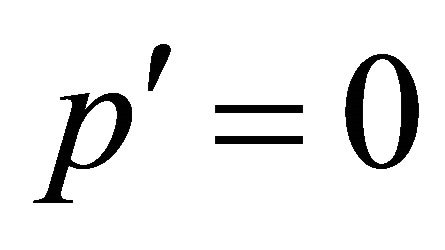 and
and 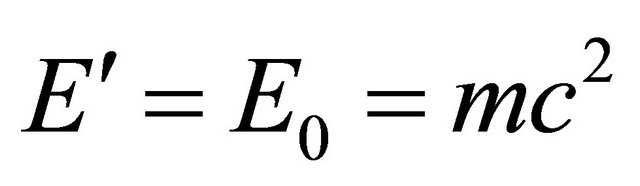 . The WF in
. The WF in  frame reads:
frame reads:
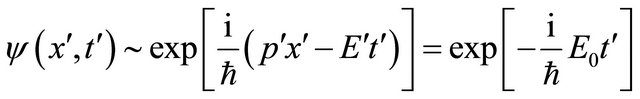 (4.4)
(4.4)
Here the space-time coordinates  are introduced and defined in the
are introduced and defined in the  frame via the phase of WF as follows: Based on the assertion that “phase remains invariant under the coordinate transformation” which was named the “law of phase harmony” by de Broglie and was regarded by himself as the fundamental achievement all his life [34], comparing the phase in Equation (4.4) with that in Equation (4.3a) and using
frame via the phase of WF as follows: Based on the assertion that “phase remains invariant under the coordinate transformation” which was named the “law of phase harmony” by de Broglie and was regarded by himself as the fundamental achievement all his life [34], comparing the phase in Equation (4.4) with that in Equation (4.3a) and using
![]() , one finds
, one finds
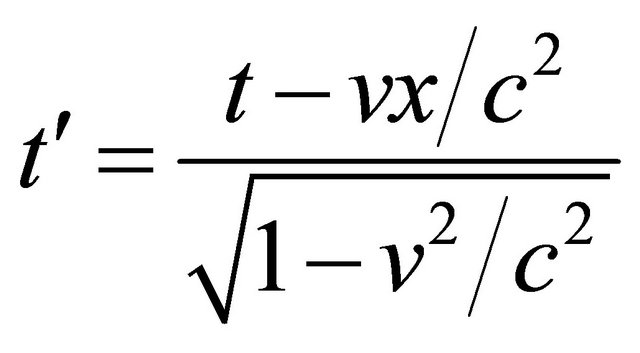 (4.5)
(4.5)
Then, all formulas in the Lorentz transformation can be obtained. In some sense, what used here is a particle’s wave-packet which serves as a microscopic “ruler”, also a “clock” simultaneously.
(b) There is a speed limit c for a massive particle.
For a free KG particle, using Equation (3.33), we may define an “impurity ratio” 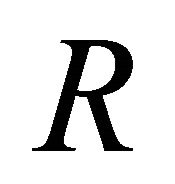 for the amplitude of hidden
for the amplitude of hidden  field to that of
field to that of  field and calculate it being
field and calculate it being
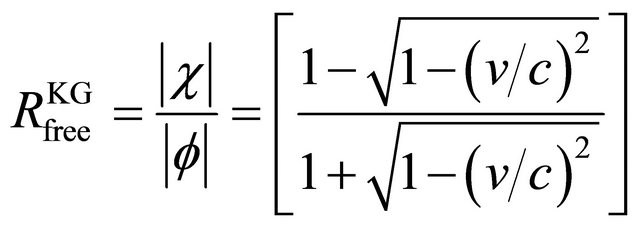 (4.6)
(4.6)
When , with the increase of v,
, with the increase of v,  increases monotonously. The particle becomes more and more “impure” until
increases monotonously. The particle becomes more and more “impure” until  as a limit of particle being still a particle. As shown by Equation (4.6), the reason why its velocity has a limiting value c (the speed of light) is because
as a limit of particle being still a particle. As shown by Equation (4.6), the reason why its velocity has a limiting value c (the speed of light) is because  and
and 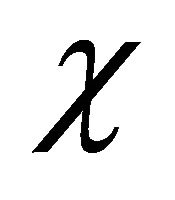 have opposite evolution tendencies in space-time as shown by Equations (4.1)- (4.3) essentially,
have opposite evolution tendencies in space-time as shown by Equations (4.1)- (4.3) essentially, 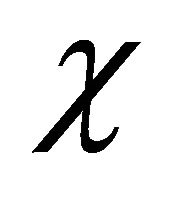 strives to hold
strives to hold  back from going forward until a balance nearly reached when
back from going forward until a balance nearly reached when 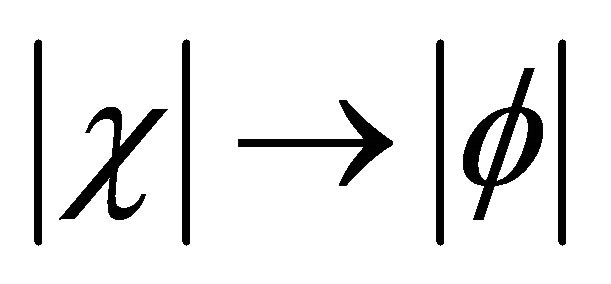 and
and![]() .
.
(c) The “length contraction” (FitzGerald-Lorentz contraction) and “time dilation”
As usual, we will show “length contraction” via a wave-packet of KG particle moving at a high-speed 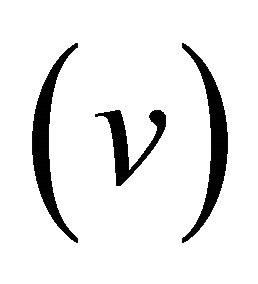 but further ascribe it to the enhancement of
but further ascribe it to the enhancement of 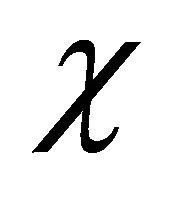 field hidden inside the particle.
field hidden inside the particle.
First, consider a wave-packet of KG particle at rest [25, 35]
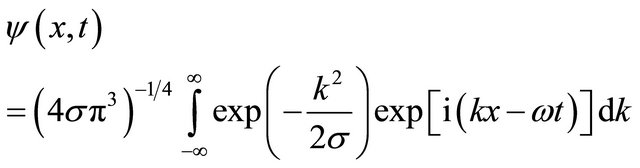 (4.7)
(4.7)
Assuming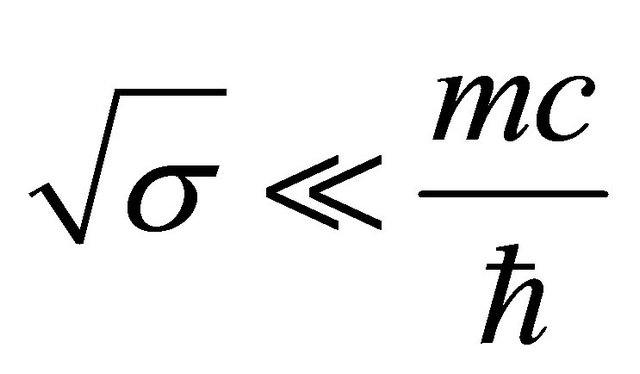 , we have approximately that
, we have approximately that
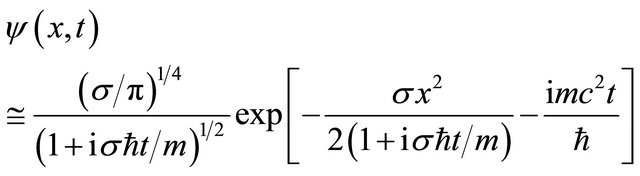 (4.8)
(4.8)
If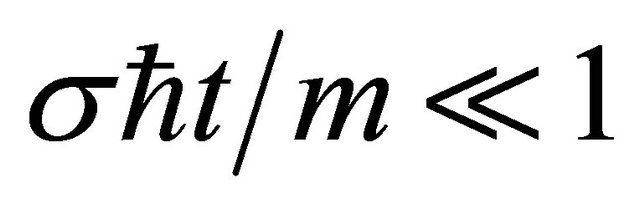 , the diffusion of wave-packet at low speed
, the diffusion of wave-packet at low speed 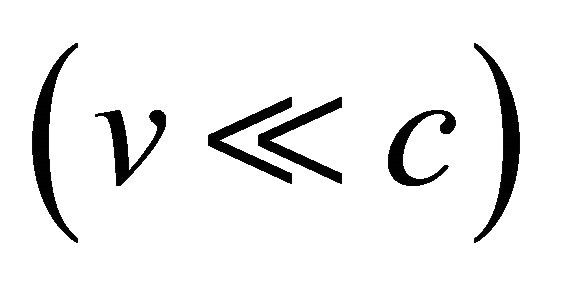 can be ignored. Then we perform a “boost transformation”
can be ignored. Then we perform a “boost transformation”
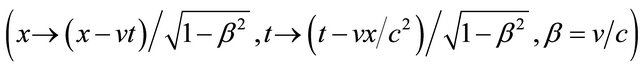
to push the wave-packet to high velocity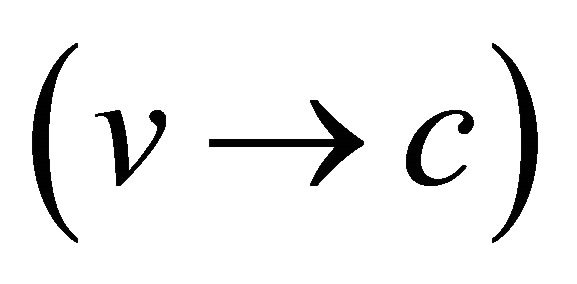 , yielding
, yielding
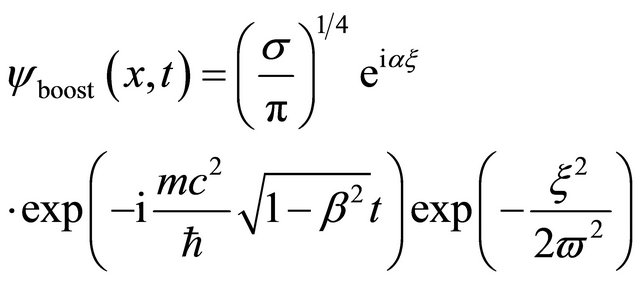 (4.9)
(4.9)
where 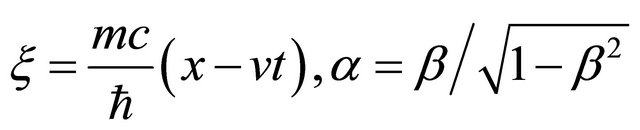 and
and
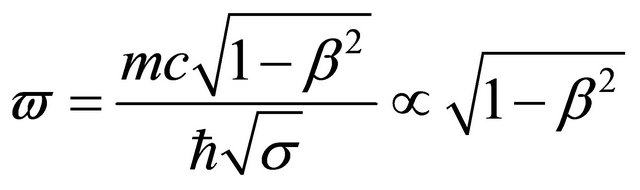 (4.10)
(4.10)
Here ![]() is the width of wave-packet measured from its center
is the width of wave-packet measured from its center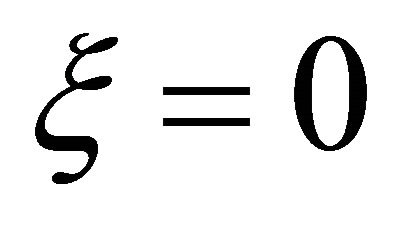 . Equations (4.7)-(4.10) show the “length contraction”.
. Equations (4.7)-(4.10) show the “length contraction”.
Second, we calculate from Equations (4.9) and (3.33)
the values of 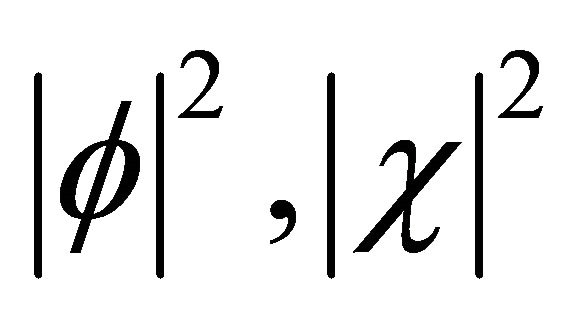 and the probability density
and the probability density
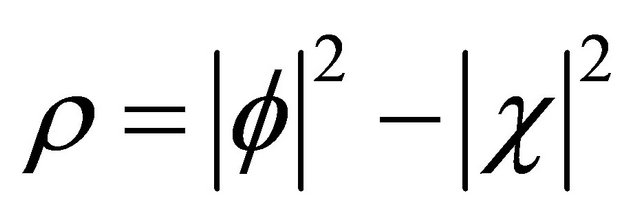 respectively.5 Their peak values all increase with the increase of v (boost effect). However, the “intensity” of
respectively.5 Their peak values all increase with the increase of v (boost effect). However, the “intensity” of 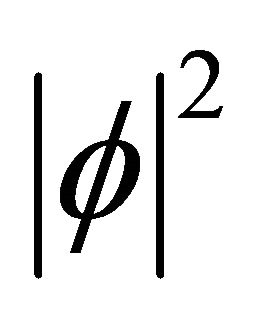 or
or 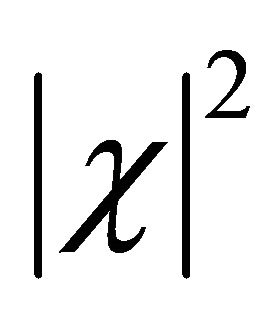 increases even faster than that of
increases even faster than that of 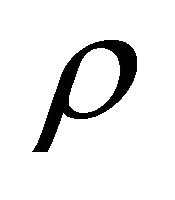 while keeping the constraint
while keeping the constraint 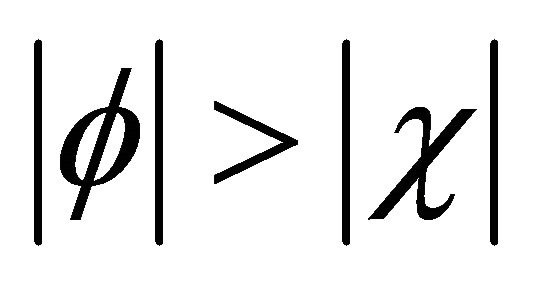 in the boosting process.
in the boosting process.
We also calculate the square of “impurity ratio”  for this moving wave-packet:
for this moving wave-packet:
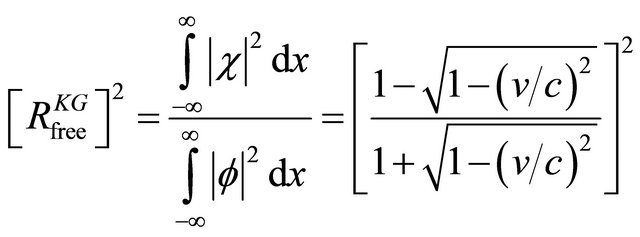 (4.11)
(4.11)
which is the counterpart of Equation (4.6) for a plane WF of KG particle.
With these calculations, we might intuitively understand the length contraction as an effect of coupling (i.e. entanglement) between  and
and 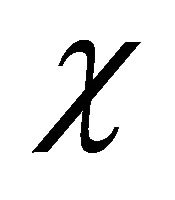 fields due to their opposite evolution tendencies in space as discussed in previous point (b).
fields due to their opposite evolution tendencies in space as discussed in previous point (b).
Let’s turn to the “time dilation” shown by the variation of the mean life
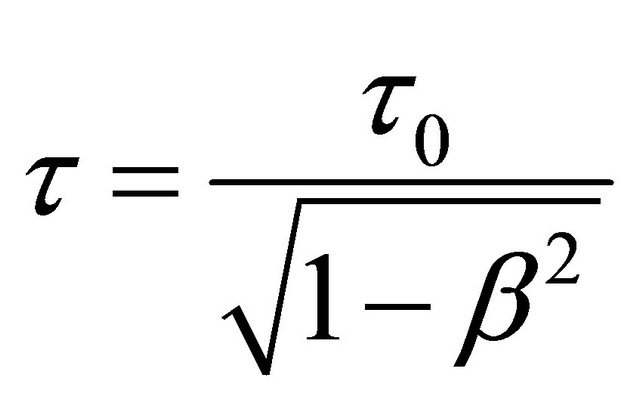 (4.12)
(4.12)
of a particle, say, a pion ( or
or ) with its velocity
) with its velocity![]() .
.
To understand it, let’s return back to Equations (4.1)- (4.3) at 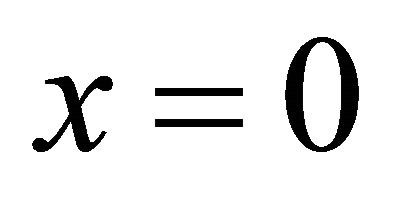 and view the WF
and view the WF 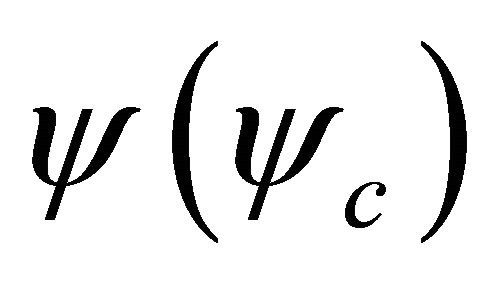 on its complex plane with
on its complex plane with 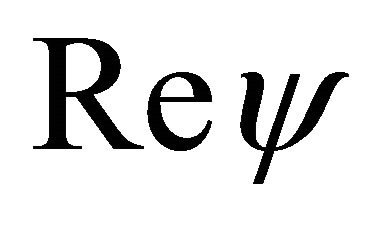 and
and 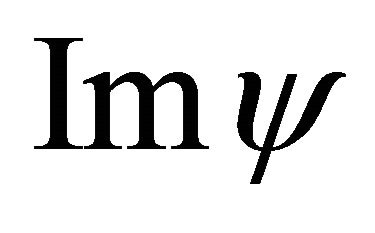 (
(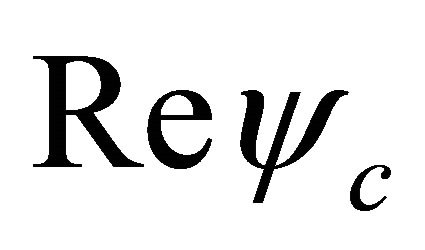 and
and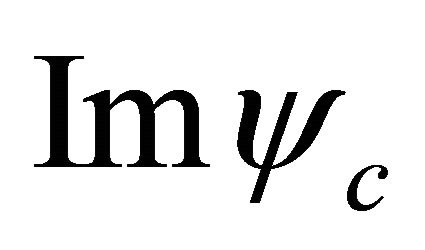 ) as abscissa and ordinate. We may see that the time reading of the “inner clock” for a particle (or an antiparticle) is “clockwise” (or “counter clockwise”). Thus with the increase of particle velocity, though the time reading remains clockwise (due to the dominance of
) as abscissa and ordinate. We may see that the time reading of the “inner clock” for a particle (or an antiparticle) is “clockwise” (or “counter clockwise”). Thus with the increase of particle velocity, though the time reading remains clockwise (due to the dominance of  field), it runs slower and slower because of the enhancement of hidden
field), it runs slower and slower because of the enhancement of hidden  field.
field.
(d) WF’s group velocity 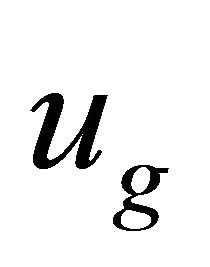 versus phase velocity
versus phase velocity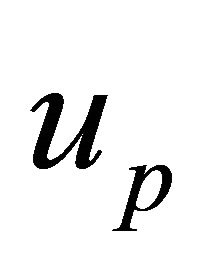 .
.
In RQM, a particle’s velocity ![]() should be identified with its group velocity
should be identified with its group velocity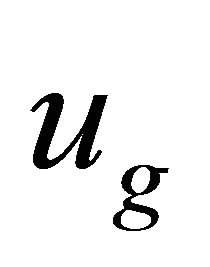 . Actually, we have
. Actually, we have
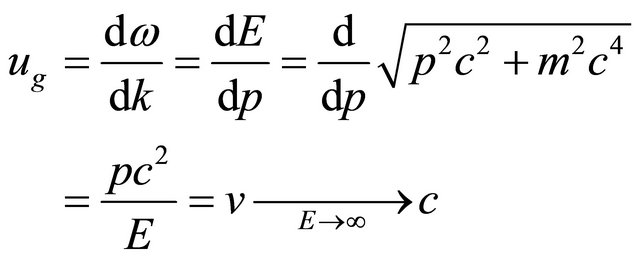 (4.13)
(4.13)
However, the fact that there is an upper bound for particle’s velocity doesn’t mean that no speed can exceed that of light,![]() . Indeed, there is another velocity
. Indeed, there is another velocity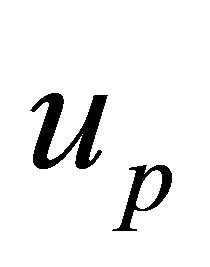 , the phase velocity in the WF
, the phase velocity in the WF
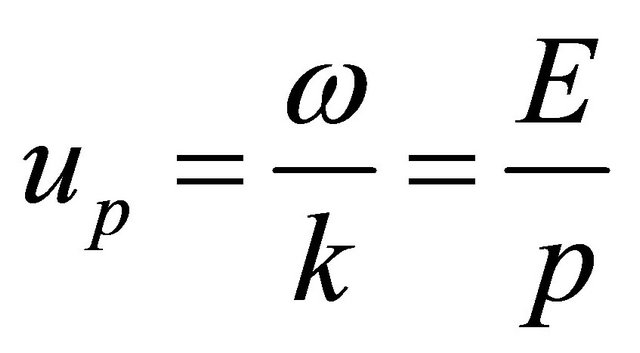 (4.14)
(4.14)
And the relation 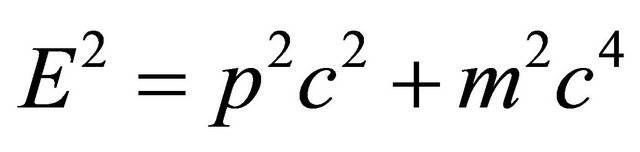 implies that
implies that
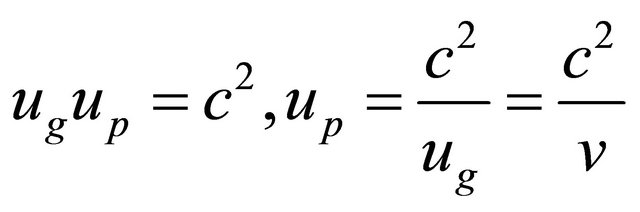 (4.15)
(4.15)
In our opinion, the role of 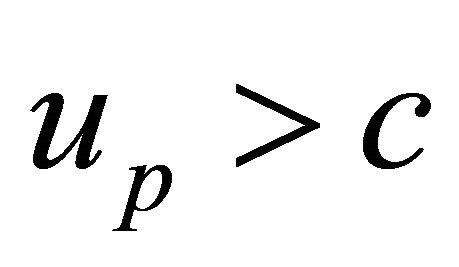 here is crucial to maintain the quantum coherence of WF in the space-time globally, we will further discuss this problem elsewhere. In 1923, de Broglie discovered Equation (4.15) in his relativistic theory. However, in the Schrödinger equation of NRQM, the phase velocity remains undefined. See Ref [34].
here is crucial to maintain the quantum coherence of WF in the space-time globally, we will further discuss this problem elsewhere. In 1923, de Broglie discovered Equation (4.15) in his relativistic theory. However, in the Schrödinger equation of NRQM, the phase velocity remains undefined. See Ref [34].
5. Dirac Equation as Coupled Equations of Two-Component Spinors
Let us turn to the Dirac equation describing an electron
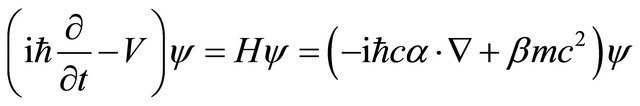 (5.1)
(5.1)
with ![]() and
and  being
being 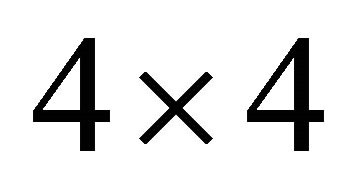 matrices, the WF
matrices, the WF 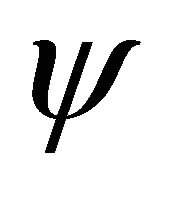 is a four-component spinor
is a four-component spinor
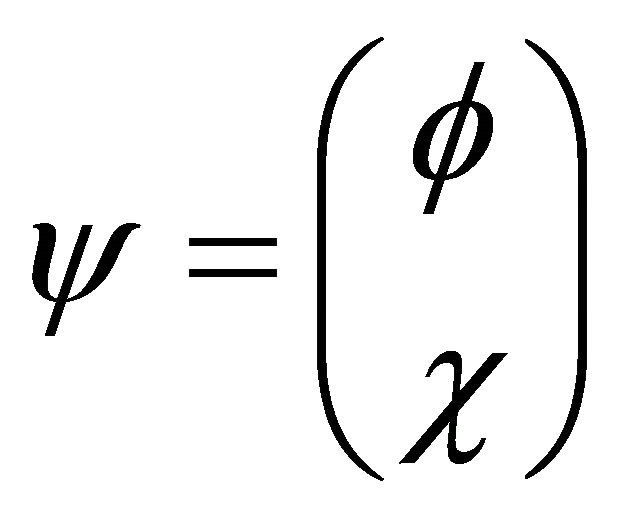 (5.2)
(5.2)
Usually, the two-component spinors  and
and 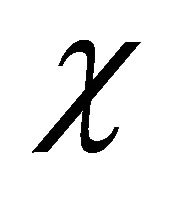 are called “positive” and “negative” energy components. In our point of view, they are the hiding “particle” and “antiparticle” fields in a particle (electron) respectively ([25], see below). Substitution of Equation (2) into Equation (1) leads to
are called “positive” and “negative” energy components. In our point of view, they are the hiding “particle” and “antiparticle” fields in a particle (electron) respectively ([25], see below). Substitution of Equation (2) into Equation (1) leads to
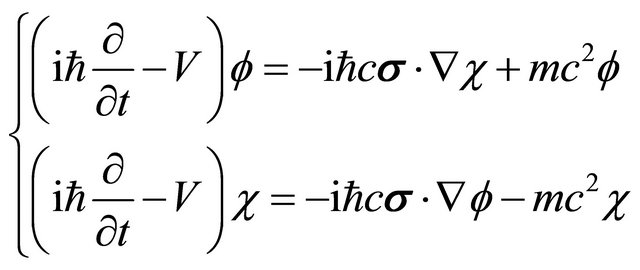 (5.3)
(5.3)
(![]() are Pauli matrices). Equation (3) is invariant under the combined space-time inversion with
are Pauli matrices). Equation (3) is invariant under the combined space-time inversion with
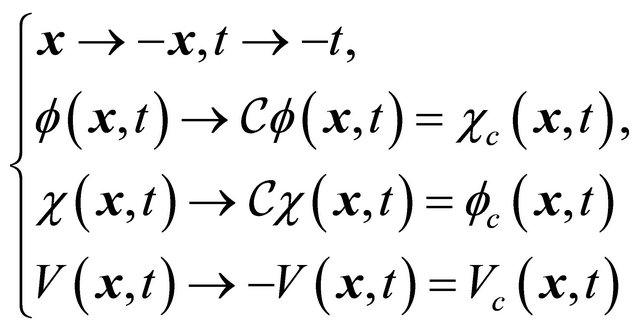 (5.4)
(5.4)
showing that in its form of two-component spinors, Dirac equation is in conformity with the underlying symmetry Equation (3.29). Note that under the space-time inversion, the ![]() remain unchanged (However, see Equations (9)- (11) below). Alternatively, Equation (3) also remains invariant under a mass inversion as
remain unchanged (However, see Equations (9)- (11) below). Alternatively, Equation (3) also remains invariant under a mass inversion as
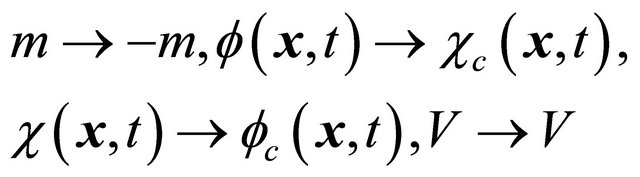 (5.5)
(5.5)
In either case of Equation (5.4) or (5.5), we have6
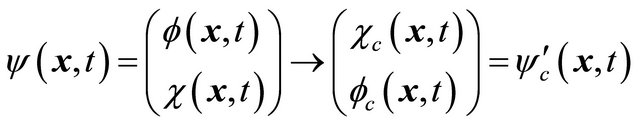 (5.6)
(5.6)
For concreteness, we consider a free electron moving along the z axis with momentum 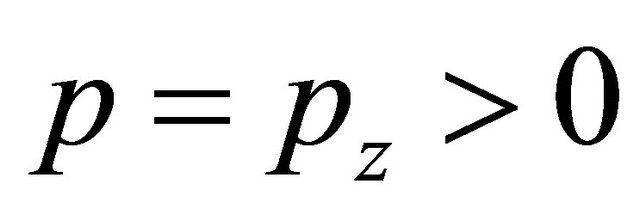 and having a helicity
and having a helicity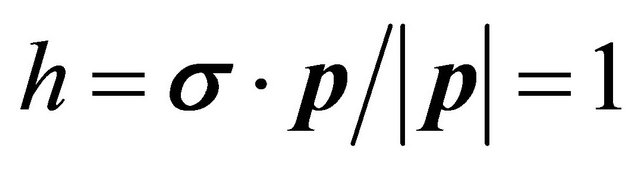 , its WF reads:
, its WF reads:
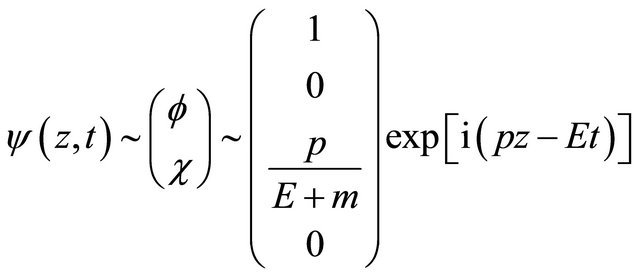 (5.7)
(5.7)
with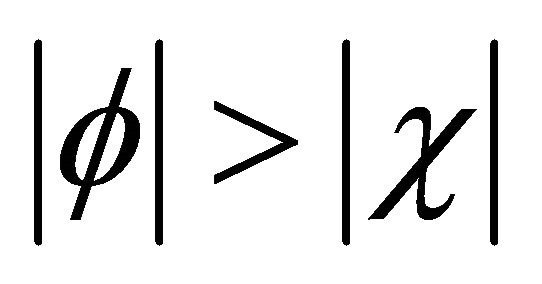 . Under a space-time inversion
. Under a space-time inversion
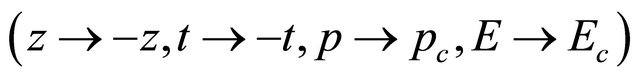 or mass inversion
or mass inversion
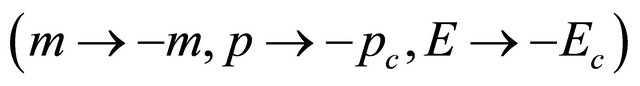 , it is transformed into a WF for positron (moving along
, it is transformed into a WF for positron (moving along  axis)
axis)
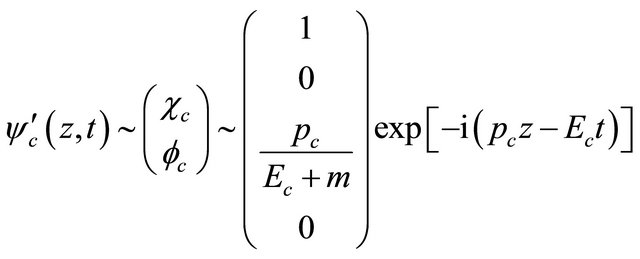 (5.8)
(5.8)
with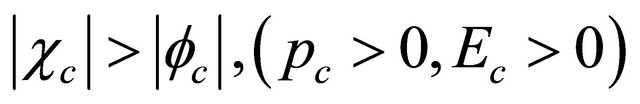 . However, the positron’s helicity becomes
. However, the positron’s helicity becomes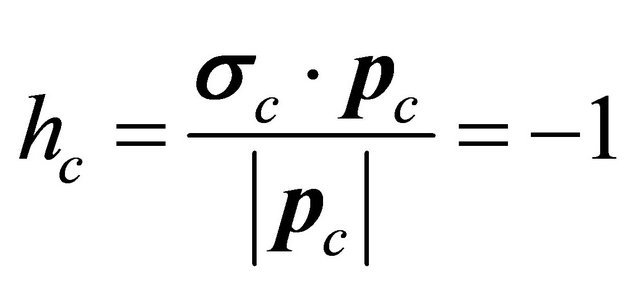 . This is because the total angular momentum operator for an electron reads
. This is because the total angular momentum operator for an electron reads
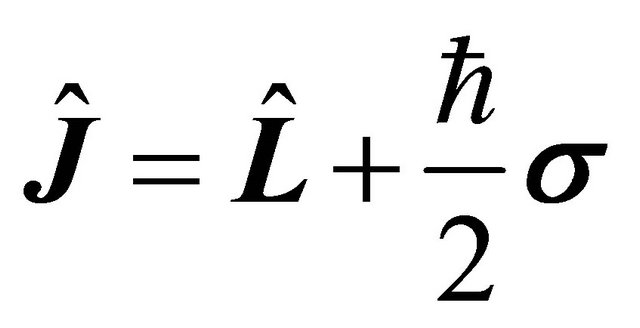 (5.9)
(5.9)
Under a space-time inversion, the orbital angular momentum operator is transformed as
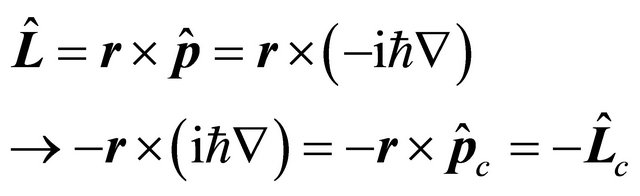 (5.10)
(5.10)
To get 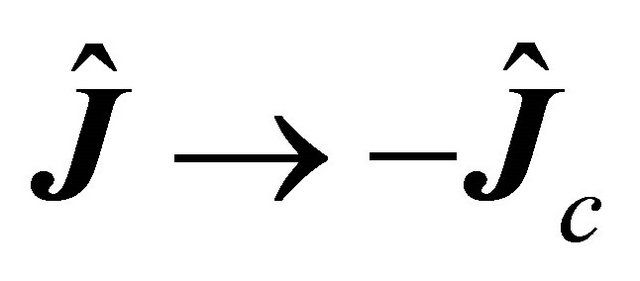 with
with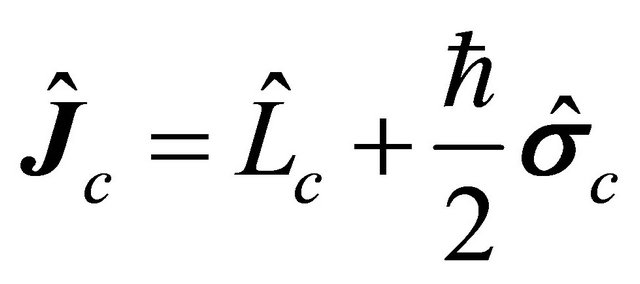 , we should have
, we should have
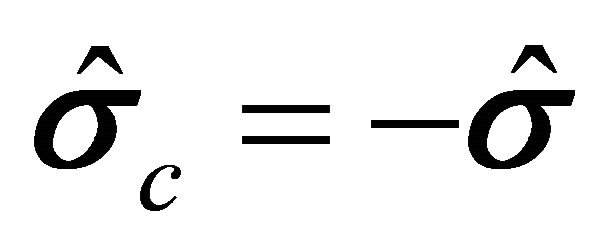 (5.11)
(5.11)
Hence the values of matrix element for positron’s spin operator 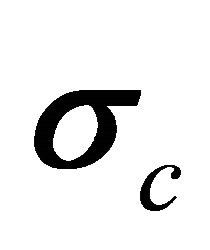 is just the negative to that for
is just the negative to that for ![]() in the same matrix representation.
in the same matrix representation.
Notice that Equation (7) describes an electron with positive helicity, i.e., 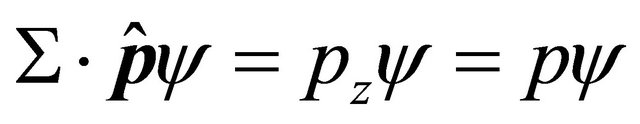 7. Under a space-time inversion, it is transformed into
7. Under a space-time inversion, it is transformed into
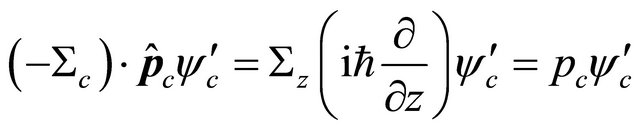 in Equation (8), i.e.,
in Equation (8), i.e.,
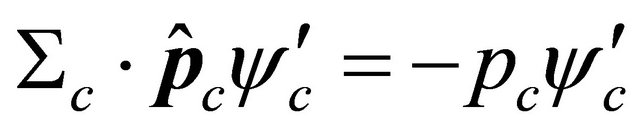 , meaning that Equation (8) describes a positron with negative helicity.
, meaning that Equation (8) describes a positron with negative helicity.
In its form of four-component spinor, Dirac equation, Equation (5.1) with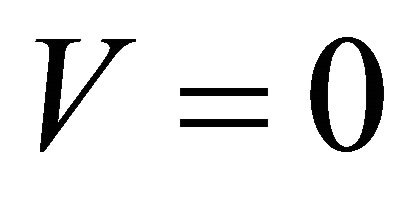 , is usually written in a covariant form as (Pauli metric is used:
, is usually written in a covariant form as (Pauli metric is used:
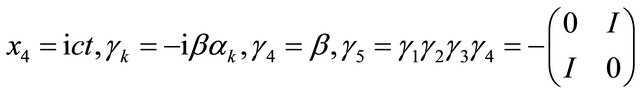 , see Ref. [25]):
, see Ref. [25]):
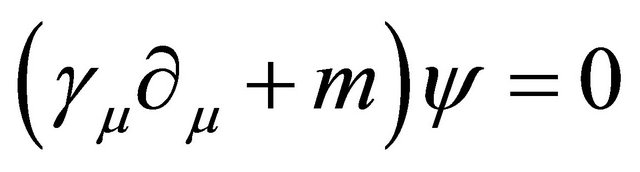 (5.12)
(5.12)
Under a space-time (or mass) inversion, it turns into an equation for antiparticle:
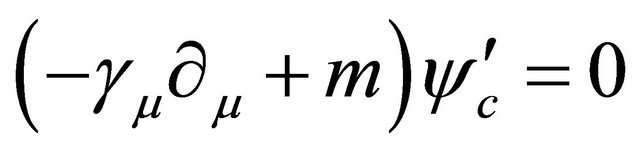 (5.13)
(5.13)
with an example of 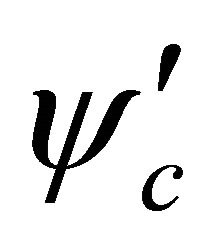 shown in Equation (8). Let us perform a representation transformation:
shown in Equation (8). Let us perform a representation transformation:
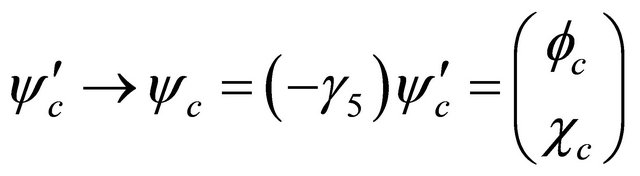 (5.14)
(5.14)
and arrive at
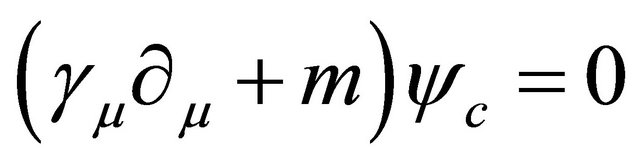 (5.15)
(5.15)
due to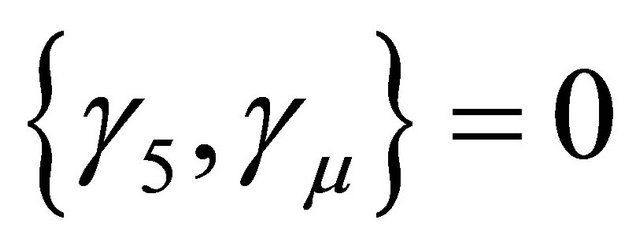 . Since
. Since 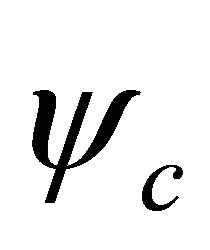 and
and 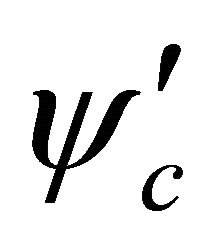 are essentially the same in physics, (this is obviously seen from its resolved form, Equation (5.3)), it is merely a trivial thing to change the position of
are essentially the same in physics, (this is obviously seen from its resolved form, Equation (5.3)), it is merely a trivial thing to change the position of 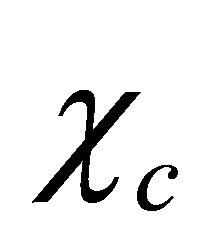 in the 4-component spinor (lower in Equation (5.14) and upper in Equation (5.8)).
in the 4-component spinor (lower in Equation (5.14) and upper in Equation (5.8)).
What important is  for characterizing an antiparticle versus
for characterizing an antiparticle versus  for a particle. Therefore, if a particle with energy E runs into a potential barrier
for a particle. Therefore, if a particle with energy E runs into a potential barrier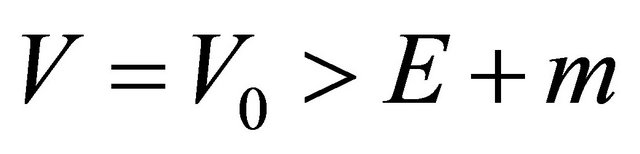 , its kinetic energy
, its kinetic energy
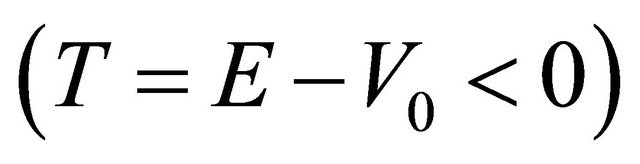 becomes negative, and its WF’s third component in Equation (5.7) suddenly turns into
becomes negative, and its WF’s third component in Equation (5.7) suddenly turns into
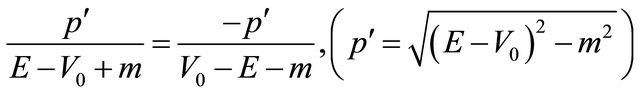 , whose absolute magnitude is larger than that of the first component. This means that it is an antiparticle’s WF satisfying Equation (5.15) (with
, whose absolute magnitude is larger than that of the first component. This means that it is an antiparticle’s WF satisfying Equation (5.15) (with 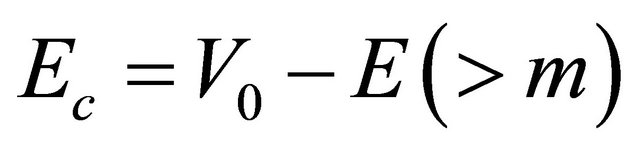 and
and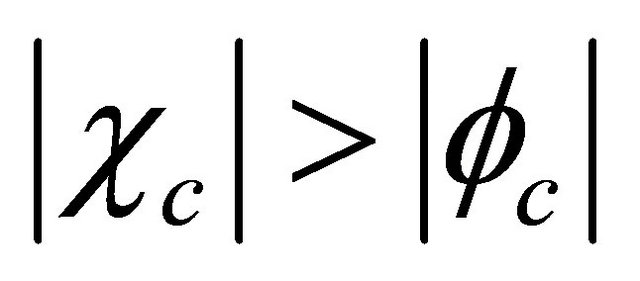 ) and will be crucial for the explanation of Klein paradox in Dirac equation (For detail, please see Appendix). However, we need to discuss the “probability density”
) and will be crucial for the explanation of Klein paradox in Dirac equation (For detail, please see Appendix). However, we need to discuss the “probability density” 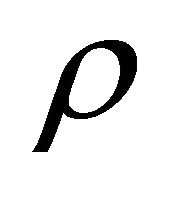 and “probability current density”
and “probability current density”  for a Dirac particle versus
for a Dirac particle versus 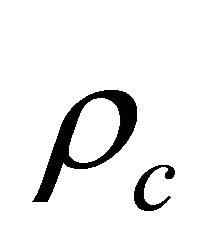 and
and  for its antiparticle. Different from that in KG equation, now we have
for its antiparticle. Different from that in KG equation, now we have
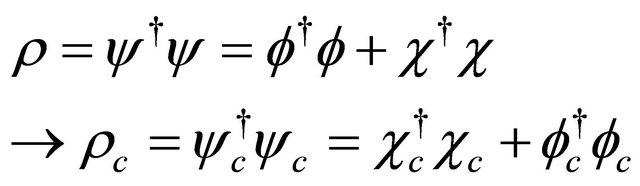 (5.16)
(5.16)
which is positive definite for either particle or antiparticle. On the other hand, we have
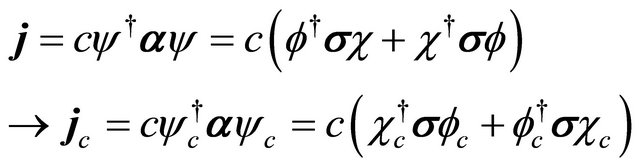 (5.17)
(5.17)
(we prefer to keep ![]() rather than
rather than 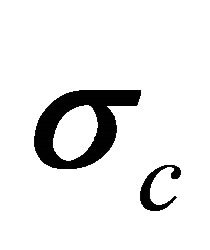 for antiparticle). For Equations (5.7), (5.8) and (5.14), we find
for antiparticle). For Equations (5.7), (5.8) and (5.14), we find 
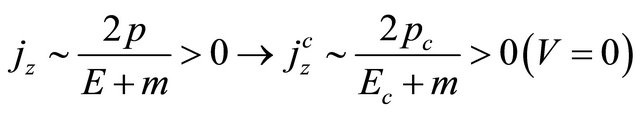 (5.18)
(5.18)
which means that the probability current is always along the momentum’s direction for either a particle or antiparticle.
Above discussions at RQM level may be summarized as follows: The first symptom for the appearance of an antiparticle is: If we perform an energy operator
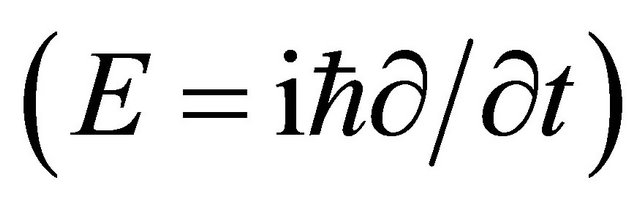 on a WF and find a negative energy
on a WF and find a negative energy
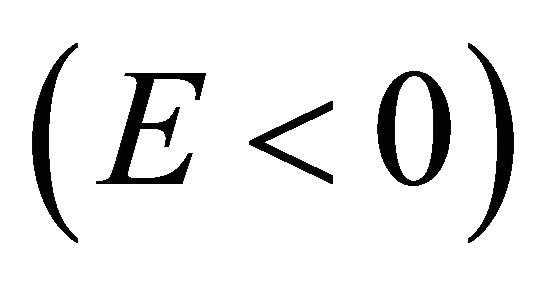 or a negative kinetic energy
or a negative kinetic energy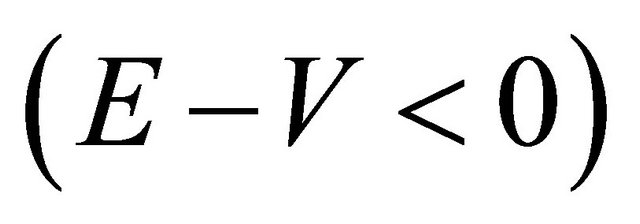 , we’d better doubt the WF being a description of antiparticle and use the operators for antiparticle, Equation (2.18). Then for further confirmation, two more criterions for
, we’d better doubt the WF being a description of antiparticle and use the operators for antiparticle, Equation (2.18). Then for further confirmation, two more criterions for 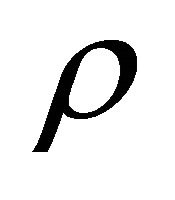 and
and  are needed (see Appendix).
are needed (see Appendix).
6. The Strong Reflection Invariance in CPT Theorem and QFT
In QFT, the starting point is the field operator which is constructed for free complex boson field as [36]
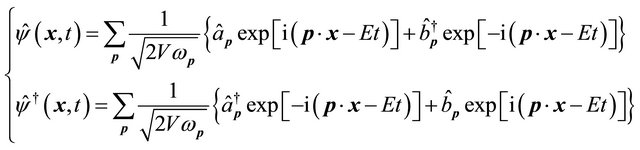 (6.1)
(6.1)
Similarly, the field operator for free Dirac field reads:
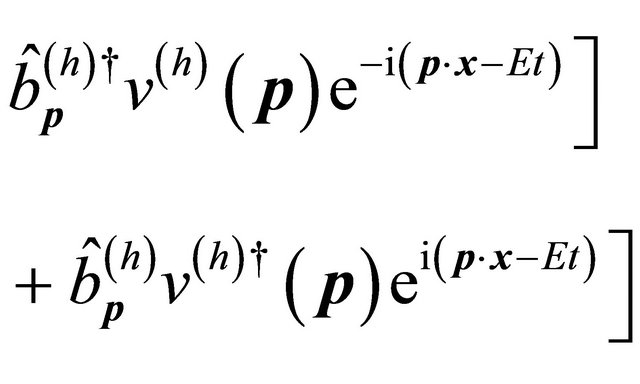
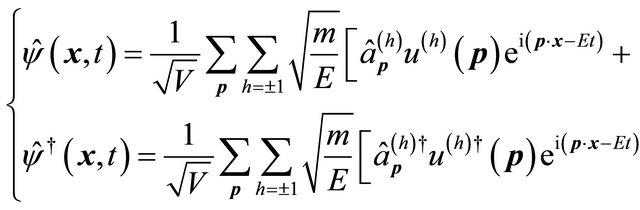 (6.2)
(6.2)
In Equation (6.1), the annihilation operator 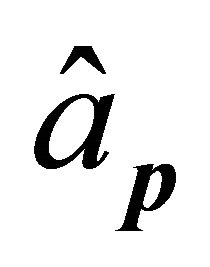 for particle and the creation operator
for particle and the creation operator 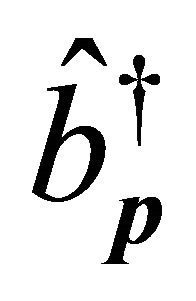 for antiparticle in Fock space are introduced. In Equation (6.2), instead of index
for antiparticle in Fock space are introduced. In Equation (6.2), instead of index ![]() (
(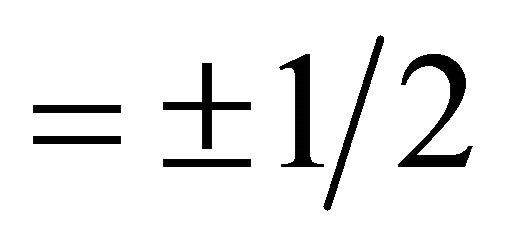 , the spin’s projection along the fixed
, the spin’s projection along the fixed  axis in space), the helicity
axis in space), the helicity  is used. See Ref. [37].
is used. See Ref. [37].
Let us return back to the CPT theorem proved by Lüders and Pauli in 1954-1957 [10-12]. The proof of CPT theorem contains a crucial step being the construction of so-called “strong reflection”, consisting in a reflection of space and time about some arbitrarily chosen origin, i.e.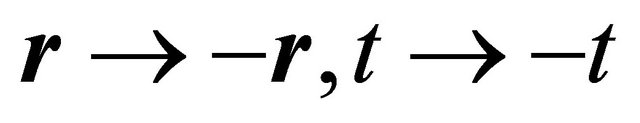 .
.
Pauli proposed and explained the strong reflection in Ref. [12] as follows: When the space-time coordinates change their sign, every particle transforms into its antiparticle simultaneously. The physical sense of the strong reflection is the substitution of every emission (absorption) operator of a particle by the corresponding absorption (emission) operator of its antiparticle. And there is no need to reverse the sign of the electric charge when the sign of space-time coordinates is reversed.
What Pauli claimed, in our understanding, means that under the strong reflection for boson field, one has
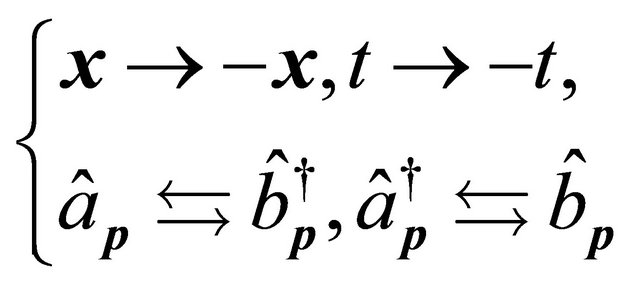 (6.3)
(6.3)
The mutual transformation, Equation (6.3), in Fock space ensures the field operators, Equation (6.1), invariant under the strong reflection in the sense of (see also [25,26]):
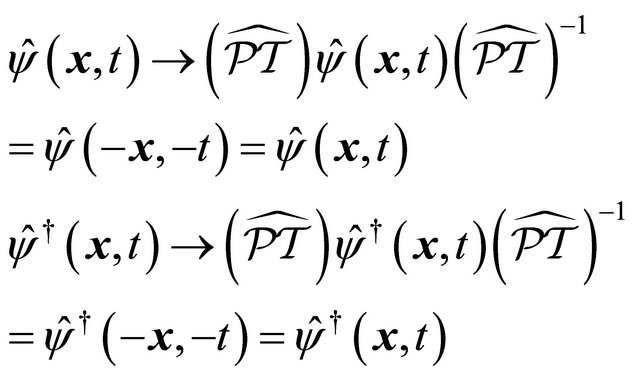 (6.4)
(6.4)
Here let us introduce the notation  to represent the strong reflection so that the presentation could be easier and clearer as shown above. Similarly, for Dirac field, under the strong reflection one has
to represent the strong reflection so that the presentation could be easier and clearer as shown above. Similarly, for Dirac field, under the strong reflection one has
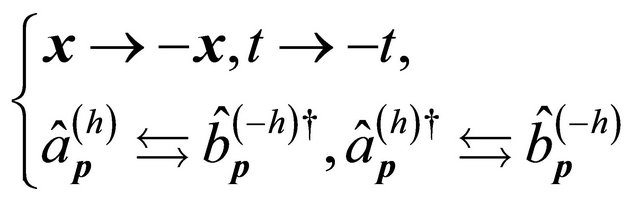 (6.5)
(6.5)
Here it is important to notice that the helicity, 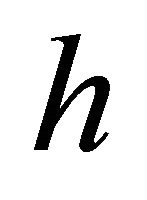 , will be reversed before and after the strong reflection for a particle and its antiparticle respectively as discussed in Section V. Because Equation (6.2) is written in 4 component spinor covariant form, the invariance of Dirac field operator under the strong reflection should be expressed rigorously as
, will be reversed before and after the strong reflection for a particle and its antiparticle respectively as discussed in Section V. Because Equation (6.2) is written in 4 component spinor covariant form, the invariance of Dirac field operator under the strong reflection should be expressed rigorously as
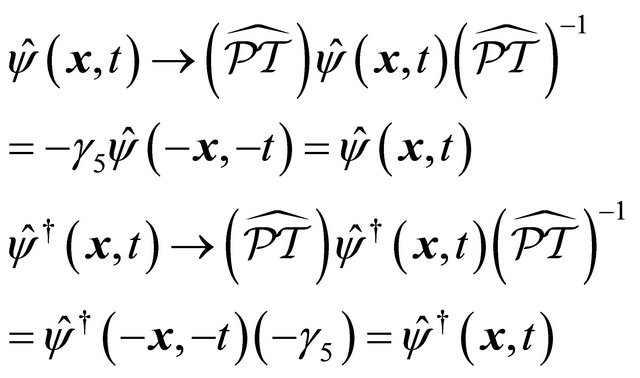 (6.6)
(6.6)
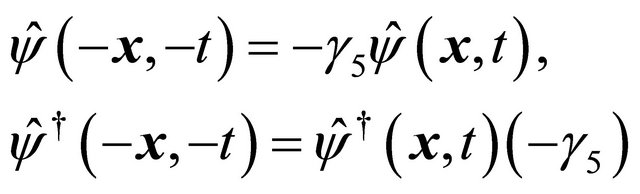 (6.7)
(6.7)
which are useful in proving the “spin-statistics connection” by strong reflection invariance.
QFT is a successful theory just because it is established on sound basis with the field operator being one of its cornerstones. Historically, through various trials and checks, Equations (6.1)-(6.2) were eventually found (see Section 3.5 of Ref. [36]). Why they are correct and why one would fail otherwise? In our understanding, it is just because they are invariant under the strong reflection as shown by Equations (6.4) and (6.6).
However, as emphasized by Pauli [12] and further stressed by Lüders [11], at least two more rules should be added in doing calculations:
(a) The order of an operator product in Fock space has to be reversed under the strong reflection, e.g.,
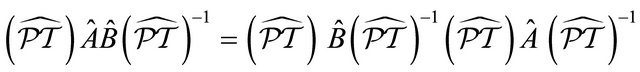 . So is the order of a process occurred in a many-particle system.
. So is the order of a process occurred in a many-particle system.
(b) Another rule is: One should always take the normal ordering when dealing with quadratic forms like 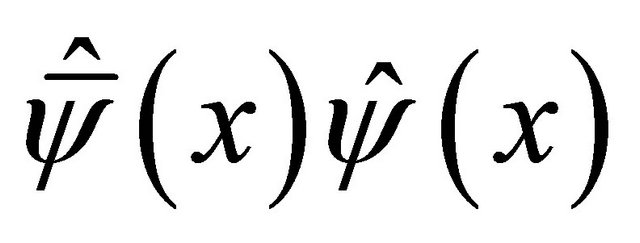 etc.
etc.
Then Pauli and Lüders were able to prove that the Hamiltonian density 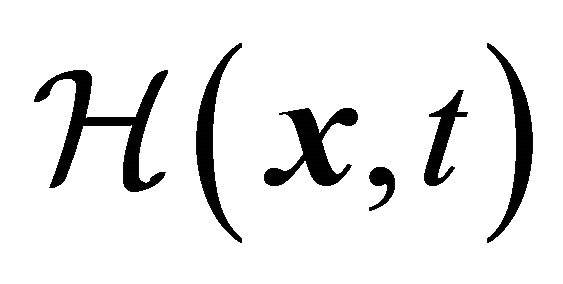 for a broad kind of model in relativistic QFT is invariant under an operation of “strong reflection”, i.e.,
for a broad kind of model in relativistic QFT is invariant under an operation of “strong reflection”, i.e.,
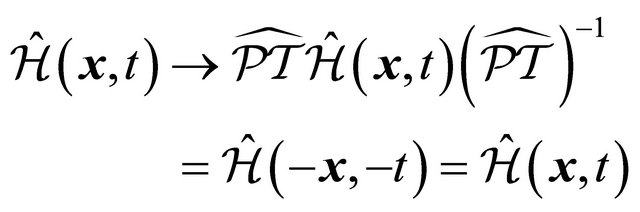 (6.8)
(6.8)
The Hamiltonian density is also invariant under a Hermitian conjugation (H.C.) as:
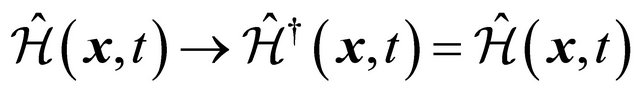 (6.9)
(6.9)
Furthermore, they proved the CPT theorem via the identification of the product of T, C, and P in QFT with the combined operation of the strong reflection and a Hermitian conjugation.
The validity of CPT invariance, i.e. Equations (6.8) and (6.9) has been verified experimentally since the discovery of parity violation ([3-8] etc.) and the establishment (and development) of standard model ([38] etc.) in particle physics till this day. See the excellent book, Ref. [19] and the Review of Particle Physics, Ref. [9].
After restudying the historical contribution of PauliLüders strong reflection invariance, we feel good in understanding that what we claim in RQM (Sections III-V) is essentially the same as or very close to their idea.
In fact, this paper is the direct continuation of our first one in 1974 [22], which was inspired jointly by the discoveries of violations in P, C, CP, T symmetries individually (but CPT invariance holds), also by Lee-Wu’s proposal in 1965 that the relationship between a particle 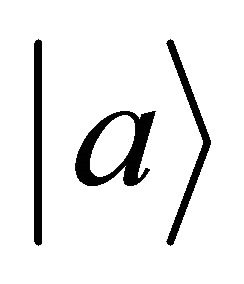 and its antiparticle
and its antiparticle 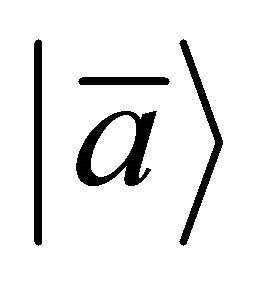 should be [13]:
should be [13]:
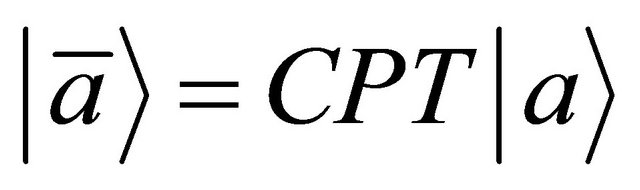 (6.10)
(6.10)
and especially by Pauli’s invention of the strong reflection in 1955 [12].
Below, we would like to show that WFs for a particle and its antiparticle given in Equations (5.7) and (5.8) are precisely that derived from QFT as expected.
Using Equation (6.2) for Dirac field, we find the WF of an electron being
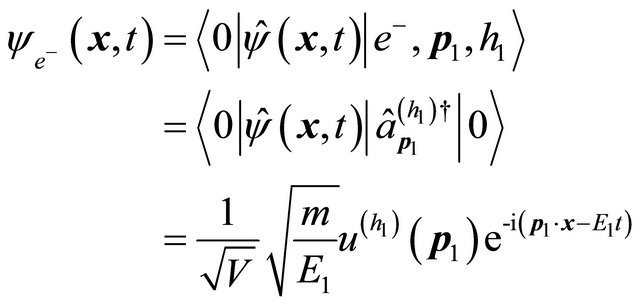 (6.11)
(6.11)
but the hermitian conjugate of a positron’s WF is given by
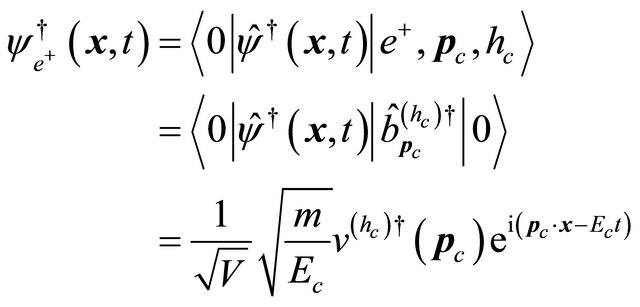 (6.12)
(6.12)
which leads to positron’s WF being
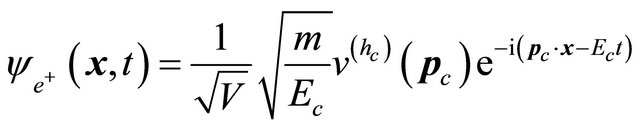 (6.13)
(6.13)
Similarly, Equations (2.20) and (2.21) can be derived from Equation (6.1) as expected.
7. An Oversight in QFT (Helicity States or Spin States?)—Why a Parity-Violation Phenomenon Was Overlooked Since 1956-1957?
Through analysis in RQM till QFT, we stress the necessity of using helicity 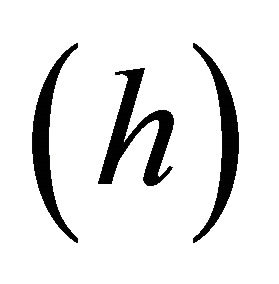 to describe a fermion or antifermion. Here is an interesting example. Since 2002, Shi and Ni [39-43] predicted a parity-violation phenomenon as follows:
to describe a fermion or antifermion. Here is an interesting example. Since 2002, Shi and Ni [39-43] predicted a parity-violation phenomenon as follows:
An unstable (decaying) fermion (e.g., neutron or muon) has different mean lifetimes for being right-handed (RH) or left-handed (LH) polarized during its flight with the same speed 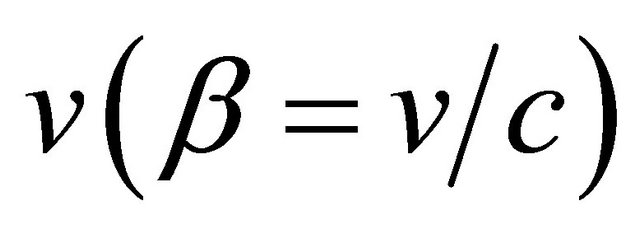
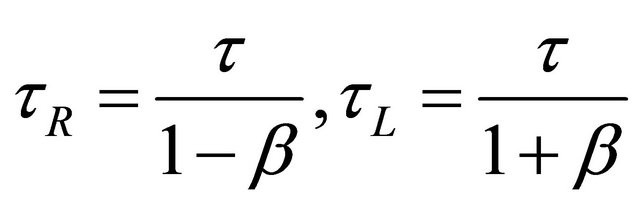 (7.1)
(7.1)
where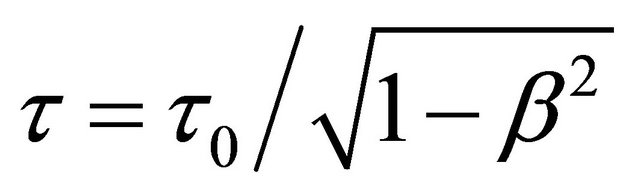 ,
, 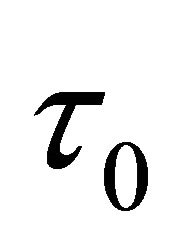 the mean lifetime when it is at rest. Similarly, for its antifermion, their lifetimes will be
the mean lifetime when it is at rest. Similarly, for its antifermion, their lifetimes will be
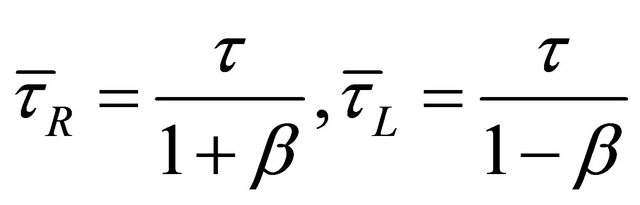 (7.2)
(7.2)
Hence, the lifetime asymmetry can be defined as
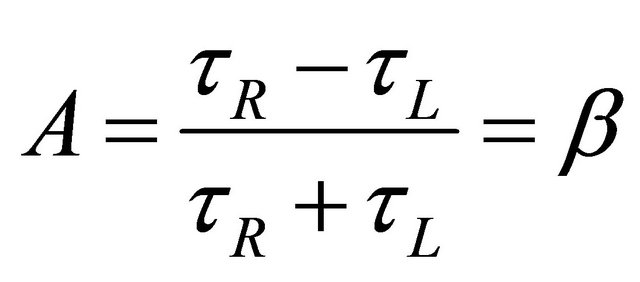 (7.3)
(7.3)
This is not a small effect. For instance, in Fermilab, physicists consider to build a muon collider [44]. The collision of 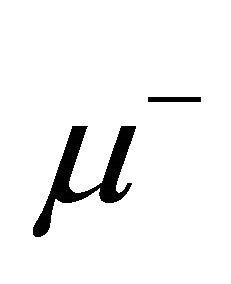 and
and 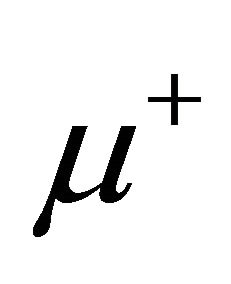 beams must happen before the muons decay. It was estimated that if a muon rings along at 1.5 TeV, the time dilation of SR stretches its lifetime to 30 milliseconds—up from 2 microseconds when it’s still. That’s time enough for 500 circuits in the final ring. However, as discussed in Ref. [43], if the prediction of life asymmetry Equation (7.1) is correct, the lifetime of RH
beams must happen before the muons decay. It was estimated that if a muon rings along at 1.5 TeV, the time dilation of SR stretches its lifetime to 30 milliseconds—up from 2 microseconds when it’s still. That’s time enough for 500 circuits in the final ring. However, as discussed in Ref. [43], if the prediction of life asymmetry Equation (7.1) is correct, the lifetime of RH 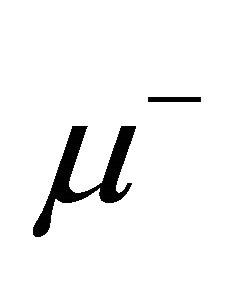 will be stretched to 146 days while that of LH
will be stretched to 146 days while that of LH 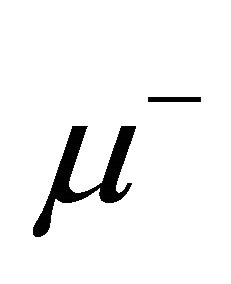 only 15 milliseconds. The lifetime asymmetry of
only 15 milliseconds. The lifetime asymmetry of 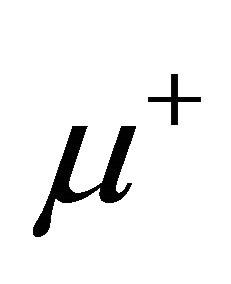 will be just the opposite as shown by Equation (7.2). Therefore, it seems necessary to take Equations (7.1)- (7.2) into account in the design of a muon collider.
will be just the opposite as shown by Equation (7.2). Therefore, it seems necessary to take Equations (7.1)- (7.2) into account in the design of a muon collider.
The problem is: How can such a parity-violation phenomenon be overlooked since 1956-1957? One theoretical reason is: in the past, for describing a fermion in flight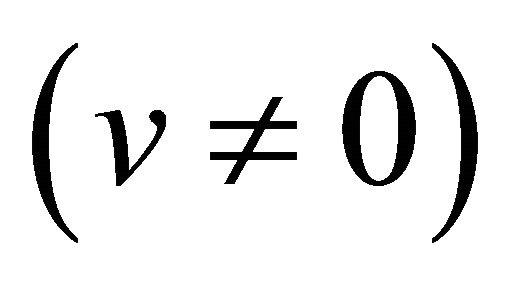 , instead of helicity states, the “spin-states” assigned by
, instead of helicity states, the “spin-states” assigned by ![]() (spin’s projection along the fixed
(spin’s projection along the fixed  axis in space) were often incorrectly used (see [40-42]). So previous calculations on the lifetime always led to a prediction that
axis in space) were often incorrectly used (see [40-42]). So previous calculations on the lifetime always led to a prediction that 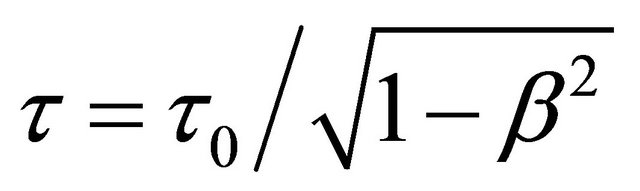 without parity-violation in contrast to Equations (7.1)-(7.3).8
without parity-violation in contrast to Equations (7.1)-(7.3).8
The interesting thing is: While Equations (7.1) and (7.2) display the violation of P or C symmetry to its maximum, their “cross-symmetry”, 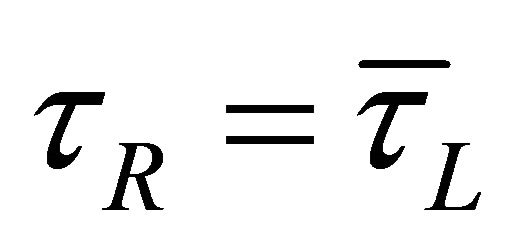 and
and 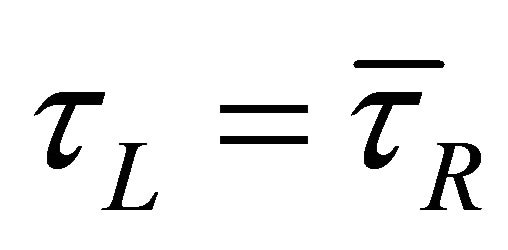 , reflects the symmetry of
, reflects the symmetry of 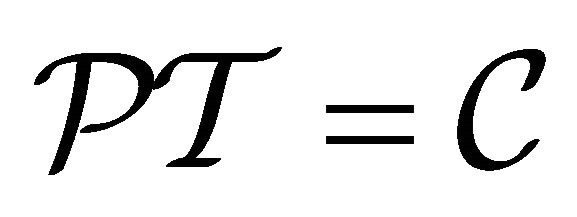 shown by Equation (6.5) exactly.
shown by Equation (6.5) exactly.
8. Dirac Particles Conserve the Parity Whereas Neutrinos Are Likely the Tachyons
8.1. Why Dirac Equation Respects the Parity Symmetry?
In the standard representation of Dirac equation for free particle 
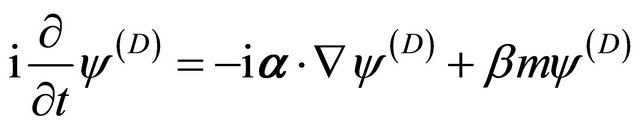 (8.1)
(8.1)
Let us choose
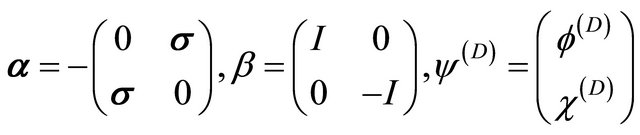 , then
, then
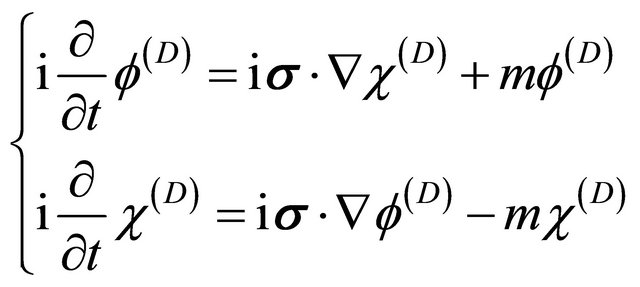 (8.2)
(8.2)
As discussed in section V, Equations (8.1) and (8.2) are invariant under the space-time inversion:
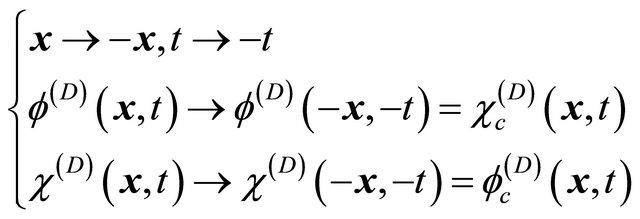 (8.3)
(8.3)
with subscript “c” meaning the antiparticle.
After transforming  into the “Weyl representation” (chiral representation) as
into the “Weyl representation” (chiral representation) as
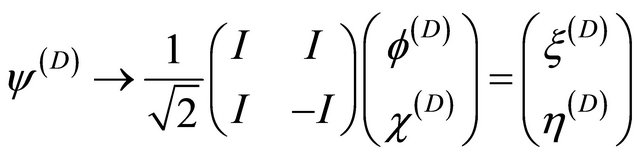 (8.4)
(8.4)
we have
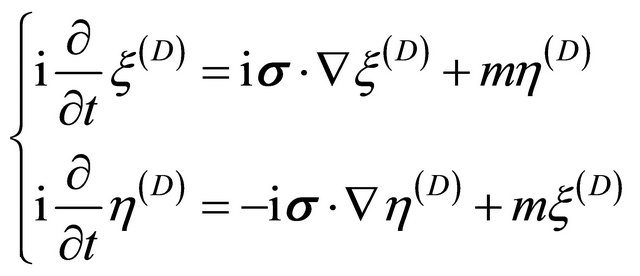 (8.5)
(8.5)
If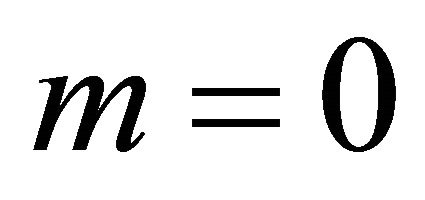 , Equation (8.5) reduces into two Weyl equations describing two kinds of permanently LH and RH polarized massless fermions respectively. So we may name
, Equation (8.5) reduces into two Weyl equations describing two kinds of permanently LH and RH polarized massless fermions respectively. So we may name 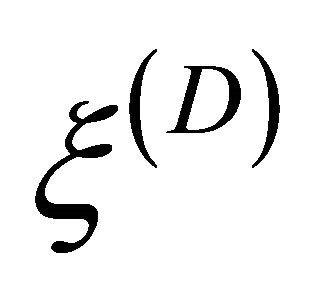 and
and 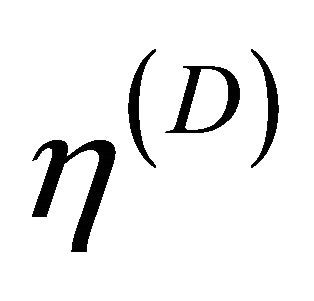 (which are usually called as chirality states or chiral fields in 4-component covariant form) as the “hidden LH and RH spinning fields” inside a Dirac particle, which can be either LH or RH polarized (with helicity
(which are usually called as chirality states or chiral fields in 4-component covariant form) as the “hidden LH and RH spinning fields” inside a Dirac particle, which can be either LH or RH polarized (with helicity 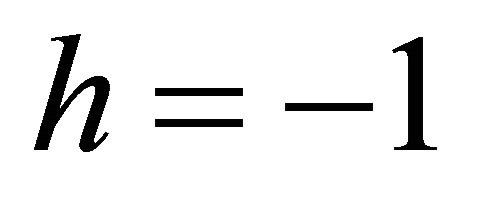 or 1) explicitly. See below.
or 1) explicitly. See below.
A new symmetry is hidden in Equation (8.5), which remains invariant under the pure space inversion 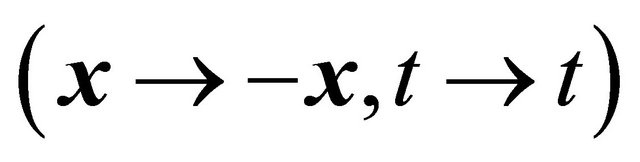 transformation, i.e., the parity operation as
transformation, i.e., the parity operation as
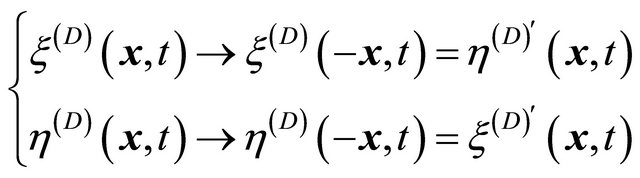 (8.6)
(8.6)
Here we add “ ” in the superscript of RHS to stress that the WF after the space inversion may be different from that at the LHS (before the space inversion). We knew that the WF in Dirac representation after a space inversion reads
” in the superscript of RHS to stress that the WF after the space inversion may be different from that at the LHS (before the space inversion). We knew that the WF in Dirac representation after a space inversion reads
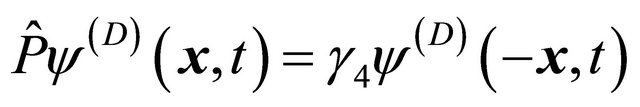 (8.7)
(8.7)
Using Equation (8.6), the RHS of Equation (8.7) turns out to be
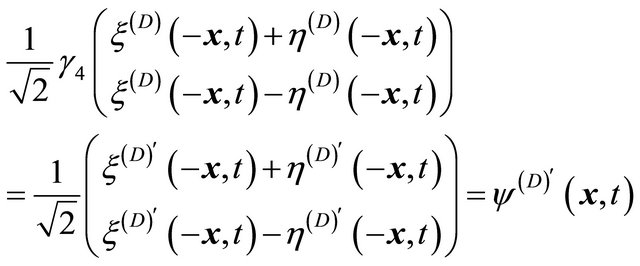 (8.8)
(8.8)
Hence, we understand the reason why a Dirac particle respects the parity symmetry as shown by Equation (8.7) is because it enjoys the symmetry Equation (8.6) hiding in the 2-component spinor form (in Weyl representation).
For concreteness, let’s write down the solution of Equation (8.1)
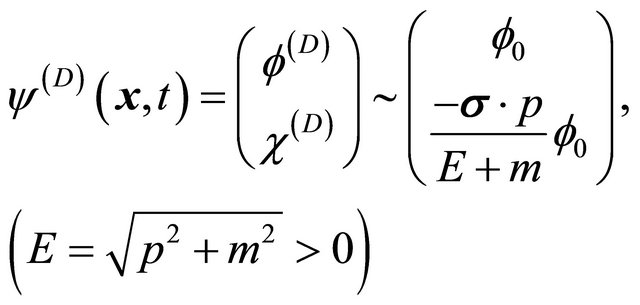 (8.9)
(8.9)
Furthermore, we choose a simplest “spin state” with
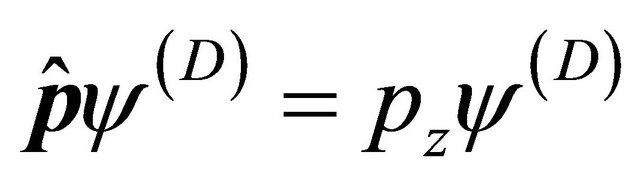 and
and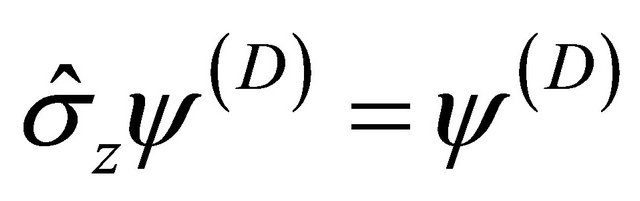 :
:
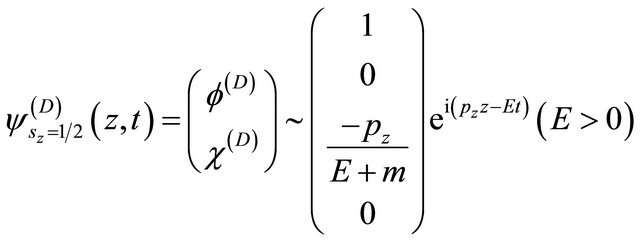 (8.10)
(8.10)
While Equation (8.10) is an eigenfunction of 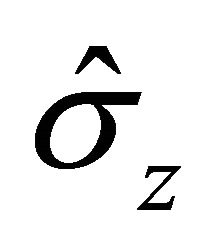 with eigenvalue
with eigenvalue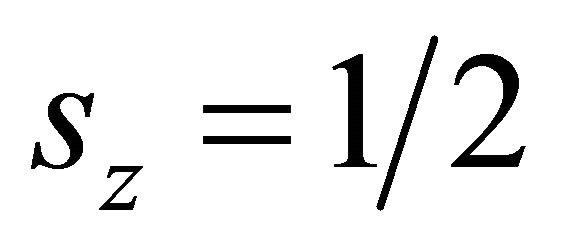 , its helicity
, its helicity 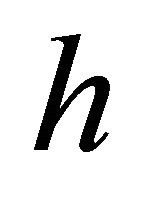 remains unfixed, depending on the value of
remains unfixed, depending on the value of 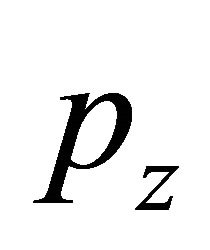 being positive or negative. Only after
being positive or negative. Only after 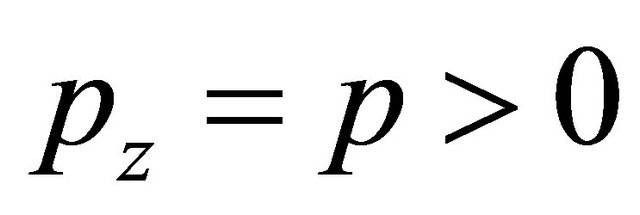 is fixed, can we have a “helicity state” describing a RH particle with
is fixed, can we have a “helicity state” describing a RH particle with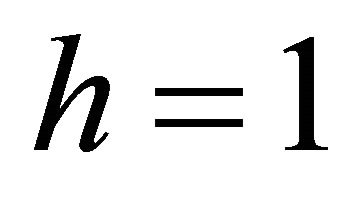 :
:
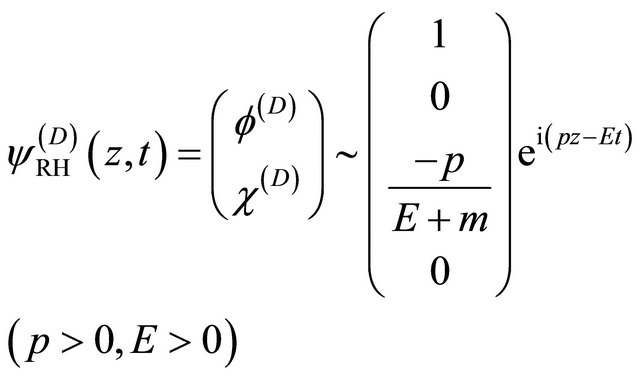 (8.11)
(8.11)
Looking at Equation (8.11) in the Weyl representation, we see that
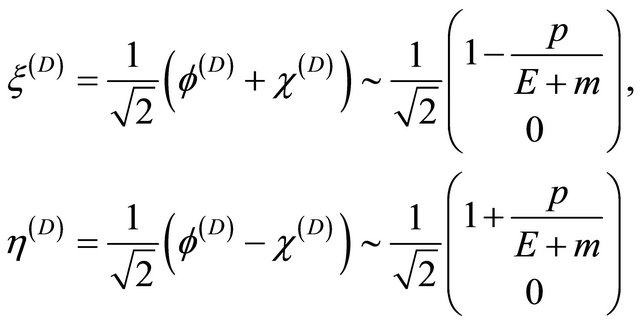 (8.12)
(8.12)
 . So Equation (8.11) describes a RH particle just because the
. So Equation (8.11) describes a RH particle just because the  field dominates the
field dominates the 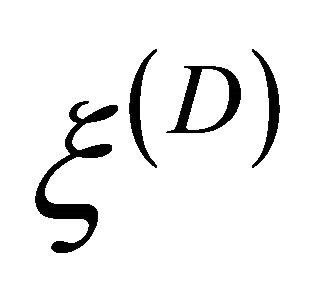 field. Now we perform a space inversion on Equation (8.11), according to the rule Equation (8.7), yielding
field. Now we perform a space inversion on Equation (8.11), according to the rule Equation (8.7), yielding
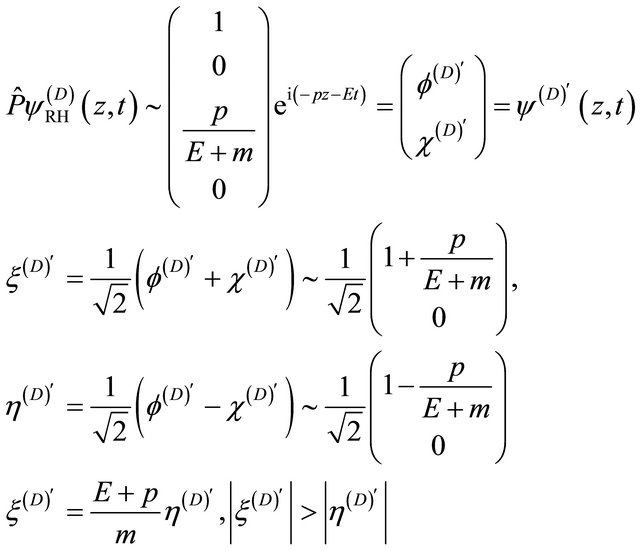
(8.13)
Hence we see that the reason why 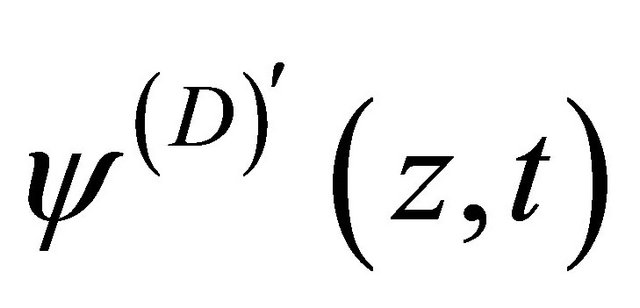 becomes a LH WF, i.e.,
becomes a LH WF, i.e.,
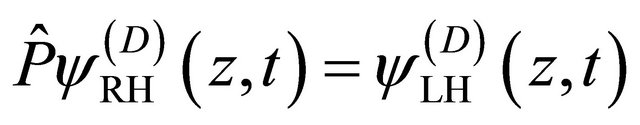 (8.14)
(8.14)
is just because of the dominance of ![]() field over
field over
![]() field after the P-operation. Before and after the operation,
field after the P-operation. Before and after the operation, 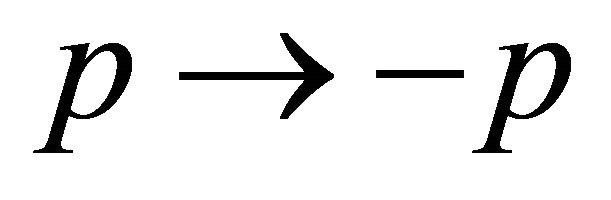 , the dominant (subordinate) field is transformed into dominant (subordinate) field:
, the dominant (subordinate) field is transformed into dominant (subordinate) field:
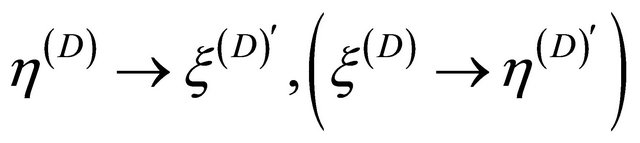 , as shown by Equation (8.6).
, as shown by Equation (8.6).
In summary, Dirac equation is invariant under a space inversion whereas its concrete solution of WF may be not. The latter may change from that for a RH particle to a LH one or vice versa, but with the same mass m, showing the law of parity conservation exactly.
8.2. Tachyon Equation as a Counterpart of the Dirac Equation
Now a question arises: Can we find an equation which violates the symmetry of pure space inversion?
The answer is “yes”. Let’s introduce a new equation in Weyl representation from Equation (8.5) by erasing the superscript (D), replacing the mass term by 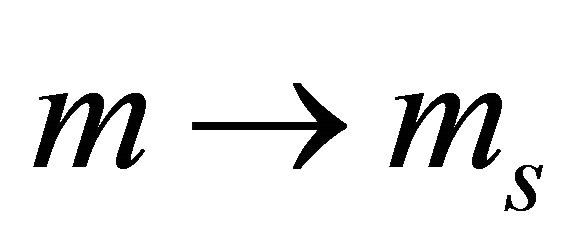 and changing its sign from “+” to “−” in the first equation of Equation (8.5) only [46]
and changing its sign from “+” to “−” in the first equation of Equation (8.5) only [46]
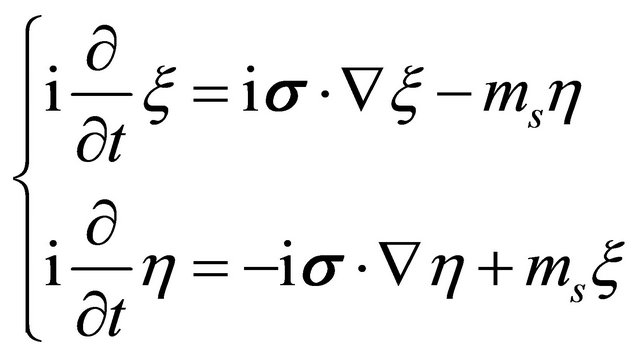 (8.15)
(8.15)
where 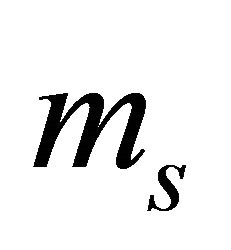 (real and positive) refers to the mass of a hypothetical particle. We will see immediately that it is a “superluminal particle” or “tachyon”.
(real and positive) refers to the mass of a hypothetical particle. We will see immediately that it is a “superluminal particle” or “tachyon”.
Indeed, substituting a plane-wave solution
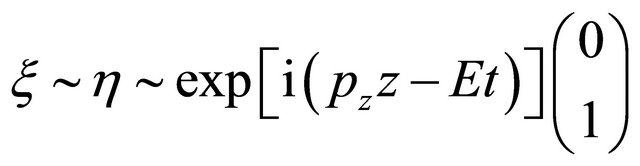 (8.16)
(8.16)
with the particle’s helicity 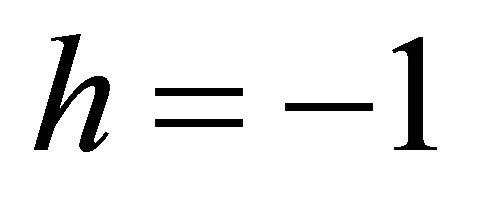 into Equation (8.15), we find that
into Equation (8.15), we find that 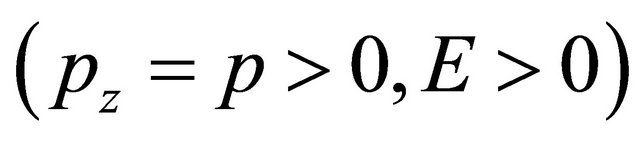
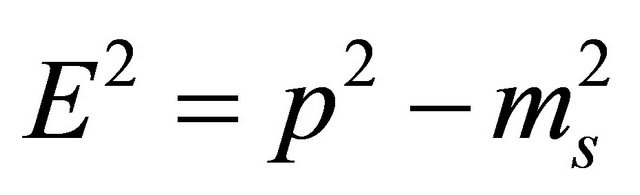 (8.17)
(8.17)
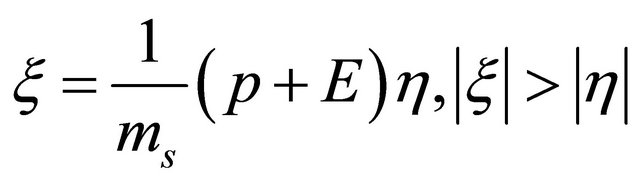 (8.18)
(8.18)
Since 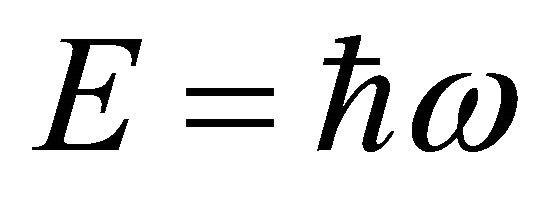 and
and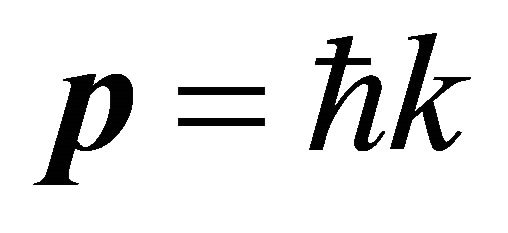 , from Equation (8.17), the dispersion-relation of wave reads
, from Equation (8.17), the dispersion-relation of wave reads
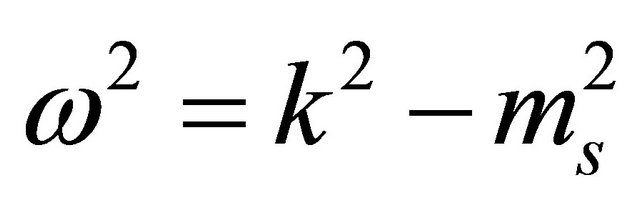 (8.19)
(8.19)
As in Section IV, we define the wave’s phase velocity 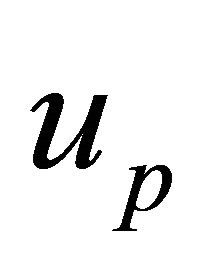 as
as
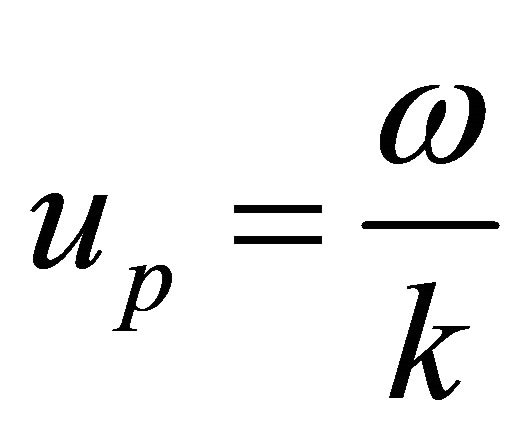 (8.20)
(8.20)
while its group velocity 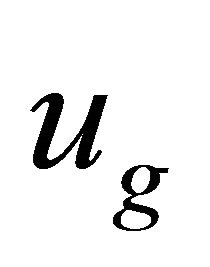
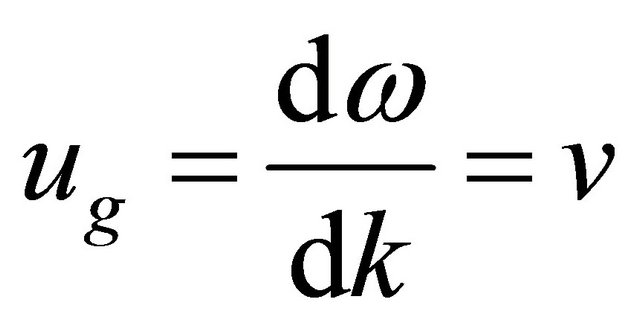 (8.21)
(8.21)
being identical with the particle’s velocity![]() . Equation (8.19) yields a relation between them coinciding with Equation (4.15) exactly:
. Equation (8.19) yields a relation between them coinciding with Equation (4.15) exactly:
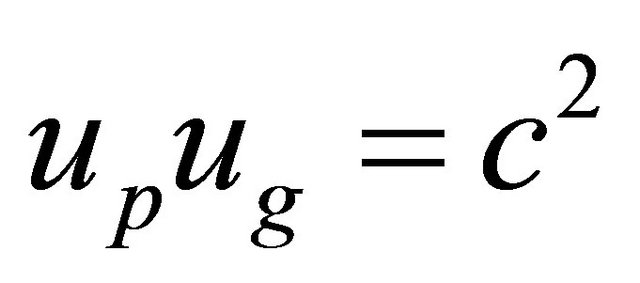 (8.22)
(8.22)
However, the relations among  and
and ![]() are dramatically different
are dramatically different
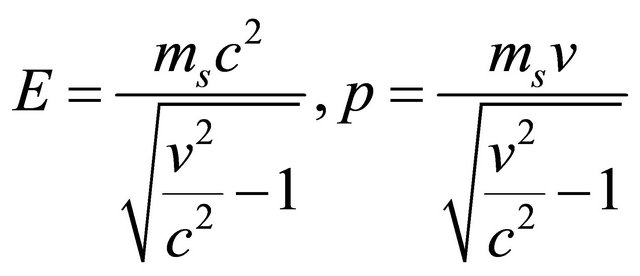 (8.23)
(8.23)
which dictate ![]() such that
such that 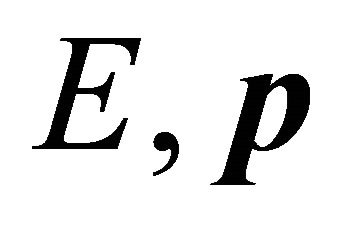 are real and
are real and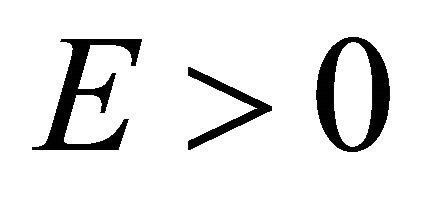 .
.
Like Equation (8.4), we define:
 (8.24)
(8.24)
and find from Equation (8.15) that (in Dirac representation)
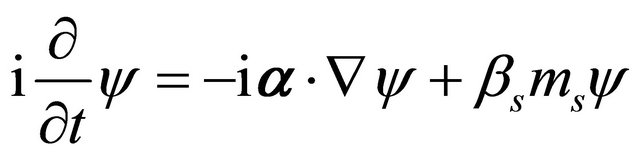 (8.25)
(8.25)
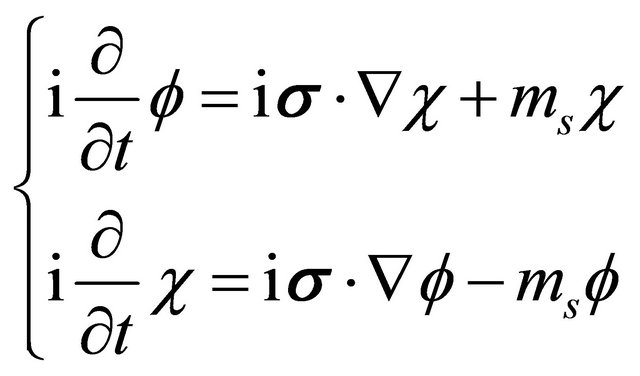 (8.26)
(8.26)
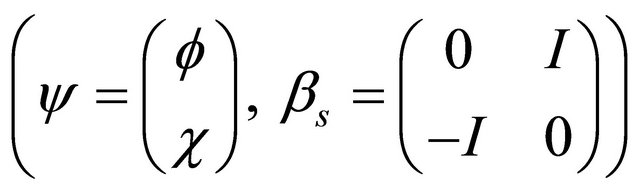 . Despite the difference between Equation (8.26) and Dirac equation, Equation (8.2), both of them respect the combined space-time inversion
. Despite the difference between Equation (8.26) and Dirac equation, Equation (8.2), both of them respect the combined space-time inversion 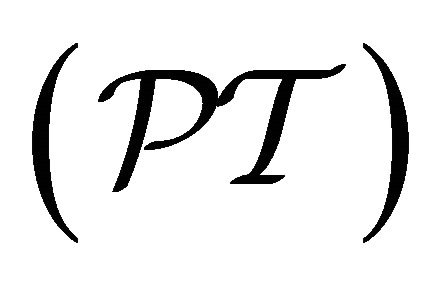 symmetry like Equation (8.3)
symmetry like Equation (8.3)
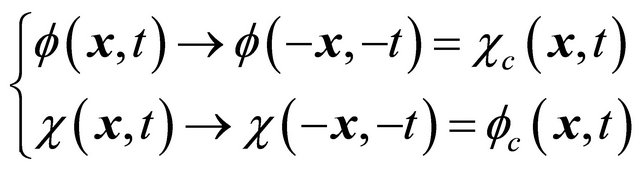 (8.27)
(8.27)
with
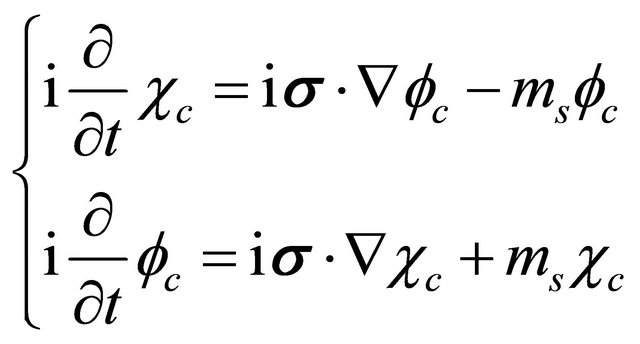 (8.28)
(8.28)
Similarly, we define the WF in Weyl representation after  inversion as:
inversion as:
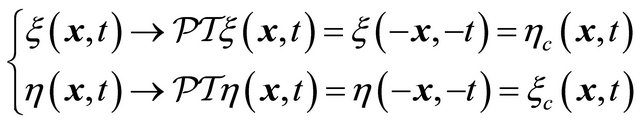 (8.29)
(8.29)
Based on Equations (8.27)-(8.29), we find
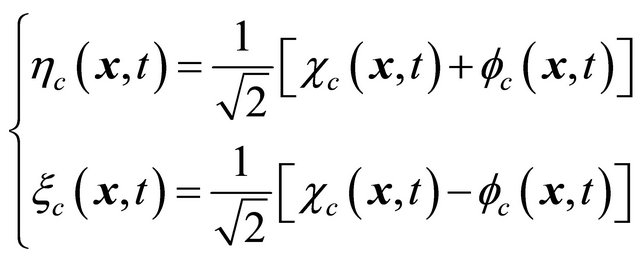 (8.30)
(8.30)
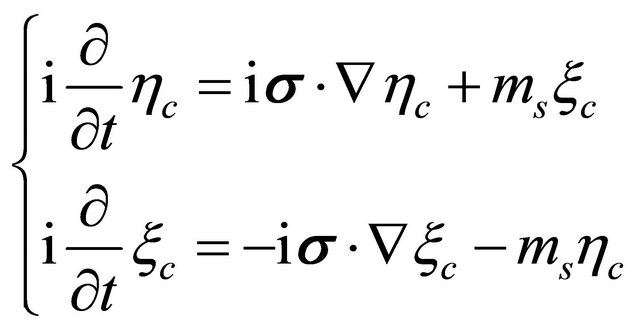 (8.31)
(8.31)
which can also be obtained via the  operation on Equation (8.15). Equations (8.15) and (8.31) are better to be compared in the following form:
operation on Equation (8.15). Equations (8.15) and (8.31) are better to be compared in the following form:
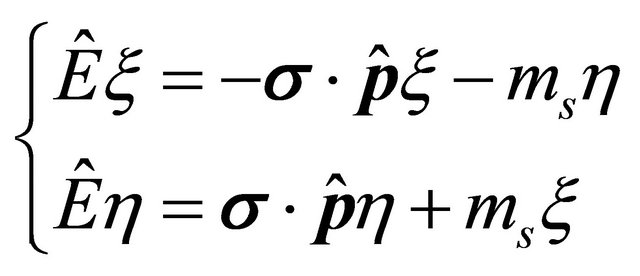 (8.32)
(8.32)
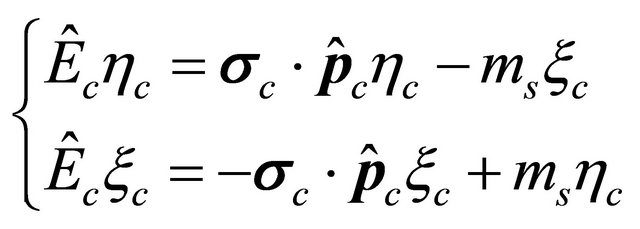 (8.33)
(8.33)
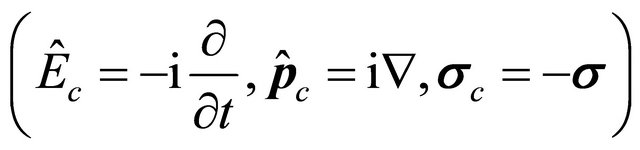 . Interestingly, Equation
. Interestingly, Equation
(8.33) can also be reached from Equation (8.32) via a “mass inversion” like that in Sections III and V:
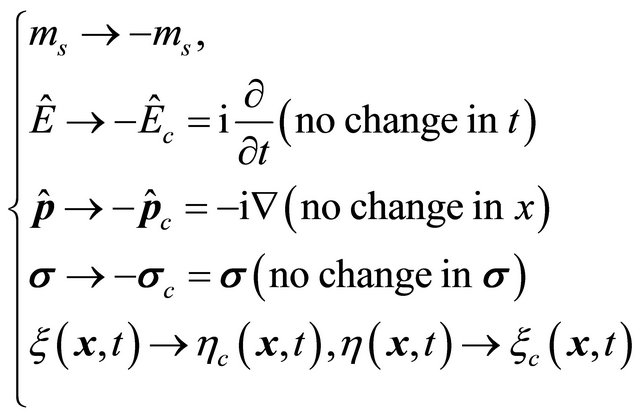 (8.34)
(8.34)
Furthermore, the probability density and probability current density before and after the  inversion can be derived as:
inversion can be derived as:
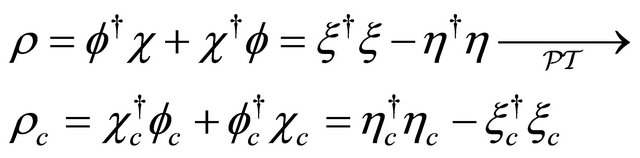 (8.35)
(8.35)
and
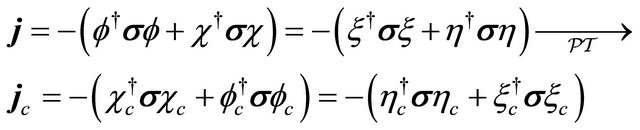 (8.36)
(8.36)
respectively. It is the sharp contrast between Equation (8.35) and Equation (5.16) for Dirac equation (i.e.,
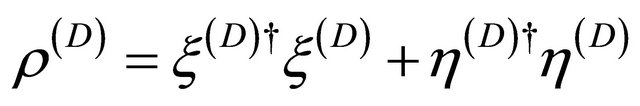 ), that makes Equation (8.15)
), that makes Equation (8.15)
so unique as shown below.
Let us look at the example of WF for tachyon, Equations (8.16)-(8.18), with 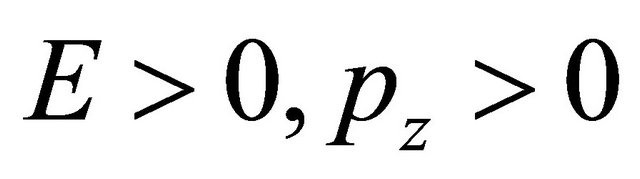 and
and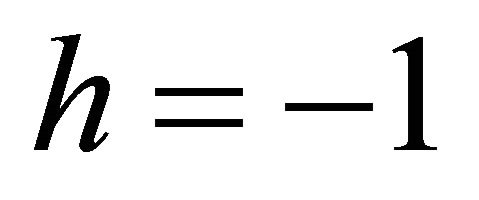 . It is allowed just because
. It is allowed just because 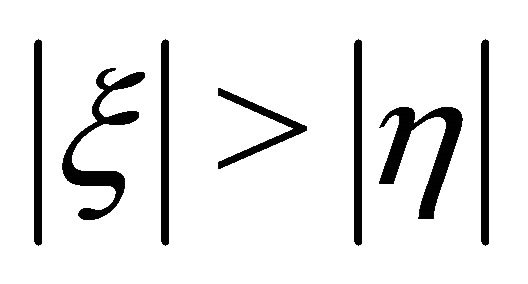 and so
and so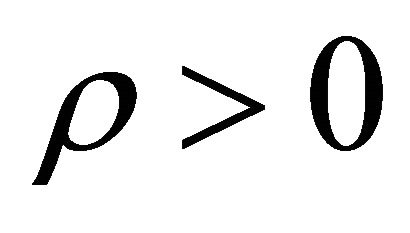 . Second choice of Equation (8.16) with
. Second choice of Equation (8.16) with
 but
but
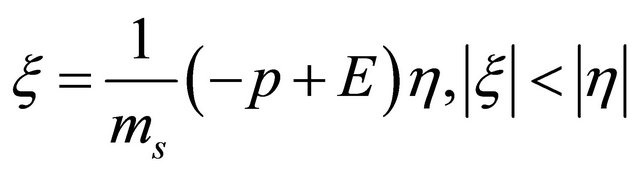 (8.37)
(8.37)
should be fobidden due to its ρ < 0. Another two possible WFs with 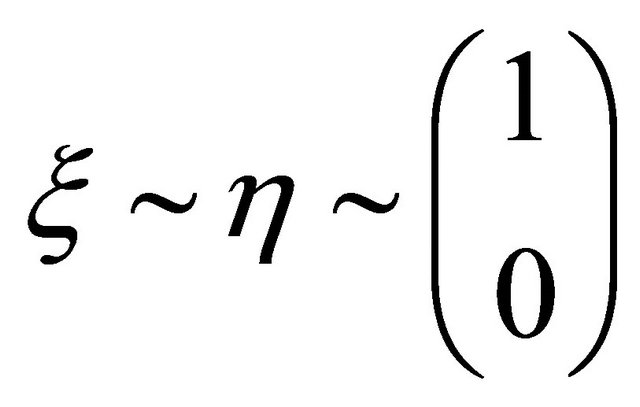 have
have 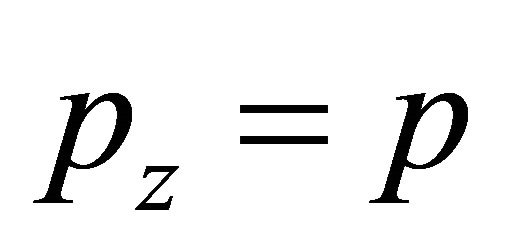 and
and 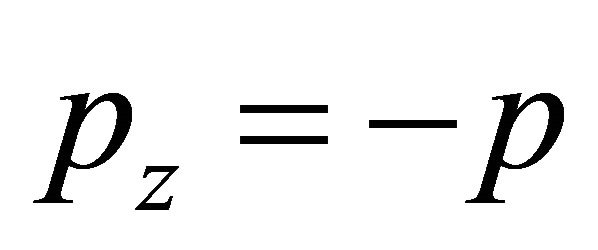 respectively, only the last one with
respectively, only the last one with
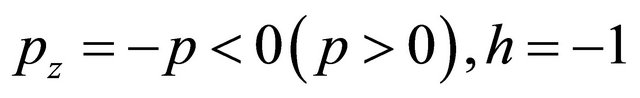 is allowed due to its
is allowed due to its
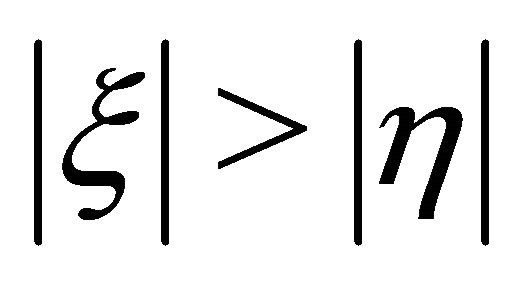 and
and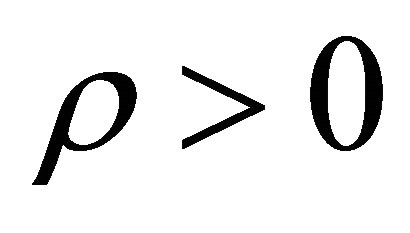 .
.
Let us turn to the solution of Equation (8.31) for antitachyon with 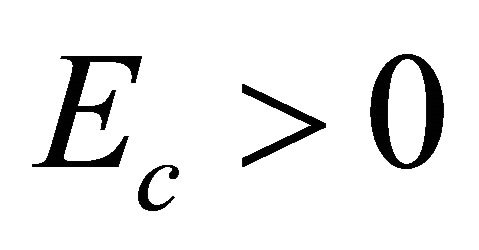 by just performing
by just performing  operation on Equation (8.16) yielding:
operation on Equation (8.16) yielding:
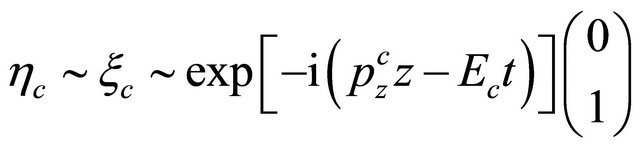 (8.38)
(8.38)
Now if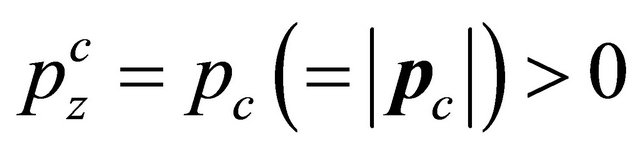 , since
, since
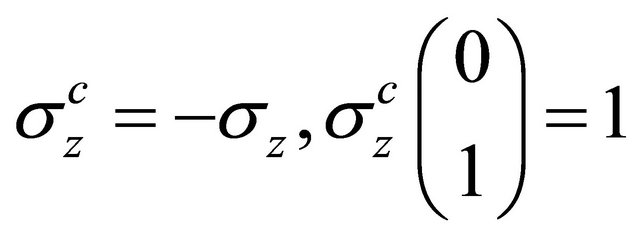 , so helicity
, so helicity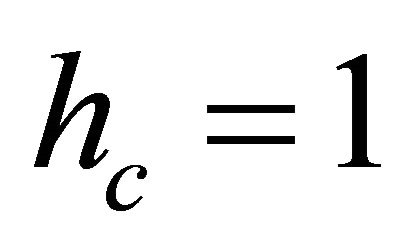 . Substitution of Equation (8.38) into Equation (8.33) yields:
. Substitution of Equation (8.38) into Equation (8.33) yields:
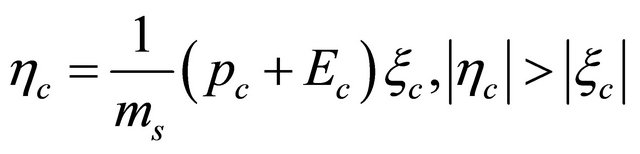 (8.39)
(8.39)
which is allowed due to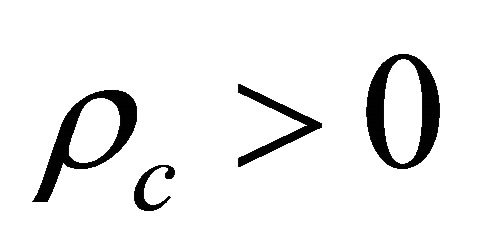 . Second choice of Equation (8.38) with
. Second choice of Equation (8.38) with 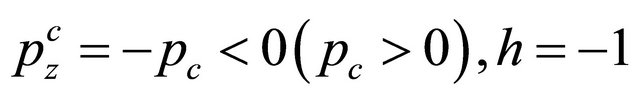 but
but
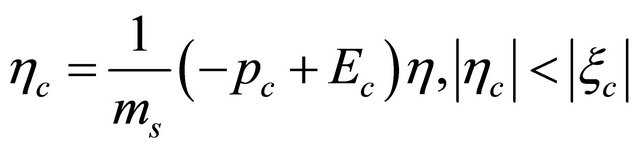 (8.40)
(8.40)
should be forbidden due to its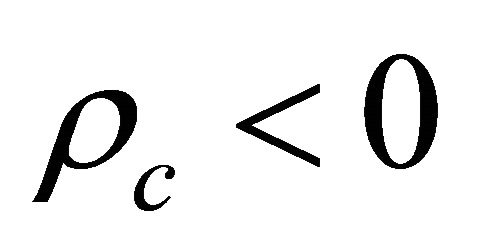 . In another two possible WFs with
. In another two possible WFs with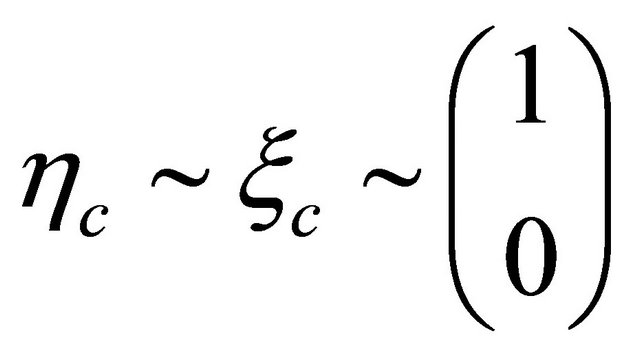 , only that with
, only that with
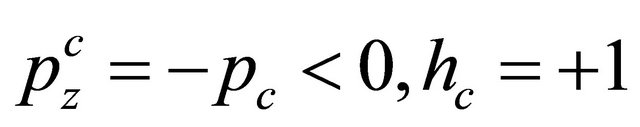 is allowed due to
is allowed due to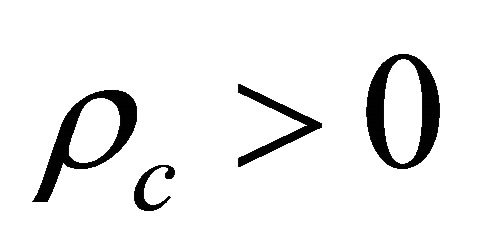 .
.
Hence we see that: The tachyon can only exist in a left-handed (LH) polarized state (with helicity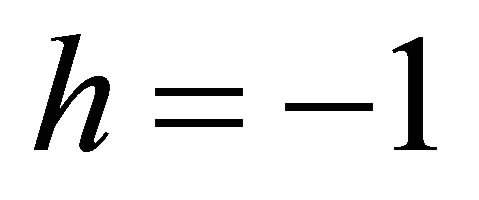 ) whereas antitachyon only in a right-handed (RH) polarized state (with
) whereas antitachyon only in a right-handed (RH) polarized state (with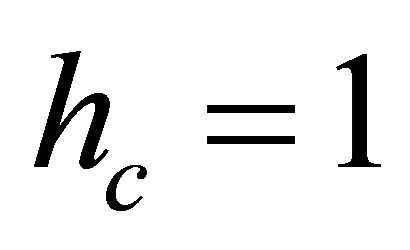 ). We tentatively link this strange feature with that found in neutrinos—only
). We tentatively link this strange feature with that found in neutrinos—only 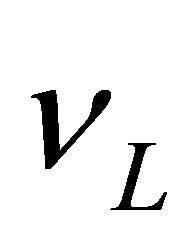 and
and 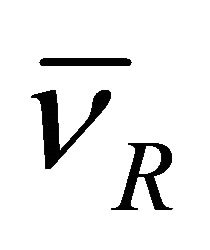 exists in nature whereas
exists in nature whereas  and
and 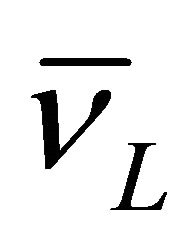 are strictly forbidden.
are strictly forbidden.
Furthermore, at first sight, although Equation (8.15) certainly has no symmetry under the space inversion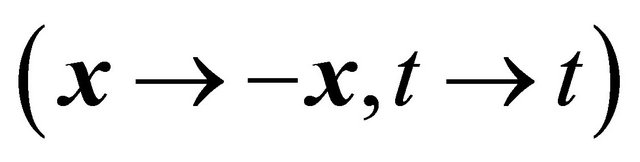 , it seems to enjoy a pure “timeinversion”
, it seems to enjoy a pure “timeinversion” 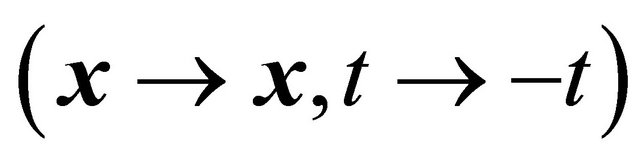 symmetry like
symmetry like
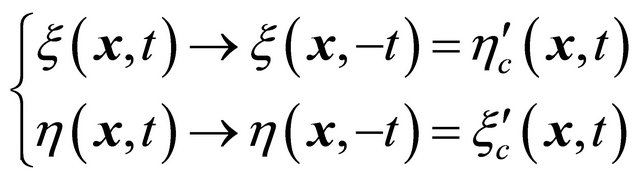 (8.41)
(8.41)
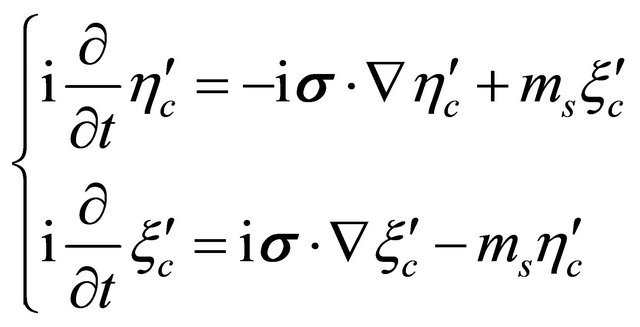 (8.42)
(8.42)
We add “ ” in the superscript of
” in the superscript of 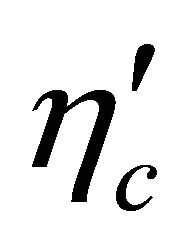 to stress that
to stress that 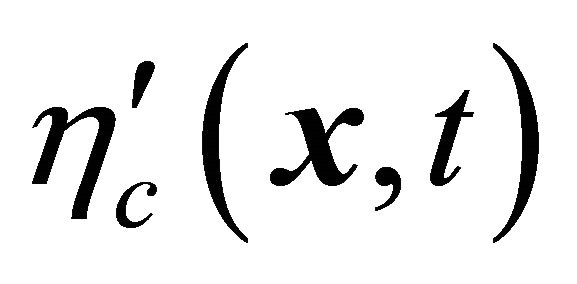 (being a time reversed WF), though looks like some antitachyon’s WF, is obviously different from
(being a time reversed WF), though looks like some antitachyon’s WF, is obviously different from 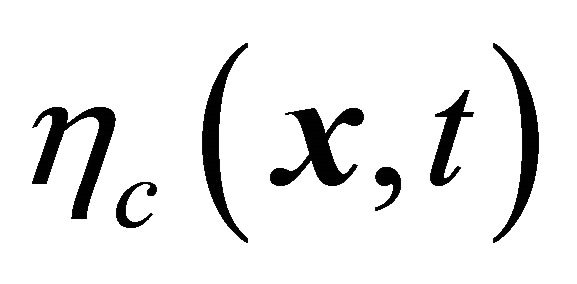 gained through the
gained through the  inversion, Equation (8.31). Actually, based on Equations (8.29)-(8.31) and (8.41)-(8.42), we have:
inversion, Equation (8.31). Actually, based on Equations (8.29)-(8.31) and (8.41)-(8.42), we have:
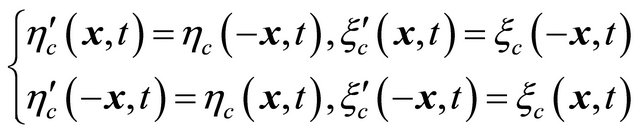 (8.43)
(8.43)
Interestingly, we cannot find from Equation (8.42) the “physical solution” of 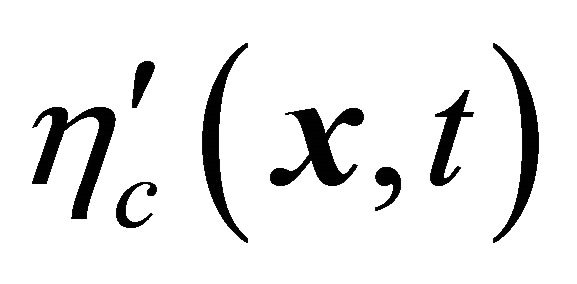 with
with  (so
(so ) and
) and  (for
(for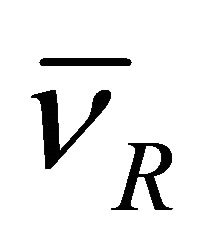 ) simultaneously. Only
) simultaneously. Only 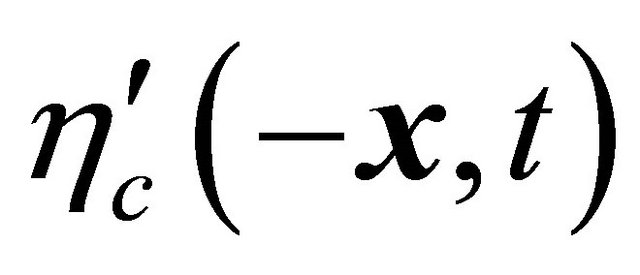 makes physical sense, but it is just
makes physical sense, but it is just 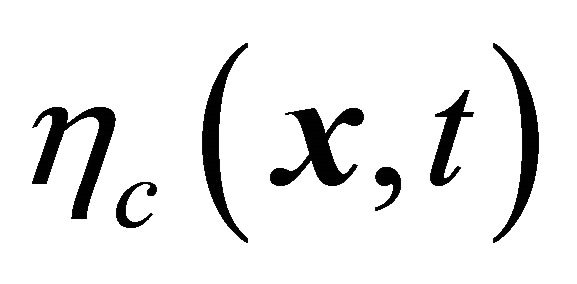 like that discussed in Equation (8.39). Notice that the sign change
like that discussed in Equation (8.39). Notice that the sign change ![]() in the phase of WF makes a change in the direction of momentum
in the phase of WF makes a change in the direction of momentum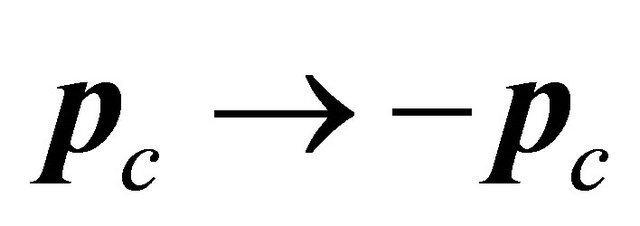 . But a WF is always composed of two fields in confrontation, like
. But a WF is always composed of two fields in confrontation, like 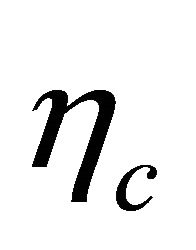 versus
versus 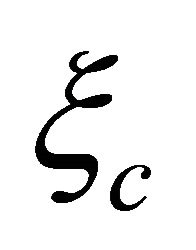 here. And the explicit helicity
here. And the explicit helicity 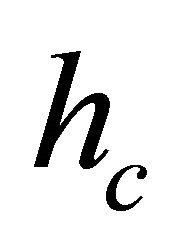 is determined by which one of these two hidden fields being in charge. So the change of
is determined by which one of these two hidden fields being in charge. So the change of ![]() in these four equalities of Equation (8.43) does reverse the status of
in these four equalities of Equation (8.43) does reverse the status of 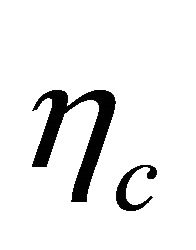 versus
versus 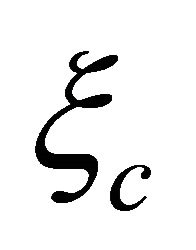 (or
(or 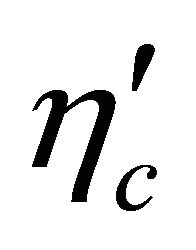 vs
vs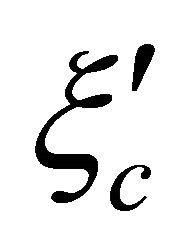 ), rendering helicity reversed explicitly. The subtlety of tachyon equation, unlike Dirac equation, lies in the fact that only
), rendering helicity reversed explicitly. The subtlety of tachyon equation, unlike Dirac equation, lies in the fact that only 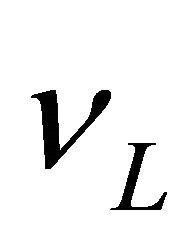 and
and 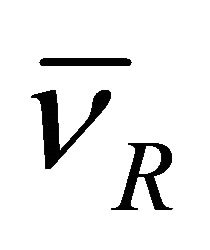 exist whereas
exist whereas  and
and 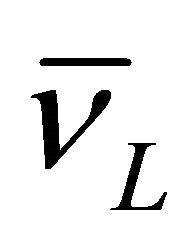 are strictly forbidden, i.e., the parity symmetry is violated to maximum. Hence, in strict sense, there is also no physically meaningful WF after the operation of pure “time inversion” on Equation (8.15). We will insist on Equation (8.31) rather than Equation (8.42)—there is only one correct way leading from tachyon to antitachyon via the
are strictly forbidden, i.e., the parity symmetry is violated to maximum. Hence, in strict sense, there is also no physically meaningful WF after the operation of pure “time inversion” on Equation (8.15). We will insist on Equation (8.31) rather than Equation (8.42)—there is only one correct way leading from tachyon to antitachyon via the  inversion essentially.
inversion essentially.
In 2000, Equation (8.25) was first proposed by Tsao Chang and then collaborated with Ni in Ref. [46] (see also [47-52] and the Appendix 9B in Ref. [25]). At first sight, the difference between Equations (8.25) and (8.1) amounts to substituting the mass term  by
by 
with  being an antihermitian matrix.
being an antihermitian matrix.
Usually, for an equation with nonhermitian Hamiltonian, there is no guarantee for the completeness of its mathematical solutions. In other words, the unitarity of its physical states is at risk. Sometimes, however, a nonhermitian Hamiltonian can be accepted in physics. For example, in the optical model for nuclear physics, an imaginary part of potential, 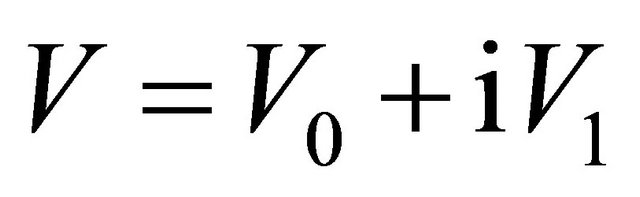 , is used to describe the absorption of incident particles successfully. The interesting thing for “tachyonic neutrino” is: Solutions of Equation (8.15) for
, is used to describe the absorption of incident particles successfully. The interesting thing for “tachyonic neutrino” is: Solutions of Equation (8.15) for 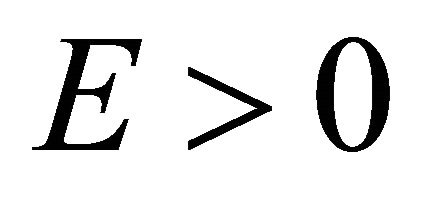
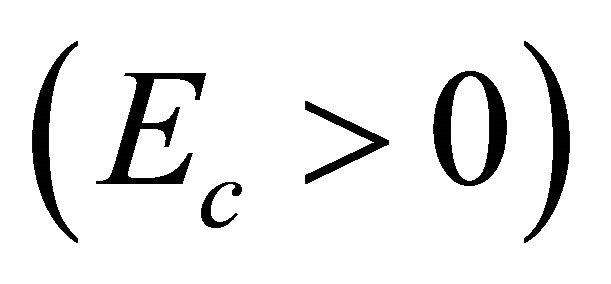 are coinciding with that for
are coinciding with that for 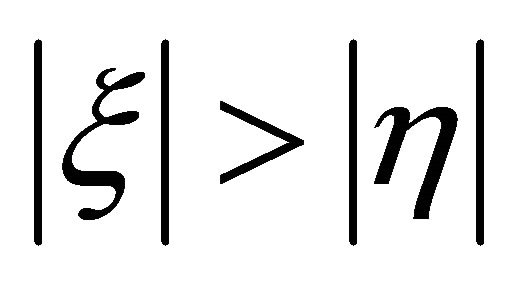
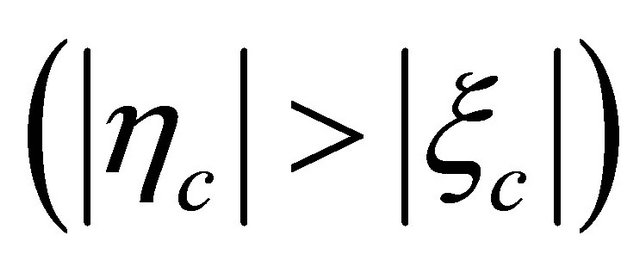 whereas another would-be solutions with
whereas another would-be solutions with 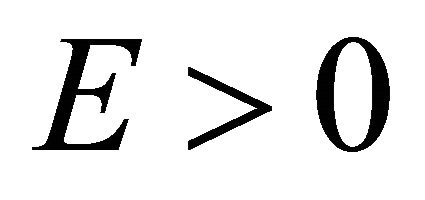 but
but 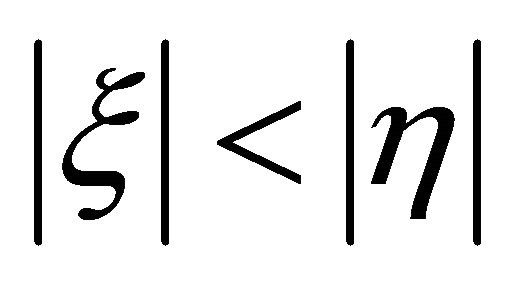 (
(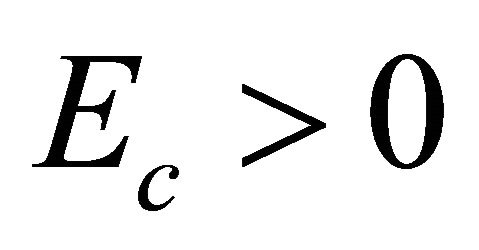 but
but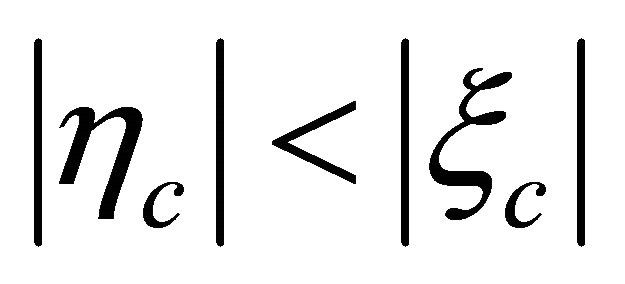 ) are forbidden, see Equations (8.37) and (8.40). It seems like half of would-be solutions disappear automatically. Equivalently, from physical point of view, only half of states with
) are forbidden, see Equations (8.37) and (8.40). It seems like half of would-be solutions disappear automatically. Equivalently, from physical point of view, only half of states with 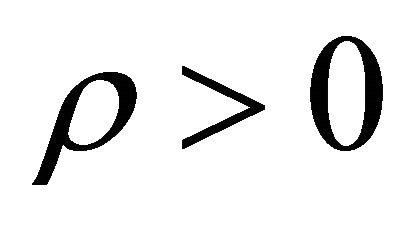 or
or 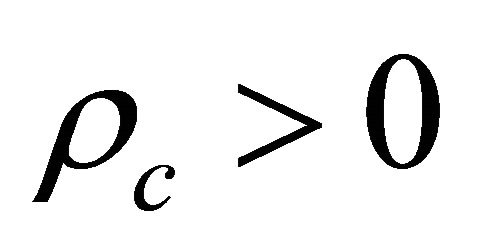 are allowed in nature whereas another half with
are allowed in nature whereas another half with 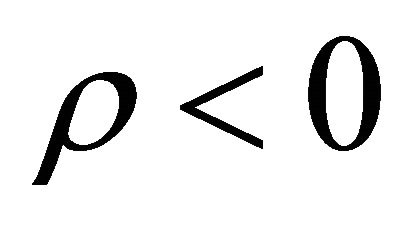 or
or 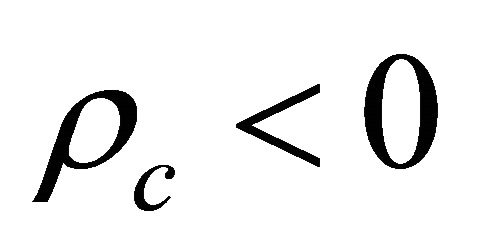 are not. Hence one unique feature of “tachyon” equation, like Equation (8.15) or (8.26), lies in its strange realization of unitarity violation that half of would-be states (being tentatively identified with
are not. Hence one unique feature of “tachyon” equation, like Equation (8.15) or (8.26), lies in its strange realization of unitarity violation that half of would-be states (being tentatively identified with  and
and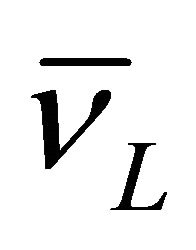 ) are absolutely forbidden whereas another half (
) are absolutely forbidden whereas another half (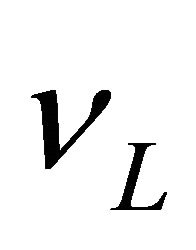 and
and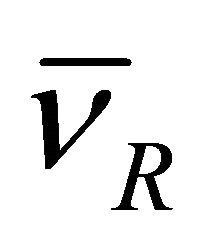 ) are stabilized. The permanently longitudinal polarization property of neutrino and antineutrino like that analysed above was first predicted by Lee and Yang in 1957 [3-5] and had been verified by GGS experiment in 1958 [53]. Further discussion on this topic is currently in preparation.
) are stabilized. The permanently longitudinal polarization property of neutrino and antineutrino like that analysed above was first predicted by Lee and Yang in 1957 [3-5] and had been verified by GGS experiment in 1958 [53]. Further discussion on this topic is currently in preparation.
9. Antigravity between Matter and Antimatter
In hindsight, there are two Lorentz invariants in the kinematics of SR:
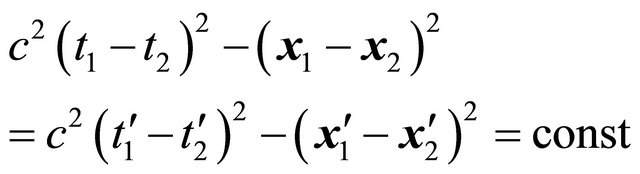 (9.1)
(9.1)
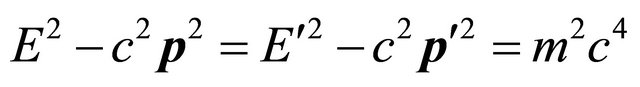 (9.2)
(9.2)
It seems quite clear that Equation (9.1) is invariant under the space-time inversion 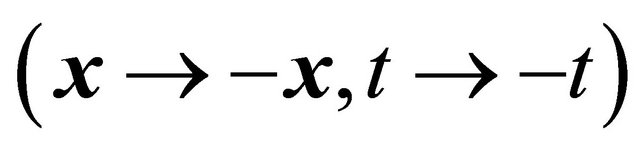 and Equation (9.2) remains invariant under the mass inversion
and Equation (9.2) remains invariant under the mass inversion 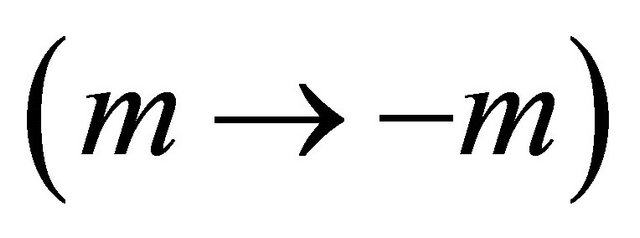 We believe that these two discrete symmetries are deeply rooted at the SR’s dynamics via its combination with QM and developing into RQM and QFT—the particle and its antiparticle are treated on equal footing and linked by the symmetry
We believe that these two discrete symmetries are deeply rooted at the SR’s dynamics via its combination with QM and developing into RQM and QFT—the particle and its antiparticle are treated on equal footing and linked by the symmetry 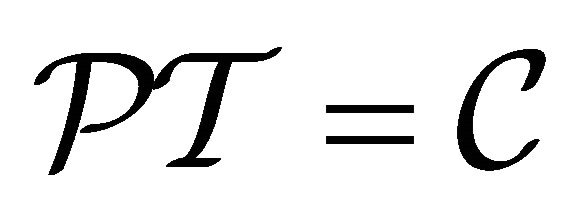 essentially. Hence we can perform a mass inversion on Equation (9.2) in each of two inertial frames with arbitrary relative velocity
essentially. Hence we can perform a mass inversion on Equation (9.2) in each of two inertial frames with arbitrary relative velocity ![]() in the sense of
in the sense of
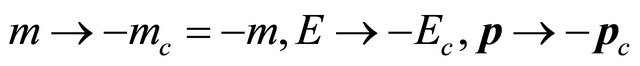 , yielding:
, yielding:
 (9.3)
(9.3)
The invariance of Equation (9.2) under mass inversion as a whole reflects the experimental fact that particle and antiparticle are equally existing in nature even at the level of classical physics.
Example: The motion equation for a charged particle (say, electron with charge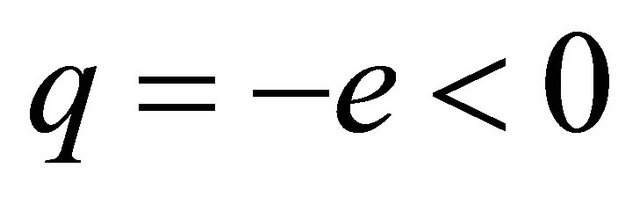 ) in the external electric and magnetic fields,
) in the external electric and magnetic fields,  and
and , is given by the Lorentz formula:
, is given by the Lorentz formula:
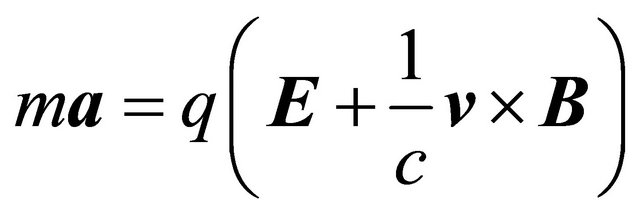 (9.4)
(9.4)
Then the operation of either 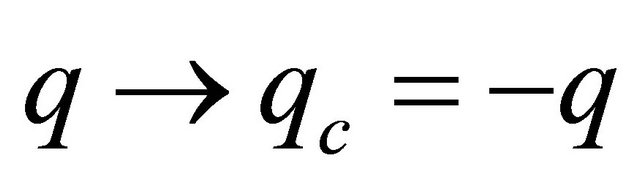 or
or
 on Equation (9.4) will realize the transformation from particle into its antiparticle (say, positron with charge
on Equation (9.4) will realize the transformation from particle into its antiparticle (say, positron with charge ) with the acceleration change from
) with the acceleration change from 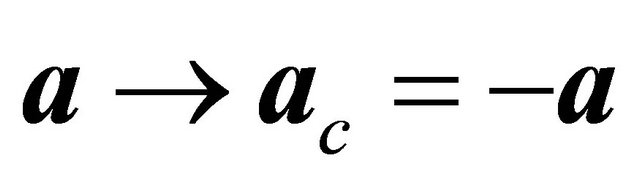 as
as
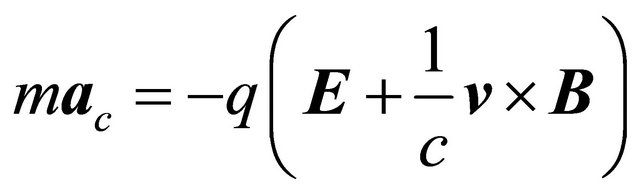 (9.5)
(9.5)
Based on what we learn from RQM (Sections III-V) as well as Equations (9.1)-(9.5), we may conjecture that for a classical theory being capable of treating matter and antimatter on an equal footing, it must be invariant under a mass inversion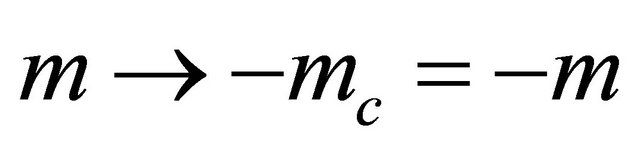 .
.
Notice that, however, Equation (9.4) (Equation (9.5)) is only valid for particle (antiparticle) moving at low speed, it must be modified to adapt to high-speed cases through the invariance of continuous Lorentz transformation. So we need “double checks” for testing a classical theory being really “relativistic” or not.
Let us restudy the theory of general relativity (GR). In a  metric, the Einstein field equation (EFE) reads (see, e.g. , Refs. [54-56])
metric, the Einstein field equation (EFE) reads (see, e.g. , Refs. [54-56])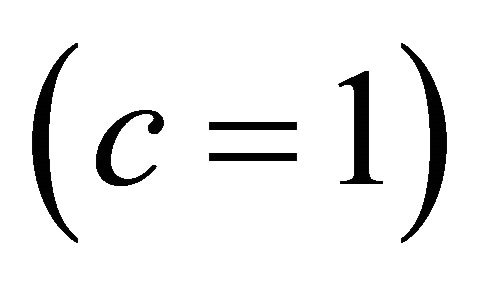 ,
,
 (9.6)
(9.6)
Of course, Equation (9.6) is covariant with respect to the Lorentz transformation. But could it withstand the test of mass inversion?
On the LHS of Equation (9.6), the Einstein tensor  contains no any mass and no charge as well. But on the RHS, the energy-momentum current density tensor
contains no any mass and no charge as well. But on the RHS, the energy-momentum current density tensor  is proportional to particle’s mass m and so changes its sign under an operation of
is proportional to particle’s mass m and so changes its sign under an operation of![]() . Hence as a whole, Equation (9.6) cannot remain invariant under the mass inversion. The reason seems rather clear that antimatter was not taking into account when GR was established in 1915. To modify EFE such that it can preserve the invariance of mass inversion, in 2004, one of us (Ni) proposed to add another term with
. Hence as a whole, Equation (9.6) cannot remain invariant under the mass inversion. The reason seems rather clear that antimatter was not taking into account when GR was established in 1915. To modify EFE such that it can preserve the invariance of mass inversion, in 2004, one of us (Ni) proposed to add another term with 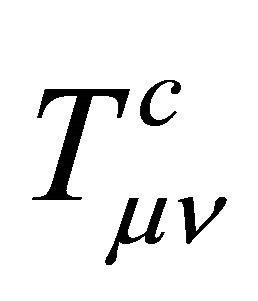 for antimatter, yielding [27]
for antimatter, yielding [27]
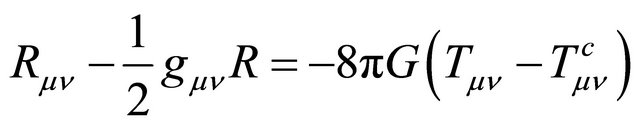 (9.7)
(9.7)
which remains invariant under a mass inversion since:
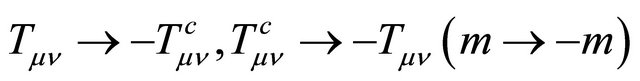 (9.8)
(9.8)
In a weak-field (or the post-Newtonian) approximation, this modified EFE, MEFE, Equation (9.7), will lead to modified Newton gravitational law as
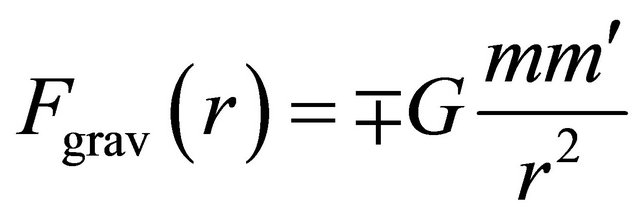 (9.9)
(9.9)
where the “ ” sign means attractive force between
” sign means attractive force between ![]() and
and 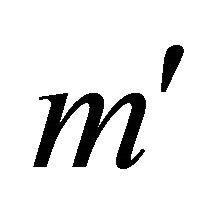 being both matter or antimatter whereas the “+” sign means repulsive force between
being both matter or antimatter whereas the “+” sign means repulsive force between ![]() and
and 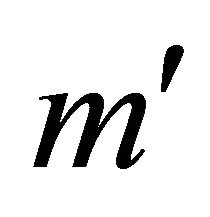 (both positive) if one of them is antimatter.
(both positive) if one of them is antimatter.
If we define the “gravitational mass” for matter and antimatter separately
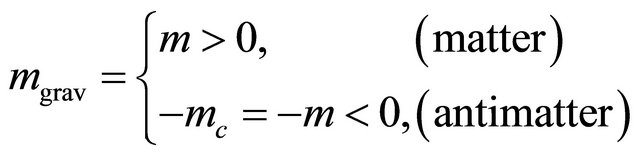 (9.10)
(9.10)
Then Equation (9.9) can be recast into one equation
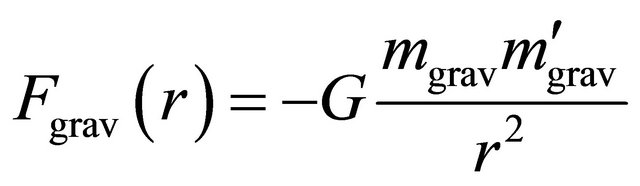 (9.11)
(9.11)
which bears a close resemblance to the Coulomb law in classical electrodynamics (CED)
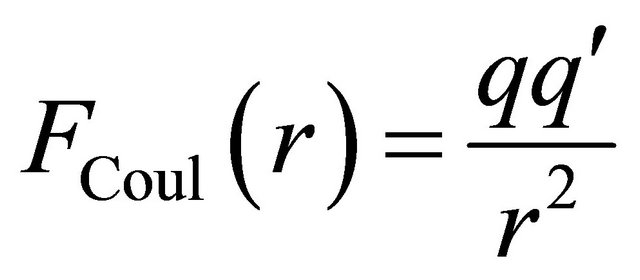 (9.12)
(9.12)
In 1986, within the framework of classical field theory (CFT) plus some assumptions, Jagannathan and Singh derived the potential energy of two static point sources as [57]
 (9.13)
(9.13)
where ![]() and
and  are spin and mass of the mediating field,
are spin and mass of the mediating field, ![]() is the “charge” of the source. For CED,
is the “charge” of the source. For CED, 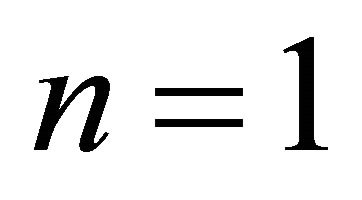 whereas
whereas 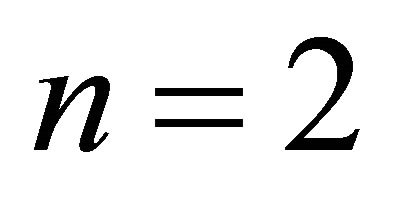 for gravitational field (
for gravitational field (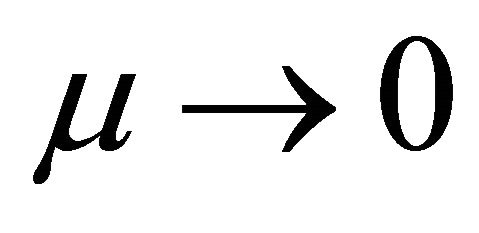 in both cases). So Equation (9.13) is in conformity with Equations (9.11) and (9.12) for the case of “like sources” (with
in both cases). So Equation (9.13) is in conformity with Equations (9.11) and (9.12) for the case of “like sources” (with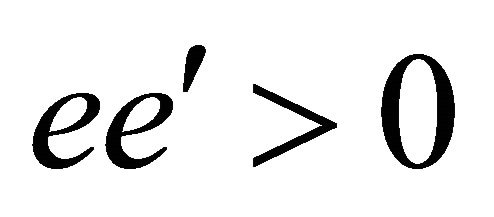 ) [57], where the case for “unlike sources”
) [57], where the case for “unlike sources” 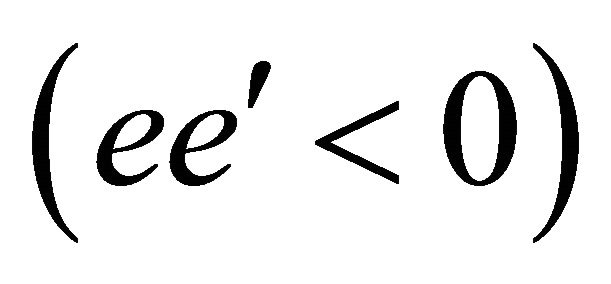 hadn’t been discussed. Here Equation (9.11) has been generalized to the case for “unlike sources”, but at a price that the “equivalence principle” in GR ceases to be valid when matter and antimatter coexist as shown by Equation (9.10).
hadn’t been discussed. Here Equation (9.11) has been generalized to the case for “unlike sources”, but at a price that the “equivalence principle” in GR ceases to be valid when matter and antimatter coexist as shown by Equation (9.10).
In 2011, the antigravity between matter and antimatter was also claimed by Villata in Ref.[58], where the argument seems different from that explained above. But theory is theory, only fact will have the final say. So we are anxiously waiting for the outcome from the AEGIS experiment [59] (at CERN), which is designed to compare the Earth gravitational acceleration on hydrogen and antihydrogen atoms.
10. Summary
1) Being the combination of SR and QM, RQM is capable of dealing with particle and antiparticle on an equal footing. As long as we admit that the antiparticle’s momentum and energy operators should be 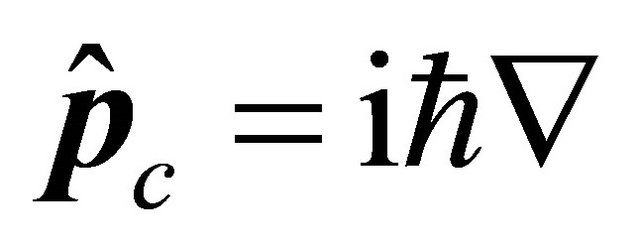
and 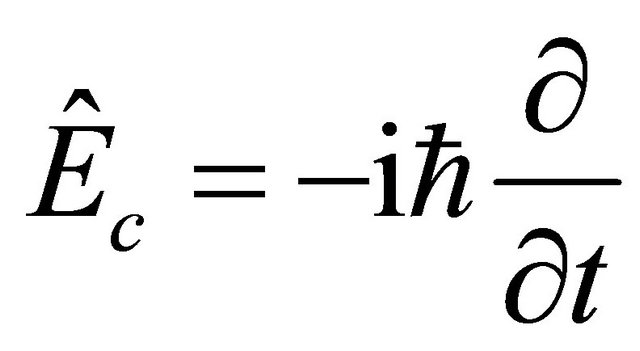 versus
versus 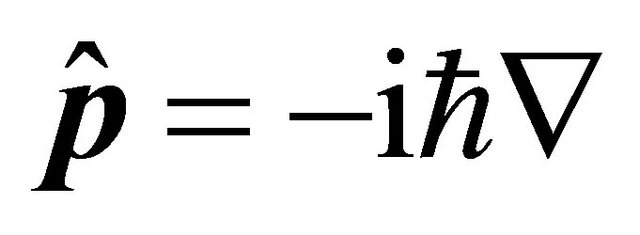 and
and 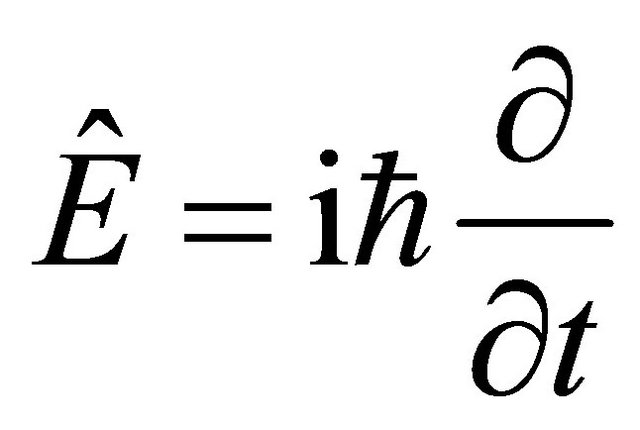 for particle, it can be proved that the “negative-energy” WF
for particle, it can be proved that the “negative-energy” WF 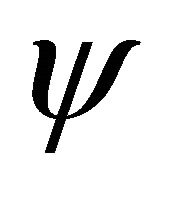 of particle corresponds to a “positive-energy” WF
of particle corresponds to a “positive-energy” WF 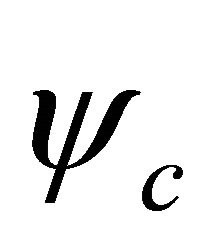 of antiparticle precisely.
of antiparticle precisely.
2) In general, an equation in RQM always has a discrete symmetry 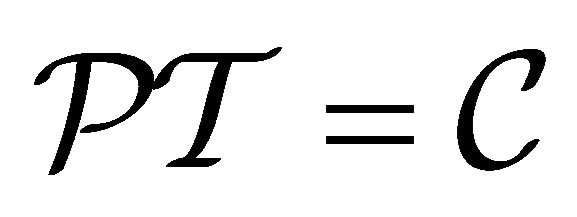 which shows up as a transformation between a particle’s WF
which shows up as a transformation between a particle’s WF 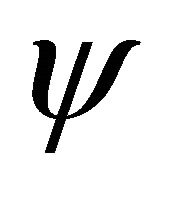 and its antiparticle’s WF
and its antiparticle’s WF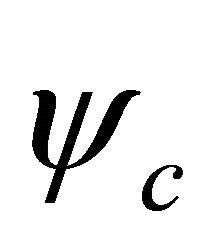 :
: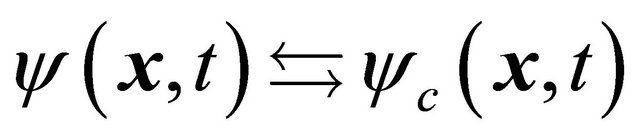 . For a free particle, it simply means
. For a free particle, it simply means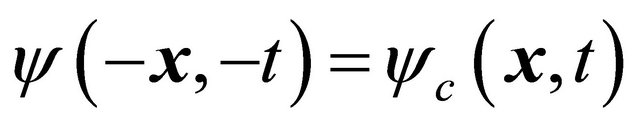 . This is in conformity with the “strong reflection” in QFT invented by Pauli and Lüders, showing that the intrinsic property of a particle cannot be detached from the space-time.
. This is in conformity with the “strong reflection” in QFT invented by Pauli and Lüders, showing that the intrinsic property of a particle cannot be detached from the space-time.
3) Following Feshbach-Villars’ deep insight, we are able to divide each and every WF 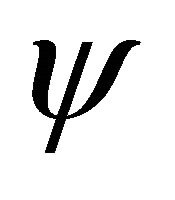 in RQM into two parts,
in RQM into two parts,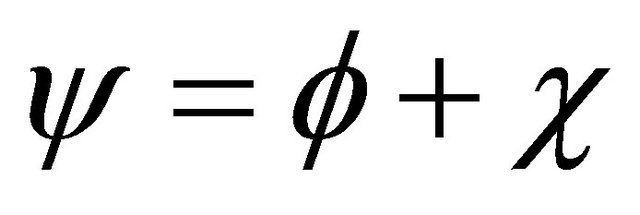 . Then the above symmetry is further rigorously expressed by an invariance of motion equation in RQM through the transformations
. Then the above symmetry is further rigorously expressed by an invariance of motion equation in RQM through the transformations 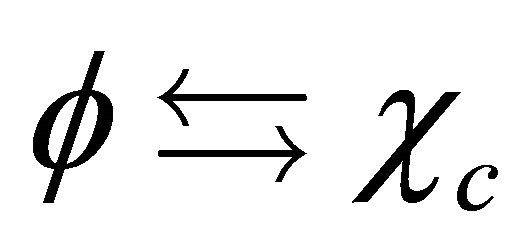 and
and 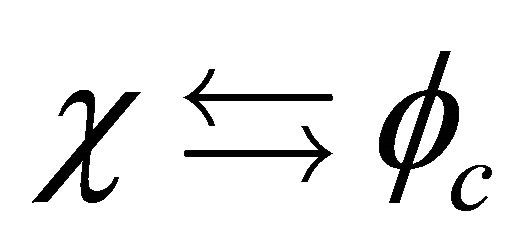 under either the space-time inversion
under either the space-time inversion
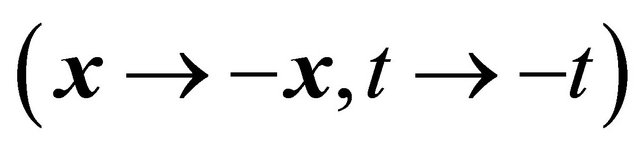 or a mass inversion
or a mass inversion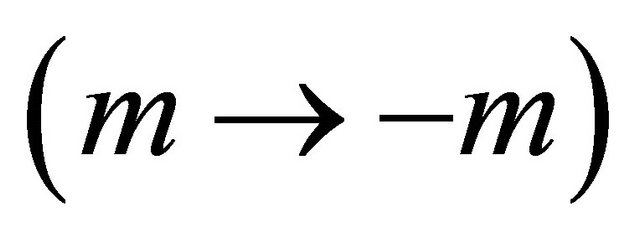 . Since
. Since  in
in 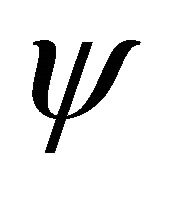 whereas
whereas 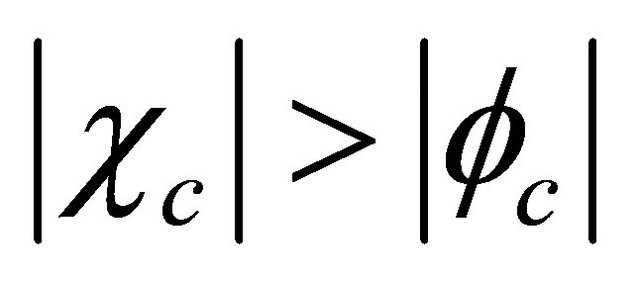 in
in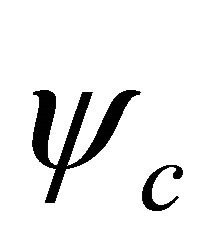 , we may name
, we may name  as the (dominant) hidden particle field in
as the (dominant) hidden particle field in  while
while  the (subordinate) hidden antiparticle field in
the (subordinate) hidden antiparticle field in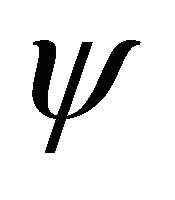 . In this way, both the “probability density”
. In this way, both the “probability density” 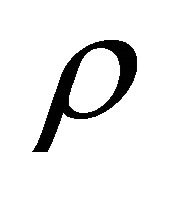 for a particle and
for a particle and 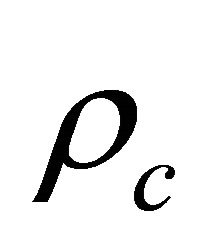 for an antiparticle can be proved to be positive definite. Now we may say that the RQM is ensured to be self-consistent and can be regarded as a sound basis for QFT.
for an antiparticle can be proved to be positive definite. Now we may say that the RQM is ensured to be self-consistent and can be regarded as a sound basis for QFT.
4) All kinematical effects in SR can be ascribed to the enhancement of the magnitude of 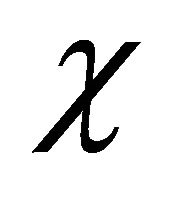 field in a particle’s WF accompanying with the increase of particle’s velocity.
field in a particle’s WF accompanying with the increase of particle’s velocity.
5) As proved for Dirac particle with spin, the helicity of a particle is just opposite to that of its antiparticle under a space-time (or mass) inversion. Therefore, the experimental tests for the CPT invariance should include not only the equal mass and lifetime of particle versus antiparticle, but also the following fact: A particle and its antiparticle with opposite helicities must coexist in nature with no exception. A prominent example is the neutrino —A neutrino 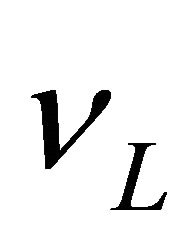 (antineutrino
(antineutrino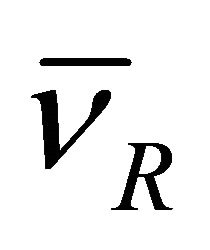 ) is permanently lefthanded (right-handed) polarized whereas the fact that no
) is permanently lefthanded (right-handed) polarized whereas the fact that no  exists in nature must means no
exists in nature must means no 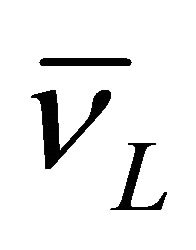 as well (as verified by the GGS experiment [53]). See also Section VII.
as well (as verified by the GGS experiment [53]). See also Section VII.
6. Based on the invariance of space-time inversion or mass inversion (at the level of RQM) and the latter’s generalization to the classical physics, we tentatively discuss some interesting problems in today’s physics, including the prediction of antigravity between matter and antimatter, as well as the reason why we believe neutrinos are likely the tachyons.
11. Acknowledgements
We thank E. Bodegom, T. Chang, Y. X. Chen, T. P. Cheng, X. X. Dai, G. Tananbaum, V. Dvoeglazov, Y. Q. Gu, F. Han, J. Jiao, A. Kellerbauer, T. C. Kerrigan, A. Khalil, R. Konenkamp, D. X. Kong, J. S. Leung, P. T. Leung, Q. G. Lin, S. Y. Lou, D. Lu, Z. Q. Ma, D. Mitchell, E. J. Sanchez, Z. Y. Shen, Z. Q. Shi, P. Smejtek, X. T. Song, R. K. Su, G. Tananbaum Y. S. Wang, Z. M. Xu, X. Xue, J. Yan, F. J. Yang, J. F. Yang, R. H. Yu, Y. D. Zhang and W. M. Zhou for encouragement, collaborations and helpful discussions.
REFERENCES
- A. Apostolakis, et al., (CPLEAR Collaboration) Physics Letters B, Vol. 422, 1998, pp. 339-348. doi:10.1016/S0370-2693(97)01545-1
- H. Feshbach and F. Villars, Review of Modern Physics, Vol. 30, 1958, pp. 24-45. doi:10.1103/RevModPhys.30.24
- T. D. Lee and C. N. Yang, Physical Review, Vol. 104, 1956, pp. 254-258.
- T. D. Lee and C. N. Yang, ibid, Vol. 105, 1957, pp. 1671-1675.
- T. D. Lee, R. Oehme and C. N. Yang, ibid, Vol. 106, 1957, pp. 340-345.
- C. S. Wu, E. Ambler, R. W. Hayward, D. D. Hoppes and R. P. Hudson, Physical Review, Vol. 105, 1957, pp. 1413-1415. doi:10.1103/PhysRev.105.1413
- J. H. Christensen, J. W. Cronin, V. L. Fitch and R. Turlay, Physical Review Letters, Vol. 13, 1964, pp. 138-140. doi:10.1103/PhysRevLett.13.138
- K. R. Schubert, B. Wolff, J.-M. Gaillard, M. R. Jane, T. J. Ratcliffe and J.-P. Repellin, Physics Letters B, Vol. 31, 1970, pp. 662-665. doi:10.1016/0370-2693(70)90029-8
- J. Beringer, et al., (Particle Data Group) Physical Review D, Vol. 86, 2012, Article ID: 010001. doi:10.1103/PhysRevD.86.010001
- G. Lüders, Kgl. Danske Vidensk. Selsk. Mat.-Fys. Medd., Vol. 28, 1954.
- G. Lüders, Annals of Physics (New York), Vol. 2, 1957, pp. 1-15.
- W. Pauli, “Exclusion Principle, Lorentz Group and Reflection of Space-Time and Charge,” In: W. Pauli, L. Rosenfeld and V. Weisskopf, Eds., Niels Bohr and the Development of Physics, McGraw-Hill, New York, 1955, pp. 30-51.
- T. D. Lee and C. S. Wu, Annual Review of Nuclear Science, Vol. 15, 1965, pp. 381-476. doi:10.1146/annurev.ns.15.120165.002121
- A. Einstein, B. Podolsky and N. Rosen, Physical Review, Vol. 47, 1935, pp. 777-780. doi:10.1103/PhysRev.47.777
- D. Bohm, “Quantum Theory,” Prentice Hall, Upper Saddle River, 1956.
- J. S. Bell, Physics, Vol. 1, 1964, pp. 195-200.
- H. Guan, “Basic Concepts in Quantum Mechanics,” High Education Press, Beijing, 1990.
- G. J. Ni, H. Guan, W. M. Zhou and J. Yan, Chinese Physics Letters, Vol. 17, 2000, pp. 393-395. doi:10.1088/0256-307X/17/6/002
- O. Nachtmann, “Elementary Particle Physics: Concepts and Phenomena,” Springer-Verlag, Berlin, 1990.
- W. Greiner and B. Müller, “Gauge Theory of Weak Interactions,” Springer-Verlag, Berlin, 1993.
- E. J. Konopinski and H. M. Mahmaud, Physical Review, Vol. 92, 1953, pp. 1045-1049. doi:10.1103/PhysRev.92.1045
- G. J. Ni, Journal of Fudan University (Natural Science), No. 3-4, 1974, pp. 125-134.
- G. J. Ni and S. Q. Chen, Journal of Fudan University (Natural Science), Vol. 35, 1996, pp. 325-334.
- G. J. Ni and S. Q. Chen, “Relation between Space-Time Inversion and Particle-Antiparticle Symmetry and the Microscopic Essence of Special Relativity,” In: V. Dvoeglazov, Ed., Photon and Poincare Group, NOVA Science Publisher, New York, 1999, pp. 145-169.
- G. J. Ni and S. Q. Chen, “Advanced Quantum Mechanics,” Rinton Press, New Jersy, 2002.
- G. J. Ni, Progress in Physics, Vol. 23, 2003, pp. 484-503.
- G. J. Ni, “A New Insight into the Negative-Mass Paradox of Gravity and the Accelerating Universe,” In: V. V. Dvoeglazov and A. A. Espinoza Garrido, Eds., Relativity, Gravitation, Cosmology, NOVA Science Publisher, New York, 2004, pp. 123-136.
- G. J. Ni, J. J. Xu and S. Y. Lou, Chinese Physics B, Vol. 20, 2011, Article ID: 020302.
- J. J. Sakurai, “Advanced Quantum Mechanics,” Addison-Wesley Publishing Company, Boston, 1978.
- J. J. Sakurai, “Modern Quantum Mechanics,” John Wiley & Sons, Inc., NewYork, 1994.
- J. D. Bjorken and S. D. Drell, “Relativistic Quantum Mechanics,” McGraw-Hill, New York, 1964,
- J. D. Bjorken and S. D. Drell, “Relativistic Quantum Fields,” McGraw-Hill, New York, 1965.
- L. B. Okun, Physics Today, Vol. 42, 1989, pp. 31-36.
- G. Lochak, “De Broglie’s Initial Conception of De Broglie Waves,” In: S. Diner, D. Fargue, G. Lochak and F. Selleri, Eds., The Wave-Particle Dualism, D. Reidal Publishing Company, Dordrecht, 1984, pp. 1-25.
- G. J. Ni, W. M. Zhou and J. Yan, “Comparison among Klein-Gordon Equation, Dirac Equation and Relativistic Schrödinger Equation,” In: A. E. Chubykalo, V. V. Dvoeglazov, D. J. Ernst, V. G. Kadyshevsky and Y. S. Kim, Eds., Lorentz Group, CPT and Neutrinos, World Scientific, London, 2000, pp. 68-81.
- M. E. Peskin and D. V. Schroeder, “An Introdution to Quantum Field Theory,” Addison-Wesley Publishing Company, Boston, 1995.
- M. Jacob and G. C. Wicks, Annals of Physics (New York), Vol. 7, 1959, pp. 404-428. doi:10.1016/0003-4916(59)90051-X
- S. Weinberg, Physical Review Letters, Vol. 19, 1967, pp. 1264-1266. doi:10.1103/PhysRevLett.19.1264
- Z. Q. Shi and G. J. Ni, Chinese Physics Letters, Vol. 19, 2002, pp. 1427-1429.
- Z. Q. Shi and G. J. Ni, Annales de la Fondation Louis de Bloglie, Vol. 29, 2004, pp. 1057-1066.
- Z. Q. Shi and G. J. Ni, Handronic Journal, Vol. 29, 2006, pp. 401-407.
- Z. Q. Shi and G. J. Ni, “Frontiers in Horizons in World Physics,” Nova Science, Marselle, 2008, pp. 53-65.
- Z. Q. Shi and G. J. Ni, Modern Physics Letters A, Vol. 26, 2011, pp. 987-998. doi:10.1142/S0217732311035250
- A. Cho, Science, Vol. 326, 2009, pp. 1342-1343. doi:10.1126/science.326.5958.1342
- L. H. Ryder, “Quantum Field Theory,” Cambridge University Press, Cambridge, 1996. doi:10.1017/CBO9780511813900
- T. Chang and G. J. Ni, “An Explanation of Possible Negative Mass-Square of Neutrinos,” FIZIKA B (Zagreb), Vol. 11, 2002, pp. 49-56. arXiv.org:hep-ph/0009291
- G. J. Ni and T. Chang, Journal of Shaanxi Normal University (Natural Science), Vol. 30, No. 3, 2002, pp. 32-39.
- G. J. Ni, Journal of Shaanxi Normal University (Natural Science), Vol. 29, No. 1, 2001, pp. 1-5.
- G. J. Ni, Journal of Shaanxi Normal University (Natural Science), Vol. 30, No. 4, 2002, pp. 1-6.
- G. J. Ni, “A Minimal Three-Flavor Model for Neutrino Oscillation Based on Superluminal Property,” In: V. V. Dvoeglazov and A. A. Espinoza, Eds., Relativity, Gravitation, Cosmology, NOVA Science Publisher, New York, 2004, pp. 137-148.
- G. J. Ni, “Principle of Relativity in Physics and in Epistemology,” In: V. Dvoeglazov, Ed., Relativity, Gravitation, Cosmology: New Development, NOVA Science Publisher, New York, 2010, pp. 237-252.
- G. J. Ni, “Cosmic Ray Spectrum and Tachyonic Neutrino,” In: V. V. Dvoeglazov and A. A. Espinoza, Eds., Relativity, Gravitation, Cosmology: New Development, NOVA Science Publisher, New York, 2010, pp. 253-265.
- M. Goldhaber, L. Grodgins and A. W. Sunyar, Physical Review, Vol. 109, 1958, pp. 1015-1017. doi:10.1103/PhysRev.109.1015
- S. Weinberg, “Gravitation and Cosmology,” John Wiley, New York, 1972.
- Z. M. Xu and X. J. Wu, “General Relativity and Contemporary Cosmology,” Press of Nanjing Normal University, Nanjing, 1999.
- T. P. Cheng, “Relativity, Gravitation and Cosmology”, 2nd Edition, Oxford University Press, Oxford, 2010.
- K. Jagannathan and L. P. S. Singh, Physical Review D, Vol. 33, 1986, pp. 2475-2477. doi:10.1103/PhysRevD.33.2475
- M. Villata, Europhysics Letters, Vol. 94, 2011, pp. 1-6. doi:10.1209/0295-5075/94/20001
- A. Kellerbauer, et al., Nuclear Instruments and Methods in Physics Research Section B, Vol. 266, 2008, pp. 351- 356. doi:10.1016/j.nimb.2007.12.010
- [61] O. Klein, Zeitschrift für Physik, Vol. 53, 1929, pp. 157-165. doi:10.1007/BF01339716
- [62] W. Greiner, “Relativistic Quantum Mechanics,” SpringerVerlag, Berlin, 1990.
- [63] W. Greiner, B. Müller and J. Rafelski, “Quantum Electrodynamics of Strong Fields,” Springer-Verlag, Berlin, 1985.
Appendix: Klein Paradox for Klein-Gordon Equation and Dirac Equation
We will discuss the Klein paradox [60] for both KG equation and Dirac equation based on Sections III and V, without resorting to the “hole” theory.
AI: Klein Paradox for KG Equation
Consider that a KG particle moves along  axis in onedimensional space and hits a step potential
axis in onedimensional space and hits a step potential
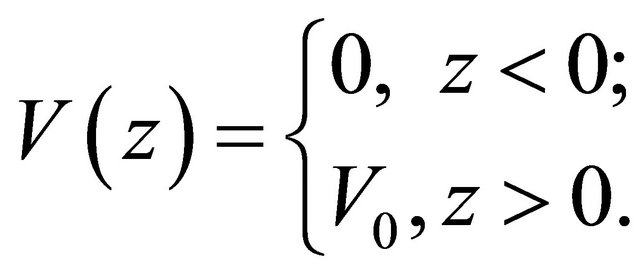 (A.1)
(A.1)
Its incident WF with momentum 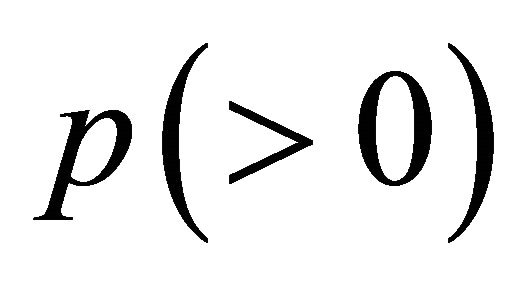 and energy
and energy 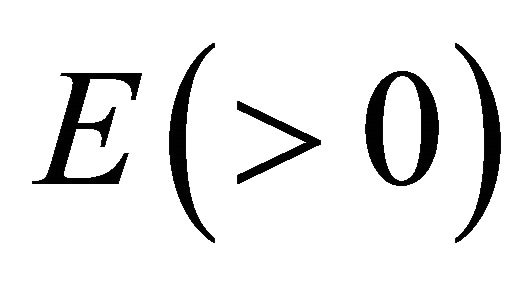 reads
reads
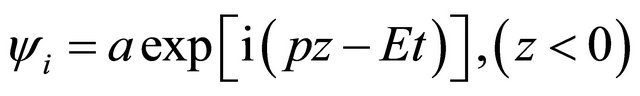 (A.2)
(A.2)
If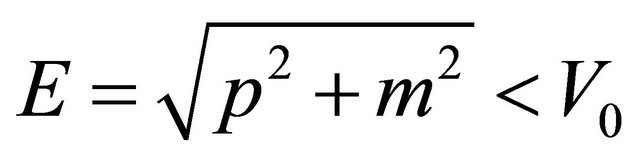 , we expect that the particle wave will be partly reflected at
, we expect that the particle wave will be partly reflected at 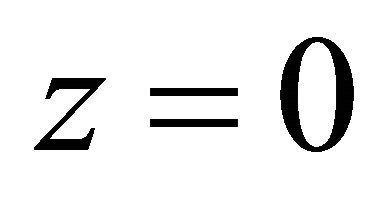 with WF
with WF 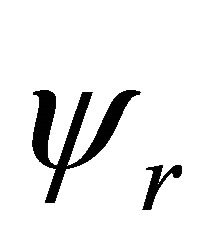 and another transmitted wave
and another transmitted wave  emerged at
emerged at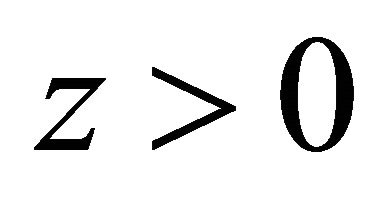 :
:
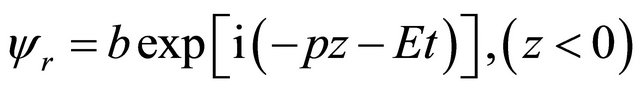 (A.3)
(A.3)
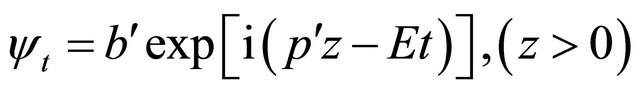 (A.4)
(A.4)
with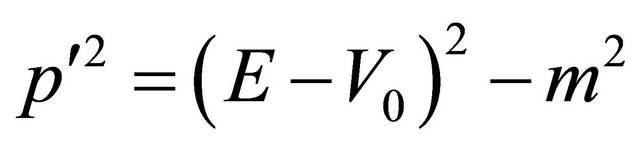 . See Figure 1(a).
. See Figure 1(a).
Two continuity conditions for WFs and their space derivatives at the boundary  give two simple equations
give two simple equations
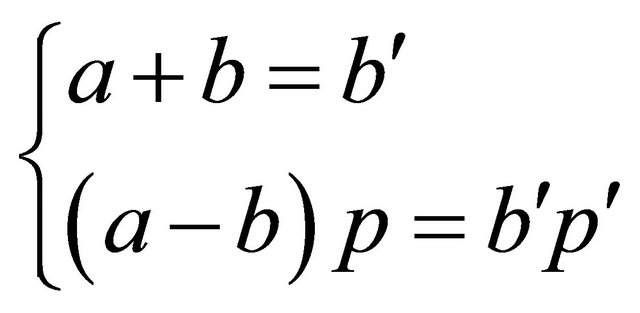 (A.5)
(A.5)
The Klein paradox happens when 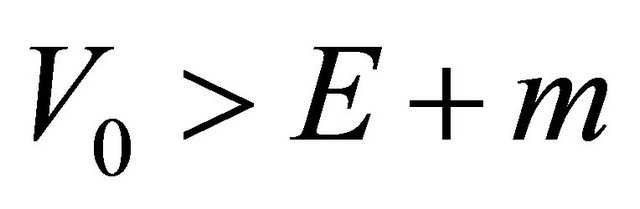 because the momentum
because the momentum 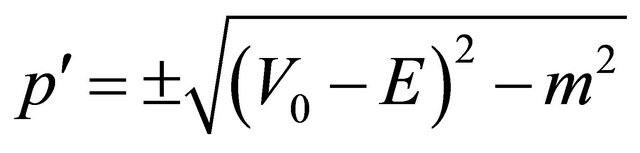 is real again and the reflectivity
is real again and the reflectivity  of incident wave reads
of incident wave reads
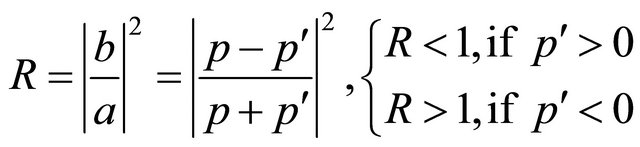 (A.6)
(A.6)
(See Ref. [18] or  9.4 in Ref. [25], where discussions are not complete and need to be complemented and corrected here). Because the kinetic energy
9.4 in Ref. [25], where discussions are not complete and need to be complemented and corrected here). Because the kinetic energy 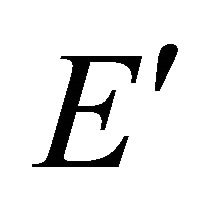 at
at 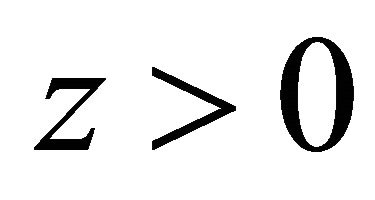 is negative:
is negative: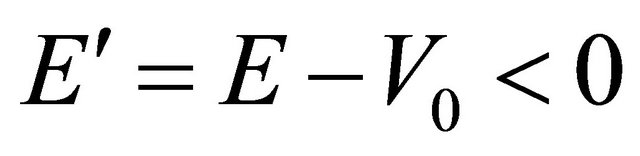 , what does it mean? Does the particle still remain as a particle?
, what does it mean? Does the particle still remain as a particle?
As discussed in Section III, for a KG particle (or its antiparticle), two criterions must be held: its probability density ρ (or ) must be positive and its probability current density
) must be positive and its probability current density  (or
(or ) must be in the same direction of its momentum
) must be in the same direction of its momentum ![]() (or
(or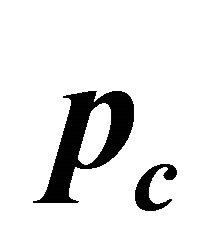 ).
).
See Figure 1(b), after making a shift in the energy scale, i.e., basing on the new vacuum at 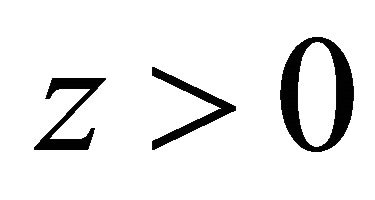 region, we redefine a WF
region, we redefine a WF 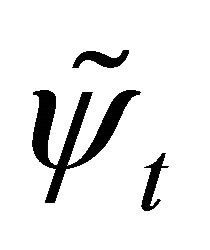 (which is actually the WF in the “interaction picture”,
(which is actually the WF in the “interaction picture”,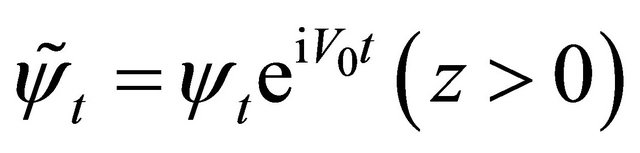 )
)
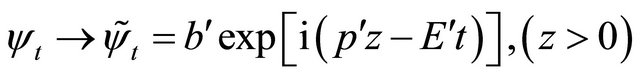 (A.7)
(A.7)
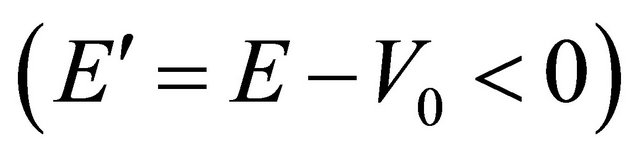 . From now on we will replace KG WF
. From now on we will replace KG WF  by
by ![]() and
and  according to Equation (3.26), if
according to Equation (3.26), if 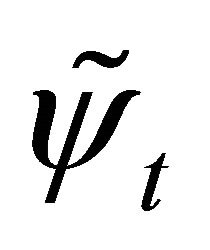 still describes a “particle”, whose probability density
still describes a “particle”, whose probability density 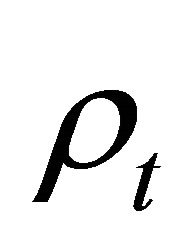 should be evaluated by Equation (27) with
should be evaluated by Equation (27) with
 yielding:
yielding:
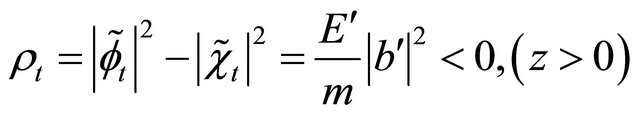 (A.8)
(A.8)
And its probability current density  should be given by Equation (3.12), yielding:
should be given by Equation (3.12), yielding:
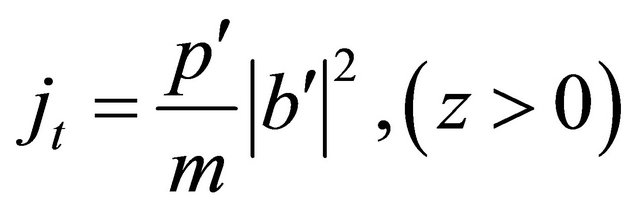 (A.9)
(A.9)
Equation (A.8) is certainly not allowed. So to consider a “particle” with momentum 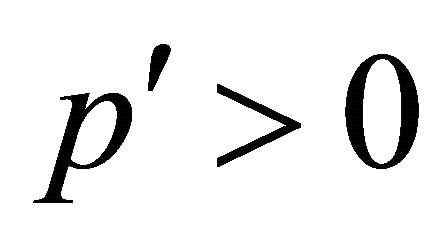 moving to the right makes no sense. Instead, we should consider
moving to the right makes no sense. Instead, we should consider 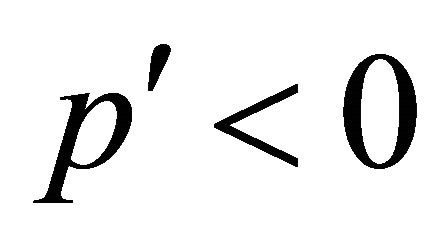 (which also makes no sense for a particle due to the boundary condition) and regard
(which also makes no sense for a particle due to the boundary condition) and regard  as an antiparticle’s WF by rewriting it as:
as an antiparticle’s WF by rewriting it as:
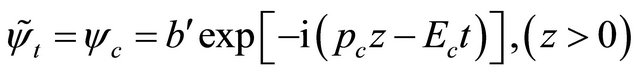 (A.10)
(A.10)
Now using Equation (2.18) we see that Equation (A.10) does describe an antiparticle with momentum
![]() and energy
and energy
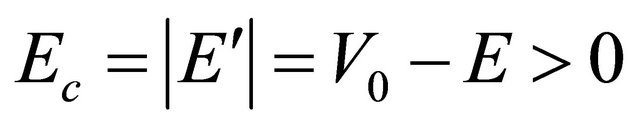 . In the mean time, from the antiparticle’s point of view (i.e., with
. In the mean time, from the antiparticle’s point of view (i.e., with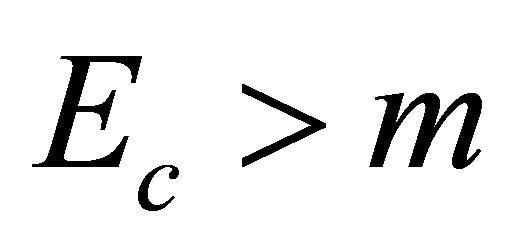 ), the potential becomes
), the potential becomes  (comparing Equation (2.21) with Equation (A.10) as shown by Figure 1(c).
(comparing Equation (2.21) with Equation (A.10) as shown by Figure 1(c).
It is easy to see from Equations (3.30), (3.31) and (A.10) that
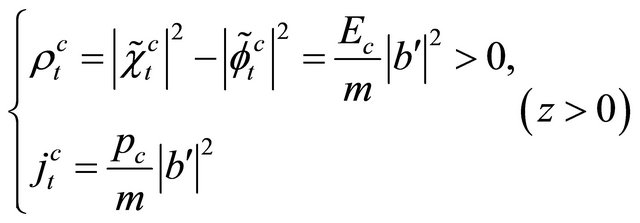 (A.11)
(A.11)
So the reflectivity, Equation (A.6), should be fixed as:
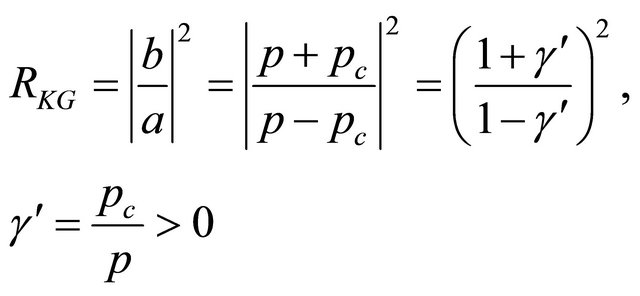 (A.12)
(A.12)
And the transmission coefficient can also be predicted as:
 (a)
(a) (b)
(b)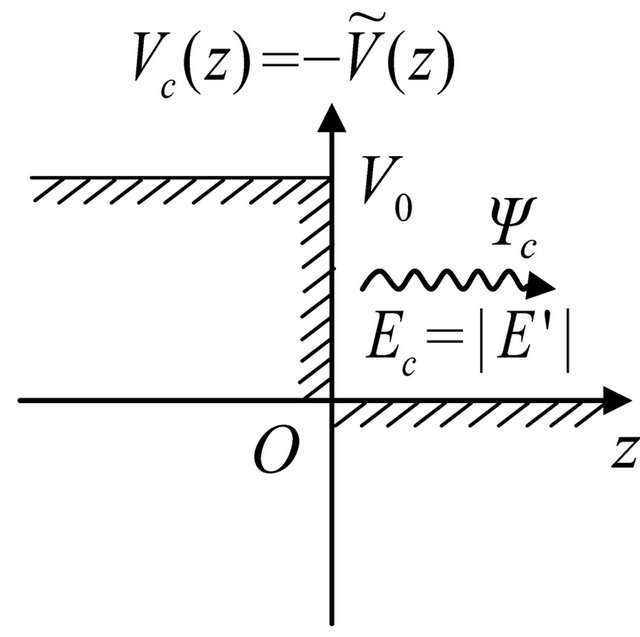 (c)
(c)
Figure 1. Klein paradox: (a) If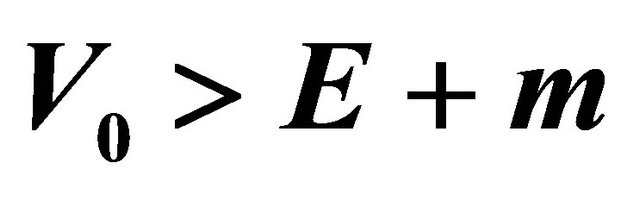 , there will be a wave
, there will be a wave 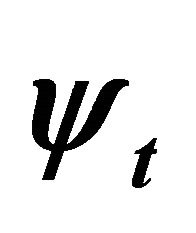 at
at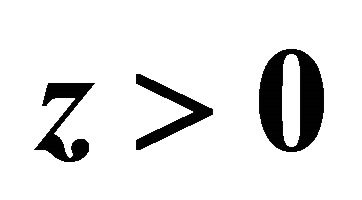 ; (b) Just look at
; (b) Just look at 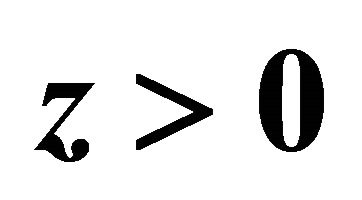 region, making a shift
region, making a shift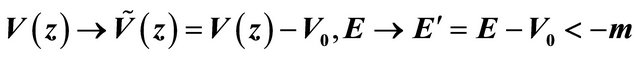 ; (c) An antiparticle (at
; (c) An antiparticle (at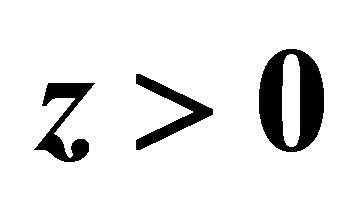 ) appears with its energy
) appears with its energy 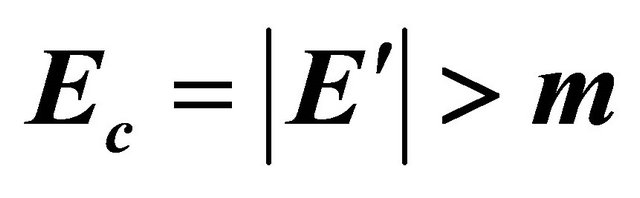 and the potential is
and the potential is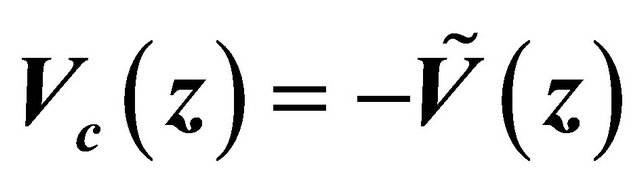 .
.
 (A.13)
(A.13)
 (A.14)
(A.14)
The variation of  seems very interesting:
seems very interesting:
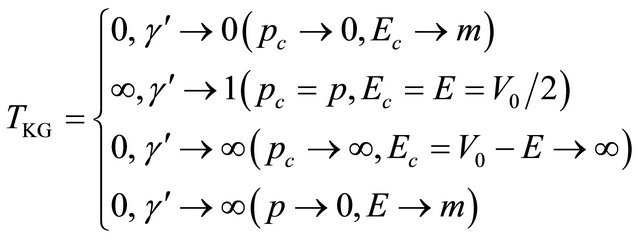 (A.15)
(A.15)
Above equations show us that the incident KG particle triggers a process of “pair creation” occurring at , creating new particles moving to the left side (to join the reflected incident particle) so enhancing the reflectivity
, creating new particles moving to the left side (to join the reflected incident particle) so enhancing the reflectivity  and new antiparticles (with equal number of new particles) moving to the right.
and new antiparticles (with equal number of new particles) moving to the right.
To our understanding, this is not a stationary state problem for a single particle, but a nonstationary creation process of many particle-antiparticle system. It is amazing to see the Klein paradox in KG equation being capable of giving some prediction for such kind of process at the level of RQM. Further investigations are needed both theoretically and experimentally.10
AII: Klein Paradox for Dirac Equation
Beginning from Klein [60], many authors e.g. Greiner et al. [61,62], have studied this topic. We will join them by using the similar approach like that for KG equation discussed above.
Based on similar picture shown in Figure 1, now we have three Dirac WFs under the condition :
:
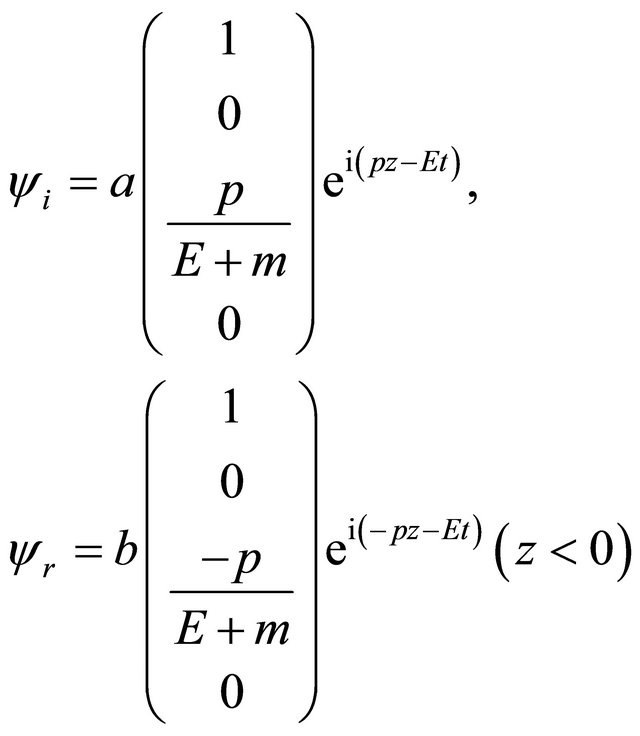 (A.16)
(A.16)
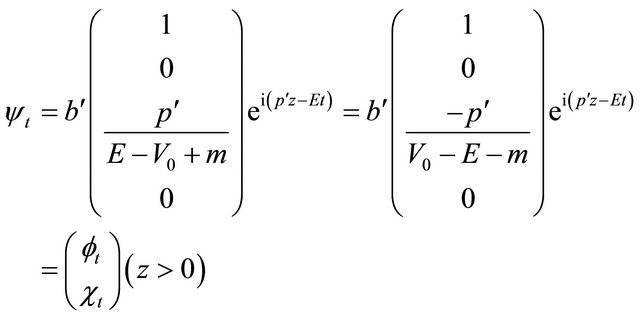
(A.17)
where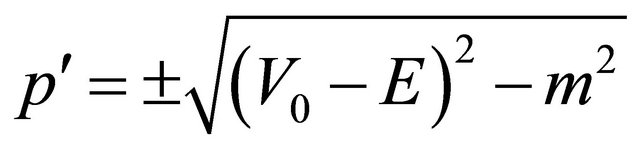 . Unlike Equation (A.8)
. Unlike Equation (A.8)
for KG equation, the probability density for Dirac WF  is positive definite (see Equation (5.16))
is positive definite (see Equation (5.16))
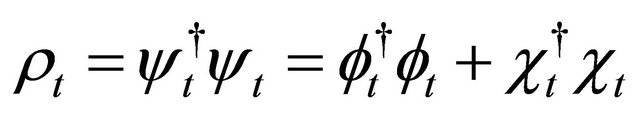 (A.18)
(A.18)
Hence we will rely on two criterions: First, the probability current density and momentum must be in the same direction for either a particle or antiparticle. For  and
and , their probability current density are
, their probability current density are 
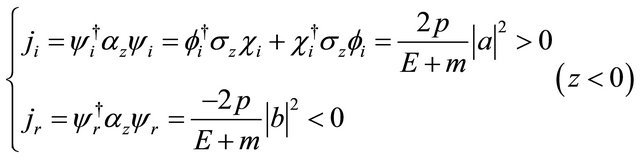
(A.19)
as expected. However, for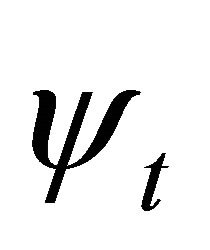 , we meet difficulty similar to that in Equation (A.9)
, we meet difficulty similar to that in Equation (A.9)
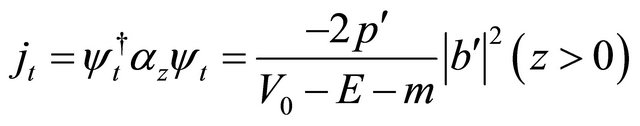 (A.20)
(A.20)
the direction of  is always opposite to that of
is always opposite to that of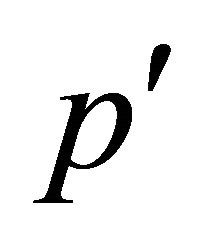 ! The second criterion is: while
! The second criterion is: while 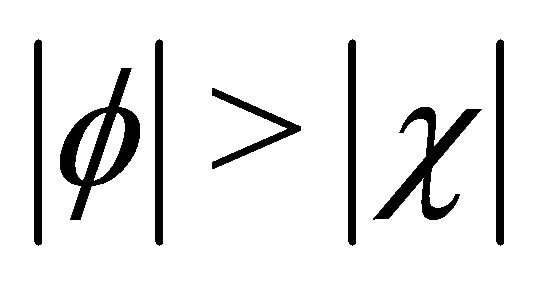 for particle, we must have
for particle, we must have 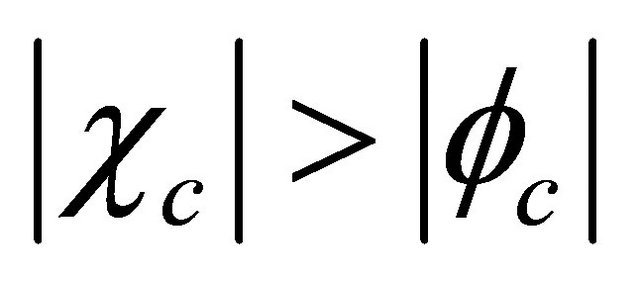 for antiparticle. Now in
for antiparticle. Now in  (or
(or
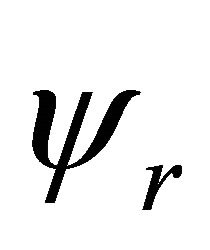 ),
), 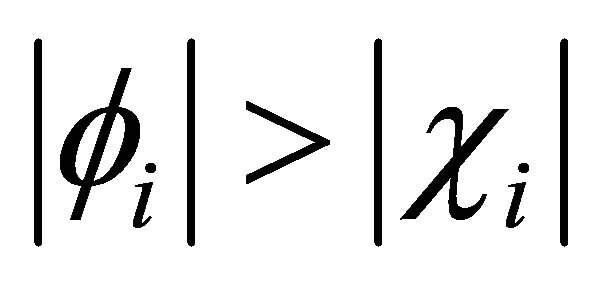 (or
(or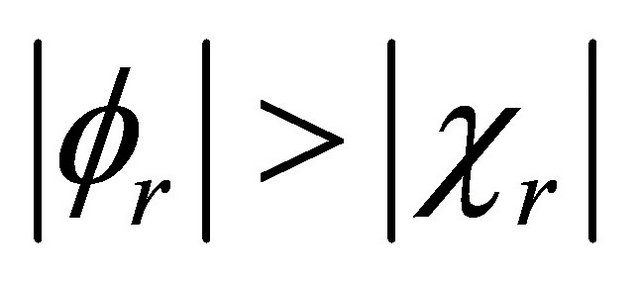 ), but the situation in
), but the situation in 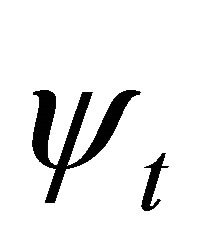
is dramatically changed, the existence of 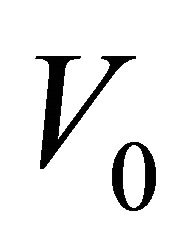 renders
renders !
!
The above two criterions, together with the experience in KG equation, prompt us to choose  and regard
and regard 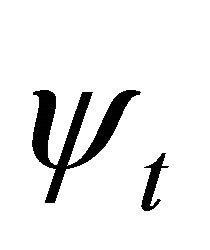 as an antiparticle’s WF. So we rewrite:
as an antiparticle’s WF. So we rewrite:
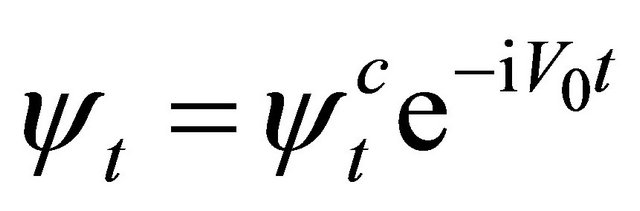 (A.21a)
(A.21a)
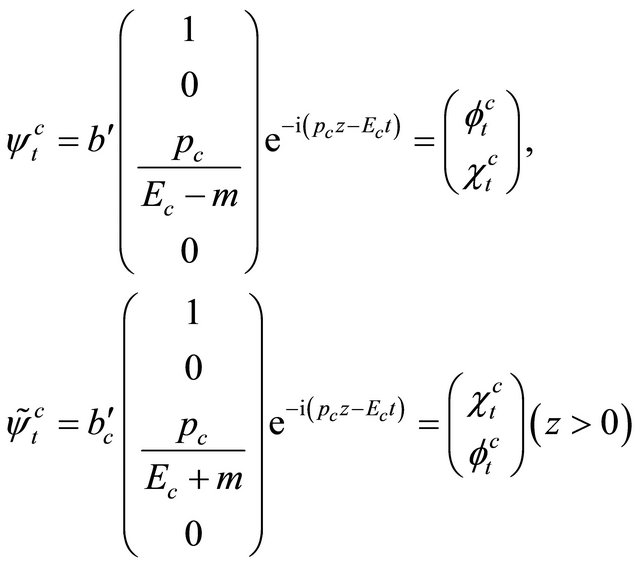 (A.21b)
(A.21b)
where 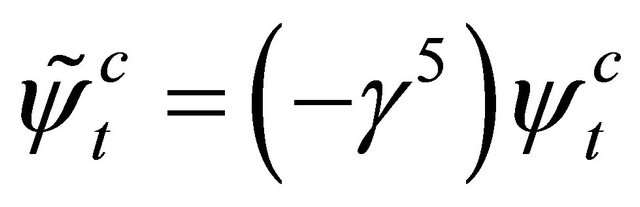 (with new normalization constant
(with new normalization constant
 replacing
replacing ) describes an antiparticle with momentum
) describes an antiparticle with momentum![]() , energy
, energy
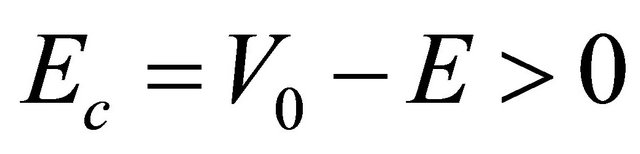 and
and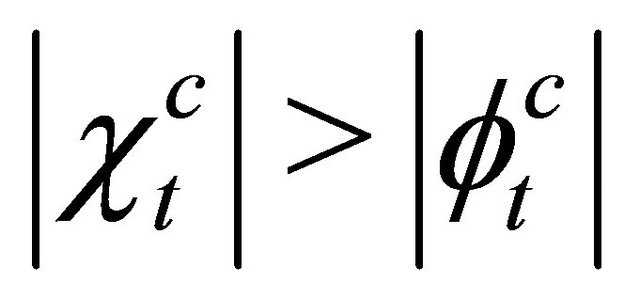 . Using Equation (5.17) we find
. Using Equation (5.17) we find
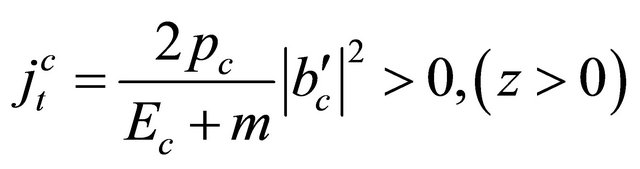 (A.22)
(A.22)
as expected. Now it is easy to match Dirac WFs at the boundary , (
, (![]() , yielding11
, yielding11
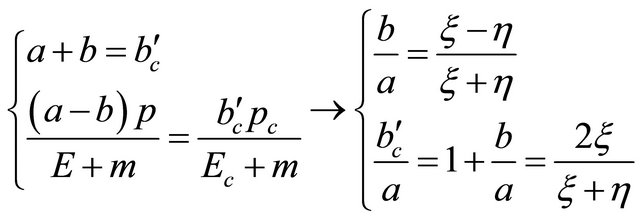 (A.23)
(A.23)
where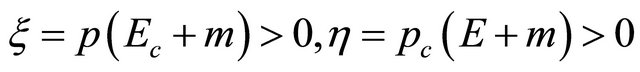 . The reflectivity
. The reflectivity  and transmission coefficient
and transmission coefficient  follow from Equations (A.19) and (A.22) as:
follow from Equations (A.19) and (A.22) as:
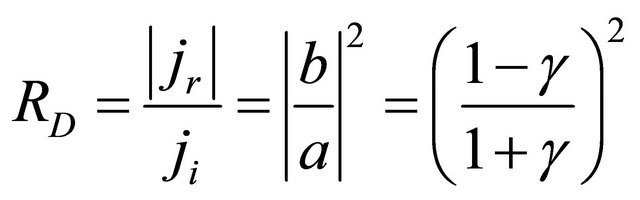 (A.24)
(A.24)
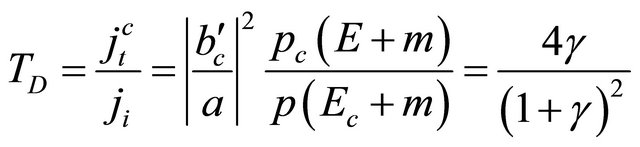 (A.25)
(A.25)
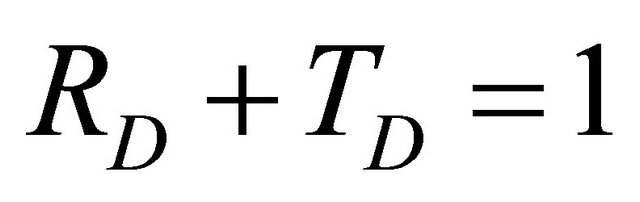 (A.26)
(A.26)
where
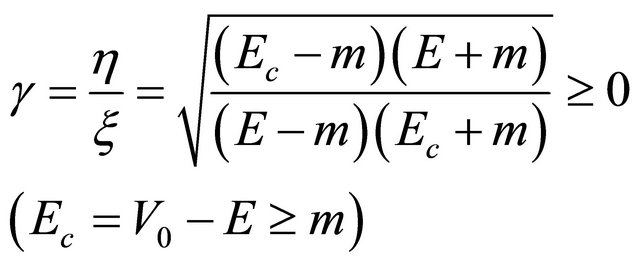 (A.27)
(A.27)
and
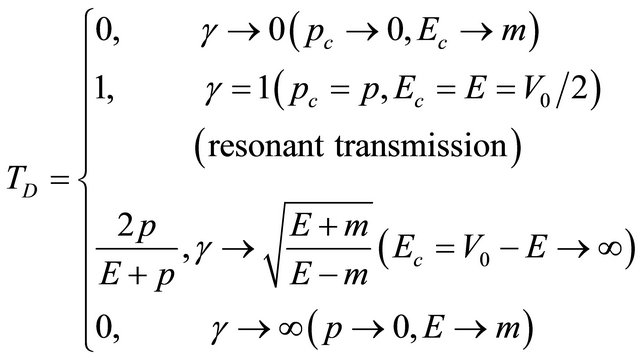 (A.28)
(A.28)
The variation of 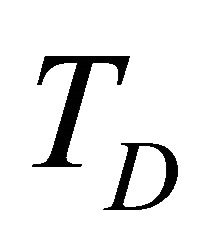 bears some resemblance to Equation (A.15) for KG equation but shows striking difference due to sharp contrast between Equations (A.24)- (A.28) and Equations (A.12)-(A.15).
bears some resemblance to Equation (A.15) for KG equation but shows striking difference due to sharp contrast between Equations (A.24)- (A.28) and Equations (A.12)-(A.15).
To our understanding, in the above Klein paradox for Dirac equation, there is no “pair creation” process occurring at the boundary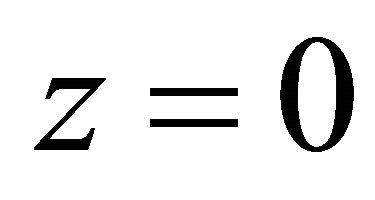 . The paradox just amounts to a steady transmission of particle’s wave
. The paradox just amounts to a steady transmission of particle’s wave  into a high potential barrier
into a high potential barrier 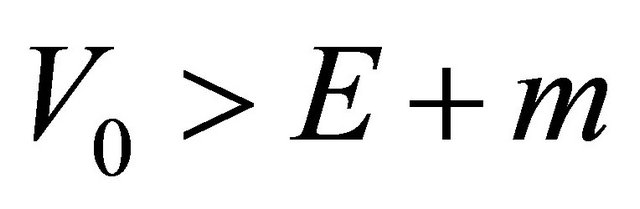 at
at 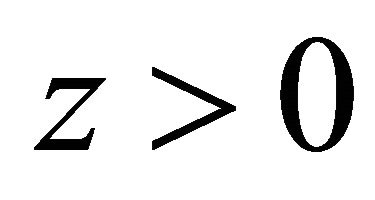 region where
region where  shows up as an antiparticle’s WF propagating to the right. In some sense, the existence of a potential barrier
shows up as an antiparticle’s WF propagating to the right. In some sense, the existence of a potential barrier  plays a “magic” role of transforming the particle into its antiparticle. Because the probability densities of both particle and antiparticle are positive definite, the total probability can be normalized over the entire space like that for one particle case:
plays a “magic” role of transforming the particle into its antiparticle. Because the probability densities of both particle and antiparticle are positive definite, the total probability can be normalized over the entire space like that for one particle case:
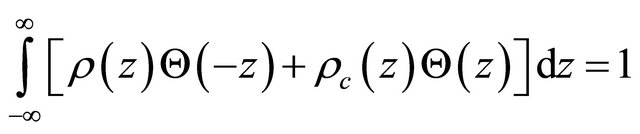 (A.29)
(A.29)
( is the Heaviside function) and the probability current density remains continuous at the boundary
is the Heaviside function) and the probability current density remains continuous at the boundary . In other words, the continuity equation holds in the whole space just like what happens in a one-particle stationary state.
. In other words, the continuity equation holds in the whole space just like what happens in a one-particle stationary state.
It is interesting to compare our result with that in Refs. [61] and [62]. In Ref. [61], Equations (13.24)-(13.28) are essentially the same as ours. But the argument there for choosing 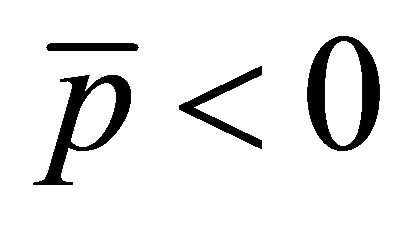 in Equation (13.23) is based on the criterion of the group velocity
in Equation (13.23) is based on the criterion of the group velocity 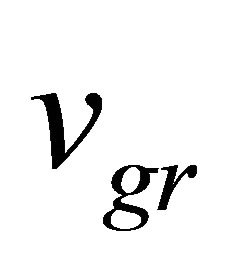 being positive (for the transmitted wave packet moving toward
being positive (for the transmitted wave packet moving toward ). And the
). And the 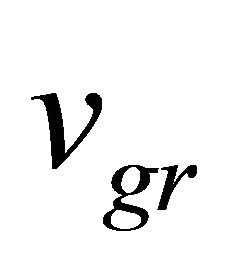 is stemming from Equation (13.16) which is essentially the probability current density in our Equations (A.21)-(A.22).
is stemming from Equation (13.16) which is essentially the probability current density in our Equations (A.21)-(A.22).
However, the author in Ref. [61] also considered the other choice 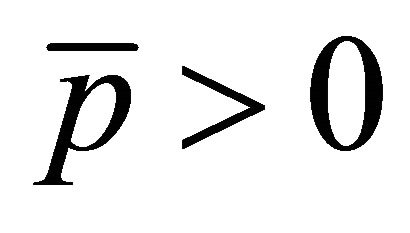 in an example (pp. 265-267 in [61]) based on the hole theory, ending up with the prediction as:
in an example (pp. 265-267 in [61]) based on the hole theory, ending up with the prediction as:
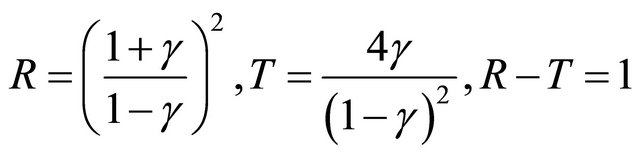 (A.30)
(A.30)
where
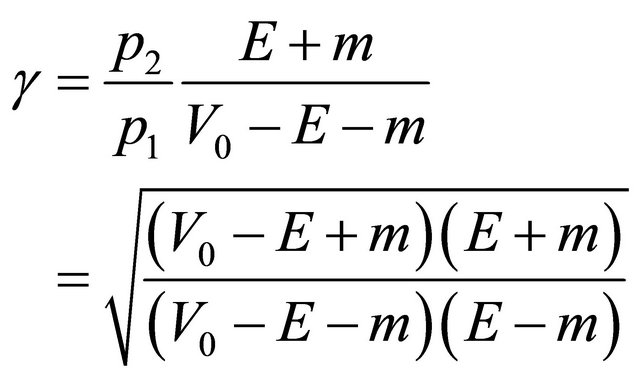 (A.31)
(A.31)
The argument for the validity of his Equations (A.30)- (A.31) is based on the hole theory (see also section 5.2 in Ref. [62]), saying that once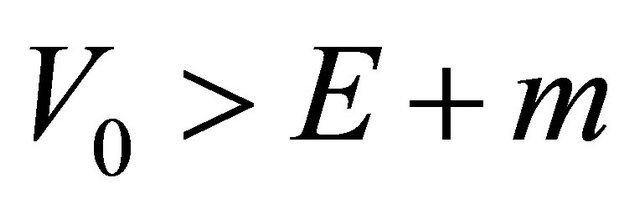 , there would be an overlap between the occupied negative continuum for
, there would be an overlap between the occupied negative continuum for 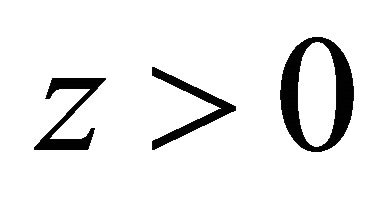 and the empty positive continuum for
and the empty positive continuum for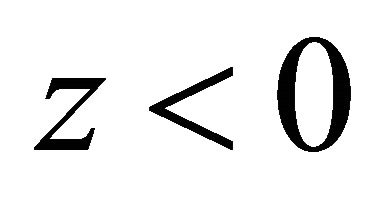 , providing a mechanism for electron-positron pair creation if the “hole” at
, providing a mechanism for electron-positron pair creation if the “hole” at 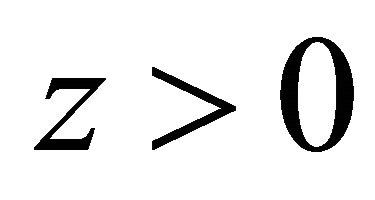 can be identified with a positron. We doubt the “hole” theory seriously because there are only two electrons (with opposite spin orientations) staying at each energy level in the negative continuum. So it seems that there is no abundant source for electrons and “holes” to account for the huge value of
can be identified with a positron. We doubt the “hole” theory seriously because there are only two electrons (with opposite spin orientations) staying at each energy level in the negative continuum. So it seems that there is no abundant source for electrons and “holes” to account for the huge value of 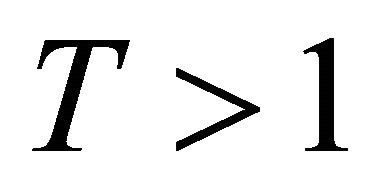 in Equation (A.30).
in Equation (A.30).
Fortunately, we learn from section 10.7 in Ref. [62] that if the Klein paradox in Dirac equation is treated at the level of QFT, their result turns out to be the same form as our Equations (A.24)-(A.28), rather than Equations (A.30) and (A.31).
NOTES
1The WF reads approximately as:
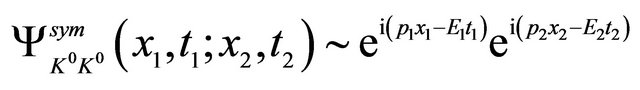 (2.14b)
(2.14b)
which can be calculated from 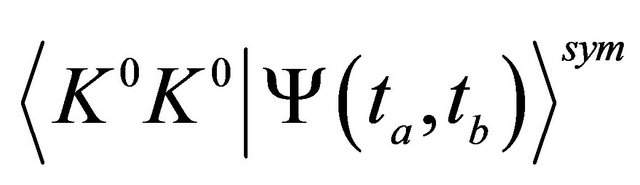 with two terms. The squares of WF’s amplitude reproduces the
with two terms. The squares of WF’s amplitude reproduces the 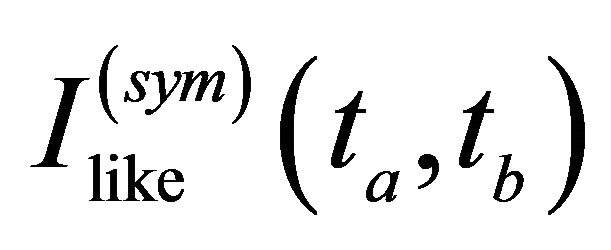 in Equation (2.12).
in Equation (2.12).
2Please see the derivation of Equations (2.20) and (2.21) from the quantum field theory (QFT) at the end of Section VI.
3Interestingly, if ignoring the coupling between  and
and ![]() and
and  in Equation (25), they satisfy respectively the “two equations” written down by Schrödinger in his 6th paper in 1926, titled “Quantisation as a problem of proper values (Part IV)” (Annalen der Physik Vol. 81, No. 4, 1926, p. 104) when he invented NRQM in the form of wave mechanics.
in Equation (25), they satisfy respectively the “two equations” written down by Schrödinger in his 6th paper in 1926, titled “Quantisation as a problem of proper values (Part IV)” (Annalen der Physik Vol. 81, No. 4, 1926, p. 104) when he invented NRQM in the form of wave mechanics.
4Here m always refers to the “rest mass” also the “inertial mass” for a particle or its antiparticle, see the excellent paper by Okun in Ref. [33].
5Some pictures of numerical calculation are shown in Ref. [35] and section 9.5C at Ref. [25], where an error in Equation (9.5.26) is corrected here.
6The reason why we use 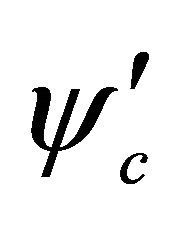 instead of
instead of 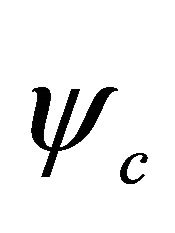 will be clear in Equations (5.12)-(5.15). Actually, we emphasize Dirac equation as a coupling equation of two two-component spinors, Equation (3), rather than merely a four-component spinor equation.
will be clear in Equations (5.12)-(5.15). Actually, we emphasize Dirac equation as a coupling equation of two two-component spinors, Equation (3), rather than merely a four-component spinor equation.
7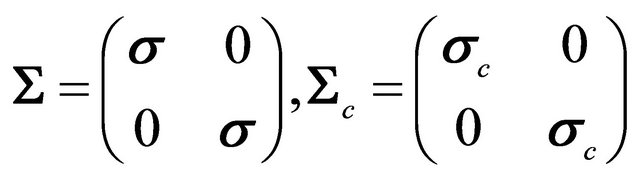
8The wonderful experiment by Wu et al. [6] reveals the decay configuration of a polarized neutron bearing a strong resemblance to a “comet” with its “head” oriented along neutron’s spin parallel to  axis in space (note that a static neutron has no helicity
axis in space (note that a static neutron has no helicity , see [45]) while its “tail” composed of emitted
, see [45]) while its “tail” composed of emitted ![]() and
and![]() . So it was expected intuitively that [39] if one pushes the “comet” along its “head”’s direction, it (suddenly has a helicity
. So it was expected intuitively that [39] if one pushes the “comet” along its “head”’s direction, it (suddenly has a helicity 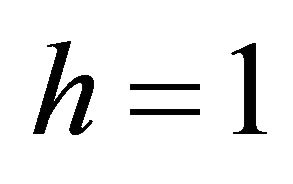 and) will be relatively more stable than it is pushed along its “tail” (when it has
and) will be relatively more stable than it is pushed along its “tail” (when it has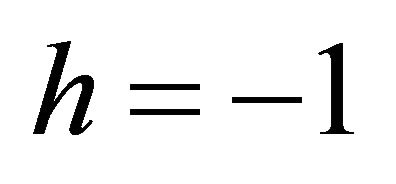 ). That’s what Equation (7.1) means and why the use of “spin state” fails to get it right.
). That’s what Equation (7.1) means and why the use of “spin state” fails to get it right.
9We had discarded the solution of  in Equations (A.7)-(A.9) as a particle. However, if we consider
in Equations (A.7)-(A.9) as a particle. However, if we consider  for an antiparticle, then similar to Equations (A.10) and (A.11), we would get
for an antiparticle, then similar to Equations (A.10) and (A.11), we would get 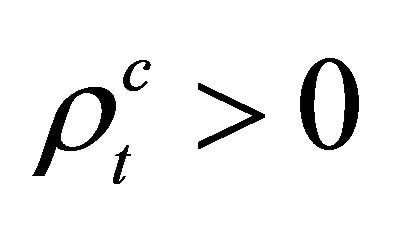 but both
but both ![]() and
and  are negative, meaning that the antiparticle is coming from
are negative, meaning that the antiparticle is coming from , not in accordance with our boundary condition. So the case of
, not in accordance with our boundary condition. So the case of  should be abandoned either as a particle or as an antiparticle.
should be abandoned either as a particle or as an antiparticle.
10We find from the Google search that R. G. Winter in 1958 had written a paper titled “Klein paradox for the Klein-Gordon equation” and reached basically the same result as ours. So he was the first author dealing with this problem. Regrettably, it seems that his paper had never been published on some journal.
11Equation (A.23) means that the large (small) component of spinor is connected with large (small) component at both sides of![]() . However, if instead of
. However, if instead of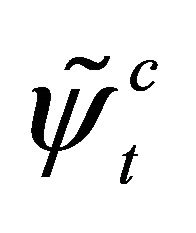 , the
, the 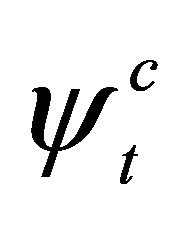 is used directly with its first (small) component being connected with the first (large) components of
is used directly with its first (small) component being connected with the first (large) components of  and
and , it would lead to a different expression of Equation (A.27):
, it would lead to a different expression of Equation (A.27):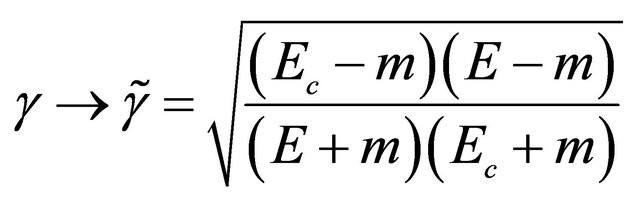 , which is just the
, which is just the  (
(![]() and
and  make no difference in the result of, say, Equations (A.24) and (A.25)) defined by Equation (8) on page 266 of Ref. [61] (see Equation (A31) below) or that by Equation (5.36) in Ref. [62]
make no difference in the result of, say, Equations (A.24) and (A.25)) defined by Equation (8) on page 266 of Ref. [61] (see Equation (A31) below) or that by Equation (5.36) in Ref. [62]

