Journal of Modern Physics
Vol.4 No.1(2013), Article ID:27242,9 pages DOI:10.4236/jmp.2013.41016
Electric Multipole Polarizabilities of Quantum Bound Systems in the Transition Matrix Formalism
Bogolyubov Institute for Theoretical Physics, National Academy of Sciences of Ukraine, Kyiv, Ukraine
Email: vkharchenko@bitp.kiev.ua
Received October 5, 2012; revised November 6, 2012; accepted November 14, 2012
Keywords: Electric Multipole Polarizabilities; Few-Body Quantum Systems; Hydrogen Atom
ABSTRACT
A new general formalism for determining the electric multipole polarizabilities of quantum (atomic and nuclear) bound systems based on the use of the transition matrix in momentum space has been developed. As distinct from the conventional approach with the application of the spectral expansion of the total Green’s function, our approach does not require preliminary determination of the entire unperturbated spectrum; instead, it makes possible to calculate the polarizability of a few-body bound complex directly based on solving integral equations for the wave function of the ground bound state and the transition matrix at negative energy, both of them being real functions of momenta. A formula for the multipole polarizabilities of a two-body bound complex formed by a central interaction potential has been derived and studied. To test, the developed t-matrix formalism has been applied to the calculation of the dipole, quadrupole and octupole polarizabilities of the hydrogen atom.
1. Introduction
Study of the few-body quantum systems persists a perspective line of the advancement of the modern physics. In atomic physics, the Efimov effect for the three-body system, the existence of which was predicted in 1970 [1], has been experimentally verified using ultracold atoms and tuning the atom-atom scattering length by the magnetic field near a Feshbach resonance [2] (see, for example, the reviews [3-5]). In nuclear physics, extensive investigations of few-body nuclei advantageously undertaken over the past fifty years make it possible to gain new important information about the nuclear force.
The investigation of the behaviour of the few-body nuclei in the external electromagnetic field permits to obtain additional data on their properties, specifically, on the electric polarizabilities and magnetic susceptibilities as important fundamental quantities of complex systems. In spite of the fact that the study of the electric polarizabilities of the few-body nuclei has attracted considerable interest from both the experimental [6-11] and theoretical [11-24] points of view and definite progress in the field has been reached, a great deal needs to be done in this area.
Up to now, there exists a discrepancy between the direct experimental result for the electric dipole polarizability of the nucleus 3He (determined by measuring deviations from the Rutherford scattering law of the lowenergy elastic 3He scattering by the Coulomb field of the heavy nucleus 208Pb [8]) and the result deduced from the data for the total 3He photoabsorption cross section using the sum rule 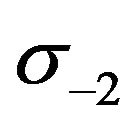 [9].
[9].
The conventional formula for the electric dipole polarizability of the 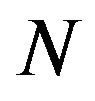 -particle bound complex has the form
-particle bound complex has the form
 (1)
(1)
where 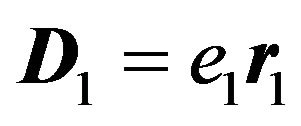 is the dipole moment operator,
is the dipole moment operator, 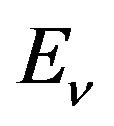 and
and 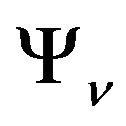 are the energy and the wave function of the v-excited state,
are the energy and the wave function of the v-excited state, 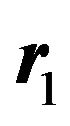 and
and 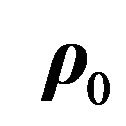 are the radius vectors of the particle 1 relative to the center of mass of the bound complex and the center of mass of the complex relative to the charged particle 0 creating the electric field, and the summation is taken over all possible excited discrete bound and continuum states.
are the radius vectors of the particle 1 relative to the center of mass of the bound complex and the center of mass of the complex relative to the charged particle 0 creating the electric field, and the summation is taken over all possible excited discrete bound and continuum states.
Although the Formula (1) using the spectral expansion can be practically applied in the case of the two-body complex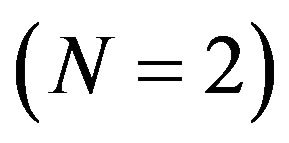 , the direct determination of
, the direct determination of 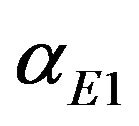 for three and more body complexes
for three and more body complexes  by this relation with the performed beforehand calculation of all discrete and continuum states is not feasible. The known method of Dalgarno and Lewis [25] permits to bypass the difficulty related with taking account of the intermediate continuum states in all possible channels in Equation (1) introducing an additional function
by this relation with the performed beforehand calculation of all discrete and continuum states is not feasible. The known method of Dalgarno and Lewis [25] permits to bypass the difficulty related with taking account of the intermediate continuum states in all possible channels in Equation (1) introducing an additional function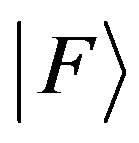 ,
,
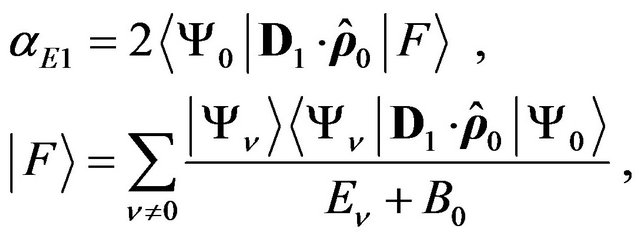 (2)
(2)
where 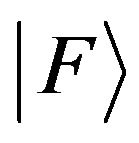 being the first-order correction to the unperturbated state satisfies an inhomogeneous differential equation. Dalgarno-Lewis method has been effectively applied in [12] and [22] to calculate the electric polarizabilities of hydrogen and helium isotopes. Though the result for
being the first-order correction to the unperturbated state satisfies an inhomogeneous differential equation. Dalgarno-Lewis method has been effectively applied in [12] and [22] to calculate the electric polarizabilities of hydrogen and helium isotopes. Though the result for 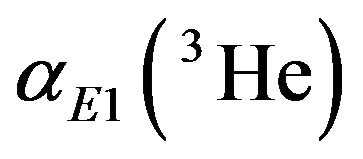 obtained therewith supports the value deduced using the sum rule
obtained therewith supports the value deduced using the sum rule 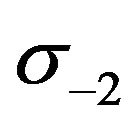 [9], the subject of the discrepancy of the experimental data for 3He under discussion may not be considered as conclusively established since indispensable consistent calculations of the electric dipole polarizabilities of the three-body nuclei on the basis of the rigorous mathematical Faddeev’s [26] formalism have not be performed yet.
[9], the subject of the discrepancy of the experimental data for 3He under discussion may not be considered as conclusively established since indispensable consistent calculations of the electric dipole polarizabilities of the three-body nuclei on the basis of the rigorous mathematical Faddeev’s [26] formalism have not be performed yet.
In this paper we formulate the direct t-matrix approach to determination of the electric polarizabilities of a bound system that relies on the solution of the integral equations for both the bound-state wave function and corresponding components of the partial transition matrix of the system. In Section 2, following the Watson-Feshbach method, we express the polarization potential describing interaction between a charge particle and a bound complex consisting of 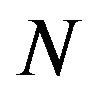 particles in terms of a “truncated” Green’s operator of the system. In this way we obtain a general expression for the electric multipole polarizability of the system. In Section 3 the t-matrix approach to determination of the electric polarizabilities is formulated and simplifications of the general formula assuming conservation of the space parity and the total orbital moment of the system are considered. Section 4 is devoted to the application of the elaborated formalism to the two-body bound systems with the central interaction. It is shown that the electric
particles in terms of a “truncated” Green’s operator of the system. In this way we obtain a general expression for the electric multipole polarizability of the system. In Section 3 the t-matrix approach to determination of the electric polarizabilities is formulated and simplifications of the general formula assuming conservation of the space parity and the total orbital moment of the system are considered. Section 4 is devoted to the application of the elaborated formalism to the two-body bound systems with the central interaction. It is shown that the electric 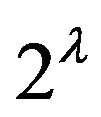 -pole polarizability of the two-particle
-pole polarizability of the two-particle  -state bound complex contains information both on derivatives (of the order
-state bound complex contains information both on derivatives (of the order  and lower) of the wave function in momentum space and on the partial component of the transition matrix that corresponds to the orbital state with
and lower) of the wave function in momentum space and on the partial component of the transition matrix that corresponds to the orbital state with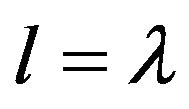 . Section 5 contains the application of the t-matrix formalism to determination of the electric multipole polarizabilities of the hydrogen atom and discussion. Section 6 is devoted to conclusion.
. Section 5 contains the application of the t-matrix formalism to determination of the electric multipole polarizabilities of the hydrogen atom and discussion. Section 6 is devoted to conclusion.
2. Polarization Potential
The formula for the polarization potential describing the interaction between a charged particle 0 and a bound complex consisting of  particles follows immediately when treating the
particles follows immediately when treating the  body problem, namely, the low-energy scattering of the complex by the Coulomb field of the charged particle 0 with the kinetic energy of the relative motion of the particle 0 and the complex
body problem, namely, the low-energy scattering of the complex by the Coulomb field of the charged particle 0 with the kinetic energy of the relative motion of the particle 0 and the complex 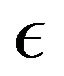 being well below the breakup threshold energy of the complex. Experimentally, to determine the polarizability of the complex in the direct way a heavy nucleus (the particle 0) is used as a source of the intense electric field. For simplicity sake assume that the
being well below the breakup threshold energy of the complex. Experimentally, to determine the polarizability of the complex in the direct way a heavy nucleus (the particle 0) is used as a source of the intense electric field. For simplicity sake assume that the  -body complex contains only one charged particle 1, the other particles
-body complex contains only one charged particle 1, the other particles 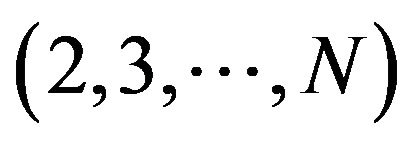 being neutral.
being neutral.
The Hamiltonian of whole system of 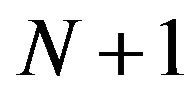 particle has the form
particle has the form
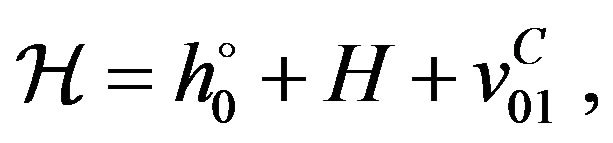 (3)
(3)
where 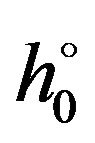 is the operator of the kinetic energy of the relative motion of the particle 0 and the center of mass of the complex,
is the operator of the kinetic energy of the relative motion of the particle 0 and the center of mass of the complex,  is the total Hamiltonian of the
is the total Hamiltonian of the  - body complex,
- body complex, 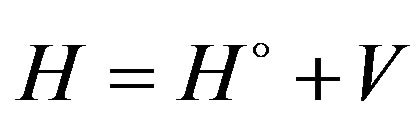 ,
, 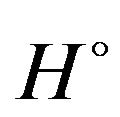 is the kinetic energy operator of the relative motion of the particles inside the complex,
is the kinetic energy operator of the relative motion of the particles inside the complex,  is the total interaction potential of the complex,
is the total interaction potential of the complex, 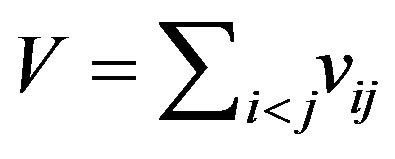 ,
, 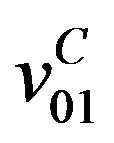 is the operator of the Coulomb interaction between the charge particles 0 and 1 (with the charges
is the operator of the Coulomb interaction between the charge particles 0 and 1 (with the charges  and
and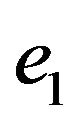 ),
), 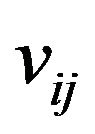 is the operator of the interaction between the particles of the complex
is the operator of the interaction between the particles of the complex 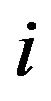 and
and .
.
Using the known Watson-Feshbach projection technique [2,27,28] with the projection operators  and
and , where
, where 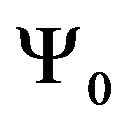 is the wave function of the ground bound state of the complex of
is the wave function of the ground bound state of the complex of 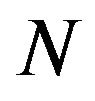 particles
particles 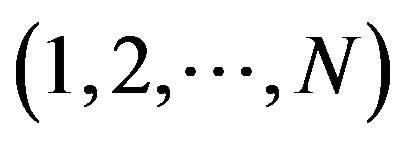 with the binding energy
with the binding energy  (normalized to one), the operator of the effective interaction may be written as
(normalized to one), the operator of the effective interaction may be written as
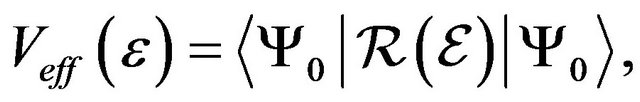 (4)
(4)
where the averaging is taken over the variables of the relative motion of the particles of the complex. The operator  satisfies the integral equation
satisfies the integral equation
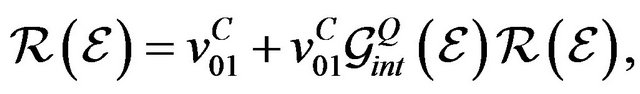 (5)
(5)
in which the potential energy operator is the “external” Coulomb interaction potential between the field source (the particle 0) and the charged particle 1 of the complex, 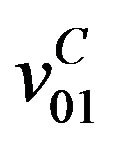 , and the propagator is a “truncated” Green’s operator containing the “internal” interaction potential of the complex
, and the propagator is a “truncated” Green’s operator containing the “internal” interaction potential of the complex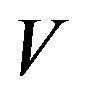 ,
,
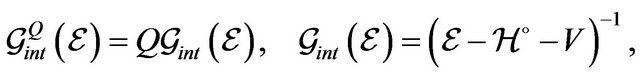 (6)
(6)
where 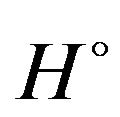 is the free Hamiltonian of the complete system (of
is the free Hamiltonian of the complete system (of  particles),
particles), 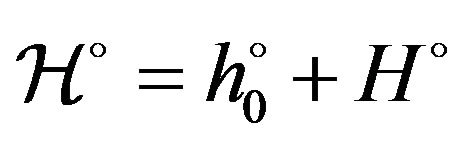 ,
,  is the total energy of the system,
is the total energy of the system,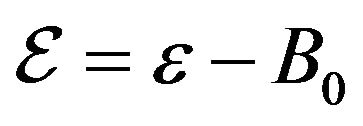 .
.
Introducing the transition operator  which satisfies the integral Lippmann-Schwinger equation
which satisfies the integral Lippmann-Schwinger equation
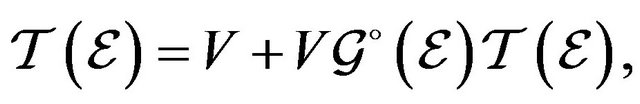 (7)
(7)
the operator 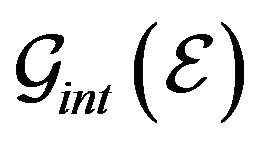 can be written in the form
can be written in the form
 (8)
(8)
where the free propagator 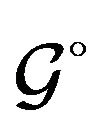 is given by
is given by
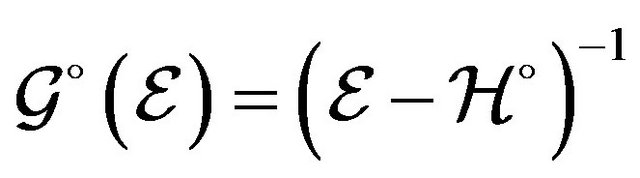 .
.
The polarization potential that corresponds to the second order of the perturbation expansion (in powers of the Coulomb interaction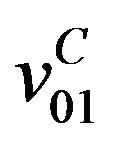 ) of the operator
) of the operator  in the expression for the effective potential (4) is given by
in the expression for the effective potential (4) is given by
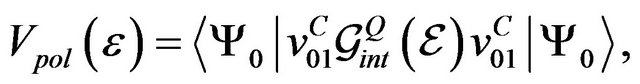 (9)
(9)
where
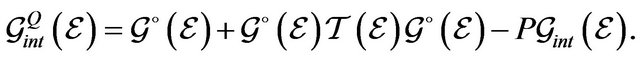 (10)
(10)
According to the uncertainty principle, in the case of asymptotically large (in comparison with the complex size) distances between the particle 0 and the complex, 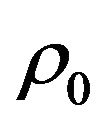 , the momentum variables of relative motion among particles inside the complex considerably exceed the momentum variable of relative motion of the particle 0 and the center of mass of the complex. In such a case, in the expression for the “truncated” Green’s function
, the momentum variables of relative motion among particles inside the complex considerably exceed the momentum variable of relative motion of the particle 0 and the center of mass of the complex. In such a case, in the expression for the “truncated” Green’s function  in Equation (9) we can neglect with the variable quantity that corresponds to the operator
in Equation (9) we can neglect with the variable quantity that corresponds to the operator  in comparison to the variable quantity that corresponds to the operator
in comparison to the variable quantity that corresponds to the operator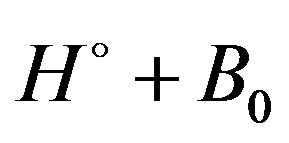 . Then the polarization potential takes the known local form
. Then the polarization potential takes the known local form
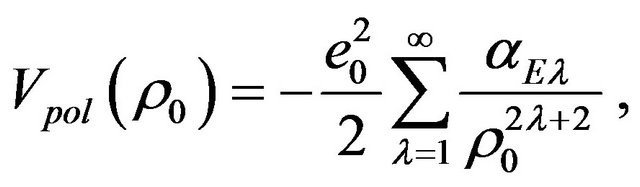 (11)
(11)
where each of coefficients in the sum (11),  , that characterizes the strength of the individual term of the polarization potential with the asymptotic
, that characterizes the strength of the individual term of the polarization potential with the asymptotic 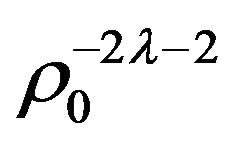 is the electric polarizability of the
is the electric polarizability of the 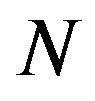 -particle complex of the multipolarity
-particle complex of the multipolarity 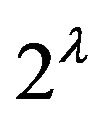
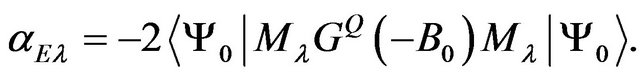 (12)
(12)
Here 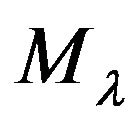 is the multipole moment operator of the charged constituent particle 1,
is the multipole moment operator of the charged constituent particle 1,
 (13)
(13)
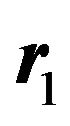 is the radius vector of the particle 1 relative to the center of mass of the bound complex; the radius vector
is the radius vector of the particle 1 relative to the center of mass of the bound complex; the radius vector  describes the position of the center of mass of the bound complex relative to the charged particle 0 creating the electric field,
describes the position of the center of mass of the bound complex relative to the charged particle 0 creating the electric field,  is Legendre polinomial (the unit vectors are marked with a hat,
is Legendre polinomial (the unit vectors are marked with a hat,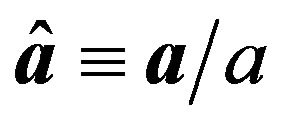 ); the quantity
); the quantity 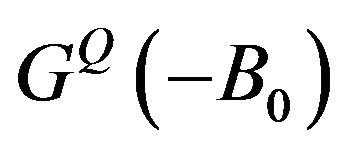 is the “truncated” Green’s operator of the complex
is the “truncated” Green’s operator of the complex 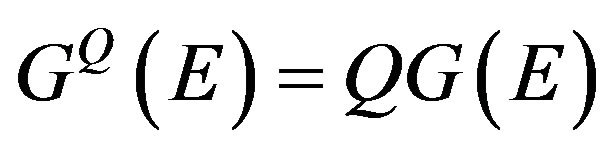 at the bound state energy
at the bound state energy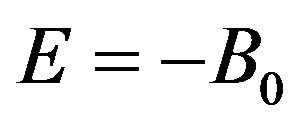 ,
, 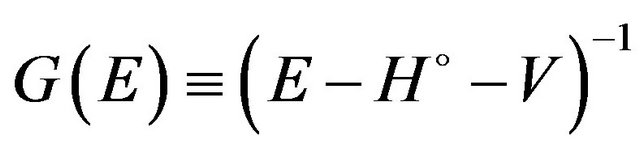 is the total Green’s function of the complex.
is the total Green’s function of the complex.
Note that Formula (1) readily follows from the general Formula (12) after applying the spectral expansion of the total Green’s operator 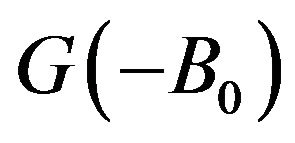 in the complete set of the eigenfunctions of the total
in the complete set of the eigenfunctions of the total 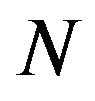 -particle Hamiltonian
-particle Hamiltonian .
.
3. T-Matrix Method of Determination of the Electric Multipole Polarizabilities of a Bound Complex
In this Section we formulate a method for the direct calculation of the polarizability of a few-particle bound system starting immediately from the definition (12) without recourse to expansion in terms of a set of excited discrete and continuum wave functions.
The general Formula (12) for the electric multipole polarizability of a bound complex of  particles
particles  contains the ground-state wave function
contains the ground-state wave function 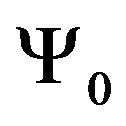 and “truncated” propagator
and “truncated” propagator
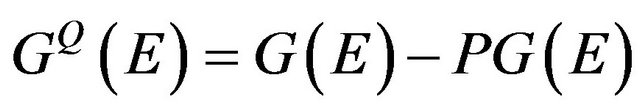 (14)
(14)
at the energy of the bound state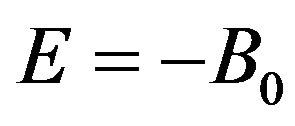 . The wave function
. The wave function 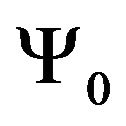 satisfies the Schrödinger equation
satisfies the Schrödinger equation
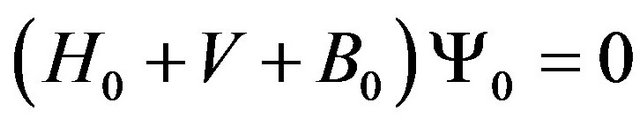 (15)
(15)
or the equivalent homogeneous integral equation
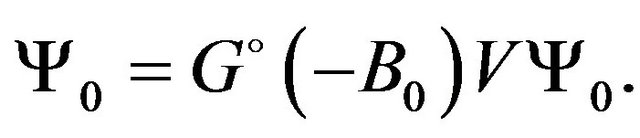 (16)
(16)
We shall restrict our consideration to the case that the complex is in the ground bound state.
The “truncated” propagator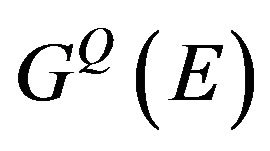 , as distinct from the total one
, as distinct from the total one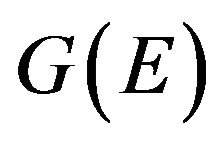 , does not contain the pole singularity at
, does not contain the pole singularity at . In an explicit form, we find the expression for
. In an explicit form, we find the expression for 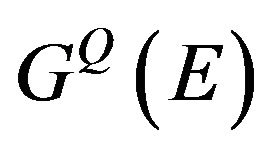 writing the total Green operator
writing the total Green operator 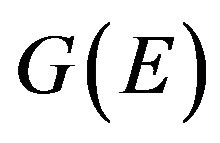 in terms of the free propagator
in terms of the free propagator

and the transition operator ,
,
 (17)
(17)
where the operator 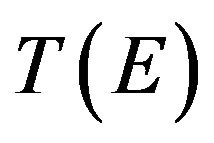 is determined by the LippmanSchwinger integral equation
is determined by the LippmanSchwinger integral equation
 (18)
(18)
In view of Equation (17) and the equality
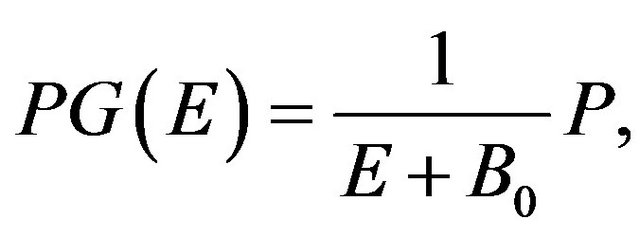 (19)
(19)
the expression (14) takes the form
 (20)
(20)
Separating out from the total transition operator 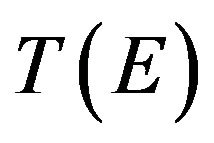 the singular pole part that corresponds to the ground bound state of the system at the energy
the singular pole part that corresponds to the ground bound state of the system at the energy , we write
, we write
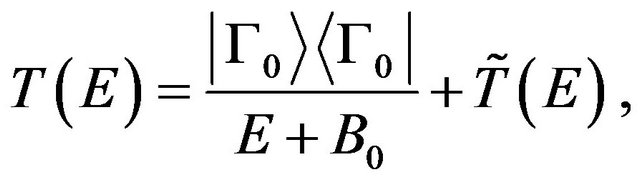 (21)
(21)
where the vertex function 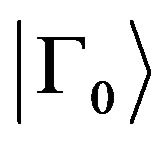 is expressed through the wave function of the ground bound state of the system,
is expressed through the wave function of the ground bound state of the system,
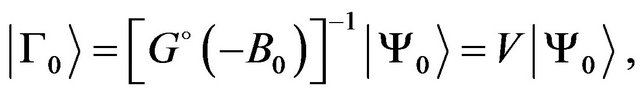 (22)
(22)
satisfying the homogeneous integral equation
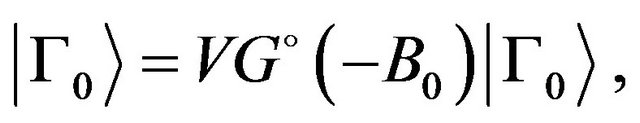 (23)
(23)
and 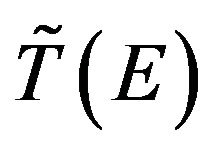 denotes the smooth (non-singular) part of the transition operator.
denotes the smooth (non-singular) part of the transition operator.
Taking into account Expression (21) we write Formula (20) for the operator  in the form
in the form
 (24)
(24)
Cancelling the pole terms in Equation (24) with the use of the identity
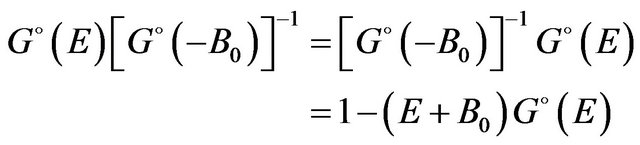 (25)
(25)
we may write Expression (24) in the form
 (26)
(26)
At the point of the negative energy of the bound state of the  -particle complex,
-particle complex, 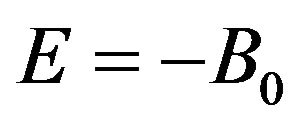 , the operator
, the operator  in the general formula for the electric dipole polarizability (12) becomes
in the general formula for the electric dipole polarizability (12) becomes
 (27)
(27)
With the use of Expression (27) the formula for the polarizability (12) takes the form
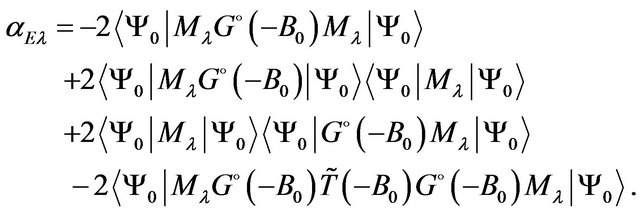 (28)
(28)
A noticeable simplification of the general formula for the electric multipole polarizability (28) takes place, if the interaction potential 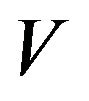 is invariant relative to the space reflection (for example, for the systems with the Coulomb or nuclear interactions). In this case the wave function of the bound complex is characterized by a definite parity. The conservation of the parity leads to nullification of the matrix elements
is invariant relative to the space reflection (for example, for the systems with the Coulomb or nuclear interactions). In this case the wave function of the bound complex is characterized by a definite parity. The conservation of the parity leads to nullification of the matrix elements
 (29)
(29)
which are present in the second and third summands of Formula (28), at odd values of .
.
Formula (28) is also simplified in the case of the invariance of the interaction relative to rotations that leads to conservation of the angular momentum. In such a situation the matrix elements (29) are proportional to the Clebsh-Gordan coefficient 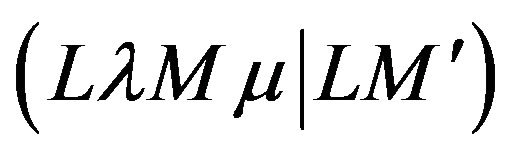 satisfying the triangle condition
satisfying the triangle condition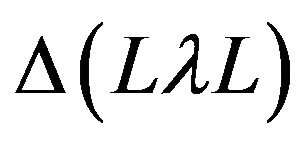 . Specifically, they vanish after integrating in angular variables for all
. Specifically, they vanish after integrating in angular variables for all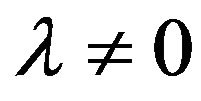 , if the total orbital moment of the complex is equal to zero,
, if the total orbital moment of the complex is equal to zero, .
.
In the case when the ground bound state of the complex is characterized with the total orbital momentum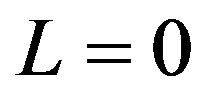 , what is realized for the simplest atomic and few-hadron systems, the formula for the electric multipole polarizability (28) is simplified to the expression
, what is realized for the simplest atomic and few-hadron systems, the formula for the electric multipole polarizability (28) is simplified to the expression
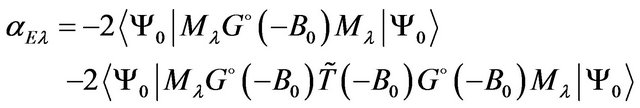 (30)
(30)
As is evident from (28) or (30), to determine the electric dipole polarizability of the bound complex, it is necessary to know not only its wave function, but the smooth part of the transition matrix at negative energy of the bound state 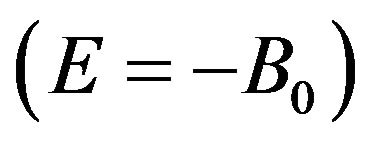 as well. The corresponding transition matrix can be determined by solving the Lippmann-Schwinger integral equation for the two-particle system, the Faddeev integral equations [26] for the threeparticle system or the Faddeev-Yakubovsky equations [29] for more complex systems.
as well. The corresponding transition matrix can be determined by solving the Lippmann-Schwinger integral equation for the two-particle system, the Faddeev integral equations [26] for the threeparticle system or the Faddeev-Yakubovsky equations [29] for more complex systems.
4. Electric Multipole Polarizabilities of the Two-Particle Bound Complex
In the case of two-particle bound complexes, the derived formula for the electric multipole polarizability (30) is simplified. Considered here is a stable bound complex consisting of a charged particle 1 and a neutral particle 2. The interaction potential between the particles is taken to be central, the complex is in S-wave ground bound state. We denote quantities describing the two-particle system by small letters as distinct to notations by capital letters in the general case of quantities for the 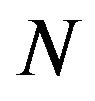 -particle complex used in the foregoing Sections:
-particle complex used in the foregoing Sections:  and
and 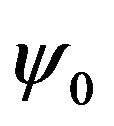 are the binding energy and the wave function of the two-particle bound complex,
are the binding energy and the wave function of the two-particle bound complex, 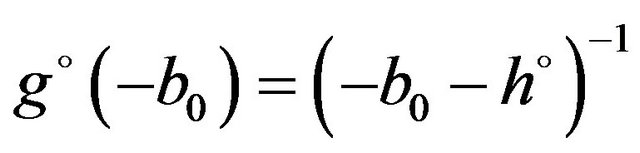
is the free Green’s operator, 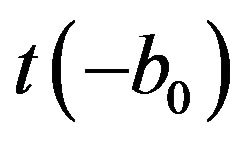 is the two-particle transition operator,
is the two-particle transition operator, 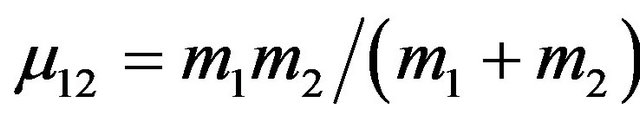 is the reduced mass of the particles 1 and 2. Further consideration we perform in the momentum space.
is the reduced mass of the particles 1 and 2. Further consideration we perform in the momentum space.
Starting from (30) and taking into consideration that the smooth part of the two-particle transition matrix 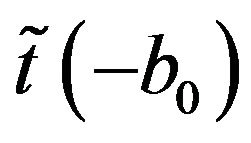 has form of the sum of the smooth part of its
has form of the sum of the smooth part of its  -wave partial component (with
-wave partial component (with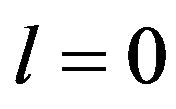 ),
), 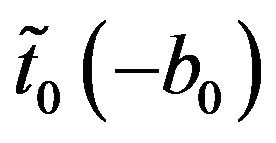 , and the sum of all higher partial orbital components (with
, and the sum of all higher partial orbital components (with ),
),  , which are non-singular at the energy of the bound state,
, which are non-singular at the energy of the bound state,
 (31)
(31)
we write the formula for the electric multipole polarizability of the two-particle system in the form
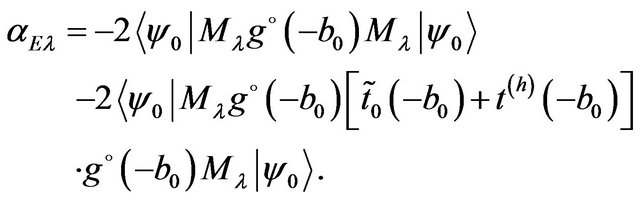 (32)
(32)
The wave function of the complex in the S-wave bound state satisfies the homogeneous integral equation
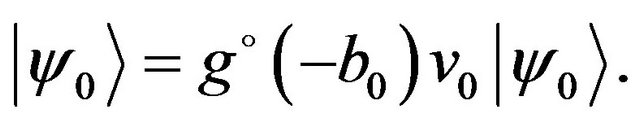 (33)
(33)
and each of the partial components of two transition matrix  satisfies the inhomogeneous integral Lippmann-Schwinger equations
satisfies the inhomogeneous integral Lippmann-Schwinger equations
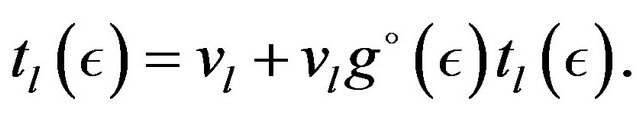 (34)
(34)
where 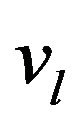 is the partial component of the interaction potential,
is the partial component of the interaction potential, 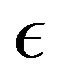 is the energy of the relative motion of the particles.
is the energy of the relative motion of the particles.
The solution of the equation for the partial transition matrix (34) that corresponds to the orbital moment of the ground state  has the form of the sum of the pole and smooth operators
has the form of the sum of the pole and smooth operators
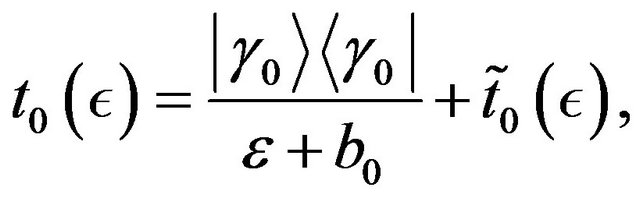 (35)
(35)
where the vertex function
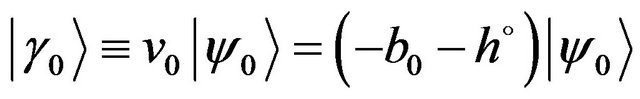
satisfies the homogeneous integral equations that follows from the Equation (33),
 (36)
(36)
Using the operator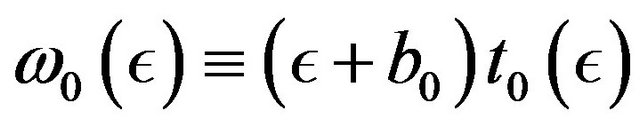 , which is determined by the inhomogeneous equation
, which is determined by the inhomogeneous equation
 (37)
(37)
we write the smooth part of the transition operator,  in the form
in the form
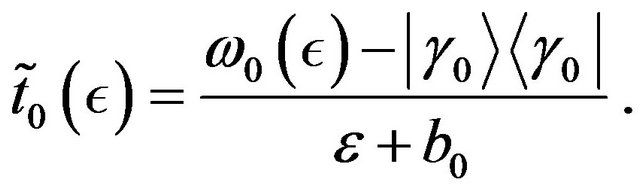 (38)
(38)
At the point , the inhomogeneous Equation (37) becomes homogeneous one,
, the inhomogeneous Equation (37) becomes homogeneous one,
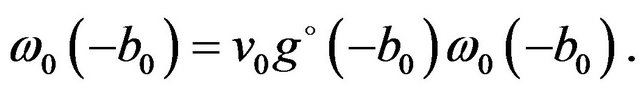 (39)
(39)
Since the kernels of the equations for the function 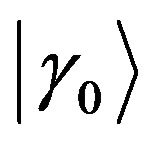 (36) and the operator
(36) and the operator 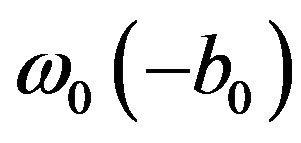 (37) coincide, the solution of the operator Equation (39) may be written as
(37) coincide, the solution of the operator Equation (39) may be written as
 (40)
(40)
According to (38), the operator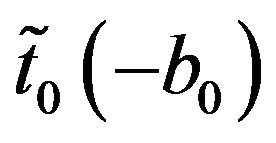 , which is contained in the formula for polarizability (32), is related to the operator
, which is contained in the formula for polarizability (32), is related to the operator  by the expression
by the expression
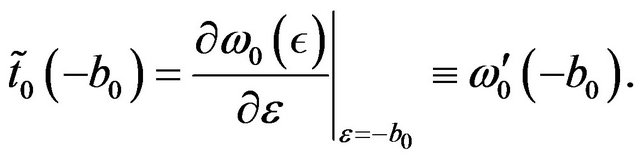 (41)
(41)
The operator 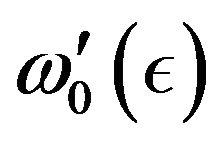 can be deduced by performing the differentiation of the Equation (37) with respect to
can be deduced by performing the differentiation of the Equation (37) with respect to  and the inverted transition from
and the inverted transition from 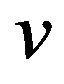 to
to 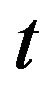 and
and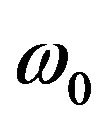 ,
,
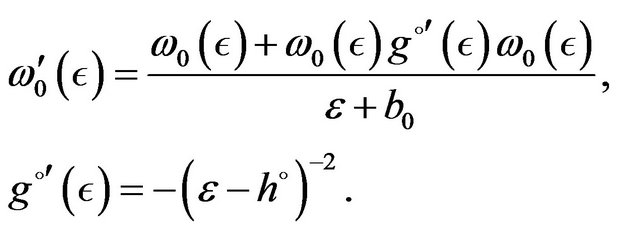 (42)
(42)
Evaluating on the right-hand side of (42) the inderterminacy of the type 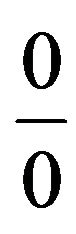 at the point
at the point , which appears in view of the relation (40) and the normalization condition
, which appears in view of the relation (40) and the normalization condition
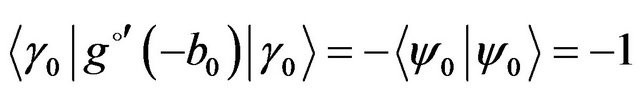 we obtain the expression for the operator
we obtain the expression for the operator ,
,
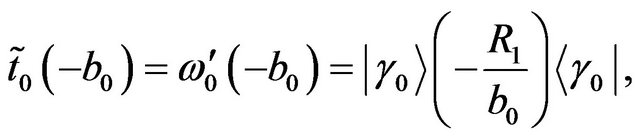 (43)
(43)
where
 (44)
(44)
In case of the central interaction, the part of the transition matrix 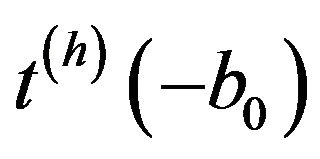 in (32) may be written in the form of expansion in the set of the spherical functions of the angular variable momenta (with
in (32) may be written in the form of expansion in the set of the spherical functions of the angular variable momenta (with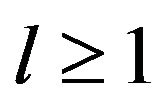 ),
),
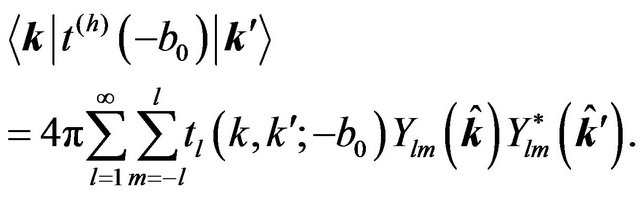 (45)
(45)
Substituting the expressions (43) and (45) for 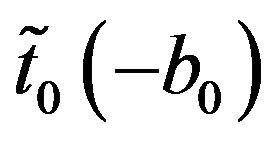 and
and 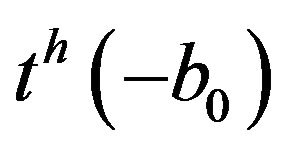 into the formula for the electric polarizability (32) and taking account of the action of the multipole moment operator
into the formula for the electric polarizability (32) and taking account of the action of the multipole moment operator 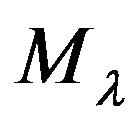 (12) on the function
(12) on the function  in the momentum space (with
in the momentum space (with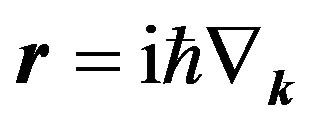 ),
),
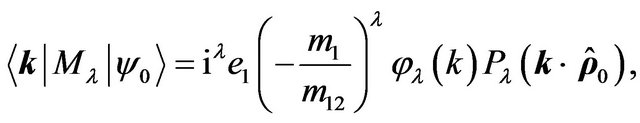 (46)
(46)
where the notations
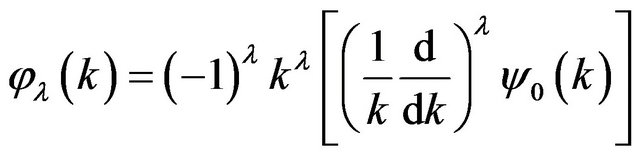 (47)
(47)
and 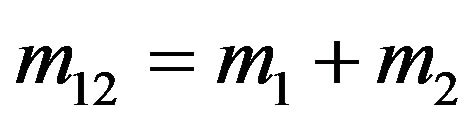 are used, we perform the integration with respect to angular variables.
are used, we perform the integration with respect to angular variables.
Notice that the contribution of the smooth part of the  -wave components of the transition matrix,
-wave components of the transition matrix,  , which is of the separable form (43), proves to be equal to zero as a result of the conservation of the space parity and the orbital moment of the relative motion (similar to zero contributions in the general case from other factorable terms of the “truncated” Green’s operator (27), see comments below Formula (28)). Non vanishing contribution in (32) makes only the partial component with
, which is of the separable form (43), proves to be equal to zero as a result of the conservation of the space parity and the orbital moment of the relative motion (similar to zero contributions in the general case from other factorable terms of the “truncated” Green’s operator (27), see comments below Formula (28)). Non vanishing contribution in (32) makes only the partial component with 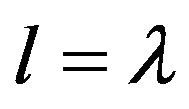 from Equation (45),
from Equation (45),  , that satisfies the Lippmann-Schwinger integral Equation (34),
, that satisfies the Lippmann-Schwinger integral Equation (34),
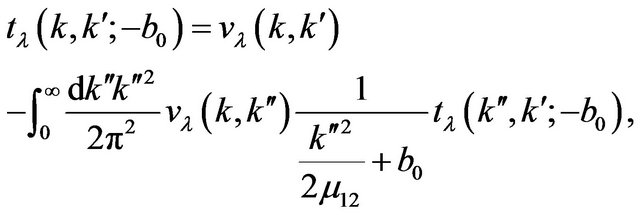 (48)
(48)
where 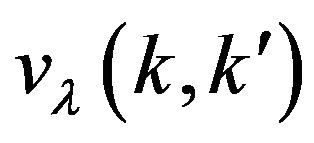 is the partial component of the interaction potential.
is the partial component of the interaction potential.
The final result for the electric multipole polarizability of the two-particle complex with a central interaction between particles following from Equation (32) is written in the form
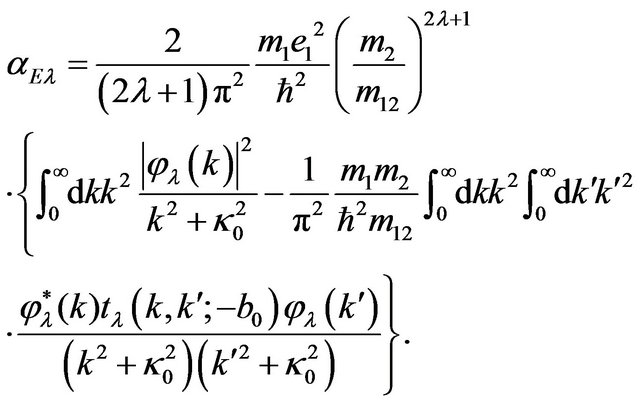 (49)
(49)
According to (47), the functions  in (49) are expressed in terms of the derivatives of the wave function of the ground bound state
in (49) are expressed in terms of the derivatives of the wave function of the ground bound state 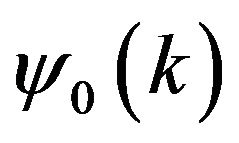 with respect to the relative momentum variable
with respect to the relative momentum variable . In the cases of the dipole
. In the cases of the dipole , quadrupole
, quadrupole  and octupole
and octupole 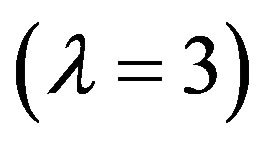 polarizabilities they are of the form
polarizabilities they are of the form
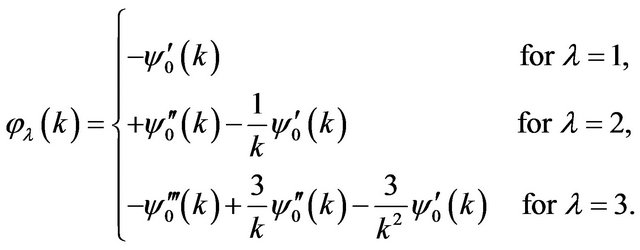 (50)
(50)
Formula (49) derived in the case of the central interaction between the constituents of the two-body complex demonstrates that the electric 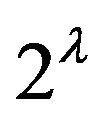 -pole polarizability of the complex contains information not only on the derivatives (of the order
-pole polarizability of the complex contains information not only on the derivatives (of the order  and lower) of its wave function, but on the partial component of the transition matrix,
and lower) of its wave function, but on the partial component of the transition matrix,  , as well.
, as well.
It is advantageous to write Formula (49) in the form more convenient for the practical use. In order to do this, instead of the two-particle t-matrix, which is the function of two momentum variables 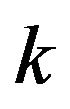 and
and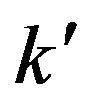 , we introduce in (49) the function of one variable
, we introduce in (49) the function of one variable
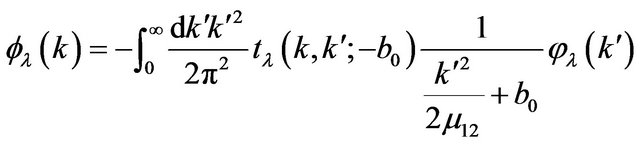 (51)
(51)
that satisfies the inhomogeneous integral equation with the kernel of the Lippmann-Schwinger Equation (48)
 (52)
(52)
in which the free term is determined by the formula
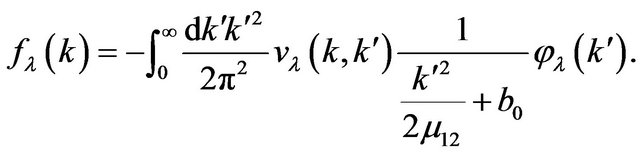 (53)
(53)
In such a case, Formula (49) takes the form
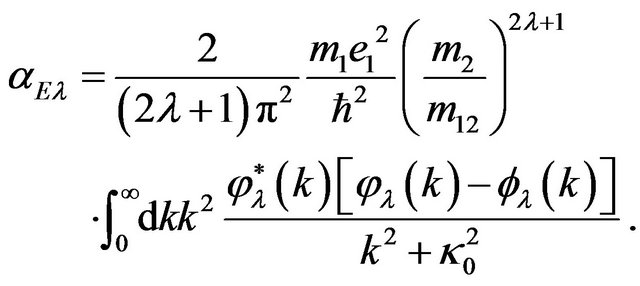 (54)
(54)
5. Application of the Direct T-Matrix Approach and Discussion
Advantages of the t-matrix approach are manifested in calculation of polarizabilities of a quantum system, even if it is two-particle (the deuteron nucleus or the hydrogen atom). In the special case that the interaction between particles is purely S-wave (for example, the separable interaction potential [30], in Formula (49) only the first term persists. The corresponding reduced formula for the dipole polarizability of the two-particle bound complex has been earlier derived in the framework of the threebody formalism of the effective interaction of a charged particle and a complex [13,14,31]. Applications of the t-matrix approach to calculation of the electric dipole polarizabilities of the deuteron, the triton and the lambda hypertriton as two cluster systems with purely  -wave interaction have been carried out in the preceding our papers [23,24].
-wave interaction have been carried out in the preceding our papers [23,24].
For the deuteron with noncentral interaction between the proton and the neutron (in the state with the total angular momentum 1) the polarization in the electric field is anisotropic. Using the separable tensor potential [32] the longitudinal and transverse (relatively to the direction of the electric field) components of the dipole polarizability of the deuteron have been calculated in the work [15]. The results of the further calculations of the components of the deuteron electric dipole polarizability obtained in the framework of the chiral effective field theory [18] are in agreement with the results of [15].
In the case of the hydrogen atom H (assuming that the proton mass is infinitely great when compared to the electron mass), the exact values of the electric multipole polarizabilities 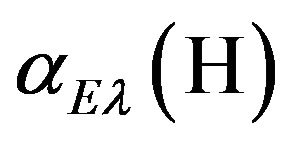 are known [25]. This is why it is possible to test directly the validity of the general formula for the polarizability of the two-particle system (49)— both of the term with free propagation in intermediate state and of the terms with the multiple scattering in the higher orbital intermediate states (with
are known [25]. This is why it is possible to test directly the validity of the general formula for the polarizability of the two-particle system (49)— both of the term with free propagation in intermediate state and of the terms with the multiple scattering in the higher orbital intermediate states (with 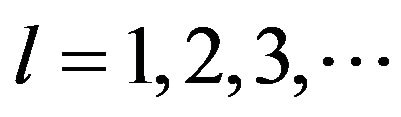 for the dipole, quadrupole, octupole and higher multipole polarizabilities, respectively).
for the dipole, quadrupole, octupole and higher multipole polarizabilities, respectively).
Inserting the analytical expression for the partial components of the Coulomb transition matrix, obtained from the representation for the three-dimensional t-matrix 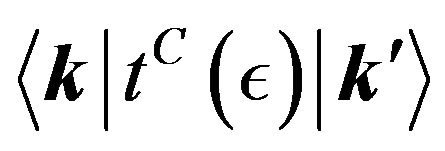 derived in [33] with the use of the O(4) rotation symmetry in four-dimensional Fock space [34], into Formula (49) and separating out the Born term from the Coulomb
derived in [33] with the use of the O(4) rotation symmetry in four-dimensional Fock space [34], into Formula (49) and separating out the Born term from the Coulomb  -matrix,
-matrix,
 (55)
(55)
we write  as a sum of three terms,
as a sum of three terms,
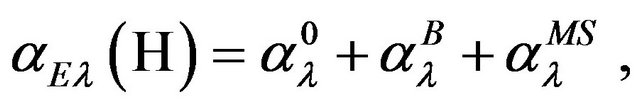 (56)
(56)
where 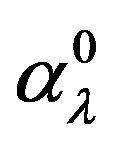 is the first term in Equation (49) that describes free virtual propagation,
is the first term in Equation (49) that describes free virtual propagation,  is a part of the second term that contains only the Born term of the partial Coulomb t-matrix,
is a part of the second term that contains only the Born term of the partial Coulomb t-matrix,  , describing the single scattering in the intermediate state, and
, describing the single scattering in the intermediate state, and 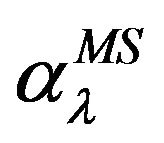 takes into account the multiple scattering contributions (of the order 2 and more).
takes into account the multiple scattering contributions (of the order 2 and more).
We show in the Table 1 the values of the components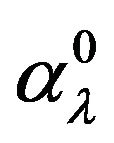 ,
, 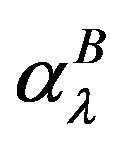 ,
, 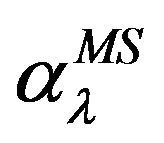 and their sum (56) (in a.u.) that determines the electric dipole
and their sum (56) (in a.u.) that determines the electric dipole , quadrupole
, quadrupole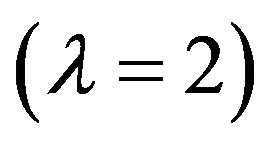 , and octupole
, and octupole 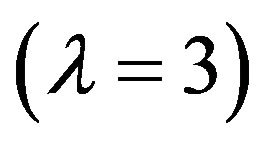 polarizabilities of the hydrogen atom,
polarizabilities of the hydrogen atom,  , obtained applying the direct t-matrix approach, together with the exact values of the polarizabilities derived by Dalgarno and Lewis [25]. Here, values of the quantities
, obtained applying the direct t-matrix approach, together with the exact values of the polarizabilities derived by Dalgarno and Lewis [25]. Here, values of the quantities 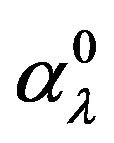 and
and 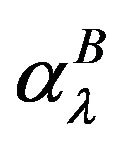 are derived from (49) analytically, and the values of
are derived from (49) analytically, and the values of  are obtained numerically calculating the integral with
are obtained numerically calculating the integral with 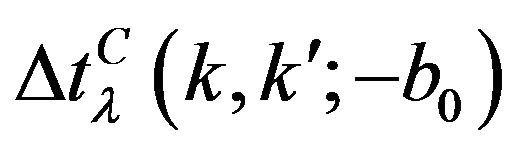 that describes the multiple scattering in intermediate states.
that describes the multiple scattering in intermediate states.
Data given in Table 1 indicate that the dipole polarizability of the hydrogen atom consists of two nearly equal parts—the first term with the free propagator,  , and the sum of two others with the
, and the sum of two others with the  -wave component of the Coulomb transition matrix,
-wave component of the Coulomb transition matrix,
 . For polarizabilities of higher polarity the contribution of the term with the free propagator
. For polarizabilities of higher polarity the contribution of the term with the free propagator  still further increases reaching
still further increases reaching  in the case
in the case 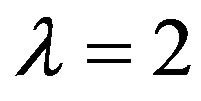 and
and  in the case
in the case . The contribution of the Born term
. The contribution of the Born term 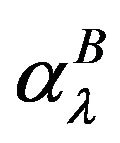 to the polarizability
to the polarizability 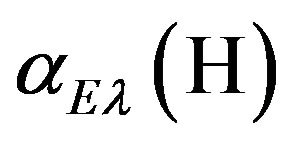 diminishes slowly with
diminishes slowly with  being equal to
being equal to  for
for ,
, 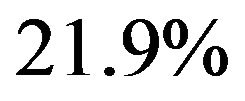 for
for 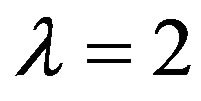 and
and  for
for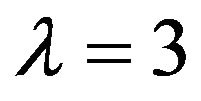 . The contribution of the term describing multiple virtual scattering,
. The contribution of the term describing multiple virtual scattering,  , lowers with increasing
, lowers with increasing  accounting for
accounting for 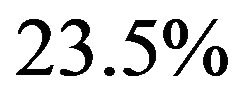 when
when ,
, 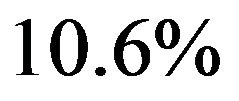 when
when 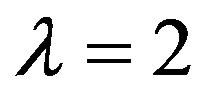 and
and 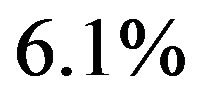 when
when . It is worthy of note that contribution of the sum of the analytically tractable terms,
. It is worthy of note that contribution of the sum of the analytically tractable terms,  , to the polarizabilities of the hydrogen atom
, to the polarizabilities of the hydrogen atom  is prevailing, it accounts for
is prevailing, it accounts for 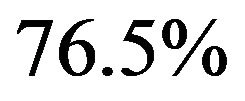 (if
(if ),
), 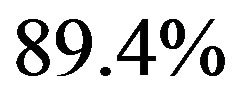 (if
(if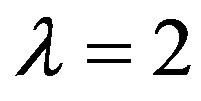 ) and
) and  (if
(if ) of the total amount.
) of the total amount.
The elaborated approach to determination of the electric multipole polarizabilities that relies on the two-particle t-matrix differs radically from the traditional
Table 1. The components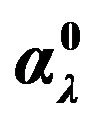 ,
,  and
and 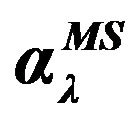 determining the electric dipole
determining the electric dipole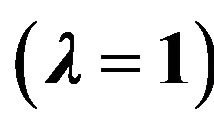 , quadrupole
, quadrupole  and octupole
and octupole  polarizabilities of the hydrogen atom,
polarizabilities of the hydrogen atom, 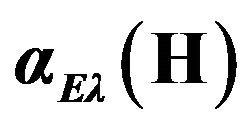 , calculated with the use of the direct t-matrix approach (Equations (49), (55) and (56)) together with the exact values of the polarizabilities (taken from [25]) (in a.u.).
, calculated with the use of the direct t-matrix approach (Equations (49), (55) and (56)) together with the exact values of the polarizabilities (taken from [25]) (in a.u.).

approach based on the spectral expansion of the Green’s function of the system that considers contributions from an infinite number of excited bound and continuum states. As evidenced by the results of the spectral-expansion calculations by Castillejo et al. [35], 65.8% of the magnitude of the electric dipole polarizability of the hydrogen atom comes from the 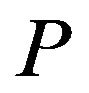 -wave excited bound states. Inclusion of all the excited bound states accounts for 81.4%. The rest 18.6% is provided taking into consideration the continuum states.
-wave excited bound states. Inclusion of all the excited bound states accounts for 81.4%. The rest 18.6% is provided taking into consideration the continuum states.
6. Conclusions
In conclusion, a new approach to the determination of the electric multipole polarizabilities of quantum bound systems (both atomic and nuclear) that is based on the use of the transition matrix has been developed. The most important advantage of the t-matrix formalism is that its application allows to avoid cumbersome calculations of individual contributions from infinitely large number of discrete and continuum excited states. Instead, the determination of one or several (depending on the interaction mode) partial components of the transition matrix is now required. It is also essential that the transition matrix in the main Formula (30) depends on the negative energy of the bound state being therefore a real function of momenta.
To test the validity of the proposed method, the calculation of the electric dipole, quadrupole and octupole polarizabilities of the hydrogen atom has been performed. The obtained results precisely reproduce the known analytically derived values of the polarizabilities. In nuclear physics, in the special case of purely S-wave separable interaction potential, the general Formula (49) is simplified and reduced to one obtained earlier for the deuteron.
The developed method can be immediately extended to more complicated interactions between constituents, specifically, to the case of tensor interactions that gives rise to anisotropic polarization properties of the system. Finally, it is quite important that the proposed approach is suitable for more complicated threeand 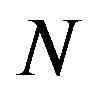 -body systems described by the Faddeev and Faddeev-Yakubovsky integral equations, since the electric polarizabilities of the few-body nuclei are important characteristics containing additional independent information about the fundamental nuclear force. In the first place, we plan to apply the t-matrix approach to study the deformation properties of the 3H and 3He nuclei in the electric field.
-body systems described by the Faddeev and Faddeev-Yakubovsky integral equations, since the electric polarizabilities of the few-body nuclei are important characteristics containing additional independent information about the fundamental nuclear force. In the first place, we plan to apply the t-matrix approach to study the deformation properties of the 3H and 3He nuclei in the electric field.
REFERENCES
- V. Efimov, “Energy Levels Arising from Resonant TwoBody Forces in a Three-Body System,” Physics Letters, Vol. 33B, No. 8, 1970, pp. 563-564.
- H. Feshbach, “A Unified Theory of Nuclear Reactions II,” Annals of Physics, Vol. 19, No. 2, 1962, pp. 287-313.
- E. Braaten and H.-W. Hammer, “Universality in Few-Body Systems with Large Scattering Length,” Physics Reports, Vol. 428, No. 5-6, 2006, pp. 259-390. doi:10.1016/j.physrep.2006.03.001
- T. Kraemer, et al., “Evidence for Efimov Quantum States in an Ultracold Gas of Caesium Atoms,” Nature (London) Vol. 440, No. 7082, 2006, pp. 315-318. doi:10.1038/nature04626
- C. Chin, P. Grimm, P. Julienne and E. Tiesinga, “Feshbach Resonance in Ultracold Atoms,” Reviews of Modern Physics, Vol. 82, No. 2, 2010, pp. 1225-1286. doi:10.1103/RevModPhys.82.1225
- N. L. Rodning, L. D. Knutson, W. G. Lynch and M. B. Tsang, “Measurement of the Electric Polarizability of the Deuteron,” Physical Review Letters, Vol. 49, No. 13, 1982, pp. 909-912. doi:10.1103/PhysRevLett.49.909
- J. L. Friar, S. Fallieros, E. L. Tomusiak, D. Skopik and E. G. Fuller, “Electric Polarizability of the Deuteron,” Physical Review C, Vol. 27, No. 3, 1983, pp. 1364-1366. doi:10.1103/PhysRevC.27.1364
- F. Goeckner, L. O. Lamm and L. D. Knutson, “Measurement of the Electric Polarizability of 3He,” Physical Review C, Vol. 43, No. 1, 1991, pp. 66-72.
- G. A. Rinker, “Nuclear Polarization in Muonic Helium,” Physical Review A, Vol. 14, No. 1, 1976, pp. 18-29. doi:10.1103/PhysRevA.14.18
- J. L. Friar, “Nuclear Polarization Corrections in μ−4 He Atoms,” Physical Review C, Vol. 16, No. 4, 1977, pp. 1540- 1548. doi:10.1103/PhysRevC.16.1540
- K. Pachucki and A. M. Moro, “Nuclear Polarizability of Helium Isotopes in Atomic Transitions,” Physical Review A, Vol. 75, No. 3, 2007, pp. 25211-25214.
- J. L. Friar and S. Fallieros, “Deuteron Electric Polarizability,” Physical Review C, Vol. 29, No. 1, 1984, pp. 232- 239. doi:10.1103/PhysRevC.29.232
- V. F. Kharchenko, S. A. Shadchin and S. A. Permyakov, “Non-Perturbative Theory of the Polarization Interaction in Three-Body Systems,” Physics Letters B, Vol. 199, No. 1, 1987, pp. 1-4. doi:10.1016/0370-2693(87)91451-1
- V. F. Kharchenko and S. A. Shadchin, “Theory of Polarization Particle-Complex Interaction in the Three-Body Approach,” Ukrainian Journal of Physics, Vol. 42, No. 8, 1997, pp. 912-920.
- A. V. Kharchenko, “Effect of the Deuteron Anisotropy: Longitudinal and Transverse Components of the Electric Dipole Polarizability,” Nuclear Physics A, Vol. 617, No. 1, 1997, pp. 34-44. doi:10.1016/S0375-9474(97)00011-0
- J. L. Friar and G. L. Payne, “Nuclear Polarizabilities and Logarithmic Sum Rules,” Physical Review C, Vol. 55, No. 6, 1997, pp. 2764-2767. doi:10.1103/PhysRevC.55.2764
- V. D. Efros, W. Leidemann and G. Orlandini, “PhotodisIntegration of the Three-Nucleon Systems and Their Polarizabilities,” Physics Letters B, Vol. 408, No. 1, 1997, pp. 1-6. doi:10.1016/S0370-2693(97)00772-7
- J.-W. Chen, H. W. Grießhammer, M. J. Savage and R. P. Springer, “The Polarizability of the Deuteron,” Nuclear Physics A, Vol. 644, No. 3, 1998, pp. 221-234. doi:10.1016/S0375-9474(98)80012-2
- D. R. Phillips, G. Rupak and M. J. Savage, “Improving the Convergence of NN Effective Field Theory,” Physics Letters, Vol. B473, No. 3-4, 2000, pp. 209-218.
- X. Ji and Y. Li, “Sum Rules and Spin-Dependent Polarizabilities of the Deuteron in Effective Field Theory,” Physics Letters, Vol. B591, No. 1-2, 2004, pp. 76-80.
- D. Gazit, N. Barnea, S. Bacca, W. Leidemann and G. Orlandini, “Photonuclear Sum Rules and the Tetrahedral Configuration of 4He,” Physical Review C, Vol. 74, No. 6, 2006, pp. 10011-10015.
- I. Stetcu, S. Quaglioni, J. L. Friar, A. C. Hayes and P. Navratil, “Electric Dipole Polarizabilities of Hydrogen and Helium Isotopes,” Physical Review C, Vol. 79, No. 6, 2009, pp. 40011-40016.
- V. F. Kharchenko and A. V. Kharchenko, “Electric Polarization of the Lambda Hypertriton Nucleus,” Collected Physical Papers (Lviv), Vol. 7, 2008, pp. 432-443.
- V. F. Kharchenko and A. V. Kharchenko, “Electric Dipole Polarizabilities of the Triton and Lambda Hypertriton,” International Journal of Modern Physics E, Vol. 19, No. 2, 2010, pp. 225-242.
- A. Dalgarno and J. T. Lewis, “The Exact Calculation of Long-Range Forces between Atoms by Perturbation Theory,” Proceeding of the Royal Society A (London), Vol. 233, No. 1192, 1955, pp. 70-74. doi:10.1098/rspa.1955.0246
- L. D. Faddeev, “Scattering Theory for a Three-Particle System,” Soviet Physics JETP, Vol. 12, 1961, pp. 1014- 1019.
- N. C. Francis and K. M. Watson, “The Elastic Scattering of Particles by Atomic Nuclei,” Physical Review, Vol. 92, No. 2, 1953, pp. 291-303. doi:10.1103/PhysRev.92.291
- C. J. Joachain, “Quantum Collision Theory,” North-Holland Publishing Company, Amsterdam, American Elsevier Publishing Co., Inc., New-York, 1975.
- O. A. Yakubovsky, “On the Integral Equations in the Theory of N Particle Scattering,” Soviet Journal of Nuclear Physics, Vol. 5, 1967, pp. 937-942.
- Y. Yamaguchi, “Two-Nucleon Problem when the Potential Is Nonlocal but Separable,” Physical Review, Vol. 95, No. 6, 1954, pp. 1628-1634. doi:10.1103/PhysRev.95.1628
- V. F. Kharchenko and S. A. Shadchin, “Three-Body Theory of the Effective Interaction between a Particle and a Two-Particle Bound System,” Institute for Theoretical Physics, ITP-93-24E, Kyiv, 1993.
- Y. Yamaguchi and Y. Yamaguchi, “Two-Nucleon Problem When the Potential Is Nonlocal but Separable II,” Physical Review, Vol. 95, No. 6, 1954, pp. 1635-1643. doi:10.1103/PhysRev.95.1635
- S. A. Shadchin and V. F. Kharchenko, “The Analytical Expression for the Two-Particle Coulomb Green’s Function with Explicitly Separated Singularities,” Journal Physics B, Vol. 16, No. 8, 1983, pp. 1319-1322. doi:10.1088/0022-3700/16/8/009
- V. A. Fock, “On the Theory of the Hydrogen Atom,” Zeitschrift für Physik, Vol. 98, No. 3-4, 1935, pp. 145-154. doi:10.1007/BF01336904
- L. Castillejo, I. C. Percival and M. J. Seaton, “On the Theory of Elastic Collisions between Electrons and Hydrogen Atoms,” Proceedings of the Royal Society A (London), Vol. 254, No. 1277, 1960, pp. 259-272. doi:10.1098/rspa.1960.0019

