Journal of Modern Physics
Vol.3 No.9A(2012), Article ID:23098,5 pages DOI:10.4236/jmp.2012.329159
The Generalized Newton’s Law of Gravitation versus the General Theory of Relativity
Department of Physics, Faculty of Science, University of Khartoum, Khartoum, Sudan
Email: aiarbab@uofk.edu
Received June 18, 2012; revised July 29, 2012; accepted August 5, 2012
Keywords: General Relativity; Gravitomagnetism; Perihelion Precession of Planets and Binary Pulsars; Origin of Planetary Spin
ABSTRACT
Einstein general theory of relativity (GTR) accounted well for the precession of the perihelion of planets and binary pulsars. While the ordinary Newton law of gravitation failed, a generalized version yields similar results. We have shown here that these effects can be accounted for as due to the existence of gravitomagnetism only, and not necessarily due to the curvature of space time. Or alternatively, gravitomagnetism is equivalent to a curved space-time. The precession of the perihelion of planets and binary pulsars may be interpreted as due to the spin of the orbiting planet (m) about the Sun (M). The spin (S) of planets is found to be related to their orbital angular momentum (L) by a simple formula, viz.,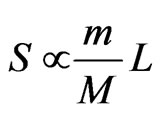 .
.
1. Introduction
We have recently introduced gravitomagnetism as a true cause of the precession of the perihelion of the orbit of planets and binary pulsars [1]. Einstein attributed these effects to the curvature of space-time. The effect of gravitomagnetism, in a similar manner to electromagnetism, is the Larmor precession of a gravitational moment in the gravitomagnetic field induced by the Sun on the planets.
Le Verrier discovered that the orbital precession of the planet Mercury was not quite what it should be; the ellipse of its orbit precesses by some minute value than the predicted by the Newtonian theory of gravitation, even after all the effects of the other planets had been accounted for [1]. This value amounts to 43 arcseconds per century. Several classical explanations were put forward, e.g., an interplanetary dust, an unobserved oblateness of the Sun, an undetected moon of Mercury, or a new planet named Vulcan. Others suggested that the Newton inverse-square law is not correct, and accordingly proposed a power law with an exponent that slightly differs from 2. Moreover, some authors argued in favor of a velocitydependent potential (see [1] and references there in).
To resolve the above mentioned dilemmas, Einstein used a pseudo-Riemannian geometry to allow for the curvature of space-time that was necessary for the reconciliation of the observed gravitational phenomena. He concluded that the space-time should be curved in order to reproduce the observed physical laws of gravitation. Owing to Einstein’s theory of general relativity, particles of negligible mass travel along geodesics in the spacetime. An exact solution to the Einstein field equations is the Schwarzschild metric, which corresponds to the external gravitational field of a stationary, uncharged, nonrotating, spherically symmetric body of mass M. It is characterized by a length scale rs, known as the Schwarzschild radius. The immediate solutions of the field equations explained the anomalous precession of Mercury, and predicted the observed bending of light, which were later confirm experimentally [2].
On the other hand, the theory of electromagnetic interaction is accomplished by Maxwell. This is coined in the four Maxwell equations relating the electric and magnetic fields to the electric charges and current. Lorentz then obtained the force experienced by a charged particle in electric and magnetic fields. Larmor has found that when an electron (magnetic moment) is placed in an external magnetic field, the magnetic moment precess about the magnetic field direction. This precession is due to the spin of the electron. This effect is prominent in the spinorbit interaction exhibited by hydrogen atom [3,4].
If we now consider gravitation with some scrutiny, we will find that, unlike electromagnetism, moving mass doesn’t create a magnetic-like field. Thus, Newton law of gravitation is not like Lorentz law of electromagnetism.
In this sense, gravity and electromagnetism are not analogous and can’t be utterly compared with gravitation. To remedy this problem, we have to look for a gravitomagnetism counterpart of gravity. In this way, we can say gravity is analogous to electricity and gravitomagnetism is analogous to magnetism. The question is what is the gravitomagnetic field? By analogy, this should be obtained by looking at Biot-Savart law that defines the magnetic field of a uniformly moving charged particle in an electric field. To complete the analogy the charge of the particle should correspond to the mass of the particle. In this way, we may call the electric charge, the electric mass in contrast with the gravitational mass. This furnishes the complete analogy between gravitation and electromagnetism.
How we then avail the electrical phenomena and rules in one paradigm to interpret the other? To answer this question, we have to trust (beforehand) the existing analogies, and base all our new interpretation of the gravitational phenomena by explaining their corresponding ones. In this manner, the precession of the perihelion of the orbit of planets and binary pulsars is obtained from the precession of the electron (magnetic moment) in an external magnetic field. Planets and binary pulsars precess when they experience a gravitomagnetic filed (if any). In this case, we use the same laws holding for the counter (analogous) phenomenon, however.
Moreover, the deflection of light by the Sun is explained by using the laws governing the deflection of a charged particle (α-particle) by the nucleus [5]. If we continue in this manner, we may persuade our selves that, to every electromagnetic phenomenon there are gravitomagnetic counter-phenomena. Hence, electromagnetism and gravitomagnetism are same but different aspects of a unified origin.
In this respect, we will find our-selves distracted to interpret the gravitational phenomena as due to the curvature of space-time. We are then not abide by the GTR to interpret our physical world. Or alternatively, we treat the curvature and gravitomagnetism as a same object, or yield the same effects. This can be trusted if we are able to show that the term responsible for the curvature of space-time in Einstein field equations is the same as the that resulting from the influence of gravitomagnetism.
In this paper, we will show that the gravitomagnetism terms in the generalized Newton law of gravitation is the same as the one in the Einstein general field equations. In this way, we upgrade Newton law of gravitation to the general theory of gravitation, but with different predictions. Thus, the correct Newton law of gravitation still works finely, and expresses gravitational phenomena in accordance with observations. Hence, gravity and electromagnetism are governed by unified laws. In Section 2 we present the potential that gives rise to the precession of perihelion in the GTR. We compare this potential with that arising from the gravitomagnetic field.
We find that the gravitomagnetic term is 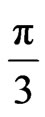 of the Einstein term (GTR). Einstein attributed this term to curvature of space.
of the Einstein term (GTR). Einstein attributed this term to curvature of space.
Can we say that the gravitomagnetism is the cause of Einstein curvature?
Do we still adopt GTR that requires advanced mathematics, as the theory of gravitation and leave the simplyunderstood Newton’s laws of gravitation aside? In effect, the gravitomagnetic theory (or Gravitational Lorentz force) is simple and can easily be handled without recourse to tensor (advanced mathematics) analysis to unravel gravitational phenomena. Besides, it is analogous to electromagnetic theory that is well understood and complies utterly with experimental facts. The idea of curvature of space is no longer adopted. Moreover, the Einstein’s dream of unification of fundamental forces in nature will become imminent within this framework.
2. The General Theory of Relativity (GTR)
Einstein attributed the gravitational phenomena, now known, to the effect of the curvature of space-time induced by the presence of a massive object [2]. The effective gravitational potential of the object of mass m moving around a massive object of mass M takes the form [6]
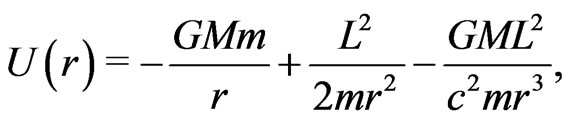 (1)
(1)
and the force, 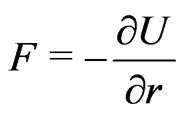 , can be written as
, can be written as
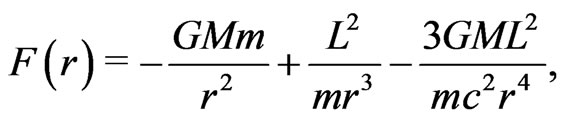 (2)
(2)
where L is the orbital angular momentum of the mass m.
This inverse-cubic energy term in Equation (1) causes elliptical orbits to precess gradually by an angle 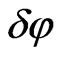 per revolution [2]
per revolution [2]
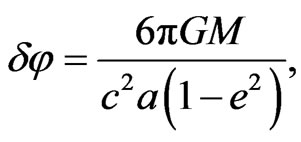 (3)
(3)
where e and a are the eccentricity and semi-major axis of the elliptical orbit, respectively. This is known as the anomalous precession of the planet Mercury.
Another prediction famously used as evidence for GTR, is the bending of light in a gravitational field. The deflection angle is given by [2]
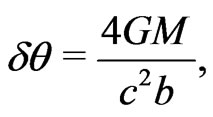 (4)
(4)
where b is the distance of closest approach of light ray to the massive object. Therefore, the gravitomagnetic force is equal to 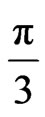 of the GTR force. Whether, the gravitational phenomena are in full agreement with our gravitomagnetic model or with GTR is a subject of the present and future observations. At any rate, we are lucky to have two complementary paradigms explaining the same effect in different ways. Can we deduce that it is the gravitomagnetic field that curves the space and not the Sun mass? Or can we say that it is the curvature that produces the gravitomagnetism?
of the GTR force. Whether, the gravitational phenomena are in full agreement with our gravitomagnetic model or with GTR is a subject of the present and future observations. At any rate, we are lucky to have two complementary paradigms explaining the same effect in different ways. Can we deduce that it is the gravitomagnetic field that curves the space and not the Sun mass? Or can we say that it is the curvature that produces the gravitomagnetism?
3. The Generalized Newton Law of Gravitation
We have shown recently that Newton law of gravitation can be written, as a Lorentz-like law, as [7]
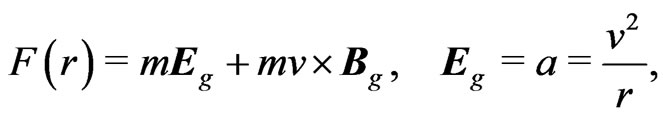 (5)
(5)
where
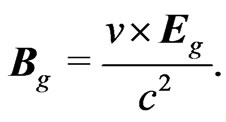 (6)
(6)
Thomas introduced a factor 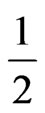 to account for the spin-orbit interaction in hydrogen atom [8]. Here
to account for the spin-orbit interaction in hydrogen atom [8]. Here 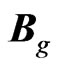 is measured in
is measured in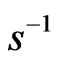 . To convert it to rad/sec, we multiply it by
. To convert it to rad/sec, we multiply it by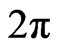 . Hence, the gravitomagnetic force becomes
. Hence, the gravitomagnetic force becomes
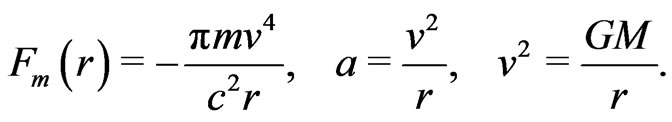 (7)
(7)
The gravitomagnetic field is divergenceless, since
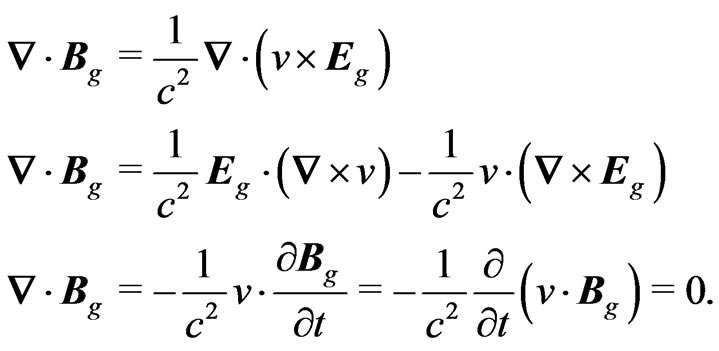
This implies that the gravitomagnetic lines curl around the moving mass (gravitational current) creating it. This may also rule out the existence of negative mass. Therefore, as no magnetic monopole exits; no gravitomagnetic monopole (antigravity) exits. Thus, the search for magnetic monopole is tantamount to that of antigravity.
The angular momentum is defined by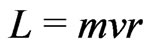 , so that Equation (7) becomes
, so that Equation (7) becomes
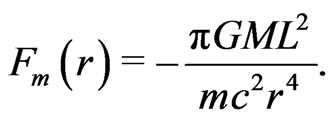 (8)
(8)
The second term in Equation (2) is due to the centrifugal term arising from a central force field. In polar coordinates the force is written as
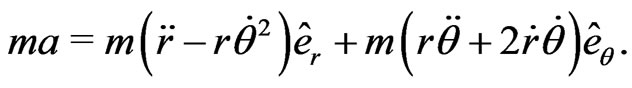 (9)
(9)
For a central force the second term vanishes. It yields,
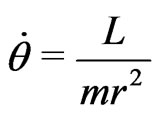 , so that the first term becomes
, so that the first term becomes
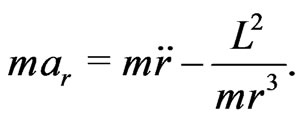 (10)
(10)
Substituting Equation (10) in Equation (5) yields the full effective central force, owing to gravitomagnetism, as
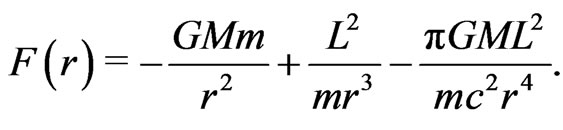 (11)
(11)
The corresponding potential will be
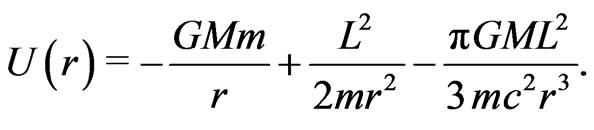
Comparison of Equations (2) and (11) reveals that the gravitomagnetic force is equal to 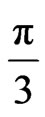 of the curvature force. Consequently, the generalized Newton law of gravitation and the general theory of relativity produce the same gravitational phenomena.
of the curvature force. Consequently, the generalized Newton law of gravitation and the general theory of relativity produce the same gravitational phenomena.
The gravitomagnetic force term, the last term in Equation (11), can be written as
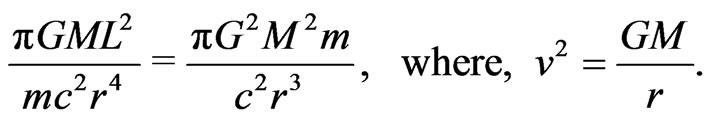 (12)
(12)
Finally, Equation (11) can be written as
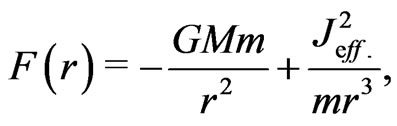 (13)
(13)
where
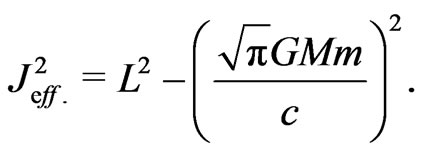 (14)
(14)
4. Precession of Planets and Binary Pulsars
Owing to the above equivalence between gravitomagnetism and GTR, we interpret the precession of the perihelion of planets and binary pulsars as a Larmor-like precession, and not due to the GTR interpretation as due to the curvature of space-time. We may attribute this precession as due to the precession of gravitational moment (mass) in a gravitomagnetic field induced by the massive objects (Sun). In electromagnetism, the Larmor precession is defined by [4]
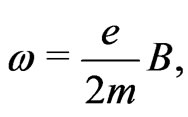 (15)
(15)
while in gravitation (since 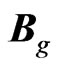 is in
is in 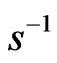 and
and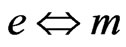 ) it is defined as [1]
) it is defined as [1]
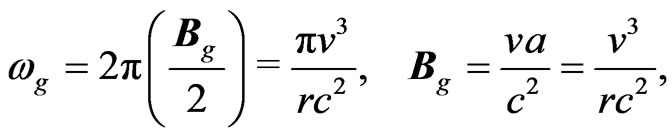 (16)
(16)
where (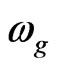 is in rad/seec) and
is in rad/seec) and
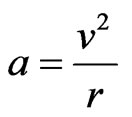 (17)
(17)
The precession rate in Equation (16) can be written as
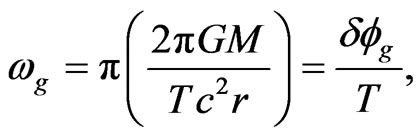 (18)
(18)
where 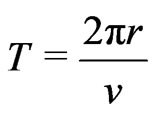 is the period of revolution. This corresponds to a precession angle of
is the period of revolution. This corresponds to a precession angle of
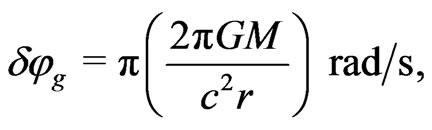 (19)
(19)
that is equal to 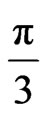 of the curvature effect, and for elliptical orbit
of the curvature effect, and for elliptical orbit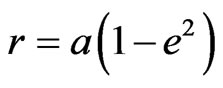 .
.
5. Deflection of α-Particles by the Nucleus
We would like here to interpret the deflection of light by the Sun gravity in an analogous way to the deflection of 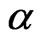 -particles by the nucleus, without resorting to the GTR calculation. The deflection angle of
-particles by the nucleus, without resorting to the GTR calculation. The deflection angle of 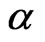 -particles by a nucleus is given by [5]
-particles by a nucleus is given by [5]
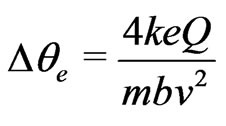 (20)
(20)
where Q is the nucleus charge, 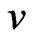 the
the 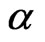 -particle speed, k Coulomb constant, and b the impact factor. The corresponding gravitational analog for the deflection of light will be,
-particle speed, k Coulomb constant, and b the impact factor. The corresponding gravitational analog for the deflection of light will be, 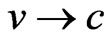 ,
, 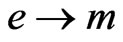 ,
, 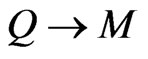 ,
, 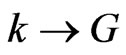 , [9]
, [9]
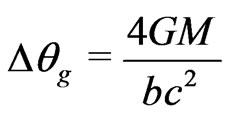 (21)
(21)
without resorting to GTR calculation. Recall that, according to Equivalence Principle, all particles in gravity accelerate without reference to their mass (whether massive or massless). Therefore, it doesn’t matter whether light has a mass or not. The relation in Equation (21) is the same as the relation obtained by GTR as in Equation (4). The minimum distance 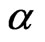 particles can approach the nucleus is given by equating the kinetic energy and the Coulomb potential energy that yields the relation
particles can approach the nucleus is given by equating the kinetic energy and the Coulomb potential energy that yields the relation
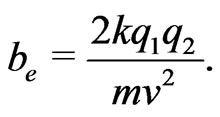 (22)
(22)
In gravitation and for light scattered by the Sun gravity, the above relation gives (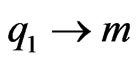 ,
,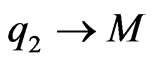 and
and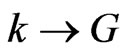 )
)
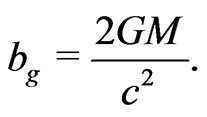 (23)
(23)
This is nothing but the Schwarzschild distance that no particle can exceed. Therefore, the complete analogy between gravitation and electricity is thus realized. In this context, we have shown recently that the Larmor dipole radiation has a gravitational analogue [10]. Similarly, the same analogy exists between hydrodynamics and electromagnetism [11].
6. The Spin of Planets
The discovery of the spin of the electron by Goudsmit and Uhlenbeck in 1926 was crucial in understanding many physical phenomena that wouldn’t have been explained without [12]. This spin is theoretically formulated by Dirac confirming the experimental finding. However, the spin of planets had been known since long time (1851) that was demonstrated by Foucault’s pendulum. In a recent paper we have introduced the gravitomagnetism produced by moving planets as the magnetic field produced by moving charge [1]. We then obtained the gravitational Ampere’s and Faraday’s laws of gravitomagnetism. The gravitomagnetic moment of a planet due to its orbital motion is given by [1]
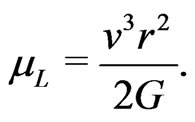 (24)
(24)
For circular orbit, Equation (24) yields
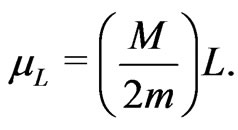 (25)
(25)
In a similar manner the gravitomagnetic moment due to spin will be twice the above value (analogous to electromagnetism)
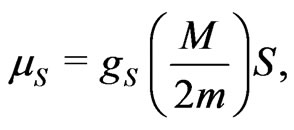 (26)
(26)
where 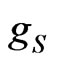 defines some gyro-gravitomagnetic ratio that is independent of the planet’s mass. If we assume the precession of planets is a spin-orbit interaction, then we can equate
defines some gyro-gravitomagnetic ratio that is independent of the planet’s mass. If we assume the precession of planets is a spin-orbit interaction, then we can equate 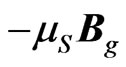 (assuming the angle to be zero) to the potential term arising from the gravitomagnetic force in Equation (11). This yields, for circular orbit,
(assuming the angle to be zero) to the potential term arising from the gravitomagnetic force in Equation (11). This yields, for circular orbit,
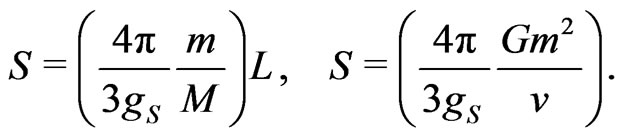 (27)
(27)
This is a very interesting equation, since it determines the spin of planets from their orbital angular momentum. With the help of the above equation, the moment of inertia of planets can be precisely determined. It then follows that the spin and the geometrical form of planets is a consequence of its dynamics. Consequently, the spin
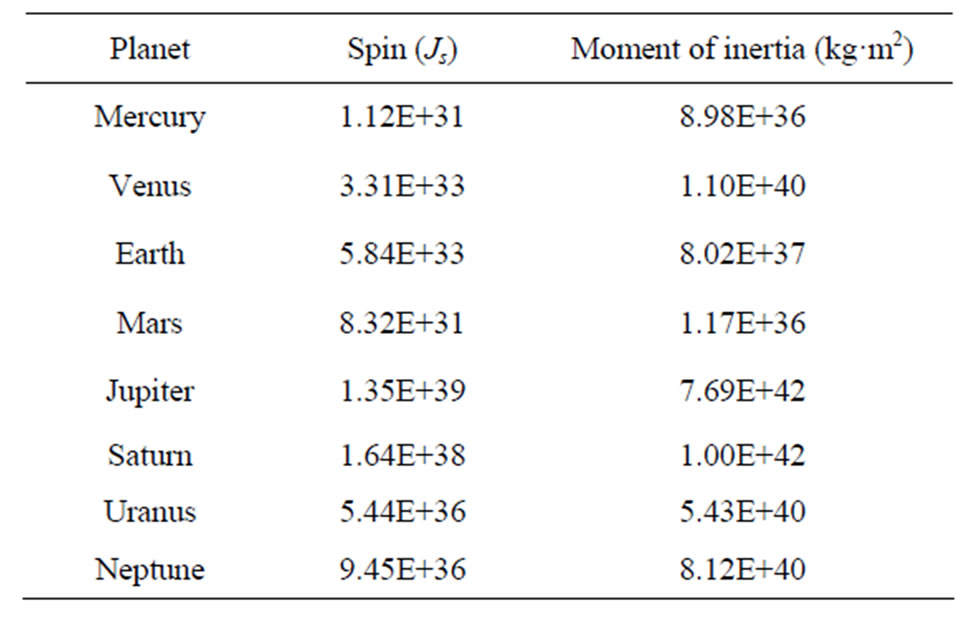
Table 1. The predicated values for spin and moment of inertia owing to Equation (27) with gS = 57. Any deviation from known values that may appear could be attributed to the uncertainty in determining the radii of planets. Alternatively, the angle between L and S will be of importance.
angular momentum is no longer an intrinsic property of the planet. The energy corresponding to this interaction may be converted into internal energy (heat) inside the planet.
Owing to Equation (27) we are entitled to say that any orbiting planet must spin! Thus, any gravitating object in curvilinear motion must spin. For consistency of the spin of the Earth with the present value with take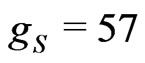 . From this law the moment of inertia of all gravitation objects can be precisely determined. Table 1 shows the anticipated values for the spin and the corresponding moment of inertia of the planetary system. Equation (27) can be used to estimate the hidden central mass around which another mass orbits. It can be generally useful in many astrophysical applications.
. From this law the moment of inertia of all gravitation objects can be precisely determined. Table 1 shows the anticipated values for the spin and the corresponding moment of inertia of the planetary system. Equation (27) can be used to estimate the hidden central mass around which another mass orbits. It can be generally useful in many astrophysical applications.
7. Conclusion
We have shown that the gravitomagnetism and the general theory of relativity are two theories of the same phenomenon. This entitles us to fully accept the analogy existing between electromagnetism and gravity. Hence, electromagnetism and gravity are unified phenomena. The precession of the perihelion of planets and binary pulsars may be interpreted as a spin-orbit interaction of gravitating objects. The spin of a planet is directly proportional to its orbital angular momentum and mass weighted by the Sun’s mass. Alternatively, the spin is directly proportional to the square of the orbiting planet’s mass and inversely proportional to its velocity.
8. Acknowledgements
I would like to thank Prof. G. Gadzirayi Nyambuyathe for critically revising the manuscript and drawing my attention to consider a formula for the spin of planets.
REFERENCES
- A. I. Arbab, “The Gravitomagnetism: A Novel Explanation of the Precession of Planets and Binary Pulsars,” Astrophysics and Space Science, Vol. 330, No. 1, 2010, pp. 61-68. doi:10.1007/s10509-010-0353-7
- S. Weinberg, “Gravitation and Cosmology,” John Wiley, New York, 1971.
- D. Griffiths, “Introduction to Electrodynamics,” PrenticeHall, Upper Saddle River, 1999.
- H. L. Malcolm, “Spin Dynamics,” John Wiley, New York, 2000.
- E. Rutherford, “The Scattering of α and β Particles by Matter and the Structure of the Atom,” Philosophical Magazine, Vol. 92, No. 4, 2012, pp. 379-398.
- T. Cheng, “Relativity, Gravitation, and Cosmology,” Oxford University Press, Oxford, 2005, p. 108.
- A. I. Arbab, “The Generalized Newton’s Law of Gravitation,” Astrophysics and Space Science, Vol. 325, No. 1, 2010, pp. 37-40. doi:10.1007/s10509-009-0145-0
- L. H. Thomas, “The Motion of the Spinning Electron,” Nature, Vol. 117, No. 2945, 1926, p. 514. doi:10.1038/117514a0
- A. I. Arbab, “A Phenomenological Model for the Precession of Planets and Bending of Light,” Astrophysics and Space Science, Vol. 325, No. 1, 2010, pp. 41-45. doi:10.1007/s10509-009-0146-z
- A. I. Arbab, “On the Gravitational Radiation of Gravitating Objects,” Astrophysics and Space Science, Vol. 323, No. 2, 2010, pp. 181-184. doi:10.1007/s10509-009-0058-y
- A. I. Arbab, “The Analogy between Electromagnetism and Hydrodynamics,” Physics Essays, Vol. 24, No. 2, 2011, pp. 254-259. doi:10.4006/1.3570825
- S. Goudsmit and G. E. Uhlenbeck, “Over Het Roteerende Electron en de Structuur der Spectra,” Physica, Vol. 6, 1926, pp. 273-290.

