Journal of Modern Physics
Vol.3 No.1(2012), Article ID:16751,8 pages DOI:10.4236/jmp.2012.31016
On Production of Hadrons in Proton-Proton Collisions at RHIC and LHC Energies and an Approach
1Department of Physics, Raghunathpur College, Raghunathpur 723133, Purulia, India
2Beramara Ram Chandrapur High School, South 24-Parganas 743609, India
3Physics and Applied Mathematics Unit (PAMU), Indian Statistical Institute, 203 B.T. Road, Kolkata 700108, India
Email: gpradeepta@rediffmail.com, sau_goutam@yahoo.com, bsubrata@isical.ac.in
Received October 10, 2011; revised November 19, 2011; accepted December 6, 2011
Keywords: Relativistic Heavy Ion Collisions; Inclusive Production
ABSTRACT
From the very early days of Particle Physics, both experimental and theoretical studies on proton-proton collisions had occupied the center-stage of attention for very simple and obvious reasons. And this intense interest seems now to be at peak value with the onset of the Large Hadron Collider (LHC)-studies at TeV ranges of energies. In this work, we have chosen to analyze the inclusive cross-sections, the rapidity density, the 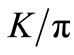 and
and 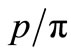 -ratio behaviours and the < PT >- values, in the light of the Sequential Chain Model (SCM). And the limited successes of the model encourage us to take up further studies on several other aspects of topmost importance in particle physics with the same approach.
-ratio behaviours and the < PT >- values, in the light of the Sequential Chain Model (SCM). And the limited successes of the model encourage us to take up further studies on several other aspects of topmost importance in particle physics with the same approach.
1. Introduction
Proton-proton collisions are known to be the most elementary interactions and form the very basis of our knowledge about the nature of high energy collisions in general. Physicists, by and large, hold the view quite firmly that the perturbative quantum-chromodynamics (pQCD) provides a general framework for the studies on high energy particle-particle collisions [1]. Obviously, the unprecedented high energies attained at Large Hadron Collider (LHC) offer new windows and opportunities to test the proposed QCD dynamics with its pros and cons. Naturally the normal expectations run high that the bulk properties of the collision system such as all the momentum spectra and correlations of all produced hadrons should follow the strictures of QCD. But this not definite and concretely-shaped knowledge about how this actually happens and to what extent the process could be understood in the perturbative and non-perturative domains. The issues involved here still remain, to a considerable extent, quite open [2,3]. Thus, having been somewhat repulsed by the so-called standard approach, we try here to explain some crucial aspects of measured data on pp reactions at the LHC range of energies with the help of some alternative approach. Our main thrust would be on the properties of time-tested familiar observables like transverse momenta spectra, rapidity distributions, the ratio-behaviours and average transverse momenta (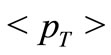 ) for the charged secondaries in high energy pp interactions. Comparison with some other model would be made whenever possible.
) for the charged secondaries in high energy pp interactions. Comparison with some other model would be made whenever possible.
The organisation of the paper is as follows: In Section 2, we provide a brief outline of the model chosen for study. In Section 3, the results obtained by the model-based study are presented. In Section 4, we end up with a discussion on the results and the observations made in Section 3 and the conclusions.
2. The Approach: An Outline
This section gives a brief overview of the model-based features for the production mechanism of the secondary hadrons in nucleon-nucleon (p + p) interaction in the context of the Sequential Chain Model (SCM). According to this Sequential Chain Model (SCM), high energy hadronic interactions boil down, essentially, to the pion-pion interactions; as the protons are conceived in this model as , where
, where  is a spectator particle needed for the dynamical generation of quantum numbers of the nucleons [4-9]. The production of pions in the present scheme occurs as follows: the incident energetic π-mesons in the structure of the projectile proton (nucleon) emits a rho(ρ)-meson in the interacting field of the pion lying in the structure of the target proton, the ρ-meson then emits a π-meson and is changed into an omega(ω)-meson, the ω-meson then again emits a π- meson and is transformed once again into a ρ-meson and thus the process of production of pion-secondaries continue in the sequential chain of ρ-ω-π mesons. The two ends of the diagram contain the baryons exclusively [4-9].
is a spectator particle needed for the dynamical generation of quantum numbers of the nucleons [4-9]. The production of pions in the present scheme occurs as follows: the incident energetic π-mesons in the structure of the projectile proton (nucleon) emits a rho(ρ)-meson in the interacting field of the pion lying in the structure of the target proton, the ρ-meson then emits a π-meson and is changed into an omega(ω)-meson, the ω-meson then again emits a π- meson and is transformed once again into a ρ-meson and thus the process of production of pion-secondaries continue in the sequential chain of ρ-ω-π mesons. The two ends of the diagram contain the baryons exclusively [4-9].
For 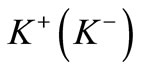 or
or 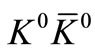 production the model proposes the following mechanism. One of the interacting π-mesons emits a ρ-mesons; the ρ-mesons in its turn emits a
production the model proposes the following mechanism. One of the interacting π-mesons emits a ρ-mesons; the ρ-mesons in its turn emits a 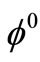 - meson and a π-meson. The π-meson so produced then again emits ρ and
- meson and a π-meson. The π-meson so produced then again emits ρ and  mesons and the process continues. The
mesons and the process continues. The 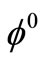 mesons so produced now decays into either
mesons so produced now decays into either 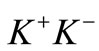 or
or  pairs. The ρ-π chain proceeds in any Fenymann diagram in a line with alternate positions, pushing the
pairs. The ρ-π chain proceeds in any Fenymann diagram in a line with alternate positions, pushing the 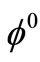 mesons (as producers of
mesons (as producers of 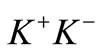 or
or  pairs) on the sides. This may appear paradoxical as the
pairs) on the sides. This may appear paradoxical as the 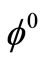 production cross-section is generally smaller than the
production cross-section is generally smaller than the  production cross-section; still the situation arises due to the fact that the
production cross-section; still the situation arises due to the fact that the  resonances produced in the collision processes will quickly decay into
resonances produced in the collision processes will quickly decay into 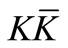 pairs, for which the number of
pairs, for which the number of 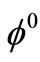 will be lower than that of the
will be lower than that of the 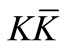 pairs. Besides, as long as
pairs. Besides, as long as 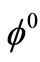 mesons remain in the virtual state, theoretically there is no problem, for
mesons remain in the virtual state, theoretically there is no problem, for  (or
(or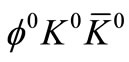 ) is an observed and allowed decay mode, wherein the strangeness conservation is maintained with the strangeantistrange coupled production. Moreover,
) is an observed and allowed decay mode, wherein the strangeness conservation is maintained with the strangeantistrange coupled production. Moreover,  (or
(or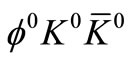 ) coupling constant is well known and is measured by experiments with a modest degree of reliability. And we have made use of this measured coupling strength for our calculational purposes, whenever necessary. It is assumed that the
) coupling constant is well known and is measured by experiments with a modest degree of reliability. And we have made use of this measured coupling strength for our calculational purposes, whenever necessary. It is assumed that the 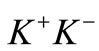 and
and  pairs are produced in equal proportions [4-9]. The entire production process of kaon-antikaons is controlled jointly by the coupling constants, involving ρ-π-φ and φ-
pairs are produced in equal proportions [4-9]. The entire production process of kaon-antikaons is controlled jointly by the coupling constants, involving ρ-π-φ and φ-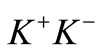 or
or 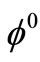 -
-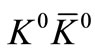 .
.
Now we describe here the baryon-antibaryon production. According to the SCM mechanism, the decay of the pion secondaries produces baryon-antibaryon pairs in a sequential chain as before. The pions producing baryonsantibaryons pairs are obviously turned into the virtual states. And the proton-antiproton pairs are just a part of these secondary baryon-antibaryon pairs. In the case of baryonantibaryon pairs it is postulated that protons-antiprotons and neutrons-antineutrons constitute the major bulk, Production of the strange baryons-antibaryons are far less due to the much smaller values of the coupling constants and due to their being much heavier.
The field theoretical calculations for the average multiplicities of the π, 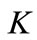 and
and  -secondaries and for the inclusive cross-sections of those secondary particles deliver some expressions which we would pick up from [4-9].
-secondaries and for the inclusive cross-sections of those secondary particles deliver some expressions which we would pick up from [4-9].
The inclusive cross-section of the π-meson produced in the 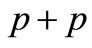 collisions given by
collisions given by
 (1)
(1)
with
 (2)
(2)
where  is the normalisation factor which will increase as the inelastic cross-section increases and it is different for different energy region and for various collisions, for example,
is the normalisation factor which will increase as the inelastic cross-section increases and it is different for different energy region and for various collisions, for example,  for Intersecting Storage Ring (ISR)energy region. The terms
for Intersecting Storage Ring (ISR)energy region. The terms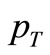 , x in Equation (1) represent the transverse momentum, Feynman Scaling variable respectively. Moreover, by definition,
, x in Equation (1) represent the transverse momentum, Feynman Scaling variable respectively. Moreover, by definition, 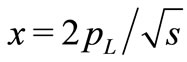 where
where  is the longitudinal momentum of the particle. The s in Equation (2) is the square of the c.m. energy.
is the longitudinal momentum of the particle. The s in Equation (2) is the square of the c.m. energy.
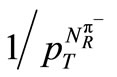 of the expression (1) is the “constituent rearrangement term” arising out of the partons inside the proton which essentially provides a damping term in terms of a power-law in
of the expression (1) is the “constituent rearrangement term” arising out of the partons inside the proton which essentially provides a damping term in terms of a power-law in 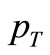 with an exponent of varying values depending on both the collision process and the specific
with an exponent of varying values depending on both the collision process and the specific 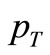 -range. The choice of
-range. The choice of  would depend on the following factors: 1) the specificities of the interacting projectile and target; 2) the particularities of the secondaries emitted from a specific hadronic or nuclear interaction; and 3) the magnitudes of the momentum transfers and of a phase factor (with a maximum value of unity) in the rearrangement process in any collision. And this is a factor for which we shall have to parameterize alongwith some physics-based points indicated earlier. The parametrization is to be done for two physical points, viz., the amount of momentum transfer and the contributions from a phase factor arising out of the rearrangement of the constituent partons. Collecting and combining all these, we proposed the relation to be given by [10]
would depend on the following factors: 1) the specificities of the interacting projectile and target; 2) the particularities of the secondaries emitted from a specific hadronic or nuclear interaction; and 3) the magnitudes of the momentum transfers and of a phase factor (with a maximum value of unity) in the rearrangement process in any collision. And this is a factor for which we shall have to parameterize alongwith some physics-based points indicated earlier. The parametrization is to be done for two physical points, viz., the amount of momentum transfer and the contributions from a phase factor arising out of the rearrangement of the constituent partons. Collecting and combining all these, we proposed the relation to be given by [10]
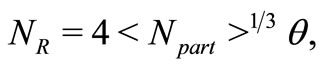 (3)
(3)
where 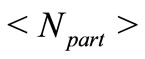 denotes the average number of participating nucleons and
denotes the average number of participating nucleons and  values are to be obtained phenomenologically from the fits to the data-points. In this context, the only additional physical information obtained from the observations made here is: with increase in the peripherality of the collisions the values of
values are to be obtained phenomenologically from the fits to the data-points. In this context, the only additional physical information obtained from the observations made here is: with increase in the peripherality of the collisions the values of 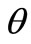 gradually grow less and less, and vise versa.
gradually grow less and less, and vise versa.
Similarly, for kaons of any specific variety (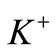 ,
, 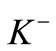 ,
,  or
or ) we have
) we have
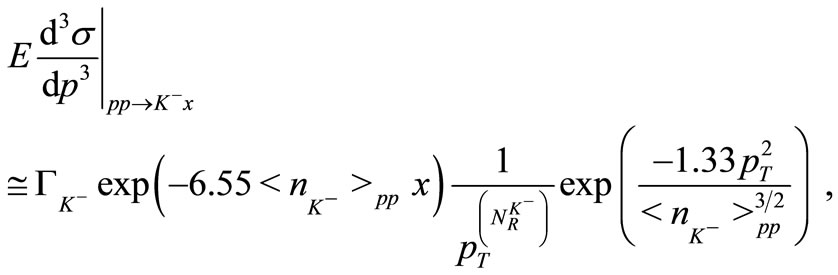 (4)
(4)
with 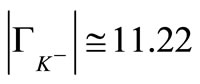 for ISR energies and with
for ISR energies and with
 (5)
(5)
And for the antiproton production in pp scattering at high energies, the derived expression for inclusive crosssection is
 (6)
(6)
with 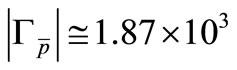 and
and  is the mass of the antiprotons. For ultrahigh energies
is the mass of the antiprotons. For ultrahigh energies
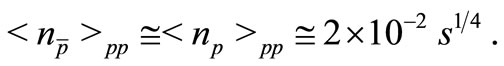 (7)
(7)
3. The Results
Now let us proceed to apply the chosen model to interpret some recent experimental results of charged hadrons production for p + p collisions at different energies. Here, the main observables are the inclusive cross-sections or invariant yields, rapidity distributions, ratio behaviour and the average transverse momenta.
3.1. Inclusive Cross-Sections
The general form of our SCM-based transverse-momentum distributions for 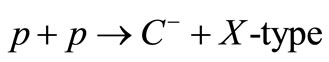 reactions can be written in the following notation:
reactions can be written in the following notation:
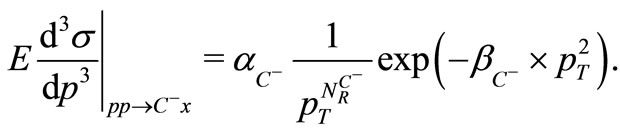 (8)
(8)
The value of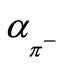 , for example, can be calculated from the following relation:
, for example, can be calculated from the following relation:
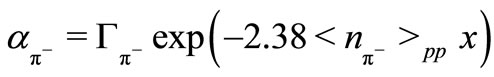 (9)
(9)
The values of ,
,  and
and  for different energies are given in Table 1. The experimental data for the inclusive cross-sections versus
for different energies are given in Table 1. The experimental data for the inclusive cross-sections versus 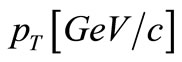 for
for 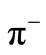 production in p + p interactions at
production in p + p interactions at 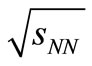 =62.4 GeV and 200 GeV are taken from Ref. [11] and they are plotted in Figures 1(a) and (b) respectively. The production of
=62.4 GeV and 200 GeV are taken from Ref. [11] and they are plotted in Figures 1(a) and (b) respectively. The production of ,
, 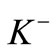 and
and 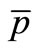 at mid-rapidity in protonproton collisions at
at mid-rapidity in protonproton collisions at  = 900 GeV has been plotted by lines in Figure 1(c). Data are taken from [12]. For the data for charged particle distribution
= 900 GeV has been plotted by lines in Figure 1(c). Data are taken from [12]. For the data for charged particle distribution at energies
at energies = 546 GeV and
= 546 GeV and  = 900 GeV we use references [3,13]. And for LHC data for charged particle distribution for energies
= 900 GeV we use references [3,13]. And for LHC data for charged particle distribution for energies 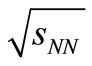 = 0.9 TeV, 2.36 Tev and 7 Tev we use references [14,15]. They are plotted in Figure 2 and Figure 3 respectively. The solid lines in those figures depict the SCM-based plots. As the main variety of the charged particles coming out are the pions, we use here Equation (1) for calculational purposes. The “NSD”- term, used by the experimentalists, has the meaning of nonsingle diffractive collisions [16].
= 0.9 TeV, 2.36 Tev and 7 Tev we use references [14,15]. They are plotted in Figure 2 and Figure 3 respectively. The solid lines in those figures depict the SCM-based plots. As the main variety of the charged particles coming out are the pions, we use here Equation (1) for calculational purposes. The “NSD”- term, used by the experimentalists, has the meaning of nonsingle diffractive collisions [16].
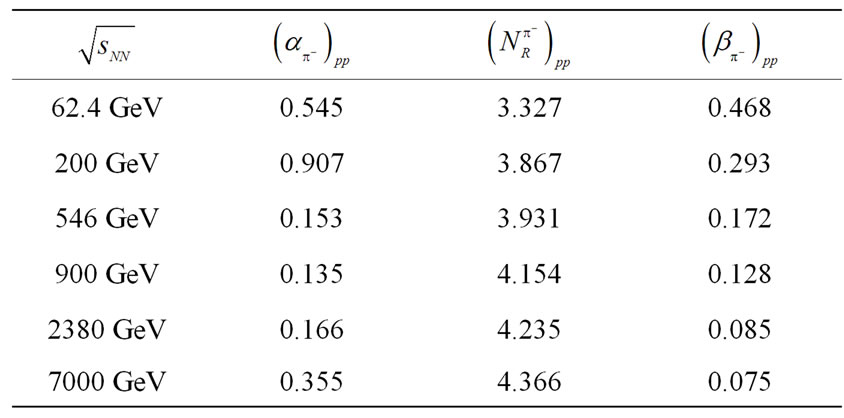
Table 1. Values of ,
,  and
and 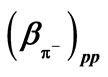 for
for 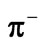 productions in p + p collisions at
productions in p + p collisions at  = 62.4, 200, 546, 900, 2380 and 7000 GeV.
= 62.4, 200, 546, 900, 2380 and 7000 GeV.
 (a)
(a)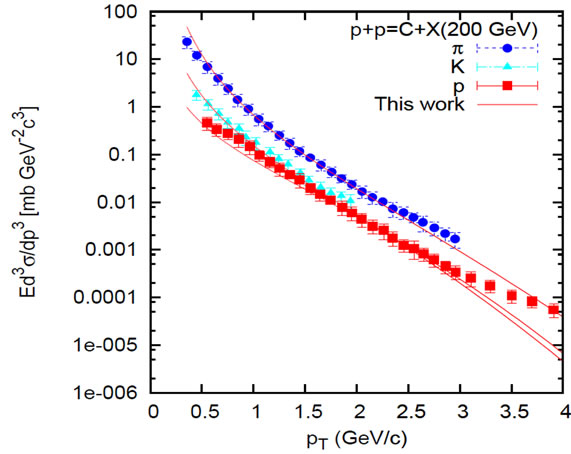 (b)
(b) (c)
(c)
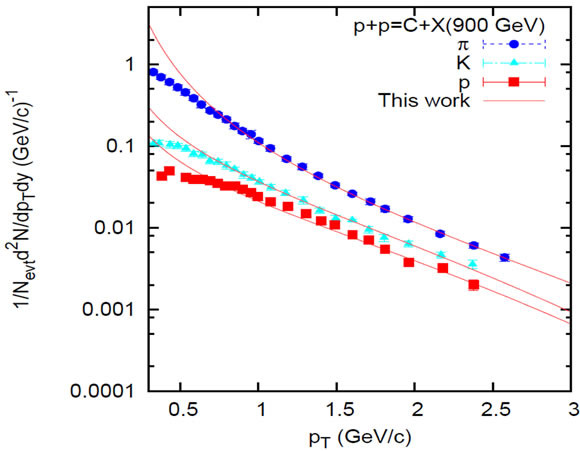
Figure 1. Plots for π, K and proton-production in p + p collisions at RHIC energies (a) 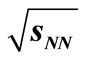 = 62.4 GeV; (b)
= 62.4 GeV; (b)  = 200
= 200
GeV; and (c) 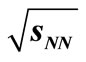 = 900 GeV. Data are taken from Ref. [11] for Figures (a)-(b), while for Figure (c) from Ref. [12]. Solid lines in the figures show the SCM-based plots.
= 900 GeV. Data are taken from Ref. [11] for Figures (a)-(b), while for Figure (c) from Ref. [12]. Solid lines in the figures show the SCM-based plots.
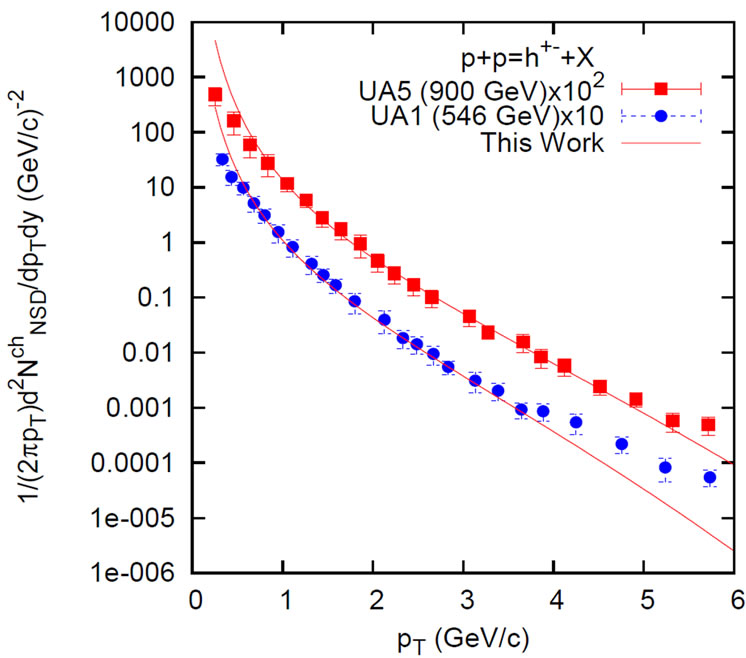
Figure 2. Transverse momentum distributions of the invariant cross section of charged particles in NSD p + p collisions at 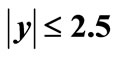 for energies
for energies 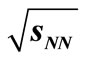 = 546 GeV and 900 GeV. Experimental data are taken from [3,13]. Lines show the theoretical plots.
= 546 GeV and 900 GeV. Experimental data are taken from [3,13]. Lines show the theoretical plots.
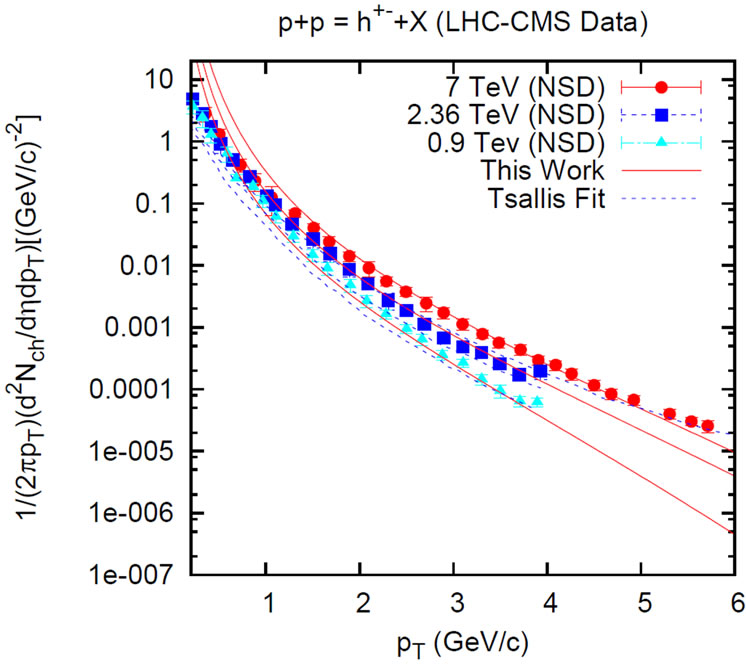
Figure 3. Charged-hadron yield for energies  = 0.9 TeV, 2.38 TeV and 7 TeV in the range η < 2.4 in NSD events as a function of pT; Data are taken from CMS collaboration [14,15]. Solid lines in the figure represent SCM based results while the dashed lines show Tsallis fit.
= 0.9 TeV, 2.38 TeV and 7 TeV in the range η < 2.4 in NSD events as a function of pT; Data are taken from CMS collaboration [14,15]. Solid lines in the figure represent SCM based results while the dashed lines show Tsallis fit.
A comparison between the SCM-based results and the Tsallis parametrization is done for energies 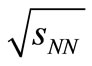 = 0.9 TeV, 2.36 TeV and 7 TeV. The Tsallis parametric equation [17,18] is given hereunder
= 0.9 TeV, 2.36 TeV and 7 TeV. The Tsallis parametric equation [17,18] is given hereunder
 (10)
(10)
with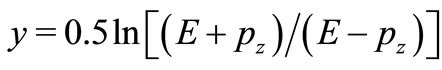 ,
, 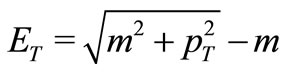 and m is the charged pion mass. The dotted lines in Figure 3 depict the Tsallis parametrization.
and m is the charged pion mass. The dotted lines in Figure 3 depict the Tsallis parametrization.
Moreover, in Figures 4(a) and (b), we have plotted theoretical values 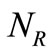 and
and  versus
versus  respectively.Similarly, by using Equations (4), (5) and (7), the values of
respectively.Similarly, by using Equations (4), (5) and (7), the values of ,
,  ,
, 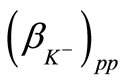 and
and ,
,  ,
,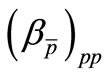 are given in Table 2. The experimental data for the inclusive cross-sections versus
are given in Table 2. The experimental data for the inclusive cross-sections versus 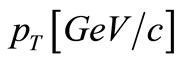 for
for  and
and 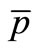 production in p + p interactions at
production in p + p interactions at  = 62.4 GeV, 200 GeV are taken from Ref. [11] and for
= 62.4 GeV, 200 GeV are taken from Ref. [11] and for  = 900 GeV we have used Ref. [12]. They are plotted in Figures 1(a)-(c) respectively. The solid lines in those figures depict the SCM-based plots.
= 900 GeV we have used Ref. [12]. They are plotted in Figures 1(a)-(c) respectively. The solid lines in those figures depict the SCM-based plots.
 (a)
(a) (b)
(b)
Figure 4. Plots of theoretical (a) 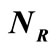 and (b)
and (b) 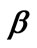 -values versus
-values versus .
.
3.2. The Rapidity Distribution
For the calculation of the rapidity distribution we can make use of a standard relation as given below:
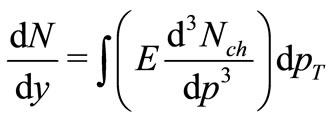 (11)
(11)
In Table 3 we had made a comparison between experimentally found  for
for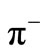 ,
, 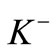 and
and 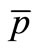 in p + p collisions for RHIC and LHC energies
in p + p collisions for RHIC and LHC energies  = 62.4 GeV, 200 GeV and 900 GeV and the SCM-based calculated results. Data are taken from Refs. [11,12]. The theoretically calculated results are coming out with the help of Equations (1), (4), (6) and (11).
= 62.4 GeV, 200 GeV and 900 GeV and the SCM-based calculated results. Data are taken from Refs. [11,12]. The theoretically calculated results are coming out with the help of Equations (1), (4), (6) and (11).
Similarly, for LHC-energies, by using Equation (1) and Equation (11), the SCM-based 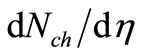 will be given hereunder
will be given hereunder

Table 2. Values of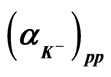 ,
, 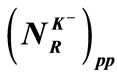 ,
,  and
and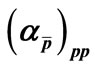 ,
, 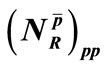 and
and 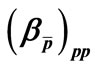 for
for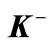 ,
, 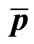 productions in p + p collisions at
productions in p + p collisions at 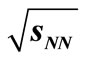 =62.4, 200 GeV and 900 GeV.
=62.4, 200 GeV and 900 GeV.
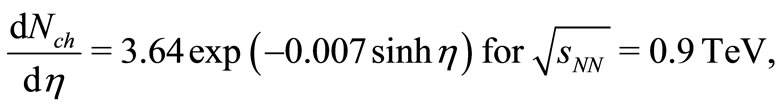 (12)
(12)
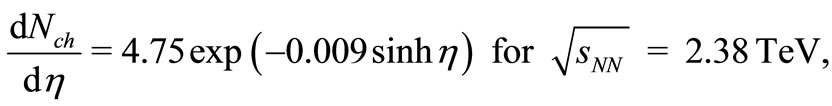 (13)
(13)
and
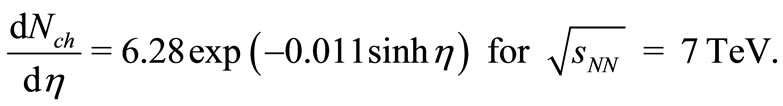 (14)
(14)
In Figure 5 we have plotted  vs
vs  at three LHC-energies
at three LHC-energies  = 0.9 TeV, 2.38 TeV and 7 TeV. The reconstructed data points for Figure 5 are from Refs. [14,16,19]. Lines in the Figure are the outcomes of Equations (12), (13) and (14) respectively.
= 0.9 TeV, 2.38 TeV and 7 TeV. The reconstructed data points for Figure 5 are from Refs. [14,16,19]. Lines in the Figure are the outcomes of Equations (12), (13) and (14) respectively.

Table 3. Comparisons of experimental  with the SCM-based theoretical ones for
with the SCM-based theoretical ones for ,
,  ,
,  productions in p + p collisions at
productions in p + p collisions at 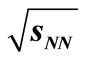 = 62.4 GeV, 200 GeV and 900 GeV.
= 62.4 GeV, 200 GeV and 900 GeV.
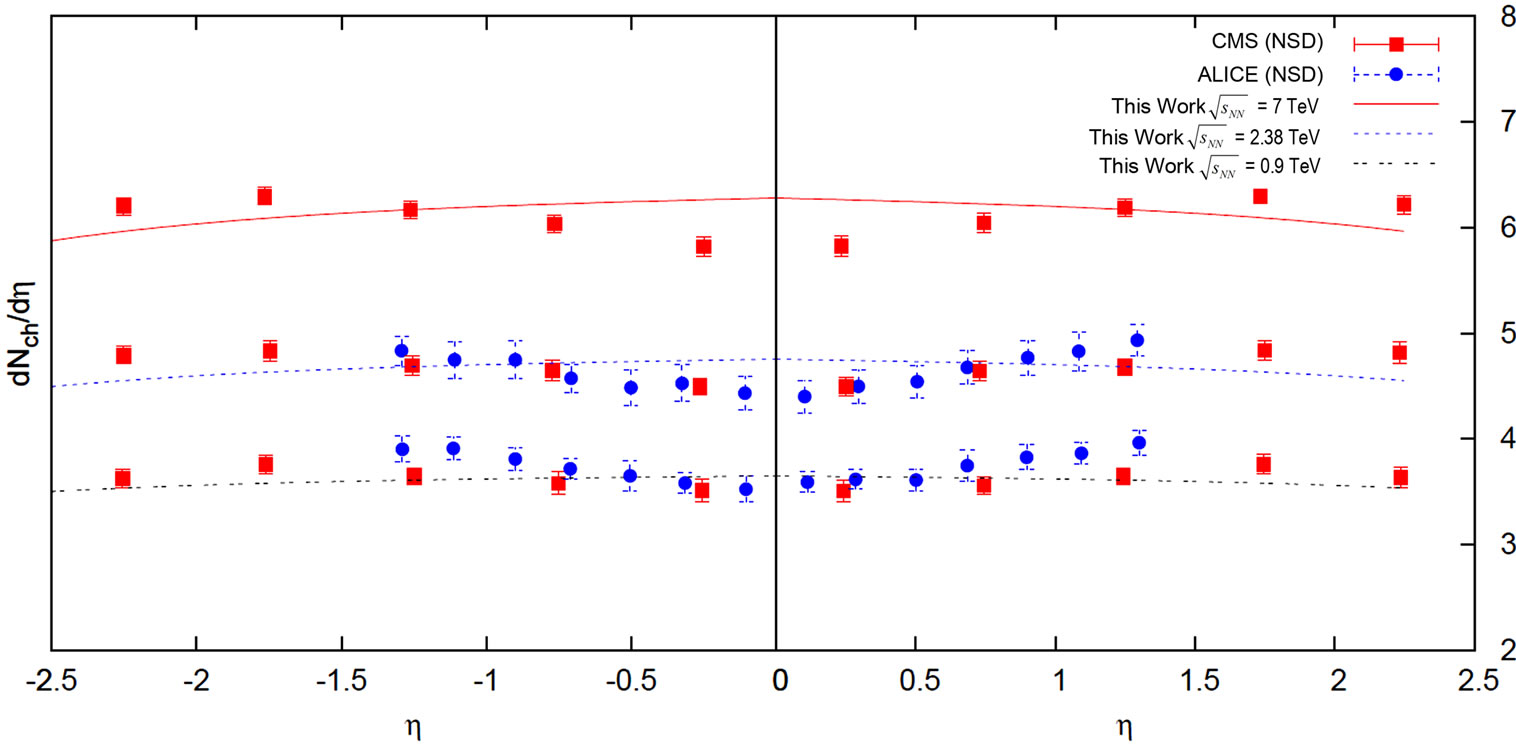
Figure 5. Plot of  vs
vs 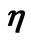 for p + p collisions at
for p + p collisions at  = 0.9 TeV, 2.38 TeV and 7 TeV. The reconstructed data points are from Refs. [14,16,19]. The lines in the figure depict the theoretical results for different energies.
= 0.9 TeV, 2.38 TeV and 7 TeV. The reconstructed data points are from Refs. [14,16,19]. The lines in the figure depict the theoretical results for different energies.
3.3. The Ratio-Behaviours for Different Secondaries
The nature of the relation of 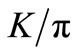 ratios with the SCM, presented in the previous work [20], would be written in the following form
ratios with the SCM, presented in the previous work [20], would be written in the following form
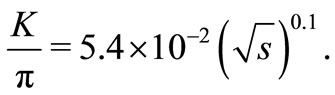 (15)
(15)
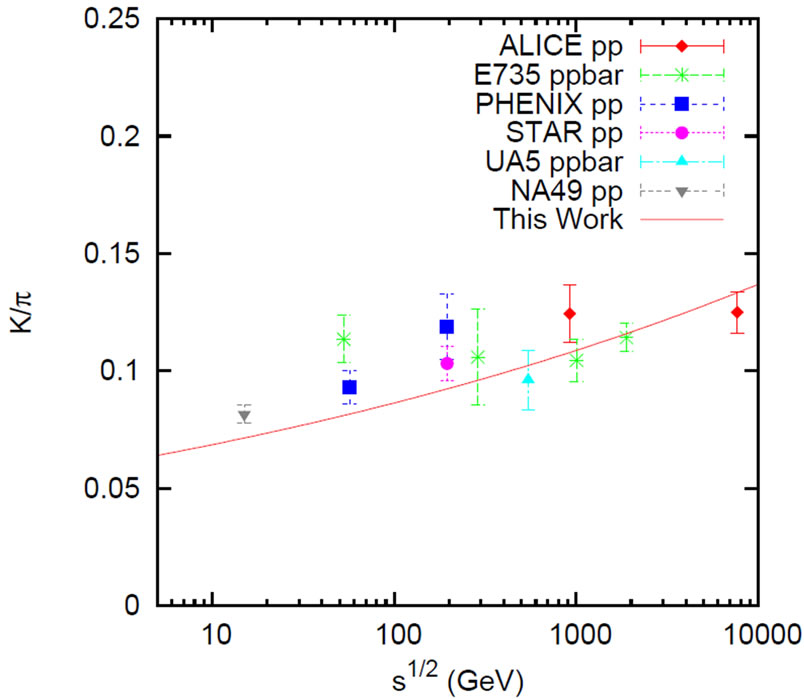
Figure 6(a) shows the nature of rise of  ratio in the light of SCM-based above relation (Equation (15)). Data are taken from Ref. [21].
ratio in the light of SCM-based above relation (Equation (15)). Data are taken from Ref. [21].
Similarly, in Figure 6(b), we have presented the 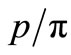 ratio for the RHIC and LHC-data [21]. The SCM-based calculations are done on the basis of Equation (1) and Table 1.
ratio for the RHIC and LHC-data [21]. The SCM-based calculations are done on the basis of Equation (1) and Table 1.
 (a)
(a)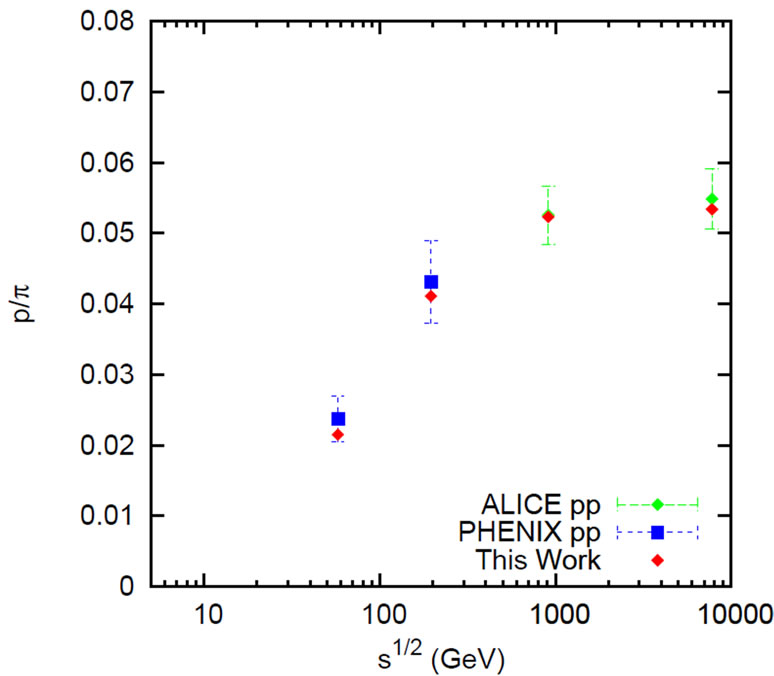 (b)
(b)
Figure 6. Presentation of plots of (a)  and (b)
and (b) 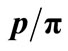 at different center-of-mass energies. Line and rhombus represent the SCM-based results in (a) and (b) respectively against the data sets taken from Ref. [21].
at different center-of-mass energies. Line and rhombus represent the SCM-based results in (a) and (b) respectively against the data sets taken from Ref. [21].
3.4.< PT >Values
Next we attempt at deriving model-based expression for .
.
The definition for average transverse momentum is < P T> given below:
 (16)
(16)
The line in the Figure 7 depicts the SCM-based calculated results of the average transverse momentum 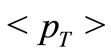 versus the c.m. energy
versus the c.m. energy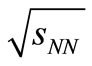 . The theoretical calculations are done on the basis of uses of Equation (1), Table 1. Data are taken from [3,14,22,23].
. The theoretical calculations are done on the basis of uses of Equation (1), Table 1. Data are taken from [3,14,22,23].
4. Discussions and Conclusions
Let us make some general observations and specific comments on the results arrived at and shown by the diagrams on a case-to-case basis.
1) The measures of inclusive cross-sections against transverse momenta  obtained on the basis of the SCM for the pions, kaons and protons for the RHIC energies
obtained on the basis of the SCM for the pions, kaons and protons for the RHIC energies 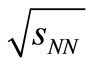 = 62.4, 200 GeV and for LHC energy=
= 62.4, 200 GeV and for LHC energy=  900 GeV are depicted in Figure 1. They describe a modest degree of success.
900 GeV are depicted in Figure 1. They describe a modest degree of success.
Of the various types particles produced, the π-mesons, constitute, the near totality of the secondaries. So, in calculating the charged hadrons yields for different transverse momenta, on the basis of the model, for different energies ranging from  = 546 GeV to 7 TeV, we use Equation (1). The results are shown in the Figure 2
= 546 GeV to 7 TeV, we use Equation (1). The results are shown in the Figure 2

Figure 7. Plot of average transverse momentum as function of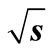 . Data are taken from [3,14,22,23]. Line shows the SCM-based calculations.
. Data are taken from [3,14,22,23]. Line shows the SCM-based calculations.
and Figure 3. Moreover, we have compared the Modelbased results with Tsallis parametrization in Figure 3. The outcomes of these plots are fairly satisfactory.
2) The theoretically calculated  and
and  -factors of Equation (8) for different
-factors of Equation (8) for different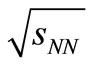 ’s have been plotted in Figure 4. With the inclusion of the power law form arising due to the physics of partonic rearrangement factor, the model has turned effectively into a mixed model. And these two factors corroborate effectively the “soft” and “hard” regimes without any extra effort.
’s have been plotted in Figure 4. With the inclusion of the power law form arising due to the physics of partonic rearrangement factor, the model has turned effectively into a mixed model. And these two factors corroborate effectively the “soft” and “hard” regimes without any extra effort.
3) The calculations of rapidity distributions for pions, kaons and protons at different RHIC and LHC energies, on the basis of the model, have been done with the help of Equation (11). The calculated values are compared with the experimental ones and they are shown in Table 3. The theoretical values are in fair agreement with the experimental data.
Similarly, in Figure 5, we have plotted the pseudorapidity distributions for different LHC energies. Here, the model modestly reproduce data consistently.
4) The agreements between the measured data on 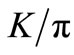 and
and  ratio and the theoretical SCM plots (shown in Figure 6) for different energies are strikingly encouraging.
ratio and the theoretical SCM plots (shown in Figure 6) for different energies are strikingly encouraging.
5) Figure 7 shows the plots of  vs
vs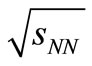 . The initial indication of the SCM-based theoretical plot shows a modest agreement with the data.
. The initial indication of the SCM-based theoretical plot shows a modest agreement with the data.
Finally, we conclude from the analysis of the results given above with the following statements: The model applied here gives fair descriptions of the 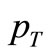 -spectra of all the light secondaries or charged hadron. Some disagreements are observed at pseudorapidity distributions at LHC energies. The model might require some finer adjustments to cope with the data for very high energy nuclear collisions. However, on an overall basis, our model is in fair agreement with the latest pp-collision results obtained from the uptodate LHC experiments. This factor is really of high important to us. Furthermore, the observables or the physical aspects that we have reckoned herewith form a clear continuum from the old ISR experiments to the recent Large Hadron Collider studies via the intermediary BNL-RHIC results cropped up over the 1st decade of this century. In so far as the rolls of the other models (including QCD versions) are considered, the results do neither speak very high about them; rather they cast doubts on the suitability of them in applying at this LHC energy band. And this certainly spurs us on to take up further studies on the SCM proposed earlier and applied in the present study.
-spectra of all the light secondaries or charged hadron. Some disagreements are observed at pseudorapidity distributions at LHC energies. The model might require some finer adjustments to cope with the data for very high energy nuclear collisions. However, on an overall basis, our model is in fair agreement with the latest pp-collision results obtained from the uptodate LHC experiments. This factor is really of high important to us. Furthermore, the observables or the physical aspects that we have reckoned herewith form a clear continuum from the old ISR experiments to the recent Large Hadron Collider studies via the intermediary BNL-RHIC results cropped up over the 1st decade of this century. In so far as the rolls of the other models (including QCD versions) are considered, the results do neither speak very high about them; rather they cast doubts on the suitability of them in applying at this LHC energy band. And this certainly spurs us on to take up further studies on the SCM proposed earlier and applied in the present study.
REFERENCES
- T. Lappi, “Energy Dependence of the Saturation Scale and the Charged Multiplicity in pp and AA Collisions,” The European Physical Journal C, Vol. 71, 2011, p. 1699. doi:10.1140/epjc/s10052-011-1699-x
- J. Schukraft, “ALICE Results from the First Pb-Pb Run at the CERN LHC,” arXiv:1106.5620v1 [hep-ex] (28 Jun 2011).
- J. Bleibel, L. V. Bravina, A. B. Kaidalov and E. E. Zabrodin, “How Many of the Scaling Trends in pp Collisions will be Violated at
 = 14 TeV?—Predictions from Monte Carlo Quark-Gluon String Model,” arXiv:1011.- 2703v1 [hep-ph] (11 Nov 2010).
= 14 TeV?—Predictions from Monte Carlo Quark-Gluon String Model,” arXiv:1011.- 2703v1 [hep-ph] (11 Nov 2010). - P. Guptaroy, G. Sau, S. K. Biswas and S. Bhattacharyya, “Understanding the Characteristics of Multiple Production of Light Hadrons in Cu + Cu Interactions at Various RHIC Energies: A Model-Based Analysis,” IL Nuovo Cimento B, Vol. 125, 2010, pp. 1071-1097. doi:10.1393/ncb/i2010-10913-4
- P. Guptaroy, B. De, G. Sau, S. K. Biswas and S. Bhattacharyya, “Some Aspects of Gold-Gold Collisions at RHIC at
 and a Version of the Sequential Chain Model (SCM),” International Journal of Modern Physics A, Vol. 22, No. 28, 2007, pp. 5121-5154. doi:10.1142/S0217751X07037251
and a Version of the Sequential Chain Model (SCM),” International Journal of Modern Physics A, Vol. 22, No. 28, 2007, pp. 5121-5154. doi:10.1142/S0217751X07037251 - P. Bandyopadhyay and S. Bhattacharyya, “Lepton-Hadron Relation, Multiparticle Production Phenomena and Average Multiplicities in Deep Inelastic pp, pi n and e n Scattering,” IL Nuovo Cimento A, Vol. 43, No. 3, 1978, pp. 305-322. doi:10.1007/BF02730432
- P. Bandyopadhyay, R. K. Roychoudhury, S. Bhattachayya and D. P. Bhattacharyya, “Lepton Hadron Relation And the Inclusive Production of Low P(t) Charged Secondaries at ISR Energies in PP Scattering,” IL Nuovo Cimento A, Vol. 50, No. 1, 1979, pp. 133-154. doi:10.1007/BF02804777
- S. Bhattacharyya, “Collisions in Space Experiments at High-Energies, Laboratory Experiments and Suggested Signatures of Quark Gluon-Plasma: An Alternative Approach to the Analysis of Actual Observations,” IL Nuovo Cimento C, Vol. 11, 1988, pp. 51-65. doi:10.1007/BF02507895
- S. Bhattacharyya, “On Some Remarkable Differences between the P Anti-p Collider Results at Cern and PP Reaction at Isr Energies,” Journal of Physics G, Vol. 14, 1988, pp. 9-17. doi:10.1088/0305-4616/14/1/005
- P. Guptaroy, G. Sau, S. K. Biswas and S. Bhattacharyya, “On Production of Direct Photons and Neutral Pions in RHIC Experiments at
 ,” Modern Physics Letters A, Vol. 23, No. 14, 2008, pp. 1031-1046. doi:10.1142/S021773230802567X
,” Modern Physics Letters A, Vol. 23, No. 14, 2008, pp. 1031-1046. doi:10.1142/S021773230802567X - A. Adare, et al. (PHENIX Collaboration), “Identified Charged Hadron Production in p + p Collisions at
 = 200 and 62.4 GeV,” Physical Review C, Vol. 83, 2011, pp. 064903-(1-29). doi:10.1103/PhysRevC.83.064903
= 200 and 62.4 GeV,” Physical Review C, Vol. 83, 2011, pp. 064903-(1-29). doi:10.1103/PhysRevC.83.064903 - K. Aamodt, et al. (ALICE Collaboration), “Production of Pions, Kaons and Protons in pp Collisions at
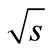 = 900 GeV with ALICE at the LHC,” The European Physical Journal C, Vol. 71, 2011, pp. 1655-(1-22). doi:10.1140/epjc/s10052-011-1655-9
= 900 GeV with ALICE at the LHC,” The European Physical Journal C, Vol. 71, 2011, pp. 1655-(1-22). doi:10.1140/epjc/s10052-011-1655-9 - G. J. Alner, et al. (UA5 Collaboration), “UA5: A General Study of Proton-Antiproton Physics at
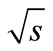 = 546 GeV,” Physics Reports, Vol. 154, No. 5-6, 1987, pp. 247-383. doi:10.1016/0370-1573(87)90130-X
= 546 GeV,” Physics Reports, Vol. 154, No. 5-6, 1987, pp. 247-383. doi:10.1016/0370-1573(87)90130-X - V. Khachatryan, et al. (CMS Collaboration), “Transverse Momentum and Pseudorapidity Distributions of Charged Hadrons in pp Collisions at
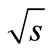 = 0.9 and 2.36 TeV,” JHEP, Vol. 2, 2010, pp. 41-(1-35). doi:10.1007/JHEP02(2010)041
= 0.9 and 2.36 TeV,” JHEP, Vol. 2, 2010, pp. 41-(1-35). doi:10.1007/JHEP02(2010)041 - V. Khachatryan, et al. (CMS Collaboration), “TransverseMomentum and Pseudorapidity Distributions of Charged Hadrons in pp Collisions at
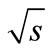 = 7 TeV,” Physical Review Letters, Vol. 105, 2010, pp. 022002-(1-14). doi:10.1103/PhysRevLett.105.022002
= 7 TeV,” Physical Review Letters, Vol. 105, 2010, pp. 022002-(1-14). doi:10.1103/PhysRevLett.105.022002 - K. Aamodt, et al. (ALICE Collaboration), “First Proton-Proton Collisions at the LHC as Observed with the ALICE Detector: Measurement of the Charged Particle Pseudorapidity Density at
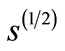 = 900-GeV,” The European Physical Journal C, Vol. 65, No. 1-2, 2010, pp. 111-125. doi:10.1140/epjc/s10052-009-1227-4
= 900-GeV,” The European Physical Journal C, Vol. 65, No. 1-2, 2010, pp. 111-125. doi:10.1140/epjc/s10052-009-1227-4 - C. Tsallis, “Possible Generalization of Boltzmann-Gibbs Statistics,” Journal of Statistical Physics, Vol. 52, No. 1-2, 1988, pp. 479-487. doi:10.1007/BF01016429
- T. S. Biró, G. Purcsel and K. Ürmössy, “Non-Extensive Approach to Quark Matter,” The European Physical
- Journal A, Vol. 40, 2009, pp. 325-340. doi:10.1140/epja/i2009-10806-6
- K. Aamodt, et al. (ALICE Collaboration), “ChargedParticle Multiplicity Measurement in Proton-Proton Collisions at
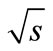 = 7 TeV with ALICE at LHC,” The European Physical Journal C, Vol. 68, 2010, pp. 345-354. doi:10.1140/epjc/s10052-010-1350-2
= 7 TeV with ALICE at LHC,” The European Physical Journal C, Vol. 68, 2010, pp. 345-354. doi:10.1140/epjc/s10052-010-1350-2 - P. Guptaroy, B. De, S. Bhattacharyya and D. P. Bhattacharyya, “Multiple Pion and Kaon Production in High Energy Nucleus-Nucleus Collisions: Measurement versus Specific Models,” Fizika B, Vol. 11, 2002, pp. 115-134.
- M. Floris for ALICE Collaboration, “Identified Particles in pp and Pb-Pb Collisions at LHC Energies with the ALICE Detector,” arXiv:1108.3257v1 [hep-ex] (16 Aug 2011).
- G. Arnison, et al. (UA1 Collaboration), “Transverse Momentum Spectra for Charged Particles at the CERN Proton Anti-Proton Collider,” Physics Letters B, Vol. 118, No. 1-3, 1982, pp. 167-172. doi:10.1016/0370-2693(82)90623-2
- T. Alexopoulos, et al. (E735 Collaboration), “Mass Identified Particle Production in
 Collisions at
Collisions at  = 300-GeV, 540-GeV, 1000-GeV, and 1800-GeV,” Physical Review D, Vol. 48, No. 3, 1993, pp. 984-997. doi:10.1103/PhysRevD.48.984
= 300-GeV, 540-GeV, 1000-GeV, and 1800-GeV,” Physical Review D, Vol. 48, No. 3, 1993, pp. 984-997. doi:10.1103/PhysRevD.48.984

