Journal of Modern Physics
Vol. 2 No. 9 (2011) , Article ID: 7146 , 4 pages DOI:10.4236/jmp.2011.29125
Properties of Phase Transformation of Ferroelectric Thin Films with Surface Layers
1Department of Physics and Electricity Information Engineering, Daqing Normol University, Daqing, China
2Center of Condensed Matter Science and Technology, Harbin Institute of Technology, Harbin, China
3Ordance Engineering Department, Air Force Aviation University, Changchun, China
E-mail: cl_19830422@126.com
Received December 1, 2010; revised April 26, 2011; accepted May 15, 2011
Keywords: Ferroelectric Thin Film, Surface Layer, Phase Transformation
ABSTRACT
Using the generalized Ginzburg-Landau-Devonshire theory, the characteristics of phase transformation of a ferroelectric thin film with surface layers are investigated. We study the effect of the surface layer on the properties (coercive field, critical thickness) of a ferroelectric thin film. Our theoretical results show that the surface layer is likely to answer for the emergence of phase transformation.
1. Introduction
With the development of the modern experiment techniques and extensive application of the ferroelectric materials in nonvolatile random access memories, ultraminiaturized electronics and nanotechnologies, characteristics of phase transformation in ferroelectric materials have aroused great interest [1,2]. Physical properties of ferroelectric thin films, such as their phase transformation characteristics, are significantly different from those of bulk ferroelectrics because of many factors including interfacial stress, defects and impurities near the surface region, electrode and substrate used. Ferroelectric thin films are also controlled via such factors [3-5]. Much work has been done on the phase transformation of a ferroelectric thin film. Experimentally, Raman scattering observations in epitaxial barium strontium titanate films on (001) MgO show that the ferroelectric phase transformation shift to higher temperatures and paraelectric phase has tetragonal symmetry [6,7]. The phase transformation was electrically investigated by Kato et al. in (100)-oriented BaTiO3 thin and thick films deposited on Si substrate using double alkoxide solutions. They indicated that the transition from paraelectric to ferroelectric phase takes place around at 100˚C instead of 130˚C for single crystals through the changes of the dielectric constant as a function of temperature in the range of −200˚C - 200˚C [8]. The characteristics of phase transformation in a ferroelectric thin film can be obviously affected by the clamped behavior from mismatch between film and substrate. This result was observed by Basceri et al. in Ba0.7Sr0.3TiO3 thin films grown by liquid-source metalorganic chemical vapor deposition [9]. In theory, the properties of the second-order transformation in ferroelectric thin films were studied by Ong et al. within the thermodynamic approach. They established an analytic model to describe the phase transformation and obtained the results which shown the importance of the size and surface effects on the phase transformation [10]. Using the time dependent Ginzburg-Landau-Devonshire (GLD) theory, Wang et al. obtained analytic expressions for the critical conditions that control the transformation between the ferroelectric and paraelectric states [11]. Paul et al. determined the effects of film thickness, epitaxial strain and the nature of electrodes on ferroelectric phase transformation in ultrathin films of BaTiO3 using a first-principles effective Hamiltonian in classical molecular dynamics simulations [12].
It is well known that the state in the vicinity of the surface of a film is different from that inside the film. The larger ratio of surface layer to volume makes the surface effects more pronounced in thinner ferroelectric films. T. Lü and W. Cao considered that the inhomogeneous polarization distribution in a ferroelectric thin film origins from this effect of surface layer [13].
In this paper, based on the idea of [13], the characteristics of phase transformation of ferroelectric thin films with surface layers are discussed.
2. The Model
The configuration of a ferroelectric thin film with two surface layers between two metallic electrodes in shortcircuit conditions is illustrated in Figure 1.
We assume that the easy polar axis of the film along the z direction is perpendicular to the film surface and the film is in single domain. The properties of the film are homogeneous in planes parallel to the surface of the film and the variation happens only along the film thickness. Taking into account the role of the surface layer is different from the bulk, so we introduce a second power of polarization in the GLD free energy and assume its coefficient to be a function of position in order to reflect the contribution of the surface layers [13]. Considering a second order system, the generalized total GLD free energy for the ferroelectric thin film with the spontaneous polarization P in unit area is given by:
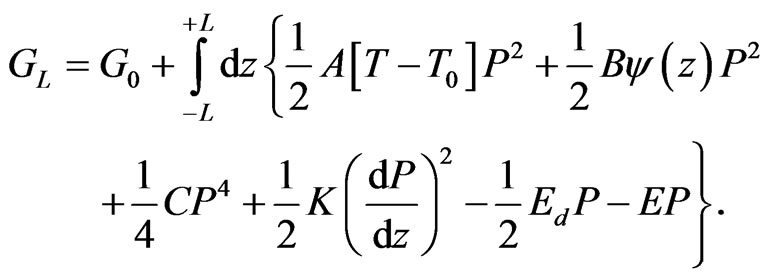 (1)
(1)
Here  is the free energy of film in the paraelectric phase. The coefficients A, B, C, and K are independent of temperature T and position z; T0 is the transformation temperature of the bulk ferroelectric; E is an applied uniform external electric field. The depolarization field produced by bound polar charges in a ferroelectric thin film that is not being screened by the surface electrodes [14] is
is the free energy of film in the paraelectric phase. The coefficients A, B, C, and K are independent of temperature T and position z; T0 is the transformation temperature of the bulk ferroelectric; E is an applied uniform external electric field. The depolarization field produced by bound polar charges in a ferroelectric thin film that is not being screened by the surface electrodes [14] is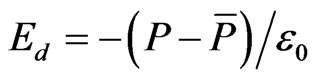 , where
, where  is the vacuum dielectric constant. The average polarization
is the vacuum dielectric constant. The average polarization 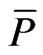 is given by
is given by
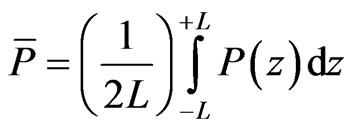 . (2)
. (2)
The function  in Equation (1) reflects the surface layer effect. In order to ensure the continuity of P(z) and its derivative, we require
in Equation (1) reflects the surface layer effect. In order to ensure the continuity of P(z) and its derivative, we require  and
and
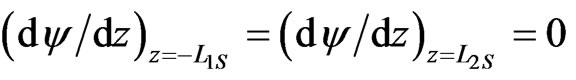 , where
, where  is the boundary position of lower (upper) surface layer in the film (see Figure 1).
is the boundary position of lower (upper) surface layer in the film (see Figure 1).
When the system is in equilibrium state,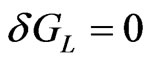 . Consequently, the Euler—Lagrange equations resulting from Equation (1) are:
. Consequently, the Euler—Lagrange equations resulting from Equation (1) are:
 (3a,b)
(3a,b)
It is convenient to readjust the variables into dimen-
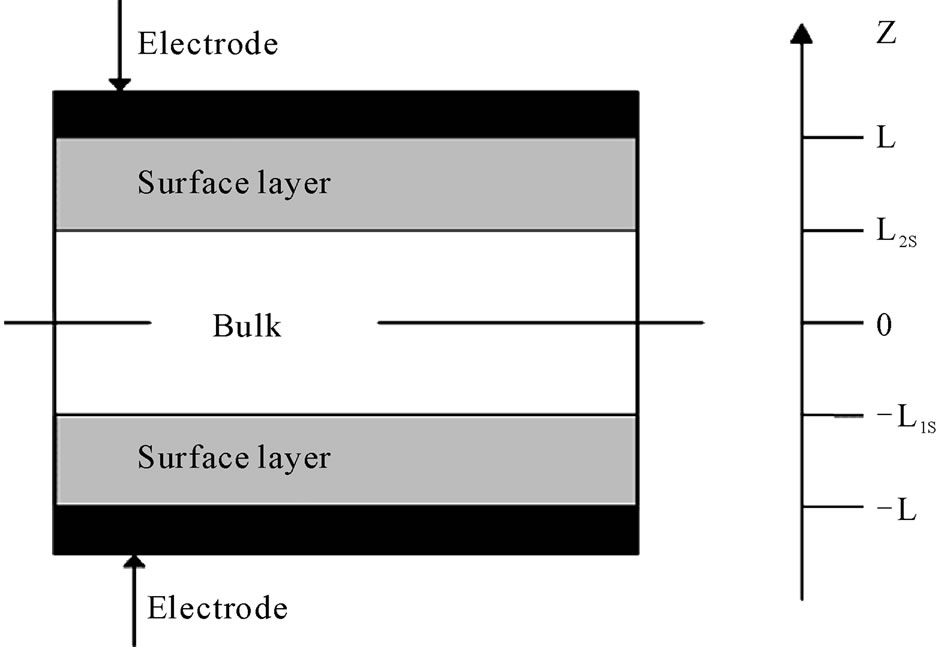
Figure 1. Geometric structure of ferroelectric thin films under study.
sionless forms. We set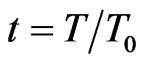 ,
,  with
with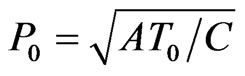 ,
, 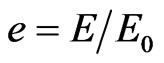 with
with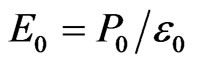 ,
, 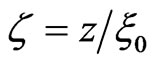 with
with ,
, 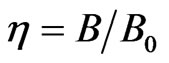 with
with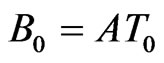 . Finally, Equations (3a,b) become:
. Finally, Equations (3a,b) become:
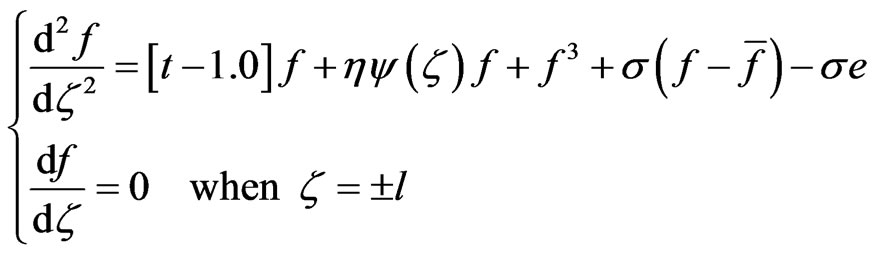 , (4a,b)
, (4a,b)
where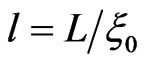 ,
,  and
and .
.
Parameter 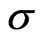 is the specific value of the Curie constant to Curie temperature of the bulk material. Considering practical examples of second-order phase transition materials (the Curie constant ~103 and the Curie temperature ~102K) we take
is the specific value of the Curie constant to Curie temperature of the bulk material. Considering practical examples of second-order phase transition materials (the Curie constant ~103 and the Curie temperature ~102K) we take  as a representative value.
as a representative value.
Since there are no real measured data available on the effects of the surface layer, a simple form is chosen for the distribution function . This peculiar choice of the
. This peculiar choice of the  does not affect the generality of the results and conclusions [13]:
does not affect the generality of the results and conclusions [13]:
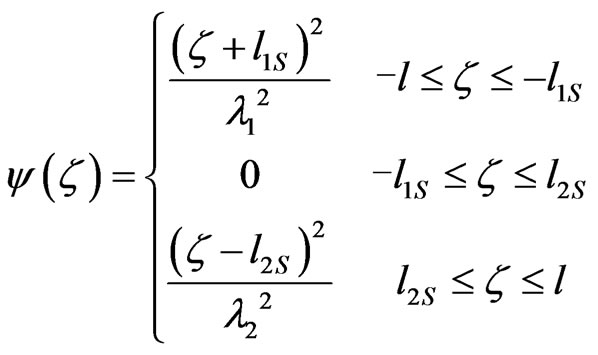 , (5)
, (5)
where  reflects the variation intensity of the free energy density in lower (upper) surface layer. We denote the relative thickness of the two surface layers in a ferroelectric thin film with
reflects the variation intensity of the free energy density in lower (upper) surface layer. We denote the relative thickness of the two surface layers in a ferroelectric thin film with 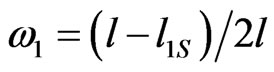 and
and
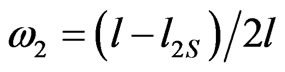 , respectively, where
, respectively, where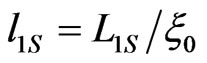 ,
, . For simplicity, the two surface layers are assumed symmetric, namely,
. For simplicity, the two surface layers are assumed symmetric, namely,  ,
, 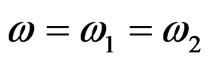 ,
,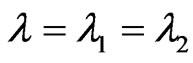 .
.
3. Results and Discussions
The phase diagram of  and the relative thickness of the surface layer
and the relative thickness of the surface layer 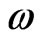 is shown in Figure 2 with the ferroelectric phase above the line and paraelectric phase below the line. Every dot in the line represents a transition point at which the polarization of a film vanishes, that means, the phase transition from the ferroelectric to paraelectric occurs. From the figure we can see if
is shown in Figure 2 with the ferroelectric phase above the line and paraelectric phase below the line. Every dot in the line represents a transition point at which the polarization of a film vanishes, that means, the phase transition from the ferroelectric to paraelectric occurs. From the figure we can see if  is fixed, a phase transformation from ferroelectric to paraelectric in the ferroelectric thin film will happen with decreasing
is fixed, a phase transformation from ferroelectric to paraelectric in the ferroelectric thin film will happen with decreasing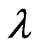 ; when
; when  is fixed, the phase transformation will also take place as
is fixed, the phase transformation will also take place as 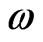 increases. And the influence of
increases. And the influence of  on the phase transformation is more obvious than
on the phase transformation is more obvious than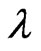 . It means the surface layer can drive phase transformation for a ferroelectric thin film system. In practice, we can obtain different cases of ferroelectric applications by controlling the surface layer.
. It means the surface layer can drive phase transformation for a ferroelectric thin film system. In practice, we can obtain different cases of ferroelectric applications by controlling the surface layer.
Figure 3 clearly illustrates the coercive field versus 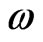 with different
with different . The coercive field reduces with increasing
. The coercive field reduces with increasing  for the same
for the same . With further increasing
. With further increasing , the coercive field deceases to zero, that is to say, a phase transformation from ferroelectric to paraelectric occurs. One can see that as
, the coercive field deceases to zero, that is to say, a phase transformation from ferroelectric to paraelectric occurs. One can see that as 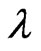 decreases, the coercive field reduces for the same relative thickness of surface layer and the curves of coercive field as a function of
decreases, the coercive field reduces for the same relative thickness of surface layer and the curves of coercive field as a function of 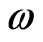 declines steeply. This phenomenon can be explained that the existence of surface layer is great disadvantage to stabilization of the ferroelectric phase, so it is easy to reverse the polarization of the film with a small coercive field for a stronger effect of surface layer. The results are in good agreement with those obtained by Tilley et al. [15], who demonstrated that the coercive field decreases with decreasing the extrapolation length. Small extrapolation length represents strong surface effects.
declines steeply. This phenomenon can be explained that the existence of surface layer is great disadvantage to stabilization of the ferroelectric phase, so it is easy to reverse the polarization of the film with a small coercive field for a stronger effect of surface layer. The results are in good agreement with those obtained by Tilley et al. [15], who demonstrated that the coercive field decreases with decreasing the extrapolation length. Small extrapolation length represents strong surface effects.
Figure 4 is a phase diagram of the thickness of a ferroelectric thin film and surface layer for different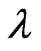 . The ferroelectric phase is above the line and paraelectric phase is below the line in the Figure 4. For the three curves, the general trend can be summarized as follows: 1) when the thickness of a ferroelectric thin film is fixed, a phase transformation from ferroelectric to paraelectric in a ferroelectric thin film will happen with increasing the thickness of surface layer; 2) when the thickness of surface layer is fixed, the phase transformation will also occur as the thickness of a ferroelectric thin film reduces, i.e., the size-driven phase transformation happens. The results are consistent with those of Reference [5], which observed that a size-driven phase transformation takes place for both tensile and compressive surfaces with decreasing film thickness. The genuine physical meaning
. The ferroelectric phase is above the line and paraelectric phase is below the line in the Figure 4. For the three curves, the general trend can be summarized as follows: 1) when the thickness of a ferroelectric thin film is fixed, a phase transformation from ferroelectric to paraelectric in a ferroelectric thin film will happen with increasing the thickness of surface layer; 2) when the thickness of surface layer is fixed, the phase transformation will also occur as the thickness of a ferroelectric thin film reduces, i.e., the size-driven phase transformation happens. The results are consistent with those of Reference [5], which observed that a size-driven phase transformation takes place for both tensile and compressive surfaces with decreasing film thickness. The genuine physical meaning
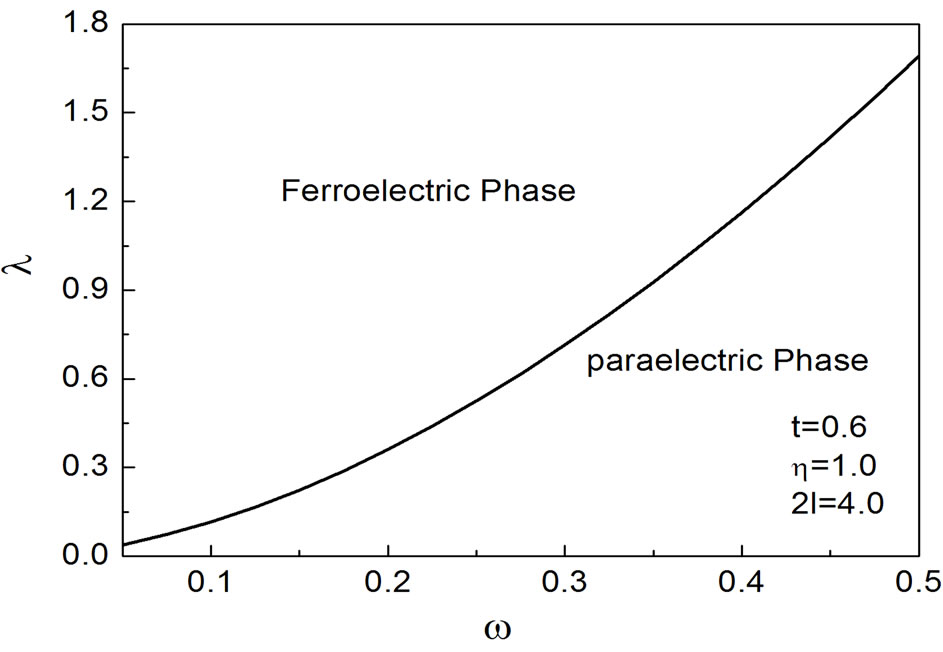
Figure 2. Phase diagram of λ and the relative thickness of the surface layer.
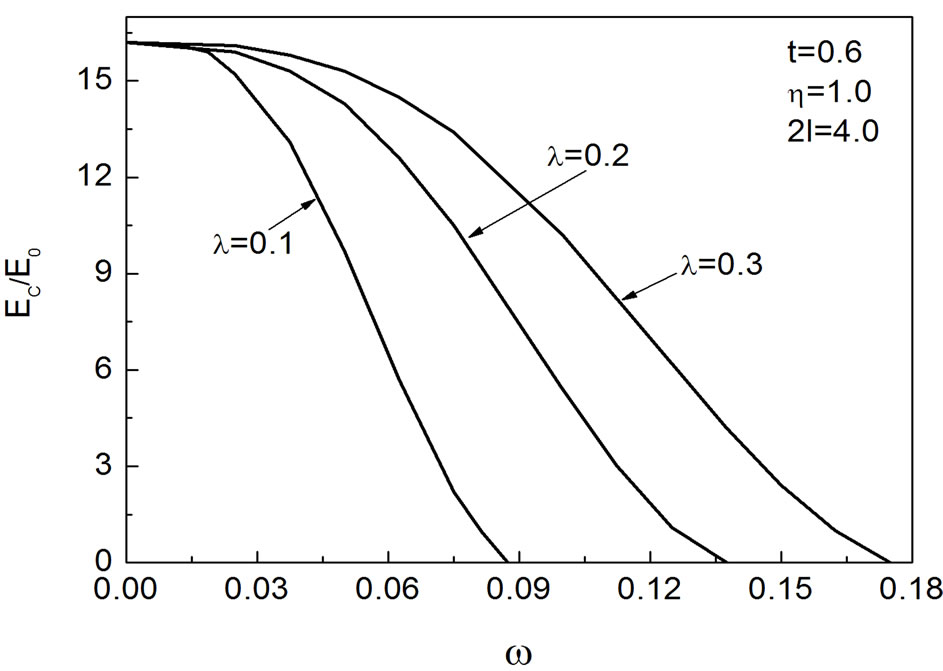
Figure 3. The coercive field as a function of the relative thickness of the surface layer with different λ.

Figure 4. Phase diagram of the thickness of ferroelectric thin film and surface layer for different λ.
behind this trend is that whether fix the thickness of a film or the surface layer, the emergence of the phase transformation is attributed to the large ratio of the surface layer to the volume of film. Moreover, with decreasing , the zone of ferroelectric phase shrinks and paraelectric phase augments. It is worth emphasizing that in the line every point represents a critical size of a ferroelectric thin film. As the thickness of surface layer increases or
, the zone of ferroelectric phase shrinks and paraelectric phase augments. It is worth emphasizing that in the line every point represents a critical size of a ferroelectric thin film. As the thickness of surface layer increases or  reduces, the critical size of a film increases, in other words, the ferroelectric phase remains stable only at a thicker thickness with the stronger effect of surface layer.
reduces, the critical size of a film increases, in other words, the ferroelectric phase remains stable only at a thicker thickness with the stronger effect of surface layer.
4. Conclusions
In summary, based on the generalized GLD theory, the characteristics of phase transformation of a ferroelectric thin film with surface layers has been studied. The characteristics of phase transformation sensitively depend on the effect of two factors ( and
and ) of surface layer. The results also show that the coercive field decreases and critical size increases with reducing
) of surface layer. The results also show that the coercive field decreases and critical size increases with reducing  or increasing the thickness of surface layer.
or increasing the thickness of surface layer.
REFERENCES
- N. Setter, D. Damjanovic, L. Eng, G. Fox, S. Gevorgian, S. Hong, A. Kingon, H. Kohlstedt, N. Y. Park, G. B. Stephenson, I. Stolitchnov, A. K. Taganstev, D. V. Taylor, T. Yamada and S. Streiffer, “Ferroelectric Thin Films: Review of Materials, Properties, and Applications,” Journal of Applied Physics, Vol. 100, No. 5, 2006, pp. 606-651. doi:10.1063/1.2336999
- J. M. Wesselinowa, “Dielectric Susceptibility of Ferroelectric Thin Film,” Solid State Communications, Vol. 121, No. 9-10, 2002, pp. 489-492. doi:10.1016/S0038-1098(02)00012-1
- G. Catalan, L. J. Sinnamon and J. M. Gregg, “The Effect of Flexoelectricity on the Dielectric Properties of Inhomogeneously Strained Ferroelectric Thin Film,” Journal of Physics: Condensed Matter, Vol. 16, No. 13, 2004, pp. 2253-2264. doi:10.1088/0953-8984/16/13/006
- Y. Zheng, B. Wang and C. H. Woo, “Critical Thickness for Dislocation Generation during Ferroelectric Transition Thin Film on A Compliant Substrate,” Applied Physics Letters, Vol. 89, No. 8, 2006, pp. 115-117. doi:10.1063/1.2338515
- K.-H. Chew, C. L. Wang, F. G. Shin, H. L. W. Chan and D. R. Tilley, “Theory of Phase Transitions in SecondOrder Ferroelectric Films: Effects of Surfaces and Surface-Induced Stresses on Polarization,” Solid State Communications, Vol. 123, No. 10, 2002, pp. 457-462. doi:10.1016/S0038-1098(02)00253-3
- Y. I. Yuzyuk, R. S. Katiyar, V. A. Alyoshin, I. N. Zakharchenko, D. A. Markov and E. V. Sviridov, “Stress Relaxation in Heteroepitaxial (Ba,Sr)TiO3/(001) MgO Thin Film Studied by Micro-Raman Spectroscopy,” Physical Review B, Vol. 68, No. 10, 2003, pp. 104-107. doi:10.1103/PhysRevB.68.104104
- Y. I. Yuzyuk, J. L. Sauvajol, P. Simon, V. L. Lorman, V. A. Alyoshin, I. N. Zakharchenko and E. V. Sviridov, “Phase Transitions in (Ba0.7Sr0.3)TiO3/(001) MgO Thin Film Studied by Raman Scattering,” Journal of Applied Physics, Vol. 93, No. 12, 2003, pp. 9930-9937. doi:10.1063/1.1574173
- K. Kato, K. Tanaka, K. Suzuki and S. Kayukawa, “Phase Transition in Bottom-up BaTiO3 Films on Si,” Applied Physics Letters, Vol. 91, No. 17, 2007, pp. 907-909. doi:10.1063/1.2794411
- C. Basceri, S. K. Streiffer, A. I. Kingon and R. Waser, “The Dielectric Response as a Function of Temperature and Film Thickness of Fiber-Textured (Ba,Sr)TiO3 Thin Films Grown by Chemical Vapor Deposition,” Journal of Applied Physics, Vol. 82, No. 5, 1997, pp. 2497-2504. doi:10.1063/1.366062
- L.-H. Ong, J. Osman and D. R. Tilley, “Landau Theory of Second-Order Phase Transitions in Ferroelectric Films,” Physical Review B, Vol. 63, No. 14, 2001, pp. 109-118. doi:10.1103/PhysRevB.63.144109
- B. Wang and C. H. Woo, “Curie Temperature and Critical Thickness of Ferroelectric Thin Films,” Journal of Applied Physics, Vol. 97, No. 8, 2005, pp. 109-118. doi:10.1063/1.1861517
- J. Paul, T. Nishimatsu, Y. Kawazoe and U. V. Waghmare, “A First-Principles Study of Phase Transitions in Ultrathin Films of BaTiO3,”Journal of Physics, Vol. 70, No. 2, 2008, pp. 263-270.
- T. Lv and W. Cao, “Generalized Continuum Theory for Ferroelectric Thin Films,” Physical Review B, Vol. 66, No. 2, 2002, pp. 102-104.
- R. Kretschmer and K. Binder, “Surface Effects on Phase Transitions in Ferroelectrics and Dipolar Magnets,” Physical Review B, Vol. 20, No. 3, 1979, pp. 1065-1076. doi:10.1103/PhysRevB.20.1065
- A. M. Musleh, L.-H. Ong and D. R. Tilley, “Effects of Extrapolation Length Δ on Switching Time and Coercive Field,” Journal of Applied Physics, Vol. 105, No. 6, 2009, pp. 602-607. doi:10.1063/1.3081964

