Applied Mathematics
Vol.07 No.09(2016), Article ID:66955,12 pages
10.4236/am.2016.79087
Homotopy Analysis Solution to Radial Diffusivity Equation of Slightly Compressible Fluid
Olugbenga Adebanjo Falode*, Victor Sunday Chukwunagolu
Department of Petroleum Engineering, University of Ibadan, Ibadan, Nigeria

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 January 2016; accepted 28 May 2016; published 31 May 2016
ABSTRACT
The salient significance of the solution of radial diffusivity equation to well testing analysis done in oil and gas industry cannot be over-emphasized. Varieties of solutions have been proposed to the radial diffusivity equation, of which the Van Everdingen-Hurst constant terminal rate solution is the most widely accepted and the others are approximate solution having their respective limitations. The main objective of this project, being its first application to oil and gas industry, is to use a new mathematical technique, the homotopy analysis method (HAM) to solve the radial diffusivity equation for slightly compressible fluid. In Using HAM, the Boltzmann transformation method was used to transform the radial PDE to ODE, then a homotopy series was then constructed for the new equation with the linear boundary condition from the original radial diffusivity equation of slightly compressible fluid and the final equation then solved using computation software Maple. The result gotten reveals that the homotopy analysis method gives good results compared to the Van Everdingen and Hurst Solution (Exact solution) and thus proves to be very effective, simple, and accurate when compared to other form of solutions. Hence from the results gotten, Homotopy Analysis Method can therefore be applied in solving other non-linear equations in the petroleum engineering field since it is simple and accurate.
Keywords:
Homotopy Analysis Method, Boltzmann Transformation, Exact Solution, Diffusivity Equation

1. Introduction
Nonlinear partial differential equations are useful in describing the various phenomena in many disciplines. Apart from a limited number of these problems, most of them do not have a precise analytical solution, so these nonlinear equations should be solved using approximate methods. In 1992, Shijun Liao employed the basic ideas of the homotopy in topology to propose a general analytic method for nonlinear problems, namely homotopy analysis method (HAM) and then modified it [1] . This method is now widely used to solve many types of nonlinear problems. For example, Ayub [2] used HAM to determine an exact flow of a third grade fluid past a porous plate. Cherniha [3] used HAM to determine the Lie and non-lie symmetries of nonlinear diffusion equations with convection term. El-Tawi [4] used HAM to get a new application for solving stochastic quadratic nonlinear diffusion equation. Hayat et al. [5] used HAM to determine an exact flow of a third grade fluid past a porous plate. Khani et al. [6] used HAM for the solutions and efficiency of the non-linear fin problem in which he showed the efficiency of HAM. Abbasbandy [7] applied HAM to solve a generalized Hirota-Satsuma coupled KdV equation. HAM was also for a Class of Holling Model with the Functional Reaction. Other researchers have since employed HAM for solutions of seeming difficult scientific and engineering problems [8] - [11] . This method has been successfully applied to solve many types of nonlinear problems. This method doesn’t depend on size of parameters whether they are small or large and is valid for most nonlinear models. HAM is different from all previous numerical methods; it contains a certain auxiliary parameter h, which provides us with a simple way to adjust and control the convergence region of solution series. The main goal of this paper is to find the approximate solution of the nonlinear radial diffusivity equation with convection term by the homotopy analysis method.
1.1. Radial Diffusivity Equation for Slightly Compressible Fluid
The Radial Diffusivity Equation is considered one of the most salient and widely used mathematical expressions in the Oil and Gas Industry. The equation is particularly applied to the analysis of well testing data. The use of this equation is to determine salient information or parameters during the testing analysis of a well and they include; Initial pressure (p), permeability (k), mechanical skin factor (s), flow efficiency, productivity index etc. The equation is also used to investigate reservoir productivity.
To develop the radial diffusivity equation, some assumptions are assumed. These are:
・ Formation is a homogenous and isotropic porous media of uniform thickness.
・ Negligible gravity effect.
・ Applicability of Darcy’s law.
・ Pressure independent rock properties.
・ Central well is perforated across the entire formation thickness. Hence; radial flow.
・ Single phase flow is present in the reservoir.
・ Small pressure gradient.
These assumptions are needed to combine the three (3) governing equations needed in deriving the radial diffusivity equation:
・ The law of conservation of mass.
・ Darcy’s law.
・ Equation of state.
We consider a radial flow of fluid towards a well in a circular reservoir. Combining the conservation of mass and Darcy’s law for the isothermal flow of fluids of small and constant compressibility, a partial differential equation is obtained that in field units simplifies to
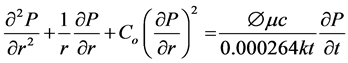 (1)
(1)
where it is assumed that compressibility, c, is small and independent of pressure, permeability, k, is constant and isotropic; viscosity, µ, is independent of pressure, porosity ɸ, is constant. The above equation is called the
non-linear radial diffusivity equation and the term 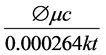 is called the hydraulic diffusivity and is fre-
is called the hydraulic diffusivity and is fre-
quently denoted by η.
Re-writing Equation (1) in terms of dimensionless variables, the following salient points are established:
1) The dimensionless radius,  , is based intuitively on the wellbore radius,
, is based intuitively on the wellbore radius,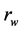 . And
. And  is always known;
is always known;
2) The dimensionless pressure, 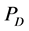 , must satisfy the following conditions;
, must satisfy the following conditions;
3) The initial condition: 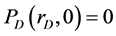 at
at  for all values of
for all values of ;
;
4) The constant rate inner boundary condition: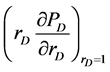 .
.
As stated above, the definition of the dimensionless radius is given as
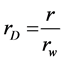 (2)
(2)
and
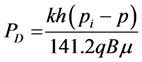 (3)
(3)
And dimensionless time is given as:
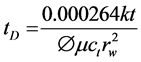 (4)
(4)
Therefore, the Dimensionless radial diffusivity equation is given as:
 (5)
(5)
When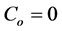 ,
,

The above Equation (6) is the linear dimensionless radial diffusivity equation.
1.2. Current Solution to the Radial Diffusivity Equation
There are four solutions to Equation (6) (when
1) Van Everdingen-Hurst constant terminal rate solution for bounded cylindrical reservoir.
2) The solution for an infinite reservoir with a well-considered to be a line source with zero wellbore radius.
3) The pseudo-steady state solution.
4) The solution that includes wellbore storage for a well in an infinite reservoir.
a) Van Everdingen-Hurst Constant Terminal rate solution for Bounded cylindrical reservoir
Van Everdingen and Hurst developed two set of solution for the linear radial diffusivity equation namely, “the constant terminal pressure case solution” and “the constant terminal rate case”. In the constant terminal pressure case, the pressure at the terminal boundary is lowered by unity at zero time, kept constant thereafter, and the cumulative amount of fluid flowing across the boundary is computed as a function of the time. The constant terminal rate solution is explained explicitly below.
Constant Terminal Rate Solution
It is solutions of the radial diffusivity Equation (1) when 
In summary, Van Everdingen and Hurst solution to the Equation (6) requires two boundary conditions and an initial condition. A realistic and practical solution is obtained if we assume that
1) A well produces a constant rate, qB, into the wellbore (q refers to flow rate in STB/D at surface conditions, and B is the formation volume factor in RB/STB);
2) The well, with wellbore radius, 

3) Before production begins, the reservoir is at uniform pressure
The most useful form of the desired solution relates flowing pressure, 





The solution after applying the above initial and boundary conditions is expressed as follows;

This solution is considered the exact solution to the radial diffusivity equation, but approximate solutions are used instead of this exact solution because of the cumbersomeness of the equation.
b) Pseudo-steady state solution for Bounded Cylindrical Reservoir
The solution here is simply a limiting form of the Van Everdingen-Hurst constant terminal rate solution (the exact solution), where the summation involving exponentials and Bessel functions is considered negligible.
The solution proposed here to the linear radial diffusivity equation is expressed as;

c) Solution for an infinite Reservoir with Line source well
Assumptions made here are that;
1) A well produces at a constant rate, qB;
2) The well has zero radius;
3) The reservoir is at uniform pressure, pi, before production begins; and
4) The well drains an infinite area (i.e., that p → pi as r → ∞).
Under these conditions, the solution to the radial diffusivity equation is;

2. Basic Idea of Homotopy Analysis Method
To describe the main idea of Homotopy Analysis Method, the following differential equations are considered:
Let U be a function of homotopy parameter q. Then,

where N is a non-linear operator, and 
The Construction of homotopy takes the form:

where 






In deriving the zeroth order deformation equation we set the homotopy Equation (10) equal to zero,

whose solution transforms continuously with respect to q.
When q = 0,


Similarly when q = 1,


Thus, as q varies from 0 to 1, the solution 


The homotopy series is gotten by expanding 

where

If the auxiliary linear operator, the initial guess, auxiliary parameter and auxiliary function are properly chosen, the series Equation (16) converges at q = 1 and we get homotopy series solution;

which must be one of the solution of the original non linear equation 

For

Differentiating Equation (11) m times with respect to the embedding parameter q and then setting q = 0 and finally dividing them by m!, we have the so-called mth-order deformtion equation:

where

and

It is of paramount importance to emphasize that 

Application of Ham to Solving Non-Linear Radial Diffusivity Equation for Slightly Comprssible Fluid
Also, transforming Equation (5) using Boltzmann transformation to ordinary differential equation for ease in solving, we have:

Equation (5) then becomes;

Initial condition

Boundary conditions

The Construction of homotopy for Equation (25) takes the form:

where 






In deriving the zeroth order deformation equation we set the homotopy Equation (28) equal to zero,

whose solution transforms continuously with respect to q.
When q = 0 ,


Similarly when q = 1,


Thus, as q varies from 0 to 1, the solution 


The homotopy series is gotten by expanding 

where

If the auxiliary linear operator, the initial guess, auxiliary parameter and auxiliary function are properly chosen, the series Equation (3.13) converges at q = 1 and we get homotopy series solution;

which must be one of the solution of the original non linear equation 

For 

Therefore from Equation (7), the mth order deformation equation is derived as;

The solution of the mth-order deformation Equation (37) is given as:

According to the rule of solution expression Equation (39), the auxilliary function 


In this way, we derive 

3. Results and Discussion
The analytical solution of the nonlinear diffusivity Equation (25) is obtained by using the Homotopy Analysis Method (HAM). The convergence parameter values for which the solution converges is shown in Figure 1. The obtained analytical solution is verified graphically in Figures 2-4 for negligible compressibility factor term in the parameters of the problem to show the behavior of the solution which satisfy the boundary conditions.
Figure 1. h curve.
Figure 2. Homotopy analysis method (Dimensionless pressure profile).
Figure 3. Plot of Exact and HAM Solutions of PD vs tD for an infinite radial system (rD = 1).
As long as we choose h in this horizontal region
Evaluating 





Homotopy Analysis Method solution was also used in solving for dimensionless pressure PD for finite radial
system with closed exterior boundary, constant rate at inner boundary (
Figure 4. Plot of Exact and HAM Solutions of PD vs tD for an infinite radial system (rD = 200).
Table 1. HAM and exact solution PD values at rD = 200.
From Table 1, it seen that there is minimal error between the Van Everdigen and Hurst solution with that of the Homotopy Analysis Method. Figure 4 is a plot of Table 2, showing the plot of the Exact solution and the values gotten from the Homotopy Analysis Method against the dimensionless time at rD = 200.
Furthermore, Homotopy Analysis Method solution gotten for the radial diffusivity equation was applied in getting the values of PD for respective Dmensionless time tD values for rD = 300 for finite radial system with closed exteriorboundary and constant rate at inner boundary. Table 2 shows the solutions gotten using HAM,
Van Everdigen and Hurst solutions against various dimensionless time tD values at rD = 300 and their respective absolute errors.
Also, from Table 1, it seen that there is minimal error between the Van Everdigen and Hurst solution with that of the Homotopy Analysis Method. Figure 5 is a plot of Table 2, showing the plot of the Exact solution and the values gotten from the Homotopy Analysis Method against the dimensionless time at rD = 300.
It is important to note that Figure 2 demonstrates the pressure distribution in a porous medium (reservoir rock) with coefficient of square of pressure gradient assumed negligible, from this figure, the efficiency and robustness
Table 2. HAM and exact solution PD values at rD = 300.
Figure 5. Plot of Exact and HAM Solutions of PD vs tD for an infinite radial system (rD = 300).
of the HAM in solving approximately the non-linear flow problem in the reservoir is evident. Also, Figures 2-4 show the accuracy of the Homotopy Analysis method when compared to the Van Everdingen and Hurst solution when the radial diffusivity equation solution used was linearized.
Figure 6 shows the comparison plot of non-linear radial diffusivity equation i.e. when compressibility factor and the pressure gradient are not negligible (≠0) and the linear radial diffusivity equation for slightly compressible fluid. Therefore, we have:
From Figure 6, we see that the respective value of dimensionless pressure against dimensionless time tends to increase as the value of the compressibility coefficient factor term of the squared pressure gradient increases.
Figure 6. Dimensionless pressure profile at different compressibility coefficient factor term of 0, 0.2, 0.4 and 0.6.
4. Conclusions
In this work, an approximate but very accurate solution of a non-linear reservoir model with coefficient of square of pressure gradient Co was successfully obtained using a powerful analytic method called the homotopy analysis method. It was shown that:
1) The pressure distribution in the reservoir with coefficient of square of pressure gradient Co, can be accurately predicted with the HAM solution.
2) The freedom of choice of the auxiliary parameter h, gives way to adjust and control the convergence of the solution series, which can be considered as a fundamental difference between the homotopy analysis method and other existing methods such as the adomian decomposition method, homotopy perturbation method and variational iteration method.
3) The Homotopy Analysis method is a mathematical model that can be used to solve the non-linear radial diffusivity equation effectively.
It is then believed that the homotopy analysis method is an efficient and capable technique in handling a wide variety of engineering problems.
Cite this paper
Olugbenga Adebanjo Falode,Victor Sunday Chukwunagolu, (2016) Homotopy Analysis Solution to Radial Diffusivity Equation of Slightly Compressible Fluid. Applied Mathematics,07,993-1004. doi: 10.4236/am.2016.79087
References
- 1. Liao, S.J. (1992) The Proposed Homotopy Analysis Method Techniques for the Solution of Nonlinear Problems. Shanghai Jiao Tong University, Shanghai.
- 2. Ayub, M.A. and Rasheed Hayat, T. (2003) Exact Flow of a Third Grade Fluid past a Porous Plate Using Homotopy Analysis. International Journal of Engineering Science, 41, 2091-2103.
http://dx.doi.org/10.1016/S0020-7225(03)00207-6 - 3. Cherniha, R. and Servo, M. (1997) Lie and Non-Lie Symmetries of Nonlinear Diffusion Equations with Convection Term. Symmetry in Nonlinear Mathematical Physics, 2, 444-449.
- 4. El-Tawi, M.A. and Hassan, H.N. (2013) A New Application of Using Homotopy Analysis Method for Solving Stochastic Quadratic Nonlinear Diffusion Equation. International Journal of Applied Mathematics and Mechanics, 9, 35-55.
- 5. Hayat, T. and Khan, M. (2005) Exact Flow of a Third Grade Fluid past a Porous Plate Using Homotopy Analysis. International Journal of Engineering Science, 56, 1012-1029.
- 6. Khani, F., Raji, M. and Nejad, H.H. (2009) Analytical Solution and Efficiency of the Nonlinear Fin Problem with Tem-perature-Dependent Thermal Conductivity and Heat Transfer Coefficient. Communications in Nonlinear Science and Numerical Simulation, 14, 3327-3338.
http://dx.doi.org/10.1016/j.cnsns.2009.01.012 - 7. Abbasbandy, S. (2007) The Application of Homotopy Analysis Method to Solve a Generalized Hirota-Satsuma Coupled KdV Equation. Physics Letters A, 361, 478-483.
http://dx.doi.org/10.1016/j.physleta.2006.09.105 - 8. Mahmoudi, Y. and Kazemian, E.M. (2013) The Homotopy Analysis Method for Solving the Kuramoto-Tsuzuki Equation. World Applied Sciences Journal, 21, 1776-1781.
- 9. Sajad, M., Hayat, T. and Asghar, S. (2006) On the Analytic Solution of the Steady Flow of a Fourth Grade Fluid. Physics Letters A, 355, 18-26.
http://dx.doi.org/10.1016/j.physleta.2006.01.092 - 10. Van Everdingen, A.F. and Hurst, W. (1949) The Application of the Laplace Transformation to Flow Problems in Reservoirs. Transactions of AIME, 186, 305-324.
- 11. Chen, X.R. and Yu, J.J. (2013) Homotopy Analysis Method for a Class of Holling Model with the Functional Reaction. The Open Automation and Control Systems Journal, 5, 150-153.
NOTES
*Corresponding author.












