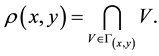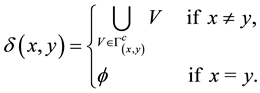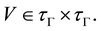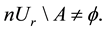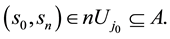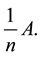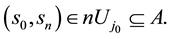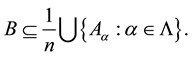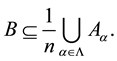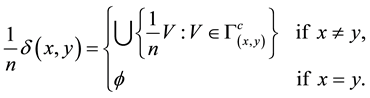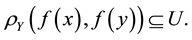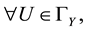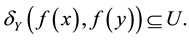Applied Mathematics
Vol.06 No.06(2015), Article ID:57037,6 pages
10.4236/am.2015.66097
More Properties of Semi-Linear Uniform Spaces
S. A. Alhihi
Department of Mathematics, Al-Balqa’ Applied University, Alsalt, Jordan
Email: suad.hihi@bau.edu.jo, suadalhihi@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 April 2015; accepted 7 June 2015; published 10 June 2015
ABSTRACT
In this paper we shall generalize the definition given in [1] for Lipschitz condition and contractions for functions on a non-metrizable space, besides we shall give more properties of semi-linear uniform spaces.
Keywords:
Lipschitz Condition, Contractions, Not Metrizable Spaces, Semi-Linear Spaces, Uniform Spaces, Fixed Point

1. Introduction
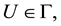
The notion of uniformity has been investigated by several mathematician as Weil [2] - [4] , Cohen [5] [6] , and Graves [7] .
The theory of uniform spaces was given by Burbaki in [8] . Also Wiels in his booklet [4] defined uniformly continuous mapping. For more information about Uniform spaces one my refer to [9] .
In 2009, Tallafha, A. and Khalil, R. [10] , defined a new type of uniform spaces, namely semi-linear uniform spaces and they gave example of semi-linear space which was not metrizable. Also they defined a set valued map  on
on , by which they studied some cases of best approximation in such spaces. More precisely, they gave the following.
, by which they studied some cases of best approximation in such spaces. More precisely, they gave the following.
Let 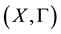 be a semi-linear uniform space;
be a semi-linear uniform space; 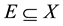 is proximinal if for any
is proximinal if for any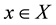 , there exists
, there exists 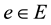 such that
such that . They asked that “must every compact is proximinal”, they gave the answer for the cases―i) E is finiate; ii) If
. They asked that “must every compact is proximinal”, they gave the answer for the cases―i) E is finiate; ii) If  converges to x, then
converges to x, then 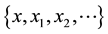 is proximinal.
is proximinal.
In [11] , Tallafha, A. defined another set valued map 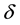 on
on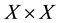 , and gave some properties of semi-linear uniform spaces using the maps
, and gave some properties of semi-linear uniform spaces using the maps 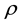 and
and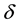 . Also in [1] [12] , Tallafha defined Lipschitz condition and con- tractions for functions on semi-linear uniform spaces, which enabled us to study fixed point for such functions. Lipschitz condition, and contractions are usually discussed in metric and normed spaces and never been studied in other weaker spaces. We believe that the structure of semi-linear uniform spaces is very rich, and all the known results on fixed point theory can be generalized.
. Also in [1] [12] , Tallafha defined Lipschitz condition and con- tractions for functions on semi-linear uniform spaces, which enabled us to study fixed point for such functions. Lipschitz condition, and contractions are usually discussed in metric and normed spaces and never been studied in other weaker spaces. We believe that the structure of semi-linear uniform spaces is very rich, and all the known results on fixed point theory can be generalized.
The object of this paper is to generalize the definition of Lipschitz condition, and contraction mapping on semi-linear uniform spaces given by Tallafha [12] . Also we shall give a new topopological properties and more properties of semi-linear uniform spaces.
2. Semi-Linear Uniform Space
Let X be a set and 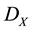 be a collection of subsets of
be a collection of subsets of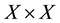 , such that each element V of
, such that each element V of  contains the diagonal
contains the diagonal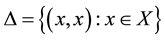
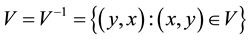
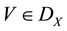
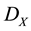
Definition 1 [10] . Let 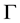

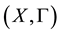
i) 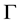
ii) For every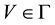


iii)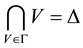
iv)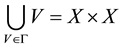
Definition 2 [10] . Let 


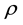
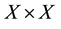
Clearly for all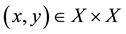
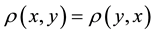
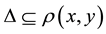
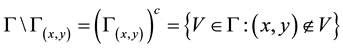
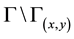
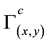
Definition 3 [11] . Let 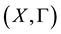

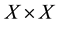
defined by,
The following results are given in [12] .
Proposition 1. Let 
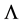
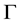
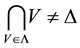


Corollary 1. Let 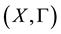

1) There exist 
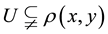
2)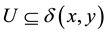
Let 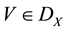


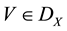
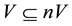
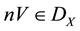
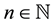
Proposition 2. Let 


Proposition 3. Let 

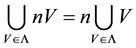
Question. Does
3. Topological Properties of Semi-Linear Uniform Spaces
Definition 4 [13] . For 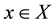
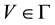
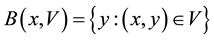
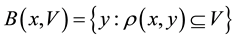
Clearly if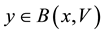
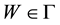
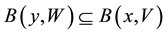

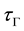
More presicly
In [10] it is shown that 
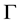
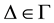
Proposition 4. Let 
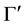
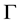
i) For every
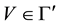

ii)
iii)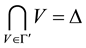
Then 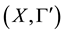
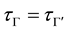
Proof. Since 
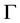
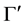
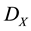
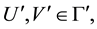
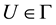
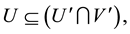
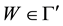

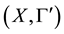
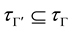
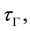

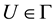
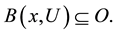
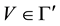

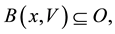
Theorem 1. Let 

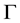
i) 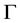
ii) Fore all 
Proof. i). Let

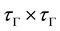
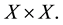

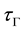

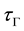

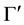
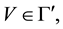
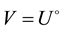
ii) Is clear by definition of
In [11] , Tallafha gave some important properties of semi-linear uniform spaces, using the set valued map 

Now we shall give more properties of semi-linear uniform spaces.
4. More Properties of Semi-Linear Uniform Spaces
Let 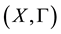

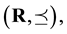
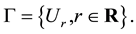
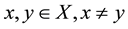
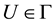

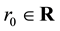
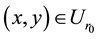


is bounded above by
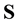
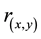
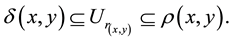
Lemma 1. Let 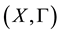


set, then for 
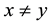
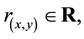
Remember that for all 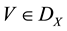
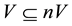



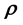

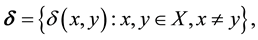


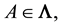
rollary 1.6, there exist 


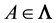
Definition 5. For 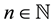

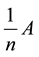
Clearly 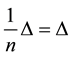
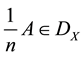
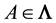


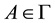
Lemma 2. Let 

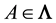
Then there exist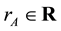
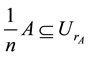
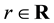

Proof. For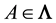
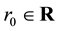
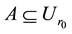

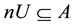

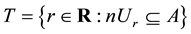

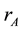
Theorem 2. Let
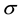

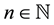
i)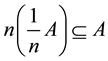
ii) If 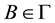


iii)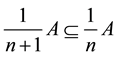
iv)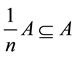
v)
vi)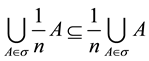
Proof. i). Let

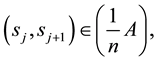
So there exist 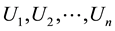
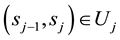
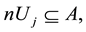


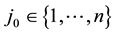
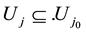

ii) and iv), are clear by definition of
iii) 
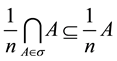
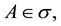
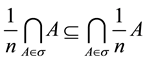
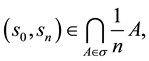

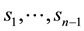
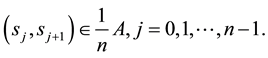
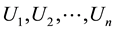

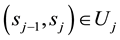
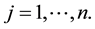

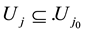
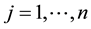
Let 
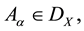
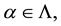


Corollary 2. For 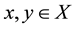
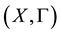
i)
ii)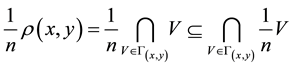
Corollary 3. Let 


i)
ii) If 

iii)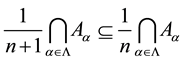
iv)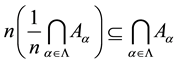
v) If 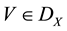
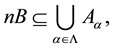
vi)
Also we have the follwing corollary.
Corollary 4. For 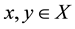
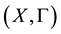

Corollary 5. For
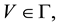

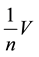
Also by Definition 3.6, for 
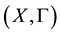
i)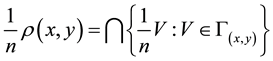
ii)
Proposition 5. Let 
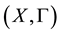
Proof. Let 
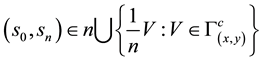

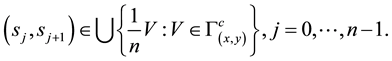


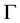
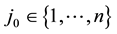
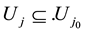

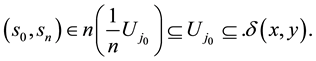
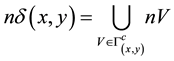


Definition 6. For

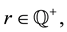
i) 
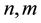
ii)
iii)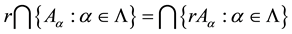
Definition 7. Let 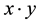

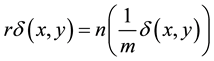


Using the a bove definition and Proposition 1.7, we have.
Proposition 6. Let 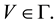
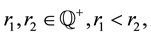
Proposition 7. Let 
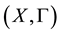
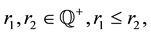
Definition 8. Let 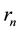
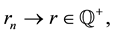

Proposition 8. Let 


Proof. It is an immediate consequence of Proposition (7) and Definition (8).
5. Contractions
In [10] the definitions of converges and Cauchy are given. Now we shall discuss some topological properties of semi-linear uniform spaces. Since the semi-linear uniform space is a topological space then the continuity of a function is as in topology. The concept of uniform continuity is given by Wiels [4] , so we have:
Definition 9 [4] . Let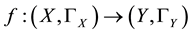
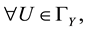
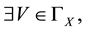
that if 
Clearly using our notation we have:
Proposition 9. Let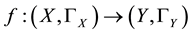



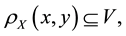
The following proposition shows that we may replace 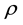
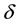
Proposition 10 [12] . Let
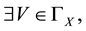


In [10] , Tallafha gave an example of a space which was the semi-linear uniform space, but not metrizable. Till now, to define a function f that satisfies Lipschitz condition, or to be a contraction, it should be defined on a metric space to another metric space. The main idea of this paper is to define such concepts without metric spaces, and we just need a semi-linear uniform space, which is weaker as we mentioned before.
Definition 10 [1] . Let 

that 
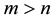
Now we shall give a new definition of Lipschitz condition and contraction called r-Lipschitz condition and r-contraction.
Definition 11. Let 
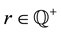
that 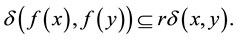
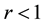
Question. Let 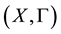

Remark 1 [12] . Let 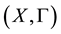
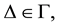
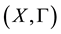
Question [1] [12] . Let 
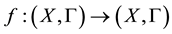
Question. Let 
References
- Tallafha, A. (2013) Open Problems in Semi-Linear Uniform Spaces. Journal of Applied Functional Analysis, 8, 223- 228.
- Weil, A. (1936) Les recouvrements des espaces topologiques: Espaces complete, espaces bicompact. Comptes Rendus de l’Académie des Sciences, 202, 1002-1005.
- Weil, A. (1937) Sur les espaces a structure uniforme et sur la topologie generale. Actuarial Science India, 551, Paris.
- Weil, A. (1938) Sur les espaces à structure uniforme et sur la topologic générale. Hermann, Paris.
- Cohen, L.W. (1937) Uniformity Properties in a Topological Space Satisfying the First Denumerability Postulate. Duke Mathematical Journal, 3, 610-615.
- Cohen, L.W. (1939) On Imbedding a Space in a Complete Space. Duke Mathematical Journal, 5, 174-183.
- Graves, L.M. (1937) On the Completing of a Housdroff Space. Annals of Mathematics, 38, 61-64.
- Bourbaki, N. (1940) Topologie Générale (General Topology). Paris.
- James, I.M. (1987) Topological and Uniform Spaces. Undergraduate Texts in Mathematics. Springer-Verlag, Berlin.
- Tallafha, A. and Khalil, R. (2009) Best Approximation in Uniformity Type Spaces. European Journal of Pure and Applied Mathematics, 2, 231-238.
- Tallafha, A. (2011) Some Properties of Semi-Linear Uniform Spaces. Boletin da Sociedade Paranaense de Matematica, 29, 9-14.
- Tallafha, A. (2015) Fixed Point in a Non-Metrizable Spaces. To Appear.
- Engelking, R. (1968) Outline of General Topology. North-Holand, Amsterdam.