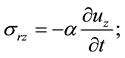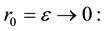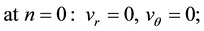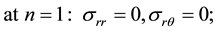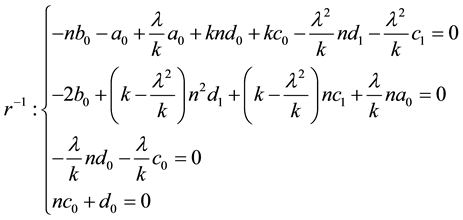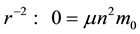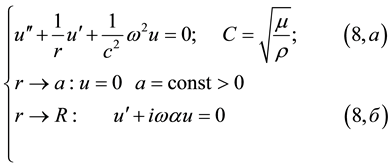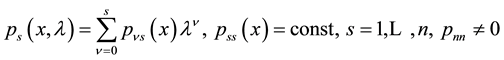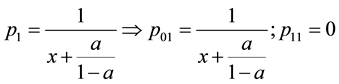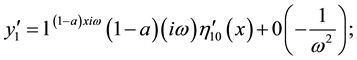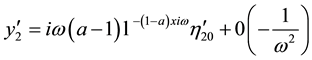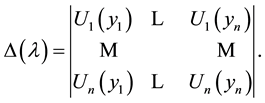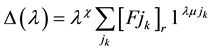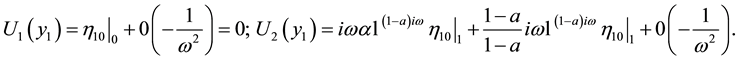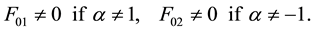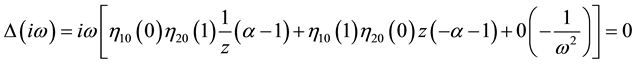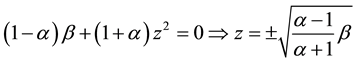Applied Mathematics Vol.06 No.03(2015), Article ID:55088,-4 pages
10.4236/am.2015.63057
Natural Oscillations of Cylindrical Bodies with External Friction on the Boundary
Safarov Ismail Ibrahimovich, Akhmedov Maqsud Sharipovich, Boltaev Zafar Ihterovich
Bukhara Engineering-Technological Institute, Bukhara, Republic of Uzbekistan
Email: maqsud.axmedov.1985@mail.ru , lazizbek.axmedov.2011@mail.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 February 2015; accepted 25 March 2015; published 26 March 2015
ABSTRACT
In this paper we consider of natural oscillations cylindrical bodies with external friction. Complex rates changes from friction parameters are shown. Rate equations are solved numerically―by method of Muller.
Keywords:
External Friction, The Natural Oscillations, Cylindrical Body, Flat Swing, Ant Plane Oscillation Frequency, Damping Factor

1. Introduction
Simulation of vibrations of bodies located in the deformable medium is studied with many scientists and by various methods [1] -[4] . Study of dynamic stress-strain state of pipelines in soil medium, refers to the complex task of solid mechanics. In some researches [5] [6] deformable surrounding in the pipe replaced by springs and considered as emerging (linear and nonlinear) reducing force. In this paper, vibrations of pipelines as a cylindrical body with radiuses r0 and R at deformable surroundings are modeled (Figure 1). Medium was replaced with viscous damping in the radial and tangential direction. The main aim of the work is to study the oscillations of a cylinder with external friction on the edge and to compare the results of the body located in an elastic medium [3] .
2. Statement of the Problem
Study fluctuations pipeline located in an elastic medium are considered different methods [6] - [9] .
In this paper, fluctuations pipelines are modeled as a cylindrical body with a radius
 and R, located in a deformable medium (Figure 1).
Medium was replaced with viscous damping in the radial and tangential direc-
and R, located in a deformable medium (Figure 1).
Medium was replaced with viscous damping in the radial and tangential direc-
Figure 1. Design model of cylindrical bodies with a viscous external friction.
tion. The main goal of the work is to study the natural oscillations a cylinder with external friction. In the study mentioned above, the optimal values of damping coefficients, in which the oscillations are, damped pipelines as possible.
Consider the problem of the oscillations of an infinite elastic cylinder with external friction at the interface (Figure 2). Closed system of equations of small oscillations of the free elastic cylindrical body has the form:
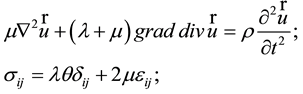 (1)
(1)
where ―displacement
vector;
―displacement
vector; ―lame
coefficients;
―lame
coefficients;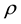 ―the
density of the cylinder;
―the
density of the cylinder;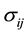 ―the
stress tensor;
―the
stress tensor; ―strain
tensor. On the part of the boundary
―strain
tensor. On the part of the boundary
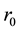 given movement:
given movement:
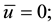 apart R-Voltage:
apart R-Voltage:
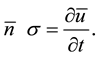 As well as
the initial conditions:
As well as
the initial conditions:
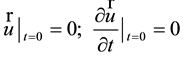
Consider the problem in cylindrical coordinates
 Assuming that z coordinate does not affect the oscil- lation, we obtain a system
of equations splits into two independent tasks [7] :
Assuming that z coordinate does not affect the oscil- lation, we obtain a system
of equations splits into two independent tasks [7] :
 (2а)
(2а)
 (2b)
(2b)
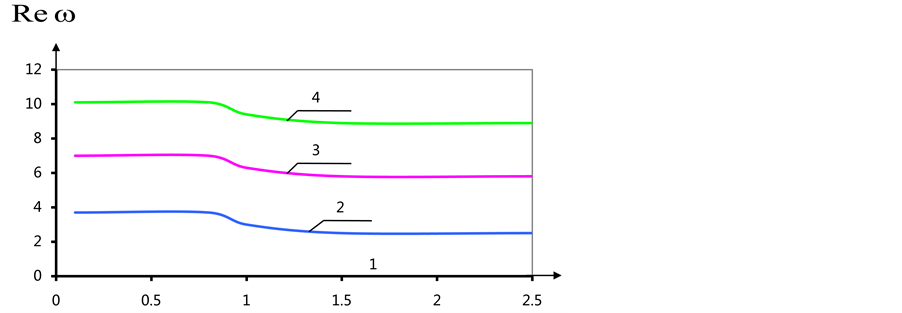
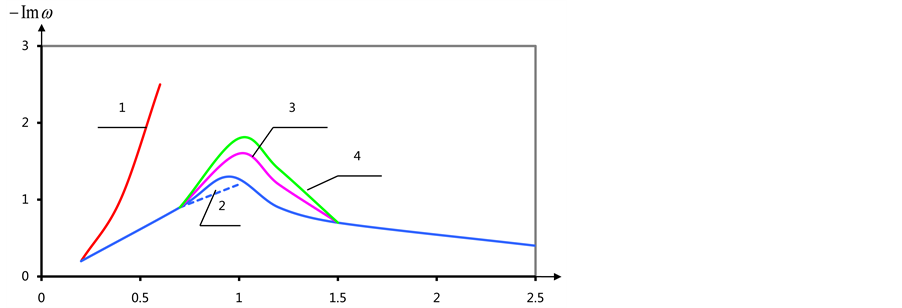
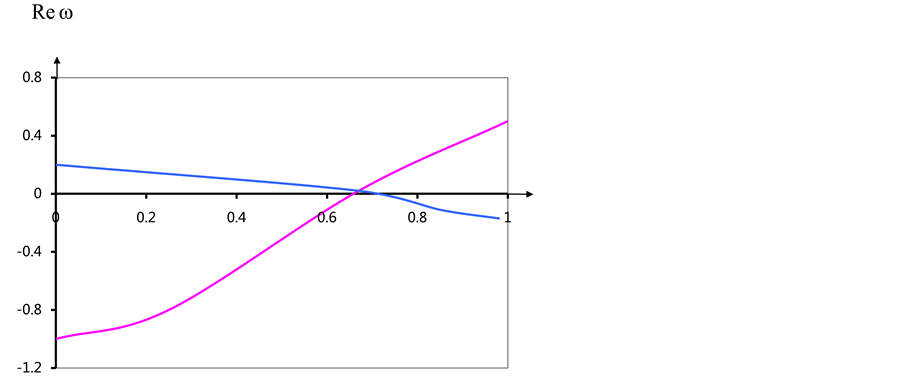
Figure 2. (a) The dependence of the real part of the eigenvalues of α (n = 0); (b) The dependence of the imaginary part of the eigenvalues of α (n = 0).
With boundary conditions:
at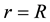

where R-radius of the cylinder;

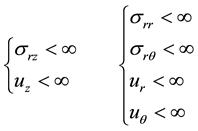
Then we call the boundary value problem (2a)-ant plane and (2b)-flat or planar problem of oscillations of a cylinder.
3. Methods for Solving the Problem of Natural Oscillations
We call the natural oscillations of an elastic cylinder solution of (2a) and (2d) (f = 0) for ant plane case types:
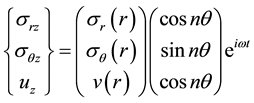
problem (2b and 2d) for the planar case types:
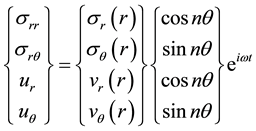
where
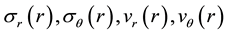
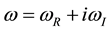
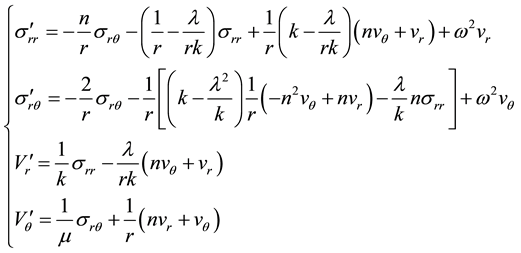
Ant planar

It can be shown that the conditions for the finiteness of all the unknowns in the center for a solid cylinder equivalent to the following boundary conditions-for flat cylinder oscillation:
At n > 1 can be set equal to zero any set of two unknowns. Indeed, if the conditions
of the limb in the center of the cylinder, then
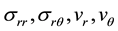
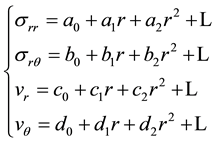
where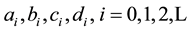
Then substituting (5a) to (4a) we obtain a system of four equations. Equating them coefficients of like powers of r we obtain the recurrence relation:
At
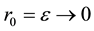
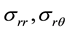
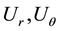


If ant planar cylinder oscillation: the n = 0
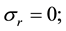
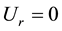
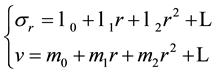
where
Substituting (5b) in (4b), we obtain a system of two equations. Equating them to obtain coefficients of the same recurrence relation:
Then for
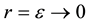


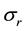
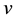
The general solution of the system of Equations (2a, 2, c) can be expressed in terms of Bessel and Neman functions n―the order:
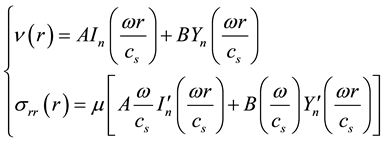
where A, B―arbitrary constants;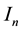
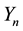
When substituting (6) into (2c and 2d), we obtain the characteristic equation for w:

Theorem. Let the Eigen values

Simple. Then the system
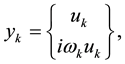
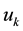
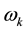

Proof. To prove the theorem using the definition from [8] . A boundary value problem can be represented as:

where


Definition 1 is the number of

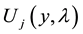
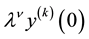
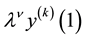
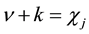
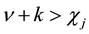
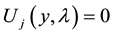
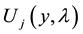
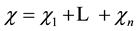
Definition 2 will be called the boundary conditions (9) normalized if any n boundary conditions, they are equivalent, i.e., received (9) are linear combinations of not less than the total order. Given the total order of the boundary conditions (9) is called a total order of the boundary conditions, we obtain from (9) after normalization.
Rewrite Equation (8a) and boundary conditions (8b) in the form (9). To make the replacement is necessary, so that the new unknown changed from zero to unity.
We introduce
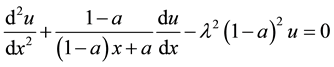
We introduce the coefficients
Boundary conditions:

c = 1 ? total order.
The characteristic equation for (9) has the form:

Its roots are denoted
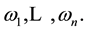
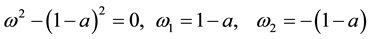
If the roots of the characteristic Equation (12) is simple, and the coefficients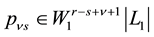
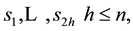
fundamental system of solutions
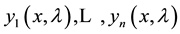


where
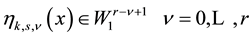
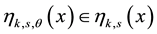

of sector and the sequence of the system of recurrence equations.
We represent the solution of our problem in the form (14):

The eigenvalues of the problem (9), (10) are determined by the zeros of the characteristic
determinant
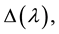
Expanding the determinant, we obtain:
where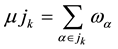
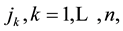
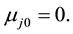
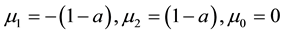
Then

We introduce the definition of [8] .
Definition 3. Boundary value problem (9), (10) is said to be regular if all the
coefficients
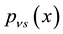

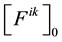

Let M denote the smallest convex polygon containing the point

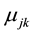
Definition 4. Regular boundary value problem is said to be strongly regular if the
zeros of the characteristic determinant

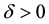
And obtained Equation (9), the coefficients
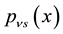
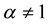
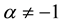

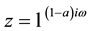
We assume without loss of generality that
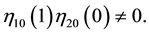
The equation becomes:
At

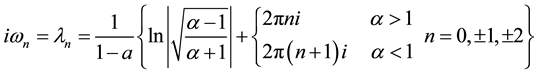
Hence the zeros of the characteristic determinant
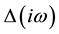
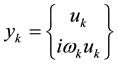
4. The Numerical Results of the Problem of Their Own Ant Planar Oscillations of the Cylinder
The results of calculations are given in dimensionless system of units in which
the value of the shear modulus m, density cylinder

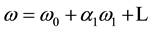
Then, after the stand (17) (7) have:

where
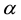
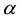
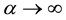
Figure 2 and Figure 3
show the dependence of the real (a) and imaginary (b) parts of the eigenvalues of
the spectral problem (9), (18) the parameter
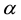
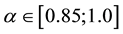
With the growing number of fashion maximum value increases, the value of a, to which
he achieved increases, while remaining less than one. Meaning a, which peaks are
shown in Table 1 and Table
2. In the zeros harmonic for any a there is zero eigenvalue and a smaller
units exist purely imaginary eigenvalues, which tends to infinity when approaching
the unit on the left. Zero eigenvalue corresponds to the motion of the cylinder
as a ri- gid body. In the case of n = 1, 2 for the first mode, there are critical
values




Figure 3. (a) The dependence of the real part of their own values of α (n = 4); (b) Dependence of the imaginary parts of the eigenvalues values of α (n = 4).

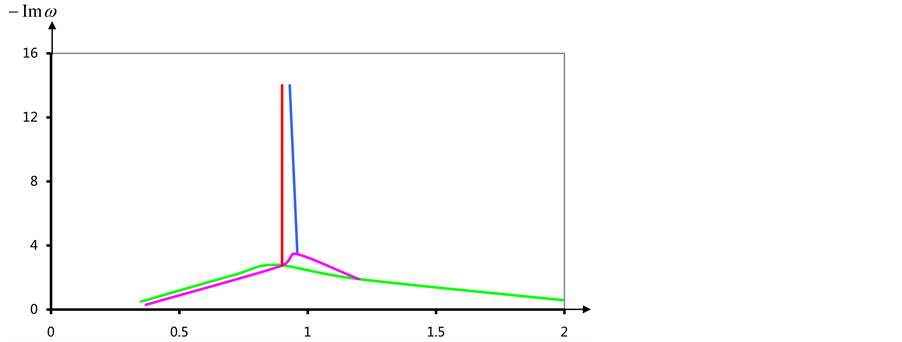
Figure 4. (а) The dependence of the real part of their own values of α (n = 1, 2); (b) Dependence of the imaginary parts of the eigenvalues values of α.
Table 1. The values of the attenuation coefficient depending on the number of harmonics.
Table 2. The values of the maximum oscillation damping depending on the number of harmonics.
with one branch tend to zero
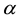
For n = 3 also exists a critical value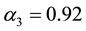


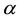
A similar case is obtained for n = 4. At the critical value
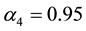
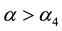
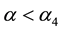
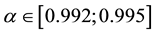

Thus for all n there is considered imaginary branch of the natural frequencies of
the parameter

Figure 4. (а) The dependence of the real part of their own values of α (n = 1, 2); (b) Dependence of the imaginary parts of the eigenvalues values of α.
Figure 5. The dependence of the imaginary part of its own values of α (n = 4).
5. Numerical Solution of the Problem on Its Own Plane Oscillations of a Cylinder
Solution of the resulting task was carried out by separation of variables and note
to the solution of the transcendental equation. All results of the calculations
are given in dimensionless system of units in which the value of the shear modulusm,
density cylinder

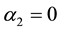


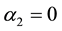
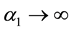
Figure 6 and Figure 7
show the dependence of the real (a) and imaginary (b) parts of the eigen values
of the spectral problem of the parameter
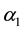

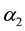

For n = 0 the problem is divided into two independent tasks. In this case, as in
the case ant planar cylinder oscillation, depending on the real parts of the eigen
values have the form of smooth decreasing steps with a maximum angle of inclination
of the tangent in the case of radial oscillations in the interval
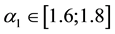

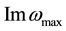


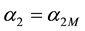
As in the case anticline, with increasing numbers of harmonics increases the maximum value, except for the first radial root (see Table 3). It differs from the rest of the eigen values of the fact that the real part vanishes that corresponds to the motion of the cylinder as a rigid body.
For all the above cases, for n > 1, there is a clear separation of the roots
into two types. The differences between these types of roots appear as a character
of the dependence of the eigen values of the parameters of the external friction,
and in the value of the form. For example, for the first root of the first harmonic-“twist”,
the maximum value of the real part of the radial component of the voltage waveform
is about three times smaller than the value of the real part component forms torsion
stresses. For the second root of the first harmonic-“radial” ―the maximum value
of the real part of the radial component of its own form of stress three times more
than the maximum torsion component (see Figure 10(a),
the first root; Figure 10(b), the second). Actual
own forms part of the deformation, on the edge of the cylinder, characterized by
two times (see Figure 11). The imaginary parts
of their own forms of valid order of magnitude smaller and do not have such a pronounced
difference. If you change depending on the real parts of the eigen values of the
first type-“radial”―the parameter of friction have the form of smooth decreasing
steps with a maximum angle of inclination of the tangent to the range

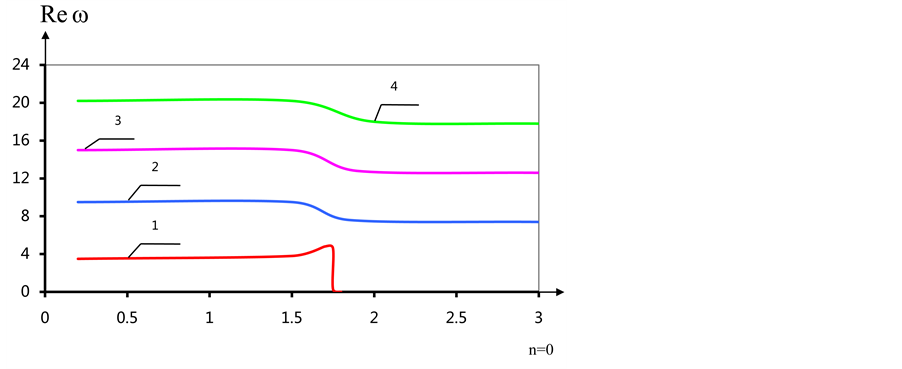
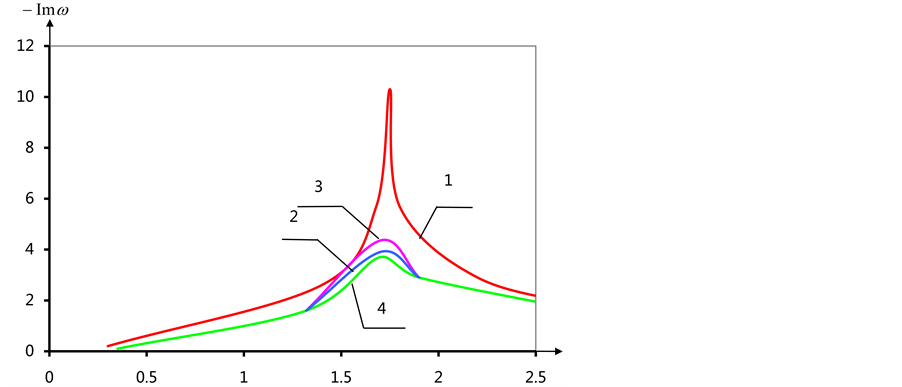
Figure 6. (a) The dependence of the real part of the eigenvalues of α; (b) The dependence of the imaginary part of the eigenvalues of α.

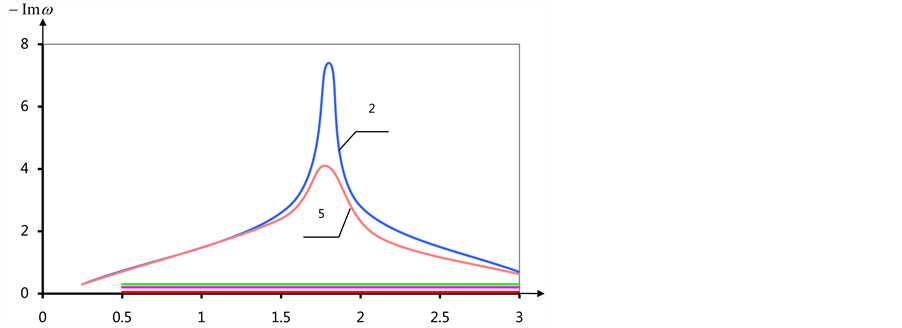
Figure 7. (a) The dependence of the real part of the eigenvalues of α; (b) The dependence of the imaginary part of the eigenvalues of α.
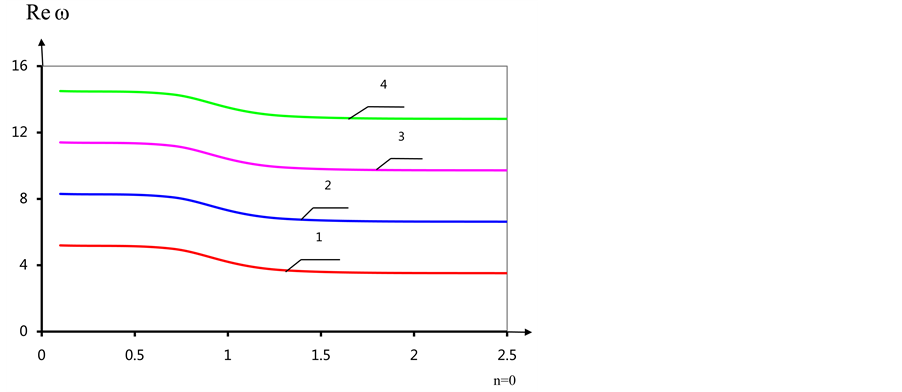
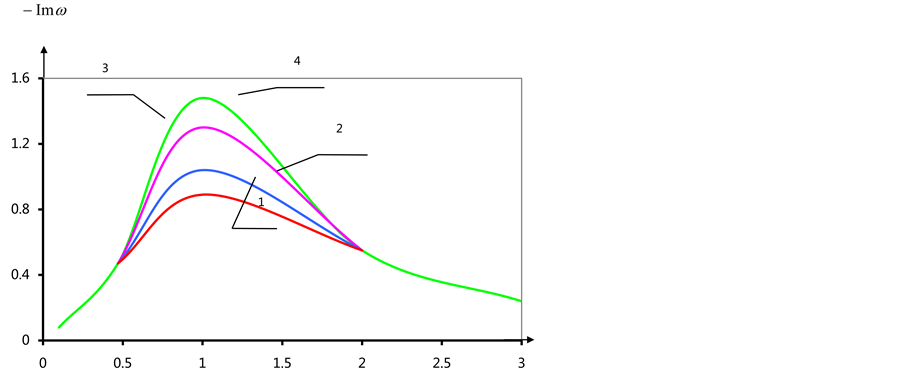
Figure 8. (a) The dependence of the imaginary part of the eigenvalues of α; (b) The dependence of the imaginary part of the eigenvalues of α.
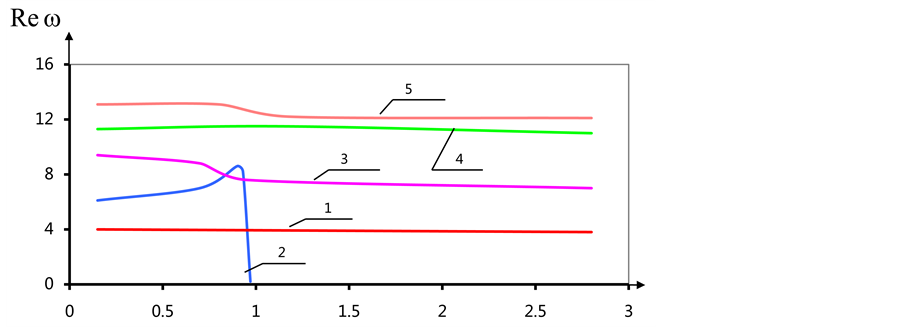

Figure 9. (a) The dependence of the real part of the eigenvalues of α (n = 3); (b) The dependence of the imaginary part of the eigenvalues of α.

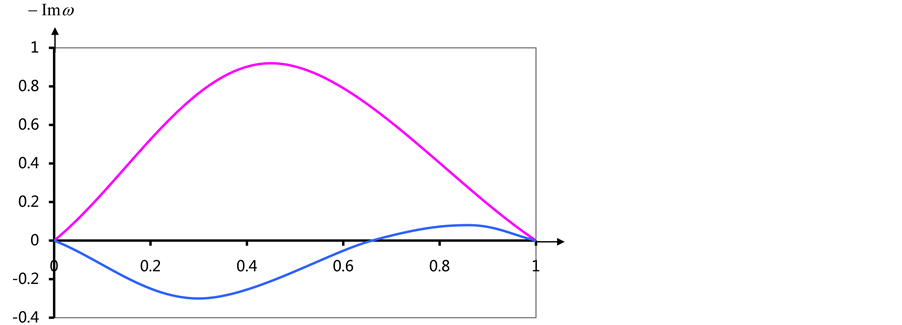
Figure 10. (a) The dependence of the real part of the eigenvalues of α; (b) The dependence of the imaginary part of the eigenvalues of α.
Figure 11. The dependence of the real part of the eigenvalues of α.
Table 3. The values of the maximum oscillation damping depending on the mode number.
ues-lose to a linear form (see Figure 8(a) and
Figure 9(a)). Actual part allocated in both cases
the eigenvalues corresponding to the above defined ranges, reaches certain values
and then decreases to zero. When changing

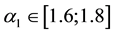
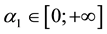
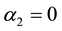


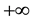
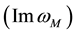

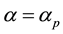
Table 4. The values of the maximum oscillation damping depending on the number of harmonics.
vibrations of the cylinder there is no expression of the growth of the maximum values
with increasing mode and shift it to the axis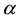
6. Conclusions
For all the cases considered flat fluctuations atn > 1, there is a clear separation of the roots into two types. The differences between these types of roots appear as a character of the dependence of the eigen values of the parameters of the external friction, and in the value of the form. For example, for the first root of the first harmonic-“twist”, the maximum value of the real part of the radial component of the voltage waveform is about three times smaller than the value of the real part component forms tensional stresses.
The imaginary parts of their own forms of valid order of magnitude smaller and do
not have such a pronounced difference. When changing
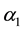

For all cases considered anti plane oscillations n there imaginary branch of the
natural frequencies of the parameter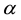
References
- Rashidov, T.R. (1973) Dynamic Theory of Seismic Stability of Complex Systems of Underground Structures. Tashkent, 182 p.
- Rashidov, T.R., Dorman, I.J. and Ishankhodjaev, A.A. (1975) Seismic Stability of Tunnel Construction of Subways. Moscow, 120 p.
- Guz, A.N. and Golovchan, V.T. (1972) Diffraction of Elastic Waves in Multiply Bodies. Kiev, 254 p.
- Kubenko, V.D. (1979) Unsteady Interaction of Structural Elements with the Environment. Kiev, 183 p.
- Safarov, I.I. (1992) Oscillations and Waves in Dissipative Media and Nedorodnyhkonstruktsiyah. Tashkent, 250 with.
- Bazarov, M.B., Safarov, I.I. and Shokin, Y.M. (1996) Numerical Modeling of Vibrations Dissipative Inhomogeneous and Homogeneous Mechanical Systems. Siberian Branch, Russian Academy of Sciences, Novosibirsk, 189 p.
- Safarov, I.I., Chat, Z.I., Rakhmonov, K.K. and Umarov, A.O. (2013) Forced to Steady-State Oscillations of Cylindrical Bodies with an External Boundary Friction. 114-123.
- Neumark, M.A. (1968) Linear Differential Operatory. Moscow, 528, p.
- Safarov, I.I., Teshaev, M.Kh. and Boltaev, Z.I. (2012) Wave Processes in the Mechanical Waveguide. LAP LAMBERT Academic Publishing, Germany, 217 p.