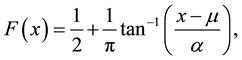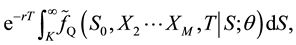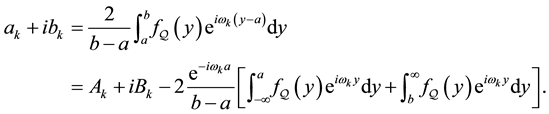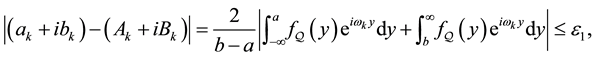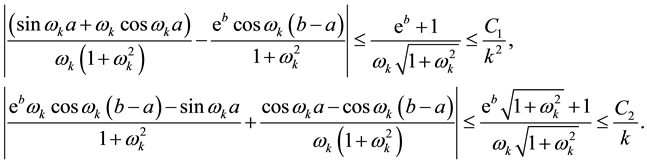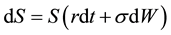Applied Mathematics
Vol.05 No.17(2014), Article ID:50802,21 pages
10.4236/am.2014.517267
On the Efficacy of Fourier Series Approximations for Pricing European Options
A. S. Hurn1, K. A. Lindsay1, A. J. McClelland2
1School of Economics and Finance, Queensland University of Technology, Brisbane, Australia
2Numerix Pty Ltd, Sydney, Australia
Email: s.hurn@qut.edu.au, kenneth.lindsay@qut.edu.au, clelland@numerix.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 July 2014; revised 26 August 2014; accepted 5 September 2014
ABSTRACT
This paper investigates several competing procedures for computing the prices of vanilla European options, such as puts, calls and binaries, in which the underlying model has a characteristic function that is known in semi-closed form. The algorithms investigated here are the half-range Fourier cosine series, the half-range Fourier sine series and the full-range Fourier series. Their performance is assessed in simulation experiments in which an analytical solution is available and also for a simple affine model of stochastic volatility in which there is no closed-form solution. The results suggest that the half-range sine series approximation is the least effective of the three proposed algorithms. It is rather more difficult to distinguish between the performance of the half- range cosine series and the full-range Fourier series. However there are two clear differences. First, when the interval over which the density is approximated is relatively large, the full-range Fourier series is at least as good as the half-range Fourier cosine series, and outperforms the latter in pricing out-of-the-money call options, in particular with maturities of three months or less. Second, the computational time required by the half-range Fourier cosine series is uniformly longer than that required by the full-range Fourier series for an interval of fixed length. Taken together, these two conclusions make a case for pricing options using a full-range range Fourier series as opposed to a half-range Fourier cosine series if a large number of options are to be priced in as short a time as possible.
Keywords:
Fourier Transform, Fourier Series, Characteristic Function, Option Price

1. Introduction
The need to price vanilla European options in a rapid manner arises in numerous activities at financial institutions. Perhaps the most well-known situation in which this need occurs in practice is model calibration, in which exotic options are priced using models with values for the (risk-neutral) parameters chosen in such a way as to ensure that the model reproduces quoted prices for liquid options. For each set of parameters considered in the search space, it is therefore necessary to evaluate the prices of all options in the calibration set using the model, before comparing these with the quoted prices. In a similar vein, there is a growing literature which uses large panels of options data for estimating model parameters ([1] -[5] ) in which the computational complexity is driven by the evaluation of vast numbers of option prices. Consequently, this paper investigates several competing procedures for computing the prices of vanilla European options, such as puts, calls and binaries and assesses their comparative performance on the basis of accuracy and computational speed.
Various strategies have been proposed for calculating the price of option contracts from knowledge of the conditional characteristic function of the underlying model. It is an important fact that a surprisingly large number of models have a semi-closed expression for their conditional characteristic function. For example, the identification of the conditional characteristic function for multivariate affine models with/without jump processes leads to the solution of a family of ordinary differential equations, albeit in the complex plane. In view of the Levy-Khintchine theorem, the identification of the conditional characteristic function for Levy processes is expressed in terms of various integrals with respect to the Levy measure.
The most commonly used techniques for taking advantage of a known conditional characteristic function have at their core the application of the Fast Fourier Transform (FFT). The best documented approaches is due to Carr and Madan [6] who construct an expression for the price of a European call option in terms of an integral over the characteristic function. This integral, which has an oscillatory kernel, is computed by an application of the FFT. Borak, Detlefsen and Hardle [7] apply the FFT strategy and demonstrate its efficacy by comparison with Monte Carlo simulation for a variety of models. Lord, Fang, Bervoets and Oosterlee [8] and Kwok, Leung and Wong [9] demonstrate how Fourier’s convolution theorem in combination with the FFT can be used to price certain exotic options from knowledge of the conditional characteristic function of the price of the underlying asset. A different approach pioneered by Fang and Oosterlee [10] uses the characteristic function to directly approximate the marginal transitional probability density of returns by a Fourier cosine series. Recently Zhang, Grzelak and Oosterlee [11] have demonstrated how this methodology can be extended to the pricing of early-exercise commodity options under the Ornstein-Uhlenbeck process.
Rather than describing in detail the nuances of these various strategies, it is useful to point out what overarching assumptions connect them. Recall that the FFT is simply a clever piece of linear algebra that reduces the arithmetical load in implementing the Discrete Fourier Transform (DFT), namely the pair of equations connecting the coefficients of a finite Fourier series with values of the underlying function and vice versa. Therefore the decision to use the FFT implicitly makes the assumption that the underlying function is periodic over an interval of finite length, in practice determined by the range of frequencies submitted to the characteristic function, and that the function has been approximated over the interval by a finite Fourier series. The values of Fourier coefficients calculated from the characteristic function are in error by the extent to which the Finite Fourier Transform1 differs from the Fourier transform.
Thus techniques using the FFT and those based on the construction of Fourier series share the same common assumptions and deficiencies. However, an important difference between an implementation using the FFT approach and one using the Fourier series approach is that the latter is parsimonious in its use of arithmetic whereas the former typically performs more arithmetic than necessary, albeit in an efficient way. For example, if the FFT is used to determine the value of a probability density function, what is recovered is the value of the function at each node of the interval, whereas all that might be needed is the value of the probability density function over a sub-interval.
The focus of this work is on the algorithm proposed by Fang and Oosterlee [10] who give a convincing demonstration of the efficacy of the Fourier cosine series. This series is more accurately called the half-range2 cosine series because the actual function to be expanded is defined only on half the interval of periodicity (or range), the function being extended to the full range as an even-valued function. Half-range cosine series usually fail to represent derivatives whereas half-range Fourier sine series usually fail to represent function values. While the use of the half-range Fourier cosine series is a solid idea, Fang and Oosterlee [10] provide no motivation or explanation as to why this choice of approximating transitional density should be preferred over the half-range Fourier sine series or the full-range Fourier series for that matter. For example, intuition would suggest that the latter might perform better simply because it uses higher frequencies, which in turn translate to a more rapidly converging Fourier expansion. Indeed this intuition is borne out in calculation, but of course speed is not the only criterion of relevance in assessing the efficacy of a numerical procedure.
An important but subtle difference shared by the half-range Fourier cosine and full-range Fourier series approximations of density, but different from representations of density based on the half-range Fourier sine series, is that the former assign unit probability to the interval of support when in reality probability lies outside this interval, whereas the latter imposes zero probability density at the endpoints of the interval of support in contravention of reality, but on the other hand does not assign unit probability to the interval of support. Is one approach always superior to the other or is it a case of horses for courses? Intuition might suggest the latter. For example, when pricing a call option the most important component of the pricing error comes from the exclusion of contributions from asset price exterior to the finite interval of support. Because the half-range cosine and full-range Fourier series necessarily capture unit density, intuition might suggest that these approximations provide potential compensation for this component of pricing error. On the other hand intuition would suggest that the same approximations, when used to price binary options, might have a tendency to exaggerate the probability of exercise and therefore overprice this option in contrast to the half-range sine series approximation of probability density.
2. Fourier Series and Transform
Suppose that
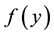 satisfies the Dirichlet conditions on
satisfies the Dirichlet conditions on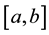 , then there are three common ways in which
, then there are three common ways in which
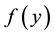 may be represented by a Fourier series. These are the half-range Fourier cosine series, the half-range Fourier sine series and the full-range Fourier series with respective representations
may be represented by a Fourier series. These are the half-range Fourier cosine series, the half-range Fourier sine series and the full-range Fourier series with respective representations
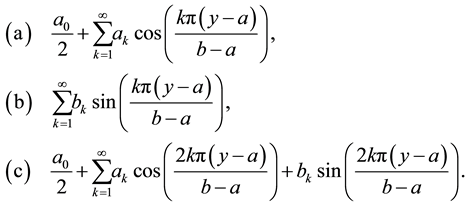 (1)
(1)
The use of the term “half-range” in describing Expressions (a) and (b) simply refers to the fact that the function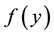 , although defined in
, although defined in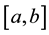 , has for the construction of the Fourier series been extended into the interval
, has for the construction of the Fourier series been extended into the interval
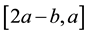 as an even-valued function in the case of the half-range cosine series (so that sine contributions vanish) and as an odd-valued function in the case of the half-range sine series (so that the constant and cosine contributions vanish). Thus both half-range series are conventional Fourier series taken over the interval
as an even-valued function in the case of the half-range cosine series (so that sine contributions vanish) and as an odd-valued function in the case of the half-range sine series (so that the constant and cosine contributions vanish). Thus both half-range series are conventional Fourier series taken over the interval
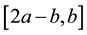 such that the function represented by the half-range Fourier cosine series is usually not differentiable at
such that the function represented by the half-range Fourier cosine series is usually not differentiable at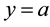 , whereas that represented by the half-range Fourier sine series is usually discontinuous at
, whereas that represented by the half-range Fourier sine series is usually discontinuous at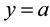 .
.
In the case of the half-range cosine and sine series in Expressions (1a) and (1b) respectively, the coefficients
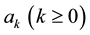 and
and
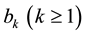 are calculated from the function
are calculated from the function
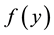 via the formulae
via the formulae
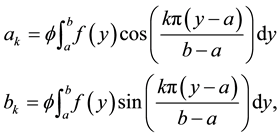 (2)
(2)
in which
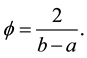
In terms of the exponential function the real coefficients
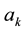 and
and
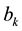

In the case of the full-range Fourier series in Expression (1c) the real coefficients
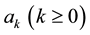
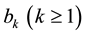
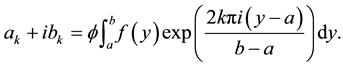
Suppose now that


where


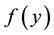

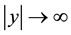

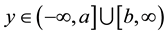
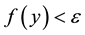




while the coefficients of the full-range Fourier series can be approximated from knowledge of the characteristic function via the formula
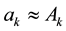


The accuracy of approximations (6) and (7) is investigated in Section 6, where it is demonstrated that the error can be made arbitrarily small by choosing a suitably large interval.
3. Approximating Probability Density Functions
The quality of this practical idea is now explored for three trial probability density functions with known closed-form expressions for their characteristic functions. The first choice is the Gaussian density which may be regarded as representative of distributions with super-exponentially decaying tail density. The second and third choices are the Gamma density and the Cauchy density which are treated as representative examples of distributions with exponentially decaying and algebraically decaying tail densities respectively.
3.1. Gaussian Density
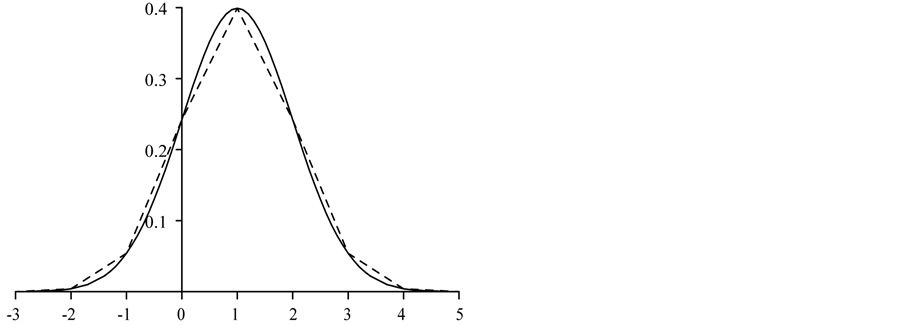
It is well known that the Gaussian density with mean value
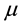
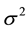

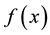
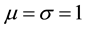
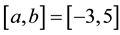
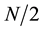

where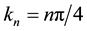
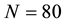
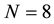
With as few as 4 frequencies it is clear that the approximating density still provides a good representation of the true density; with 40 frequencies the approximating density function is indistinguishable from the true density function, at least in terms of the resolution in Figure 1. It will be seen that this excellent performance is explained by the fact that the cumulative distribution function of the Gaussian probability density function converges to zero super-exponentially as

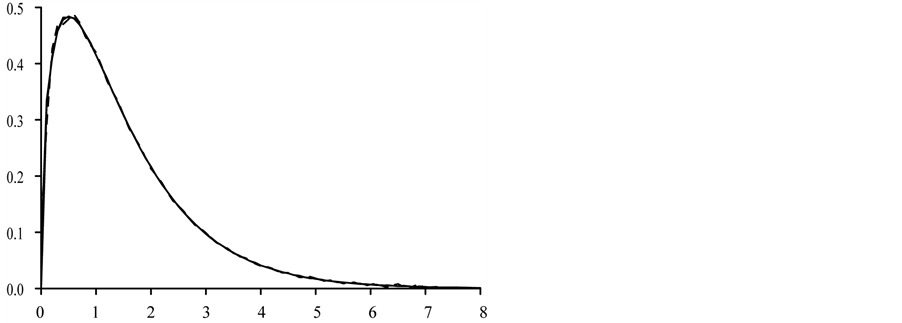
3.2. Gamma Density
The Gamma density with shape parameter

The approximating density is identical to Expression (8) with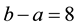
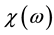
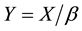

strates the quality of this approximation for
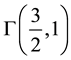
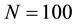
cies (dashed line,
The quality of the approximation is again due to the fact that the cumulative distribution function of the Gamma density converges exponentially to zero as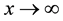
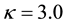
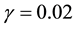

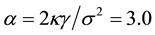
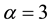
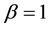
The important observation from both of these experiments is that distributions with exponentially decaying tail density can also be well described by a relatively small range of frequencies.
Figure 1. Comparison of the true Gaussian density and its approximation based on 40 frequencies (solid line, N = 80) and 4 frequencies (dashed line, N = 8).
Figure 2. Comparison of the Gamma density
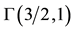
Figure 3. Comparison of the Gamma density

3.3. Cauchy Density
The Cauchy density with median


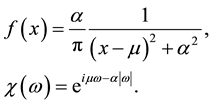
The approximating density is again Expression (8) with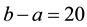


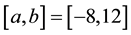
which in this case converges algebraically to zero as
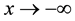

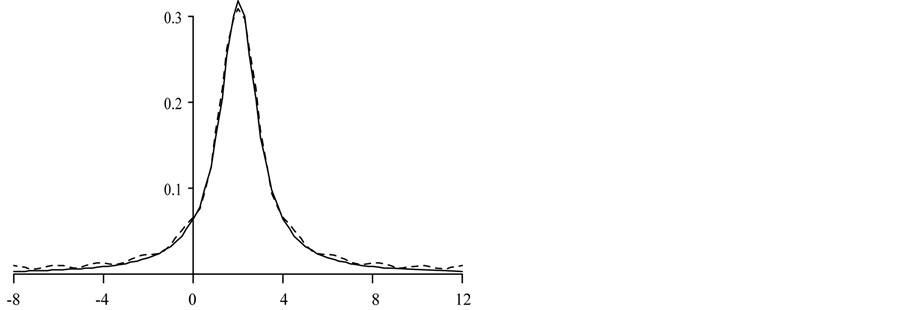
Figure 4. Comparison of the Cauchy density with parameters
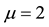

While some erratic behaviour is evident in the tails of the approximating density, nevertheless the quality of the approximation is remarkably good considering the small number of frequencies in use.
In general, the approximate representations of the Gaussian, Gamma and Cauchy probability density functions all share the common fact that

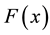
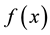

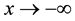

3.4. Comparison of True and Approximating Densities
While the illustrations of Figures 1-4 suggest that the Fourier series approximation of density is effective, it would be useful to quantify just how well density is approximated by the various Fourier methods. Instinctively it would seem that one possible way to achieve this objective is to use the Kullback-Leibler (KL) divergence criterion
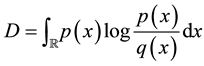
to measure the “distance” or departure of the probability density function




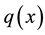
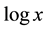


The central idea of each Fourier approximation is to replace the true probability density function by a function of compact support, that is,



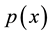





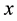
As might be anticipated, the Gaussian distribution is most efficiently approximated by Fourier methods followed by the Gamma distribution and finally the Cauchy distribution. However, it is clear that all of these distributions are well approximated by the half range Fourier cosine and full range Fourier series for sufficiently large intervals of support and an adequate number of frequencies. The results in these tables also reinforce the
Table 1. Values of the KL measure (Dc for the half range Fourier cosine series and Df for the full Fourier series) are given for the Gaussian density with unit mean and unit standard deviation. Values measure the deviation of the true density deviates from the approximating density for intervals of length 6, 8, 10, 12 and 14 standard deviations centred about the mean of the Gaussian distribution using 5, 10, 25, 50, 100 and 200 frequencies.
Table 2. Values of the KL measure (Dc for the half range Fourier cosine series and Df for the full Fourier series) are given for the Gamma density with shape parameter 3 and unit scale factor. Values measure the deviation of the true density deviates from the approximating density for intervals [0, L] of length 6, 8, 10, 12 and 14 scale factors using 5, 10, 25, 50, 100 and 200 frequencies.
Table 3. Values of the KL measure (Dc for the half range Fourier cosine series and Df for the full Fourier series) are given for the Cauchy density with median two and unit scale factor. Values measure the deviation of the true density deviates from the approximating density for intervals of length 14, 20, 26, 32 and 38 scale factors centred about the median of the Cauchy distribution using 5, 10, 25, 50, 100 and 200 frequencies.
idea that the number of frequencies used in the approximation is of secondary importance to the size of the interval of support once sufficient frequencies are in use. This observation accords with intuition in the respect that larger intervals of support capture more of the true density and reduce the distortion in the approximating density, which as has already been commented, will always integrate to one. It would seem that approximations based on 50 frequencies are adequate in all of these examples. The results suggest that using more frequencies provides no meaningful improvement in accuracy. Moreover, for practical purposes there is little to choose between approximation based on the half range Fourier cosine and the full range Fourier series, although the latter has a slight edge for sufficiently large intervals and an adequate number of frequencies.
4. Pricing European Options
The successfully pricing of European option contracts for affine models of stochastic volatility requires knowledge of the marginal density of the asset price under the risk-neutral measure. The difficulty, however, is that no closed-form expression for this density is available for even the simplest of the multivariate affine models used in finance, although it is well known that such models have characteristic function,
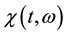
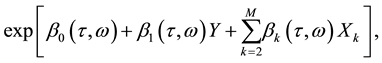
where






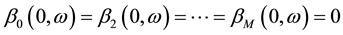
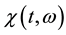
4.1. European Call Option
In the case of a European call option with strike price


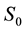
where

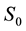




where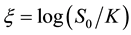

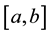

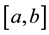
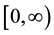

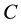

where
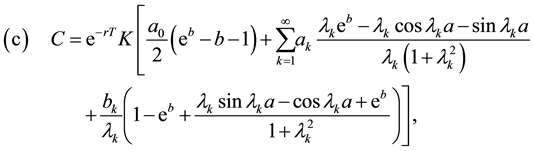
where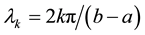
4.2. Binary Option
The price of a binary (call) option with strike price
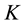
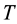
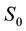
where
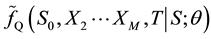
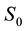

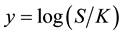
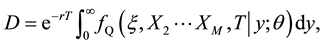
where
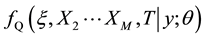

where

where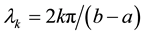
5. The Heston Model of Stochastic Volatility
Heston’s [12] risk-neutral model of stochastic volatility has expression
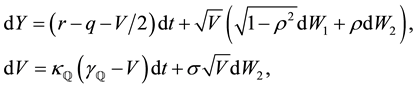
where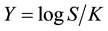
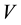
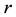
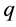
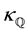


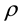
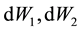
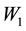

Suppose that
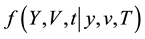
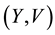
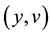
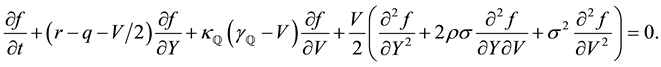
Let
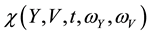


By taking the Fourier transform of Equation (20) with respect to the backward variables, the characteristic function
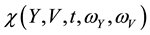
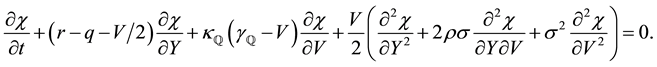
with terminal condition
Thereafter, it is straightforward to show that the anzatz
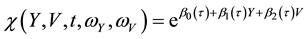
with
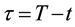




The characteristic function of the marginal density of the terminal value of
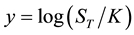
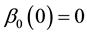
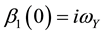


On a practical note, the fact that the characteristic function of
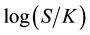





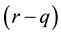

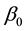
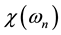
6. Error Analysis
Let
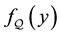
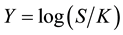




6.1. Truncation Error
Truncation error occurs when the semi-infinite interval in Expression (13) or (16) is replaced by an integral over a finite interval, say

resulting in an error due to the loss of the contribution to the price from values of
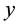
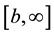
which in turn simplifies to give
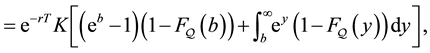
where

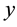




The inference from this observation is that approximations of

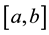
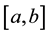
6.2. Approximation Errors
Suppose now that the transitional density

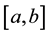
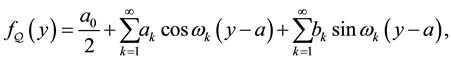
where the choice of frequencies

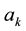
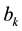
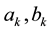

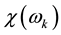

Table 4. Percentage errors recorded by the half-range cosine series, half-range sine series and full-range Fourier series of pricing a European call option and a binary option with strike K = 1200 and maturities one month (panel (a)), three months (panel (b)) and six months (panel (c)). The factor refers to the multiple of
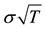
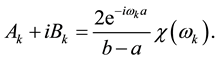
Consequently a misspecification error arises in the Fourier coefficients. Second, the truncation of the Fourier series (27) to a finite number of terms, say
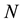

in which


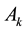

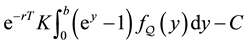
which has explicit expression

The misspecification error in the coefficients
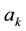
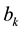

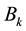
Standard properties of integral Calculus guarantee that
where
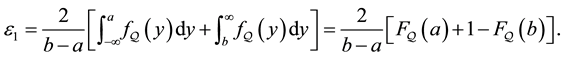
It therefore follows directly that
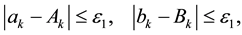
for all values of

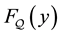
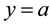

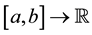



In conclusion, the total error in pricing a call option, namely
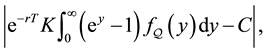
is formed by connecting together Equation (26) for the error arising in the truncation of the density
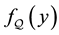


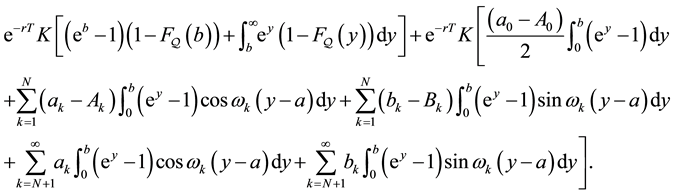
Each integral is replaced by its value and the triangle inequality is used to deduce that

The contributions to the error from the first, second, third and fourth terms on the right hand side of inequality (36) are dominated by the behaviour of


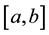
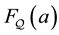
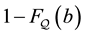



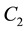
The well known result that if
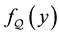
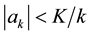
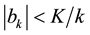
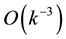
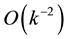
In conclusion, the error in pricing a call option can be made arbitrarily small by restricting the marginal probability density to a finite interval

7. Performance under Simulation
A series of simulation experiments was undertaken in order to examine the efficacy of the half-range Fourier cosine series, half-range Fourier sine series and full-range Fourier series in respect of how accurately these approximations price European call options and binary options. The first experiment prices options in a Black- Scholes world so that a closed-form solution may be used to assess the pricing error, whereas the second experiment prices the same options using Heston’s model of stochastic volatility.
7.1. Black-Scholes Pricing
Assume that the asset price,

in which



Three major experiments are performed. In each of these experiments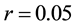


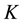



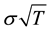
Two very clear general conclusions emerge from these results.
1) For options that are deep in-the-money (Table 6) in which
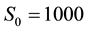
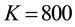
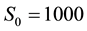
2) For options that are deep out-of-the-money (Table 4) in which
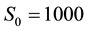

a) The half-range Fourier sine series does not perform as well as the other two approximations and its use is therefore not recommended. This finding accords well with our previous intuition based on a consideration of the contribution to the price of a call option lost as a result of truncating marginal density.
b) The half-range Fourier cosine series and the full-range Fourier series both perform relatively well. When the size of the interval of approximation is a relatively small multiple of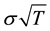
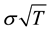

On the basis of this analysis and on accuracy grounds, it is hard to ignore the claim that the full-range Fourier series is the algorithm of choice when using Fourier methods to price options. Moreover, the full-range Fourier series converges faster than either the half-range sine or cosine series and is therefore likely to price options more rapidly. These themes are explored in more detail in the pricing of call options under Heston’s model of stochastic volatility.
7.2. Heston’s Model
A total of approximately 40,000 options over ten years were generated by simulation of Heston’s model. Sixteen
Table 5. Percentage errors recorded by the half-range cosine series, half-range sine series and full-range Fourier series of pricing a European call option and a binary option with strike K = 1000 and maturities one month (panel (a)), three months (panel (b)) and six months (panel (c)). The factor refers to the multiple of

options were generated each day spread over 4 maturities ranging from 92 to 5 days and 4 strikes two of which are initialised at 20% out of and into the money and two of which are initialised at 7% out of and into the money. The half-range Fourier cosine series and the full-range Fourier series are then used to price call options and binary options with these strikes. In this instance no exact solutions are available, and so the accuracy of each method in respect of each type of option is gauged by comparison against values calculated using a large interval. The left hand and middle columns of Table 7 show respectively the
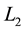
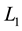
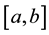
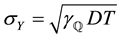



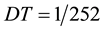
A clear finding from Table 7 is that the half-range Fourier cosine series performs well in respect of the
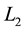

Table 6. Percentage errors recorded by the half-range cosine series, half-range sine series and full-range Fourier series of pricing a European call option and a binary option with strike K = 800 and maturities one month (panel (a)), three months (panel (b)) and six months (panel (c)). The factor refers to the multiple of
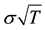
performance of the full-range Fourier series is poor with regard to both measures for shorter intervals. However, the quality of approximation provided by the half-range cosine series is erratic as the size of the Fourier window increases whereas that provided by the full-range Fourier series improves systematically to the extent that its performance surpasses that of the half-range Fourier cosine series for intervals of length 24 standard deviations or more. Furthermore, this level of accuracy is achieved by the full-range Fourier series in approximately 25% quicker than that required by the half-range Fourier cosine series.
Fang and Oosterlee [10] suggest choosing intervals of length 20 standard deviations. In this problem, it is evident that the half-range Fourier cosine series still enjoys an advantage over the full-range Fourier series for intervals of this length. The suggestion of this investigation is that 20 standard deviations should be regarded as a minimum length of interval. Table 8 shows the


Table 7. The L2 and L1 relative pricing errors calculated from the half-range Fourier cosine series and the full-range Fourier series for out-of-the-money call options based on Heston’s model. The timings refer to the times (seconds) needed to price 12 daily call options over 10 years with maturities ranging from 5 to 92 days. The factor refers to the multiple of σY used to establish the interval over which the numerical approximation is computed.
Table 8. The L2 and L1 relative pricing errors calculated from the half-range cosine series and the full-range Fourier series for in-the-money call options based on Heston’s model. The timings refer to the times (seconds) needed to price 12 daily call options over 10 years with maturities ranging from 5 to 92 days. The factor refers to the multiple of σY used to establish the interval over which the numerical approximation is computed.
The results reported in Table 8 exhibit a similar pattern of behaviour to those reported in Table 7, namely that for intervals of short length the half-range Fourier cosine series outperforms the full-range Fourier series with respect to both the
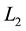

The results presented in Table 9 and Table 10 demonstrate that both the half-range Fourier cosine series and the full-range Fourier series both generate good estimates of the price of binary options with the former performing better than the latter for intervals of short length, but with this advantage disappearing when the length of the interval is increased.
Table 9. The L2 and L1 relative pricing errors calculated from the half-range cosine series and the full-range Fourier series for out-of-the-money binary options based on Heston’s model. The timings refer to the times (seconds) needed to price 12 daily call options over 10 years with maturities ranging from 5 to 92 days. The factor refers to the multiple of σY used to establish the interval over which the numerical approximation is computed.
Table 10. The L2 and L1 relative pricing errors calculated from the half-range cosine series and the full-range Fourier series for in-the-money binary options based on Heston’s model. The timings refer to the times (seconds) needed to price 12 daily call options over 10 years with maturities ranging from 5 to 92 days. The factor refers to the multiple of σY used to establish the interval over which the numerical approximation is computed.
The results reported in Tables 7-10 are characterised by two common denominators. First, the computational time required by the half-range Fourier cosine series is uniformly longer than that required by the full-range Fourier series for an interval of fixed length. The simple explanation for this observation is that the full-range Fourier series uses larger frequencies for a given length of interval, and therefore the full-range Fourier series converges more rapidly. Second, the pricing of call options and binary options using the half-range Fourier cosine series representation of transitional density is noticeably better than the corresponding pricing using the full-range Fourier series for short intervals
For an interval of given length, the frequencies present in the half-range Fourier cosine expansion are smaller that the frequencies present in the full-range Fourier series, and therefore when the length of the interval
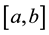

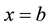


8. Conclusion
One clear conclusion from these calculations is that the half-range Fourier cosine series and the full-range Fourier series perform uniformly better than the half-range Fourier sine series. The half-range Fourier cosine series and the full-range Fourier series both perform with credit. When the length of the interval

References
- Johannes, M.S., Polson, N.G. and Stroud, J.R. (2009) Optimal Filtering of Jump Diffusions: Extracting Latent States from Asset Prices. Review of Financial Studies, 22, 2759-2799. http://dx.doi.org/10.1093/rfs/hhn110
- Broadie, M., Chernov, M. and Johannes, M. (2007) Model Specification and Risk Premia: Evidence from Futures Options. Journal of Finance, 62, 1453-1490. http://dx.doi.org/10.1111/j.1540-6261.2007.01241.x
- Christoffersen, P., Jacobs, K. and Mimouni, K. (2010) Volatility Dynamics for the S&P500: Evidence from Realized Volatility, Daily Returns and Option Prices. Review of Financial Studies, 23, 3141-3189. http://dx.doi.org/10.1093/rfs/hhq032
- Hurn, A.S., Lindsay, K.A. and McClelland, A.J. (2012) Estimating the Parameters of Stochastic Volatility Models Using Option Price Data. Unpublished Working Paper, NCER.
- Andersen, T.G., Fusari, N. and Todorov, V. (2012) Parametric Inference and Dynamic State Recovery from Option Pa- nels. NBER Working Paper Series.
- Carr, P.P. and Madan, D.B. (1999) Option Evaluation Using the Fast Fourier Transform. Journal of Computational Fi- nance, 2, 61-73.
- Borak, S., Detlefsen, K. and Hardle, W. (2005) FFT Based Option Pricing. SFB Discussion Paper 649.
- Lord, R., Fang, F. Bervoets, F. and Oosterlee, C.W. (2007) A Fast and Accurate FFT-Based Methodology for Pricing Early-Exercise Options under Levy Processes. SIAM Journal of Scientific Computing, 20, 1678-1705.
- Kwok, Y.K., Leung, K.S. and Wong, H.Y. (2012) Efficient Options Pricing Using the Fast Fourier Transform. In: Duan, J.C., Ed., Handbook of Computational Finance, Springer, Berlin, 579-604. http://dx.doi.org/10.1007/978-3-642-17254-0_21
- Fang, F. and Oosterlee, C.W. (2008) A Novel Pricing Method for European Options Based on Fourier-Cosine Series Expansions. SIAM Journal on Scientific Computing, 31, 826-848. http://dx.doi.org/10.1137/080718061
- Zhang, B., Grzelak, L.A. and Oosterlee, C.W. (2012) Efficient Pricing of Commodity Options with Earlyexercise under the Ornstein-Uhlenbeck Process. Applied Numerical Mathematics, 62, 91-111. http://dx.doi.org/10.1016/j.apnum.2011.10.005
- Heston, S.L. (1993) A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Cu- rrency Options. Review of Financial Studies, 6, 327-343.
- Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637-654. http://dx.doi.org/10.1086/260062
NOTES
1The Finite Fourier Transform is the integral expression defining the coefficients of a Fourier series.
2Historically, half-range Fourier series have largely arisen as analytical tools for handling various types of boundary conditions when solving partial differential equations using integral transforms.
3Sharper results can be obtained if