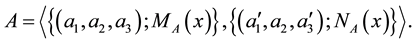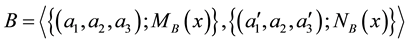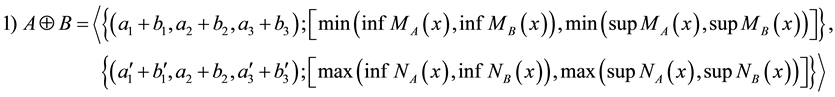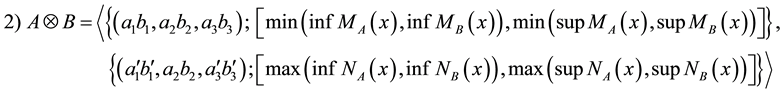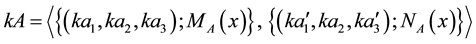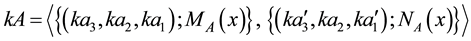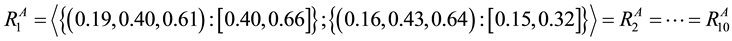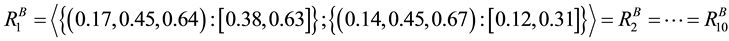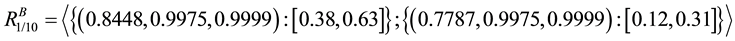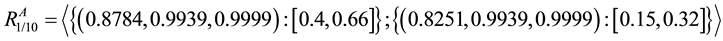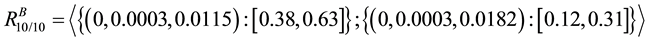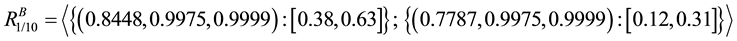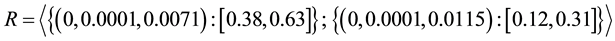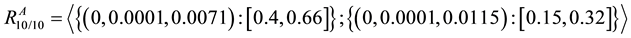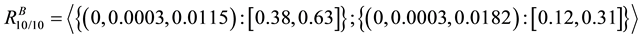Applied Mathematics
Vol.05 No.13(2014), Article ID:47879,7 pages
10.4236/am.2014.513193
Reliability Analysis of a Powerloom Plant Using Interval Valued Intuitionistic Fuzzy Sets
Sanjay Kumar Tyagi
General Requirements Department, Ibri College of Applied Sciences, Ministry of Higher Education, Ibri, Sultanate of Oman
Email: sanjay_tyagi94@rediffmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 April 2014; revised 18 May 2014; accepted 2 June 2014
ABSTRACT
In this paper, we investigate the reliability analysis of a powerloom plant by using interval valued intuitionistic fuzzy sets (IVIFS). Herein, we modeled a powerloom plant as a gracefully degradable system having two units A(n) and B(m) connected in series. The reliability of n components of unit A and m components of unit B is assumed to be an IVIFS defined over the universe of discourse [0, 1]. Thus, the reliability of the system obtained is an IVIFS that covers the inherited uncertainty in data collection and reliability evaluation of a powerloom plant.
Keywords:
Reliability, Interval Valued Intuitionistic Fuzzy Sets, Powerloom Plant, Parallel Redundancy, Graceful Degradation

1. Introduction
It is well established that the classical set theoretic approach in reliability analysis fails to address the uncertainty up to a desired level. For systems with built-in multi-component parallel redundancy, graceful degradation [1] describes a smooth change to a lower performance level of the system. For such systems, it is therefore unrealistic to assign a number to the reliability of the different components of unit A and B. In 1965, Zadeh [2] introduced the concept of fuzzy sets. Since the inception of fuzzy set, it is widely used in reliability evaluation by many authors. Using it, Cai et al. [3] introduced the fuzzy state assumption and possibility assumption to give Profust and Possbist reliability respectively. Singer [4] presented fuzzy state theoretic approach to fault tree analysis. Chen [5] used arithmetic of fuzzy numbers to evaluate system reliability. Bowles and Palaez [6] obtained the Profust reliability estimates for a single unit gracefully degradable system. Fuzzy set theoretic approach for failure rate estimation developed by Pandey and Tyagi [7] provides comprehensive results in reliability estimation of a gracefully degradable system.
Since the introduction of fuzzy set by Zadeh [2] in 1965, the concept of fuzzy sets has been extended by various researchers such as L-fuzzy sets [8] , fuzzy multisets [9] , etc. But in the words of Gehrke et al. [10] , many people believe that assigning an exact number to an expert’s opinion is too restrictive, and that the assignment of an interval values is more realistic. Taking view of that apparently Sambuc [11] introduced interval valued fuzzy sets (IVFS). He called them 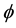 -flou functions. Later, intuitionistic fuzzy set (IFS) was introduced by Atanassov [12] in 1983. IFS provides the opportunity to model hesitation and uncertainty by introducing a non-membership function in addition to membership function. Tyagi and Akram [13] used IFS to evaluate human reliability of a man-machine system. Wu and Mendel [14] made linguistic summarization using IF-THEN rules and interval type-2 fuzzy sets. Beliakov et al. [15] analyzed the median aggregation operator of IFS and IVFS. In 1989, Atanassov and Gargov [16] introduced the concept of IVIFS along with several of their properties. Unlike IFS, IVIFS maps the universe of discourse E to the set of intervals over [0, 1].
-flou functions. Later, intuitionistic fuzzy set (IFS) was introduced by Atanassov [12] in 1983. IFS provides the opportunity to model hesitation and uncertainty by introducing a non-membership function in addition to membership function. Tyagi and Akram [13] used IFS to evaluate human reliability of a man-machine system. Wu and Mendel [14] made linguistic summarization using IF-THEN rules and interval type-2 fuzzy sets. Beliakov et al. [15] analyzed the median aggregation operator of IFS and IVFS. In 1989, Atanassov and Gargov [16] introduced the concept of IVIFS along with several of their properties. Unlike IFS, IVIFS maps the universe of discourse E to the set of intervals over [0, 1].
In our work, we use IVIFS to investigate the reliability evaluation of a powerloom plant. A powerloom plant is a small scale industrial setup that weaves threads of different varieties of colours to produce a long piece of cloth of standard size [17] . In the present model, let A(n) and B(m) be two units having n and m 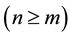 components respectively in parallel redundancy. Units A(n) carries n threads of different colours through its n-identical parallel components, and after weaving threads of some specified colour combination together provides m threads to unit B(m). Unit B(m) receives these m threads through its m-identical parallel components and weaves them together to produce a long piece of cloth of some standard size. Failure of any component of either unit would result in missing a thread of that unit and deteriorate the quality of that product. Without any loss of generality, we can assume that at the most one component of these units may fail at any point of time. This shows that both the units of the system are gracefully degradable. Further, we may assume that owing to
components respectively in parallel redundancy. Units A(n) carries n threads of different colours through its n-identical parallel components, and after weaving threads of some specified colour combination together provides m threads to unit B(m). Unit B(m) receives these m threads through its m-identical parallel components and weaves them together to produce a long piece of cloth of some standard size. Failure of any component of either unit would result in missing a thread of that unit and deteriorate the quality of that product. Without any loss of generality, we can assume that at the most one component of these units may fail at any point of time. This shows that both the units of the system are gracefully degradable. Further, we may assume that owing to 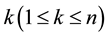 and
and  missing threads in unit A(n) and B(m) respectively, the quality of the product deteriorates beyond the acceptable limits. Therefore, system will be considered failed in view of reliability estimation, if k components of unit A(n) and l components of unit B(m) fail. Choice of k and l depends upon the tolerable limit to be prescribed by quality control.
missing threads in unit A(n) and B(m) respectively, the quality of the product deteriorates beyond the acceptable limits. Therefore, system will be considered failed in view of reliability estimation, if k components of unit A(n) and l components of unit B(m) fail. Choice of k and l depends upon the tolerable limit to be prescribed by quality control.
2. Preliminaries
2.1. Interval Valued Fuzzy Sets
An IVFS A over a basic set E is specified by a function 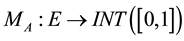 , where
, where  is the set of all intervals within
is the set of all intervals within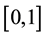 , i.e. for all
, i.e. for all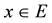 ,
,  is an interval over
is an interval over .
.
2.2. Intuitionistic Fuzzy Sets
An IFS 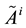 [12] on X is given by
[12] on X is given by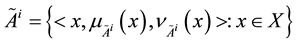 , where
, where 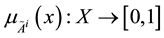 and
and 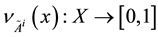 such that
such that 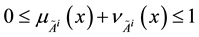 for all
for all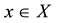 .
.
The value 
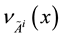
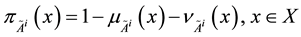

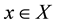
When the universe of discourse X is discrete, an IFS 
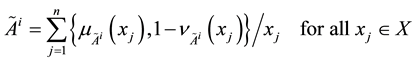
An IFS 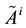

Figure 1. Intuitionistic fuzzy set explanation of a real number.
2.3. Interval Valued Intuitionistic Fuzzy Sets
An IVIFS [16] [18] is an extension of both, the IFS and IVFS. An IVIFS A over a universal set E is defined as an object of the form:
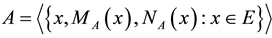
where 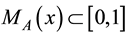
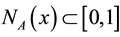
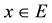
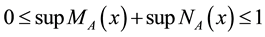
This definition of IVIFS is analogous to the definition of IFS, where 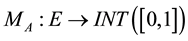
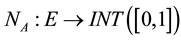
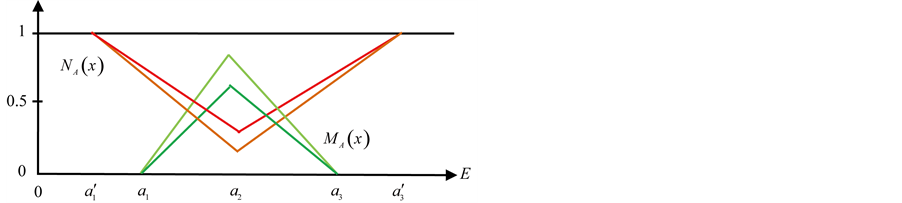
2.4. Triangular Interval-Valued Intuitionistic Fuzzy Sets
A triangular interval valued intuitionistic fuzzy sets (TIVIFS) A over the universe E shown in Figure 2 is defined as:
2.5. Arithmetic Operations on TIVIFS
Here, we introduce some basic arithmetic operations on TIVIFS. For this, let
and
are two TIVIFS defined over a universal set E as shown in Figure 2, then following arithmetic operations between A and B can be defined [18] .
3) a) If k > 0, then,
b) If k < 0, then,
3. Reliability Analysis of a Series and Parallel Network
3.1. Series Network
Let, 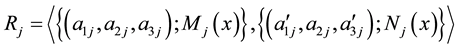
Figure 2. Membership and non-membership function of TIVIFS.
Figure 3. Series network.
series network would be given as:
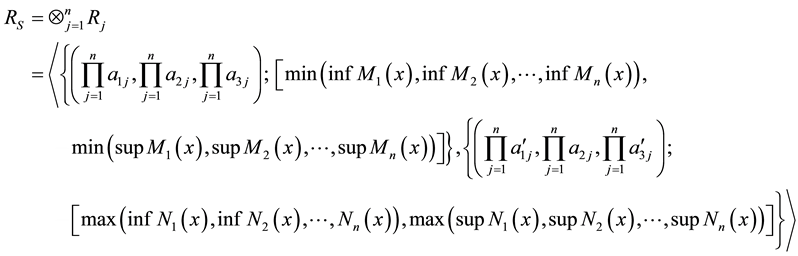
3.2. Parallel Network
Let, 
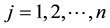
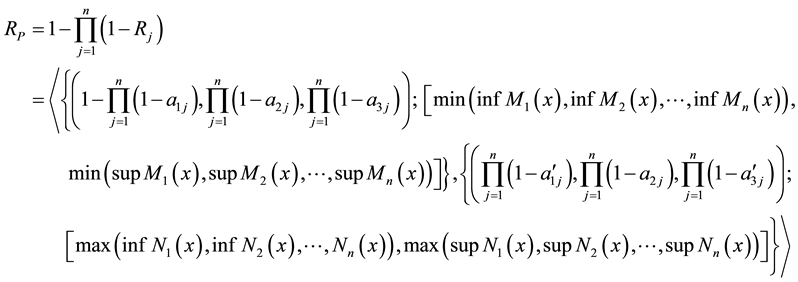
4. Reliability Analysis of a Powerloom Plant
As mentioned earlier, failure of any component of unit A(n) or B(m) results in missing a thread in either unit and causes the deterioration in the quality of the product. Herein, we considered that both the units in powerloom are gracefully degradable. Further, we may assume that if, 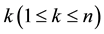
Now, let, 
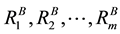
Figure 4. Parallel network.
Also, let 
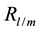
On substituting 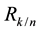
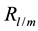
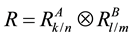
The choice for the value of k and l components depends upon the tolerable limit prescribed by the quality control department. For numerical estimation of reliability of powerloom plant, we consider that both the units A(n) and B(m) have 10 components each, i.e. n = m = 10.
Since all 10 components of unit A(n) are identical, it may be assumed that they have equal probability of success (reliability) i.e.
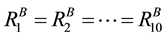
We consider the following cases for different values of k and l.
Case I: k = 1, l = 1 represents the system in which at least one component of both the units is required to be working for the smooth functioning of the powerloom plant. In other word, we can say that all components of unit A as well as of unit B are connected in parallel as shown in Figure 5.
Using TIVIFS assigned to the reliability of each component and (2), we evaluate the reliability 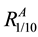
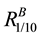
On substituting the values of 
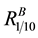
Case II: k = 1 and l = 10 represents the system, where all components of unit A are connected in parallel and that of unit B are connected in series as shown in Figure 6.
We substitute TIVIFS assigned to the reliability of each component, in (1) and (2) to obtain the reliability 

Further, we substitute the values of 
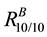
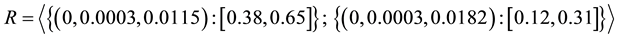
Figure 5. Powerloom plant for k = 1 and l = 1.
Figure 6. Powerloom plant for k = 1 and l = 10.
Case III: k = 10 and l = 1 represents the system in which all components of unit A should be working to keep unit A functioning i.e. all components of unit A are connected in series. In a similar manner, the unit B will be functioning if at least one component of unit B is working i.e. all components of unit B are connected in parallel as shown in Figure 7.
On substituting the values of 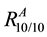
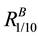
Case IV: k = 10 and l = 10 represents the system in which all components of each unit should be working i.e. all components of both the units are connected in series as shown below in Figure 8.
We substitute TIVIFS assigned to the reliability of each component in (1) to obtain the reliability 
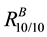
Further, we substitute the values of 
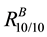
5. Conclusion
In the present paper, we used IVIFS for reliability estimation of a powerloom plant. The important reason for using IVIFS is that in case of fuzzy or intuitionistic fuzzy sets, one needs a number to assign to each element of universal set. However, in some case, we may only be able to find the lower as well as upper bound of membership/non-membership grades. Herein, a powerloom plant is modeled as a two unit system connected in series and the reliability of each component of unit A(n) and B(m) is assumed to be IVIFS. Unit A(n) and B(m) are consisting of 10 components each. Further, it is evident that the failure of each component affects the failure of the powerloom plant. Therefore, the minimum number of components k and l required for unit A and B depends upon the tolerable limit prescribed by quality control. Using different values of k and l, we considered four cases
Figure 7. Powerloom plant for k = 10 and l = 1.
Figure 8. Powerloom plant for k = 10 and l = 10.
for different values of k and l and obtained the reliability of powerloom. The reliability of powerloom plant results as an IVIFS in each case. Obviously, IVIFS are most generalized form of fuzzy sets. Thus, the new approach using IVIFS provides comprehensive results and rules out under/over estimation of reliability of the powerloom plant.
Acknowledgements
The author would like to extend his heartfelt gratitude to the editor and anonymous reviewers for their critical evaluation and constructive suggestions.
References
- Cai, K.Y. (1996) Introduction to Fuzzy Reliability. Kluwer Academic Publishers, Boston. http://dx.doi.org/10.1007/978-1-4613-1403-5
- Zadeh, L.A. (1965) Fuzzy Sets. Information Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- Cai, K.Y. and Wen, C.Y. (1990) Street Lighting Lamp Replacement: A Fuzzy Viewpoint. Fuzzy Sets and Systems, 37, 161-172. http://dx.doi.org/10.1016/0165-0114(90)90039-9
- Singer, D. (1990) A fuzzy set approach to fault tree and reliability analysis. Fuzzy Sets and Systems, 34, 145-155. http://dx.doi.org/10.1016/0165-0114(90)90154-X
- Chen, S.M. (1994) Fuzzy System Reliability Analysis Using Fuzzy Number Arithmetic Operations. Fuzzy Set and Systems, 64, 31-38. http://dx.doi.org/10.1016/0165-0114(94)90004-3
- Bowles, J.B. and Palaez, C.E. (1995) Application of Fuzzy Logic to Reliability Engineering. Proceedings of the IEEE, 83, 435-449. http://dx.doi.org/10.1109/5.364489
- Pandey, D. and Tyagi, S.K. (2007) Profust Reliability of a Gracefully Degradable System. Fuzzy Sets and Systems, 158, 794-803. http://dx.doi.org/10.1016/j.fss.2006.10.022
- Goguen, J.A. (1967) L-Fuzzy Sets. Journal of Mathematical Analysis and Applications, 18, 145-174. http://dx.doi.org/10.1016/0022-247X(67)90189-8
- Ramer, A. and Wang, C. (1996) Fuzzy Multisets. Proceedings of 1996 Asian Fuzzy System Symposium, Taiwan, 11-14 December 1996, 429-434.
- Gehrke, M., Walker, C. and Walker, E. (1996) Some Comments on Interval Valued Fuzzy Sets. International Journal of Intelligent Systems, 11, 751-759. http://dx.doi.org/10.1002/(SICI)1098-111X(199610)11:10<751::AID-INT3>3.3.CO;2-N
- Sambuc, R. (1975) Fonctions φ-floues: Application a l'aide au diagnostic en pathologie thyroidienne. Ph.D. Thesis, University of Marseille, France.
- Atanassov, K.T. (1986) Intuitionistic Fuzzy Sets. Fuzzy Sets and Systems, 20, 87-96. http://dx.doi.org/10.1016/S0165-0114(86)80034-3
- Tyagi, S.K. and Akram, M. (2013) Human Reliability Evaluation for Offshore Platform Musters Using Intuitionistic Fuzzy Sets. IEEE Transactions on Fuzzy Systems, 21, 1115-1122. http://dx.doi.org/10.1109/TFUZZ.2013.2243734
- Wu, D. and Mendel, J.M. (2011) Linguistic Summarization Using IF-THEN Rules and Interval Type-2 Fuzzy Sets. IEEE Transactions on Fuzzy Systems, 19, 136-151. http://dx.doi.org/10.1109/TFUZZ.2010.2088128
- Beliakov, G., Bustince, H., James, S., Calvo, T. and Fernandez, J. (2012) Aggregation for Atanassov’s Intuitionistic and Interval Valued Fuzzy Sets: The Median Operator. IEEE Transactions on Fuzzy Systems, 20, 487-498. http://dx.doi.org/10.1109/TFUZZ.2011.2177271
- Atanassov, K. and Gargov, G. (1989) Interval-Valued Fuzzy Set. Fuzzy Sets and Systems, 31, 343-349. http://dx.doi.org/10.1016/0165-0114(89)90205-4
- Pandey, D., Jacob, M. and Yadav, J. (1996) Reliability Analysis of a Powerloom Plant with Cold Standby for Its Strategic Unit. Microelectronics Reliability, 36, 115-119. http://dx.doi.org/10.1016/0026-2714(95)00013-R
- Atanassov, K.T. (1999) Intuitionistic Fuzzy Sets: Theory and Applications. Springer Verlag, Berlin.