Applied Mathematics
Vol.06 No.01(2015), Article ID:53339,9 pages
10.4236/am.2015.61016
Travelling Wave Solutions of Kaup-Kupershmidt Equation Which Describes Pseudo Spherical Surfaces
G. M. Gharib
Mathematics Department, College of Science and Information Technology, Zarqa University, Zarqa, Jordan
Email: Gharibmusa@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 December 2014; accepted 16 December 2014; published 19 January 2015
ABSTRACT
In this paper I introduce the geometric notion of a differential system describing surfaces of a constant negative curvature and describe a family of pseudo-spherical surface for Kaup-Ku- pershmidt Equation with constant Gaussian curvature −1. I obtained new soliton solutions for Kaup-Kupershmidt Equation by using the modified sine-cosine method.
Keywords:
Soliton Solutions, Pseudo Spherical Surfaces, Nonlinear Evolution Equations

1. Introduction
Many partial differential equations which continue to be investigated due to their role in mathematics and physics exhibit interrelationships with the geometry of surfaces, or submanifolds, immersed in a three-dimensional space [1] . In particular, it has been known for a while that there is a relationship between surfaces of a constant negative Gaussian curvature in Euclidean three-space, the Sine-Gordon Equation and Bäcklund transformations which are relevant to the given equation [2] . Moreover, the original Bäcklund transformation for the Sine-Gor- don Equation is also a simple geometric construction for pseudospherical surfaces [3] -[5] . It is well known that nonlinear complex physical phenomena are related to nonlinear partial differential equations (NLPDEs) which are involved in many fields from physics to biology, chemistry, mechanics, etc.
As mathematical models of the phenomena, the investigation of exact solutions to the NLPDEs reveals to be very important for the understanding of these physical problems. Many mathematicians and physicists have well understood this importance when they decided to pay special attention to the development of sophisticated methods for constructing exact solutions to the NLPDEs. Thus, a number of powerful methods have been presented.
We can cite the inverse scattering transform [6] , the Bäcklund and Darboux transform [7] - [10] , Hirota’s bilinear method [11] , the homogeneous balance method [12] , Jacobi elliptic function method [13] , the tanh method and extended tanh-function method [14] - [20] , F-expansion method [21] - [23] and so on. The notion of conservation laws is important in the study of nonlinear evolution equations (NLEEs) appearing in mathematical physics [24] .
Consider Kaup-Kupershmidt Equation,
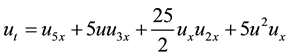 (1)
(1)
where 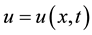 is a function of two independent variables
is a function of two independent variables  and
and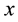 .
.
2. Kaup-Kupershmidt Equation Which Describes Pseudo Spherical Surfaces
I recall the definition [25] -[28] of a differential equation (DE) that describes a pss. Let 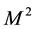 be a two dimensional differentiable manifold with coordinates
be a two dimensional differentiable manifold with coordinates . A DE for a real function
. A DE for a real function 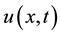 describes a pss if it is a necessary and sufficient condition for the existence of differentiable functions
describes a pss if it is a necessary and sufficient condition for the existence of differentiable functions
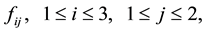 (2)
(2)
depending on u and its derivatives such that the one-forms
 (3)
(3)
satisfy the structure equations of a pss, i.e.,
 (4)
(4)
I obtain that the Kaup-Kupershmidt Equation (1) describes pseudospherical surfaces, with associated one forms 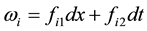
 given by
given by
 (5)
(5)
As a consequence, each solution of the DE provides a local metric on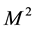 , whose Gaussian curvature is constant, equal to −1. Moreover, the above definition is equivalent to saying that DE for
, whose Gaussian curvature is constant, equal to −1. Moreover, the above definition is equivalent to saying that DE for 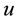 is the integrability condition for the problem [19] [29] :
is the integrability condition for the problem [19] [29] :
 (6)
(6)
where 




3. Exact Solution for Kaup-Kupershmidt Equation
With the rapid development of science and technology, the study kernel of modern science is changed from linear to nonlinear step by step. Many nonlinear science problems can simply and exactly be described by using the mathematical model of nonlinear equation. Up to now, many important physical nonlinear evolution equations are found, such as Sine-Gordon Equation, KdV Equations, Schrodinger Equation all possess solitary wave solutions. There exist many methods to seek for the solitary wave solutions, such as inverse scattering method, Hopf-Cole transformation, Miura transformations, Darboux transformation and Bäcklund transformation [7] -[10] , but solving nonlinear equations is still an important task [27] -[30] . In this paper, with the aid of Mathematica, a traveling wave solution for a class of Kaup-Kupershmidt Equation,
In order to obtain the soliton solution of (1), I will use the modified sine-cosine to develop traveling wave solutions to this equation. The modified sine-cosine method admits the use of solutions [30]

and

where 





From Equation (9), I obtain

With the aid of Mathematica or Maple, from (8) and (10), we can get

Now, from Equation (12) equating the exponents n − 5 and 2n − 3 leads

Also from Equation (12) equating the coefficients of like powers of





Solving the above system by the aid of Wu elimination method [31] , I obtain the three solutions

and

and

Then the soliton solutions of the Kaup-Kupershmidt Equation is given by

and

and

If setting

and

and

The double-kink solutions (19), (20), and (21) are characterized by the eigenvalue 

4. Conclusions
The new types of exact traveling wave solution obtained in this paper for the Kaup-Kupershmidt Equation will
Figure 1. See [6] : solution 



Figure 2. See [20] : solution 


Figure 3. See [6] : solution 



Figure 4. See [20] : solution 


Figure 5. See [6] : solution 



Figure 6. See [20] : solution 


Figure 7. See [6] : solution 



Figure 8. See [20] : solution 


Figure 9. See [6] : solution 



Figure 10. See [20] : solution 


Figure 11. See [6] : solution 



Figure 12. See [20] : solution 


be of benefit to future studies.
The Soliton Equations play a central role in the field of integrable systems and also play a fundamental role in several other areas of mathematics and physics.
A soliton is a localized pulse-like nonlinear wave that possesses remarkable stability properties. Typically, problems that admit soliton solutions are in the form of evolution equations that describe how some variable or a set of variables evolves in time from a given state. The equations may take a variety of forms, for example, PDEs, differential difference equations, partial difference equations, integro-differential equations, as well as coupled ODEs of finite order.
In this paper, we considered the construction of exact solutions to Kaup-Kupershmidt Equation. I obtain travelling wave solutions for the above equation by using the modified sine-cosine method with the aid of Mathematica.
A travelling wave of permanent form has already been met; this is the solitary wave solution of the nonlinear evolution equation itself. Such a wave is a special solution of the governing equation which does not change its shape and propagates at constant speed.
The soliton phenomena of nonlinear evolution equations represent an important and well-established field of modern physics, mathematical physics and applied mathematics. Solitons are found in various areas of physics from hydrodynamics and plasma physics, nonlinear optics and solid state physics, to field theory and gravitation. NLEEs which describe soliton phenomena have a universal character.
Funding
This research is funded by the Deanship of Research and Graduate Studies in Zarqa University/Jordan.
References
- Rogers, C. and Schief, W.F. (2002) Bäcklund and Darboux Transformations, Geometry and Modern Applications in Soliton Theory. In: Ablowitz, M.J., Eds., Cambridge Texts in Applied Mathematics, Cambridge University Press, Cambridge.
- Matveev, V.A. and Salle, M.A. (1991) Darboux Transformation and Solitons. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-662-00922-2
- Sayed, S.M. and Gharib, G.M. (2009) Canonical Reduction of Self-Dual Yang-Mills Equations to Fitzhugh-Nagumo Equation and Exact Solutions. Chaos, Solitons & Fractals, 39, 492-498. http://dx.doi.org/10.1016/j.chaos.2007.01.076
- Klingenberg, W. (1982) Riemannian Geometry. Walter de Gruyter, Berlin, New York.
- Bracken, P. (2010) Surfaces Specified by Integrable Systems of Partial Differential Equations Determined by Structure Equations and Lax Pair. Journal of Geometry and Physics, 60, 562-569. http://dx.doi.org/10.1016/j.geomphys.2009.12.004
- Abolwitz, M.J. and Clarkson, P.A. (1991) Solitons, Nonlinear Evolution Equation and Inverse Scattering. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511623998
- Rogers, C. and Wong, P. (1984) On Reciprocal Bäcklund Transformations of Inverse Scattering Schemes. Physica Scripta, 30, 10-14. http://dx.doi.org/10.1088/0031-8949/30/1/003
- Wazwaz, A.M. (2006) Two Reliable Methods for Solving Variants of the KdV Equation with Compact and Noncompact Structures. Chaos, Solitons & Fractals, 28, 454-462. http://dx.doi.org/10.1016/j.chaos.2005.06.004
- Geng, X.G. and Wang, H. (2013) Coupled Camassa-Holm Equations―Peakons and Infinitely Many Conservation Laws. Journal of Mathematical Analysis and Applications, 403, 262-271. http://dx.doi.org/10.1016/j.jmaa.2013.02.030
- Khater, A.H., Callebaut, D.K. and Sayed, S.M. (2004) Conservation Laws for Some Nonlinear Evolution Equations Which Describe Pseudo-Spherical Surfaces. Journal of Geometry and Physics, 51, 332-352. http://dx.doi.org/10.1016/j.geomphys.2003.11.009
- Cavalcante, J.A. and Tenenblat, K. (1988) Conservation Laws for Nonlinear Evolution Equations. Journal of Mathematical Physics, 29, 1044-1059. http://dx.doi.org/10.1063/1.528020
- Beals, R., Rabelo, M. and Tenenblat, K. (1989) B cklund Transformations and Inverse Scattering Solutions for Some Pseudo-Spherical Surfaces. Studies in Applied Mathematics, 81, 125-134.
- Reyes, E.G. (2000) Conservation Laws and Calapso-Guichard Deformations of Equations Describing Pseudo-Spherical Surfaces. Journal of Mathematical Physics, 41, 2968-2979. http://dx.doi.org/10.1063/1.533284
- Reyes, E.G. (2001) On Geometrically Integrable Equations and Hierarchies of Pseudo-Spherical Type. Contemporary Mathematics, 285, 145-156.
- Chern, S.S. and Tenenblat, K. (1986) Pseudospherical Surfaces and Evolution Equations. Studies in Applied Mathematics, 74, 55-83.
- Khater, A.H., Callebaut, D.K., Abdalla, A.A., Shehata, A.R. and Sayed, S.M. (1999) B cklund Transformations and Exact Solutions for Self-Dual SU(3) Yang-Mills Equations. IL Nuovo Cimento B, 114, 1-10.
- Qu, C., Si, Y. and Liu, R. (2003) On Affine Sawada-Kotera Equation. Chaos, Solitons & Fractals, 15, 131-139. http://dx.doi.org/10.1016/S0960-0779(02)00121-2
- Wright, O.C. (2003) The Darboux Transformation of Some Manakov Systems. Applied Mathematics Letters, 16, 647- 652. http://dx.doi.org/10.1016/S0893-9659(03)00061-2
- Hirota, R. (2004) The Direct Method in Soliton Theory. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511543043
- Khater, A.H., Callebaut, D.K. and Sayed, S.M. (2006) Exact Solutions for Some Nonlinear Evolution Equations Which Describe Pseudo-Spherical Surfaces. Journal of Computational and Applied Mathematics, 189, 387-411. http://dx.doi.org/10.1016/j.cam.2005.10.007
- Liu, S.K., Fu, Z.T., Liu, S.D. and Zhao, Q. (2001) Jacobi Elliptic Function Expansion Method and Periodic Wave Solutions of Nonlinear Wave Equations. Physics Letters A, 289, 69-74. http://dx.doi.org/10.1016/S0375-9601(01)00580-1
- Fan, E. (2000) Extended Tanh-Function Method and Its Applications to Nonlinear Equations. Physics Letters A, 277, 212-218. http://dx.doi.org/10.1016/S0375-9601(00)00725-8
- Malfliet, W. and Hereman, W. (1996) The Tanh Method: I. Exact Solutions of Nonlinear Evolution and Wave Equations. Physica Scripta, 54, 569-575.
- Chadan, K. and Sabatier, P.C. (1977) Inverse Problems in Quantum Scattering Theory. Springer, New York. http://dx.doi.org/10.1007/978-3-662-12125-2
- Ablowitz, M.J., Chakravarty, S. and Halburd, R. (1998) On Painlevé and Darboux-Halphen Type Equations. In: Conte, R., Ed., The Painlev Property: One Century Later, CRM Series in Mathematical Physics, Springer, Berlin.
- Al-Ali, E.M. (2013) Traveling Wave Solutions for a Generalized Kawahara and Hunter-Saxton Equations. International Journal of Mathematical Analysis, 7, 1647-1666.
- Sayed, S.M. (2013) The Bäcklund Transformations, Exact Solutions, and Conservation Laws for the Compound Modified Korteweg-de Vries-Sine-Gordon Equations Which Describe Pseudospherical Surfaces. Journal of Applied Mathematics, 2013, Article ID: 613065. http://dx.doi.org/10.1155/2013/613065
- Matveev, V.B. and Salle, M.A. (1991) Darboux Transformations and Solitons. Springer-Verlag, Berlin.
- Tenenblat, K. (1998) Transformations of Manifolds and Applications to Differential Equations. Pitman Monographs and Surveys in Pure and Applied Mathematics 93, Addison Wesley Longman, England.
- Wazwaz, A.M. (2004) New Compactons, Solitons and Periodic Solutions for Nonlinear Variants of the KdV and the KP Equations. Chaos, Solitons & Fractals, 22, 249-260. http://dx.doi.org/10.1016/j.chaos.2004.01.005
- Wu, W.T. (1994) Polynomial Equations-Solving and Its Applications. In: Algorithms and Computation, Lecture Notes in Computer Science 834, Springer-Verlag, Berlin, 1-9.















