Applied Mathematics
Vol.05 No.03(2014), Article ID:42801,10 pages
10.4236/am.2014.53048
Some Mixed Soft Operations and Extremally Soft Disconnectedness via Two Soft Topologies
Nihal Arabacıoğlu Tas, Ahu Acikgoz
Department of Mathematics, Balikesir University, Balikesir, Turkey
Email: nihalarabacioglu@hotmail.com, ahuacikgoz@gmail.com
Copyright © 2014 Nihal Arabacıoğlu Tas, Ahu Acikgoz. This is an open access article distributed under the Creative Commons At- tribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is prop- erly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Nihal Arabacıoğlu Tas, Ahu Acikgoz. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
ABSTRACT
Received October 23, 2013; revised November 23, 2013; accepted November 30, 2013
In this paper, we study the concept of soft sets which is introduced by Molodtsov [5]. We give the definition of
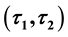 -semi open soft (resp.
-semi open soft (resp.
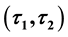 -pre open soft,
-pre open soft,
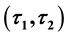 -
- -open soft,
-open soft,
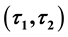 -
-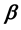 -open soft,
-open soft,
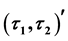 -semi open soft,
-semi open soft,
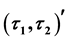 -pre open soft,
-pre open soft,
 -
-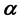 -open soft,
-open soft,
 -
-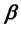 -open soft) set via two soft topologies. Also we introduce
-open soft) set via two soft topologies. Also we introduce
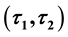 -regular open soft and ESDC on two soft topologies. The aim of this paper is to investigate properties of some mixed soft operations and characterizations of ESDC. Finally, we study
-regular open soft and ESDC on two soft topologies. The aim of this paper is to investigate properties of some mixed soft operations and characterizations of ESDC. Finally, we study
 -ESDC soft topologies
-ESDC soft topologies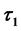 .
.
Keywords:
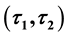 -Semi Open Soft;
-Semi Open Soft;
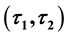 -Pre Open Soft;
-Pre Open Soft;
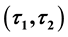 -
-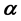 -Open Soft;
-Open Soft;
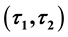 -
-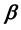 -Open Soft;
-Open Soft;
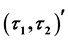 -Semi Open Soft;
-Semi Open Soft;
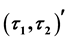 -Pre Open Soft;
-Pre Open Soft;
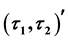 -
-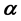 -Open Soft;
-Open Soft;
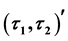 -
- -Open Soft;
-Open Soft;
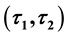 -Regular Open Soft; ESDC
-Regular Open Soft; ESDC
1. Introduction
Some set theories can be dealt with unclear concepts, for example theory of rough sets and theory of fuzzy sets. Unfortunately, these theories are not sufficient to deal with some difficulties and encounter some problems. In 2009, Ali, Feng, Liu, Min and Shabir [1] investigated several operations on soft sets and introduced some new notions such as the restricted intersection, the restricted union etc. In 2011, Hussain and Ahmad [2] researched some properties of soft topological space. Kandil et al. [3] had defined semi-open (pre-open,
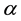 -open,
-open,
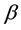 - open) soft set and semi (pre,
- open) soft set and semi (pre,
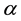 ,
,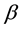 )-soft continuity via these soft sets. In 2003, Maji, Biswas and Roy [4] introduced equality of two soft sets, subset of a soft set, null soft set, absolute soft set etc. In 1999, Molodtsov [5] introduced the soft theory as a general mathematical tool for dealing with these problems. He accomplished very significant applications of soft set theory such as solving some complications in economics, social science, medical science, engineering etc. In 2011, Shabir and Naz [6] defined and studied some notions such as soft topological space, soft interior, soft closure etc. In 2012, Zorlutuna et al. [7] introduced the concepts of soft interior point, soft interior, soft neighborhood, soft continuity and soft compactness. Later there has been an extensive study on the applications of soft set theory. Many people have studided soft theory and investigated some properties of this theory.
)-soft continuity via these soft sets. In 2003, Maji, Biswas and Roy [4] introduced equality of two soft sets, subset of a soft set, null soft set, absolute soft set etc. In 1999, Molodtsov [5] introduced the soft theory as a general mathematical tool for dealing with these problems. He accomplished very significant applications of soft set theory such as solving some complications in economics, social science, medical science, engineering etc. In 2011, Shabir and Naz [6] defined and studied some notions such as soft topological space, soft interior, soft closure etc. In 2012, Zorlutuna et al. [7] introduced the concepts of soft interior point, soft interior, soft neighborhood, soft continuity and soft compactness. Later there has been an extensive study on the applications of soft set theory. Many people have studided soft theory and investigated some properties of this theory.
The aim of the present paper is to introduce and study notions of
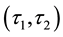 -semi open soft (resp.
-semi open soft (resp.
 -pre
-pre
open soft,
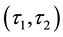 -
-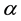 -open soft,
-open soft,
 -
-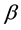 -open soft,
-open soft,
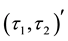 -semi open soft,
-semi open soft,
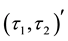 -pre-open soft,
-pre-open soft,
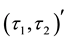 -
-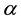 -open soft,
-open soft,
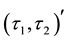 -
- -open soft) set via two soft topologies. For this purpose, we consider two soft topologies
-open soft) set via two soft topologies. For this purpose, we consider two soft topologies
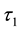 and
and
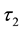 over
over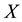 . Also we define
. Also we define
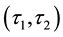 -regular open soft and ESDC on two soft topologies. Furthermore, we investigate some properties of some mixed soft operations and some characterizations of ESDC. Finally, we show
-regular open soft and ESDC on two soft topologies. Furthermore, we investigate some properties of some mixed soft operations and some characterizations of ESDC. Finally, we show
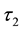 -ESDC soft topologies
-ESDC soft topologies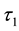 .
.
2. Preliminaries
Soft sets and Soft Topology
Definition 2.1 [1]. The complement of a soft set (F,A) is defined as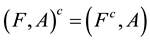 , where
, where
 , for all
, for all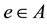 .
.
Theorem 2.1 [2]. Let
 be a soft topological space over
be a soft topological space over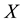 ,
,
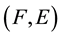 and
and
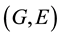 are soft sets over
are soft sets over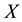 . Then
. Then
1)
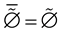 and
and .
.
2) .
.
3)
 is a closed set if and only if
is a closed set if and only if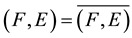 .
.
4)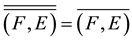 .
.
5)
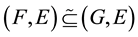 implies
implies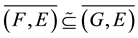 .
.
6) .
.
7)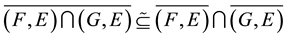 .
.
Theorem 2.2 [2]. Let
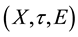 be a soft topological space over
be a soft topological space over
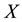 and
and
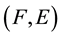 and
and
 are soft sets over
are soft sets over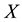 . Then
. Then
1)
 and
and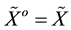 .
.
2)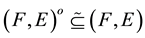 .
.
3)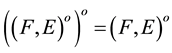 .
.
4)
 is a soft open set if and only if
is a soft open set if and only if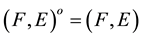 .
.
5)
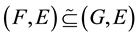 implies
implies .
.
6) .
.
7) .
.
Theorem 2.3 [2]. Let
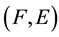 be a soft set of soft topological space over
be a soft set of soft topological space over . Then
. Then
1)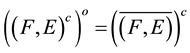 .
.
2)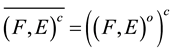 .
.
3) .
.
Definition 2.2 [3]. Let
 be a soft topological space and
be a soft topological space and . Then
. Then
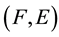 is said to be
is said to be
1) pre-open soft set if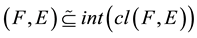 ;
;
2) semi-open soft set if ;
;
3)
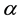 -open soft set if
-open soft set if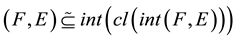 ;
;
4)
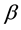 -open soft set if
-open soft set if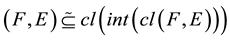 .
.
Definition 2.3 [4]. Let
 and
and
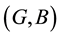 be two soft sets over a common universe X. Then
be two soft sets over a common universe X. Then
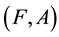 is said to be a soft subset of
is said to be a soft subset of
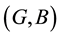 if
if
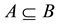 and
and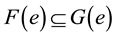 , for all
, for all . This relation is denoted by
. This relation is denoted by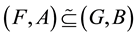 .
.
Definition 2.4 [4]. A soft set (F,A) over X is said to be a null soft set if , for all
, for all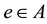 . This is denoted by
. This is denoted by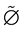 .
.
Definition 2.5 [4]. A soft set (F,A) over X is said to be an absolute soft set if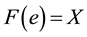 , for all
, for all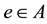 . This denoted by
. This denoted by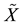 .
.
Definition 2.6 [4]. The union of two soft sets
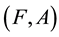 and
and
 over the common universe
over the common universe
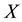 is the soft set
is the soft set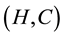 , where
, where
 and
and
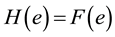 if
if
 or
or
 if
if
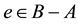 or
or
 if
if
 for all
for all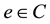 .
.
Definition 2.7 [4]. The intersection of two soft sets
 and
and
 over the common universe
over the common universe
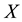 is the soft set
is the soft set , where
, where
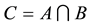 and for all
and for all ,
,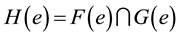 .
.
Definition 2.8 [5]. A pair , where
, where
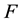 is mapping from
is mapping from
 to
to , is called a soft set over
, is called a soft set over . The family of all soft sets on
. The family of all soft sets on
 is denoted by
is denoted by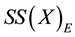 .
.
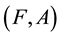 is said to be soft equal to
is said to be soft equal to
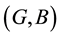 if
if
 and
and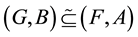 . This relation is denoted
. This relation is denoted
by .
.
Definition 2.9 [6]. Let
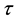 be the collection of soft sets over X. Then
be the collection of soft sets over X. Then
 is said to be a soft topology on X if
is said to be a soft topology on X if
1)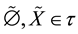 ;
;
2) the intersection of any two soft sets in
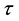 belongs to
belongs to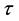 ;
;
3) the union of any number of soft sets in
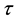 belongs to
belongs to .
.
The triple
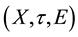 is called a soft topological space over X. The members of
is called a soft topological space over X. The members of
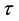 are said to be
are said to be
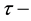 soft open sets or soft open sets in X. A soft set over X is said to be soft closed in X if its complement belongs to
soft open sets or soft open sets in X. A soft set over X is said to be soft closed in X if its complement belongs to . The set of all soft open sets over
. The set of all soft open sets over
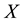 denoted by
denoted by
 or
or
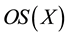 and the set of all soft closed sets denoted by
and the set of all soft closed sets denoted by
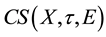 or
or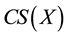 .
.
Definition 2.10 [6]. The difference of two soft sets (F,A) and (G,A) is defined by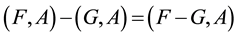 ,
,
where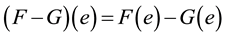 , for all
, for all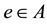 .
.
Definition 2.11 [6]. Let
 be a soft topological space and
be a soft topological space and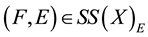 . The soft closure of
. The soft closure of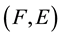 , denoted by
, denoted by
 is the intersection of all closed soft super sets of
is the intersection of all closed soft super sets of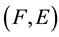 .
.
Definition 2.12 [7]. Let
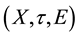 be a soft topological space and
be a soft topological space and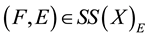 . The soft interior of
. The soft interior of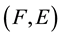 , denoted by
, denoted by
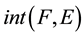 is the union of all open soft subsets of
is the union of all open soft subsets of .
.
3. Some Properties of Some Mixed Soft Operations
In this section we investigated some properties of some mixed operations such as
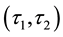 -semi open soft,
-semi open soft,
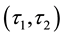 -pre open soft. Also we will write
-pre open soft. Also we will write
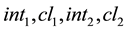 for
for , respectively.
, respectively.
Definition 3.1. Let
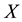 be an initial universe and
be an initial universe and
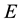 be a set of parameters. Let
be a set of parameters. Let
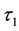 and
and
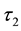 be two soft topologies on
be two soft topologies on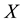 . Then
. Then
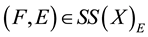 is said to be
is said to be
1)
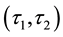 -semi open soft if
-semi open soft if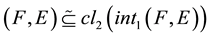 ;
;
2)
 -pre open soft if
-pre open soft if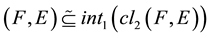 ;
;
3)
 -
-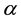 -open soft if
-open soft if ;
;
4)
 -
-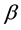 -open soft if
-open soft if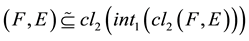 .
.
The complement of
 -semi open (resp.
-semi open (resp.
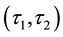 -pre open,
-pre open,
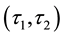 -
-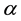 -open,
-open,
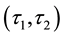 -
-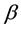 -open) soft set is called
-open) soft set is called
 -semi closed (resp.
-semi closed (resp.
 -pre closed,
-pre closed,
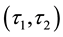 -
-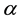 -closed,
-closed,
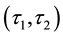 -
-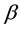 -closed) soft (See Figure 1).
-closed) soft (See Figure 1).
Definition 3.2. Let
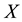 be an initial universe and
be an initial universe and
 be a set of parameters. Let
be a set of parameters. Let
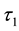 and
and
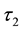 be two soft topologies on
be two soft topologies on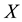 . Then
. Then
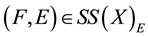 is said to be
is said to be
1)
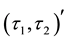 -semi open soft if
-semi open soft if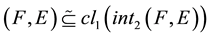 ;
;
2)
 -pre open soft if
-pre open soft if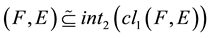 ;
;
3)
 -
- -open soft if
-open soft if ;
;
 -soft open
-soft open
 -
- -open soft
-open soft
 -semi open soft
-semi open soft


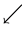



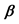 -open soft
-open soft
Figure 1. The relations among


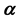 -open soft,
-open soft,

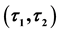

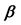 -open soft.
-open soft.
4)
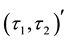 -
-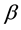 -open soft if
-open soft if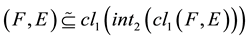 .
.
The complement of
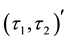 -semi open (resp.
-semi open (resp.
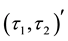 -pre open,
-pre open,
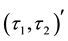 -
- -open,
-open,
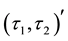 -
-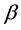 -open)
-open)
soft set is called
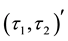 -semi closed (resp.
-semi closed (resp.
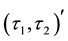 -pre closed,
-pre closed,
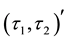 -
-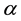 -closed,
-closed,
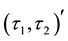 -
-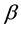 -closed)
-closed)
soft (See Figure 2).
Theorem 3.1. Let
 be an initial universe and
be an initial universe and
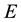 be a set of parameters. Let
be a set of parameters. Let
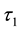 and
and
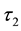 be two soft topologies on
be two soft topologies on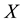 . Then
. Then
1) If
 and
and ,
, .
.
2) If
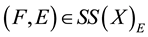 and
and ,
,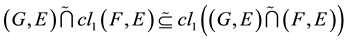 .
.
Proof. It is seen from Definition .
.
Theorem 3.2. Let
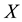 be an initial universe and
be an initial universe and
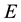 be a set of parameters. Let
be a set of parameters. Let
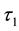 and
and
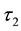 be two soft topologies on
be two soft topologies on . Then
. Then
1)
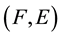 is a
is a
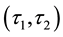 -semi open soft set if and only if
-semi open soft set if and only if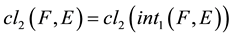 .
.
2)
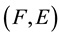 is a
is a
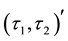 -semi open soft set if and only if
-semi open soft set if and only if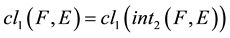 .
.
Proof. 1) Necessity. Let
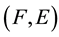 be a
be a
 -semi open soft set. Since
-semi open soft set. Since , we
, we
have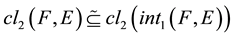 . Also
. Also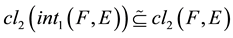 . Hence
. Hence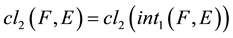 .
.
Sufficieny. Let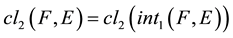 . Therefore
. Therefore
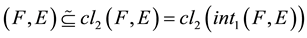 and
and
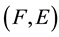 is a
is a
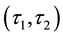 -semi open soft.
-semi open soft.
2) By a similar way.
Theorem 3.3. Let
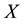 be an initial universe and
be an initial universe and
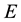 be a set of parameters. Let
be a set of parameters. Let
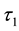 and
and
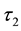 be two soft topologies on
be two soft topologies on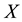 . Then
. Then
1) If
 is a
is a
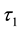 -soft open set and
-soft open set and
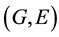 is a
is a
 -pre open soft set,
-pre open soft set,
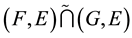 is a
is a
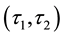 - pre open soft.
- pre open soft.
2) If
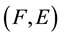 is a
is a
 -soft open set and
-soft open set and
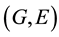 is a
is a
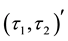 -pre open soft set,
-pre open soft set,
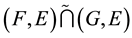 is a
is a
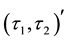 -pre open soft.
-pre open soft.
Proof. (1). Let
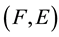 be
be
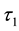 -soft open and
-soft open and
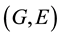 be
be
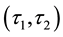 -pre open soft set. Then
-pre open soft set. Then
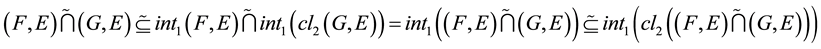
from Theorem
 Hence
Hence
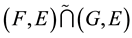 is a
is a
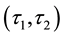 -pre open soft.
-pre open soft.
(2). By a similar way.
Theorem 3.4. Let
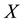 be an initial universe and
be an initial universe and
 be a set of parameters. Let
be a set of parameters. Let
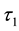 and
and
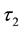 be two soft topologies on
be two soft topologies on . Then
. Then
1) If either
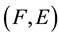 is a
is a
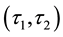 -semi open soft or
-semi open soft or
 is a
is a
 -semi open soft set,
-semi open soft set,
 .
.
2) If either
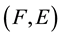 is a
is a
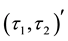 -semi open soft or
-semi open soft or
 is a
is a
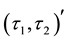 -semi open soft set,
-semi open soft set,
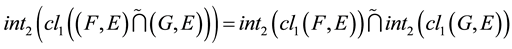 .
.
Proof. 1) Let . We have
. We have
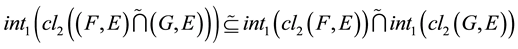 .
.
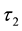 -soft open
-soft open
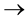
 -
-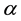 -open soft
-open soft

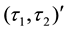 -semi open soft
-semi open soft




Figure 2. The relations among







We assume that



from Theorem 3.1. Hence we have
2) By a similar way.
Theorem 3.5. Let





1) If






2) If






Proof. 1) Let




from Theorem



2) By a similar way.
Theorem 3.6. Let






1)






2) If







3)






4) If







Proof. 1) Necessity. Let

Sufficiency. Let





is


2) Let





Thus



3)-4) By a similar way.
Theorem 3.7. Let





1) If









2) If






is


Proof. 1) Let






from Theorem




2) By a similar way.
Proposition 3.1. Let






1)
2)
Proof. It is obvious from Definition 2.1., 2.11. and
Theorem 3.8. Let





1)



2)



Proof. 1) Necessity. Let





Thus
Sufficiency. Let

Hence




2) By a similar way.
Theorem 3.9. Let





1)




2)




Proof. 1) Necessity. Let






soft, that is

Sufficiency. Let

Hence






2) By a similar way.
Theorem 3.10. Let





1)



2)



Proof. 1) Necessity. Let




open soft set, that is

Sufficiency. Let

Hence




2) By a similar way.
Theorem 3.11. Let





1) If







2) If







Proof. 1) Let






Therefore


2) By a similar way.
Theorem 3.12. Let





1)
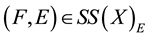



2)




Proof. 1) Necessity. Let






soft set, that is
fore,
Sufficiency. Let

Hence






2) By a similar way.
4. Extremally Soft Disconnectedness on Two Soft Topologies
In this section we introduced extremally soft disconnectedness (briefly, ESDC) via two soft topological spaces over

Definition 4.1. Let









Definition 4.2. Let








Theorem 4.1. Let





1)


2) If

3) If

4) Every


5) If




6) Every



7) Every



8) If



Proof. 1) Þ 2) Let


1),


2) Þ 3) Let

is





3) Þ 4) Let


from 3). Hence,


4) Þ 5) Let








pre open soft.

5) Þ 6) Let





Hence,


6) Þ 7) Let










7) Þ 1) Let

and





and


1) Þ 8) Let




Therefore,
8) Þ 1) Let

is




Hence, we have


Theorem 4.2. Let





1)


2) If



3) If



4) If



Proof. 1) Þ 2) Every




2) Þ 4). Every



From 2),
1) Þ 3) Since every



3) Þ 4) Since every



4) Þ 1) If

is


by



Therefore
Lemma 4.1.




Proof. Obvious.
Theorem 4.3. Let






1)


2) If



3) If



4) If



Proof. 1) Þ 2) Let




2) Þ 3) Let



3) Þ 4) Let







4) Þ 3) Let



Then we have



Hence
3) Þ 1) Let



Thus

5. t2-ESDC Soft Topologies t1
The family of all semi-open (resp. pre-open,
















Theorem 5.1. If





Proof. Let






Hence



Therefore, we obtain
Theorem 5.2. If





Proof. Let






Hence,


Therefore, we obtain
6. Conclusion
We give the definition of












set via two soft topologies. Also we introduce

References
- M. I. Ali, F. Feng, X. Liu, W. K. Min and M. Shabir, “On Some New Operations in Soft Set Theory,” Computers & Mathe- matics with Applications, Vol. 57, No. 9, 2009, pp. 1547-1553. http://dx.doi.org/10.1016/j.camwa.2008.11.009
- S. Hussain and B. Ahmad, “Some Properties of Soft Topological Space,” Computers & Mathematics with Applications, Vol. 62, No. 11, 2011, pp. 4058-4067. http://dx.doi.org/10.1016/j.camwa.2011.09.051
- A. Kandil, O. A. E. Tantawy, S. A. El-Sheikh and A. M. Abd El-Latif, “γ-Operation and Decompositions of Some Forms of Soft Continuity in Soft Topological Spaces,” Annals of Fuzzy Mathematics and Informatics, 2014, to appear.
- P. K. Maji, R. Biswas and A. R. Roy, “Soft Set Theory,” Computers & Mathematics with Applications, Vol. 45, No. 4-5, 2003, pp. 555-562. http://dx.doi.org/10.1016/S0898-1221(03)00016-6
- D. Molodtsov, “Soft Set Theory―First Results,” Computers & Mathematics with Applications, Vol. 37, No. 4-5, 1999, pp. 19-31. http://dx.doi.org/10.1016/S0898-1221(99)00056-5
- M. Shabir and M. Naz, “On Soft Topological Spaces,” Computers & Mathematics with Applications, Vol. 61, No. 7, 2011, pp. 1786-1799. http://dx.doi.org/10.1016/j.camwa.2011.02.006
- I. Zorlutuna, M. Akdag, W. K. Min and S. Atmaca, “Remarks on Soft Topological Spaces,” Annals of Fuzzy Mathematics and Informatics, Vol. 3, No. 2, 2012, pp. 171-185.
















