Applied Mathematics
Vol.4 No.4(2013), Article ID:30758,4 pages DOI:10.4236/am.2013.44097
Strongly Balanced 4-Kite Designs Nested into OQ-Systems
1Dipartimento di Matematica e Informatica, Universitá di Catania, Catania, Italy
2Dipartimento di Matematica, Universitá di Roma Tre, Roma, Italy
Email: gionfriddo@dmi.unict.it, milazzo@dmi.unict.it, rota@mat.uniroma3.it
Copyright © 2013 Mario Gionfriddo et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 20, 2012; revised December 10, 2012; accepted December 18, 2012
Keywords: Graphs; Designs; 4-Kite
ABSTRACT
In this paper we determine the spectrum for octagon quadrangle systems [OQS] which can be partitioned into two strongly balanced 4-kitedesigns.
1. Introduction
Let 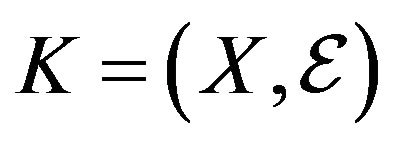 be a graph defined on the vertex set X. Let G be a subgraph of K. A G-decomposition of K is a pair
be a graph defined on the vertex set X. Let G be a subgraph of K. A G-decomposition of K is a pair , where
, where  is a partition of the edge set of K into subsets isomorphic to G. If
is a partition of the edge set of K into subsets isomorphic to G. If  is the complete undirected graph defined on the vertex set X, a G-decomposition
is the complete undirected graph defined on the vertex set X, a G-decomposition 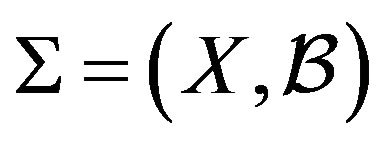 of
of  is called a G-design of order v and the classes of the partition
is called a G-design of order v and the classes of the partition  are said to be the blocks of
are said to be the blocks of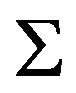 . A G-design is called balanced if for each vertex
. A G-design is called balanced if for each vertex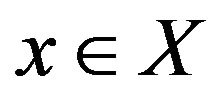 , the number of blocks of
, the number of blocks of  containing x is a constant. Observe that if G is a regular graph then a G-design is always balanced, hence the notion of a balanced G-design becomes meaningful only for a non-regular graph G.
containing x is a constant. Observe that if G is a regular graph then a G-design is always balanced, hence the notion of a balanced G-design becomes meaningful only for a non-regular graph G.
Let G be a graph and let 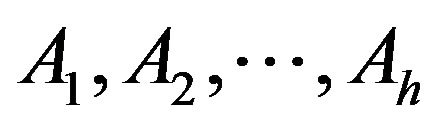 be the orbits of the automorphism group of G on its vertex-set. Let
be the orbits of the automorphism group of G on its vertex-set. Let 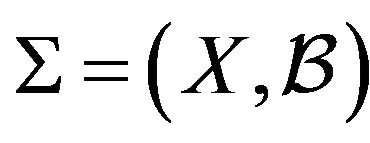 be a G-design. We define the degree
be a G-design. We define the degree 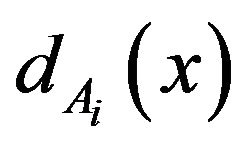 of a vertex
of a vertex  as the number of blocks of
as the number of blocks of 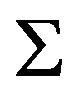 containing x as an element of Ai. We say that
containing x as an element of Ai. We say that 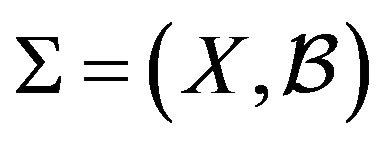 is a strongly balanced G-design if, for every
is a strongly balanced G-design if, for every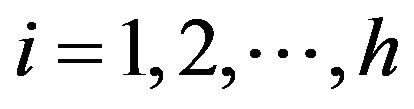 , there exists a constant Ci such that
, there exists a constant Ci such that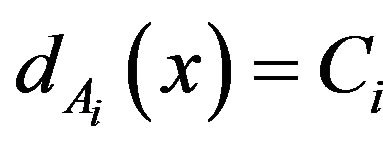 , for every
, for every 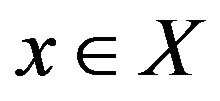 [1-3]. Clearly, since for each vertex
[1-3]. Clearly, since for each vertex  the relation
the relation 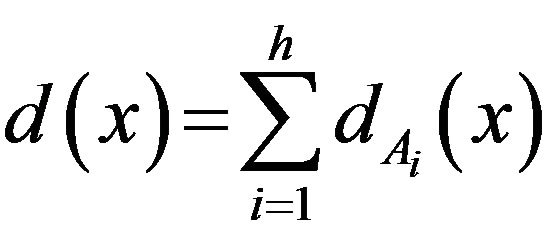 holds, we have that “a strongly balanced G-design is always a balanced G-design”. We say that a G-design is simply balanced if it is balanced, but not strongly balanced.
holds, we have that “a strongly balanced G-design is always a balanced G-design”. We say that a G-design is simply balanced if it is balanced, but not strongly balanced.
A cycle of length 4 with a pendant edge, i.e. the graph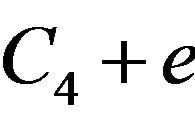 , is called a 4-kite and is denoted by
, is called a 4-kite and is denoted by 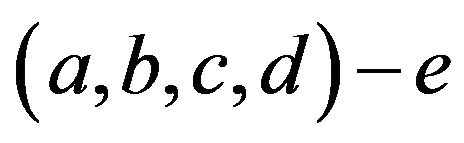 or
or , where
, where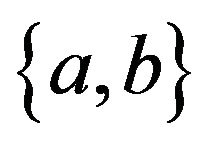 ,
,  ,
, 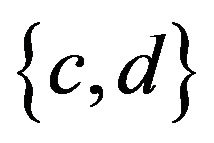 ,
, 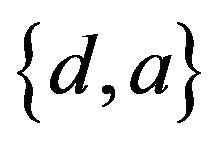 ,
,  are the edges of the 4-kite. Note that a cycle of length 3 with a pendant edge is called a 3-kite or just a kite. In the case when G is a 4-kite, a G-design is called a 4-kite-design or also a 4-kite-system. It is known that a 4-kite design of order v exists when
are the edges of the 4-kite. Note that a cycle of length 3 with a pendant edge is called a 3-kite or just a kite. In the case when G is a 4-kite, a G-design is called a 4-kite-design or also a 4-kite-system. It is known that a 4-kite design of order v exists when  or
or . Further research on 4-kite designs can be found in [2]. We will call the vertices a and c of the 4-kite
. Further research on 4-kite designs can be found in [2]. We will call the vertices a and c of the 4-kite  the lateral vertices, b the middle vertex, d the center vertex and e the terminal vertex [4-6]. Some balanced Gdesigns, when G is a path, have been studied in [1,3]. Strongly balanced G-designs were first introduced in [1], in which the spectrum of simply balanced and strongly balanced
the lateral vertices, b the middle vertex, d the center vertex and e the terminal vertex [4-6]. Some balanced Gdesigns, when G is a path, have been studied in [1,3]. Strongly balanced G-designs were first introduced in [1], in which the spectrum of simply balanced and strongly balanced 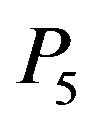 and
and 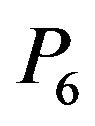 -designs have been determined, where
-designs have been determined, where  denotes a path with k vertices.
denotes a path with k vertices.
An octagon quadrangle is a graph denoted by  and formed by an 8- cycle
and formed by an 8- cycle 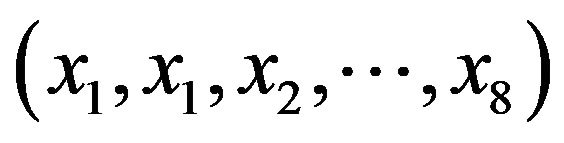 with the two additional edges
with the two additional edges 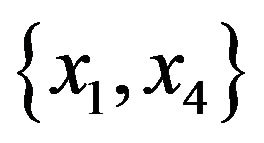 and
and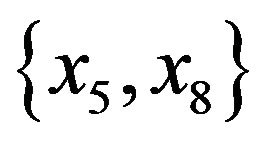 . An octagon quadrangle system [OQS] is a G-design, where G is an octagon quadrangle.
. An octagon quadrangle system [OQS] is a G-design, where G is an octagon quadrangle. 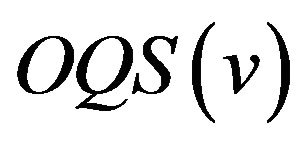 s have been defined and studied in [4,7-9]. In these papers, the main idea was to follow the research about hexagon triangle systems and all the others already introduced in the literature, where we can find many authors who have studied in many ways polygon triangle systems using triangulations of polygons [5,10,11]. With the study of octagon quadrangles the authors have considered quadrangulations of polygons with new ideas for the research [12,13].
s have been defined and studied in [4,7-9]. In these papers, the main idea was to follow the research about hexagon triangle systems and all the others already introduced in the literature, where we can find many authors who have studied in many ways polygon triangle systems using triangulations of polygons [5,10,11]. With the study of octagon quadrangles the authors have considered quadrangulations of polygons with new ideas for the research [12,13].
In what follows, if  is an
is an 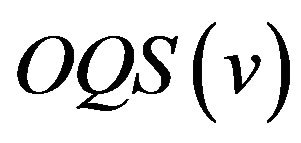 in which the family of all
in which the family of all 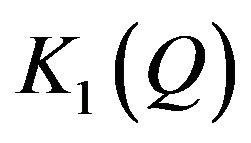 contained in the blocks of
contained in the blocks of  forms a 4-kite design
forms a 4-kite design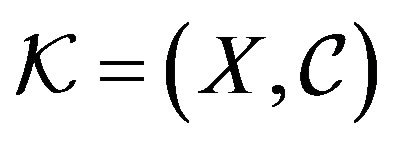 , we will say that
, we will say that 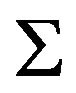 is nesting
is nesting 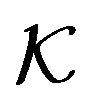 or also that
or also that 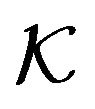 is nested in
is nested in . Similar problems, including colorings, can be found also in [14,15].
. Similar problems, including colorings, can be found also in [14,15].
In this paper, starting from the remark that an octagon quadrangle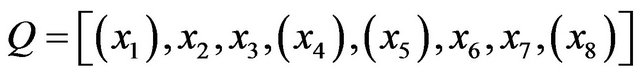 , can be partitioned into two 4-kites
, can be partitioned into two 4-kites
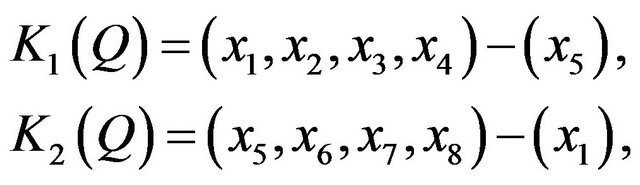
the authors study OQSs which can be partitioned into two strongly balanced 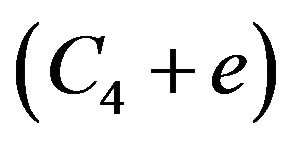 -designs, determining their spectrum.
-designs, determining their spectrum.
2. Necessary Existence Conditions
If 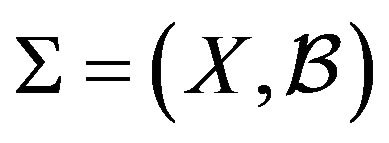 is strongly balanced 4-kite design, its vertices describe four orbits in the automorphism group of a block, which is a graph
is strongly balanced 4-kite design, its vertices describe four orbits in the automorphism group of a block, which is a graph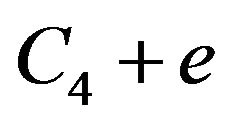 . We will indicate by C the number of blocks containing any vertex as a center of the 4-kite block, by T the number of blocks containing any vertex as a terminal, by L and M the number of blocks containing any vertex as lateral or median, respectively.
. We will indicate by C the number of blocks containing any vertex as a center of the 4-kite block, by T the number of blocks containing any vertex as a terminal, by L and M the number of blocks containing any vertex as lateral or median, respectively.
In this section, we determine necessary conditions for the existence of strongly balanced 4-kite designs (order v, index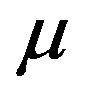 ) and for the existence of OQS (order v, index
) and for the existence of OQS (order v, index ) nesting strongly balanced 4-kite designs. These conditions are preliminary for conclusive Theorems of Section 3.
) nesting strongly balanced 4-kite designs. These conditions are preliminary for conclusive Theorems of Section 3.
Theorem 2.1. If 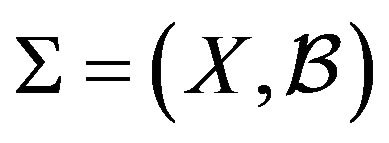 is a strongly balanced 4-kite design of order v and index
is a strongly balanced 4-kite design of order v and index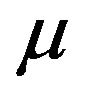 , then:
, then:
1) ;
;
2)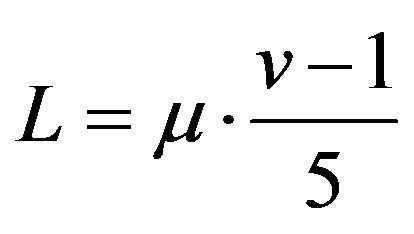 ;
;
3) .
.
Proof. If 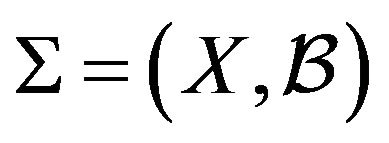 is a strongly balanced 4-kite design of order v and index
is a strongly balanced 4-kite design of order v and index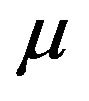 , following the terminology described above and considering that each vertex occupies C times the central position in the blocks, necessarily:
, following the terminology described above and considering that each vertex occupies C times the central position in the blocks, necessarily:
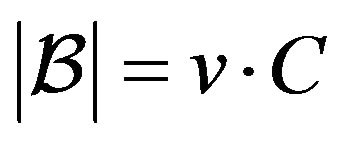 from which
from which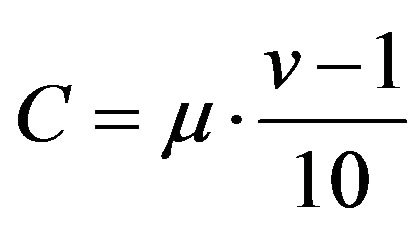 .
.
The same considerations can be done to calculate the parameters T, M, which have the same value of C. For the last parameter L, we can consider that:
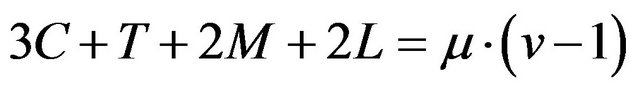 hence
hence
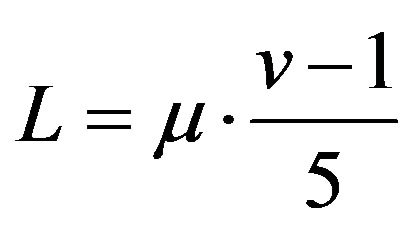 .
.
Thus, 1) and 2) are verified and from them 3) holds. 
Theorem 2.2. Let  be an OQS of order v and index
be an OQS of order v and index , nesting a strongly balanced 4-kite design
, nesting a strongly balanced 4-kite design  of index
of index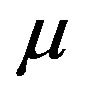 . Then:
. Then:
1) ;
;
2)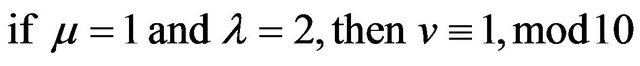 .
.
Proof. 1) Since:

and necessarily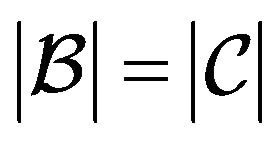 , it follows
, it follows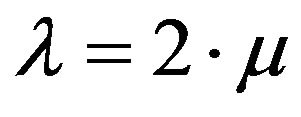 . 2) From 3) of Theorem 2.1, if
. 2) From 3) of Theorem 2.1, if  then
then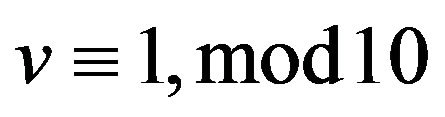 .
. 
3. Main Existence Theorems
In what follows, if 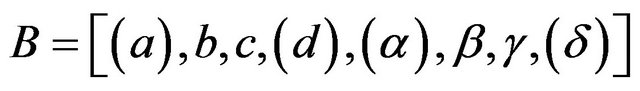 is a block of an OQ-system
is a block of an OQ-system 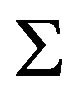 defined in
defined in , then the translates of B are all the blocks of type
, then the translates of B are all the blocks of type
for every . B is called a base block of
. B is called a base block of .
.
Theorem 3.1. There exists an OQS, of order v and index two, nesting a strongly balanced 4-kite design of index one if and only if:

Proof.  Let
Let  be an OQS of order v and index
be an OQS of order v and index , nesting a 4-kite design
, nesting a 4-kite design 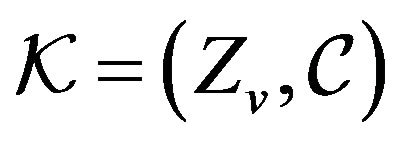 of order v and index one. From Theorem 2.2 it is
of order v and index one. From Theorem 2.2 it is  and
and

 Consider the following octagon quadrangles:
Consider the following octagon quadrangles:

Consider the system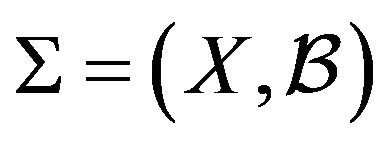 , defined in
, defined in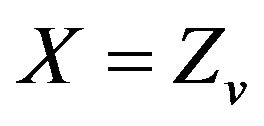 , having
, having  as base blocks. This means that the blocks
as base blocks. This means that the blocks 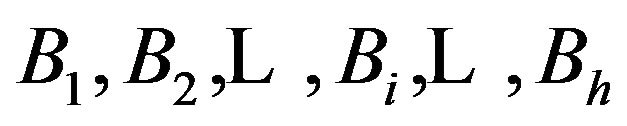 belong to
belong to  and with all their translates.
and with all their translates.
Observe that, for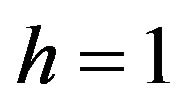 , the correspondent system defined in
, the correspondent system defined in 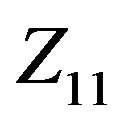 has for blocks all the translates of the following base block:
has for blocks all the translates of the following base block:
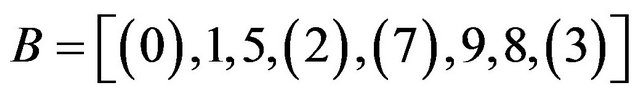 .
.
In every case, it is possible to verify that 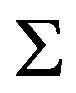 is an OQS of order
is an OQS of order 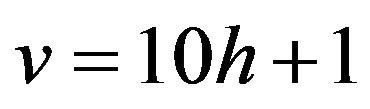 and index
and index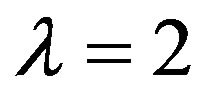 . Further, if we partition every block
. Further, if we partition every block

into the two 4-kites:

we can verify that the collection of all the upper 4-kites forms a 4-kite-design  of index one. Observe also that the collection of all the lower 4-kites forms a 4-kite-design
of index one. Observe also that the collection of all the lower 4-kites forms a 4-kite-design  of index one.
of index one.
We can verify that both the systems 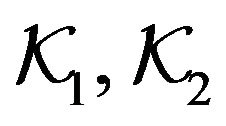 are strongly balanced. In fact, for them it is
are strongly balanced. In fact, for them it is , and
, and .
.
To verify this, it is enough to consider that the system  is constructed by base blocks and difference method.
is constructed by base blocks and difference method.
This proves that  is an OQS of order
is an OQS of order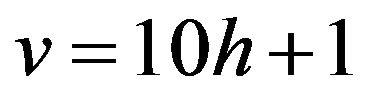 ,
, 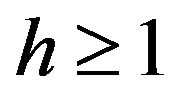 , where the two 4-kites designs nested in it have both index one and are both strongly balanced.
, where the two 4-kites designs nested in it have both index one and are both strongly balanced. 
At last, it follows a result about the existence of strongly balanced 4-kite designs, whose spectrum is unknown.
Theorem 3.2. For every  there exists strongly balanced 4-kite designs of index one.
there exists strongly balanced 4-kite designs of index one.
4. Conclusive Remarks and Problems
Theorem 3.1 gives completely the spectrum of OQS which can be partitioned into two strongly balanced 4- kite designs. For a given v belongs to the spectrum, Theorem 3.1 gives also the method to construct an OQS of order v with the said properties.
For example, if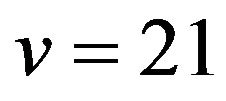 , the translates of the two base blocks:
, the translates of the two base blocks:
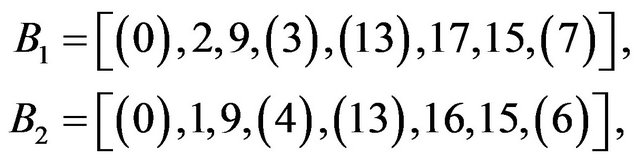
constructed on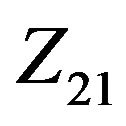 , define an OQS of order
, define an OQS of order 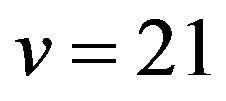 and index
and index . We can observe that B1 can be partitioned into the two 4-kites
. We can observe that B1 can be partitioned into the two 4-kites

and  into the two 4-kites
into the two 4-kites
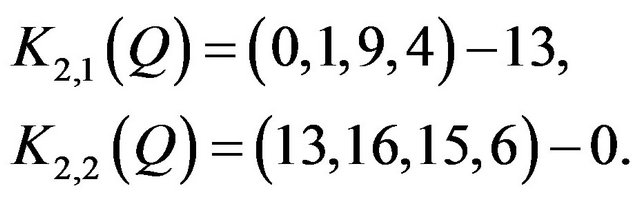
We can verify that the translates of 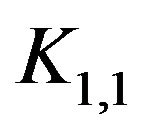 and
and  define a strongly balanced 4-kite designs of order
define a strongly balanced 4-kite designs of order 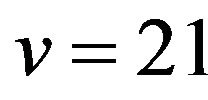 and index
and index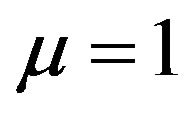 . Further, a system of the same type and parameters is defined by the translates of
. Further, a system of the same type and parameters is defined by the translates of 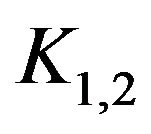 and
and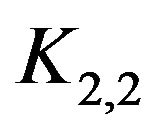 .
.
The Theorem 3.1 permits also to find values of v for which there exist strongly balanced 4-kite designs, whose spectrum is still unknown. Thus, the statement of Theorem 3.2 can be the starting point for its determination.
In conclusion, we observe that from Theorem 3.1 follows the more general:
Theorem 4.1. There exists an OQS, of order v and index , nesting a strongly balanced 4-kite design of order v and of index
, nesting a strongly balanced 4-kite design of order v and of index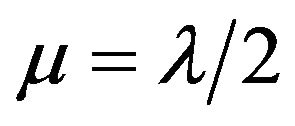 , if and only if:
, if and only if:

Proof. From Theorem 2.2, it is necessarily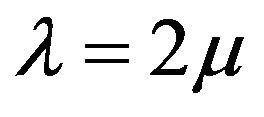 . So, from Theorem 3.1, by a repetition of blocks, the statement follows.
. So, from Theorem 3.1, by a repetition of blocks, the statement follows. 
We can also point out that, after the determination of the spectrum, found in this paper, it is possible to study other problems about octagon quadrangle systems. It is possible to study the intersection problem among them, about which there exist an important literature, following the technique introduced in [16,17]. Also, it should be interesting to examine the conjecture of Berge for linear hypergraphs, in the case in which these are OQSs, following the ideas seen in [18,19].
REFERENCES
- L. Berardi, M. Gionfriddo and R. Rota, “Balanced and Strongly Balanced Pk-Designs,” Discrete Mathematics, Vol. 312, No. 3, 2012, pp. 633-636. doi:10.1016/j.disc.2011.05.015
- M. Gionfriddo, S. Kucukcifci and L. Milazzo, “Balanced and Strongly Balanced 4-Kite Systems,” Utilitas Mathematica, Vol. 90, 2013.
- M. Gionfriddo and G. Quattrocchi, “Embedding Balanced P3-Designs into (Balanced) P4-Designs,” Discrete Mathematics, Vol. 308, No. 2-3, 2008, pp. 155-160. doi:10.1016/j.disc.2006.11.027
- L. Berardi, M. Gionfriddo and R. Rota, “Perfect Octagon Quadrangle Systems with an Upper C4-System and a Large Spectrum,” Computer Science Journal of Moldova, Vol. 18, No. 3, 2010, pp. 303-318.
- L. Gionfriddo, “Hexagon Kite Systems,” Discrete Mathematics, Vol. 309, No. 2, 2009, pp. 505-512. doi:10.1016/j.disc.2008.02.042
- M. Gionfriddo and S. Milici, “Octagon Kite Systems,” Electronic Notes in Discrete Mathematics, Vol. 41, 2013.
- L. Berardi, M. Gionfriddo and R. Rota, “Perfect Octagon Quadrangle Systems,” Discrete Mathematics, Vol. 310, No. 13-14, 2010, pp. 1979-1985. doi:10.1016/j.disc.2010.03.012
- L. Berardi, M. Gionfriddo and R. Rota, “Perfect Octagon Quadrangle Systems with Upper C4-Systems,” Journal of Statistical Planning and Inference, Vol. 141, No. 7, 2011, pp. 2249-2255. doi:10.1016/j.jspi.2011.01.015
- L. Berardi, M. Gionfriddo and R. Rota, “Perfect Octagon Quadrangle Systems—II,” Discrete Mathematics, Vol. 312, No. 3, 2012, pp. 614-620. doi:10.1016/j.disc.2011.05.009
- S. Kucukcifci and C. C. Lindner, “Perfect Hexagon Triple Systems,” Discrete Mathematics, Vol. 279, No. 1-3, 2004, pp. 325-335. doi:10.1016/S0012-365X(03)00278-4
- C. C. Lindner and A. Rosa, “Perfect Dexagon Triple Systems,” Discrete Mathematics, Vol. 308, No. 2-3, 2008, pp. 214-219. doi:10.1016/j.disc.2006.11.035
- L. Gionfriddo, “Hexagon Quadrangle Systems,” Discrete Mathematics, Vol. 308, No. 2-3, 2008, pp. 231-241. doi:10.1016/j.disc.2006.11.037
- L. Gionfriddo and M. Gionfriddo, “Perfect Dodecagon Quadrangle Systems,” Discrete Mathematics, Vol. 310, No. 22, 2010, pp. 3067-3071. doi:10.1016/j.disc.2009.02.029
- M. Gionfriddo, L. Milazzo, A. Rosa and V. Voloshin, “Bicolouring Steiner Systems S(2,4,v),” Discrete Mathematics, Vol. 283, No. 1-3, 2004, pp. 249-253. doi:10.1016/j.disc.2003.11.016
- S. Milici and G. Ragusa, “Maximum Embedding of an H(v-w,3,1) into a TS(v, λ),” Australasian Journal of Combinatorics, Vol. 46, 2010, pp. 121-127.
- M. Gionfriddo and C. C. Lindner, “Construction of Steiner Quadruples Systems Having a Prescribed Number of Blocks in Common,” Discrete Mathematics, Vol. 34, No. 1, 1981, pp. 31-42. doi:10.1016/0012-365X(81)90020-0
- Y. Chang and G. Lo Faro, “Intersection Numbers of Kirkman Triple Systems,” Journal of Combinatorial Theory A, Vol. 86, No. 2, 1999, pp. 348-361. doi:10.1006/jcta.1998.2948
- M. Gionfriddo and Z. Tuza, “On Conjectures of Berge and Chvátal,” Discrete Mathematics, Vol. 124, No. 1-3, 1994, pp. 79-86. doi:10.1016/0012-365X(94)90086-8
- M. Gionfriddo and S. Milici, “A Result Concerning Two Conjectures of Berge and Chvátal,” Discrete Mathematics, Vol. 155, No. 1-3, 1996, pp. 77-79. doi:10.1016/0012-365X(94)00371-O

