Applied Mathematics
Vol. 3 No. 11 (2012) , Article ID: 24518 , 3 pages DOI:10.4236/am.2012.311233
Symmetric Solutions of a Nonlinear Elliptic Problem with Neumann Boundary Condition
1Group of Waves, Program of Mathematics, Faculty of Exact and Natural Sciences, Cartagena University, Cartagena de Indias, Colombia
2Morelia Institute of Technology, Morelia, Mexico
Email: amarinr@unicartagena.edu.co, rortizo@unicartagena.edu.co, joel@ifm.umich.mx
Received September 3, 2012; revised October 3, 2012; accepted October 11, 2012
Keywords: Nonlinear Boundary Value Problems; Elliptic
ABSTRACT
We show a result of symmetry for a big class of problems with condition of Neumann on the boundary in the case one dimensional. We use the method of reflection of Alexandrov and we show one application of this method and the maximum principle for elliptic operators in problems with conditions of Neumann. Some results of symmetry for elliptic problems with condition of Neumann on the boundary may be extended to elliptic operators more general than the Laplacian.
1. Introduction
The maximum principle is one of the most used tools in the study of some differential equations of elliptic type. It is a generalization of the following well-known theorem of the elemental calculus “If f is a function of class 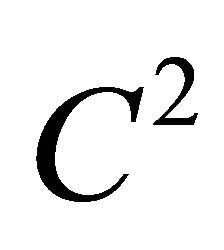 in
in  such that the second derivative is positive on (a, b) then the maximum value of f attains at the ends of
such that the second derivative is positive on (a, b) then the maximum value of f attains at the ends of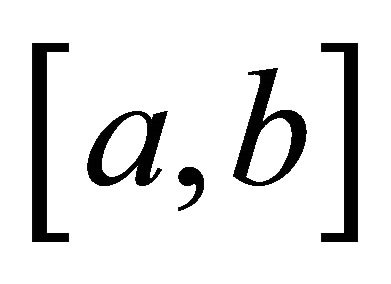 ”. It is important to point out that the maximum principle gives information about the global behavior of a function over a domain from the information of qualitative character in the boundary and without explicit knowledge of the same function. The maximum principle allows us, for example, to obtain uniqueness of solution of certain problems with conditions of the Dirichlet and Neumann type. Also it allows to obtain a priori estimates for solutions. These reasons make interesting the study of the maximum principle on several forms and its generalizations and the Hopf lemma. For example a geometric version of the maximum principle allows us to compare locally surfaces that coincide at a point. On the other hand, the maximum principle and the Alexandrov reflection principle in [1] have been used to prove symmetries with respect to some point, some plane, symmetries of domain and to determine asymptotic-symmetric behavior of the solutions of some elliptic problems. (See Serrin [2], Gidas, Ni and Nirenberg [3], Gidas, Ni and Nirenberg [4], Caffarelli, Gidas and Spruck [5], Berestycki and Nirenberg [6]). The first person in use this technic was Serrin. Serrin proved that: “If
”. It is important to point out that the maximum principle gives information about the global behavior of a function over a domain from the information of qualitative character in the boundary and without explicit knowledge of the same function. The maximum principle allows us, for example, to obtain uniqueness of solution of certain problems with conditions of the Dirichlet and Neumann type. Also it allows to obtain a priori estimates for solutions. These reasons make interesting the study of the maximum principle on several forms and its generalizations and the Hopf lemma. For example a geometric version of the maximum principle allows us to compare locally surfaces that coincide at a point. On the other hand, the maximum principle and the Alexandrov reflection principle in [1] have been used to prove symmetries with respect to some point, some plane, symmetries of domain and to determine asymptotic-symmetric behavior of the solutions of some elliptic problems. (See Serrin [2], Gidas, Ni and Nirenberg [3], Gidas, Ni and Nirenberg [4], Caffarelli, Gidas and Spruck [5], Berestycki and Nirenberg [6]). The first person in use this technic was Serrin. Serrin proved that: “If 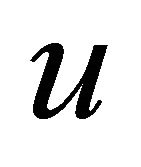 is a positive solution of the problem
is a positive solution of the problem

which is zero on the boundary and its outer normal derivative on the boundary is constant, then  is a ball and
is a ball and  is radially symmetric with respect to the center of
is radially symmetric with respect to the center of ”. Using the ideas of Serrin and a version of the maximum principle for functions that do not change of sign, Gidas Ni and Nirenberg proved that: “If
”. Using the ideas of Serrin and a version of the maximum principle for functions that do not change of sign, Gidas Ni and Nirenberg proved that: “If  is a ball,
is a ball,  and
and  is a positive solution of the problem,
is a positive solution of the problem,

which is zero on the boundary, then u is radially symmetric with respect to the center of the ball”. Using the method of reflection and a version of maximum principle for thin domains Berestycki and Nirenberg made a generalization of this statement. Our proof shows that the technic used by Berestycki and Nirenberg for the study of symmetries of solutions of the elliptic problem with Dirichlet condition, can be applied in elliptic problems with Neumann conditions with nonlinear term .
.
2. Maximum Principle and Hopf Lemma
Our result is based on the well known maximum principle and on the Hopf lemma for the differential operator of the form (see [7-9])
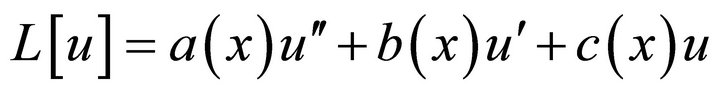 (1)
(1)
where  is in
is in  We suppose that the coefficients
We suppose that the coefficients 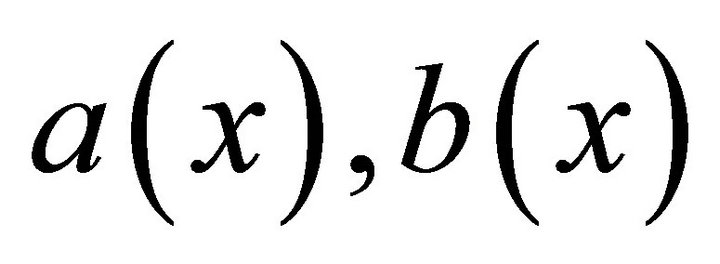 and
and 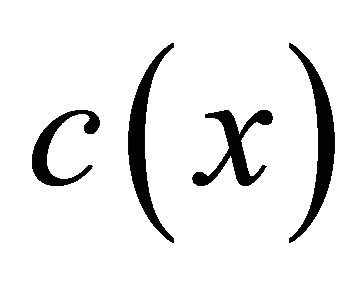 are bounded on
are bounded on  and
and 
 for all
for all 
Theorem 2.1. (Maximum principle)
Let 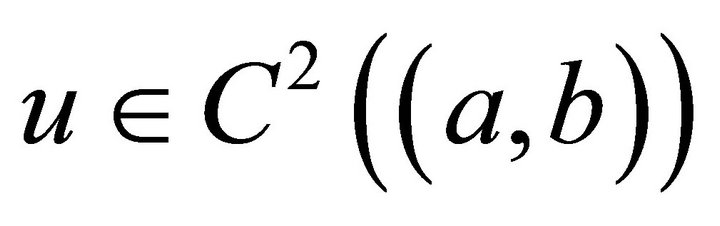 be such that
be such that  Then
Then  cannot attain its maximum value in
cannot attain its maximum value in 
Lemma 2.2. (Hopf)
Suppose 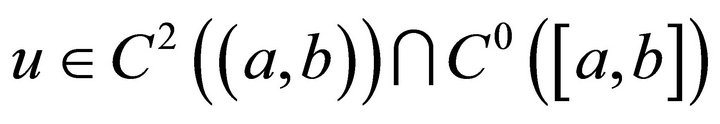 satisfies
satisfies

Let  be such that
be such that
•  is continuous at
is continuous at 
• 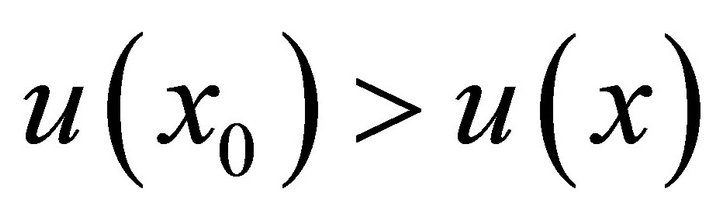 for all
for all 
•  existe.
existe.
Then 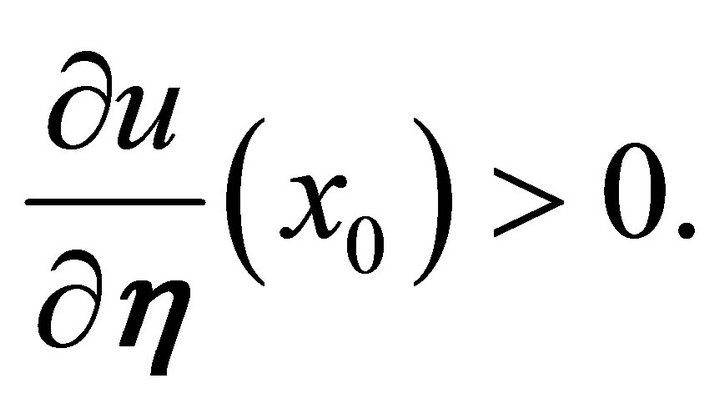
3. Main Result
Theorem 3.3. Let 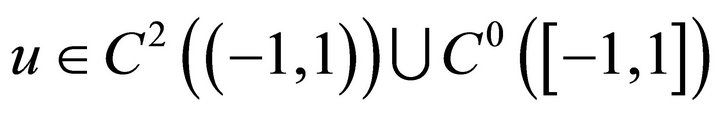 be a solution of
be a solution of
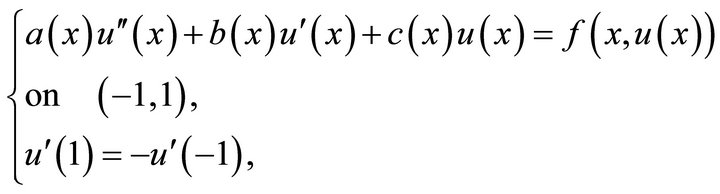
where 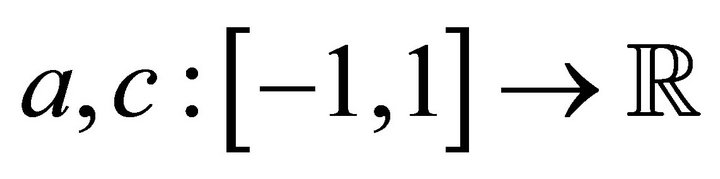 are bounded functions and symmetric with respect to the origin such that
are bounded functions and symmetric with respect to the origin such that 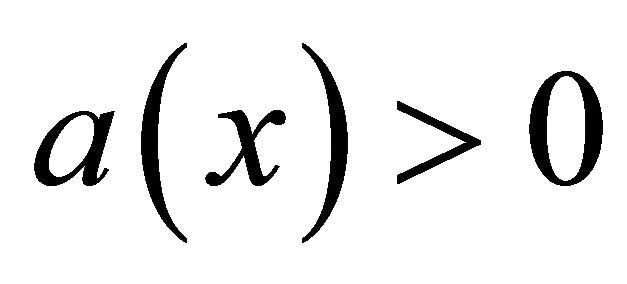
and  for all
for all 
 is such that
is such that 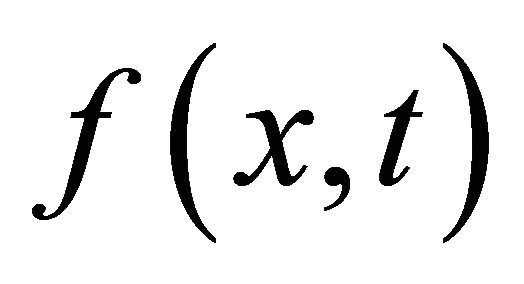 is strictly increasing in
is strictly increasing in  for all
for all  and is symmetric to
and is symmetric to 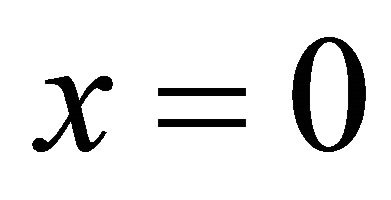 for all
for all  and
and 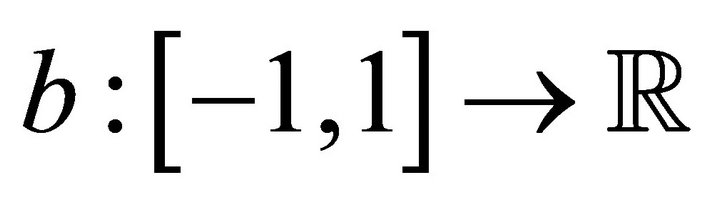 is a bounded function and odd. Then
is a bounded function and odd. Then  is symmetric with respect to the origin.
is symmetric with respect to the origin.
Proof: Define the reflected function of  in
in 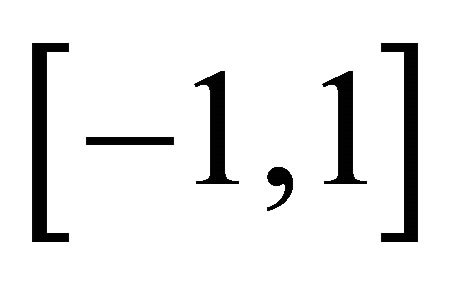 by
by

Hence,  Then v satisfies
Then v satisfies
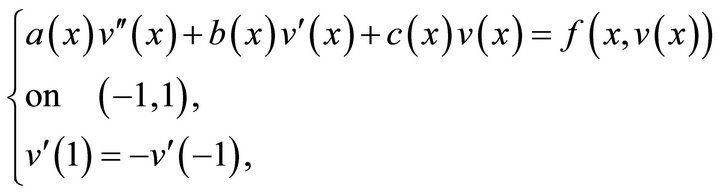
Define

Then  satisfies
satisfies
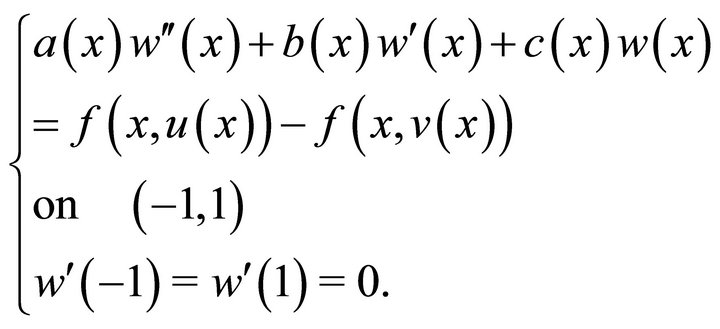
Since  is continuous in
is continuous in , there are
, there are 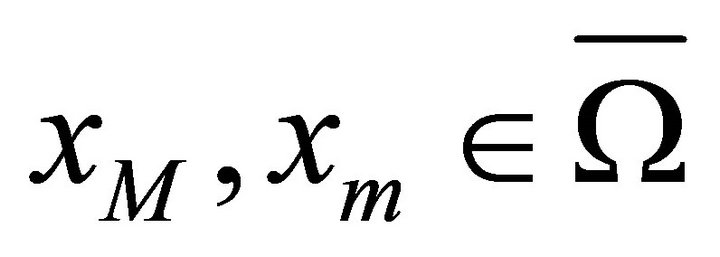 such that
such that

Suppose that  or
or 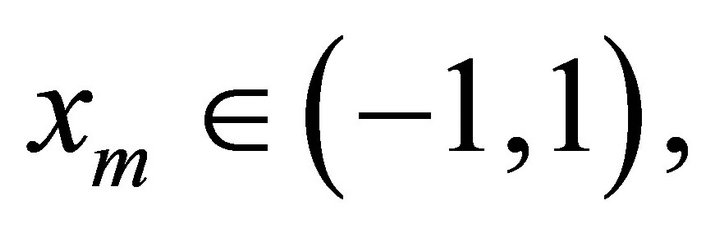 then if
then if
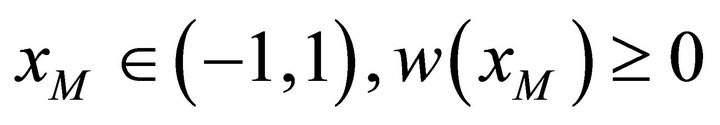 since
since 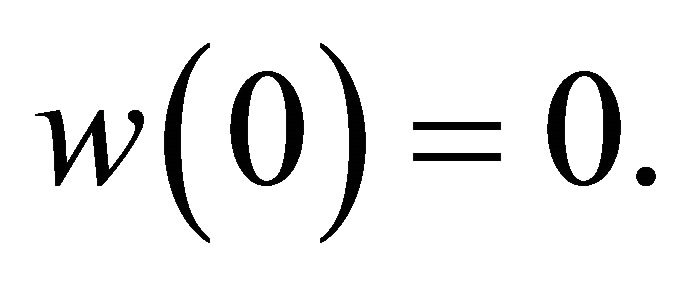 Further
Further
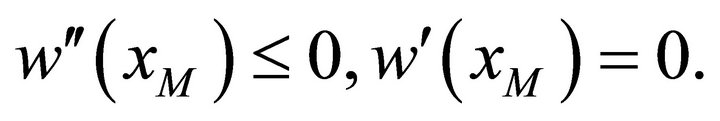 Therefore
Therefore
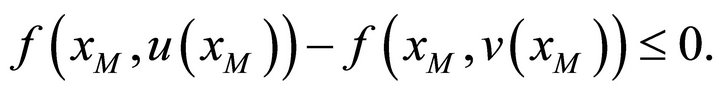
Since  is strictly increasing in
is strictly increasing in 

Then
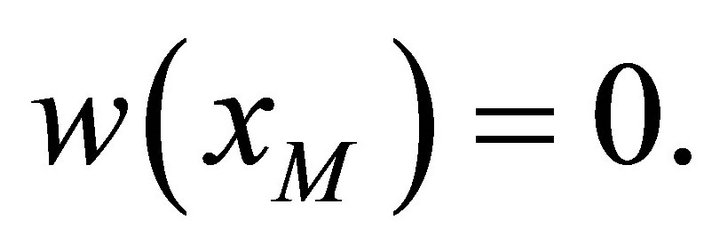
Therefore
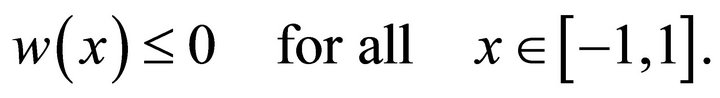
If 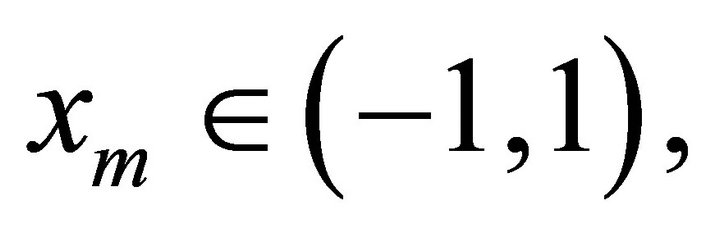 using a similar argue we demonstrate that
using a similar argue we demonstrate that  and we obtain the same conclusion. Suppose that
and we obtain the same conclusion. Suppose that 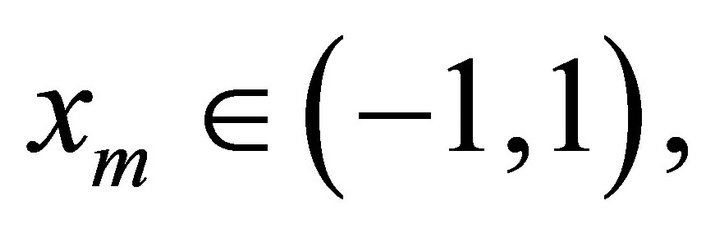 then
then 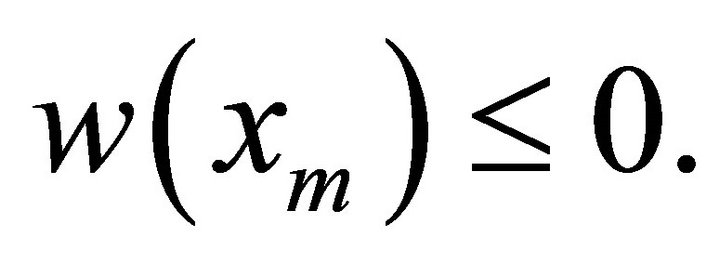 since w(0) = 0 Further
since w(0) = 0 Further 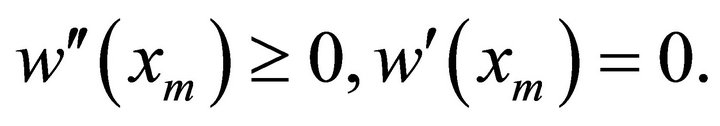 Therefore
Therefore
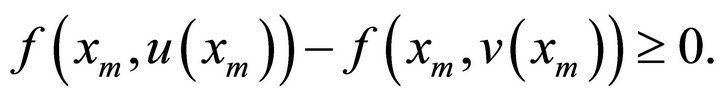
Since  is strictly increasing in
is strictly increasing in 
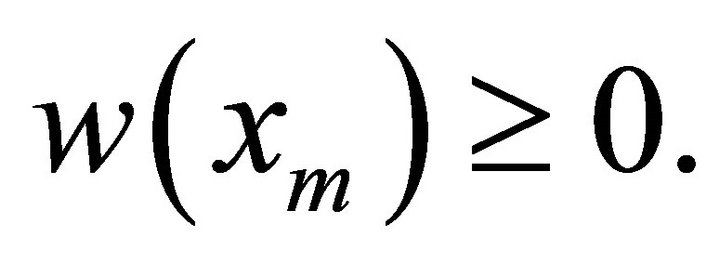
Then
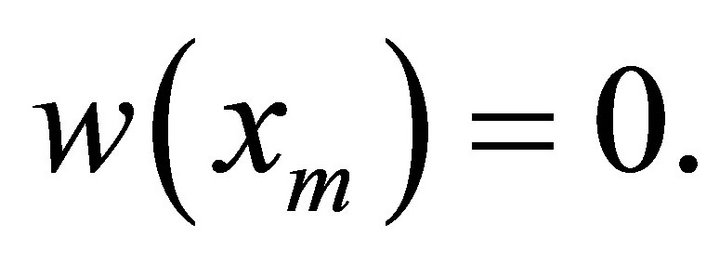
Therefore

We conclude

So 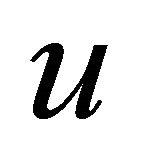 is symmetric with respect to the origin.
is symmetric with respect to the origin.
We will prove that  do not belong to
do not belong to  Suppose now that
Suppose now that  and
and
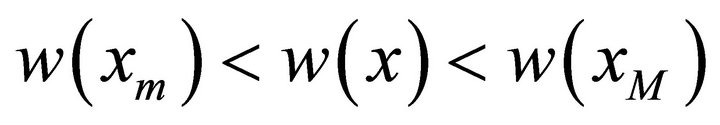 for all
for all 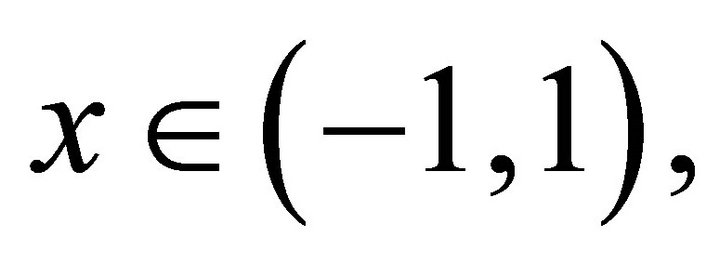 then
then
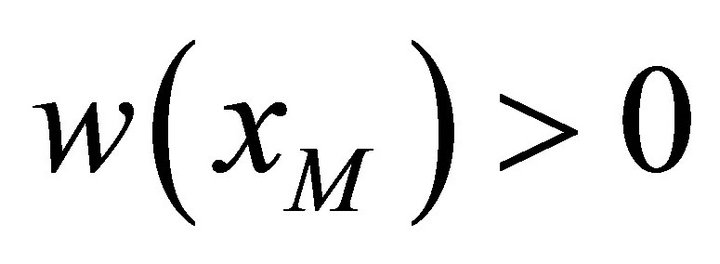 and
and  If
If 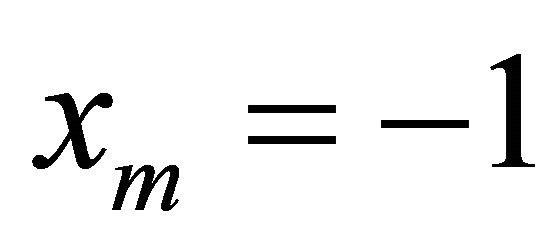 and
and 
then 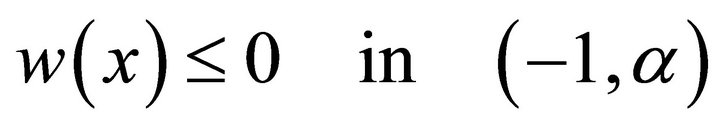 and
and 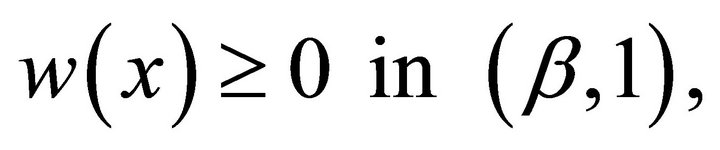 where
where 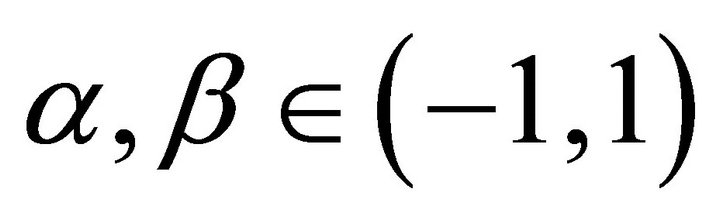 are such that
are such that 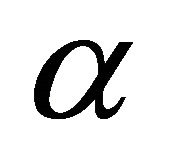 is the first zero of w and
is the first zero of w and  is the last. Since
is the last. Since 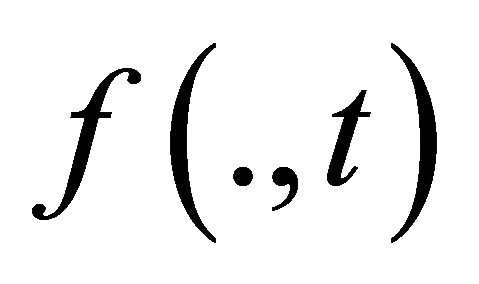 is strictly increasing in
is strictly increasing in , then
, then
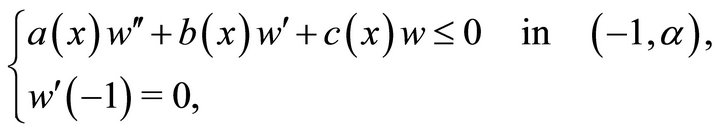
and
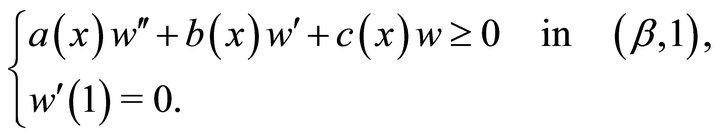
Applying maximum principle and Hopf lemma,

since 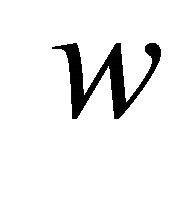 is not constant. Which contradicts the fact that
is not constant. Which contradicts the fact that

Hence this case is impossible. It happens equally to 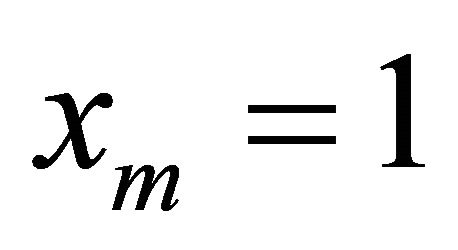 and
and 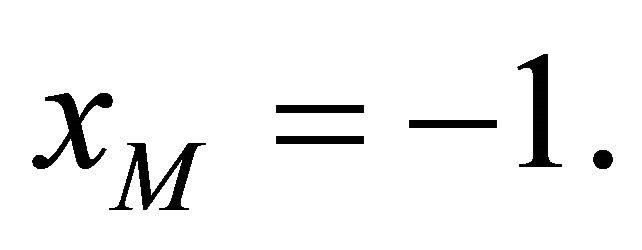 In conclusion we have that
In conclusion we have that  on
on 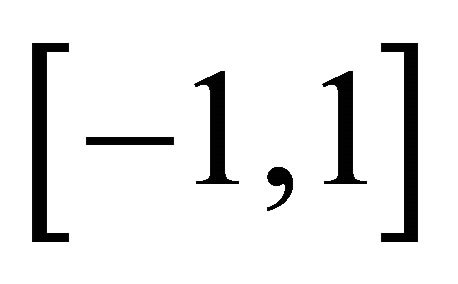 and therefore
and therefore 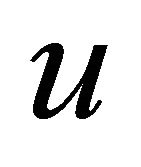 is symmetric with respect to
is symmetric with respect to 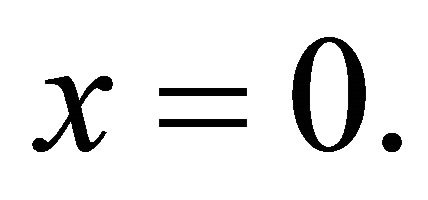
4. Example
Taking
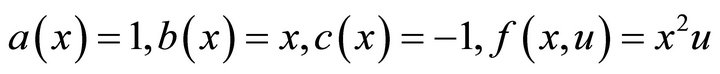
in Theorem 3.3, we have the following system
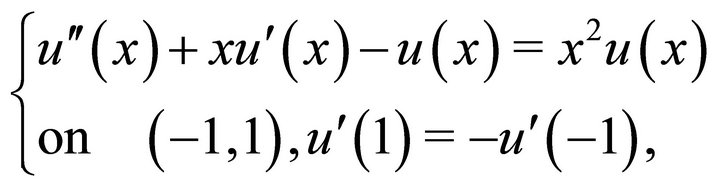
following the steps of the demonstration, it follows that u is symmetric with respect to the origin.
5. Acknowledgements
The authors express their deep gratitude to CONACYT México, Programa de Mejoramiento del Profesorado (PROMEP)-México and Universidad de Cartagena for financial support.
REFERENCES
- A. D. Alexandrov, “Uniqueness Theorems for Surfaces in the Large,” Vestnik Leningrad University: Mathematics, Vol. 13, No. 19, 1958, pp. 5-8.
- J. Serrin, “A Symetry Problem in Potential Theory,” Archive for Rational Mechanics and Analysis, Vol. 43, No. 4, 1971, pp. 304-318. doi:10.1007/BF00250468
- B. Gidas, W.-M. Ni and L. Nirenberg, “Symmetry and Related Properties via Maximum Principle,” Communications in Mathematical Physics, Vol. 68, No. 3, 1979, pp. 209-243. doi:10.1007/BF01221125
- B. Gidas, W.-M. Ni and L. Nirenberg, “Symmetry of Positive Solutions of Nonlinear Elliptic Equations in
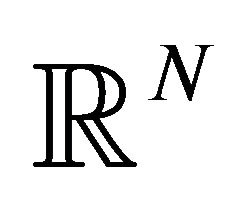 ,” In: Mathematical Analysis and Applications, Part A, Academic Press, New York, 1981, pp. 369-402.
,” In: Mathematical Analysis and Applications, Part A, Academic Press, New York, 1981, pp. 369-402. - L. Cafarelli, B. Gidas and J. Spruck, “Asymptotic Symmetry and Local Behavior of Semilinear Elliptic with Critical Sobolev Growth,” Communications on Pure and Applied Mathematics, Vol. 42, No. 3, 1989, pp. 271-297. doi:10.1002/cpa.3160420304
- H. Berestycki and L. Nirenberg, “On the Method of Moving Planes and the Sliding Method,” Bulletin of the Brazilian Mathematical Society, Vol. 22, No. 1, 1991, pp. 1-37.
- F. John, “Partial Differential Equations,” Springer-Verlag, New York, 1982.
- M. Protter and H. Weinberger, “Maximum Principle in Differential Equations,” Springer-Verlag, New York, 1984. doi:10.1007/978-1-4612-5282-5
- D. Gilbarg and N. Trudinger, “Elliptic Partial Differential Equations of Second Order,” Springer-Verlag, Berlin, Heidelberg, New York, 1977.

