ABSTRACT

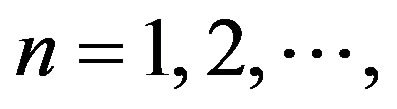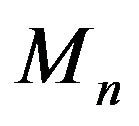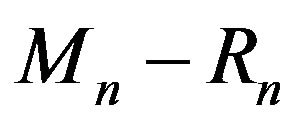In this paper, we propose a new class of discrete time stochastic processes generated by a two-color generalized Pólya urn, that is reinforced every time. A single urn contains a white balls, b black balls and evolves as follows: at discrete times we sample balls and note their colors, say are white and are black. We return the drawn balls in the urn. Moreover, 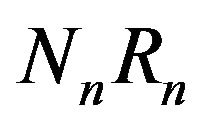new white balls and 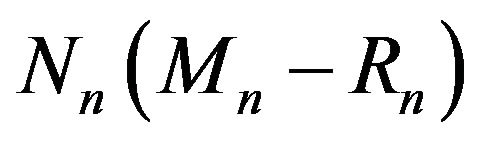new black balls are added in the urn. The numbers 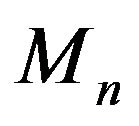and 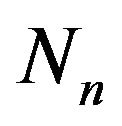are random variables. We show that the proportions of white balls forms a bounded martingale sequence which converges almost surely. Necessary and sufficient conditions for the limit to concentrate on the set 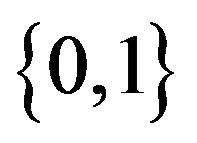are given.

1. Introduction

Urn models have been among the most popular probabilistic schemes and have received a lot of attention in the literature (see [1,2]). Let us describe the Pólya urn scheme briefly. In 1923, [3] proposed the following urn scheme to model processes such as the spread of infectious diseases. In this scheme, a single urn contains 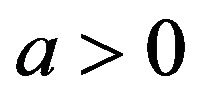white balls and black balls. One ball is drawn at random and then replaced, together with balls of the same color. The procedure is repeated n times. It is known that the sequence of the proportions of white balls is a martingale converging almost surely to a random variable having a beta distribution with parameters and. Since then, numerous generalizations and extentions of the Pólya urn have been studied : see [4-14]. In 1990, [6] generalized the Pólya urn model with the single change that the number of extra balls added in the urn is a function of time. One ball is drawn and is replaced in the urn along with F(n) balls of the same color. In his setup can be any function. He showed that the proportions of white balls converge almost surely and the limit has no atom except possibly at 0 or 1.

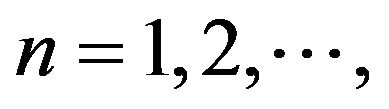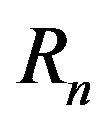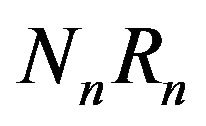In this paper, we propose a new class of discrete time stochastic processes generated by a two-color generalized Pólya urn that is reinforced every time. This is a generalization of the urn model considered in [10]. A single urn contains white balls and black balls: at discrete times we draw balls and note their colors, say are black and are white. We return the drawn balls to the urn. Moreover, new white balls and 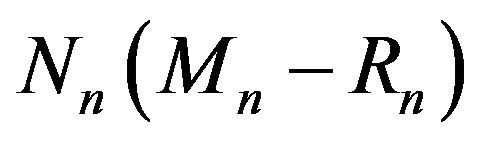new black balls are added in the urn. The numbers and 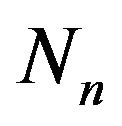are random variables in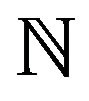. We show that the proportions of white balls form a bounded martingale sequence which converges almost surely. Necessary and sufficient conditions for the limit to have no atoms at 0 or 1 are given.

This paper is organized as follows. In Section 2, we set the probabilistic model for a randomly reinforced urn. In Section 3, we show that the proportions of white balls form a bounded martingale sequence which converges almost surely. Necessary and sufficient conditions for the limit to concentrate on the set 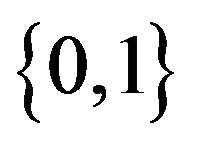are given. We conclude the paper by proving that interacting reinforced urn process are asymptotically exchangeable.

2. Model Description and Notation

On a rich enough probability space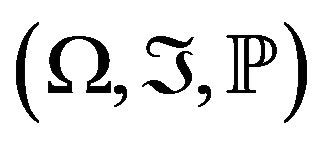, define two sequences 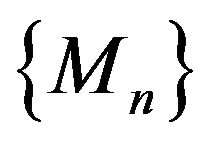and 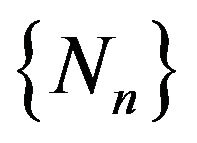of positive, integervalued random variables and let and 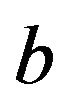are fixed positive integers. A randomly reinforced urn generates the stochastic processes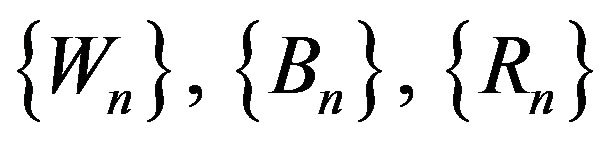. The sequences and 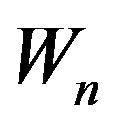respectively denote the number of black balls and white balls in the urn at time. The dynamics of the processes 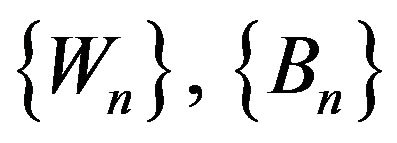and 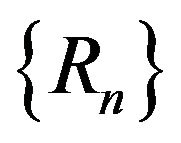are governed by the following: set 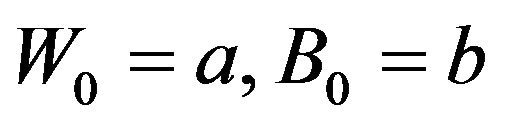and let

be a 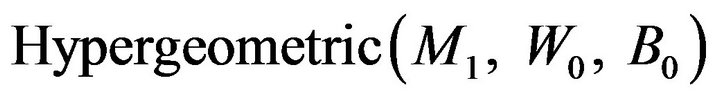random variable. Now we iterate this sampling scheme forever. Thus, at time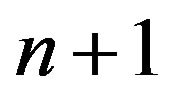, given the sigma-field 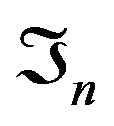generated by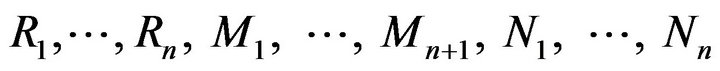, we consider that 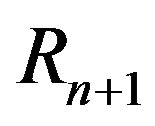is a Hypergeometric 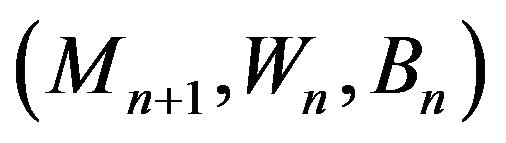random variable and we assume that and are independent conditionaly on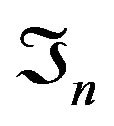. Finally, we set

(2.1)

This is a generalization of the reinforced urn model considered in [10]. Assume that, at each time periode a new firm appears on the market and have to choose operative systems among the systems A and B, for its computers. The firm can choose 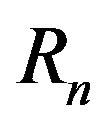blocks of size of computers having the operative system. This choice depends on the number of computers having the operative system A on the market. The process 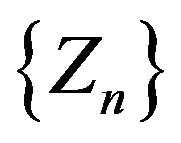given in (2.1) is going to describe the evolution along time of the proportion of computers operating systems A.

3. Martingale Property

The process 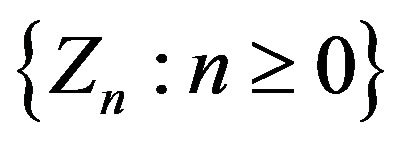is of primary interest for studying the stochastic processes generated by this generalization of Pólya’s urn. Here represents the proportion of white balls in the urn at time. We show that these proportions form a bounded martingale. This martingale converges almost surely. The next theorem is of fundamental importance, this is our main result.

Theorem 3.1. The sequence 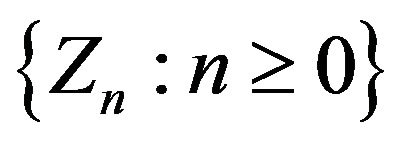is a bounded martingale with respect to the filtration 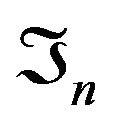taking values in Therefore, it converges almost surely to a random variable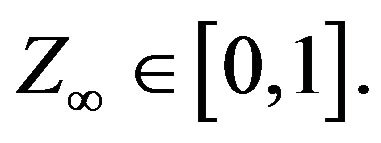

Proof.

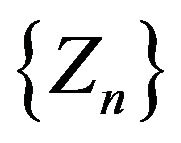Here with being the total number of balls in the urn at time. Now let us show that is a martingale. In fact

This shows that 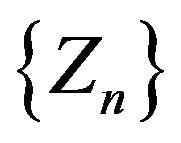is 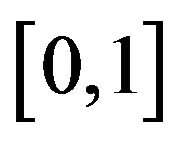-bounded martingale with respect to the filtration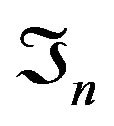. Hence, there exists a random variable 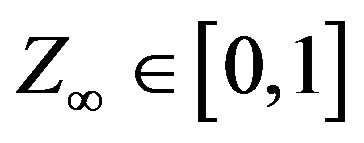such that 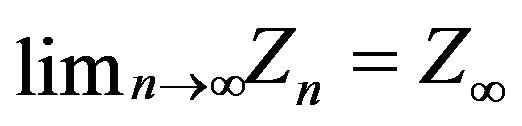on a set of probability one.

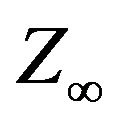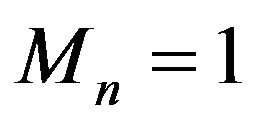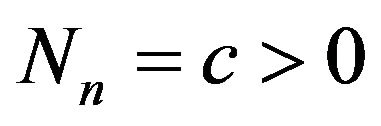The exact distribution of is unknown except in a few particular cases. The situation where almost surely for all and almost surely for all n corresponds to the classical Pólya-Eggenberger contagious urn scheme. In this case 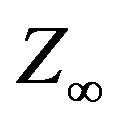has a beta distribution with parameters 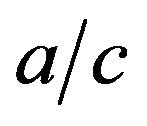and. Let us continue with the general case.

Theorem 3.2. The limit is Bernoulli distributed if and only if

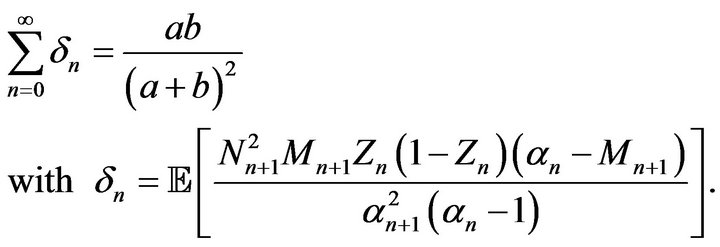
Proof. From (2.1) we have

thus we get

The transition between the second equality and the third equality relies on the fact that, conditionally on are independent. As a result

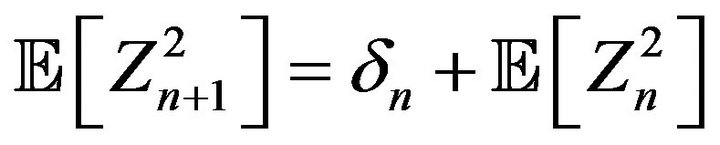, (3.1)

with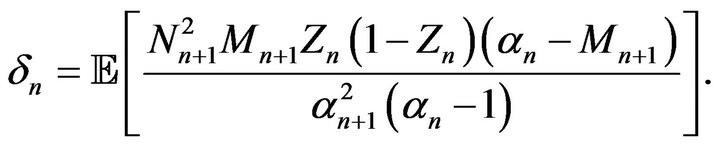

Now we set, and we have from (3.1)

Consequently, converges to if and only if V_n converges to, which happens whenever

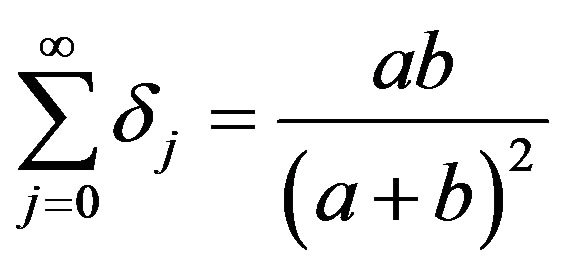. This is the desired result because a random variable 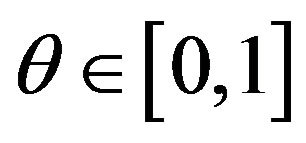satisfies the condition

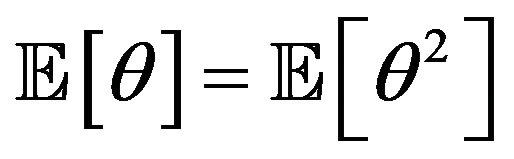if and only if is concentrated on the set.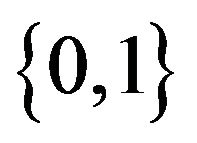

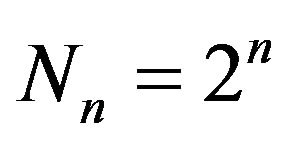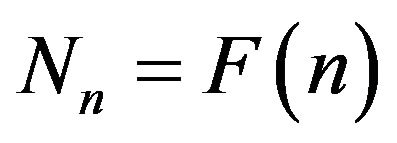This theorem applies, for example, when and almost surely. In fact from (3.1), we remark that when and almost surely (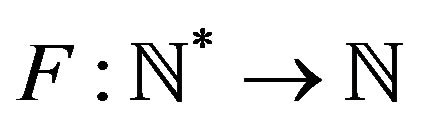and be any function) we have

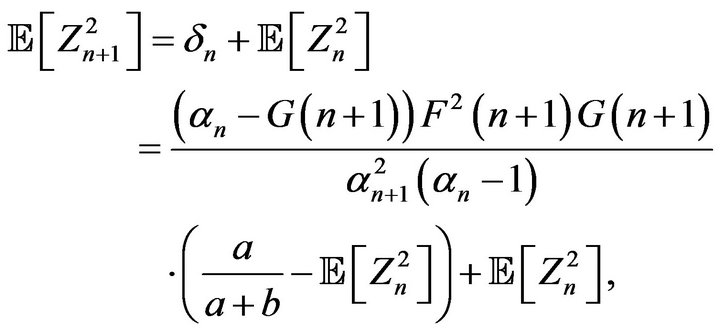
and we deduce

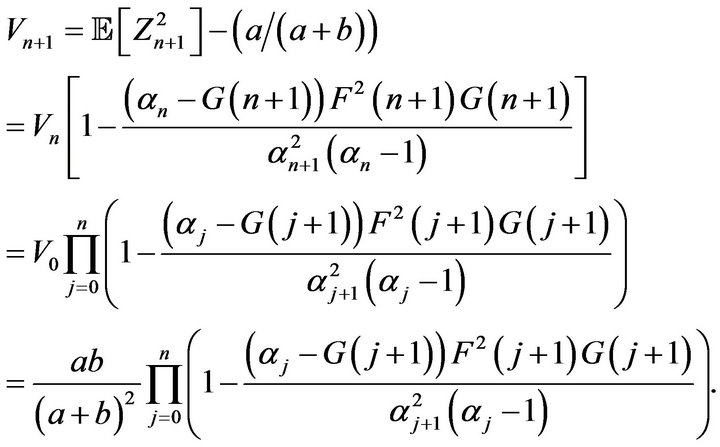
Consequently, 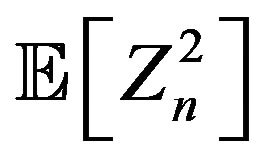converges to if and only if 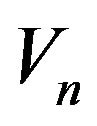converges to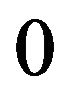, which happens whenever the product values

converges to

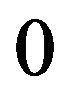. This happens whenever

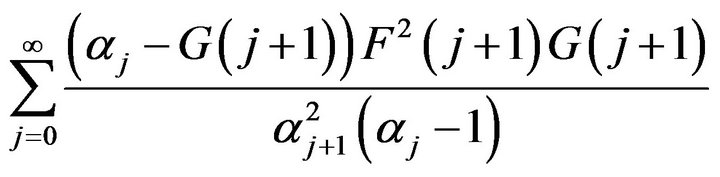diverges.

Moreover, if 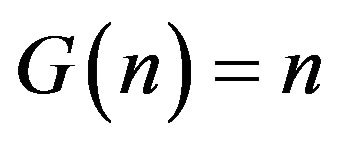and then

the general term of the series being proportional to.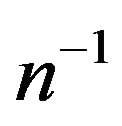

From Theorem 3.1 we deduce thatCorollary 3.3. Assume that the sequence satisfies the following conditions

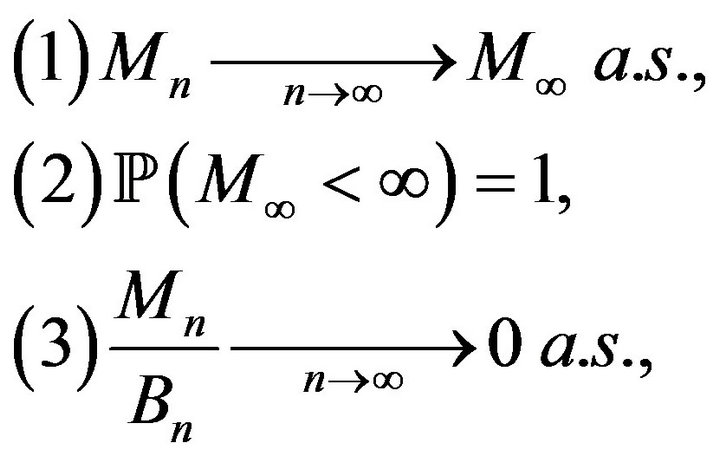
then

and

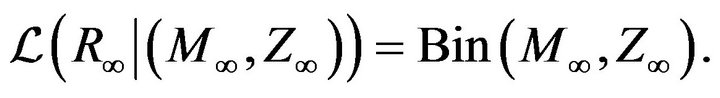
Proof. For every fixed 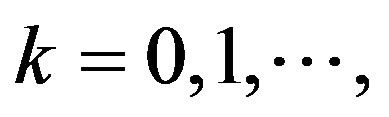and for sufficiently large,

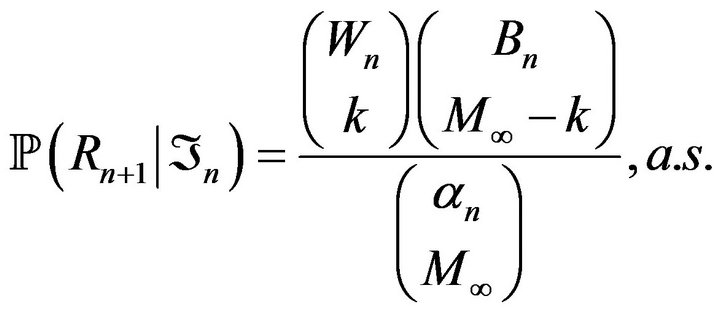
Then, using the well know convergence of the hypergeometric probabilities to the binomial, we have

and the conclusion follows from the bounded convergence theorem.

As a consequence of Theorem (3.2), we have the following.

Corollary 3.4. Assume that the sequences 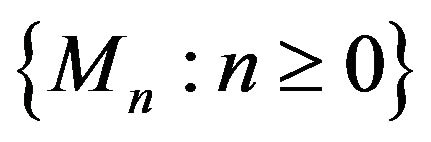and 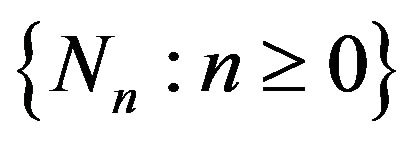are bounded then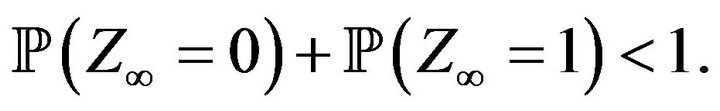

Proof. Since the sequences 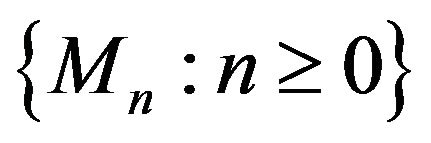and 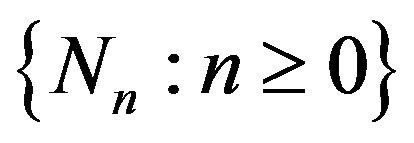are bounded by some constant 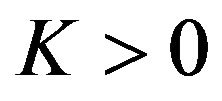and for all 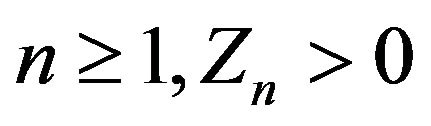we obtain from (3.1) that

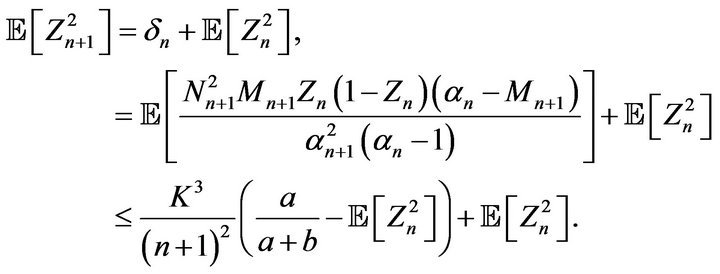
Let 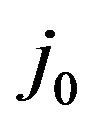be such that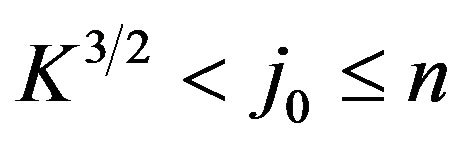. We obtain that

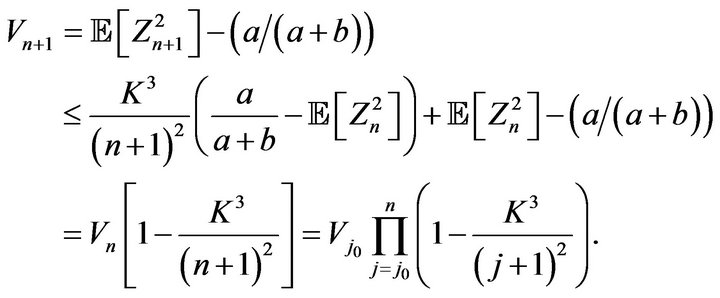
Now, since, then

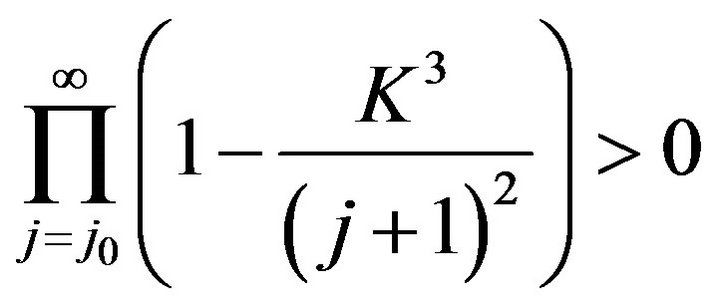and

so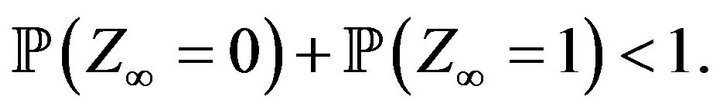

The final result in this section shows that the law of large numbers holds for interacting reinforced urn systems.

Theorem 3.5. We have

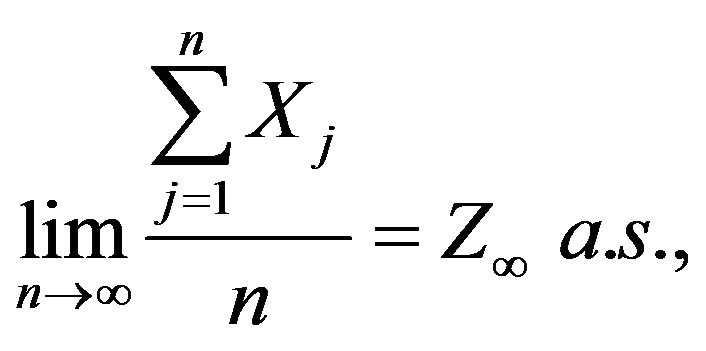
with

Proof. Using Cesàro’s summability result we obtain that,

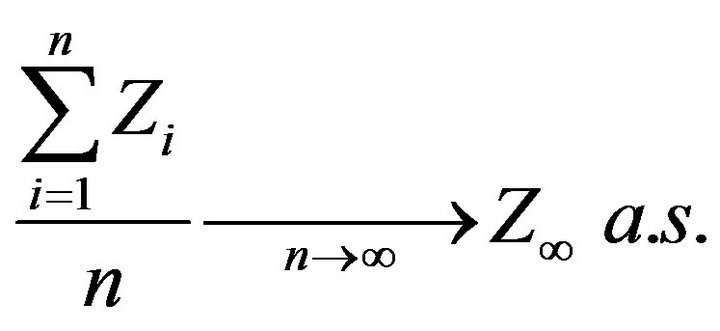
Let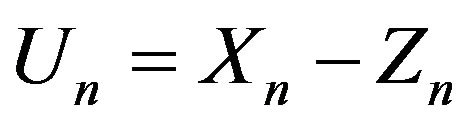. Since 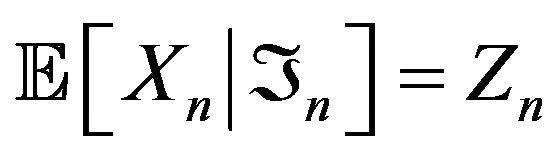then we have the following1), for all.

2) For all we have

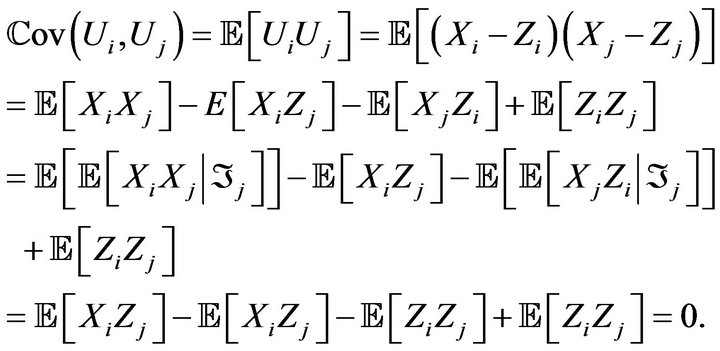
This shows that the sequence is orthogonal, with zero mean.

3) For, we have

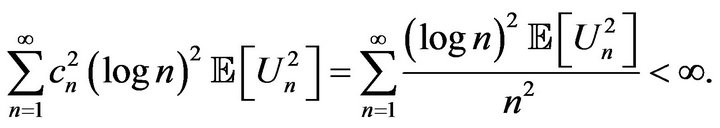
Therefore, the sequence satisfies the conditions of Hall’s theorem (see [15], Theorem 2.8, p. 22), and we can conclude that the series

(3.2)

Finally, Kronecker’s lemma yields

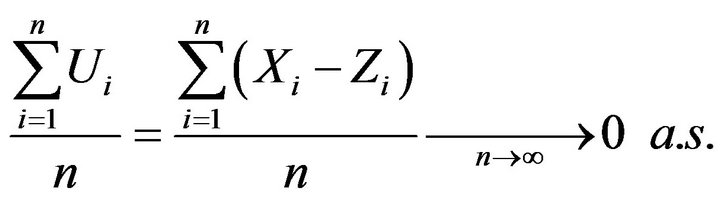(3.3)

This shows that

(3.4)

which is the announced result.

4. Asymptotic Exchangeability

According to [16] a sequence of random variables is asymptotically exchangeable if the joint distribution of the sequence 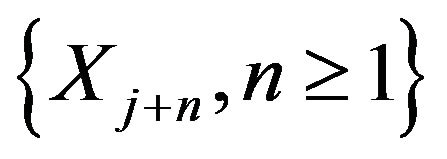converges as to the distribution of some exchangeable sequence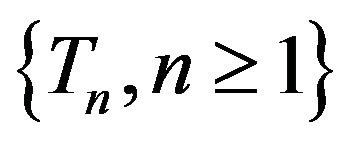. In particular, we have the following lemma due to [17].

Lemma 6. (Aldous)

Consider 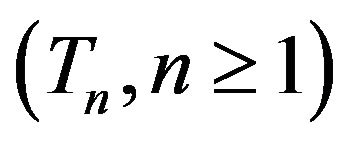be an infinite exchangeable sequence directed by.

1) Let 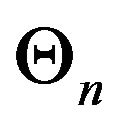be a regular conditional distribution for 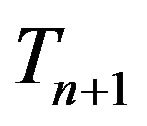given.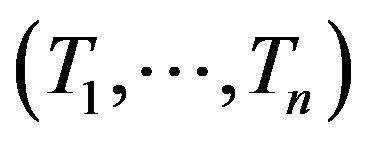

Then

(4.1)

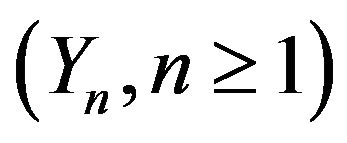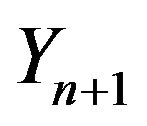2) Let be an infinite sequence. Let be a regular conditinal distribution for given, and suppose that

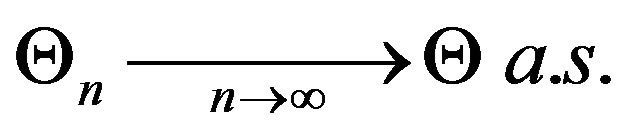
Then

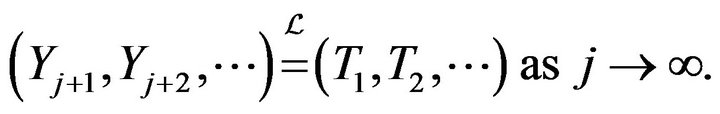(4.2)

Theorem 3.1 together with Lemma yield that the sequence of random variables 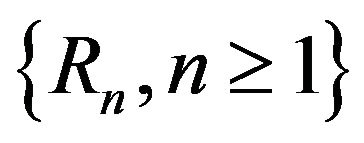is asymptotically exchangeable. The main result of this section is the following.

Theorem 4.1. Under the conditions of Corollary 3.3, the sequence of random variables 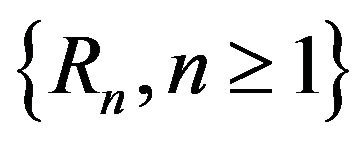is asymptotically exchangeable.

Proof. For all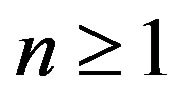, the conditional distribution of given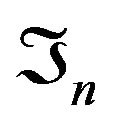, is such that

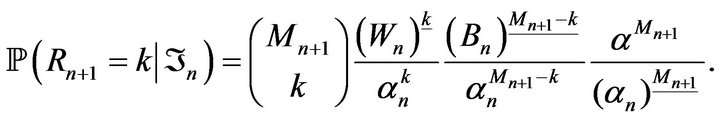
Hence, as in Corollary 3.3, we obtain that

The conclusion comes from Lemma 4.1, part (b).

5. Conclusions

Urn model have been widely studied and applied in both scientific and social science disciplines. In this paper, we have proposed a general class of discrete stochastic processes generated by a two-color generalized Pólya urn. This model generalizes a model previously studied by [10]. This paper also shows that the proportion of white balls form a bounded martingale sequence which converge almost surely. Asymptotic properties and asymptotic exchangeability are given. However, the complete characterization of the limit still remains to be resolved in the future and it would be interesting to explore the possibility extensions to more than two colors.

Another important application of this urn models is to randomize treatments to patients in a clinical trial (see [18]). Consider an urn containing balls of two type, representing two treatements. Patients normally arrive sequentially, and treatment assigned on the urn composition and previous treatment outcomes. For more details analysis on this application, we refer to [13].

6. Acknowledgements

The authors want to thank Professor Éric Marchand for his numerous advices and helpful discussions. The second author wants to thank NSERC for the financial support.

REFERENCES

NOTES

^*Corresponding author.