Applied Mathematics
Vol. 3 No. 1 (2012) , Article ID: 16757 , 7 pages DOI:10.4236/am.2012.31016
A Statistical Analysis of Intensities Estimation on the Modeling of Non-Life Insurance Claim Counting Process
Department of Statistics, Kasetsart University, Bangkok, Thailand
Email: ur_jaroen@yahoo.com, {fsciwnb, fsciamu}@ku.ac.th
Received October 1, 2011; revised November 19, 2011; accepted November 28, 2011
Keywords: Estimating Function; Zero Mean Martingale; Non-Life Insurance Claim Counting Process; Poisson Process; Bell-Shaped Intensity
ABSTRACT
This study presents an estimation approach to non-life insurance claim counts relating to a specified time. The objective of this study is to estimate the parameters in non-life insurance claim counting process, including the homogeneous Poisson process (HPP) and the non-homogeneous Poisson process (NHPP) with a bell-shaped intensity. We use the estimating function, the zero mean martingale (ZMM) as a procedure of parameter estimation in the insurance claim counting process. Then, Λ (t), the compensator of N (t) is proposed for the number of claims in the time interval (0, t]. We present situations through a simulation study of both processes on the time interval (0, t]. Some examples of the situations in the simulation study are depicted by a sample path relating N (t) to its compensator Λ (t). In addition, an example of the claim counting process illustrates the result of the compensator estimate misspecification.
1. Introduction
Nowadays, insurance is a common way of managing risks and the insurance industry has grown rapidly over time. Insurance industry owners, especially, consider the components of risk management, such as the premiums which are the main income of insurance businesses, reserves, underwriting, investment planning, reinsurance planning, etc. Also, estimating claims play an important part in each component in the non-life insurance field. In the past four decades, a few researchers have studied the claim counts model for non-life insurance. Klugman et al. [1] and Denuit et al. [2] were interested in studying the frequency distribution of insurance claims, including the parameter estimation methods. Bühlmann [3,4] presented the credibility approach in the form of a linear function to estimate and predict the expected claim counts in upcoming periods, using past experience of claims as a risk class or related risk classes. Bühlmann’s credibility approach is interesting and can be extended to other approaches, such as the Bühlmann-Straub model, Jewell’s model or the Exact credibility approach, etc., (see Klugman et al. [1]). Calculating the expected claim counts using the credibility approach only depends on the information from prior experience of claim counts, and does not consider the occurrence behavior of claim counts over time. Some authors have found an alternative approach to claim counts relating to a specified time or their behavior over time, for example, Mikosch [5] viewed the claim counting process as a homogeneous Poisson process (HPP) in the Cramér-Lundberg model, one of the most popular and useful risk models in non-life insurance, and Matsui and Mikosch [6] also considered a Poisson cluster model for the modeling of a total claims amount by a point of claim counts as an HPP with a constant rate of occurrence called the constant intensity. For some non-life insurance portfolios, the claim counts during a time period are caused by periodic phenomena or seasonality. These claim counts are modeled in terms of a non-homogeneous Poisson process (NHPP) with a period time-dependent intensity rate. Morales [7] presented the periodic risk model consisting of the claim counting process with a bell-shaped intensity function (called the Gaussian intensity) of the form
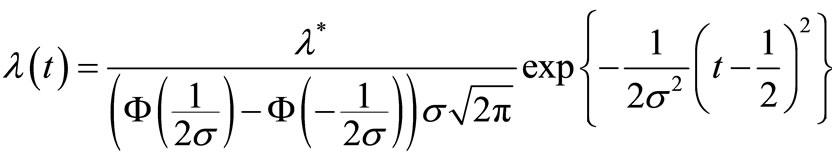 ;
;
 ,
, 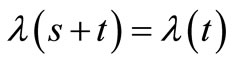 , where s is an initial season, s = 0, 1, 2, ···, σ and
, where s is an initial season, s = 0, 1, 2, ···, σ and 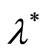 are parameters, and
are parameters, and 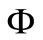 is the standard normal distribution function. He estimated the unknown parameters of the periodic model intensity by using the maximum likelihood estimation (MLE), and he also considered evaluating the ruin probability through a simulation study. Furthermore, Lu and Garrido [8] explored the periodic NHPP model with a Beta-shaped intensity function.
is the standard normal distribution function. He estimated the unknown parameters of the periodic model intensity by using the maximum likelihood estimation (MLE), and he also considered evaluating the ruin probability through a simulation study. Furthermore, Lu and Garrido [8] explored the periodic NHPP model with a Beta-shaped intensity function.
The precision of claim count estimation is a key to running the insurance business successfully. In this study, we will present an estimation approach to non-life insurance claim counts related to a specification of the two different claim counting processes, i.e., HPP, and NHPP with a bell-shaped intensity function, through a simulation study. Our purpose is to estimate the parameters in the non-life insurance claim counting process. The parameters in the insurance claim counting process, intensity function ( ) in terms of mean value function
) in terms of mean value function 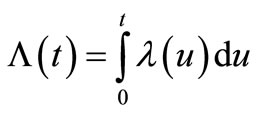 , makes a complicated distribution function of insurance claim counts. An estimating function, such as the zero mean martingale (ZMM), is used here as a procedure of parameter estimation of an insurance claim counts model, and the parameters of model intensity are estimated by the MLE method.
, makes a complicated distribution function of insurance claim counts. An estimating function, such as the zero mean martingale (ZMM), is used here as a procedure of parameter estimation of an insurance claim counts model, and the parameters of model intensity are estimated by the MLE method.
2. A Definition of the Non-Life Insurance Claim Counting Process
We define the insurance claim counting process 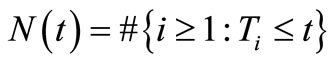 ;
;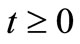 , and the insurance claim counts which have occurred in the time interval (0,t] where
, and the insurance claim counts which have occurred in the time interval (0,t] where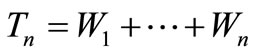 ;
;  is a claim arrival time and
is a claim arrival time and 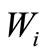 is independent and identically distributed (iid) Exponential with the parameter
is independent and identically distributed (iid) Exponential with the parameter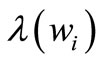 , called the intensity rate,
, called the intensity rate, 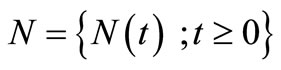 is a counting process which is non-decreasing,
is a counting process which is non-decreasing, 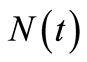 can be written as
can be written as 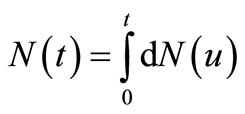 where
where 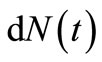 is an increment of
is an increment of  in a small fraction period. The Poisson distribution is often considered as a common distribution modeling of insurance claim counts, and our main interest in the process of insurance claim counts is the Poisson process, i.e., HPP, and NHPP with the bell-shaped intensity function. This interest lies in the intensity rate, in which the insurance claim counts occur, and whether these change over time. In an HPP, the intensity rate is constant for a given time, and the process is called an NHPP, if it changes as a function of time [2,5,9].
in a small fraction period. The Poisson distribution is often considered as a common distribution modeling of insurance claim counts, and our main interest in the process of insurance claim counts is the Poisson process, i.e., HPP, and NHPP with the bell-shaped intensity function. This interest lies in the intensity rate, in which the insurance claim counts occur, and whether these change over time. In an HPP, the intensity rate is constant for a given time, and the process is called an NHPP, if it changes as a function of time [2,5,9].
On a probability space ,
, 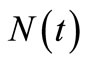 is Poisson distributed with the parameter
is Poisson distributed with the parameter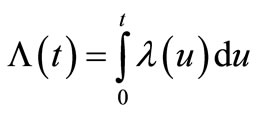 , with a mean value function
, with a mean value function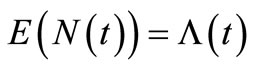 . As
. As 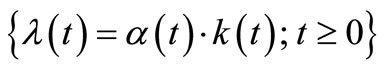 is called the multiplicative intensity, where
is called the multiplicative intensity, where  and
and 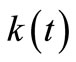 are defined as the intensity rate and the exposure risk, respectively. We consider
are defined as the intensity rate and the exposure risk, respectively. We consider 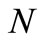 as a non-decreasing right continuous step function 0 at time t = 0 and jumps of size 1, and
as a non-decreasing right continuous step function 0 at time t = 0 and jumps of size 1, and
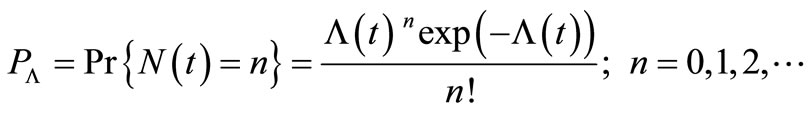
and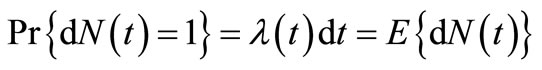 .
.
In this study we consider the insurance claim counting process which are the HPP with , a constant intensity, and the NHPP with a bell-shaped intensity function as an initial season, s = 0 [7],
, a constant intensity, and the NHPP with a bell-shaped intensity function as an initial season, s = 0 [7],
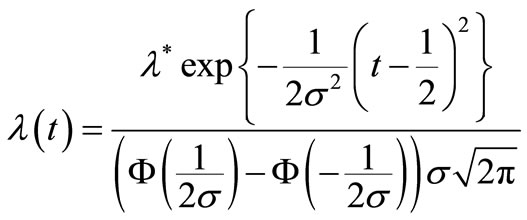 (1)
(1)
where 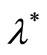 (an average number of claims over a period) and
(an average number of claims over a period) and  are the parameters,
are the parameters, 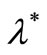 ,
,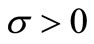 .
.
3. Parameter Estimation in the Non-Life Insurance Claim Counting Process
In this section, we introduce the methods which are useful for parameter estimation in the non-life insurance claim counting process, including the estimating function, the martingale method, and the MLE.
3.1. Estimating Function
On a probability space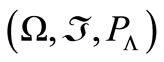 , where
, where ,
,  is an open interval on the real line,
is an open interval on the real line, 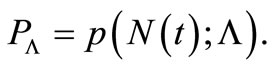 Suppose that the observation
Suppose that the observation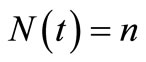 , the estimating functions,
, the estimating functions, 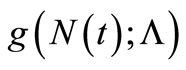 , are functions of
, are functions of  and the parameter
and the parameter . By solving
. By solving , a so-called estimating equation, an estimate of
, a so-called estimating equation, an estimate of  is obtained. Then
is obtained. Then 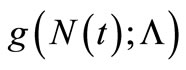 is an unbiased estimating function if
is an unbiased estimating function if  for all
for all 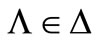 [10].
[10].
In this study, the estimating function for parameter estimation in the insurance claim counting process is provided by the martingale method.
3.2. The Martingale Method
The martingales are random processes relating to time. On a probability space , we suppose the increasing family
, we suppose the increasing family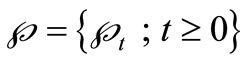 , a filtration or history
, a filtration or history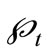 , which is the available data at the time
, which is the available data at the time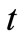 . The process
. The process  is a martingale with respect to
is a martingale with respect to 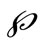 if
if 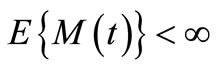 exist, and
exist, and 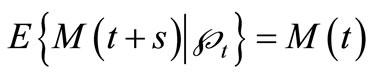 for all
for all . As a result of the properties of the martingale,
. As a result of the properties of the martingale,  for all
for all , then
, then 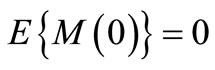 for a ZMM [11,12].
for a ZMM [11,12].
This study of the martingale method is useful for constructing an estimating function for a parameter estimation in the insurance claim counting process. The process takes place over a small time interval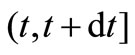 ,
,  and as a result of the meaning of martingale property, the martingale can be written as
and as a result of the meaning of martingale property, the martingale can be written as
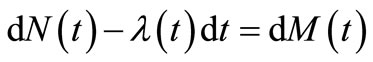 (2)
(2)
which is a martingale-difference. Then, the following martingale is
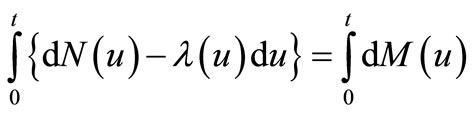 or it is rewritten in the form of
or it is rewritten in the form of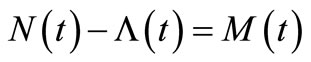 , is a ZMM. Based on ZMM, we obtain
, is a ZMM. Based on ZMM, we obtain
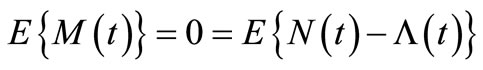 .
.
Thus,  is an estimating equation for the parameter estimation in the insurance claim counting process. Also, as a result of the parameter estimate in the process, this can be interpreted as an
is an estimating equation for the parameter estimation in the insurance claim counting process. Also, as a result of the parameter estimate in the process, this can be interpreted as an 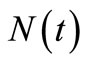 estimate or, in other words,
estimate or, in other words, 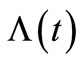 is called the compensator of
is called the compensator of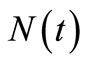 , and this estimate is useful for predicting the times of occurrence of insurance claim counts [12]. We can depict the systematic part of the process of insurance claim counts,
, and this estimate is useful for predicting the times of occurrence of insurance claim counts [12]. We can depict the systematic part of the process of insurance claim counts,  , related to its compensator,
, related to its compensator, 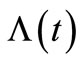 , and the associated martingale
, and the associated martingale 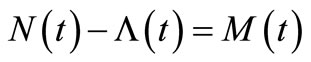 in Figures 1(a) and (b), respectively, based on a sample of 15 independent random times of claims occurrence in the NHPP with an intensity of
in Figures 1(a) and (b), respectively, based on a sample of 15 independent random times of claims occurrence in the NHPP with an intensity of
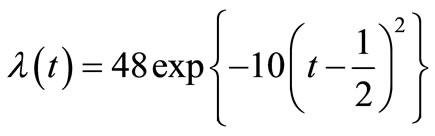 .
.
3.3. A Maximum Likelihood Estimation of the Model Intensity
In order to get the estimate of the compensator of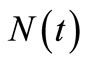 ,
, 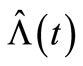 , on the modeling of the non-life insurance claim counting process, both the HPP and NHPP, the parameters of the intensity function are estimated by the MLE method. Given
, on the modeling of the non-life insurance claim counting process, both the HPP and NHPP, the parameters of the intensity function are estimated by the MLE method. Given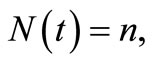 we suppose that
we suppose that 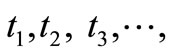
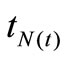 are the arrival times of the claims in the time interval
are the arrival times of the claims in the time interval 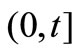 with a cumulative distribution function (a general order statistics model)
with a cumulative distribution function (a general order statistics model)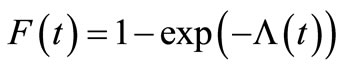 . The likelihood function [5,13] is given by
. The likelihood function [5,13] is given by
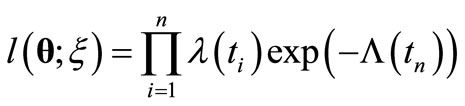 (3)
(3)
where 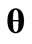 is a vector of the parameters of the model intensity,
is a vector of the parameters of the model intensity,  denotes the set of arrival times, the intensity
denotes the set of arrival times, the intensity  in the HPP is
in the HPP is 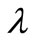 as
as  and the intensity
and the intensity 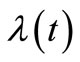 in the NHPP is given in equation (1) as
in the NHPP is given in equation (1) as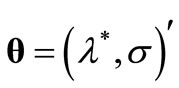 . The estimate of
. The estimate of 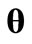 can be simply found if we take the logarithm of the likelihood function and we seek a value of
can be simply found if we take the logarithm of the likelihood function and we seek a value of 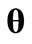 that maximizes the log likelihood function. The following parameter estimate of the HPP model is:
that maximizes the log likelihood function. The following parameter estimate of the HPP model is:
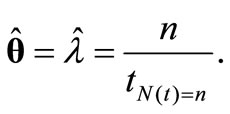 For the NHPP, the calculation of the
For the NHPP, the calculation of the
 (a) (b)
(a) (b)
Figure 1. In a sample of 15 independent random times of claims occurrence with the intensity , (a) Non-life insurance claim counting process
, (a) Non-life insurance claim counting process 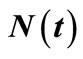 related to its compensator
related to its compensator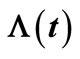 ; and (b) Martingale
; and (b) Martingale 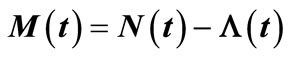 .
.
MLE estimator of the model intensity, which is a complicated system of equations, requires an iterative procedure, i.e. the Newton-Raphson algorithm, to solve these equations [2].
4. Simulation Study
In this study, a simulation study is used to investigate how the observation of the non-life insurance claim counting process can be used to estimate its model parameter, i.e. intensity 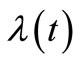 or in term
or in term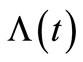 , using the estimating function provided by the martingale method with ZMM. In particular, the HPP of the insurance claim counts, with
, using the estimating function provided by the martingale method with ZMM. In particular, the HPP of the insurance claim counts, with  as a constant intensity and the NHPP of the insurance claim counts, with
as a constant intensity and the NHPP of the insurance claim counts, with 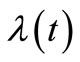 given in equation (1) as a bell-shaped intensity, we must first consider the simulation study of the HPP of the insurance claim counts in the time interval (0,t] in which the observation involves the claim arrival times,
given in equation (1) as a bell-shaped intensity, we must first consider the simulation study of the HPP of the insurance claim counts in the time interval (0,t] in which the observation involves the claim arrival times, 
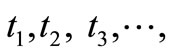 , generated by applying an exponential law with the intensity
, generated by applying an exponential law with the intensity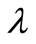 , i.e. with a mean
, i.e. with a mean 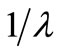 as λ = 0.1 and 10. The second simulation study of the insurance claim counting process, in which we consider the NHPP with a bell-shaped intensity function, or as the general form of mean value function
as λ = 0.1 and 10. The second simulation study of the insurance claim counting process, in which we consider the NHPP with a bell-shaped intensity function, or as the general form of mean value function
 ,
,
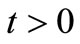 , where
, where 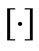 is the greatest integer function, the claim arrival times,
is the greatest integer function, the claim arrival times,  , can be simulated by using the mean value function
, can be simulated by using the mean value function 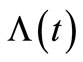 as a claim arrival time of the HPP with mean one [7]. It implies that
as a claim arrival time of the HPP with mean one [7]. It implies that  are independent and exponentially distributed with mean one, where
are independent and exponentially distributed with mean one, where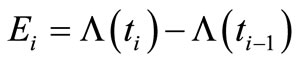 , for all
, for all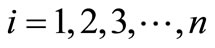 . So, in this study, the
. So, in this study, the 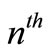 claim arrival time,
claim arrival time, 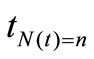 , is generated by
, is generated by
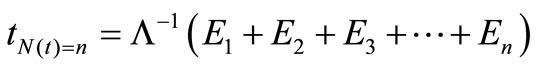 (4)
(4)
where 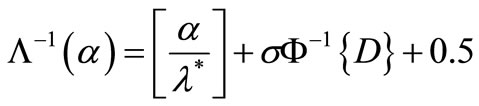 is the invertible function of
is the invertible function of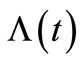 ,
, 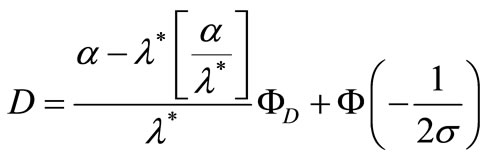 ,
, 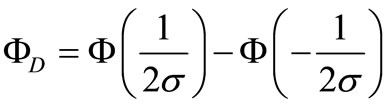 and
and 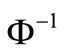 is the quantile function of a standard normal distribution, with
is the quantile function of a standard normal distribution, with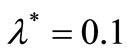 ,
, 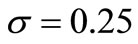 ,
,  ,
, 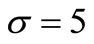 ,
, 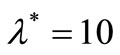 ,
, 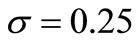 and
and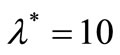 ,
, .
.
In this simulation study of both the HPP and the NHPP of the insurance claim counts in the time interval (0,t], the number of observations,  , is composed of 5, 10, 15 and 20. The HPP and the NHPP are carried out with 5000 sample paths. In each sample path, the parameter estimate of the model intensity is computed using the MLE method and the estimating function, such as the ZMM which is used to estimate the parameter
, is composed of 5, 10, 15 and 20. The HPP and the NHPP are carried out with 5000 sample paths. In each sample path, the parameter estimate of the model intensity is computed using the MLE method and the estimating function, such as the ZMM which is used to estimate the parameter 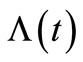 in the process (or the compensator
in the process (or the compensator 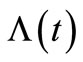 of
of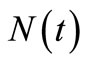 ), i.e. fitting the compensator estimate
), i.e. fitting the compensator estimate 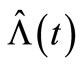 to
to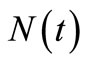 . Also, the mean squared error (MSE) is provided to measure things, fitting
. Also, the mean squared error (MSE) is provided to measure things, fitting 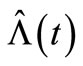 to
to 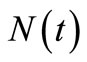 as the following form,
as the following form,
 where
where 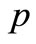 denotes the number of sample paths. Notice that the MSE of the compensator estimate
denotes the number of sample paths. Notice that the MSE of the compensator estimate 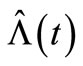 of
of 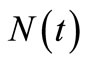 for both processes, as shown in Tables 1 and 2, depends on the parameters of the model intensity as the following details, for the HPP with a constant intensity
for both processes, as shown in Tables 1 and 2, depends on the parameters of the model intensity as the following details, for the HPP with a constant intensity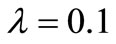 , a small intensity rate, and the MSE of the compensator estimate
, a small intensity rate, and the MSE of the compensator estimate 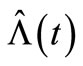 of
of 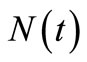 increases exponentially as the number of observations increases. On the other hand, the same process with
increases exponentially as the number of observations increases. On the other hand, the same process with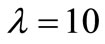 , the MSE of the compensator estimate
, the MSE of the compensator estimate 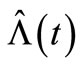 of
of 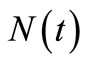 decreases exponentially, while the observation number increases until the observed 15 times of claims occurrence, and then the MSE value begins to increase as the observation number increases. For the NHPP with a bell-shaped intensity, the
decreases exponentially, while the observation number increases until the observed 15 times of claims occurrence, and then the MSE value begins to increase as the observation number increases. For the NHPP with a bell-shaped intensity, the
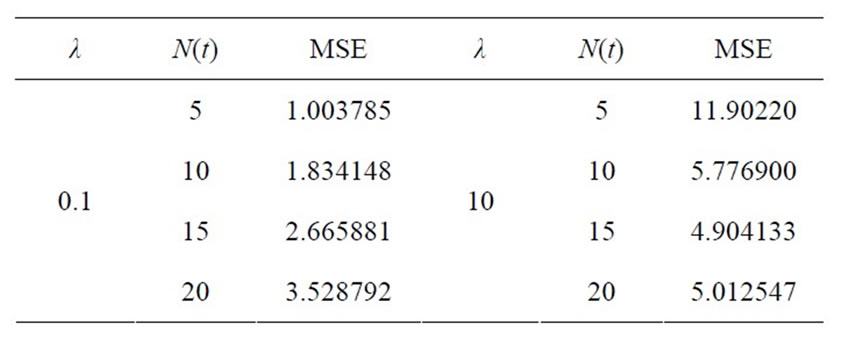
Table 1. MSE of the compensator estimate 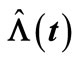 of
of 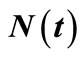 in the HPP of non-life insurance claim counts.
in the HPP of non-life insurance claim counts.
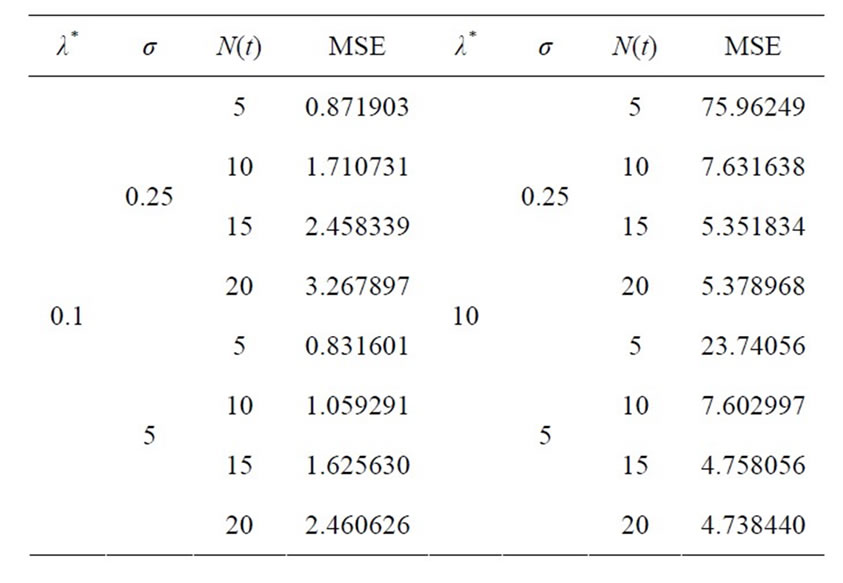
Table 2. MSE of the compensator estimate  of
of  in the NHPP of non-life insurance claim counts.
in the NHPP of non-life insurance claim counts.
parameters of its model intensity ,
,  and
and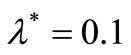 ,
, 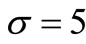 (a small average number of a claims over a period), the MSE of the compensator estimate
(a small average number of a claims over a period), the MSE of the compensator estimate  of
of 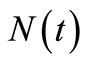 increases as the observation number increases. When we consider the NHPP between the parameters of the model intensity
increases as the observation number increases. When we consider the NHPP between the parameters of the model intensity ,
, 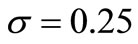 and
and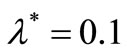 ,
, 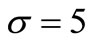 , we found that in the process with the parameters of the model intensity
, we found that in the process with the parameters of the model intensity ,
,  , the MSE of the compensator estimate
, the MSE of the compensator estimate 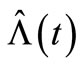 of
of  is much lower. In the same NHPP with the parameters of model intensity
is much lower. In the same NHPP with the parameters of model intensity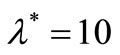 ,
, 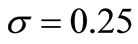 , the MSE of the compensator estimate
, the MSE of the compensator estimate  of
of  decreases while its observation number increases until the observed 15 times of claims occurrence, and then its MSE values begins to increase as the observation number increases. The MSE of the compensator estimate
decreases while its observation number increases until the observed 15 times of claims occurrence, and then its MSE values begins to increase as the observation number increases. The MSE of the compensator estimate 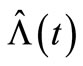 of
of  in the same NHPP with the parameters
in the same NHPP with the parameters ,
, 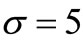 decreases exponentially as its observation number increases. When we consider the NHPP between the parameters of the model intensity
decreases exponentially as its observation number increases. When we consider the NHPP between the parameters of the model intensity ,
, 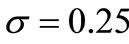 and
and ,
, 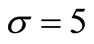 , we found that in the process with the parameters of the model intensity
, we found that in the process with the parameters of the model intensity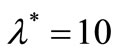 ,
, 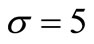 , the MSE of the compensator estimate
, the MSE of the compensator estimate  of
of  is much lower than the other one.
is much lower than the other one.
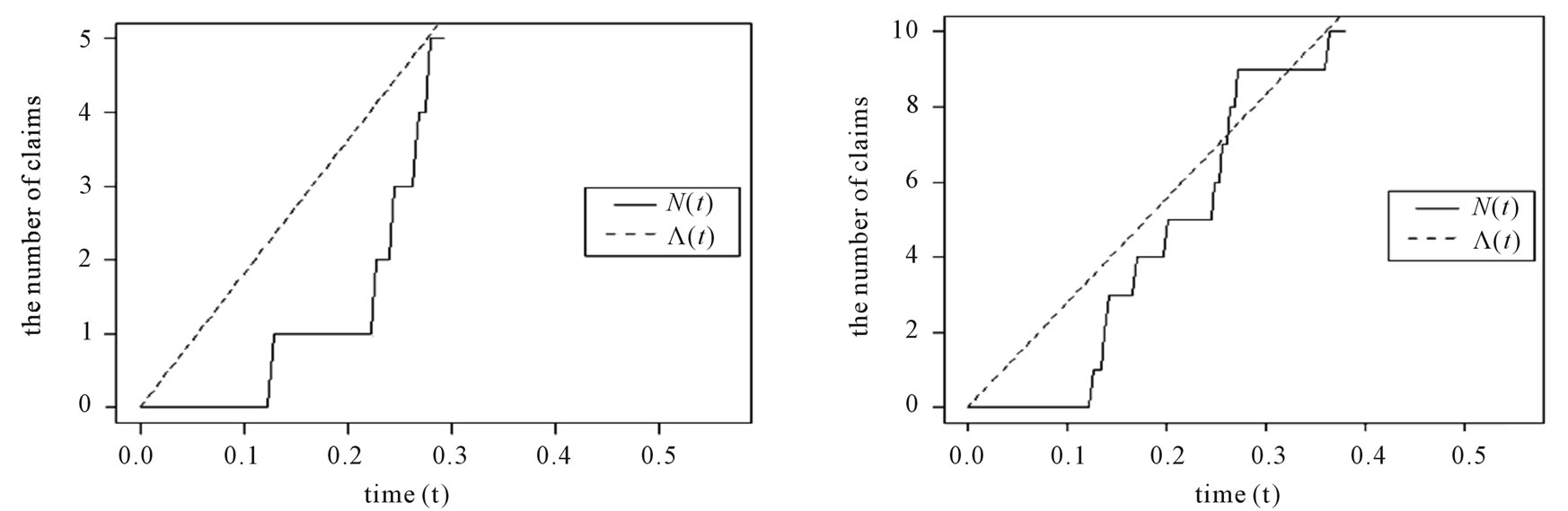
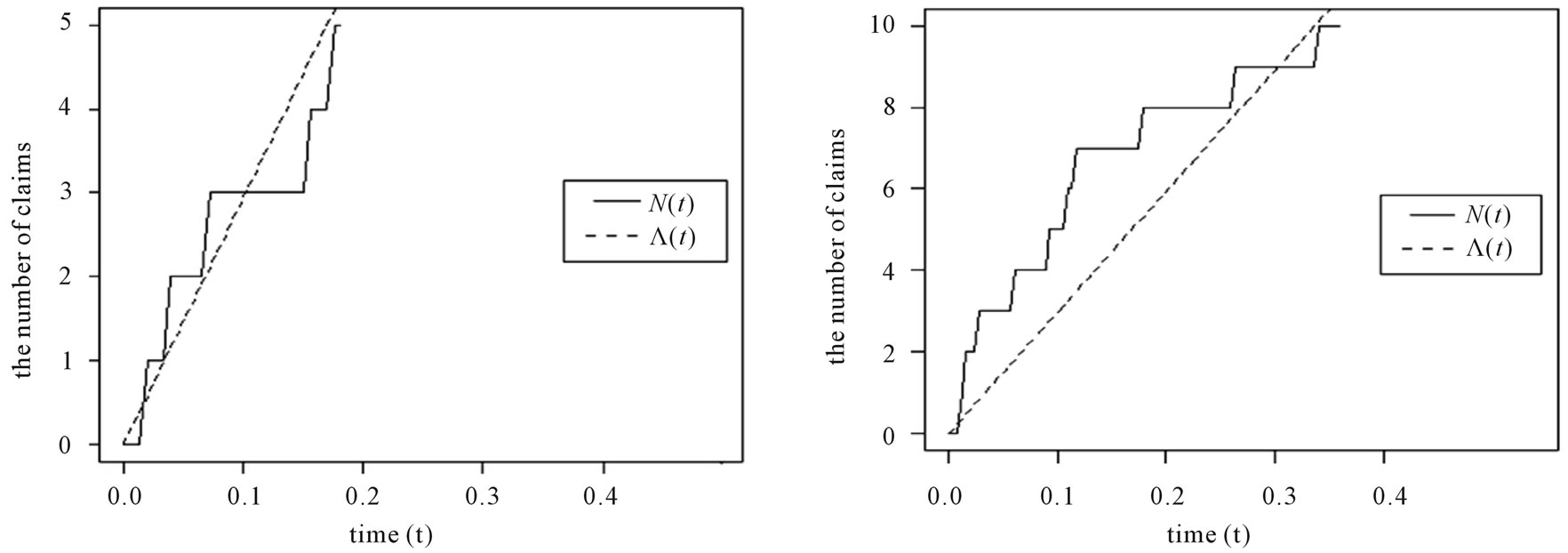
Some examples in these situations of both the HPP and the NHPP with a bell-shaped intensity of non-life insurance claim counts based on a sample of 5, 10, 15 and 20 times of claims occurrence are illustrated in Figures 2 and 3, including the  and its compensator
and its compensator . Figure 2 shows a sample path of the HPP with a constant intensity
. Figure 2 shows a sample path of the HPP with a constant intensity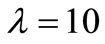 . The
. The 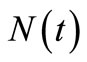 and its compensator
and its compensator 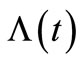 are characterized by the intensity
are characterized by the intensity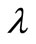 , i.e.
, i.e.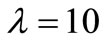 , the compensator
, the compensator 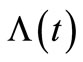 fits well with
fits well with , as the observation number is 15 and 20 (slightly larger than the intensity
, as the observation number is 15 and 20 (slightly larger than the intensity ). Similarly, the
). Similarly, the 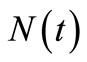 and its compensator
and its compensator 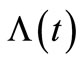 in the NHPP are characterized by the parameters of the model bell-shaped intensity
in the NHPP are characterized by the parameters of the model bell-shaped intensity ,
, 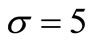 in Figure 3. The compensator
in Figure 3. The compensator 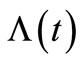 fits with
fits with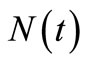 , as the observation number is 15 and 20 (slightly larger than the parameter of model intensity
, as the observation number is 15 and 20 (slightly larger than the parameter of model intensity ). Figure 4 illustrates a sample path of NHPP, and we can see the difference with the compensator estimate which
). Figure 4 illustrates a sample path of NHPP, and we can see the difference with the compensator estimate which
 (a)
(a)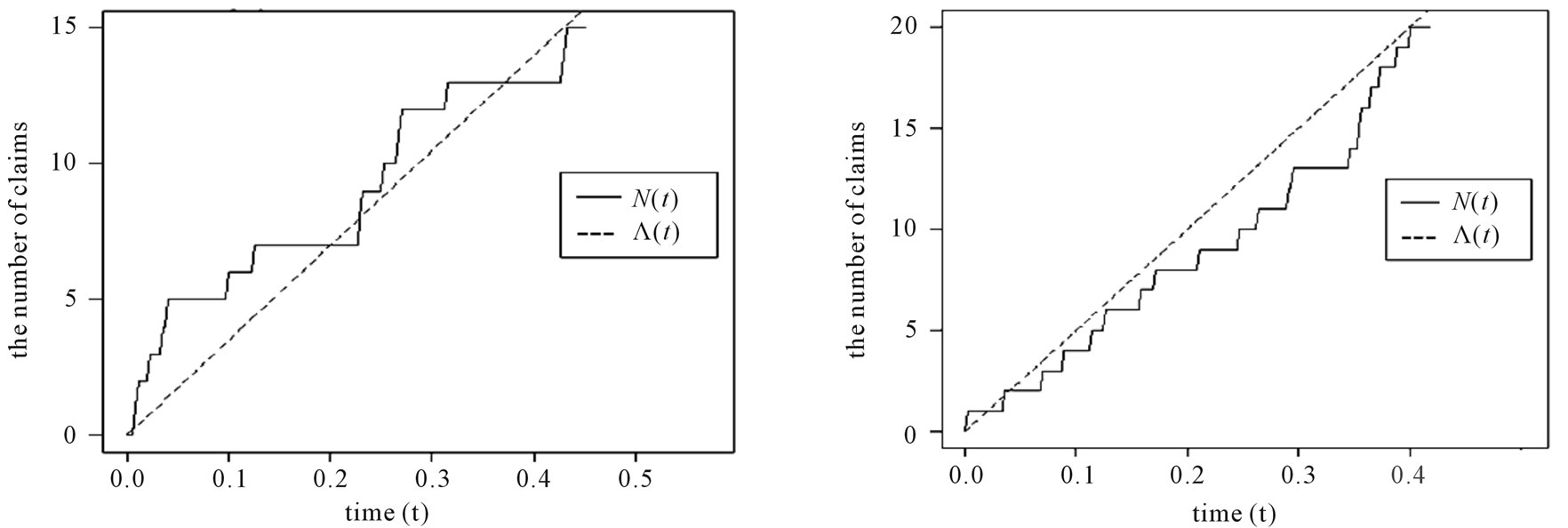 (b)
(b)
Figure 2.  and its compensator
and its compensator 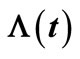 in the HPP with the intensity λ = 10 based on a sample of (a) 5 claims; (b) 10 claims; (c) 15 claims; and (d) 20 claims.
in the HPP with the intensity λ = 10 based on a sample of (a) 5 claims; (b) 10 claims; (c) 15 claims; and (d) 20 claims.
 (a)
(a)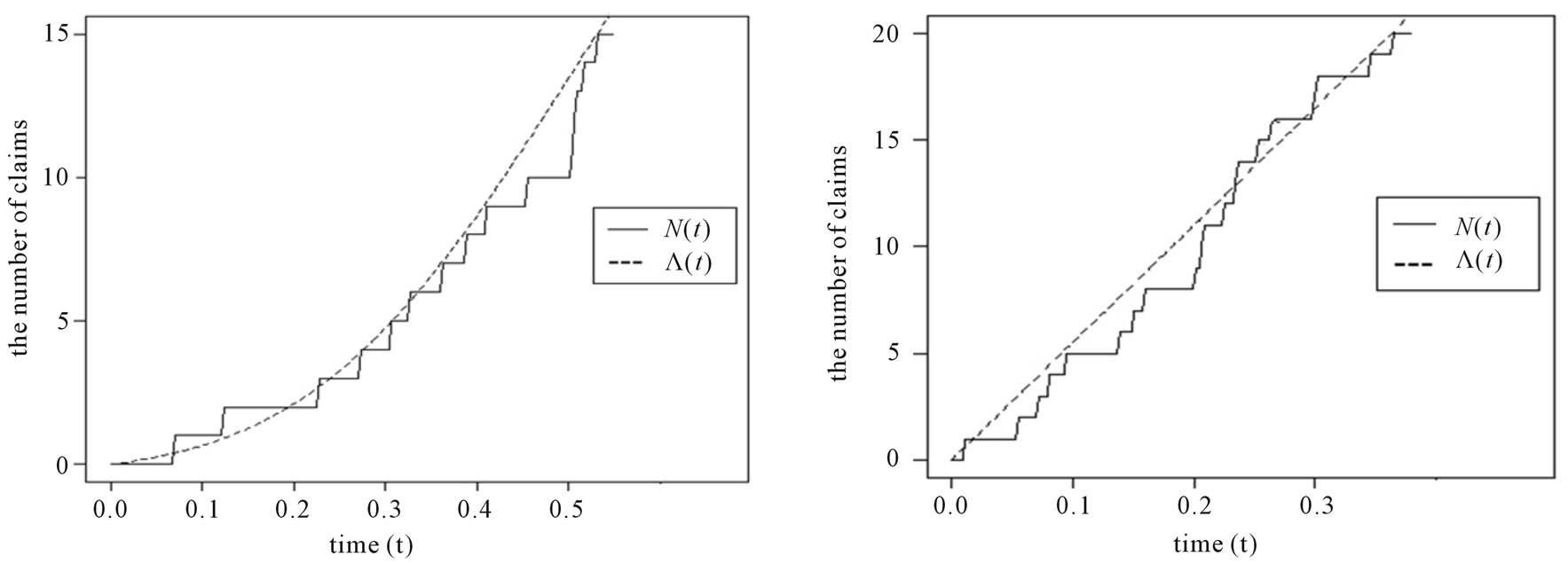 (b)
(b)
Figure 3. 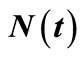 and its compensator
and its compensator 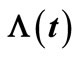 in the NHPP with the parameters of a bell-shaped intensity
in the NHPP with the parameters of a bell-shaped intensity 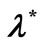 = 10, σ = 5 based on a sample of (a) 5 claims; (b) 10 claims; (c) 15 claims; and (d) 20 claims.
= 10, σ = 5 based on a sample of (a) 5 claims; (b) 10 claims; (c) 15 claims; and (d) 20 claims.
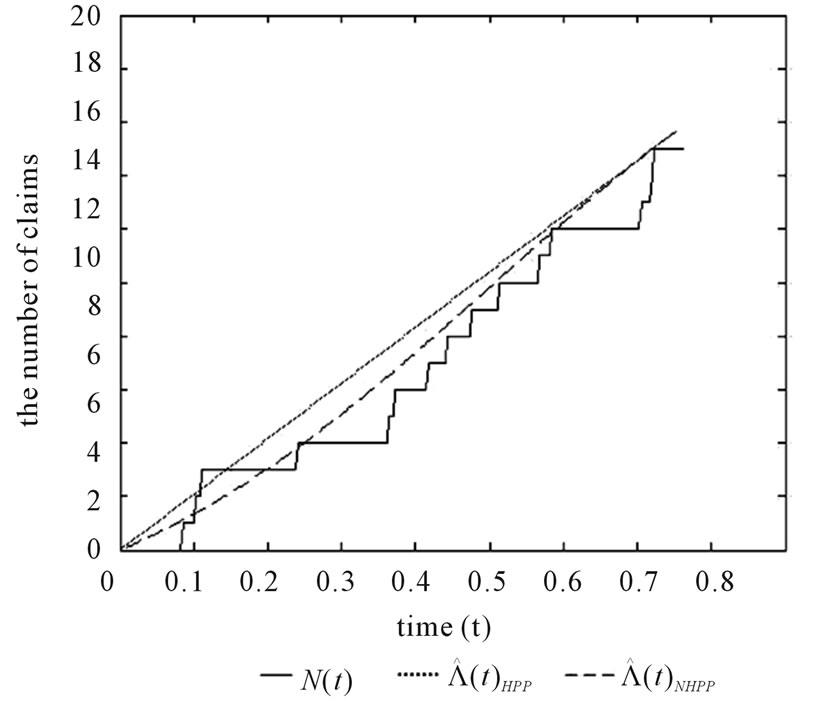
Figure 4. ,
, 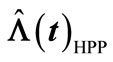 , and
, and  in the NHPP of non-life insurance claim counts.
in the NHPP of non-life insurance claim counts.
uses the estimation method of NHPP with a period timedependent intensity, 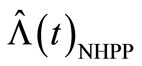 , fits well with
, fits well with  by MSE = 1.48 shown with a dashed line and the MSE = 5.35 along 5000 sample paths. It is notable that if, instead, the compensator estimate misspecification
by MSE = 1.48 shown with a dashed line and the MSE = 5.35 along 5000 sample paths. It is notable that if, instead, the compensator estimate misspecification 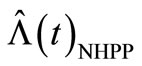 is calculated more easily by using the estimation method of HPP with a constant intensity, and the compensator estimate misspecification
is calculated more easily by using the estimation method of HPP with a constant intensity, and the compensator estimate misspecification  fluctuates a lot from
fluctuates a lot from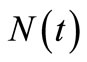 , shown on the dotted line in Figure 4. The MSE of fitting the compensator estimate misspecification
, shown on the dotted line in Figure 4. The MSE of fitting the compensator estimate misspecification 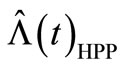 to
to 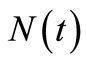 is 2.72, and the MSE = 5.53 along 5000 sample paths are larger than the fitting of the compensator estimate
is 2.72, and the MSE = 5.53 along 5000 sample paths are larger than the fitting of the compensator estimate  to
to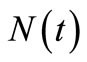 .
.
5. Conclusion
This simulation study of the non-life insurance claim counting process, of both the HPP and the NHPP with a bell-shaped intensity, demonstrates that the fitting of the compensator estimate 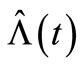 to
to 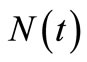 in the time interval
in the time interval 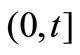 depends on the parameters of model intensity as in the following details, firstly, regarding the HPP with a small intensity rate, with almost no claim occurrences, while the number of observations is very small, the compensator estimate
depends on the parameters of model intensity as in the following details, firstly, regarding the HPP with a small intensity rate, with almost no claim occurrences, while the number of observations is very small, the compensator estimate  is a good fit to
is a good fit to  with less of a MSE. In the same process with a constant intensity rate, the claims occurrence rate, when the number of observations is slightly larger than the constant intensity, the MSE of the compensator estimate
with less of a MSE. In the same process with a constant intensity rate, the claims occurrence rate, when the number of observations is slightly larger than the constant intensity, the MSE of the compensator estimate 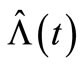 of
of 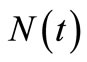 is much less. Secondly, as regards to the NHPP with the parameters of the model intensity, a
is much less. Secondly, as regards to the NHPP with the parameters of the model intensity, a 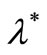 has a very small average number of claims over a period, almost no claim occurrences over a period, and any
has a very small average number of claims over a period, almost no claim occurrences over a period, and any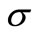 , as the number of observations is very small, the compensator estimate
, as the number of observations is very small, the compensator estimate 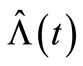 is a good fit to
is a good fit to 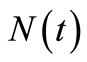 with less of a MSE. Using the same process with the parameters of the model intensity, with an average number of claims over a period
with less of a MSE. Using the same process with the parameters of the model intensity, with an average number of claims over a period  is no less than one and any
is no less than one and any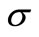 , while the number of observations is slightly larger than the value of
, while the number of observations is slightly larger than the value of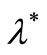 , the MSE of the compensator estimate
, the MSE of the compensator estimate 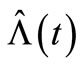 of
of 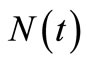 is much less. Some examples of the situations in the simulation study are also depicted by a sample path relating
is much less. Some examples of the situations in the simulation study are also depicted by a sample path relating 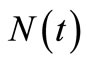 and its compensator
and its compensator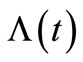 . Furthermore, the result of the compensator estimate misspecification
. Furthermore, the result of the compensator estimate misspecification 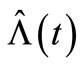 of
of  is illustrated by a sample path of the NHPP so that the MSE of fitting the compensator estimate misspecification
is illustrated by a sample path of the NHPP so that the MSE of fitting the compensator estimate misspecification 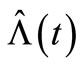 to
to 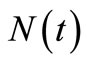 is much larger than the fitting of the compensator
is much larger than the fitting of the compensator  to
to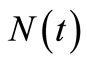 .
.
REFERENCES
- S. A. Klugman, H. H. Panjer and G. E. Willmot, “Loss Models from Data to Decisions,” 3rd Edition, John Wiley & Sons, Hoboken, 2008.
- M. Denuit, X. Maréchal, S. Pitrebois and J. F. Walhin, “Actuarial Modelling of Claim Counts,” John Wiley & Sons, Hoboken, 2007. doi:10.1002/9780470517420
- H. Bühlmann, “Introduction Report Experience Rating and Credibility,” ASTIN Bulletin, Vol. 4, No. 3, 1967, pp. 199-207.
- H. Bühlmann, “Credibility Procedures,” Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, University of California Press, Berkeley, Vol. 1, 1972, pp. 515-525.
- T. Mikosch, “Non-Life Insurance Mathematics,” 2nd Edition, Springer-Verlag, Berlin, 2009. doi:10.1007/978-3-540-88233-6
- M. Matsui and T. Mikosch, “Prediction in a Poisson Cluster Model,” Journal of Applied Probability, Vol. 47, No. 2, 2010, pp. 350-366. doi:10.1239/jap/1276784896
- M. Morales, “On a Surplus Process under a Periodic Environment: A Simulation Approach,” North American Actuarial Journal, Vol. 8, No. 2, 2004, pp. 76-87.
- Y. Lu and J. Garrido, “On Double Periodic Non-Homogeneous Poisson Processes,” Bulletin of the Swiss Association of Actuaries Swiss Association of Actuaries-Bern, Bern, 2004, pp. 195-212.
- S. M. Ross, “Introduction to Probability Models,” 5th Edition, Academic Press, Inc., San Diego, 1993.
- P. Mukhopadhyay, “An Introduction to Estimating Functions,” Alpha Science International Ltd., Harrow, 2004.
- P. K. Andersen, O. Borgan, R. D. Gill and N. Keiding, “Statistical Models Based on Counting Processes,” SpringerVerlag, New York, 1993.
- P. Yip, “Estimating the Number of Error in a System Using a Martingale Approach,” IEEE Transactions on Reliability, Vol. 44, No. 2, 1995. pp. 322-326. doi:10.1109/24.387389
- J. E. R. Cid and J. A. Achcar, “Bayesian Inference for Nonhomogeneous Poisson Processed in Software Reliability Models Assuming Nonmonotonic Intensity Functions,” Computational Statistics & Data Analysis, Vol. 32, No. 2, 1999, pp.147-159. doi:10.1016/S0167-9473(99)00028-6

