ABSTRACT

By employing the Srivastava-Owa fractional operators, we consider a class of fractional differential equation in the unit disk. The existence of the univalent solution is founded by using the Schauder fixed point theorem while the uniqueness is obtained by using the Banach fixed point theorem. Moreover, the integral mean of these solutions is studied by applying the concept of the subordination.

1. Introduction

Recently, the theory of fractional calculus has found interesting applications in the theory of analytic functions. The classical definitions of fractional operators and their generalizations have fruitfully been applied in obtaining, for example, the characterization properties, coefficient estimates [1], distortion inequalities [2] and convolution structures for various subclasses of analytic functions and the works in the research monographs. In [3], Srivastava and Owa, gave definitions for fractional operators (derivative and integral) in the complex z-plane 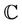as follows:

Definition 1.1. The fractional derivative of order 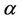is defined, for a function 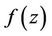by

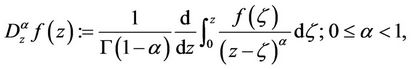
where the function 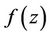is analytic in simply-connected region of the complex z-plane 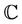containing the origin and the multiplicity of 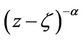is removed by requiring to be real when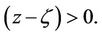

Definition 1.2. The fractional integral of order 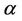is defined, for a function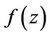, by

where the function 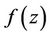is analytic in simply-connected region of the complex z-plane (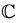) containing the origin and the multiplicity of 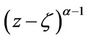is removed by requiring 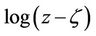to be real when

Remark 1.1.

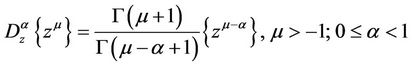
and

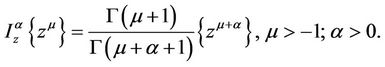
Further properties of these operators can be found in [4,5].

2. Preliminaries

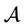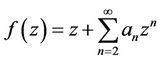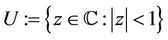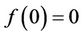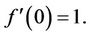Let be the class of all normalized analytic functions in the open unit disk satisfying and Let 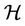be the class of analytic functions in U and for any 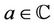and 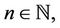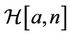be the subclass of 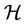consisting of functions of the form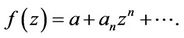

For given two functions F and G, which are analytic in U, the function F is said to be subordinate to G in U if there exists a function h analytic in U with

such that

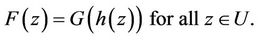
We denote this subordination by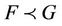. If G is univalent in U, then the subordination 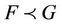is equivalent to 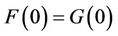and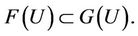

Lemma 2.1 [6]. If the functions f and g are analytic in U then

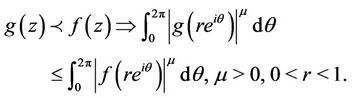
Lemma 2.2 [7]. Let f, g be analytic function in U. Assume that 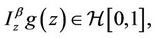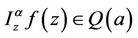and 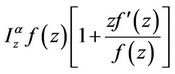is univalent in U. If

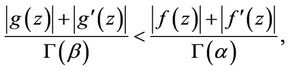
then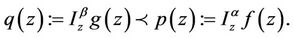

Our work is organized as follows: In Section 2, we will derive the integral means for normalized analytic functions involving fractional integral in the open unit disk U

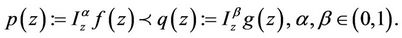
In Section 3, we study the existence of locally univalent solution for the fractional diffeo-integral equation

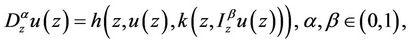(1)

subject to the initial condition 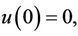where 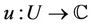is an analytic function for all 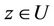and 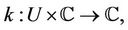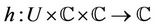are analytic univalent functions in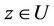. The existence is shown by using Schauder fixed point theorem while the uniqueness is verified by using Banach fixed point theorem.

For that purpose we need the following definitions and results:

Let M be a subset of Banach space X and 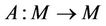an operator. The operator A is called compact on the set M if it carries every bounded subset of M into a compact set. If A is continuous on M (that is, it maps bounded sets into bounded sets) then it is said to be completely continuous on M. A mapping 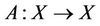is said to be a contraction if there exists a real number 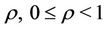such that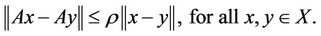

Theorem 2.1. Arzela-Ascoli let E be a compact metric space and 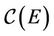be the Banach space of real or complex valued continuous functions normed by

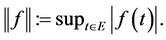
If 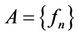is a sequence in 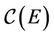such that 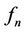is uniformly bounded and equi-continuous, then 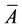is compact.

Theorem 2.2. (Schauder) Let X be a Banach space, 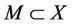a nonempty closed bounded convex subset and 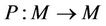is compact. Then P has a fixed point.

Theorem 2.3. (Banach) If X is a Banach space and 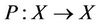is a contraction mapping then P has a unique fixed point.

3. Existence and Uniqueness

In this section, we established the existence and uniqueness solution for the diffeo-integral Equation (1). Let 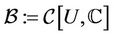be a Banach space of all continuous functions on U endowed with the sup. norm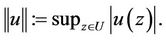

Lemma 3.1. If the function h is analytic, then the initial value problem (1) is equivalent to the nonlinear Volterra integral equation

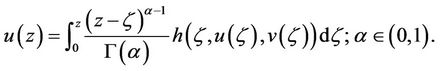(2)

In other words, every solution of the Volterra Equation (2) is also a solution of the initial value problem (1) and vice versa.

The following assumptions are needed in the next theorem:

(H1) There exists a continuous function 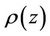on U and increasing positive function 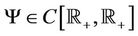such that

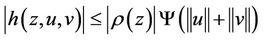
with the property that

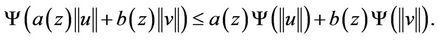
Note that 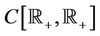is the Banach space of all continuous positive functions.

(H2) There exists a continuous function p in U, such that

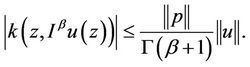
Remark 3.1. By using fractional calculus we observe that Equation (2) is equivalent to the integral equation of the form

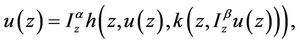(3)

that is, the existence of Equation (2) is the existence of the Equation (3).

Theorem 3.1. Let the assumptions (H1) and (H2) hold. Then Equation (1) has a univalent solution 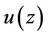on U.

Proof. We need only to show that has a fixed point by using Theorem 1.2 where

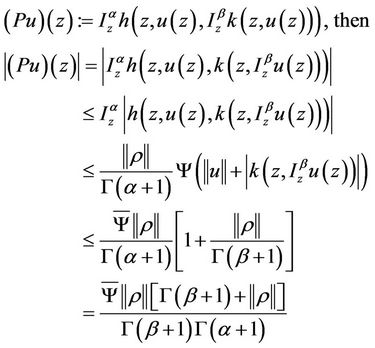(4)

where 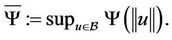Thus we obtain that

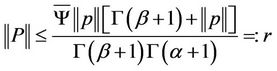
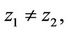
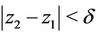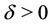that is Then P mapped into itself. Now we proceed to prove that P is equicontinuous. For such that ,. Then for all 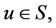where

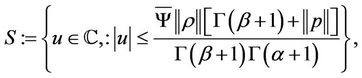
we obtained

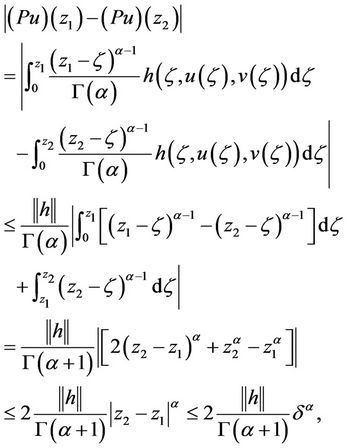
which is independent of u.

Hence P is an equicontinuous mapping on S. Moreover, for, such that 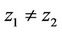and under assumption (H1), we show that P is a univalent function. The Arzela-Ascoli theorem yields that every sequence of functions 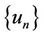from 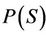has a uniformly convergent subsequence, and therefore 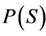is relatively compact. Schauder’s fixed point theorem asserts that P has a fixed point. The univalency of the function h yields that u is a univalent solution.

Now we discuss the uniqueness solution for the problem (1). For this purpose let us state the following assumptions:

(H3) Assume that there exists a positive number L such that for each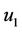, 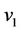and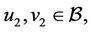

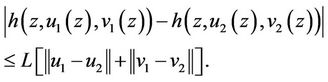
(H4) Assume that there exists a positive number such that for each 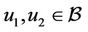we have

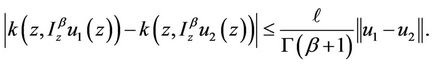
Theorem 3.2. Let the hypotheses (H1-H4) be satisfied. If 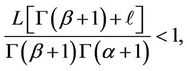then (1) admits a unique univalent solution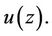

Proof. Assume the operator P defined in Equation (4), we only need to show that P is a contraction mapping that is P has a unique fixed point which is corresponding to the unique solution of the Equation (1). Let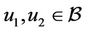, then for all 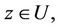we obtain that

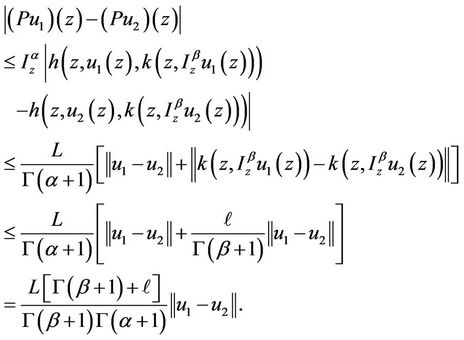
Thus by the assumption of the theorem we have that P is a contraction mapping. Then in view of Banach fixed point theorem, P has a unique fixed point which corresponds to the univalent solution (Theorem 3.1) of Equation (1). Hence the proof.

The next result shows the integral means of univalent solutions of problem (1).

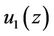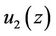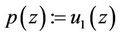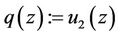Theorem 3.3. Let, be two analytic univalent solutions for the Equation (1) satisfying the assumptions of Lemma 2.2 with and then

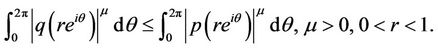
Proof. Setting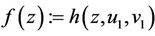, , 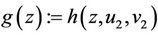Lemma 2.2 implies that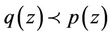. Hence in view of Lemma 1.2, we obtain the result.

Example 3.1. Consider the fractional problem

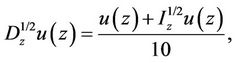(5)

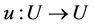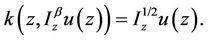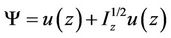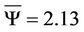where and We observe that and and

where 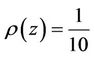and 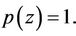Thus in view of Theorem 3.1, the problem (5) has a solution in the unit disk.

REFERENCES