Advances in Pure Mathematics
Vol.2 No.6(2012), Article ID:24990,7 pages DOI:10.4236/apm.2012.26068
Approximation of Common Fixed Points of Pointwise Asymptotic Nonexpansive Maps in a Hadamard Space
1Department of Mathematics, Statistics and Physics, Qatar University, Doha, Qatar
2Department of Mathematics and Statistics, King Fahd University of Petroleum and Minerals, Dhahran, KSA
Email: safeer@qu.edu.qa, safeerhussain5@yahoo.com, hfdin@kfupm.edu.sa
Received July 18, 2012; revised September 18, 2012; accepted September 27, 2012
Keywords: Pointwise Asymptotic Nonexpansive Map; Common Fixed Point; Ishikawa Iteration Process; Strong Convergence; Weak Convergence
ABSTRACT
We establish weak and strong convergence of Ishikawa type iterates of two pointwise asymptotic nonexpansive maps in a Hadamard space. For weak and strong convergence results, we drop “rate of convergence condition”, namely 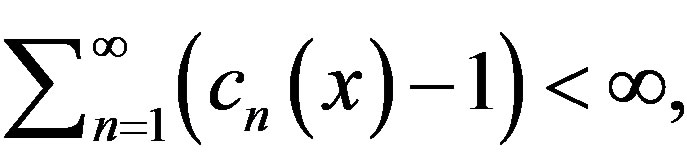 to answer in the affirmative to the open question posed by Tan and Xu [1] even in a general setup.
to answer in the affirmative to the open question posed by Tan and Xu [1] even in a general setup.
1. Introduction
A metric space 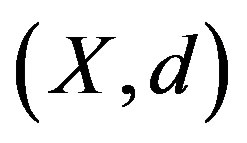 is a length space if any two points of X are joined by a rectifiable path (that is, a path of finite length) and the distance between any two points of X is taken to be the infimum of the lengths of all rectifiable paths joining them. In this case, d is known as length metric (otherwise an inner metric or intrinsic metric). In case, no rectifiable path joins two points of the space, the distance between them is taken to be
is a length space if any two points of X are joined by a rectifiable path (that is, a path of finite length) and the distance between any two points of X is taken to be the infimum of the lengths of all rectifiable paths joining them. In this case, d is known as length metric (otherwise an inner metric or intrinsic metric). In case, no rectifiable path joins two points of the space, the distance between them is taken to be 
A geodesic path joining 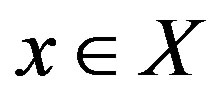 to
to 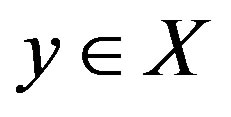 (or, more briefly, a geodesic from x to y) is a map c from a closed interval
(or, more briefly, a geodesic from x to y) is a map c from a closed interval 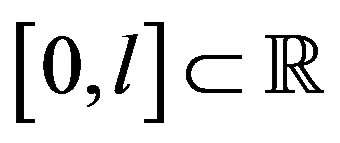 to X such that
to X such that 
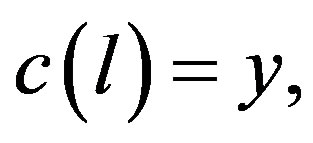 and
and 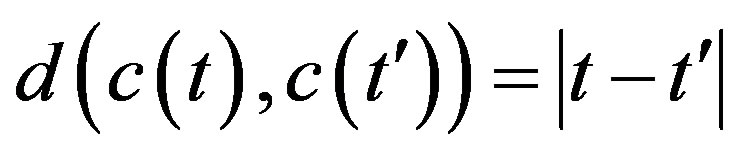 for all
for all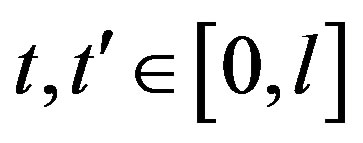 . In particular, c is an isometry and
. In particular, c is an isometry and 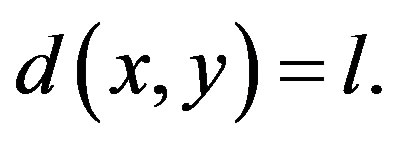 The image
The image 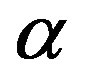 of c is called a geodesic (or metric) segment joining x and y. We say X is: 1) a geodesic space if any two points of X are joined by a geodesic and 2) uniquely geodesic if there is exactly one geodesic joining x and y. for each
of c is called a geodesic (or metric) segment joining x and y. We say X is: 1) a geodesic space if any two points of X are joined by a geodesic and 2) uniquely geodesic if there is exactly one geodesic joining x and y. for each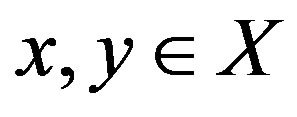 , which we will denote by
, which we will denote by  called the segment joining x to y.
called the segment joining x to y.
A geodesic triangle 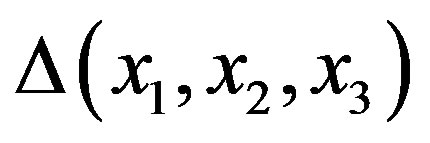 in a geodesic metric space
in a geodesic metric space 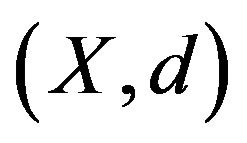 consists of three points in X (the vertices of Δ) and a geodesic segment between each pair of vertices (the edges of Δ). A comparison triangle for geodesic triangle
consists of three points in X (the vertices of Δ) and a geodesic segment between each pair of vertices (the edges of Δ). A comparison triangle for geodesic triangle 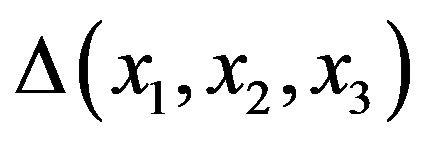 in
in 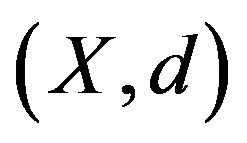 is a triangle
is a triangle  in
in  such that
such that
 for
for 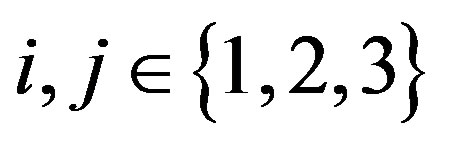 and such a triangle always exists (see [2]). A geodesic metric space is a
and such a triangle always exists (see [2]). A geodesic metric space is a 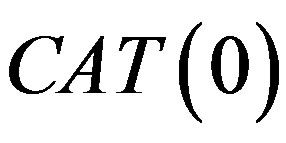 space if all geodesic triangles of appropriate size satisfy
space if all geodesic triangles of appropriate size satisfy 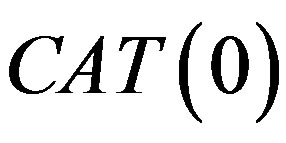 comparison axiom: Let Δ be a geodesic triangle in X and let
comparison axiom: Let Δ be a geodesic triangle in X and let 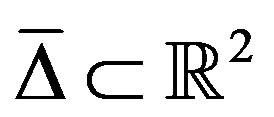 be a comparison triangle for Δ. Then Δ is said to satisfy the
be a comparison triangle for Δ. Then Δ is said to satisfy the  inequality if for all
inequality if for all 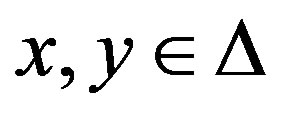 and all comparison points
and all comparison points  we have
we have
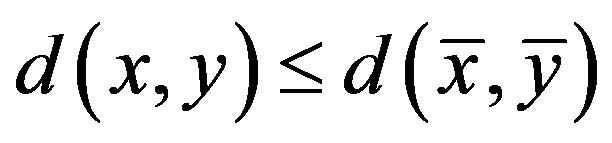 .
.
For any  and
and 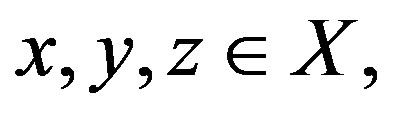 Dhompongsa and Panyanak [3] modified the (CN) inequality of Bruhat and Tits [4] as
Dhompongsa and Panyanak [3] modified the (CN) inequality of Bruhat and Tits [4] as
 (1.1)
(1.1)
If  then (1.1) reduces to the original (CN) inequality of Bruhat and Tits [4].
then (1.1) reduces to the original (CN) inequality of Bruhat and Tits [4].
Let us recall that a geodesic metric space is a  space if and only if it satisfies the (CN) inequality (see [2, p. 163]). Complete
space if and only if it satisfies the (CN) inequality (see [2, p. 163]). Complete 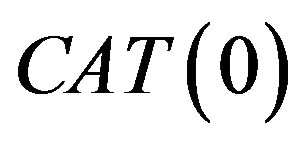 spaces are often called Hadamard spaces (see [5]). Moreover, if X is a
spaces are often called Hadamard spaces (see [5]). Moreover, if X is a  metric space and
metric space and  then there exists a unique point
then there exists a unique point 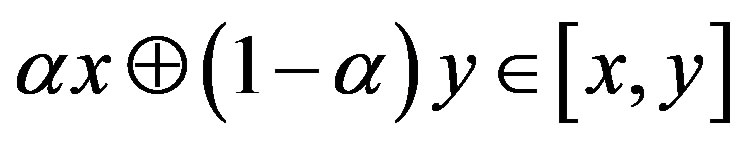 such that
such that
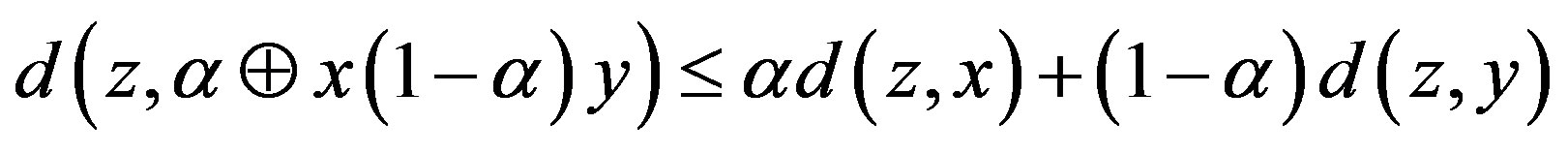 .
.
A subset  of a
of a 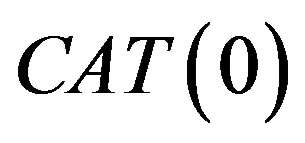 space
space  is convex if for any
is convex if for any 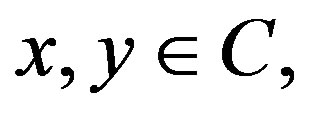 we have
we have 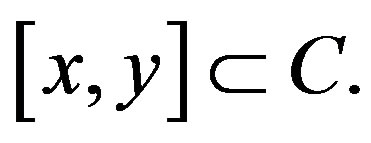
In 2008, Kirk and Xu [6] studied (in Banach spaces) the existence of fixed points of asymptotic pointwise nonexpansive selfmap 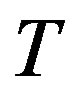 on
on  defined by:
defined by:
 for all
for all  where
where 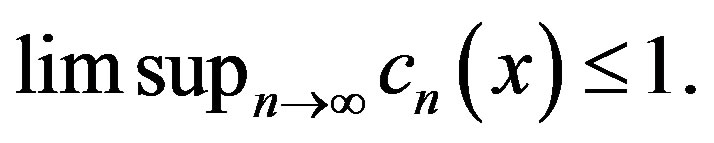
Their main result ([6], Theorem 3.5) states that every asymptotic pointwise nonexpansive selfmap of a nonempty closed bounded convex subset C of a uniformly convex Banach space has a fixed point. This result of Kirk and Xu is a generalization of Goebel and Kirk fixed point theorem [7] for a narrower class of maps, the class of asymptotic nonexpansive maps, where (using our notation) every function  is a constant function. In 2009, the results of [6] were extended to the case of metric spaces by Hussain and Khamsi [8]. As pointed out by Kirk and Xu in [6], asymptotic pointwise maps seem to be a natural generalization of nonexpansive maps. The conditions on
is a constant function. In 2009, the results of [6] were extended to the case of metric spaces by Hussain and Khamsi [8]. As pointed out by Kirk and Xu in [6], asymptotic pointwise maps seem to be a natural generalization of nonexpansive maps. The conditions on 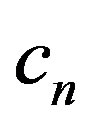 can be, for instance, expressed in terms of the derivatives of iterations of T for differentiable T.
can be, for instance, expressed in terms of the derivatives of iterations of T for differentiable T.
T is said to be asymptotic pointwise nonexpansive map if there exists a sequence of maps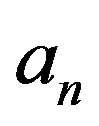 :
: 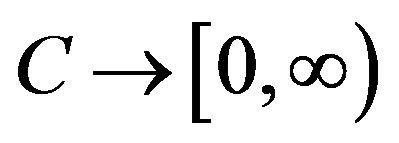 such that
such that 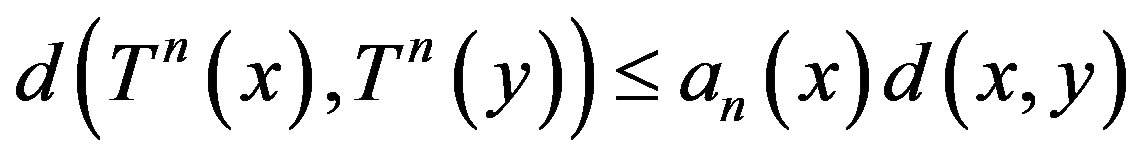 for all x,
for all x, 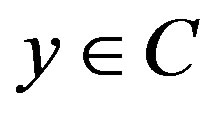 ,
,  , where
, where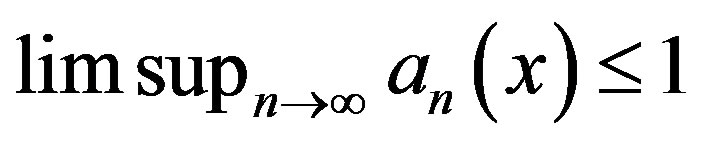 . Denoting
. Denoting
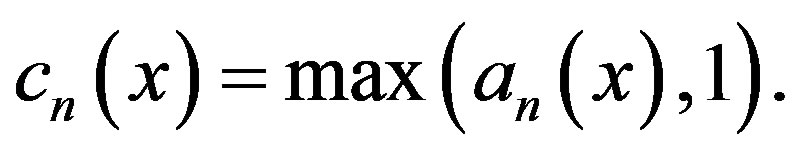 Then note that without any loss of generality, T is an asymptotic pointwise nonexpansive map if
Then note that without any loss of generality, T is an asymptotic pointwise nonexpansive map if 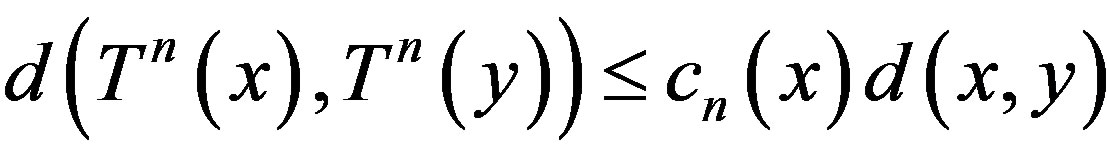 for all x,
for all x, 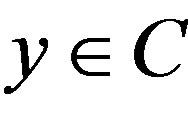 ,
, 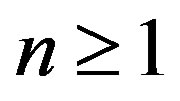 , where
, where  and
and  Moreover, we recall that
Moreover, we recall that  is uniformly LLipschitzian if for some
is uniformly LLipschitzian if for some 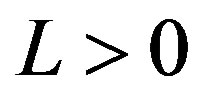 we have that
we have that  for
for 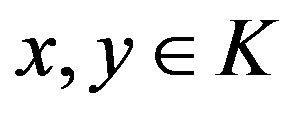 and
and  asymptotic nonexpansive if there is a sequence
asymptotic nonexpansive if there is a sequence 
 with
with 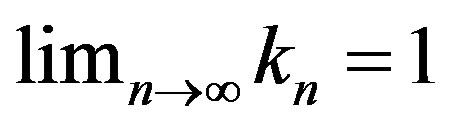 such that
such that
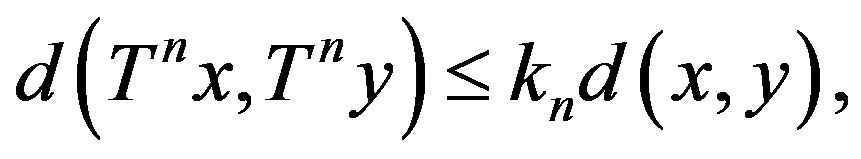 for all
for all 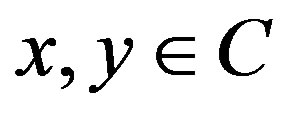 and
and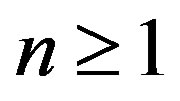 ;
;
semi-compact (completely continuous) if for any bounded sequence 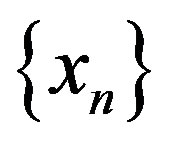 in C with
in C with  as
as 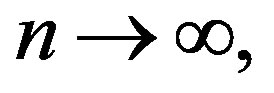 there is a subsequence
there is a subsequence 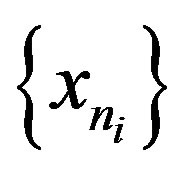 of
of 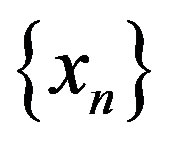 such that
such that 
 as
as 
Let 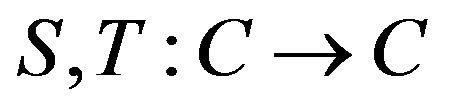 be asymptotic pointwise nonexpansive maps with function sequences
be asymptotic pointwise nonexpansive maps with function sequences 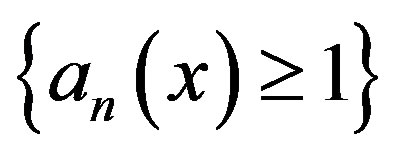 and
and 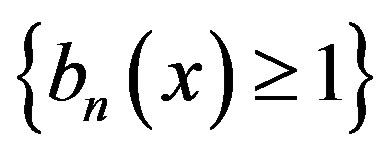 satisfying
satisfying 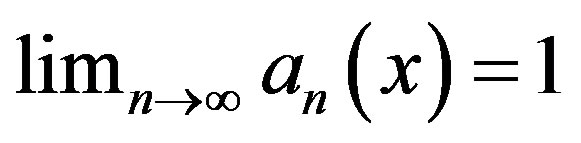 and
and
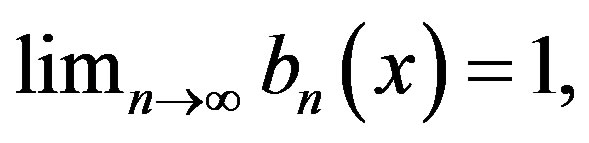 respectively. Set
respectively. Set
 Then
Then
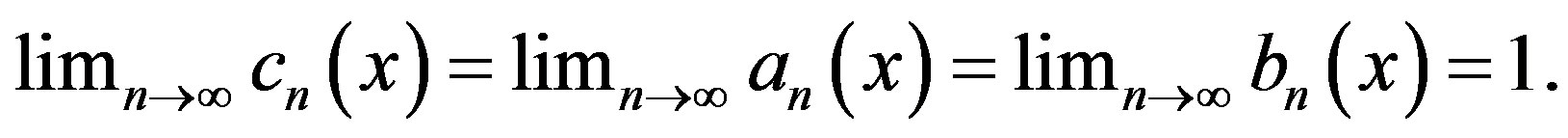
Therefore throughout the paper, we shall take  as the class of all pointwise asymptotic nonexpansive self maps T on C with function sequence
as the class of all pointwise asymptotic nonexpansive self maps T on C with function sequence 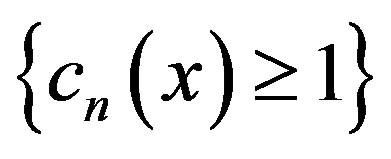 with
with 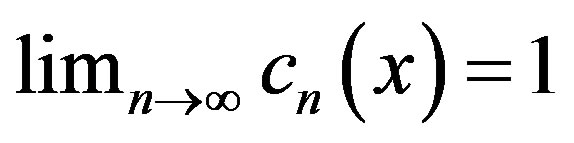 for every
for every 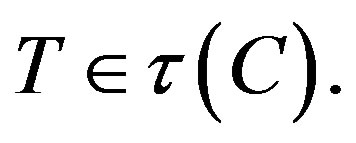 Also F will stand for the set of common fixed points of the two maps
Also F will stand for the set of common fixed points of the two maps 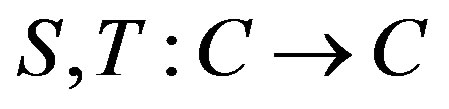 We assume that cn is a bounded function for every
We assume that cn is a bounded function for every 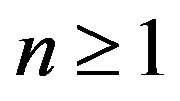 and all the functions cn are not bounded by a common constant, therefore a pointwise asymptotic nonexpansive map is not uniformly Lipschitzian. However, an asymptotic nonexpansive map is a pointwise asymptotic nonexpansive as well as uniformly Lipschitzian.
and all the functions cn are not bounded by a common constant, therefore a pointwise asymptotic nonexpansive map is not uniformly Lipschitzian. However, an asymptotic nonexpansive map is a pointwise asymptotic nonexpansive as well as uniformly Lipschitzian.
A strictly increasing sequence 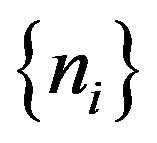 of natural numbers is quasi-periodic if the sequence
of natural numbers is quasi-periodic if the sequence 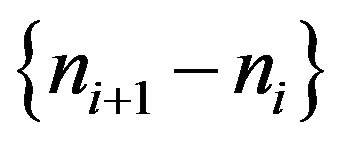 is bounded or equivalently if there exists a natural number q such that any block of q consecutive natural numbers must contain a term of the sequence
is bounded or equivalently if there exists a natural number q such that any block of q consecutive natural numbers must contain a term of the sequence 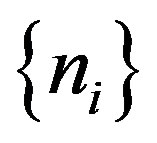 The smallest of such numbers q will be called a quasi-period of
The smallest of such numbers q will be called a quasi-period of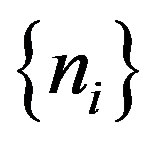 .
.
Hussain and Khamsi [8] have shown that if X is a Hadamard space and C a nonempty bounded closed convex subset of X, then any pointwise asymptotic nonexpansive selfmap on C has a fixed point. Moreover, this fixed point set is closed and convex. The proof of this important theorem is of the existential nature and does not describe any algorithm for constructing a fixed point of an asymptotic pointwise nonexpansive map. This paper aims at complementing their paper. It is also well known that the fixed point construction iteration processes for generalized nonexpansive maps have been successfully used to develop efficient and powerful numerical methods for solving various nonlinear equations.
Several authors have studied the generalizations of known iterative fixed point construction processes like the Mann process (see e.g. [9,10]) or the Ishikawa process (see e.g. [11]) to the case of asymptotic (but not pointwise asymptotic) nonexpansive maps. There is huge literature on the iterative construction of fixed points for asymptotic nonexpansive maps in Hilbert, Banach and metric spaces, see e.g. [1,3,7,9-25,27-32] and the references therein. Schu [32] proved the weak convergence of the Mann iteration process to a fixed point of asymptotic nonexpansive maps in uniformly convex Banach spaces with the Opial property [28] and the strong convergence for compact asymptotic nonexpansive maps in uniformly convex Banach spaces. Tan and Xu [1] proved the weak convergence of Mann and Ishikawa iteration processes for asymptotic nonexpansive maps in uniformly convex Banach spaces either satisfying the Opial condition or possessing Fréchet differentiable norm. Moreover, the rate of convergence condition namely 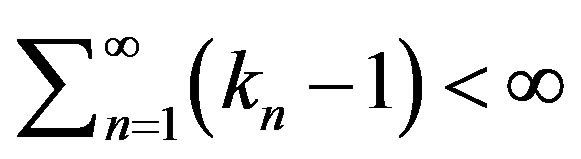 has remained in extensive use to prove both weak and strong convergence theorems to approximate fixed points of asymptotic nonexpansive maps in uniformly convex Banach spaces. Also Tan and Xu [1] remarked: we do not know whether our Theorem 3.1 remains valid if
has remained in extensive use to prove both weak and strong convergence theorems to approximate fixed points of asymptotic nonexpansive maps in uniformly convex Banach spaces. Also Tan and Xu [1] remarked: we do not know whether our Theorem 3.1 remains valid if  (the sequence associated with the asymptotic nonexpansive map T) is allowed to approach 1 slowly enough so that
(the sequence associated with the asymptotic nonexpansive map T) is allowed to approach 1 slowly enough so that 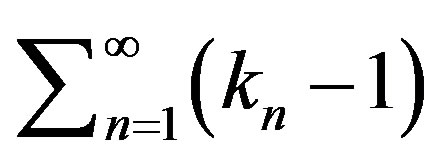 diverges.
diverges.
Recently Kozlowski [23] defined Mann type and Ishikawa type iterative processes to approximate fixed points of pointwise asymptotic nonexpansive maps in Banach spaces. We follow his idea and the concept of unique geodesic path denoted by  of two points x, y in geodesic space and define Ishikawa type iterative process of two pointwise asymptotic nonexpansive maps in a geodesic space.
of two points x, y in geodesic space and define Ishikawa type iterative process of two pointwise asymptotic nonexpansive maps in a geodesic space.
Let C be a nonempty and convex subset of a geodesic space X Let  be pointwise asymptotic nonexpansive maps and let
be pointwise asymptotic nonexpansive maps and let 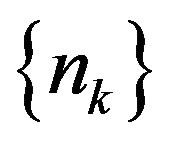 be an increasing sequence of natural numbers and
be an increasing sequence of natural numbers and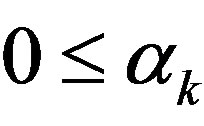 ,
,  Then the Ishikawa iteration process denoted by
Then the Ishikawa iteration process denoted by 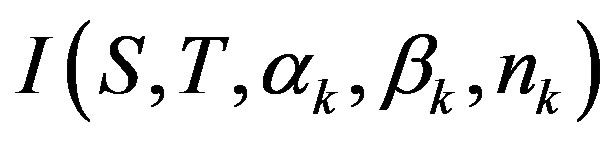 in a geodesic space X is as under:
in a geodesic space X is as under:
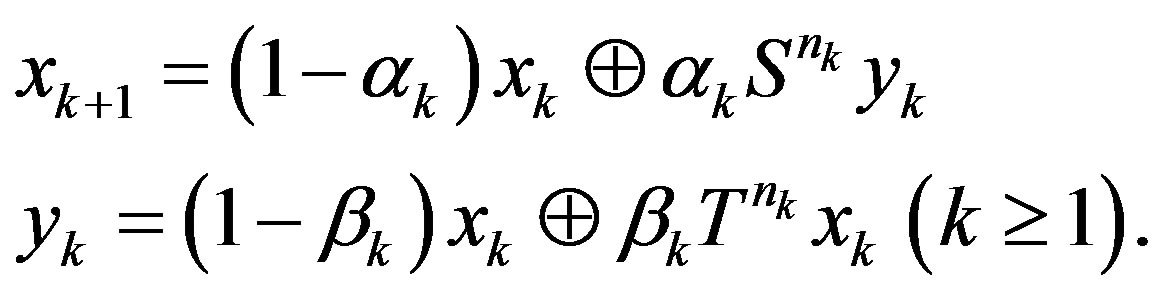 (1.2)
(1.2)
We say that 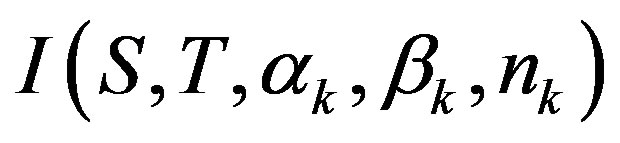 is well-defined if
is well-defined if 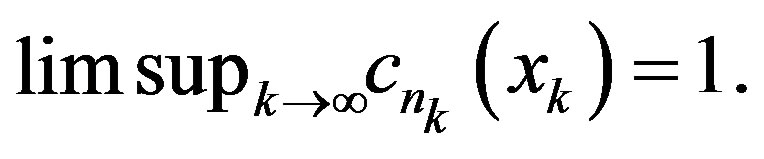
2. Fixed Point Approximation
Following the investigations of Hussain and Khamsi [8], the existence of the fixed point of pointwise asymptotic nonexpansive map can not be achieved without its bounded domain. We shall follow them for the purpose. We start with proving the following lemma.
Lemma 2.1. Let C be a nonempty, bounded, closed and convex set in a geodesic space X and let  Let
Let 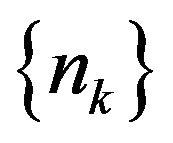 be such that the sequence
be such that the sequence  in (1.2) is well defined. If the set
in (1.2) is well defined. If the set 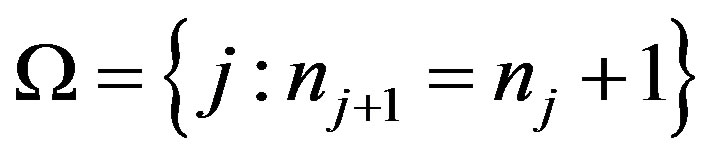 is quasiperiodic and
is quasiperiodic and
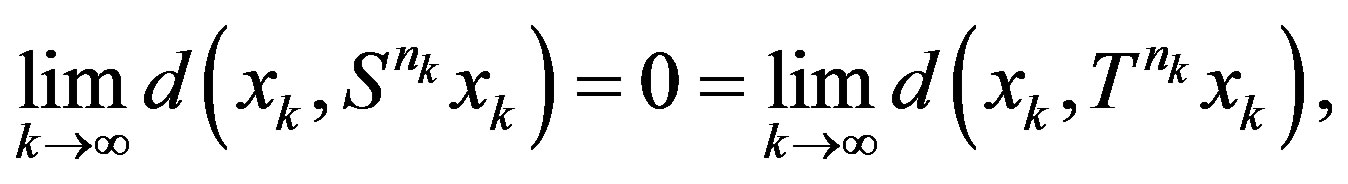 (2.1)
(2.1)
then

Proof. Set 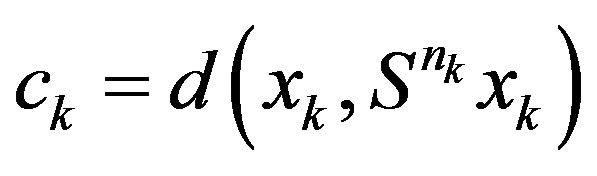 and
and 
From

we have
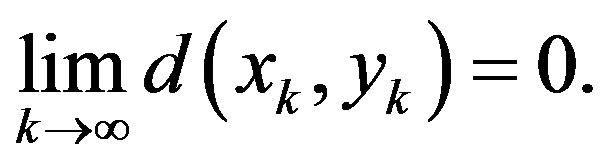 (2.2)
(2.2)
Also
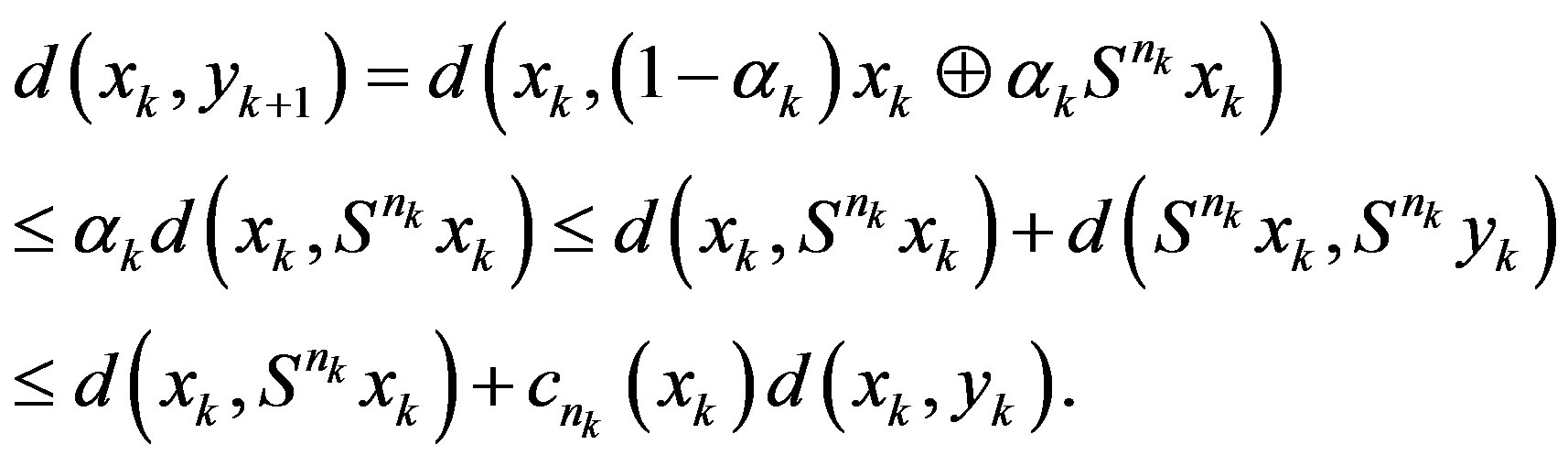 (2.3)
(2.3)
Using (2.1) and (2.2) in (2.3), we have
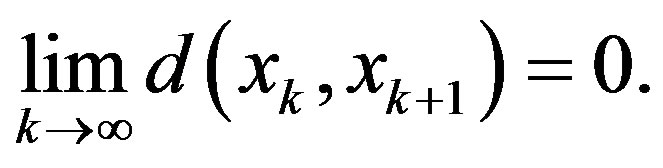 (2.4)
(2.4)
Since
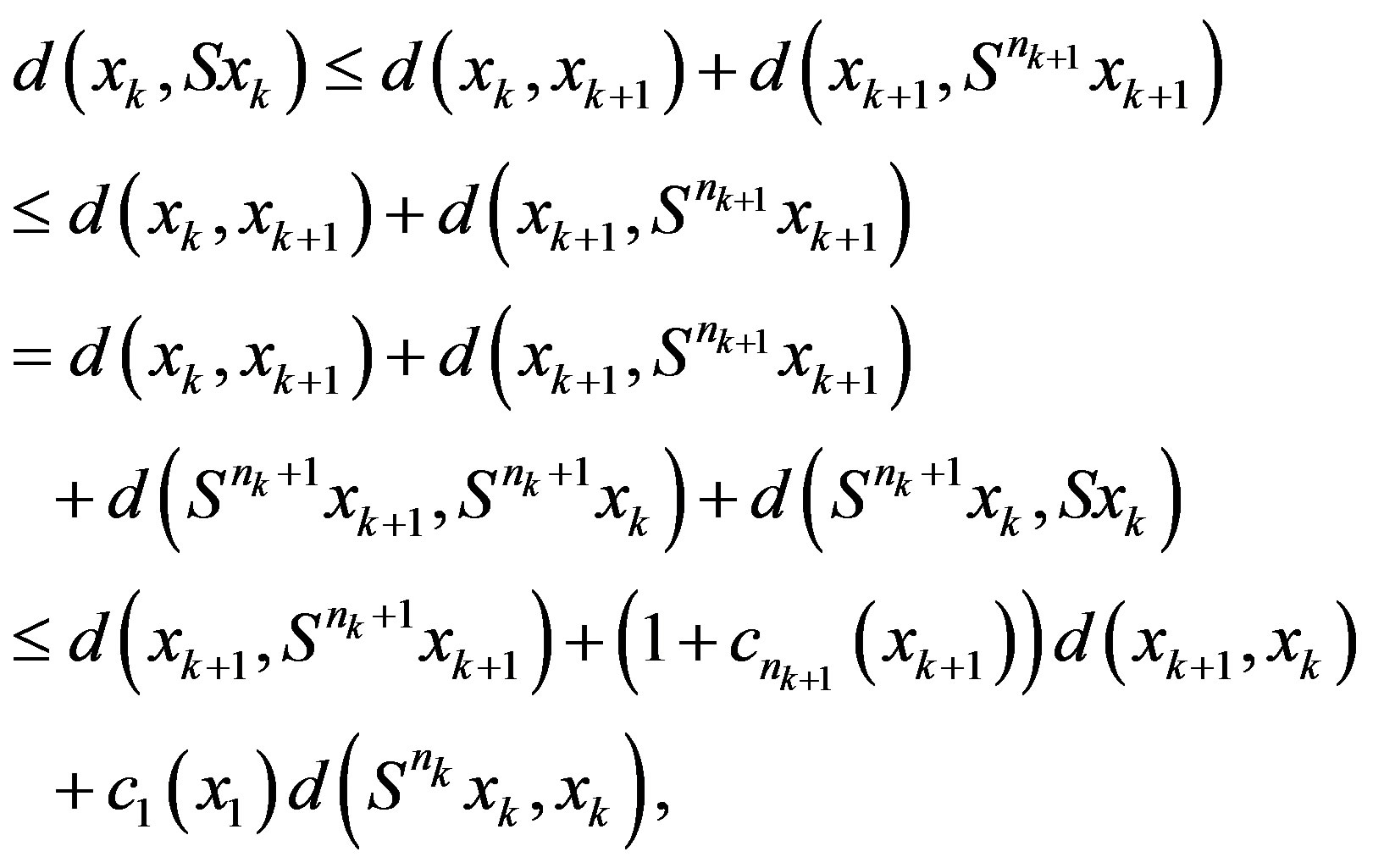 (2.5)
(2.5)
therefore taking  on both the sides of inequality (2.5) and using (2.1) and (2.4), we get
on both the sides of inequality (2.5) and using (2.1) and (2.4), we get
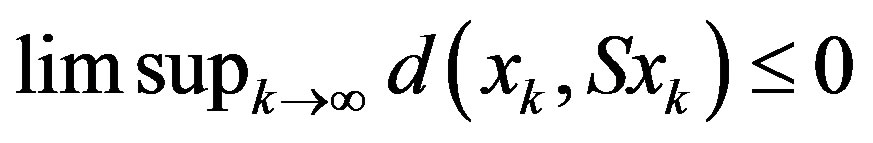 and hence
and hence
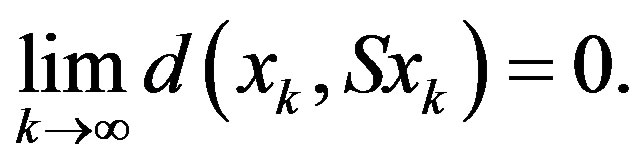
Similarly
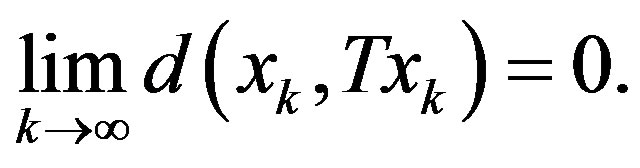
That is,
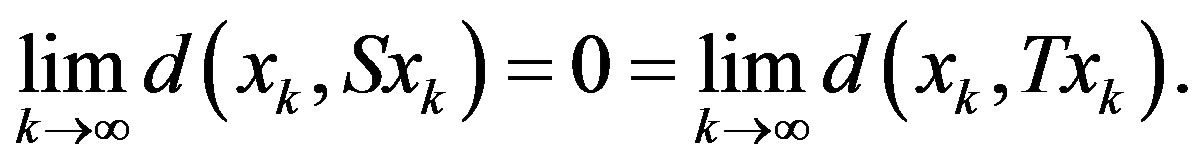
Remark 2.2. Lemma 2.1 extends the corresponding Lemma 3 of Khan and Takahashi [22] from Lipschitzian to non-Lipschitzian maps.
Lemma 2.3. Let 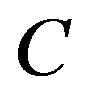 be a nonempty, bounded, closed and convex subset of a Hadamard space
be a nonempty, bounded, closed and convex subset of a Hadamard space 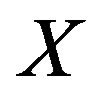 and let
and let
 . Let
. Let 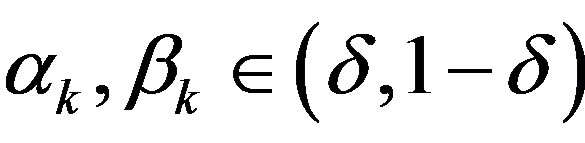 for some
for some 
and  be such that the sequence
be such that the sequence 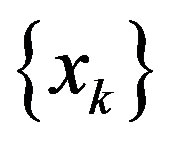 in
in 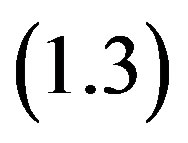 is well-defined. If the set
is well-defined. If the set 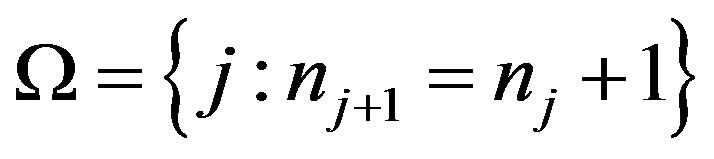 is quasiperiodic and
is quasiperiodic and  then
then

Proof. Let 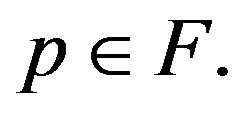 Then use (CN) inequality (1.1) for the scheme (1.2) to have
Then use (CN) inequality (1.1) for the scheme (1.2) to have

Since 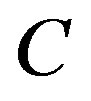 is bounded, there exists
is bounded, there exists 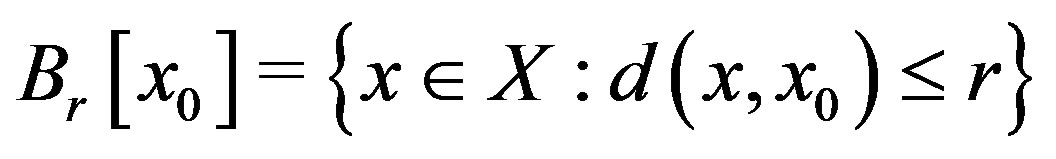 such that
such that 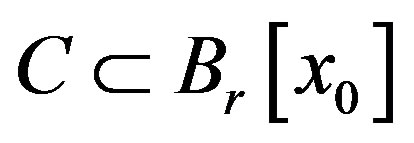 for some
for some 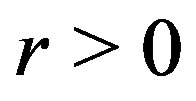 Therefore the above inequality becomes
Therefore the above inequality becomes
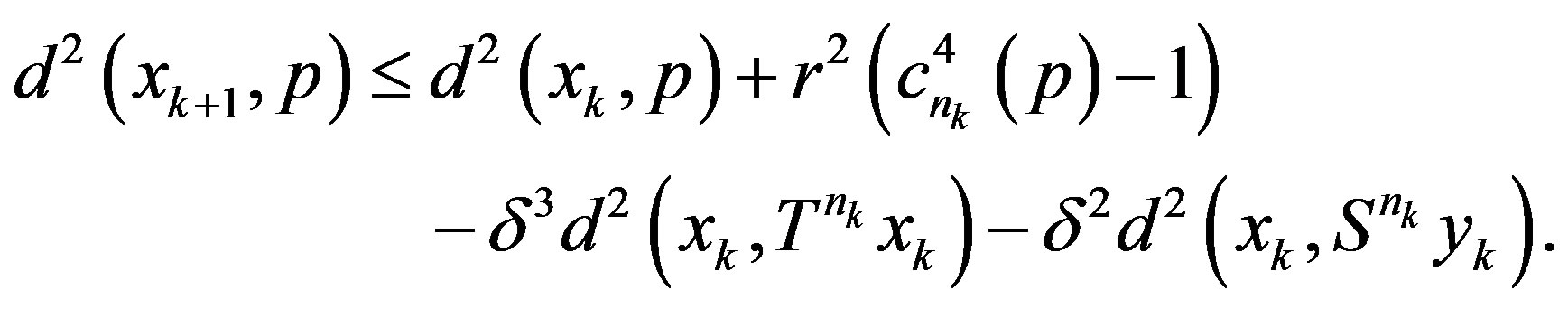 (2.6)
(2.6)
From (2.6), the following two inequalities are obtained
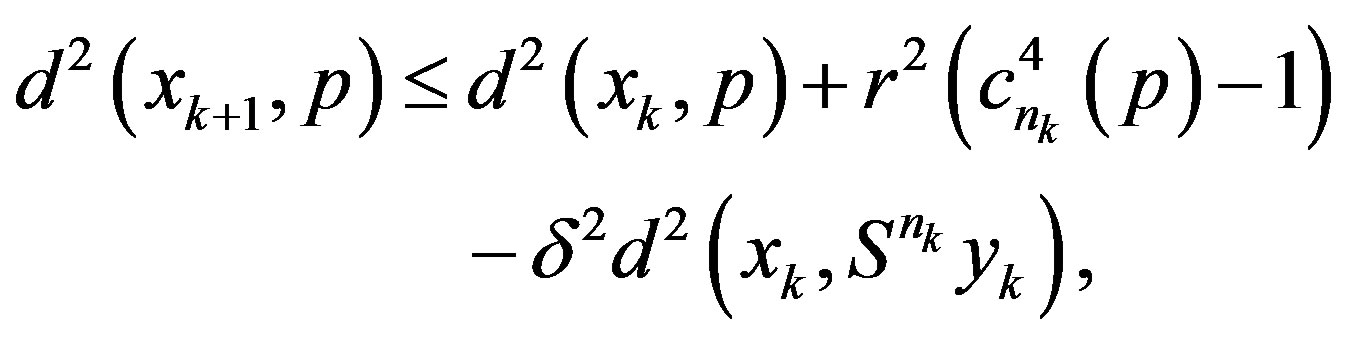 (2.7)
(2.7)
and
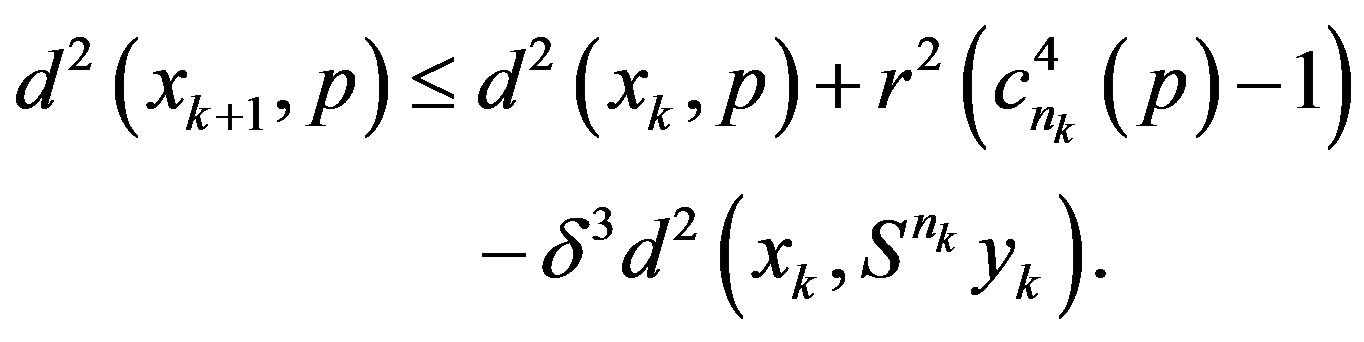 (2.8)
(2.8)
Now, we prove that
 (2.9)
(2.9)
First assume 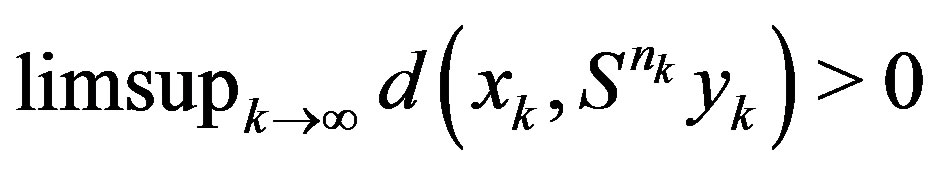 Then there exists a subsequence(use the same notation for subsequence as for the sequence) of
Then there exists a subsequence(use the same notation for subsequence as for the sequence) of 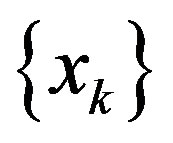 and
and  such that
such that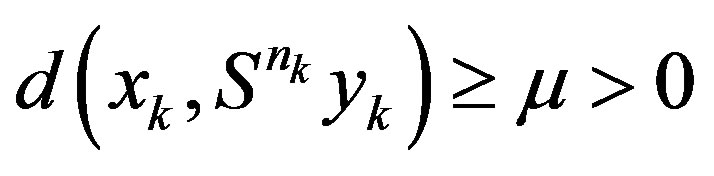 .
.
From (2.7), it follows that
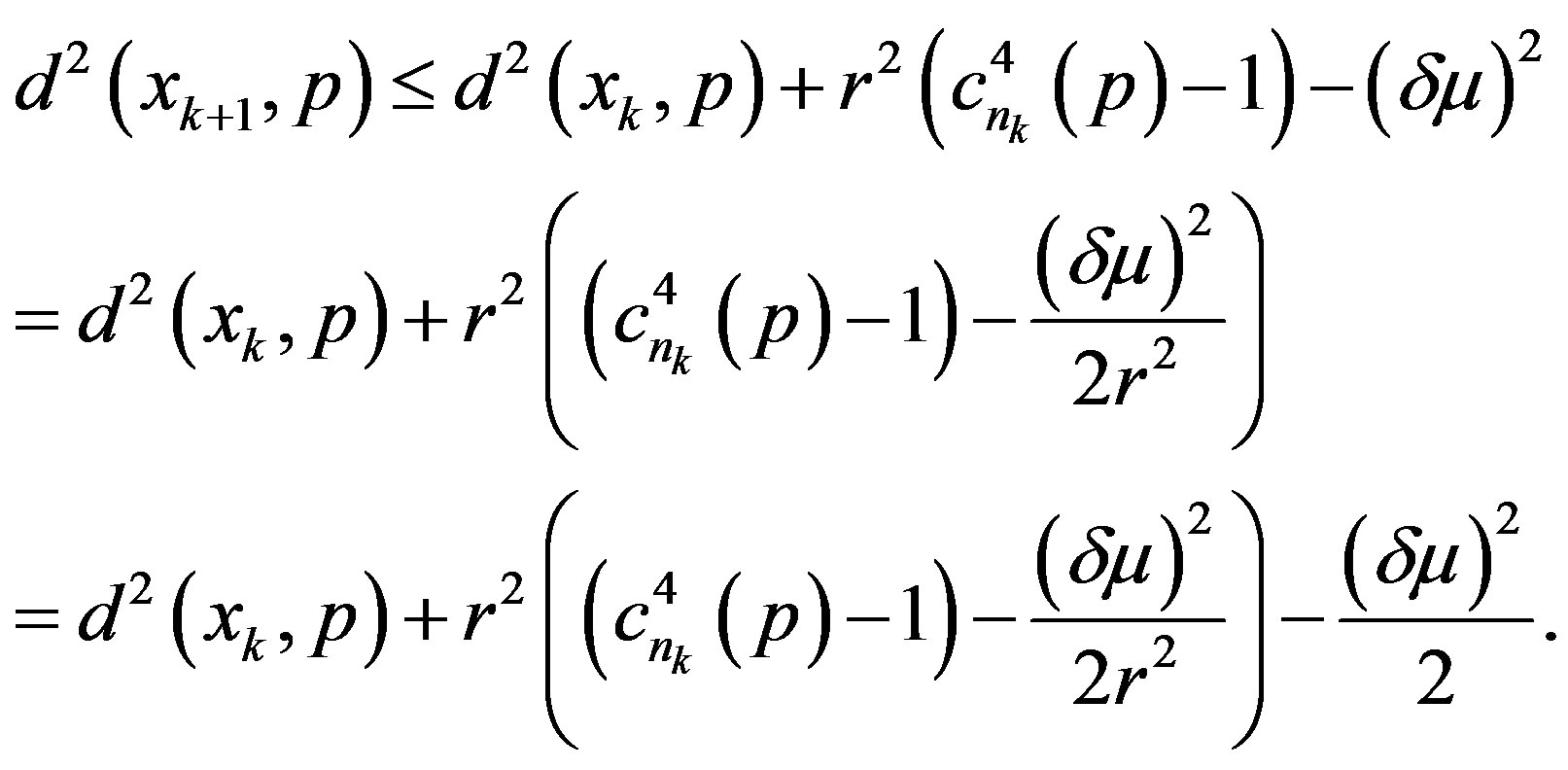
Since 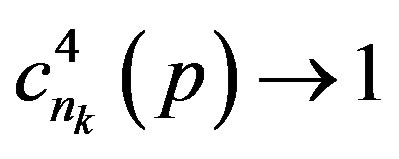 and
and  so there exists
so there exists 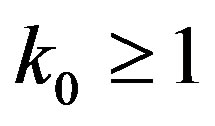 such that
such that 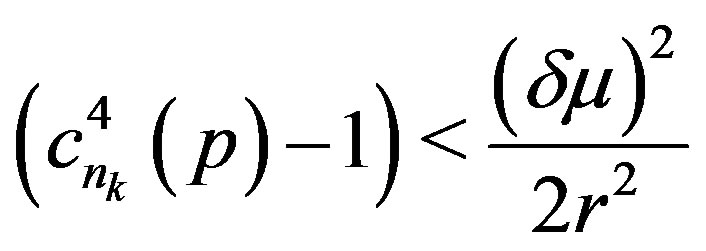 for all
for all 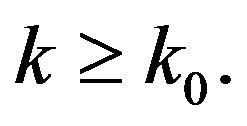
Hence the above inequality reduces to
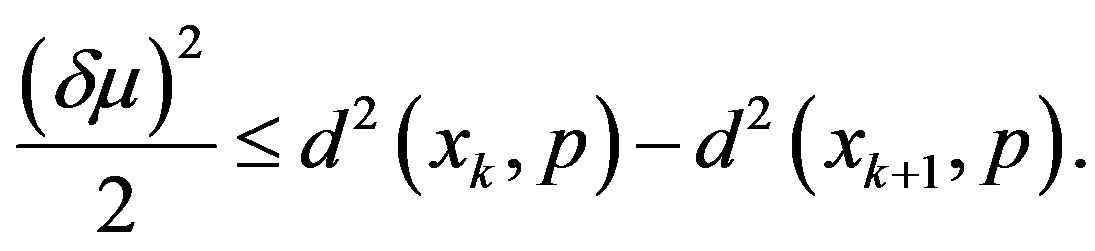 (2.10)
(2.10)
Let  be any positive integer. Then from (2.10), we have
be any positive integer. Then from (2.10), we have
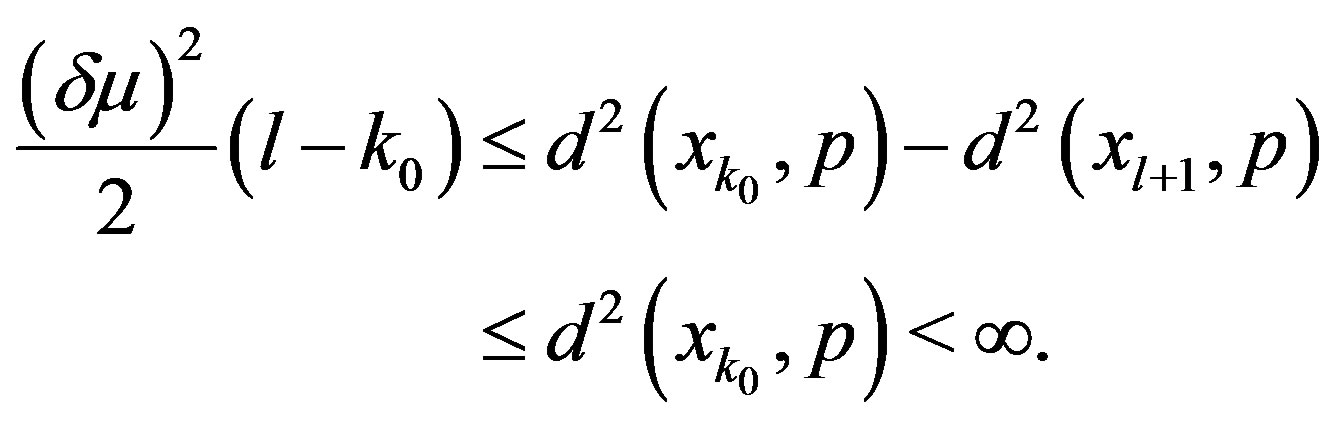 (2.11)
(2.11)
Letting  in (2.11), we get
in (2.11), we get

a contradiction.
Hence

Consequently, we have
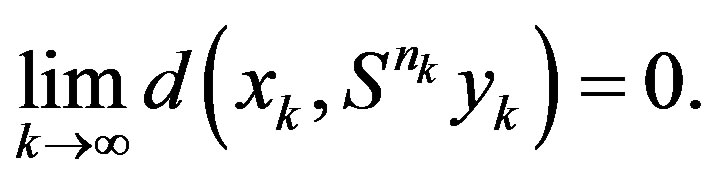 (2.12)
(2.12)
Following the similar procedure of proof with (2.8), we conclude
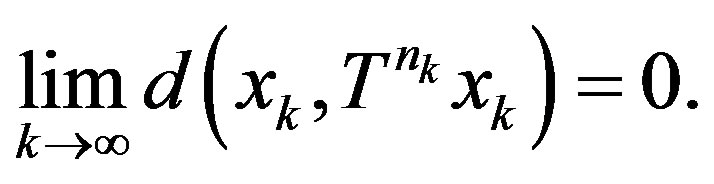 (2.12.1)
(2.12.1)
Since
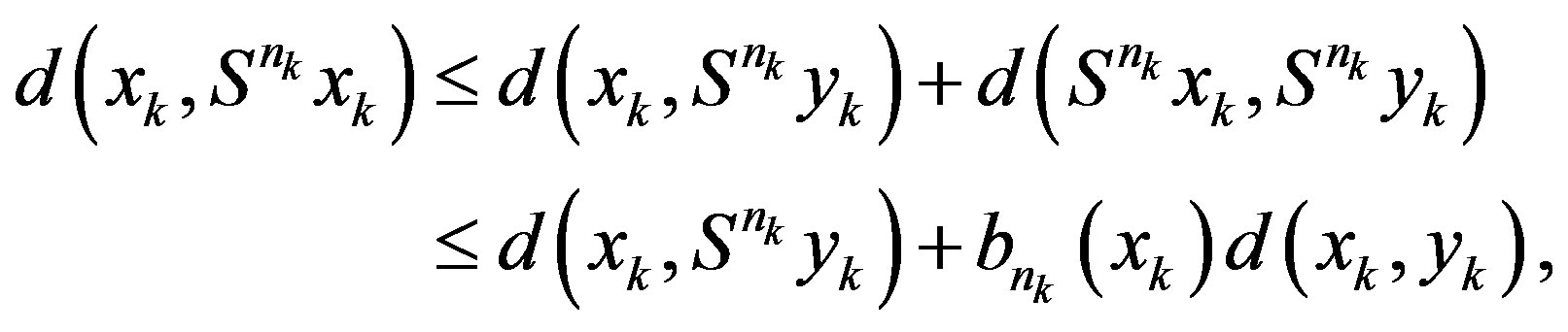
therefore with the help of (2.2) and (2.12), we get
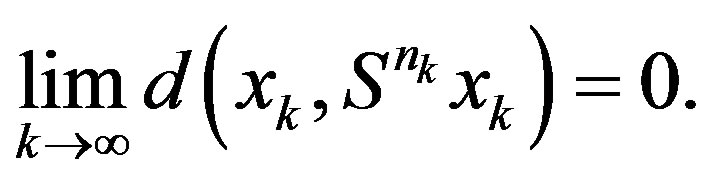
Finally, Lemma 2.1 appeals that
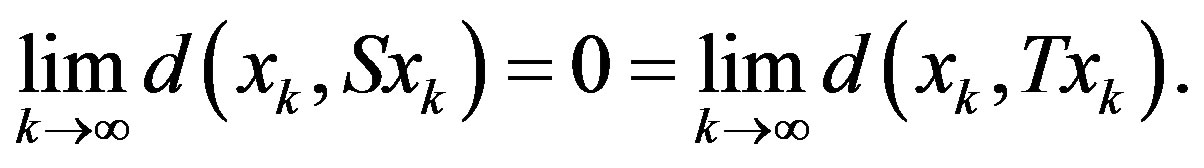 (2.13)
(2.13)
Let 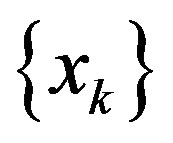 be a bounded sequence in a metric space X. For
be a bounded sequence in a metric space X. For  define
define 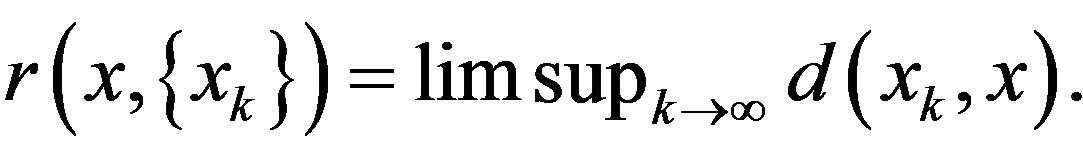 The asymptotic radius
The asymptotic radius  of
of 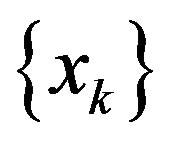 is given by:
is given by:
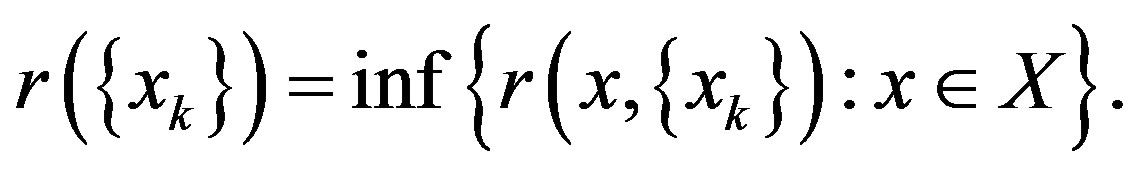
A bounded sequence  in
in 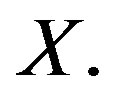 is regular if
is regular if 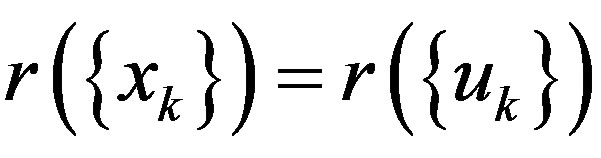 for every subsequence
for every subsequence  of
of 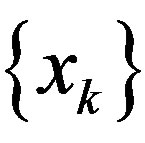
The asymptotic center of a bounded sequence  with respect to
with respect to 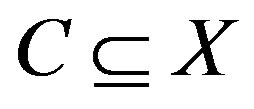 is defined
is defined

If the asymptotic center is taken with respect to 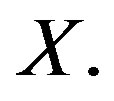 then it is simply denoted by
then it is simply denoted by 
A bounded sequence  in X. is said to be regular if
in X. is said to be regular if 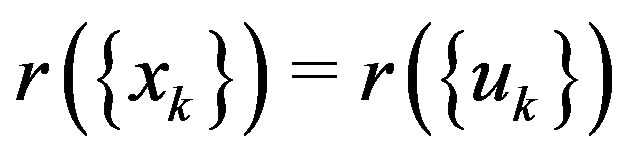 for every subsequence
for every subsequence  of
of  Recall that a sequence
Recall that a sequence  converges weakly to w (written as
converges weakly to w (written as ) if and only if
) if and only if 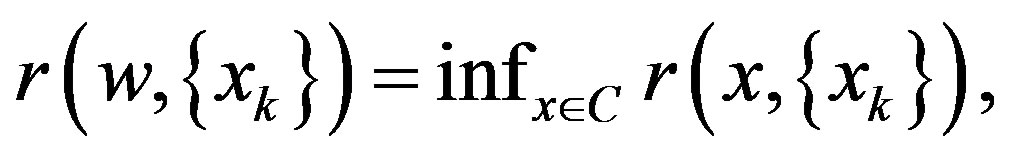 where C is a closed and convex subset containing the bounded sequence
where C is a closed and convex subset containing the bounded sequence 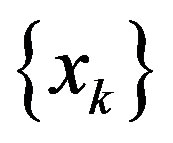 Moreover, a sequence
Moreover, a sequence  (in X.) Δ-converges to
(in X.) Δ-converges to 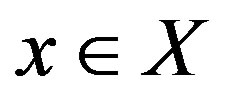 if x is the unique asymptotic center of
if x is the unique asymptotic center of  for every subsequence
for every subsequence 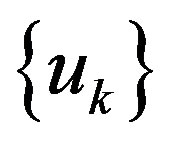 of
of 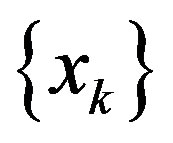 In this case, we write
In this case, we write 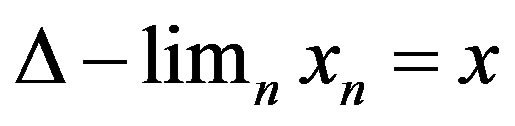 and x is called Δ-limit of
and x is called Δ-limit of 
In a Banach space setting, Δ-convergence coincides with weak convergence. A connection between weak convergence and Δ-convergence in geodesic spaces is characterized in the following lemma due to Nanjaras and Panyanak [26].
Lemma 2.4. ([26], Proposition 3.12). Let  be a bounded sequence in a
be a bounded sequence in a 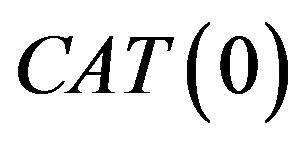 space
space 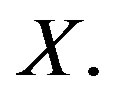 and let
and let  be a closed and convex subset of
be a closed and convex subset of  and contains
and contains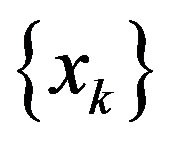 . Then 1)
. Then 1) 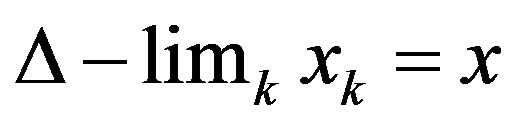 implies that
implies that 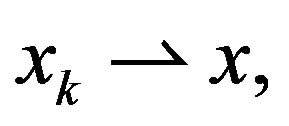
2) the converse of (1) is true if 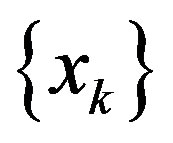 is regular.
is regular.
Next, we state the demiclosed principle in 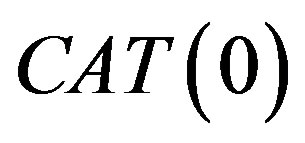 spaces due to Hussain and Khamsi [8] needed in the next convergence theorem.
spaces due to Hussain and Khamsi [8] needed in the next convergence theorem.
Lemma 2.5. Let 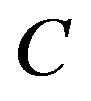 be a nonempty, bounded, closed and convex set in a
be a nonempty, bounded, closed and convex set in a  space X. and
space X. and 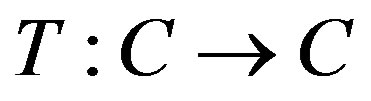 be a pointwise asymptotic nonexpansive map. Let
be a pointwise asymptotic nonexpansive map. Let  be a sequence in
be a sequence in 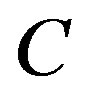 such that
such that  and
and 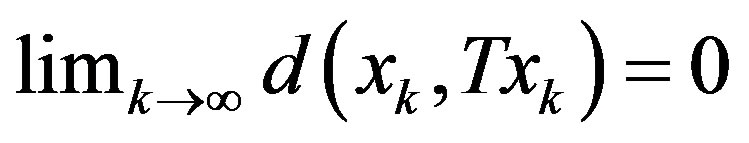 Then
Then 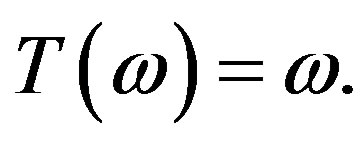
Next, we prove our weak convergence theorem.
Theorem 2.6. Let C be a nonempty, bounded, closed and convex set in a Hadamard space X. and let
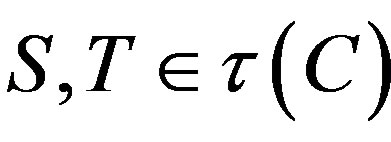 . Let
. Let  for some
for some 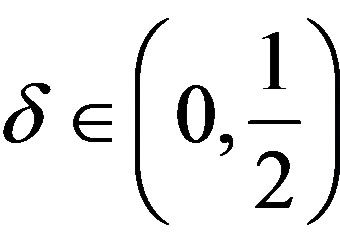
and 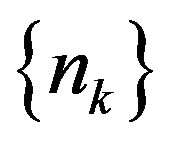 be such that the sequence
be such that the sequence 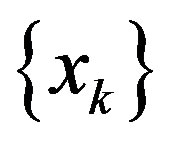 in
in 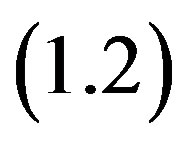 is well defined. If the set
is well defined. If the set 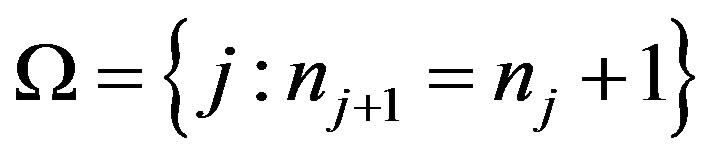 is quasiperiodic and
is quasiperiodic and 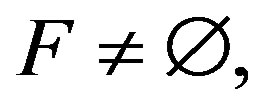 then
then 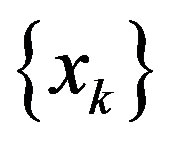 converges weakly to a point in
converges weakly to a point in 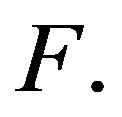
Proof. Let  be the weak
be the weak 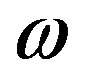 -limit set of
-limit set of 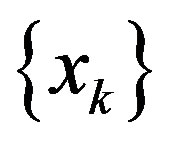 given by
given by

Since C is a nonempty bounded closed convex subset of a Hadamard space, there exists a subsequence 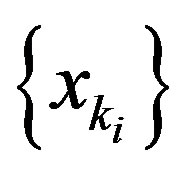 of
of 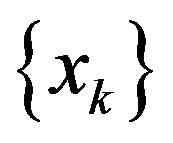 such that
such that  as
as 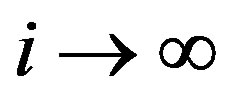 and vice versa. This shows that
and vice versa. This shows that 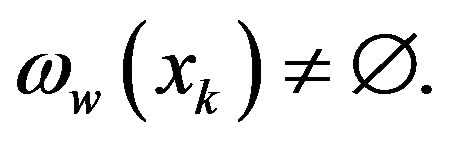 As
As 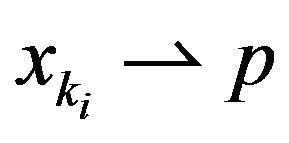
and 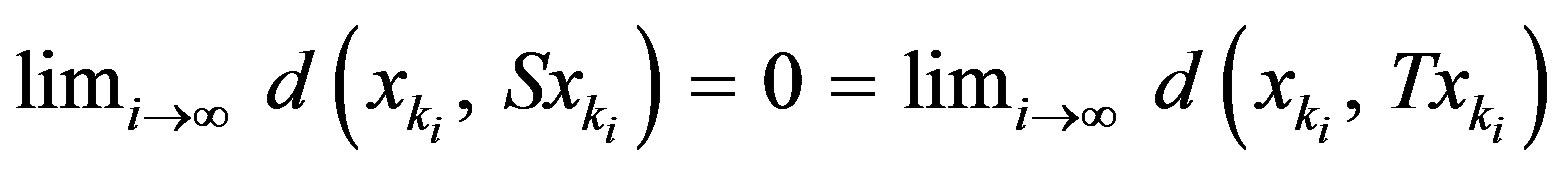 (by Lemma 2.1), therefore by Lemma 2.5,
(by Lemma 2.1), therefore by Lemma 2.5,  That is,
That is, 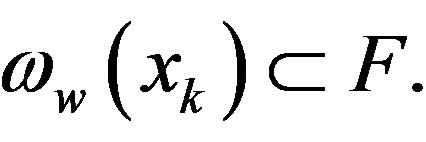 Next, we follow the idea of Chang et al. [14]. For any
Next, we follow the idea of Chang et al. [14]. For any 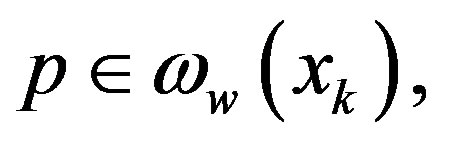 there exists a subsequence
there exists a subsequence  of
of 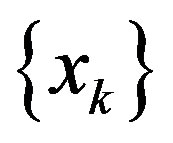 such that
such that
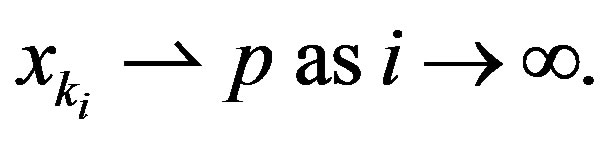 (2.14)
(2.14)
Hence from (2.12) and (2.14), it follows that
 (2.15)
(2.15)
Now from (1.2), (2.14) and (2.15), we get that
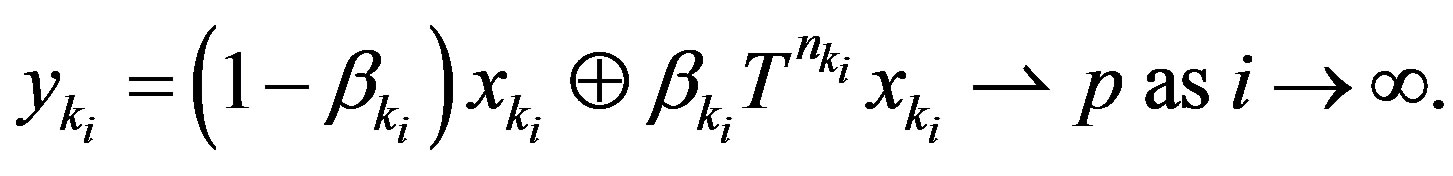 (2.16)
(2.16)
Also from (2.12) and (2.14), we have that
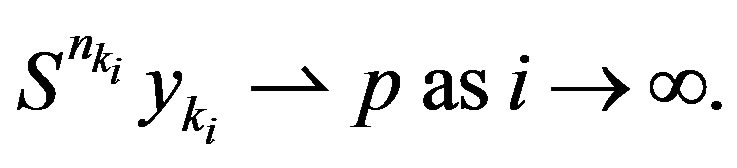 (2.17)
(2.17)
Again from (1.2), (2.14) and (2.17), we conclude that

Continuing in this way, by induction, we can prove that, for any 
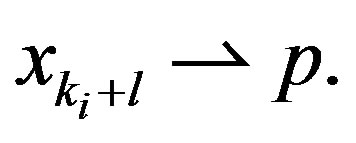
By induction, one can prove that  converges weakly to
converges weakly to 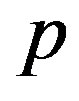 as
as 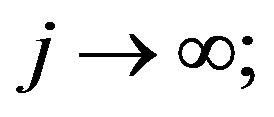 in fact
in fact  gives that
gives that  as
as 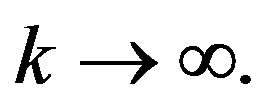
Remark 2.7. If 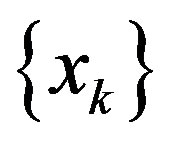 is regular in a geodesic space, then
is regular in a geodesic space, then 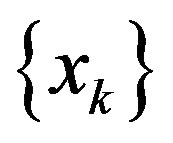 is Δ-convergent.
is Δ-convergent.
Our strong convergence theorem is as follows. We do not use the rate of convergence condition namely
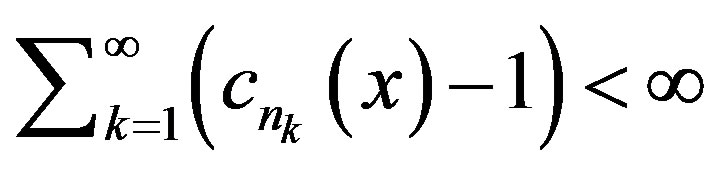 in its proof.
in its proof.
Theorem 2.8. Let C be a nonempty, bounded, closed and convex set in a Hadamard space X and let
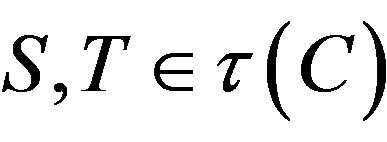 . Let
. Let 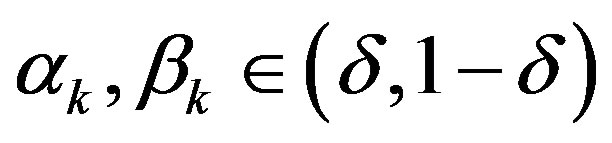 for some
for some 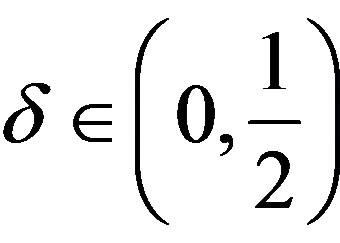
and 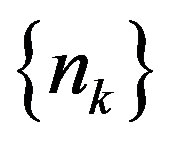 be such that the sequence
be such that the sequence 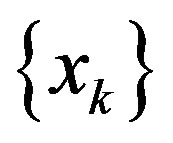 in
in 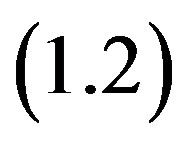 is well defined. If the set
is well defined. If the set 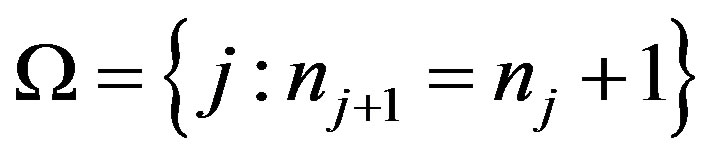 is quasiperiodic,
is quasiperiodic,  and either
and either 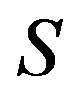 or
or 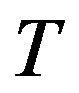 is semi-compact (completely continuous), then
is semi-compact (completely continuous), then 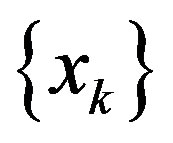 converges strongly to a point in F.
converges strongly to a point in F.
Proof. Let S be semi-compact. As 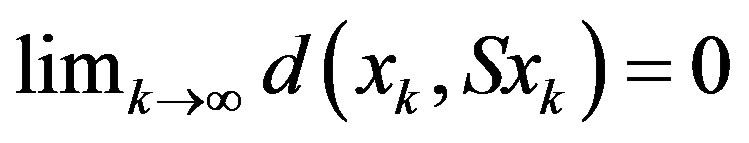 , there exists a subsequence
, there exists a subsequence  of
of  such that
such that
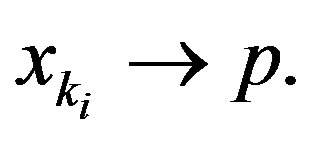
Using 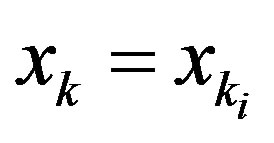 in (2.13) and continuity of
in (2.13) and continuity of 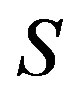 and
and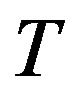 , we obtain that
, we obtain that 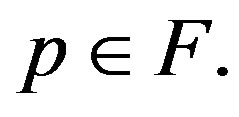 The rest of the proof follows by replacing
The rest of the proof follows by replacing  with
with  in Theorem 2.6 and we, therefore, omit the details.
in Theorem 2.6 and we, therefore, omit the details.
Finally, we state a theorem due to Nanjaras and Panyanak [26] proved in Hadamard spaces in which rate of convergence condition is necessary for Δ-convergence of the sequence.
Theorem 2.9. Let C be a nonempty, bounded, closed and convex set in a Hadamard space X and let 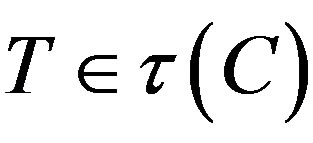 with a sequence
with a sequence 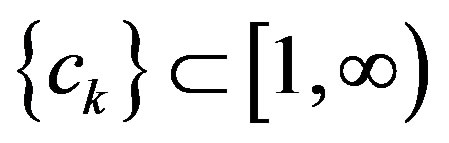 for which
for which 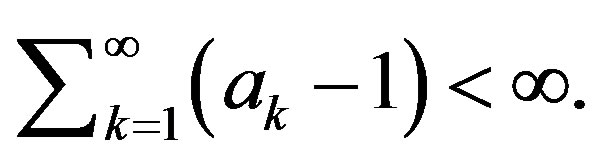 Suppose that
Suppose that 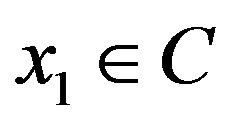 and
and  is a sequence in
is a sequence in 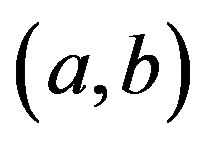 for some
for some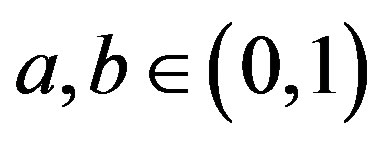 . Then the sequence
. Then the sequence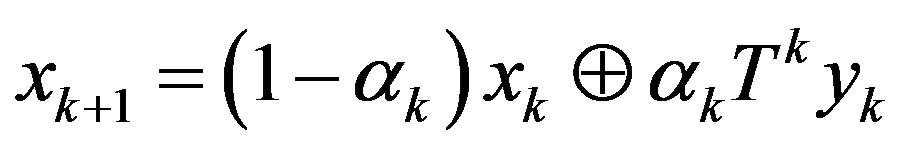 , Δ-converges to a fixed point of T.
, Δ-converges to a fixed point of T.
We pose the following open question.
Open question: Does Theorem 2.6 hold if we replace weak convergence by Δ-convergence?
REFERENCES
- K. K. Tan and H. K. Xu, “Fixed Point Iteration Processes for Asymptotically Nonexpansive Mapping,” Proceedings of the American Mathematical Society, Vol. 122, No. 3, 1994, pp. 733-739. doi:10.1090/S0002-9939-1994-1203993-5
- M. Bridson and A. Haefliger, “Metric Spaces of Non-Positive Curvature,” Springer-Verlag, Berlin, 1999.
- S. Dhompongsa and B. Panyanak, “On Δ-Convergence Theorems in CAT(0) Spaces,” Computers & Mathematics with Applications, Vol. 56, No. 10, 2008, pp. 2572-2579. doi:10.1016/j.camwa.2008.05.036
- F. Bruhat and J. Tits, “Groupes Réductifs Sur Un Corps Local. I. Données Radicielles Valuées,” Institut des Hautes Études Scientifiques Publications Mathématiques, Vol. 41, No. 1, 1972, pp. 5-251. doi:10.1007/BF02715544
- W. A. Kirk, “A Fixed Point Theorem in CAT(0) Spaces and R-Trees,” Fixed Point Theory and Applications, Vol. 4, 2004, pp. 309-316.
- W. A. Kirk and H. K. Xu, “Asymptotic Pointwise Contractions,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 69, No. 12, 2008, pp. 4706-4712. doi:10.1016/j.na.2007.11.023
- K. Goebel and W. A. Kirk, “A Fixed Point Theorem for Asymptotically Nonexpansive Mappings,” Proceedings of the American Mathematical Society, Vol. 35, 1972, pp. 171-174. doi:10.1090/S0002-9939-1972-0298500-3
- N. Hussain and M. A. Khamsi, “On Asymptotic Pointwise Contractions in Metric Spaces,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 71, No. 10, 2009, pp. 4423-4429. doi:10.1016/j.na.2009.02.126
- C. W. Groetsch, “A Note on Segmenting Mann Iterates,” Journal of Mathematical Analysis and Applications, Vol. 40, No. 2, 1972, pp. 369-372. doi:10.1016/0022-247X(72)90056-X
- W. R. Mann, “Mean Value Methods in Iteration,” Proceedings of the American Mathematical Society, Vol. 4, No. 3, 1953, pp. 506-510. doi:10.1090/S0002-9939-1953-0054846-3
- S. Ishikawa, “Fixed Points by a New Iteration Method,” Proceedings of the American Mathematical Society, Vol. 44, No. 1, 1974, pp. 147-150. doi:10.1090/S0002-9939-1974-0336469-5
- S. C. Bose, “Weak Convergence to the Fixed Point of an Asymptotically Nonexpansive,” Proceedings of the American Mathematical Society, Vol. 68, No. 3, 1978, pp. 305-308. doi:10.1090/S0002-9939-1978-0493543-4
- R. Bruck, T. Kuczumow and S. Reich, “Convergence of Iterates of Asymptotically Nonexpansive Mappings in Banach Spaces with the Uniform Opial Property,” Collectanea Mathematica, Vol. 65, No. 2, 1993, pp. 169-179.
- S. Chang, Y. J. Cho and H. Zhou, “Demiclosed Principle and Weak Convergence Problems for Asymptotically Nonexpansive Mappings,” Journal of the Korean Mathematical Society, Vol. 38, 2001, pp. 145-1260.
- H. Fukhar-ud-din and S. H. Khan, “Convergence of TwoStep Iterative Scheme with Errors for Two Asymptotically Nonexpansive Mappings,” International Journal of Mathematics and Mathematical Sciences, Vol. 2004, No. 37, 2004, pp. 1965-1971. doi:10.1155/S0161171204308161
- H. Fukhar-ud-din and S. H. Khan, “Convergence of Iterates with Errors of Asymptotically Quasi-Nonexpansive Mappings and Applications,” Journal of Mathematical Analysis and Applications, Vol. 328, No. 2, 2007, pp. 821-829. doi:10.1016/j.jmaa.2006.05.068
- H. Fukhar-ud-din and A. R. Khan, “Approximating Common Fixed Points of Asymptotically Nonexpansive Maps in Uniformly Convex Banach Spaces,” Computers & Mathematics with Applications, Vol. 53, No. 9, 2007, pp. 1349-1360. doi:10.1016/j.camwa.2007.01.008
- H. Fukhar-ud-din and A. R. Khan, “Convergence of Implicit Iterates with Errors for Mappings with Unbounded Domain in Banach Spaces,” International Journal of Mathematics and Mathematical Sciences, Vol. 10, 2005, pp. 1643-1653. doi:10.1155/IJMMS.2005.1643
- H. Fukhar-ud-din, A. R. Khan, D. O’Regan and R. P. Agarwal, “An Implicit Iteration Scheme with Errors for a Finite Family of Uniformly Continuous Mappings,” Functional Differential Equations, Vol. 14, No. 3-4, 2007, pp. 245-256.
- S. H. Khan and H. Fukhar-ud-din, “Weak and Strong Convergence of a Scheme with Errors for Two Nonexpansive Mappings,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 61, No. 8, 2005, pp. 1295-1301. doi:10.1016/j.na.2005.01.081
- A. R. Khan and N. Hussain, “Iterative Approximation of Fixed Points of Nonexpansive Maps,” Scientiae Mathematicae Japonicae, Vol. 54, No. 3, 2001, pp. 503-511.
- S. H. Khan and W. Takahashi, “Approximating Common Fixed Points of Two Asymptotically Nonexpansive Mappings,” Scientiae Mathematicae Japonicae, Vol. 53, No. 1, 2001, pp. 143-148.
- W. M. Kozlowski, “Fixed Point Iteration Processes for Asymptotic Pointwise Nonexpansive Mappings in Banach Spaces,” Journal of Mathematical Analysis and Applications, Vol. 377, No. 1, 2011, pp. 43-52. doi:10.1016/j.jmaa.2010.10.026
- T. Laokul and B. Panyanak, “Approximating Fixed Points of Nonexpansive Mappings in CAT(0) Spaces,” International Journal of Mathematics and Mathematical Sciences, Vol. 3, No. 25-28, 2009, pp. 1305-1315.
- W. Laowang and B. Panyanak, “Approximating Fixed Points of Nonexpansive Nonself Mappings in CAT(0) Spaces,” Fixed Point Theory and Applications, 2010, 11 pages, Article ID: 367274.
- B. Nanjaras and B. Panyanak, “Demiclosed Principle for Asymptotically Nonexpansive Mapping in CAT(0) Spaces,” Fixed Point Theory and Applications, 2010, 14 pages, Article ID: 268780.
- M. A. Noor and B. Xu, “Fixed Point Iterations for Asymptotically Nonexpansive Mappings in Banach Spaces,” Journal of Mathematical Analysis and Applications, Vol. 267, No. 2, 2002, pp. 444-453. doi:10.1006/jmaa.2001.7649
- Z. Opial, “Weak Convergence of Successive Approximations for Nonexpansive Mappings,” Bulletin of the American Mathematical Society, Vol. 73, 1967, pp. 591-597. doi:10.1090/S0002-9904-1967-11761-0
- G. B. Passty, “Construction of Fixed Points for Asymptotically Nonexpansive Mappings,” Proceedings of the American Mathematical Society, Vol. 84, 1982, pp. 212- 216. doi:10.1090/S0002-9939-1982-0637171-7
- B. E. Rhoades, “Fixed Point Iterations for Certain Nonlinear Mappings,” Journal of Mathematical Analysis and Applications, Vol. 183, No. 1, 1994, pp. 118-120. doi:10.1006/jmaa.1994.1135
- J. Schu, “Iterative Construction of Fixed Points of Asymptotically Nonexpansive Mappings,” Journal of Mathematical Analysis and Applications, Vol. 158, No. 2, 1991, pp. 407-413. doi:10.1016/0022-247X(91)90245-U
- J. Schu, “Weak and Strong Convergence to Fixed Points of Asymptotically Nonexpansive Mappings,” Bulletin of the Australian Mathematical Society, Vol. 43, No. 1, 1991, pp. 153-159. doi:10.1017/S0004972700028884

