Atmospheric and Climate Sciences
Vol.3 No.1(2013), Article ID:27585,9 pages DOI:10.4236/acs.2013.31016
On the Chain Length and Rate of Ozone Depletion in the Main Stratospheric Cycles
Institute of Energy Problems of Chemical Physics, Russian Academy of Sciences, Moscow, Russia
Email: iklarin@narod.rut
Received October 6, 2012; revised November 8, 2012; accepted November 16, 2012
Keywords: Ozone Depletion; Stratospheric Cycles; Chain Propagation; Chain Limitation; Limiting Step
ABSTRACT
Algorithm for calculation of the chain length and rate of stratospheric ozone depletion in Ox, HOx, NOx, ClOx and BrOx cycles has been developed. The most important new element in the theory of stratospheric chain processes is the correct determination the propagation rate, taking into account all reactions involved rather than a single reaction, which has the lowest rate, as it was usually done before. The role of null chain processes in the cycles has been considered and shown that these processes play a decisive role in formation of families of the odd oxygen, nitrogen, chlorine and bromine in the daytime while at night they play no role. Using two-dimensional model Socrates, and algorithm developed correct rate of ozone depletion and chain length in the cycles above for model conditions of June 2020 at 50˚N have been calculated.
1. Introduction
1.1. Short History of the Problem
For the first time the photochemical theory of stratospheric ozone was developed by the outstanding English geophysicist Sydney Chapmen [1]. The theory was applied to model of ozone distribution in the atmosphere to explain ozone layer existence. An important consequence of the Chapman’s finding was a conclusion that ozone in the stratosphere can be destroyed only by the depletion of odd oxygen (i.e. ozone molecules and atoms of oxygen) that today is a base of all known cycles of stratospheric ozone depletion. Forty years later, stratospheric ozone attracted an overall attention in connection with the threat of destruction of the ozone layer under action of anthropogenic chlorine-containing compounds found in the early 1970-ies by Molina and Rowland [2]. Among the works to precede this discovery (besides Chapman’s one) it should be noted the paper by Hampson [3], where the first chain mechanism of the ozone depletion in reactions with hydrogen oxides, which amplifies an action of the Chapman mechanism, has been described. Intensive studies of stratosphere chemistry at that time has led to the discovery of catalytic cycles with participation of nitrogen oxides [4], chlorine oxides [5], bromine oxides [6,7] and iodine oxides [8]. In last year problems of stratosphere chemistry and processes of formation and decomposition of the stratosphere ozone have been examined in a number books [9-13], including the one by G. Braseur and S. Solomon [14], that is most fully throwing light on all questions, connected with chemistry of ozone in the middle atmosphere. To the list of ozone references it should be added the work by Grenfell et al. [15], on chemical reaction pathways affecting stratospheric and mesospheric ozone and the one by D. J. Lary [16], which is probably the only one addressed the issue of the chain length in stratospheric ozone depletion cycles.
The chain length (in this case it’s a number of molecules of ozone, destroyed by one active particle in its life time in the stratosphere) is one of the most important characteristics of chain process. Special importance this index has acquired in the contemporary conditions, when it was convincingly demonstrated, that because of the chain processes the anthropogenic factors proved to be capable of competing with the natural processes. Therefore it is important to understand, what a future potential participants of the chain stratospheric processes are danger for the ozone layer and what is their effectiveness in comparison with the chlorine components, having played the dominant role in the anthropogenic depletion of the ozone layer in the end of the past century. A definition of the chain length makes it possible to successfully solve the task as well as task of a comparison of the effectiveness of these cycles, similarly, as this is done with respect to various halogen-containing chemicals, for which an index of Ozone Depletion Potential is used (see, for example, [17]). In the present work we have considered some new conceptions of the stratospheric chain processes theory, and also we have demonstrated how this theory can be used for description of the ozone depletion in Ox, HOx, NOx, ClOx and BrOx cycles which are considered now to be the main cycles of destruction of stratospheric ozone. New key points in our analysis are a correct determination of the rate of chain propagation and finding algorithm for the chain length calculations in the cycles mentioned above.
1.2. On Some Peculiarity of the Stratospheric Chain Processes
In the simplest case the chain process of the ozone depletion in the stratosphere can be written as follows [18]:
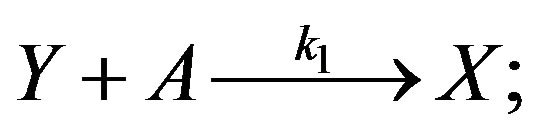 (R1)
(R1)
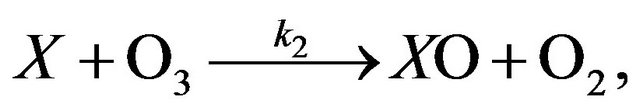 (R2)
(R2)
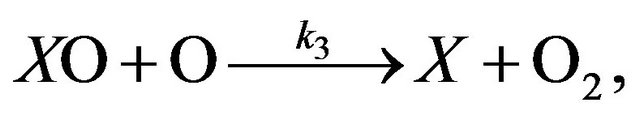 (R3)
(R3)
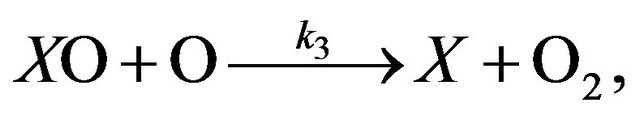
 (R4)
(R4)
Here (R1) is a reaction of chain initiation, (R2), (R3) are the ones of chain propagation and (R4) is the one of chain termination. The length of chain, ν, which in this case is a number of odd oxygen particles, destroyed by one active particle X in time of its stratospheric life, can be calculated using Equation (1):
 (1)
(1)
If reactions (R2) and (R3) are unique processes of a mutual exchange between X and XO, their rates become identical already after several cycles. However, as a rule, besides reactions (R2) and (R3) other processes of exchange between X and XO run in the stratosphere. As a result, it does not lead to alignment of the reaction rates even at considerable chain length. But in any case because the reactions of chain propagation are consecutive ones, the rate of destruction of odd oxygen (i.e. O3 + O) are defined by the rate of so-called limiting step of the process. Usually the limiting step refers to the reaction with the lowest rate. But in most real situations in the stratosphere it is difficult to determine a true limiting step (as a single reaction) for all heights. For example, in the NOx cycle the chain propagation reactions are
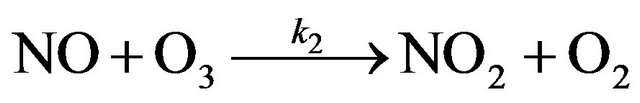 (R5)
(R5)
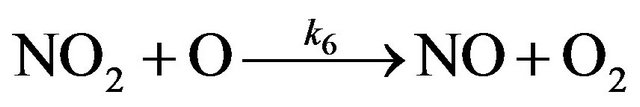 (R6)
(R6)
and reaction (R6) is considered to be a limiting step in NOx cycle because it has a minimal rate in the stratosphere [12-14]. But as it seen from Figure 1 near 40 km the rates of reactions (R6) and (R5) change places and at

Figure 1. Reactions of chain propagation and the limiting step in NOx cycle.
more height reaction (R5) is getting slower than reaction (R6).
In addition, around 40 km reaction rates are the same and formally a limiting step here is missing.
To resolve the problem we offer a simple rule for calculating the rate of limiting step (=the rate propagation)— in case of two reactions of propagation, (R2) and (R3), the rate of the limiting step, 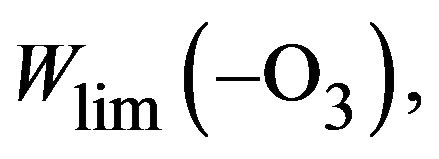 should be defined by Equation (2):
should be defined by Equation (2):
 (2)
(2)
where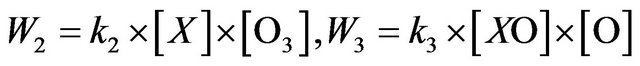 , and the rate of ozone depletion,
, and the rate of ozone depletion, 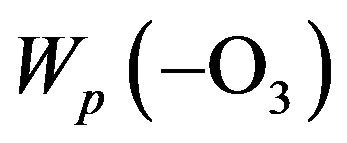 , should be defined by Equation (3):
, should be defined by Equation (3):
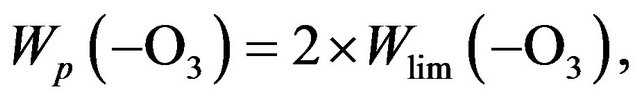 (3)
(3)
where factor 2 appears as two particles of odd oxygen are destroyed in the chain process. Rate of limiting step by Equation (2) is shown in Figure 1 (dotted cutve). It’s seen that Equation (2) allow one fully satisfy a concept of the lowest rate for limiting step at all stratospheric heights. Note also, that as it follows directly from Equation (2), at W2 = W3 the rate of destruction of odd oxygen equals 0.5 × W2 or 0.5 × W3. The last conclusion is a logical consequence of the fact that two successive steps require two times longer than one.
From here it is easy to conclude that under three reactions of chain propagation run with rates W2, W3 and W4, 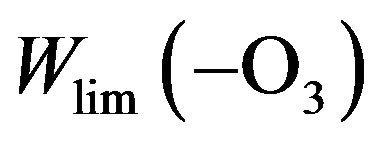 is expressed by Equation (4):
is expressed by Equation (4):
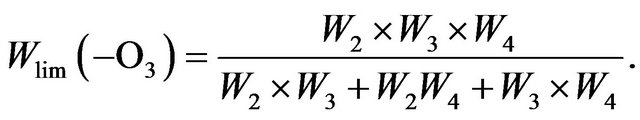 (4)
(4)
Similarly, it is possible to calculate the rate of a limiting step at any number of propagation reactions at any small differences in their rates that would represent a significant challenge for the limiting step in usual formulation. The concept of a limiting step of chain process introduced and its definition through inverse rates of chain propagation reactions is a basic new feature of stratospheric chain process, which was not considered till now at description of the chain stratospheric processes. We’ll show how to use the new concept at consideration of main cycles of stratospheric ozone depletion in the next section.
2. Results and Discussion
This section presents the results of calculation of the chain lengths, as well as the rates of limiting steps and chain limitation in Ox, HOx, NOx, ClOx and BrOx cycles. The chain length has been determined by Equation (1). All numerical data have been obtained using 2D model Socrates [18] for conditions of June 2020 at the latitude 50˚N and IPCC Scenarios for greenhouse gases [19,20]. By consideration of the chemistry of cycles only the reactions involved in the calculations specified above have been taken into account.
2.1. Ox Cycle or Chapman’s One
It’s assumed that odd oxygen [Ox] = [O3] + [O(3P)] + [O(1D)] where O(3P) is atom O in the ground state and O(1D) is the one in exited state with energy 1.96 eV. According [14] Chapman’s cycle includes the reactions (R7)-(R12):
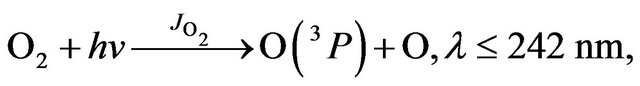 (R7)
(R7)
 (R8)
(R8)
![]() (R9)
(R9)
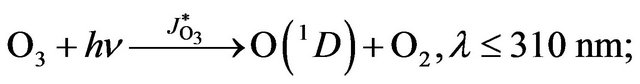 (R10)
(R10)
 (R11)
(R11)
 (R12)
(R12)
where M is molecules of air, 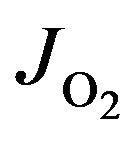 ,
,  and
and 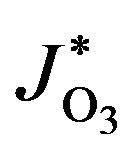 are coefficients of photodissociation of O2 and O3, respectively.
are coefficients of photodissociation of O2 and O3, respectively.
Since reaction (R11) converts O(1D) to O(3P), it follows that the reaction (R12) determines the loss of all three component of odd oxygen, i.e. (R12) may be seen as a reaction of chain termination, Wd(−Ox). On the other hand, reaction (R12) should be considered as a chain propagation reaction in Ox cycle because just this one does destroy odd oxygen. It follows that chain length in Ox cycle, ![]() is equal to 1 (see Equation (1)) and the rate of chain propagation, Wp(−Ox), is:
is equal to 1 (see Equation (1)) and the rate of chain propagation, Wp(−Ox), is:
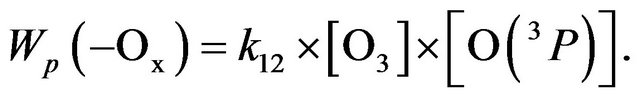 (5)
(5)
It can be shown that stratospheric lifetime of Ox, τ(Ox), is much more than τ(O3), τ(O(3P)) and τ(O(1D)) if the latter are defined through its individual ways of destruction. The situation is realized thank to so called Ox null cycle which doesn’t destruct O3 or O(3P). The reactions of Ox null cycle are (R13) and (R9):
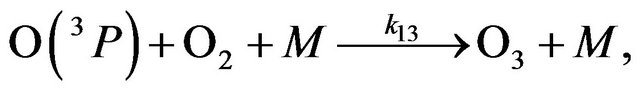 (R13)
(R13)
![]() (R9)
(R9)
So using Equation (2) one can find that the rate of the limiting step in Ox null cycle
 (6)
(6)
where 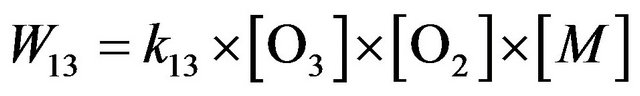 and
and
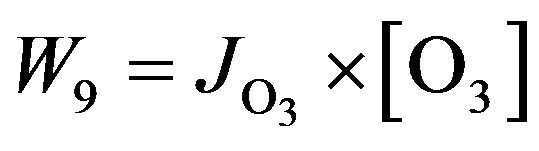 . The rate of chain termination in null cycle is the same as in the main cycle, i.e.
. The rate of chain termination in null cycle is the same as in the main cycle, i.e. 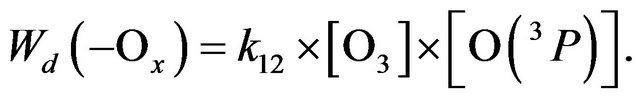 So we obtain that
So we obtain that
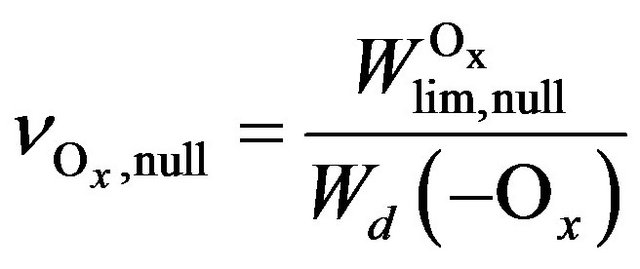 . (7)
. (7)
Height profile of 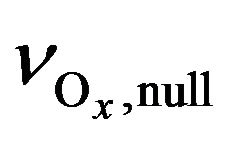 is shown in Figure 2. One can see that in the low stratosphere, chain length is about 106, and at the altitude of 55 km it’s about 50. In our case the chain length means a number of mutual conversion of Ox components occurring during stratospheric lifetime of Ox, τ(Ox). So, a condition of
is shown in Figure 2. One can see that in the low stratosphere, chain length is about 106, and at the altitude of 55 km it’s about 50. In our case the chain length means a number of mutual conversion of Ox components occurring during stratospheric lifetime of Ox, τ(Ox). So, a condition of 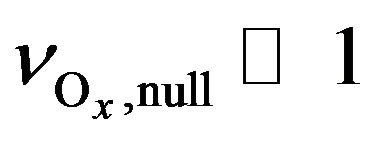 means that mutual conversion of O3, O(3P) and O(1D) occur so fast in comparison with τ(Ox) that they are getting chemically indistinguishable and one can consider lifetime of these components to be the same as τ(Ox). But it should be the case only for daytime conditions. At night
means that mutual conversion of O3, O(3P) and O(1D) occur so fast in comparison with τ(Ox) that they are getting chemically indistinguishable and one can consider lifetime of these components to be the same as τ(Ox). But it should be the case only for daytime conditions. At night , W9 and
, W9 and 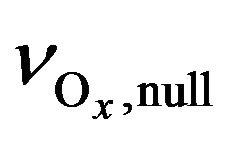 are getting to zero, Ox family disappears and lifetime of O3, O(3P) and O(1D) are getting dependent on
are getting to zero, Ox family disappears and lifetime of O3, O(3P) and O(1D) are getting dependent on

Figure 2. Height profile of the chain length in Ox null cycle.
its individual loss processes.
Finally, let’s underline that to understand a daytime chemistry of ozone it is possible only through a method of families. It is the only way to define correctly atmospheric lifetime of ozone as well as to show that a unique source of ozone in the stratosphere is photodissociation of О2, and a unique sink is a reaction O3 with O(3P).
2.2. HOx Cycle
Family of odd hydrogen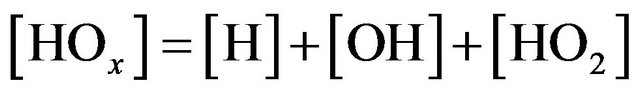 . Destruction of odd oxygen in HOx cycle occurs through the following chain mechanisms.
. Destruction of odd oxygen in HOx cycle occurs through the following chain mechanisms.
Cycle I:
 (R14)
(R14)
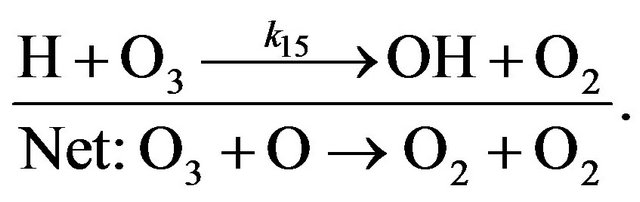 (R15)
(R15)
Cycle II:
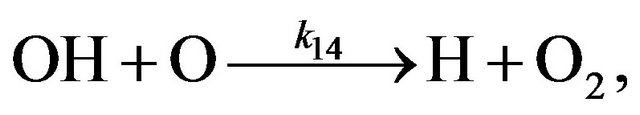 (R14)
(R14)
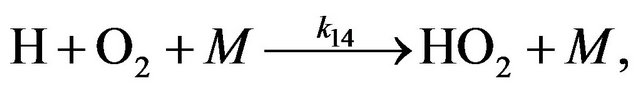 (R16)
(R16)
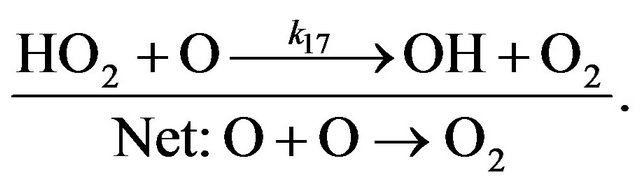 (R17)
(R17)
Cycle III:
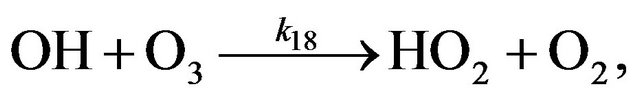 (R18)
(R18)
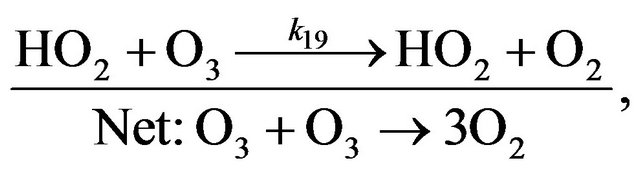 (R19)
(R19)
Cycle IV:
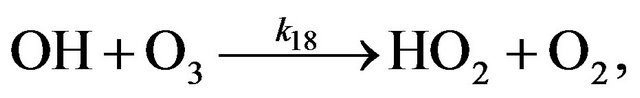 (R18)
(R18)
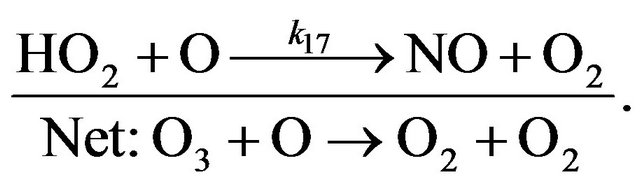 (R17)
(R17)
Rate of the limiting steps in Cycles I-IV is determined by Equations (8)-(11):
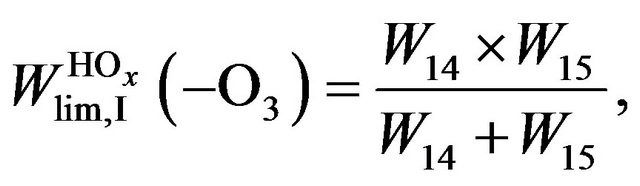 (8)
(8)
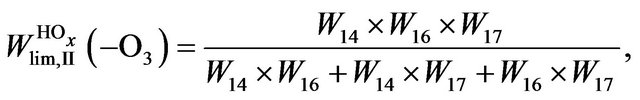 (9)
(9)
 (10)
(10)
 (11)
(11)
where W# is the rate of reaction (R#). Height profiles of 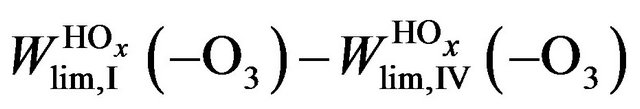 and their sum are shown in Figure 3. Rate of destruction of odd oxygen in a hydrogen cycle,
and their sum are shown in Figure 3. Rate of destruction of odd oxygen in a hydrogen cycle,  one can define as a sum of
one can define as a sum of 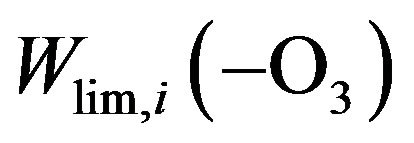 times factor 2,
times factor 2,
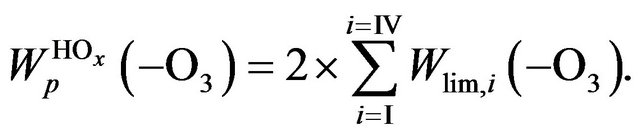 (12)
(12)
Chain termination processes in HOx cycle and their rates are shown in Figure 4. As it follows from Figure 4 chain termination in HOx cycle is due to the reaction (R20):
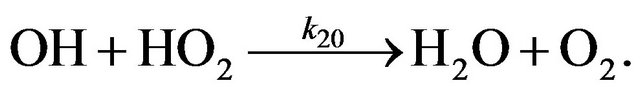 (R20)
(R20)
So the rate of chain termination in hydrogen cycle,  , can be written as Equation (13):
, can be written as Equation (13):
 (13)
(13)
Chain length in HOx cycle one can find using Equation (14)
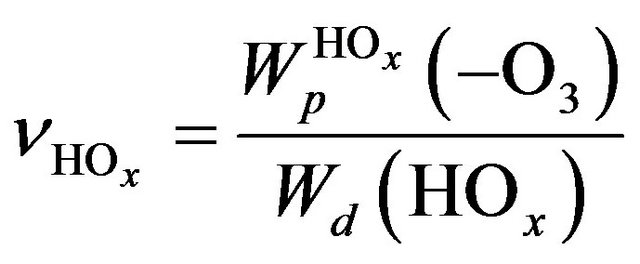 . (14)
. (14)
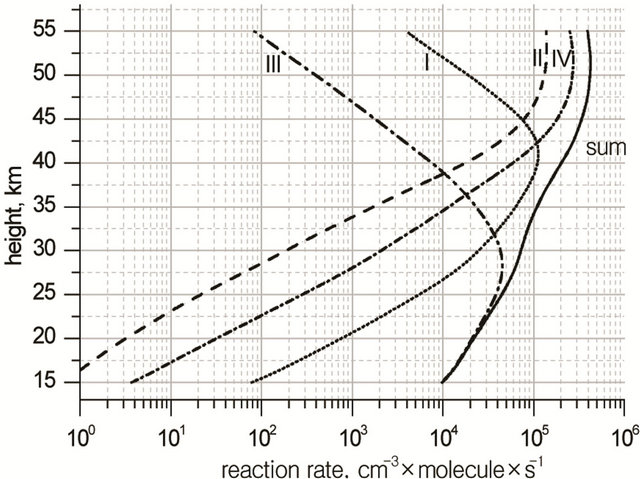
Figure 3. Heigt profiles of 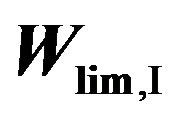 (−O3) −
(−O3) − 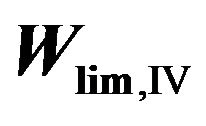 (−O3) and their sum in HOx cycle.
(−O3) and their sum in HOx cycle.
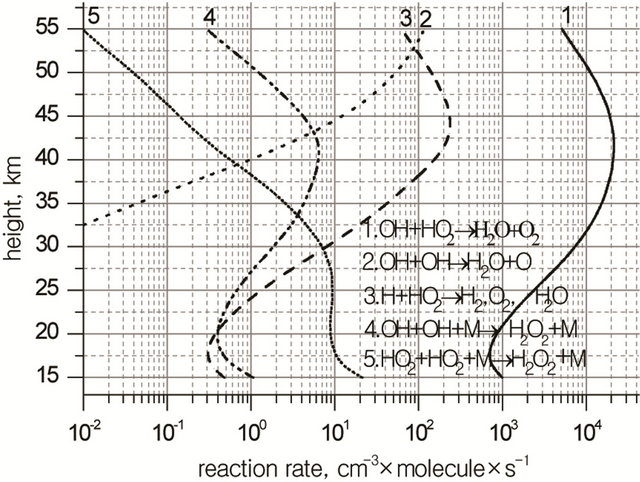
Figure 4. Chain termination processes in HOx cycle and their rates.
In conclusion it should be noted that under description of ozone depletion in HOx cycle usually reactions with individual participation O3 or O are taking into account (see [11,14]). In this connection it should be underlined that as it follows from Chapman’s mechanism, ozone can be destructed only through depletion of the odd oxygen which requires at least two reaction of chain propagation. But in this case the rate of ozone depletion is expressed using limiting steps as it was done above. Using individual reaction with O3 or O means, in fact, an ignoring chain mechanism of ozone depletion in the stratosphere.
2.3. NOx Cycle
NOx family includes NO and NO2. Like HOx, cycle NOx includes three chain mechanisms Cycle I:
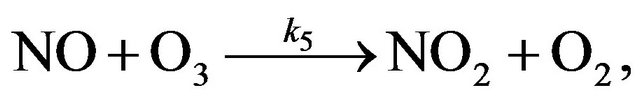 (R5)
(R5)
 (R6)
(R6)
Cycle II:
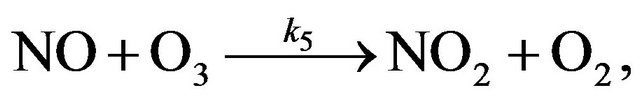 (R5)
(R5)
 (R21)
(R21)
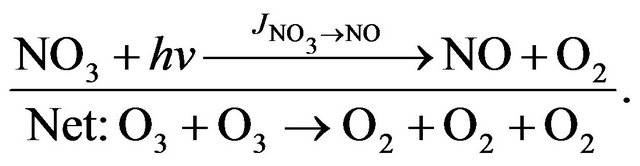 (R22)
(R22)
Cycle III:
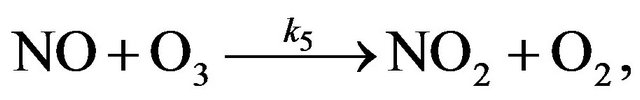 (R5)
(R5)
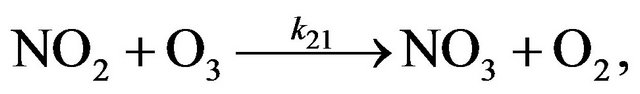 (R21)
(R21)
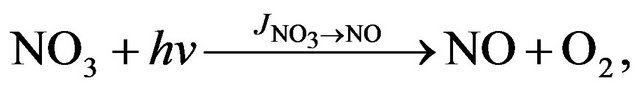 (R22)
(R22)
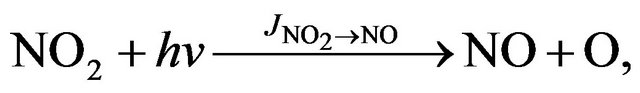 (R23)
(R23)
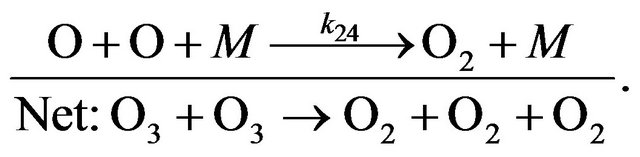 (R24)
(R24)
Height profiles of the rate of limiting steps in Cycles I-III are shown in Figure 5.
It’s seen that the most important cycles in that case are Cycles I and II. So the rate of ozone depletion in total NOx cycle, 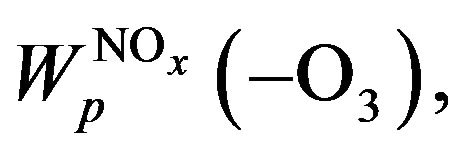 can be expressed by Equation (15):
can be expressed by Equation (15):
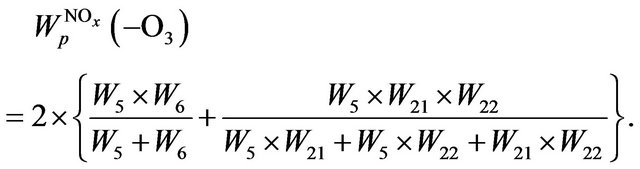 (15)
(15)
Chain limitation in NOx cycle occur through chemical conversion of NO in N2:
 (R25)
(R25)
and physical process of the turbulent transport characterized by time τd expressed by Equation (16):
 (16)
(16)
Here H is scale height, kzz is a vertical coefficient of turbulent diffusion. So the rate of chain limitation in NOx cycle, Wd(NOx), can be expressed as
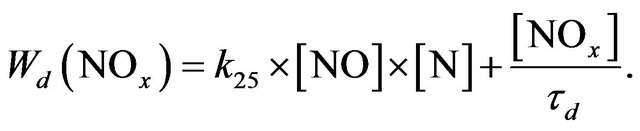 (17)
(17)
Height profiles of Wd(NOx) are shown in Figure 6.
Knowledge of the rates of chain propagation and of chain limitation allows one to express a chain length in NOx cycle,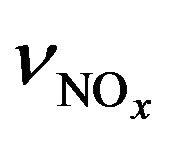 :
:
 (18)
(18)
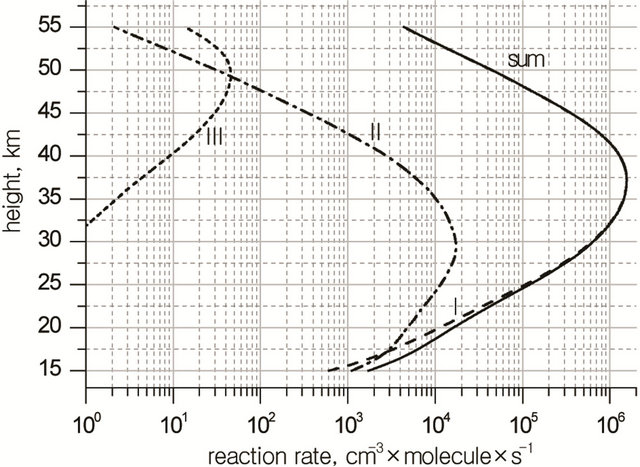
Figure 5. Height profiles of the limiting step rates of Cycles I-III in NOx cycle and their sum.
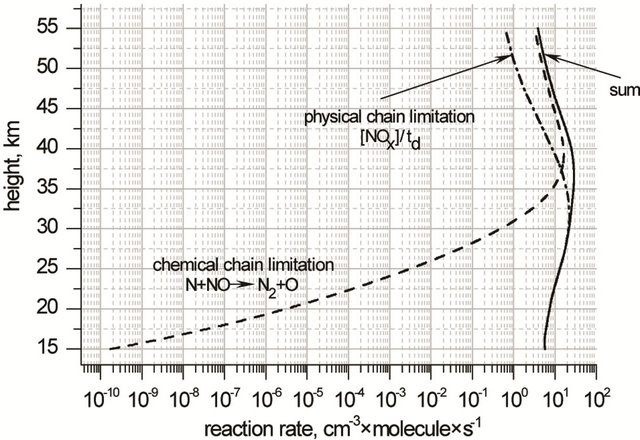
Figure 6. Height profiles of chain limitation rate in NOx cycle.
It should add that in the low and middle stratosphere NOx cycle runs mainly not destroying odd oxygen. It’s explained by a null cycle, a chain length of which here is much higher than the one of main cycle determined by Equation (18). Reactions of the NOx null cycle are the following:
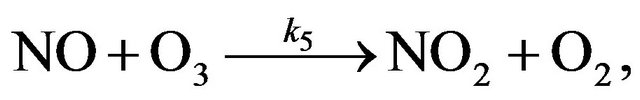 (R5)
(R5)
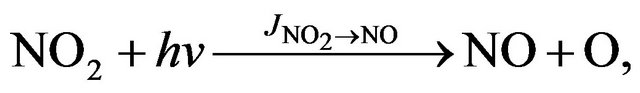 (R23)
(R23)
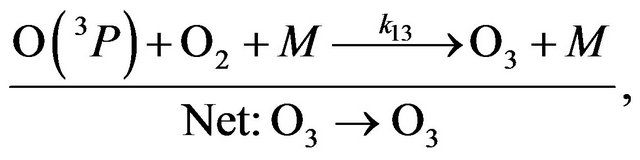 (R13)
(R13)
Limiting step of null cycle includes reactions (R5) and (R23) and its rate can be easily calculated by the same rules as above. Chain limitation is the same as in the main cycle (see Equation (17)). Let’s remind, that the null cycle acts only in day conditions that provides a possibility of existence of NOx family. At night the rate of the reaction (R23) is getting to zero and NOx family disintegrates.
Figure 7 shows chain lengths of the main cycle (Equation (18)) and the null one in NOx cycle.
2.4. ClOx Cycle
Depletion of the odd oxygen in that case includes two cycles.
Cycle I:
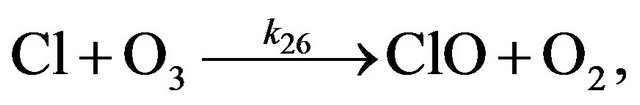 (R26)
(R26)
 (R27)
(R27)
Cycle II:
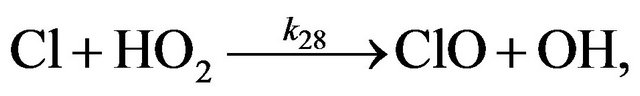 (R28)
(R28)
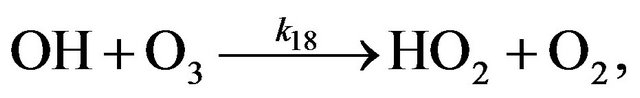 (R18)
(R18)
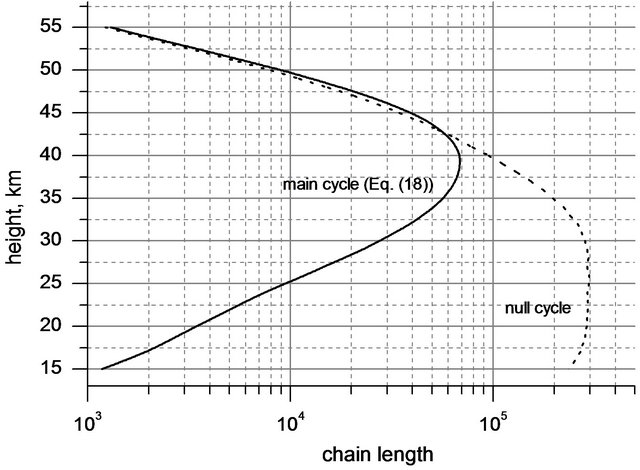
Figure 7. Chain lengths of the main cycle (Equation (18)) and the null one in NOx cycle.
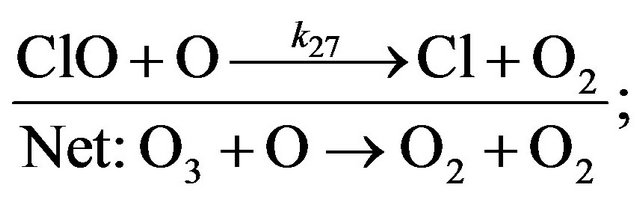 (R27)
(R27)
Rates of the limiting step in Cycles I, II are calculated just as in case of a hydrogen cycle. The results of the calculations are shown in Figure 8.
It’s seen from Figure 8 that one can neglect limiting step of Cycle II and express the rate of ozone depletion in ClOx cycle, 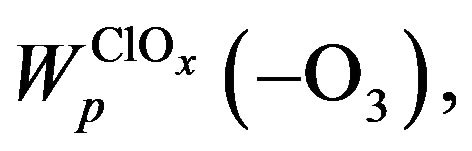 as follows:
as follows:
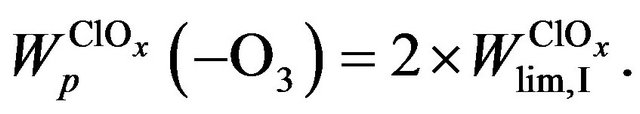 (19)
(19)
Chemical chain limitation in ClOx cycle occures by reactions with formation of HCl, HOCl and ClONO2. However stratospheric lifetime of these species appears to be less than a transport time τd (see Equation (16)). Consequently, the real chain limitation should be determined by the processes of turbulent transport, the rate of which is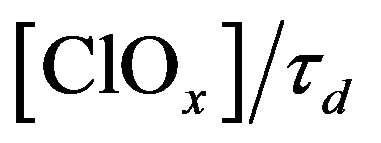 . So one can consider that
. So one can consider that
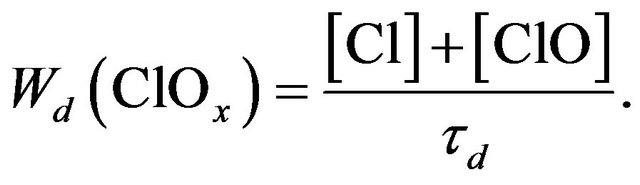 (20)
(20)
Respectively, ClOx chain length, 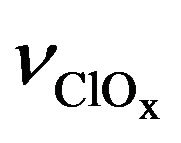 , one can find using Equation (21):
, one can find using Equation (21):
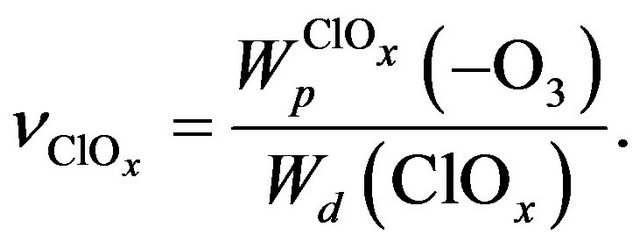 (21)
(21)
Like NOx cycle, ClOx one has a null cycle as well which provides a mutual exchange of Cl and ClO:
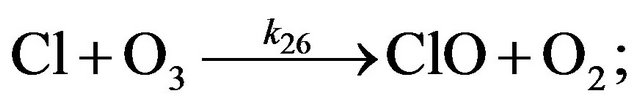 (R26)
(R26)
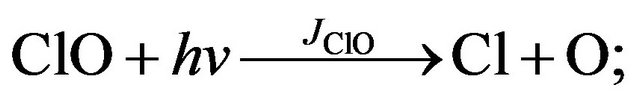 (R27)
(R27)
 (R13)
(R13)
It can be shown that like NOx cycle the null cycle of ClOx family appears to be faster than main (“working”) cycle.
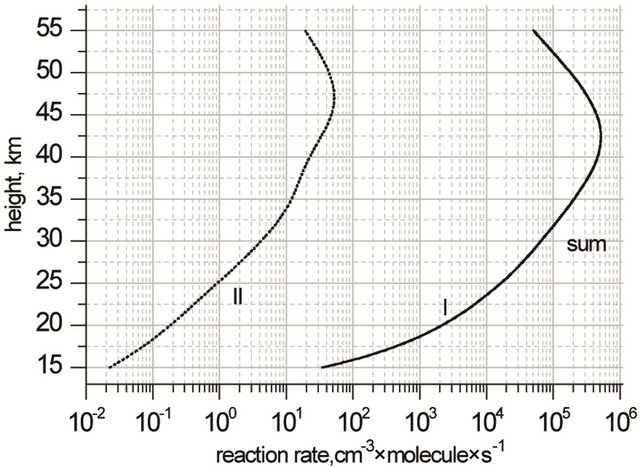
Figure 8. Height profiles of the limiting step rates of Cycles I and II in ClOx cycle and their sum.
2.5. BrOx Cycle
First two BrOx cycles have been suggested by Wofsy et al. in 1975 [6].
Cycle I:
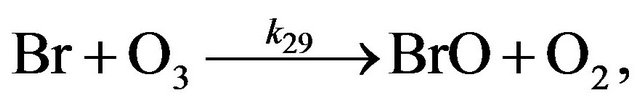 (R29)
(R29)
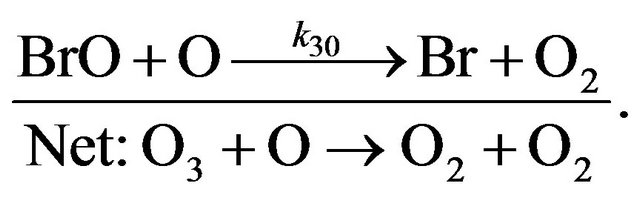 (R30)
(R30)
Cycle II:
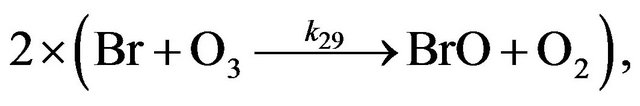 (R29)
(R29)
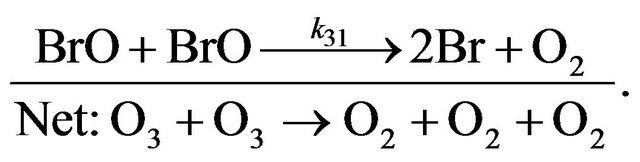 (R31)
(R31)
In 1980 Yung et al. [7] have added next four cycles.
Cycle III:
 (R29)
(R29)
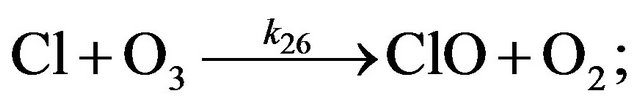 (R26)
(R26)
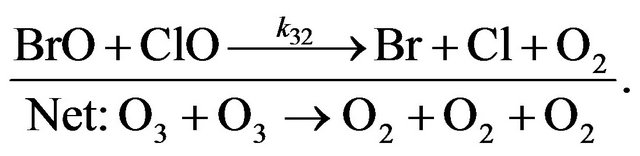 (R32)
(R32)
Cycle IV:
 (R29)
(R29)
 (R33)
(R33)
 (R34)
(R34)
 (R22)
(R22)
 (R5)
(R5)
Cycle V:
 (R29)
(R29)
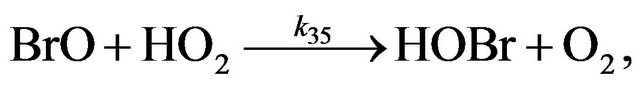 (R35)
(R35)
 (R36)
(R36)
 (18)
(18)
Cycle VI:
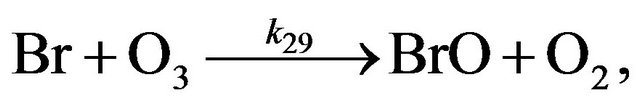 (R29)
(R29)
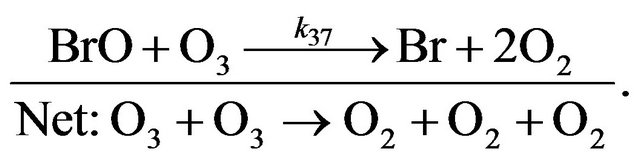 (R37)
(R37)
The rates of limiting steps in Cycles I-VI can be found as above. They are shown in Figure 9.
So using Equation (22) one can get the rate of ozone depletion in BrOx cycle:
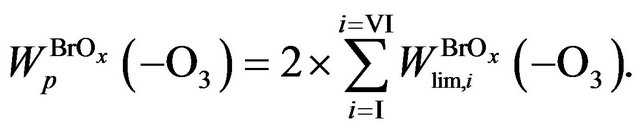 (22)
(22)
Formally chemical chain limitation in BrOx cycle run with formation HBr, HOBr and BrONO2. But it doesn’t stop chain propagation because a stratospheric lifetime of these species is much less than τd. So one can get for the real chain limitation in BrOx cycle the same expression as in case of ClOx cycle:
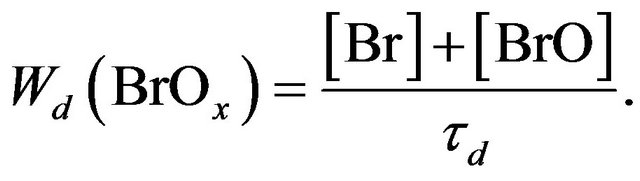 (23)
(23)
From here follows, that chain length in BrOx cycle is:
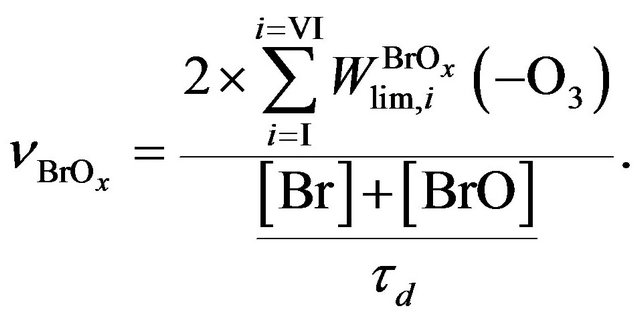 (24)
(24)
Chain length 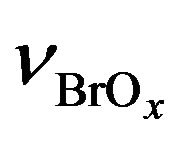 as well as ones of all other cycles considered above are shown in Figure 10.
as well as ones of all other cycles considered above are shown in Figure 10.
Finally, Figures 11 and 12 show the absolute and relative contribution in ozone depletion all cycles for conditions specified above.
3. Conclusions
Algorithm for calculation of the limiting step rates in the chain propagation reactions of stratospheric ozone depletion has been developed. It allows one to calculate the rate of limiting steps with any number of propagation reactions and any arbitrarily small difference in the rates of these reactions. This provided the opportunity for the first time correctly to calculate the rate of ozone destruction in the main cycles of the stratospheric ozone depletion.
Using algorithm developed, 2D model Socrates and
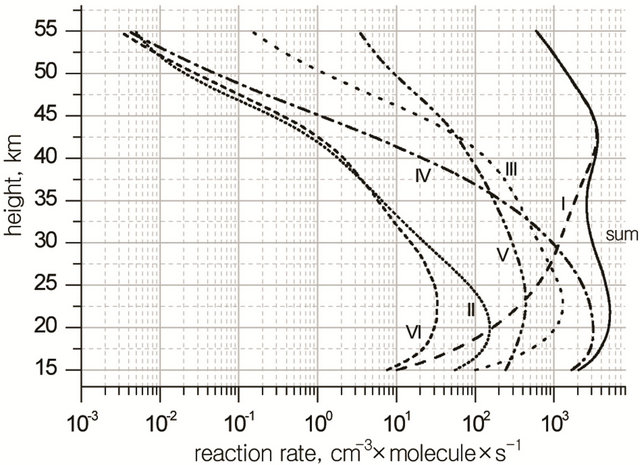
Figure 9. Height profiles of the limiting step rates in BrOx cycle.
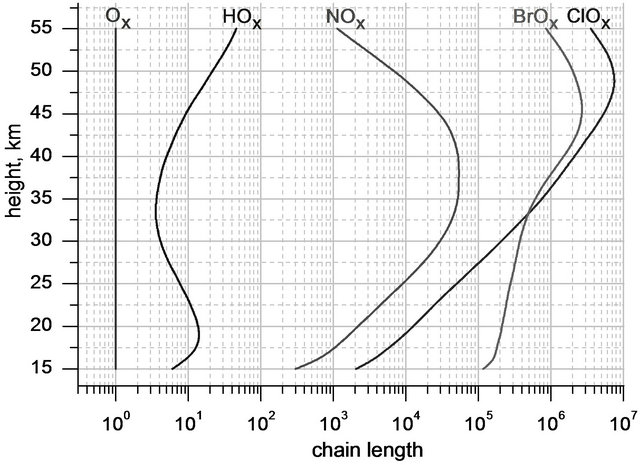
Figure 10. Height profiles of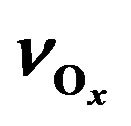 ,
, ![]() ,
, 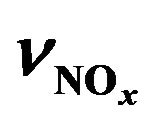 ,
, 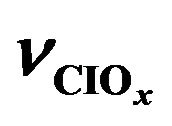 and
and 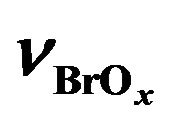 for June 2020 at latitude 50˚N obtained using algorithm developed, 2D model Socrates and IPCC scenarios of greenhouse gases RCP 4.5.
for June 2020 at latitude 50˚N obtained using algorithm developed, 2D model Socrates and IPCC scenarios of greenhouse gases RCP 4.5.
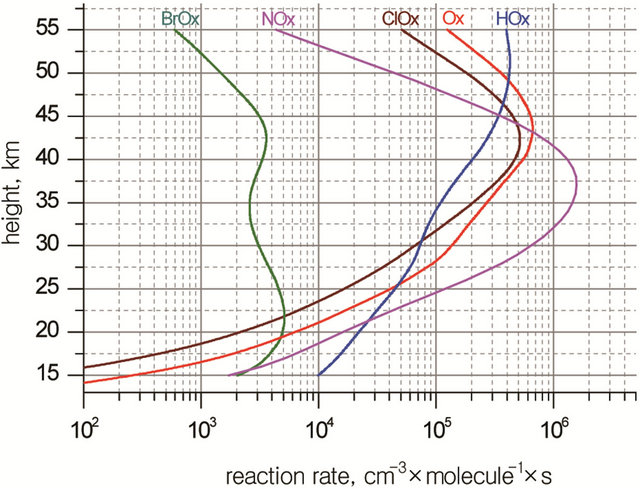
Figure 11. Rates of ozone depletion in Ox, HOx, NOx, ClOx and BrOx cycles in the stratosphere for model conditions of June 2020 at 50˚N.
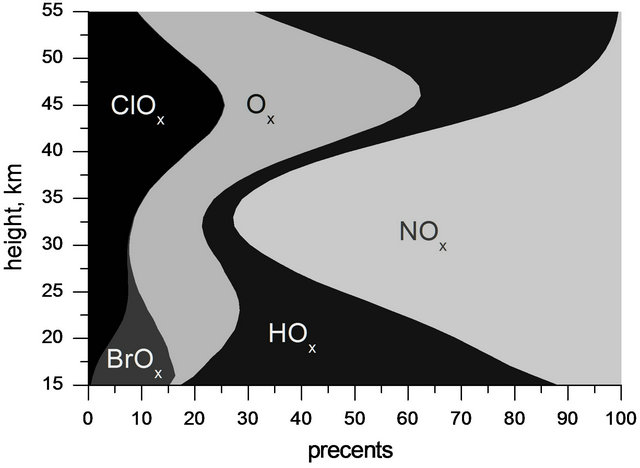
Figure 12. Relative contribution of main cycles into ozone depletion in the stratosphere for model conditions as in Figure 11.
other approaches chain lengths of the main stratospheric cycles have been calculated.
The role of the stratospheric null cycles has been considered. It has been shown that null cycles along with main cycles of ozone depletion provides a mutual exchange of the species participating in the chain processes and thereby does conditions of an existence of the stratospheric families such as Ox, NOx, HOx. It has also been shown that null cycles act only in daytime conditions. At night their action stops, families are disintegrating and their participants start to exist as individual species without any connection with a former family.
Finally, comparing the present results with data in [16], which also provides the chain lengths for major stratospheric cycles, shows that in case of HOx cycle chain length in [16] slightly more than in this work. This is due to the fact that in [16] a single reaction (instead of pair) has been considered as limiting step, that has increased the rate of the chain propagation. In case of NOx, ClOx and BrOx cycles chain lengths in [16] were noticeably smaller than obtained here. This is due to the fact that in [16] chain limitation in these cycles is mistakenly attributed to the formation of reservoirs of HNO3, HCl and HBr. It can be shown that the atmospheric lifetime of these reservoirs much less than time of transport τd and, therefore, a true chain limitation should be connected not with fast chemical reactions and slow transport processes, that significantly decreases the rate of limitation and increases the chain length.
4. Acknowledgements
Author wishes to thank his colleagues, Prof. Alex Yermakov and Dr. Michael Kuskov for help under preparation of this paper.
REFERENCES
- S. Chapman, “On Ozone and Atomic Oxygen in the Upper Atmosphere,” Philosophical Magazine, Vol. 10, No. 7, 1930, pp. 369-383.
- M. J. Molina and F. S. Rowland, “Stratospheric Sink for Chlorofluoromethanes: Chlorine Atom Catalyzed Destruction of Ozone,” Nature, Vol. 249, No. 5460, 1974, pp. 810-814. doi:10.1038/249810a0
- J. Hampson, “Chemical Instability of the Stratosphere,” International Association of Meteorology and Atmospheric Physics (IUGG) Symposium on Atmospheric Radiation, Leningrad, 1964.
- P. J. Crutzen, “Ozone Production Rates in an Oxygen, Hydrogen, Nitrogen-Oxide Atmosphere,” Journal of Geophysical Research, Vol. 76, No. 30, 1971, pp. 7311-7327. doi:10.1029/JC076i030p07311
- R. S. Stolarski and R. J. Cicerone, “Stratospheric Chlorine: A Possible Sink for Ozone,” Canadian Journal of Chemistry, Vol. 52, No. 8, 1974, pp. 1610-1615. doi:10.1139/v74-233
- S. C. Wofsy, M. B. McElroy and Y. L. Yung, “Chemistry of Atmospheric Bromine,” Geophysical Research Letters, Vol. 2, No. 6, 1975, pp. 215-218. doi:10.1029/GL002i006p00215
- Y. L. Yung, J. P. Pinto, R. T. Watson and S. P. Sander, “Atmospheric Bromine and Ozone Perturbations in the Lower Stratosphere,” Journal of the Atmospheric Sciences, Vol. 37, No. 2, 1980, pp. 339-353. doi:10.1175/1520-0469(1980)037<0339:ABAOPI>2.0.CO;2
- W. L. Chameides and D. D. Davis. “Iodine: Its possible role in Tropospheric Photochemistry,” Journal of Geophysical Research, Vol. 85, No. C12, 1980, pp. 7383- 7397. doi:10.1029/JC085iC12p07383
- M. Nicolet, “Etude des Reactions Chimiques de l’Ozone dans la Stratosphere,” Institut Royal Meteorologique de Belgique, Koninklijk Meteorologisch Instituut van Belgiё, Belgiё, 1978.
- J. R. Barker, “Progress and Problems in Atmospheric Chemistry,” World Scientific Publishing Co., Singapore, 1995, pp. 1-33.
- P. Brasseur, J. J. Orlando and G. S. Tyndall, “Atmospheric Chemistry and Global Change,” National Center for Atmospheric Research, Boulder, 1998.
- D. J. Jacob, “Introduction in Atmospheric Chemistry,” Princeton University Press, Princeton, 1999.
- C. N. Hewitt and A. V. Jackson, “Atmospheric Science for Environmental Scientists,” Wiley-Blackwell, West Sussex, 2009, pp. 198-217.
- G. Brasseur and S. Solomon, “Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere,” 3rd Edition, Springer, Montreal, 2005, pp. 265-501.
- J. L. Grenfell, R. Lehmann, P. Mieth, U. Langematz and B. Steil, “Chemical Reaction Pathways Affecting Stratospheric and Mesospheric Ozone,” Journal of Geophysical Research: Atmospheres, Vol. 111, No. D17, 2006, doi:10.1029/2004JD005713
- D. J. Lary, “Catalytic Destruction of Atmospheric Ozone,” Journal of Geophysical Research, Vol. 102, No. D17, 1997, pp. 21515-21526. doi:10.1029/97JD00912
- “Scientific Assessment of Ozone Depletion: 1994,” Global Ozone Research and Monitoring Project—Report, WMO, Geneva, 1995.
- A. P. Purmal, “A, B, C… Khimicheskoi Kinetiki,” Akademkniga, Moskva, 2004, pp. 166-215 (in Russian).
- 2001. http://acd.ucar.edu/models/SOCRATES/
- L. Clarke, J. Edmonds, H. Jacoby, H. Pitcher, J. Reilly and R. Richels, “Scenarios of Greenhouse Gas Emissions and Atmospheric Concentrations,” US Climate Change Science Program and the Subcommittee on Global Change Research, Department of Energy, Office of Biological & Environmental Research, Washington, 2007.

