Journal of Signal and Information Processing
Vol. 3 No. 2 (2012) , Article ID: 19580 , 4 pages DOI:10.4236/jsip.2012.32033
Non-Fragile Controller Design for 2-D Discrete Uncertain Systems Described by the Roesser Model
![]()
Department of Electronics and Communication Engineering, Motilal Nehru National Institute of Technology, Allahabad, India.
Email: amit_dhawan2@rediffmail.com
Received November 7th, 2011; revised December 13th, 2011; accepted January 17th, 2012
Keywords: 2-D Discrete Systems; Non-Fragile Control; Roesser Model; Linear Matrix Inequality; Lyapunov Methods
ABSTRACT
This paper is concerned with the design problem of non-fragile controller for a class of two-dimensional (2-D) discrete uncertain systems described by the Roesser model. The parametric uncertainties are assumed to be norm-bounded. The aim of this paper is to design a memoryless non-fragile state feedback control law such that the closed-loop system is asymptotically stable for all admissible parameter uncertainties and controller gain variations. A new linear matrix inequality (LMI) based sufficient condition for the existence of such controllers is established. Finally, a numerical example is provided to illustrate the applicability of the proposed method.
1. Introduction
In the past decades, the two-dimensional (2-D) discrete systems have received much attention due to its practical and theoretical importance in the fields such as multidimensional digital filtering, image processing, seismographic data processing, thermal processes, gas absorption, water stream heating etc. [1-4]. The stability analysis and feedback stabilization problems are among the central issues of 2-D discrete systems. Many significant results on the solvability of the stability problem for 2-D discrete systems described by the Roesser model [5] have been proposed in [6-12].
In [13], the solutions for the 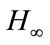 control and robust stabilization problems for 2-D systems in Roesser model using the 2-D system bounded realness property have been presented. The design methods for the
control and robust stabilization problems for 2-D systems in Roesser model using the 2-D system bounded realness property have been presented. The design methods for the  and mixed
and mixed  control of 2-D systems in Roesser model have been developed in [14]. In [15], the optimal guaranteed cost control problem for 2-D discrete uncertain systems described by the Roesser model has been discussed.
control of 2-D systems in Roesser model have been developed in [14]. In [15], the optimal guaranteed cost control problem for 2-D discrete uncertain systems described by the Roesser model has been discussed.
In the recent years, the problem of non-fragile control has been an attractive topic in theory analysis and practical implement. In the implement for the state feedback control, there are often some perturbations appearing in the controller gain, which may result from either the actuator degradations or the requirements for readjustment of controller gains during the controller implementation stage [16]. Since controller fragility is basically the performance deterioration of a feedback control system due to inaccuracies in controller implementation, the nonfragile control problem for 1-D system has been investigated in [17-23]. The non-fragile control problem for uncertain 2-D systems described by the Roesser model is an important problem. However, to the best of the authors’ knowledge, such problem has not been addressed so far in the literature.
This paper, therefore, addresses the non-fragile robust stabilization problem for 2-D discrete uncertain systems described by the Roesser model. The paper is organized as follows. Section 2 deals with the problem formulation of non-fragile control for the uncertain 2-D discrete system described by the Roesser model. Some useful results are also recalled in this section. In Section 3, an LMI based sufficient condition for the existence of non-fragile state feedback controller is established and the feasible solutions to this LMI provide a parameterized representation of the controller. In Section 4, a numerical example is given to illustrate the feasibility and effectiveness of the proposed technique.
Throughout the paper the following notations are used: The superscript T stands for matrix transposition,  denotes real vector space of dimension n,
denotes real vector space of dimension n,  is the set of n ´ m real matrices, 0 denotes null matrix or null vector of appropriate dimension, I is the identity matrix of appropriate dimension,
is the set of n ´ m real matrices, 0 denotes null matrix or null vector of appropriate dimension, I is the identity matrix of appropriate dimension,  denotes direct sum, i.e.,
denotes direct sum, i.e.,  , and G < 0 stands for the matrix G is symmetric and negative definite.
, and G < 0 stands for the matrix G is symmetric and negative definite.
2. Problem Formulation and Preliminaries
This paper deals with the design problem of non-fragile controller for a class of 2-D discrete uncertain systems described by the Roesser model [5]. Specifically, the system under consideration is given by
 (1a)
(1a)
where  and
and 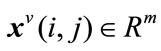 are the horizontal and vertical state, respectively,
are the horizontal and vertical state, respectively,  is the control input. The matrices
is the control input. The matrices 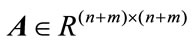 and
and  are known constant matrices representing the nominal plant. The matrix
are known constant matrices representing the nominal plant. The matrix 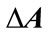 represents parameter uncertainty which is assumed to be of the form
represents parameter uncertainty which is assumed to be of the form
 (1b)
(1b)
In the above, 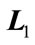 and
and 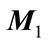 are known real constant matrices with appropriate dimensions and
are known real constant matrices with appropriate dimensions and  is an unknown matrix representing parameter uncertainty which satisfies
is an unknown matrix representing parameter uncertainty which satisfies
 (1c)
(1c)
Here, the objective of this paper is to develop a procedure to design a memoryless non-fragile state feedback control law
 (2)
(2)
such that the resulting closed-loop system given by
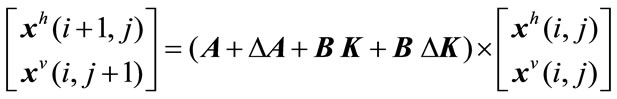 (3)
(3)
is asymptotically stable for all admissible uncertainties and controller gain variations.
In non-fragile state feedback control law (2), K is the nominal controller gain, 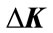 represents the gain perturbation, which is assumed to be of the form
represents the gain perturbation, which is assumed to be of the form
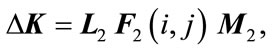 (4a)
(4a)
where 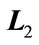 and
and 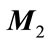 are known real constant matrices with appropriate dimensions and
are known real constant matrices with appropriate dimensions and  is an unknown matrix representing parameter uncertainty which satisfies
is an unknown matrix representing parameter uncertainty which satisfies
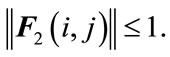 (4b)
(4b)
Before concluding this section, we recall the following lemmas which will be used in the next section. As an extension of the result for the global asymptotic stability condition of the 2-D discrete Roesser model given in [6], one can easily arrive at the following lemma.
Lemma 2.1. [6] The system (3) is quadratically stable if there exists a 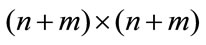 positive definite symmetric block diagonal matrix
positive definite symmetric block diagonal matrix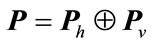 , satisfying
, satisfying
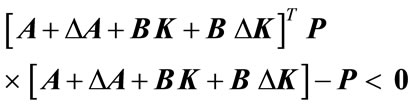 (5)
(5)
for all admissible uncertainties satisfying 1(b), 1(c) and (4), where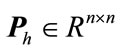 ,
, .
.
The following well-known lemmas are needed in the proof of our main result.
Lemma 2.2. [24] Let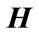 ,
, 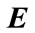 ,
, 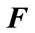 , and
, and 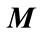 be real matrices of appropriate dimension with
be real matrices of appropriate dimension with  satisfying
satisfying  then
then
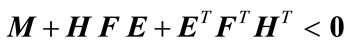 (6a)
(6a)
for all 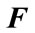 satisfying
satisfying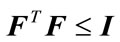 , if and only if there exists a scalar
, if and only if there exists a scalar 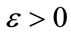 such that
such that
 (6b)
(6b)
Lemma 2.3. [24] For real matrices M, L, Q of appropriate dimensions, where  and
and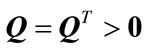 , then
, then 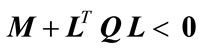 if and only if
if and only if

or equivalently
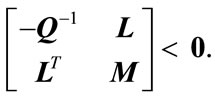 (7)
(7)
3. Main Result
In this section, we are interested in designing a memoryless non-fragile state feedback controller (2) for the system (1) such that the resulting closed-loop system (3) is asymptotically stable for all admissible uncertainties and controller gain variations. Based on Lemma 2.1, we have the following main theorem which can be recast to an LMI feasibility problem.
Theorem 3.1. Consider the system (1) and controller gain perturbation 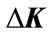 in (4). The system (1) is nonfragile stabilizable if there exist a
in (4). The system (1) is nonfragile stabilizable if there exist a 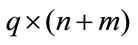 matrix U, a
matrix U, a 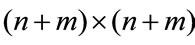 positive definite symmetric block diagonal matrix
positive definite symmetric block diagonal matrix  and scalars
and scalars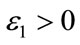 ,
, 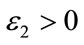 such that the following LMI is feasible:
such that the following LMI is feasible:
 (8)
(8)
where . In this situation, a suitable nonfragile state feedback controller is given by K =
. In this situation, a suitable nonfragile state feedback controller is given by K = 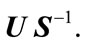 (9)
(9)
Proof: Using (1b), (1c), (4) and Lemma 2.3, (5) can be rearranged as
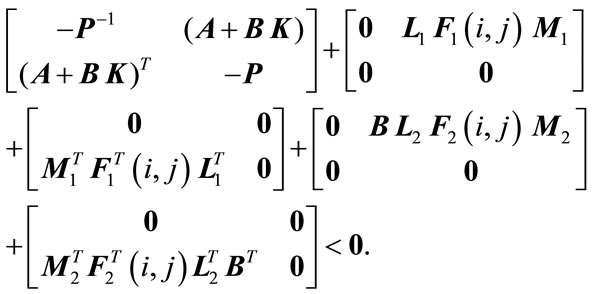 (10)
(10)
Equation (10) can be rewritten as
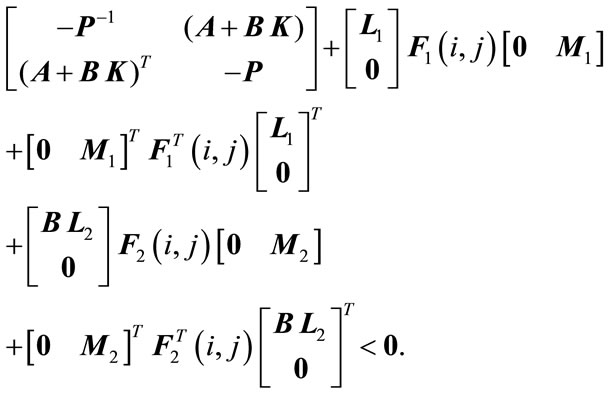 (11)
(11)
Using Lemma 2.2, (11) can be rearranged as
 (12)
(12)
Premultiplying and postmultiplying (12) by the matrix
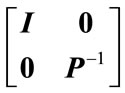 one obtains
one obtains
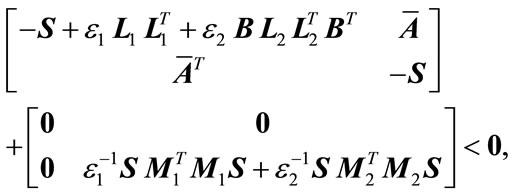 (13)
(13)
where
 (14)
(14)
The equivalence of (13) and (8) follows trivially from Lemma 2.3. This completes the proof of the Theorem 3.1.
Remark 3.1. Note that (8) is linear in the variables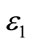 ,
, 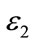 ,
,  , and
, and 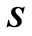 which can be easily solved using Matlab LMI Toolbox [24,25].
which can be easily solved using Matlab LMI Toolbox [24,25].
4. Numerical Example
To illustrate the applicability of Theorem 3.1, we now consider a specific example. Consider the 2-D discrete uncertain system represented by (1) with
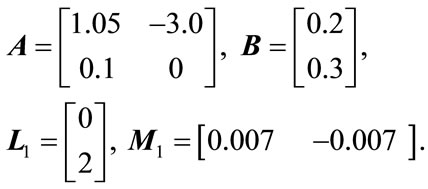 (15)
(15)
We wish to design a memoryless non-fragile state feedback controller for this system with controller gain variations satisfying (4) with
 (16)
(16)
It is found using Matlab LMI toolbox [24,25] that the LMI (8) is feasible for the present example and the feasible solution is given by
 (17)
(17)
Therefore, by Theorem 3.1, a non-fragile stabilizing state feedback control law can be obtained as
 (18)
(18)
5. Conclusion
In this paper, we have considered the non-fragile controller design problem for a class of 2-D discrete uncertain systems described by the Roesser model with norm bounded parametric uncertainties. LMI based sufficient condition for the existence of such controllers has been derived. A non-fragile stabilizing state feedback control law can be obtained if this condition is feasible. Furthermore, a numerical example has been provided to illustrate the effectiveness of the proposed technique.
6. Acknowledgements
The author wish to thank the reviewers for their constructive comments and suggestions.
REFERENCES
- T. Kaczorek, “Two-Dimensional Linear Systems,” SpringerVerlag, Berlin, 1985.
- R. N. Bracewell, “Two-Dimensional Imaging,” Prentice-Hall Signal Processing Series, Prentice-Hall, Englewood Cliffs, 1995.
- W.-S. Lu and A. Antoniou, “Two-Dimensional Digital Filters,” Marcel Dekker, New York, 1992.
- N. K. Bose, “Applied Multidimensional System Theory,” Van Nostrand Reinhold, New York, 1982.
- R. P. Roesser, “A Discrete State-Space Model for Linear Image Processing,” IEEE Transactions on Automatic Control, Vol. 20, No. 1, 1975, pp. 1-10.
- B. D. O. Anderson, P. Agathoklis, E. I. Jury and M. Mansour, “Stability and the Matrix Lypunov Equation for Discrete 2-Dimensional Systems,” IEEE Transactions on Circuits and Systems, Vol. 33, 1986, pp. 261-267. doi:10.1109/TCS.1986.1085912
- H. Kar and V. Singh, “Stability Analysis of 2-D StateSpace Digital Filters Using Lyapunov Function: A Caution,” IEEE Transactions on Signal Process, Vol. 45, No. 10, 1997, pp. 2620-2621. doi:10.1109/78.640734
- H. Kar and V. Singh, “Stability Analysis of 1-D and 2-D Fixed-Point State-Space Digital Filters Using Any Combination of Overflow and Quantization Nonlinearities,” IEEE Transactions on Signal Process, Vol. 49, 2001, pp. 1097-1105. doi:10.1109/78.917812
- D. Liu and A. N. Michel, “Stability Analysis of StateSpace Realizations for Two-Dimensional Filters with Overflow Nonlinearities,” IEEE Transactions on Circuits and Systems I, Vol. 41, No. 2, 1994, pp. 127-137. doi:10.1109/81.269049
- H. Kar and V. Singh, “Stability Analysis of 2-D StateSpace Digital Filters with Overflow Nonlinearities,” IEEE Transactions on Circuits and Systems I, Vol. 47, No. 4, 2000, pp. 598-601. doi:10.1109/81.841865
- V. Singh, “New LMI Condition for the Nonexistence of Overflow Oscillations in 2-D State-Space Digital Filters Using Saturation Arithmetic,” Digital Signal Process, Vol. 17, No. 1, 2007, pp. 345-352. doi:10.1016/j.dsp.2006.01.003
- H. Kar, “Comments on ‘New LMI Condition for the Nonexistence of Overflow Oscillations in 2-D State-Space Digital Filters Using Saturation Arithmetic’,” Digital Signal Process, Vol. 18, No. 2, 2008, pp. 148-150. doi:10.1016/j.dsp.2007.02.001
- C. Du, L. Xie and C. Zhang, “
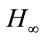 Control and Robust Stabilization of Two-Dimensional Systems in Roesser Models,” Automatica, Vol. 37, No. 2, 2001, pp. 205-211. doi:10.1016/S0005-1098(00)00155-2
Control and Robust Stabilization of Two-Dimensional Systems in Roesser Models,” Automatica, Vol. 37, No. 2, 2001, pp. 205-211. doi:10.1016/S0005-1098(00)00155-2 - R. Yang, L. Xie and C. Zhang, “
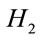 and Mixed
and Mixed  Control of Two-Dimensional Systems in Roesser Model,” Automatica, Vol. 42, No. 9, 2006, pp. 1507-1514. doi:10.1016/j.automatica.2006.04.002
Control of Two-Dimensional Systems in Roesser Model,” Automatica, Vol. 42, No. 9, 2006, pp. 1507-1514. doi:10.1016/j.automatica.2006.04.002 - A. Dhawan and H. Kar, “An LMI Approach to Robust Optimal Guaranteed Cost Control of 2-D Discrete Systems Described by the Roesser Model,” Signal Process, Vol. 90, No. 9, 2010, pp. 2648-2654. doi:10.1016/j.sigpro.2010.03.008
- D. Yue and J. Lam, “Non-Fragile Guaranteed Cost Control for Uncertain Descriptor Systems with Time-Varying State and Input Delays,” Optimal Control Applications & Methods, Vol. 26, 2005, pp. 85-105. doi:10.1002/oca.753
- L. H. Keel and S. P. Bhattacharya, “Robust, Fragile or Optimal,” IEEE Transactions on Automatic Control, Vol. 42, No. 8, 1997, pp. 1098-1105. doi:10.1109/9.618239
- W. M. Haddad and J. R. Corrado, “Robust Resilient Dynamic Controllers for Systems with Parameter Uncertainty and Controller Gain Variations,” International Journal of Control, Vol. 73, No. 15, 2000, pp. 1405-1423. doi:10.1080/002071700445424
- C. Lien, W. Cheng, C. Tsai and K. Yu., “Non-Fragile Observer-Based Controls of Linear System via LMI Approach,” Chaos, Solitons and Fractals, Vol. 32, No. 4, 2007, pp. 1530-1537. doi:10.1016/j.chaos.2005.11.092
- S. Xu, J. Lam, G. Yang and J. Wang, “Stabilization and
 Control for Uncertain Stochastic Time-Delay Systems via Non-Fragile Control,” Asian Journal of Control, Vol. 8, No. 2, 2006, pp. 197-200. doi:10.1111/j.1934-6093.2006.tb00270.x
Control for Uncertain Stochastic Time-Delay Systems via Non-Fragile Control,” Asian Journal of Control, Vol. 8, No. 2, 2006, pp. 197-200. doi:10.1111/j.1934-6093.2006.tb00270.x - J. H. Park, “Robust Non-Fragile Control for Uncertain Discrete-Delay Large-Scale Systems with a Class of Controller Gain Variations,” Applied Mathematics and Computation, Vol. 149, No.1, 2004, pp. 147-164. doi:10.1016/S0096-3003(02)00962-1
- C. Lien, “
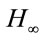 Non-Fragile Observer-Based Controls of Dynamical Systems via LMI Optimization Approach,” Chaos, Solitons and Fractals, Vol. 34, No. 2, 2007, pp. 428-436. doi:10.1016/j.chaos.2006.03.050
Non-Fragile Observer-Based Controls of Dynamical Systems via LMI Optimization Approach,” Chaos, Solitons and Fractals, Vol. 34, No. 2, 2007, pp. 428-436. doi:10.1016/j.chaos.2006.03.050 - C. Lien, “Non-Fragile Guaranteed Cost Control for Uncertain Neutral Dynamic Systems with Time-Varying Delays in State and Control Input,” Chaos, Solitons and Fractals, Vol. 31, No. 4, 2007, pp. 889-899. doi:10.1016/j.chaos.2005.10.080
- S. Boyd, L. El Ghaoui, E. Feron and V. Balakrishnan, “Linear Matrix Inequalities in System and Control Theory,” SIAM, Philadelphia, 1994. doi:10.1137/1.9781611970777
- P. Gahinet, A. Nemirovski, A. J. Laub and M. Chilali, “LMI Control Toolbox—For Use with Matlab,” The MATH Works Inc., Natick, 1995.

