Advances in Nanoparticles
Vol.2 No.2(2013), Article ID:31894,13 pages DOI:10.4236/anp.2013.22028
New Kinetic Computerized Model for Multicomponent Mass Transfer in Bi-Functional Matrix of NanoComposites
Institute for Physical Chemistry and Electro Chemistry, Russian Academy of Science, Moscow, Russia
Email: kalina@phyche.ac.ru
Copyright © 2013 Anatoliy Kalinitchev. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Bi-Functional Matrix; Active Nano-Sites
Received December 27, 2012; revised January 29, 2013; accepted February 5, 2013
Keywords: NanoComposites; Mass Transfer; Concentration Waves; Diffusion; Multicomponent Kinetics;
ABSTRACT
The aim of this theoretical investigation is the description of the multicomponent mass transfer process in the NanoComposites (NC)—novel materials with the bi-functional matrix. The new theoretical NC Model is assigned for the modern theoretical investigations of the multicomponent mass transfer kinetics in the bi-functional NC materials. This NC Model for the multicomponent mass transfer in the bi-functional NC matrix includes into the consideration the proposed key conception—two co-existing routes: I—chemical reactions onto the active NC centers-sites, and II—diffusion mass transfer inside the bi-functional NC matrix. All the results are presented in the terms of the additional key concept: propagating multicomponent concentration waves (W+) in the NC matrix. The used W+ concept for the description of the multicomponent NC mass transfer kinetics give the clear interpretation of the computerized results. The mass transfer process in the NC matrix has been described theoretically by computerized simulation. The results of the calculations are new and illustrated by author’s animations showing visually the propagation of the multicomponent concentration waves (W) inside the various NC matrixes: r-beads, cylindrical ro-fibers, or planar L-membranes. Two variants of modeling for mass transfer diffusion kinetics in the bi-functional NC matrixes with one (Variant 1), or two (Variant 2) dissociation-association reactions at the active nano-sites (R0) are considered theoretically.
1. Introduction
The created new theoretical NanoComposite (NC) Model is developed for the modern investigations of the multicomponent mass transfer kinetics in the bi-functional NC materials [1,2]. The detailed description of the properties of the such type novel NC materials with the example: “NC Metal-Ion Exchangers”, including the methods of their synthesis has been published recently in the Russian recent monograph [3]. Theoretical aspects for the synthesis of the NC with a number of practical applications have been discussed in details in the monograph [3]. The NC includes numerious NanoParticles (NP) embedded inside the matrix-medium of the NC. The details of the NC synthesis with zero valent Metal (Me0) in the ion exchanger matrix are presented [3]. Synthesized NC with the bi-functional matrixes, as for example: “Me0-Ion Exchangers”, have practical advantages compared with the usual IEx materials [3,4]. Corresponding obvious experimental micrography and pictures for the NC structure with the NP are presented (Figuгes 1(a) and (b)) as the illustration of the NP agglomerates embedded into the NC media [3]. Figure 1(a) shows one of the experimental microphotography of the structure for the NC “Me0— Ion Exchangers” including zero valent Metal0 NP (Figures 1(b) and (c), (5), shaded) inside the bi-functional NC matrix. The microphotography of the experimentally synthesized NC (Figure 1(a)) is obtained by prof. T. Kravchenko group from Voronezh State University [3]. The experimental examples are presented as the illustrations of the NC media [2,3]. The Me0-NP ((Figures 1(a)-(c)): NP—light points, (a); Me0 (shaded regions)— (b)(5), (c)), play the role of the active nano centers-sites R0 (Figure 1(c)) located at the bi-functional matrix [1,2]. The modern multicomponent kinetic theoretical Model is developed for the NC with the key conception: two coexisting routes—(I) and (II) for the multicomponent mass transfer inside the bi-functional NC matrix-medium [1,2]. These two co-existing routes reflect the two simultaneous processes: (Ia,b)—sorption-desorption for the components at the active nano-sites (R0) of the NC matrix and (II)—diffusion of the components in the pores
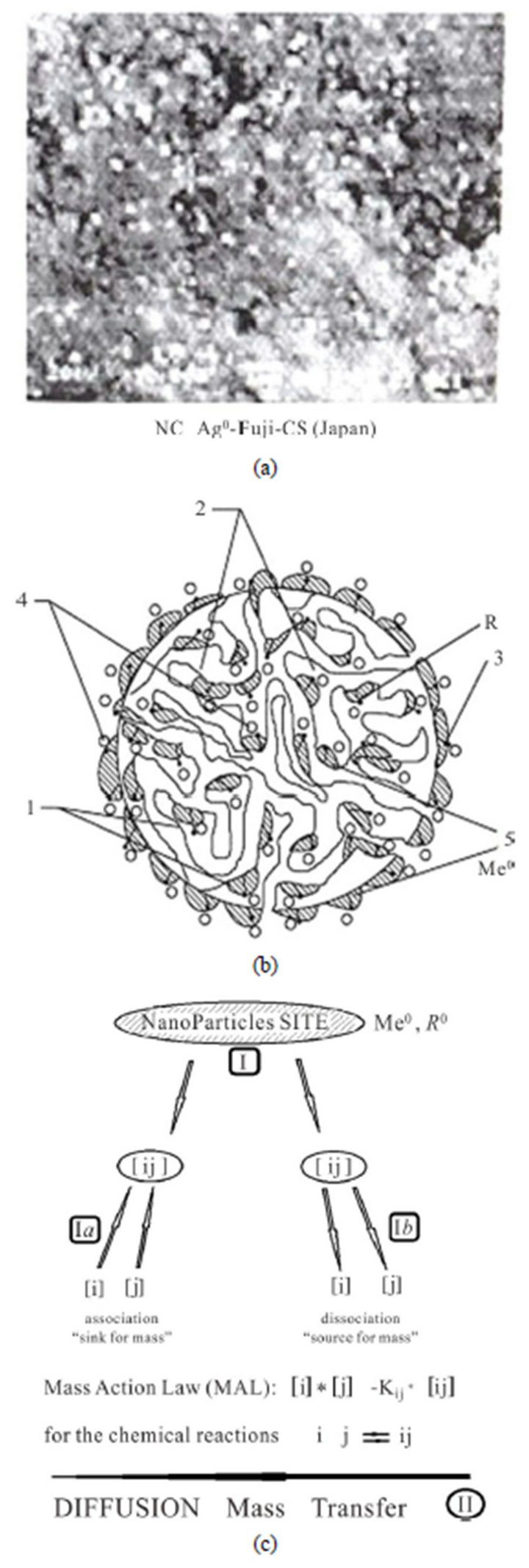
Figure 1. (a)-(c) Mass transfer schemes inside the bi-functional NC matrix: (a)—experimental NC microphotography [3]; (b)—picture of NC r-bead (ro-fiber); 2—micro-pores, 3—fixed groups R, 4—counter-ions, 5—Me0-NP ag glomerates ((b), (c), shaded); (c)—mass “transformations” scheme at the active nano-sites (Me0, R0): (Ia)—
association stage of reactions (left); (Ib) —dissociation stage of reactions (right); (II)-diffusion mass transfer along the NC pores ((b), 2).
of the NC matrix (Figure 1(c)). Along with the diffusion mass transfer (II) the “sorption-desorption” process is realized in the NC Model via the mechanism of the “association-dissociation” reactions (Ia,b). Figure 1(c) represents the schemes-illustrations of the NC bead [1,2] with all accompanying mass transfer elements [2,3]. Figure 1(c) shows the scheme of the two accompanying co-existing routes: I—active nano-sites of the NC with the “sinks” (I(a)) and “sources” (Ib) of the [ij]—mass component “transformation”: [ij]↔[i]+[j] (Ia,b), and II—the diffusion mass transfer in the NC matrix pores [1,2].
The various components participate in the reactions (I(a), (b)) and in the diffusion mass transfer (II) inside the pores (Figure 1(b)-2) of the NC bi-functional matrix during the kinetic process. The mechanism of the “association-dissociation” reactions (Ia, b) (Figure 1(c)) retards the whole kinetic process. Typical composition of the components may include: ions, complexes, neutral substances with zero charges and, in addition, the immovable m-components (with zero diffusivity, m(R0i)à Dm=0) at the fixed R0 nano-sites (Figure 1(c)) of the bi-functional NC matrix.
The created modern Model has common points with the preceding approaches published previously at the end of the last century for IEx kinetics [5-10]. However, the previous kinetic models have been applied to the IEx kinetic processes, accompanied by the chemical reactions only in the usual IEx resins (and for r-beads only), but not for the new NC bi-functional materials, which are shown in Figures 1(a) and (b).
The created new multicomponent NC Model [1,2] is used for the computer simulation of the multicomponent mass transfer into the bi-functional NC matrix of the three various shapes: r-beads, cylindrical ro-fibers and planar L-membranes. There is used here the modern bi-functional NC Me0-Ion Exchanger [3], as the real example for the new Model applications. For the generalization of the calculated examples (Section 4) the active nano-sites hereinafter are labeled as the k-component: kR0 (here number of any component is represented by the left index). So for any NC the R0 label means the nano-site and absolutely the same as Me0 for the example “Me0-Ion Exchanger” in Figures 1(b) and (c), shaded regions).
The modern multicomponent NC Model [1,2] with the key conception (I, II, co-routes for mass transfer, Figure 1(c)) is represented by the adequate computerized description of the mass transfer in the bi-functional matrix of the novel NC materials. There are considered two real factors of the multicomponent mass transfer in the NC materials: Diffusion (Di,j) of the i,j-components, together with the Reaction and co-existing routes (Ia,b) for the “sinks & sources” of the masses at the active nano-sites R0 (Figure 1(c), dashed region) of the bi-functional NC matrix. The specific role of the reaction factor (routes Ia, Ib) concludes in the retardation of the whole diffusion process due to the equilibrium of the associationdissociation reaction at the nano-sites (R0) of the NC (Figure 1(c)). It will be shown here the full similarity between the reaction influence for the retardation of the diffusion kinetics in the bi-functional NC and the sorption isotherms factor influence in the dynamic theory of chromatography. Such similarity will be discussed in details in Sections 6 and 7. The multicomponent mass transfer kinetics in the bi-functional NC matrix represent the process, in which the reactions (i.e. equilibrium transformations of various k,j-components due to the routes Ia, Ib) must undoubtedly consider mass transport in the bi-functional NC materials.
Examples of IEx kinetics with the actual processes occurring via the mechanism of “sinks and sources” of masses are discussed in details [5-13]. Herewith, the effect of reactions on the kinetic behavior of the bifunctional NC system may be crucial: the kinetic process rate may be decreased by one or two orders of magnitude with the decisive dependence of the process on the solution concentration changes. Therefore, distinctive changes in the mechanism of the kinetic mass transport process may occur due to the reaction (Ia, Ib) factors influence.
Consideration of the active nano-sites influence in the bi-functional NC matrix (routes Ia, Ib; Figure 1(c)), at which changes of the mass for the components occur, is especially relevant in the case of the mass transport processes in the new bi-functional NC materials [1-4].
2. Modeling of Multicomponent Mass
Transfer Kinetics in Bi-functional
NC Matrix
Herewith the general phenomenological approach of the non-equilibrium thermodynamics [11] has been used for the multicomponent mass transfer in the new Model with the bi-functional NC matrix [1,2]. Postulates for the various Ion Exchange (IEx) multicomponent Models for IEx kinetics have been used during long-time period (around 50 years) starting from prof. F. Helfferich [12] with his review [13] and emphasizing STATE-of-theART-REPORT [8], till 80 - 90th [5-10].
Here is a short list of mathematical approaches used in the description of IEx kinetics: mass balance partial differential equations, quasi homogeneous medium, isothermal process, electro-neutrality, fundamental NernstPlanck relationship for fluxes, constant diffusion coefficients (Di) for i-components. As usual in the theory, the influence of the gradient of the electric field is expressed via the sum of the j-concentration gradients by using the absence of the electric current relationships [1,5-13]. In result the flux of each i-ion is described by its own gradient with addition of the multicomponent superposition of the j-concentrations gradients. Such superposition is called “diffusion potential” in the theory of irreversible thermodynamics (Ch. 4 in the monograph [11]).
For the bi-functional NC matrix the additional mass fluxes are formed due to the transformations of the components, which are expressed by MALS relations at the NP nano-sites (Figure 1(c), MAL). These sinks and sources of masses are considered by the corresponding fluxes of i-components and bring the redistributions of masses for various components participated. The effects of mass transport for the created NC Model [1,2] by the mechanism “sinks-sources” at the nano-sites R0 (Figures 1(b) and (c)) are included in the material balance equations due to the introduction of the additional terms describing decrease of a mass (with negative term for “sink”) or increase of a mass (with positive term for “source”).
For further advance of the Model the chemical reactions equilibrium uses the classical MALS relationships [11] (Ch. 2). In the computerized Model they are presented in the generalized form:
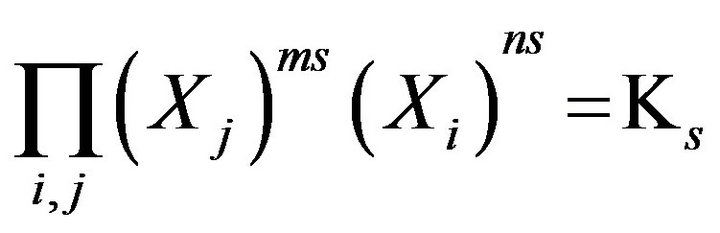 , s = 1, 2,…(MALS), (1)
, s = 1, 2,…(MALS), (1)
where expression Пi (I ≠ j) is the product of concentrations (Xi)ms (i = 1,2,..); ns, ms (negative, or positive)— are stoichiometric coefficients of the chemical s-reaction; s—is the corresponding index; KS—are equilibrium constants in the MALS relationships (Equation 1), (Figure 1(c)). In principle the stoichiometric coefficients (ms, ns) for the chemical reactions equilibrium (1) might be fractional [7]. During the computerized simulations all the ms, ns values are assumed to be (± 1). However in need all these values may easily be used in the NC Model as fractional or larger than unity.
The modern approach with all mentioned postulates and equations of the NC Model [1,2] has been realized by modern computer modeling. The set of corresponding computer FORTRAN programs has been composed for the simulation of various multicomponent mass transfer in the NC systems, describing the kinetic behavior inside the bi-functional NC matrix. The various shapes of the NC medium: r-beads, cylindrical ro-fibers, or planar Lmembranes are included into the theoretical computer simulation. Thus, the computerized investigations of the influence of the equilibrium reactions parameters in cooperation with the diffusion coefficients (Di) of the icomponents on the kinetics inside the bi-functional NC matrix of the various three NC matrix shapes are realized.
The basic properties in the development of the created generalized NC Model accounting for the multicomponent character of the system are introduced. There are included the new properties of the bi-functional NC matrix based on the proposed key two routes concept (I & II) including “association-dissociation” mechanism onto nano-sites: kR0 (Figure 1). For further consideration let us simplify the generalized approach (Equation 1) to be closer to the multicomponent examples, which have been realized here by computers. The mathematical realization of the diffusion and relations for the chemical reactions inside the bi-functional NC matrix is based on the approach with the application of the simple form of MAL (Figure 1(c)) in the modern NC Model for the arbitrary i, j, ij-components concentrations: [i], [j], [ij]. The corresponding simple scheme, as for example for the simple reactions: i + j ↔ ij may be represented by the simple MALS relations for monovalent components: Ks [i] × [j] = [ij] (Figure 1(c))..
The specific case is realized for the p-components, which are transformed into the complex—m(R0p), (mth- component) with zero diffusivity (Dm=0). Meanwhile such p-components may participate in the associationdissociation transformation: ip à m(R0p) ip + kR0 ↔ m (R0p) with the following change of the masses. It will be shown (Section 4) that due to this components transformation at the nano-sites (kR0, Figure 1(c)), the kR0- component concentration wave (Figures 2, 3 and 5 solids, brown curves – k = 5,6) propagates in the bi-functional NC matrix (though DkR = 0). The obtained results of the computerized simulation on the basis of the created NC Model [1,2] are presented via the well known “multicomponent concentration waves” (W+) concept [14-21].
Concentration waves arise and propagate along the distance (r-, ro-radius, or L-thickness) inside the NC matrix during multicomponent mass transfer. The multicomponent waves with their propagation in the bi-functional NC matrix play the decisive role in the description of the multicomponent NC kinetics of the mass transfer. Therefore this well known and widely used “wave” approach [14-26] is shortly reviewed in the next Section 3.
3. Concept of Concentration Waves (W+) for
Multicomponent Kinetics and Dynamics
of Mass Transfer
During the mass transfer kinetics the concentration profiles—“waves” of the components are formed inside the porous media. Figures 2, 3 and 5 represent a lot of computerized examples of the waves propagating during the multicomponent NC kinetics. The key concept (W+) of “multicomponent waves” is widely used in theoretical description for many scientific fields of the multicomponent transport for various kinetic and dynamic systems. The “multicomponent waves” concept has wide area for applications in such research fields, as percolation processes [18,19], mechanics of liquids, gas dynamics [22], theory of burning and even street traffic [19,23,24]. The term “wave” (W+ concept) has been used in all these publications [14-26] including the mentioned excellent monograph [14] and the books [23,24] concerned with car traffic and kinematic waves.
There are phenomenological concepts potentially common to all filtration processes, which can also be extended to a whole series of migration phenomena such as chromatography, sedimentation, electrophoresis and some others [14-26]. The review [21] and presentations [25,26] published by author in cooperation with W. Hoell (Karlsruhe Research Center, Germany) include the application of the multicomponent wave concept with the description of the SCT (Surface Complexation Theory)-Model. The SCT-Model for the multicomponent IEx equilibrium had been elaborated by prof. W. Hoell group at the end of the last century (Refs. in the review [21]).
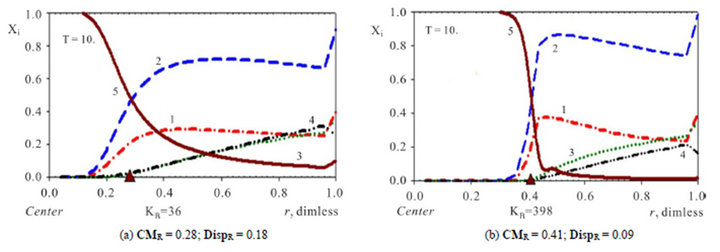
Figure 2. (a), (b) Comparison of concentration waves—Xi(r,T) inside NC matrix (r-bead). Variant 1. (5—component system, Anion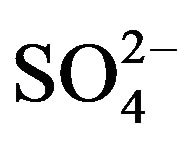 ). Influence of KB value: KB = 36 ((a), left); KB = 398 ((b), right). Triangles (brown) show CMR positions for 5R0-waves (brown solids, 5) at r axis. Number of components are at curves.
). Influence of KB value: KB = 36 ((a), left); KB = 398 ((b), right). Triangles (brown) show CMR positions for 5R0-waves (brown solids, 5) at r axis. Number of components are at curves. 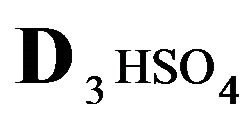 = 0.0085 <
= 0.0085 < 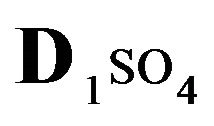 = 0.01 <
= 0.01 < 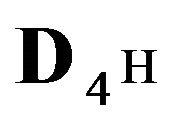 = 0.03. T = 10.
= 0.03. T = 10.
Waves propagation, as well as their concurrent interference-interaction should be used for the simulation and consideration of all the details of the mass transfer kinetics and dynamics. The fundamental monograph [14] (including additionally a lot of chromatographic papers by prof. F. Helfferich) is devoted to the all aspects of the travelling “concentration waves” conception. There is a lot of research papers adjoined, which are included into the special issue [15] dedicated to F. Helfferich (Festschrift) with the detailed consideration of the travelling “multicomponent concentration waves” (W+) concept [15-21], including some others related. A fairly detailed discussion of the wave concept, as well as many fundamental examples and definitions, are presented in a number of books and reviews (Refs. in [15-22]). In the presence of the effects of the non-ideality of the sorption medium the travelling concentration waves propagate with their broadening, including results of their consequent interference [14-26].
The concept of “multicomponent concentration waves” (W+) is widely used here to consider the results of the computer simulation of the multicomponent NC kinetics in the bi-functional matrix. The examples of the multicomponent concentration waves are presented in Figures 2, 3 and 5 for the NC bi-functional matrix. Comparison of the concentration waves behavior for the kinetic and dynamic system shows compatibility and differences for the interfering waves: there is the similarity between mass balance equations for multicomponent kinetics and dynamics. The travelling multicomponent concentration waves are involved in both cases of the kinetic and dynamic systems. However in addition, there are the differences:
1) In the dynamic IEx systems, as a rule, the travelling concentration waves used to reach the stage (named by F. Helfferich as “coherence” [14,17]), in which the linear dimensions of the system are large, while multicomponent waves achieve the so called “coherent state” [14,15,17- 19]. In this state the waves are separated by the concentration plateaus [14-21,25,26];
2) In the kinetic diffusion multicomponent IEx systems the behavior of the waves and its interpretation differs in the presence of the diffusion phenomenon (even in the absence of reactions). Concentration waves in the kinetic systems propagate without the formation of the concentration plateaus between the waves [16]. In this case, due to a limited small size of the matrix the concentration waves are unable to disperse with the formation of concentration plateaus. Therefore, the coherent state is unattainable in these kinetic variants of the mass transport. However, in the case of multicomponent kinetics the effect of the interference of the diffusion kinetic concentration waves of the components still takes place [9,16]. Further, this behavior of the multicomponent system with the wave interference are shown in Figures 2, 3 and 5 based on the approach with the multicomponent kinetic equations of the mass transport in the bi-functional NC matrix.
The quantitative description of the waves behavior is successfully described here by the well known two integral parameters used for the characterization of any distributions: “Center of Mass” (CMk) and “Dispersion” (Dispk). The “CMk” parameter describes the integral “Center” of k-concentration (frontal) distribution-wave kR0. The “Dispk” parameter describes “the integral width” of the k-wave distribution. Parameters “CM” and “Disp” are well known in the mathematical statistics as “average of distribution” and “dispersion” correspondingly [27]. Such types of the descriptions are used (Section 4, CMR and DispR, Figure 4) for the estimation of the “completion Time”: Tfin of the kinetic process and “width” of the kR0-concentration frontal k-wave in Figures 2 and 3 (5R0-wave, solids, 5-brown curves). The con centration waves propagate across the various NC medium (L-membrane, ro-fiber, r-bead) from the boundary points (L0, ro0, r0 = 1) to the final “zero points”: L, ro, r = 0 correspondingly (Figures 2-4). The kinetic processes are finished at the completion moment T = Tfin , when the understandable relation CMR + DispR = 1 is realized. This moment Tfin correspons to “the crossing” (Figure 4) of solid and dashed curves correspondingly. The more detailed description and discussion of the integral parameters are given below (Sections 4 and 5).
The description of the created NC Model [1,2] has been followed by the computerized simulation of the multicomponent system behavior in the bi-functional NC matrix. All the parameters of the system in the computer simulations are dimensionless (see Nomenclature) as it is better for any modeling (and for understanding) especially in Fundamentals. The obtained results of the computerized simulation for the multicomponent mass transfer in the NC are original and new. The results of modeling are demonstrated and discussed in Sections 4-7.
The results of the computer simulations are presented here in the set of various pictures (Figures 2-5) where part of the images (Figures 2, 3 and 5) shows the multicomponent concentration distributions-waves.
Additional visual illustrations may be shown via the author’s computerized animations prepared for the oral presentations (or for posters) via lap-top computer. The animations are framed by the real calculated multicomponent concentration profiles-waves for the successive time moments. The propagations of the travelling concentration waves in the NC matrix via animations may be demonstrated visually. Such type of the computerized visual representations of the theoretical results with the dynamic and kinetic waves has been using by author repeatedly (including the sessions of “IEX 2004, 2008 and 2012” Conferences) [2,25,26].
4. Concentration Waves in the Multicomponent NC Kinetics
The described postulates of the mathematical Model were realized for all relationships including multicomponent mass transfer kinetic partial differential equations, electro-neutrality relations, classical Nernst-Plank equations for the fluxes of the components and Mass Action Laws for the chemical reactions equilibrium (Equation 1, Figure 1(c)) [1,2].
All the systems describing the multicomponent kinetic behavior in the bi-functional NC matrix of the various shapes (r-bead, ro-fiber, L-membrane) were involved in the simulation with several author’s FORTRAN computer programs for such NC systems. The computer calculations were fulfilled for a number of variants with different values of the diffusion coefficients and various constants of the MAL chemical reactions (Equations 1, Figure 1(c)). The results of the simulations for the multicomponent NC systems are presented below. All the computer calculations have been obtained by using dimensionless values, including concentrations (Xi); diffusion coefficients Di; constants of chemical association-dissociation reactions (KS). The mass transfer kinetics in the NC Model include the multicomponent concentration waves propagation along the dimensionless distance: r, ro, or L in the course of the dimensionless time (T = D0t/r02). All the author’s results of the computer simulation are obtained for the first time. The results of such calculations for the bi-functional NC matrix are presented in the next SubSections.
4.1. Computerized Simulation of Multicomponent Diffusion Kinetics with Additional Mass Transfer at the Nanosites (kR0)
There is productive for the quantitative estimation and description of the travelling concentration k-waves behavior to use the integral characteristics: Center of Mass —CMk(T) and Dispersion—Dispk(T). Such characteristics have wide spread occurrence in mathematical statistics [27]. For the computer modeling these integral CMk(T), Dispk(T)—parameters may be easily calculated during computerized simulation of the process. The CMk(T)—dependence describes the position of the kwave along the distance in the NC matrix: radius for r-bead (ro-fiber) or through the thickness (L) of the planar L-membrane. The Dispk(T) dependence describes the change of the width of the Xi concentration (frontal) wave in correspondence with its physical meaning. The illustrations are presented in Figures 2-5 for the k-wave profiles with the CMk positions. These CMk positions are indicated by the brown triangles on abscissa r (ro or L) (Figures 2, 3 and 5). The dependences—CMk (T) are presented by solid lines in Figure 4. The results of the computer calculations of the both integral parameters are presented in Figures 3(a)-(f) and Figure 4 (Dispk(T)— dashed lines).
This investigation shows that the time dependences of this two parameters: CMk(T), Dispk(T) (Figure 4) are suitable for the description of the behavior of the kR0-component wave, where kR0 are the nano-sites R0- concentrations. Examples of such description will be presented in this Section 4.1 below for two various cases for kR0 sites: Variant 1 with the one association-dissociation reaction (1B), and Variant 2 with the two reactions (2.2), (2.3) correspondingly. The lists of the components for each Variant 1 and Variant 2 in the bi-functional NC matrix are shown in Section 4.1.
The kR0—wave (Figures 2, 3 and 5—solids, brown curves—5,6) is formed in the bi-functional NC matrix due to the transformation of the 4th-component (4H+ ↔ kRH+) at kR0 nano-sites with the change of [kR0]—concentration in the k-wave (k = 5, Variant 1, Figures 3 and 4), or k = 6 (Variant 2, Figure 5).
All the relations (1A), (1B) or (2.1) - (2.3) are presented here in the simple MALS type: 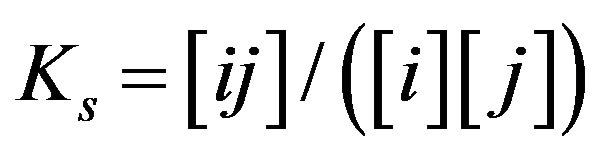 (Figure 1(c)).
(Figure 1(c)).
4.1.1. Kinetics of H2SO4 Acid inside the NC Matrix
with One Reaction at the Nano-Sites (5R0)
Variant 1. Sorption Kinetics of H2SO4 acid for 5-component NC System. The i-components (numbers—indexes to the left of the Symbols) with the corresponding diffusivities Di:
 —anions of acid with the diffusivity (
—anions of acid with the diffusivity ( = 0.01) in the NC pores (2, Figure 1(b));
= 0.01) in the NC pores (2, Figure 1(b));
2RH+—immovable 2nd-component, formed by nano-sites, protonated by acid cations (4H+) due to the association reaction (1B), (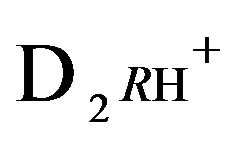 = 0);
= 0);
 —anions of the acid (reaction (1A)) with the diffusivity (D3 = 0.008) inside NC pores;
—anions of the acid (reaction (1A)) with the diffusivity (D3 = 0.008) inside NC pores;
4H+—cations of H2SO4 acid with the diffusivity (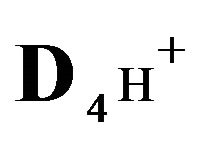 = 0.03) in the NC pores;
= 0.03) in the NC pores;
5R0—zero valent nano-sites (D5R = 0), generated by the NP agglomerates (Figure 1(c)).
The IEx, NC system is characterized by these 5 components, three diffusion coefficients (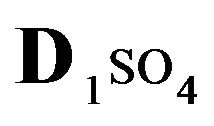 ;
; ;
; ) with two reactions: in the NC pores (Equation (1A)) and at the active nano-sites: 5R0 (Equation (1B)) correspondingly: for NC pores,
) with two reactions: in the NC pores (Equation (1A)) and at the active nano-sites: 5R0 (Equation (1B)) correspondingly: for NC pores,

 (MALA) (1A)
(MALA) (1A)
At active nano-sites, 5R0 
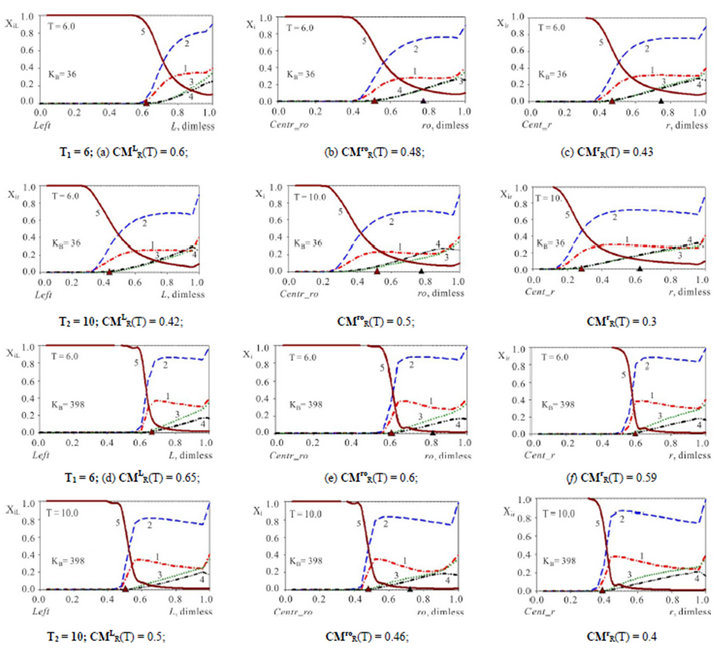
Figure 3. (a)-(f) (Variant 1. Anion ) Comparison of propagating 5R0(T)-waves (5, brown solids) inside the NC matrix for various shapes with KB values: XiL(L, T), L-membrane (left, a, d); Xi(ro, T); ro-fiber (middle, b, e); Xir(r, T); r-bead (right (c), (f). Triangles (brown) show CMR positions at L, ro, r-axes (abscissa); KB = 36 (a)-(c); KB= 398 (d)-(f). T1,2 = 6, 10. Component numbers are at curves.
) Comparison of propagating 5R0(T)-waves (5, brown solids) inside the NC matrix for various shapes with KB values: XiL(L, T), L-membrane (left, a, d); Xi(ro, T); ro-fiber (middle, b, e); Xir(r, T); r-bead (right (c), (f). Triangles (brown) show CMR positions at L, ro, r-axes (abscissa); KB = 36 (a)-(c); KB= 398 (d)-(f). T1,2 = 6, 10. Component numbers are at curves.
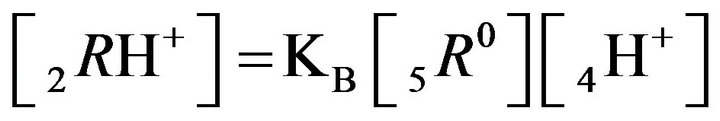 , (MALB) (1B)
, (MALB) (1B)
The relationships (1A), (1B) are presented by MALS with the constants: KA, KB.
It follows (Variant 1) that the expression (1C) holds in equilibrium at the nano-sites 5R0 for the [5R0] concentration, where 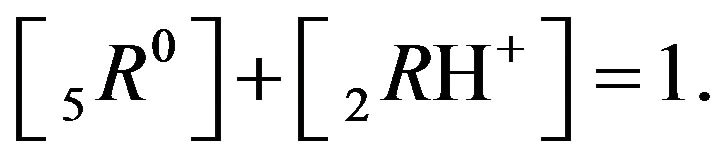 And
And
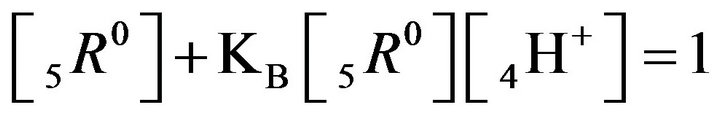 ,
,
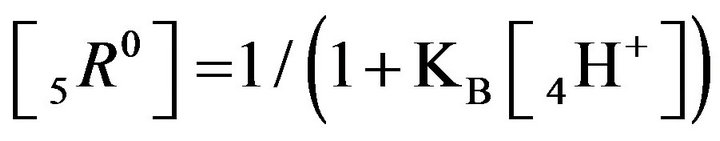 (1C)
(1C)
There is described in Variant 1 the sorption of H2SO4
acid with the sulphate anions (An− =1 ) including concentrations [Xi] of all five components (I = 1,2,…5; left indexes): {[1
) including concentrations [Xi] of all five components (I = 1,2,…5; left indexes): {[1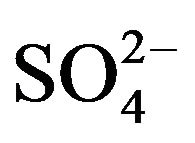 ], [2RH+], [3
], [2RH+], [3 ], [4H+], [5R0]}. Such diffusion 5-component process in the bi-functional NC matrix is accompanied by two MALS relations: (1A), (1B) with
], [4H+], [5R0]}. Such diffusion 5-component process in the bi-functional NC matrix is accompanied by two MALS relations: (1A), (1B) with ;
; ;
; )—diffusivities of 1,3,4- components. The relationship (1C) shows that for Variant 1 the 5R0-wave depends on [4H+]-concentration with the KB constant value (1B). This dependence influences the concentration waves 5R0 behavior shown in Figures 2(a) and (b) and Figures 3(a)-(f). The results are calculated on the basis of the NC Model (Section 1) with the computerized simulation.
)—diffusivities of 1,3,4- components. The relationship (1C) shows that for Variant 1 the 5R0-wave depends on [4H+]-concentration with the KB constant value (1B). This dependence influences the concentration waves 5R0 behavior shown in Figures 2(a) and (b) and Figures 3(a)-(f). The results are calculated on the basis of the NC Model (Section 1) with the computerized simulation.
4.1.2. Kinetics of HCl Acid inside the NC Matrix with
Two Reactions at the Nano-Sites (6R0)
Variant 2. Sorption Kinetics of HCl acid for 6-component NC System. The i-components with the diffusion coefficients Di: 6(six)-component system:
1Cl−—anions of acid with diffusivity (D1Cl = 0.01) in the NC pores (2, Figure 1(b));
2RH+—immovable 2nd-component, formed by 6R0 nanosites protonated by acid cations (4H+) due to the association reaction (2.2), ( = 0);
= 0);
3RHCl—immovable 3d-component, generated by the reaction (2.3), (D3RHCl = 0);
4H+—cations of HCl acid with diffusivity ( = 0.03) in the NC pores;
= 0.03) in the NC pores;
5HCl—acid in dissociation-association reaction (2.1) with diffusivity (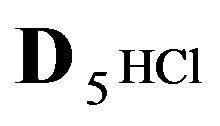 = 0.008) in the NC pores;
= 0.008) in the NC pores;
6R0—zero valent immovable (D6R = 0) nano-sites generated by NP agglomerates (Figure 1(c)).
The NC system (2.1) - (2.3) is characterized by n = 6 components, three diffusion coefficients (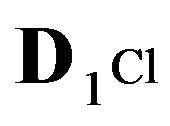 ;
;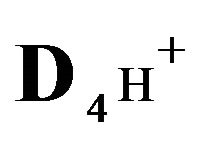 ;
; ) with three reactions: one in the NC pores (2.1) with additional two association-dissociation reactions (2.2), (2.3) at the active 6R0 nano-sites correspondingly:
) with three reactions: one in the NC pores (2.1) with additional two association-dissociation reactions (2.2), (2.3) at the active 6R0 nano-sites correspondingly:
for NC pores,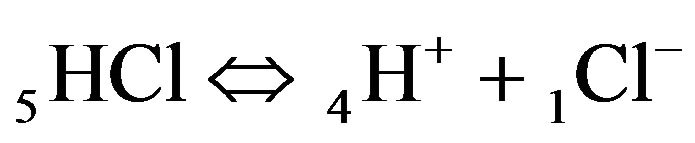 ;
;
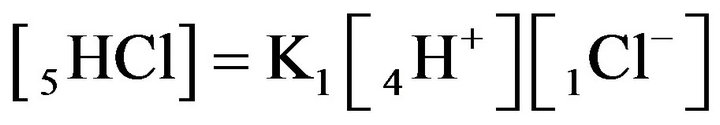 (K1, MAL1), (2.1)
(K1, MAL1), (2.1)
at active nanosites 6R0, 1st step:
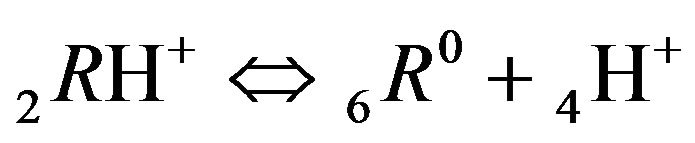 ;
;
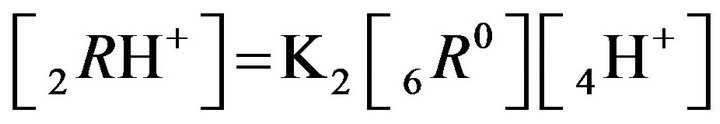 (K2, MAL2) (2.2)
(K2, MAL2) (2.2)
at active nano-sites 6R0, 2nd step:,
 ;
;
 (K3, MAL3) (2.3)
(K3, MAL3) (2.3)
The second relations in (2.1), (2.2) and (2.3) (multiplication) are described by MALS with the corresponding constants: K1, K2, K3.
There is described in Variant 2 the sorption of HCl acid with chloride anions (An− = 1Cl−) including concentrations [Xi] of all six components (i = 1,2,…6; left indexes): {[1Cl−], [2RH+], [3RHCl], [4H+], [5HCl], [6R0]}. Such diffusion 6- component process in the bi-functional NC matrix is accompanied by three MALS relations (2.1)-(2.3); (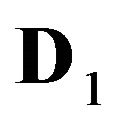 Cl;
Cl;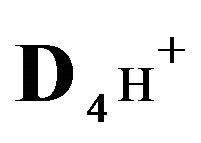 ;
;  HCl)-diffusivities of 1,4,5- components:
HCl)-diffusivities of 1,4,5- components:
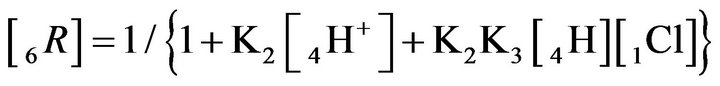 (2.4)
(2.4)
The relationship (2.4) shows that the profile of the 6R0-wave for Variant 2 depends on two concentrations [4H+] and [1Cl−] together with two MALS constants K2 and K3. The 6R0-wave profile is shown in Figures 5(a)– (d).
Thus the comparison of the (1C) and (2.4) relations shows that the propagation of the 6R0-wave (Variant 2, 6- components, two MALS constants: K2 and K3) is more complex (and more variable) than for the 5R0-wave (with one K2-constant, Variant 1). Taking the relationships: (1A), (1B) and (2.1-2.4) into account with comparing Variant 1 and Variant 2 it is clear that for two considered NC systems—Variant 2 is more complex and has more degrees of freedom (the ability for more variations) than Variant 1.
5. Multicomponent Waves Behavior in the
Modeling of NC Kinetics
The multicomponent concentration wave behavior in the bi-functional NC matrix is described here on the basis of the considered NC Model (Figure 1(c)) with the computerized modeling including the wave (W+) concept. There are considered two various different multicomponent NC kinetic systems: 5-component NC system with one association-dissociation reaction-(1B) (Variant 1) and 6component NC system with two association-dissociation reactions—(2.2), (2.3) (Variant 2).
5.1. Concentration Waves in 5-component NC
System {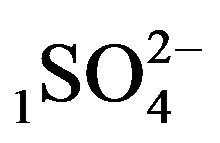 , 2RH+,
, 2RH+,  , 4H+, 5R0} with One Association-Dissociation Reaction
, 4H+, 5R0} with One Association-Dissociation Reaction
The investigation of the waves propagation with the results of the computerized simulation are presented in Figures 2-4 for Variant 1 with one association-dissociation reaction (1B) at 5R0 nano-sites (including 5R0- wave, sorption of H2SO4 acid, 5-components). Comparison of the 5R0-waves (5, brown solids) in Figure 2 shows that with the small KB value (a, left) the 5R0- wave propagates to the Center (for r-bead) faster, than for the large KB value (b, right): CMR (left) < CMR (right). For the dispersion the inequality is reverse: DispR(left) > DispR (right). In other words 5R0-wave (right) propagates slower with the profile, which is sharper (Figure 2(b)) in comparison with the 5R0-wave (left) (Figure 2(a)). If KB is increased: from (a) to (b), it means that the equilibrium of the reaction (1B) shifts to the left hand side of the reaction (1B). In this case (from (a) to (b)) such shift of the equilibrium (1B) clearly slows down the kinetic process. Figure 2 illustrate the influence of the KB value in the reaction (1B): the increase of the KB increases the completion time (Tfin) for the kinetic process.
Figures 3(a)-(f) illustrate the influence of the three various shapes of the NC matrix: r-bead (right), ro-fiber (middle), and L-membrane (left) on the 5R0-waves behavior in the course of time (T1,2 = 6à10) for the various KB values: KB =36 (a)-(c) or 398 (d)-(f). Comparison of propagating 5R0-waves in Figures 3(a)-(f), shows that 5R0-wave moves faster in the r-bead (right, c,f) of the NC Matrix than in the planar L-membrane or ro-fiber: CMLR(T)(a), (d) > CMroR(b), (e) > CMrR(T)(c), (f) (compare the positions for CMR (triangles, brown) in Figures 3(a)-(c) and also in Figures 3(d)-(f). The reason of such differences in the wave velocity is geometric: for r-bead the diffusion occurs in the fewer volume in the course of time T (for ro-fiber the change in volume is smaller than for r-bead, for L-membrane the volume is permanent—no change). In Figure 4 the dependencies for the integral parameters: CMR(T), and DispR(T) are presented for 5R0 waves (Variant 1) with various shapes of the bi-functional NC matrix: r-bead, ro-fiber, L-membrane.
Figure 4 represents the time dependent estimations of the mass transfer kinetics for the three various shapes - L,ro,r(T) of the NC matrix. The completion time (Tfin) of the kinetic process corresponds to the criterion (see also Section 3): the amount of sum (CMR + DispR)L,ro,r = 1.0. It means, that the distance covered by the [5R0]—concentration wave to the moment Tfin is equal to the length of the matrix: L0 (thickness), ro0 (radius of cylinder) or r0 (radius of sphere). In other words the completion time Tfin corresponds to the “crossing” of two curves: CMR(T), (solids) with DispR(T), (dashed) (Figure 4). In accordance with this criterion of “crossing” it is obvious from all Figures 3 and 4 that for any conditions the kinetic mass transfer process in the NC matrix is the fastest inside r-bead and the slowest inside L-membrane. The Dispersion (DispR(T) —width) of the 5R0 wave (dashed lines, Figures 4(a) and (b)) is the largest for the L-membrane—DispRL(T). The conclusions are obvious and follow from Figures 3 and 4.
(Figure 4, DispR(T), dashed). In accordance with this criterion of “crossing” it is obvious from all Figures 3,4 that for any conditions the kinetic mass transfer process in the NC matrix is the fastest inside r-bead and the slowest inside L-membrane. The Dispersion (width—DispR(T)) of the 5R0 wave (dashed lines, Figures 4(a) and (b)) is the largest for the L-membrane—DispRL(T). The conclusions are followed from Figures 3 and 4.
5.2. Concentration Waves in 6-Component NC System {1Cl−, 2RH+, 3RHCl, 4H+, 5HCl, 6R0} with Two Association-Dissociation Reactions
The 6R0-waves (brown curve-6, Figures 5) formed during the kinetic process in 6-component system (Variant 2) have the principal characteristic feature in comparison with the 5R0-waves for 5-component system (Variant 1, Figures 2-4). The 6R0 wave is “divided” partly into two sub-waves: rather sharp part of 6R0 frontal wave (for large concentrations) and rather diffuse 6R0-frontal wave (for small ones) (Variant 2, Figures 5(a)-(d)). This is explained by the influence of the two sequential effects of the two steps of the association-dissociation reactions (2.2), (2.3) with the corresponding constants -K2, K3. The velocity and profile of the 6R0-wave (Figures 5) depend on the combined influence of the K2, K3-constants including additional effects of the [4H+], [1Cl−]-concentrations values in relation (2.4). The point of transition from one sub-wave to the other depends mainly on the K2-value (compare Figure 5 (left—(a),c) with Figure 5 (right—b,d).
6. Discussion
The computerized simulation of the mass transfer kinetics inside the NC matrix (Sections 4,5) discovers the clear analogies of the multicomponent NC kinetics with the main theoretical basis of the theory of nonlinear multicomponent chromatography [14,19]. These analogies concern here the multicomponent concentration waves
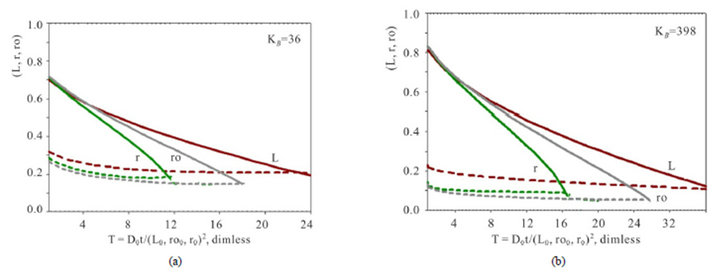
Figure 4. Variant 1. (Sulphate Anion: 1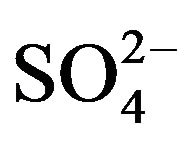 ). Time dependence of integral parameters: CMRL,ro,r(T), (solids) & DispRL,ro,r (T), (dashed) during propagation of 5R0-wave in the NC matrix: KB =36 (a), left); 398 (b), right); L-membrane (brown), rofiber (grey), r-bead (green).
). Time dependence of integral parameters: CMRL,ro,r(T), (solids) & DispRL,ro,r (T), (dashed) during propagation of 5R0-wave in the NC matrix: KB =36 (a), left); 398 (b), right); L-membrane (brown), rofiber (grey), r-bead (green). 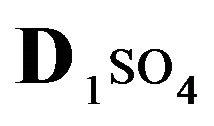 = 0.01;
= 0.01; 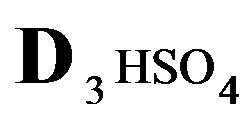 = 0.0085;
= 0.0085;  H = 0.03. Ordinate axis: distance from boundary (L0, r0, ro0 = 1) to “zero” points (L, r, ro = 0). Distances: 1. > L, r, ro > 0.
H = 0.03. Ordinate axis: distance from boundary (L0, r0, ro0 = 1) to “zero” points (L, r, ro = 0). Distances: 1. > L, r, ro > 0.

Figure 5. (a)-(d) (Variant 2. Chloride: 1Cl−). Comparison of propagating 6R0(T)-waves (6, brown solids) inside the NC matrix (ro, L) with two various K1-3 values for : ro-fiber-Xi(ro, T), (up, (a), (b)); L-membrane-XiL(L, T), (down, (c), (d)). Triangles (brown) show CMR positions at ro, L-axes (abscissa); K2 = 56 (left—(a), (c)); K2 = 100 (right—(b), (d)). Component Numbers (1, 6) are at the corresponding curves: 6R0, 1Cl−. T = 12.
behavior in the bi-functional NC matrix. The physical meaning of the reasons for the explanation of the propagating concentration waves behavior (Figures 2-4) is described by the joint influence of the two co-existing factors in the bi-functional NC matrix: Chemical Reaction (I) and Diffusion (II) (Figure 1(c)). Such type of the same joint effect (Reaction equilibrium + Diffusion effects in the NC matrix) is represented in the theory of chromatography by: multicomponent isotherms for equilibria (I) and set of the broadening factors for the concentration waves in columns (II), (i.e. well known effective HETP parameters (see Nomenclature) for chromatographic columns [9,14,19,20].
The first part of the Sections 5,6 concerns mainly the Variant 1: mass transfer of 5 components in the bi-functional NC matrix with one assocition-dissociation reaction (1B) at the nanosites—5R0. The influence of the first factor (I-Reaction equlibrium) is expressed by the KB (MALB) value: the more is KB-value (1B)-the less is the Dispersion (DispR) of the 5R0-concentration wave. In other words the width of the wave profile becomes narrower with the large KB value (Figure 3(b) and Figure 4(b)). The comparison of the DispR, in Figure 3a with Figure 3b (brown solids, curve 5) shows the narrowing distinctly. The same effect is shown via comparison Figure 4(a) with Figure 4(b) (DispRL,ro,r-dashed, corresponding color). The influence of the second factor (II-Diffusion) gives, as usual, the widening of the concentration 5R0- waves with the increase of the diffusivity. It should be emphasized here the non-trivial, specific effect for the NC system: there is no diffusivity for the 5,6R0-component (D5,6R = 0), nevertheless the propagation of the 5,6R0-waves takes place (Figures 2, 3 and 5). The physical reason of such propagation is not the diffusivity (D5,6R = 0) but the chemical reaction (1B) (or (2.2),(2.3)) influence: the transformation for the components (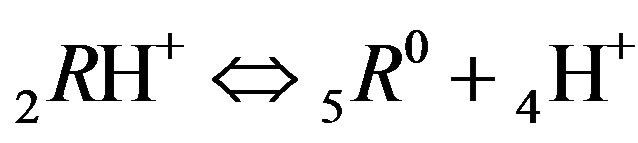 ), and diffusion coefficients of other moveable components (D1SO4; D3HSO4; D4H) bring the resulting mass transfer of the [5R0]-, (or [6R0])-concentrations with the propagation of the corresponding 5,6R0waves.
), and diffusion coefficients of other moveable components (D1SO4; D3HSO4; D4H) bring the resulting mass transfer of the [5R0]-, (or [6R0])-concentrations with the propagation of the corresponding 5,6R0waves.
One more interesting result with the evidence of the above marked analogy can be seen from Figure 4. In this cases it takes place the typical behavior of the parameter—DispR in the course of Time (T, abscissa): the dispersion (DispR) of 5R0-waves tends asymptotically to the permanent value at the end of T-abscissa (Figure 4, see dashed curves behavior along the abscissa T with the asymptotic tendency to the constant value). In the theory of chromatography the same effect takes place for the concentration waves in columns, when the favourable isotherm factor (I) used to compensate the unfavourable influence of the broadening HETP factors (II) for the concentration waves in columns: favourable equilibrium (I) compensate the widening of the concentration wave with the same type of the asymptotic tendency [14,19,20] There are considered these effects on the basis of the NC Model with the results of the multicomponent kinetic system for Variant 1 (k = 5) and Variant 2 (k = 6).
Variant 1. Association-dissociation reaction (1B) at the nano-sites 5R0 brings the retardation (in the NC medium) of the i-component due to the partial transformation in the association-dissociation reaction (1B):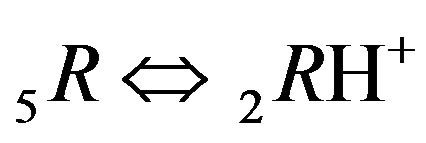 . Therefore the movement and broadening of the 5R0- concentration wave (5-component system) depend on the one KB value and on [4H+] concentration (1C). The comparison between Figure 2(a, left) and Figure 2(b, right) shows that the width of the 5R0-wave (5, brown solids, a, left) is much larger than for the right 5R0-wave (b). In addition Figure 2 shows that the 5R0-wave (curve 5, a, left) moves faster than the 5R0-wave (curve 5, b, right).
. Therefore the movement and broadening of the 5R0- concentration wave (5-component system) depend on the one KB value and on [4H+] concentration (1C). The comparison between Figure 2(a, left) and Figure 2(b, right) shows that the width of the 5R0-wave (5, brown solids, a, left) is much larger than for the right 5R0-wave (b). In addition Figure 2 shows that the 5R0-wave (curve 5, a, left) moves faster than the 5R0-wave (curve 5, b, right).
Variant 2. Association-dissociation two steps reactions (2.2), (2.3) at the nano-sites 6R0 bring also the retardation (in the NC matrix) of the i-component due to the partial transformations with both reactions: 1st step: 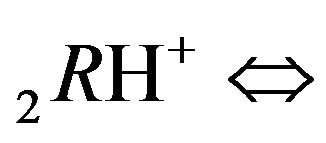
 (2.2) and then, 2nd step:
(2.2) and then, 2nd step: 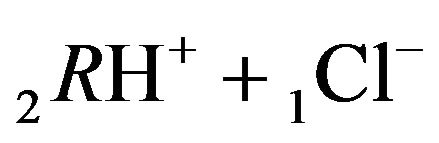
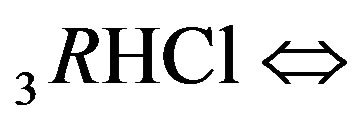 (2.3). The total effect of the two step reactions is determined by the values of the two coefficients—K2, K3 with additional influence of the concentrations [4H+], [1Cl−] (2.4) on the [6R0]-concentration wave behavior. Therefore the movement of the 6R0-concentration wave is influenced by the [1Cl−], [4H+]-concentrations with the additional influences of K2, K3 values. The behavior of the 6R0-wave (6-component NC system with two association-dissociation reactions) is more complex and more variable (with more degrees of freedom) than for the 5-component system (Variant 1), where there is only one association-dissociation reaction (1B). This difference is expressed in the combined character of the 6R0 wave profile (Figure 5).
(2.3). The total effect of the two step reactions is determined by the values of the two coefficients—K2, K3 with additional influence of the concentrations [4H+], [1Cl−] (2.4) on the [6R0]-concentration wave behavior. Therefore the movement of the 6R0-concentration wave is influenced by the [1Cl−], [4H+]-concentrations with the additional influences of K2, K3 values. The behavior of the 6R0-wave (6-component NC system with two association-dissociation reactions) is more complex and more variable (with more degrees of freedom) than for the 5-component system (Variant 1), where there is only one association-dissociation reaction (1B). This difference is expressed in the combined character of the 6R0 wave profile (Figure 5).
Thus more variable 6-component NC system (Variant 2) has more complex behavior. For 6-component NC system the number of the determining parameters (including concentrations) is larger than for 5-component NC system (Variant 1). The mentioned analogies between multicomponent chromatography and NC kinetics in the NC Model is not so visual and becomes more complex for the 6 component NC system (Variant 2). The main reason is the influence of the two association dissociation constants K2, K3 (2.2), (2.3) for the 6-component system in contrast to the simple influence of one KB constant (Variant 1). The discussion of the regularities in the behavior of the integral parameters: CM6 and Disp6 for the 6R0-wave needs thorough future analyses with the multicomponent calculations of mass transfer in the 6-component NC system.
The corresponding computer animations are prepared by author for the visual demonstration of the obtained results of the modeling. The animations obtained on the basis of the computer calculations with the corresponding successive visual frames for the waves are perceived easily by any audience.
7. Conclusions
The modern kinetic NC Model for the multicomponent mass transfer in the novel NC materials is created. The computerized simulations of the nonlinear NC systems on the basis of the Model bring the new results describing the behavior of the multicomponent concentration waves (W) in the bi-functional NC matrixes for the three various shapes: r-bead, ro-fiber, L-membrane.
The results demonstrate rather comprehensive analogy between theory of nonlinear chromatography and multicomponent NC kinetics in the bi-functional matrix. This analogy is used for the description of the multicomponent concentration waves behavior. In the interpretation of the marked analogy there are shown the decisive influences of the two characteristics of the NC model: the equilibrium parameters of the Reactions (I) and Diffusion effects (II) on the propagation of the concentration waves inside the bi-functional NC matrix during the NC kinetic process.
The “multicomponent concentration wave” (W+) concept in the study of the bi-functional NC matrix with the two factors: (I) Reactions on the active nano-sites and (II) Diffusion in the NC medium is effective. It brings the clear, and understandable treatment of the multicomponent mass transfer kinetics in the bi-functional NC matrix. The quantitative estimations of the concentration waves behavior are obtained by using the two integral parameters of the wave distributions: “Center of MassCM” and “Dispersion—Disp”. The corresponding conclusions concerning co-influence of the Reactions and Diffusion coefficients inside the bi-functional NC matrix on the kR0-concentration wave behavior are obtained.
All the obtained results are presented in terms of the additional key concept (W+): propagating multicomponent concentration waves (W) in the bi-functional NC matrix. The used W+ concept for the description of the multicomponent NC mass transfer kinetics gives the clear interpretation of the computerized results. The obtained original, new results on the basis of the NC Model show the behavior of the broadening and interacting propagating concentration waves (especially concentration 5,6R0-waves) inside the bi-functional NC matrix during multicomponent mass transfer NC kinetics.
8. Acknowledgements
Author is grateful for the support of part of this research, which has been fulfilled in Karlsruhe, (KIT) under the support of DFG (Deutsche Forschung Gemeindschaft, 2011, German-Russian grant N 436 RUS 113/989/9 - 1).
REFERENCES
- Kalinitchev, “Kinetic and Dynamic Chromatographic Systems, and Models of Mass Transport: Behavior of Multicomponent Concentration Waves,” Protection of Metals and Physical Chemistry of Surfaces Journal, Vol. 47, No. 6, 2011, pp. 570-579.
- A. Kalinitchev, “Mass Transfer Kinetics Modeling in Bifunctional Ion Exchangers with Chemical Reactions on Active Centers,” In: M. Cox, Ed., IEX 2012 Intern. IEx Conference, Version of full Papers. S. “Fundamentals” (Book-El.). SCI & Ext. Abstracts, 2012, pp. 1-18 & pp. 123-125.
- T. Kravchenko, L. Polyansky, A. Kalinitchev and D. Konev, “Nano Composites Metal-Ion Exchangers,” 2009.
- E. Kiprianova, T. Kravchenko, D. Konev, A. Kalinitchev and W. Hoell, “Reducing Sorption of the Molecular Oxygen from Water by Silver-Sulpho-Cation Exchanger Nano Composite with Various Ionic Forms,” Russian Journal of Physical Chemistry, Vol. 84, No. 6, 2010, pp. 1104- 1110.
- F. Helfferich and Y-I. Hwang, “Kinetics of Acid Uptake by Weak Base Anion Exchangers. Mechanism of Proton Transfer,” Am. I. Ch. E. Symp. Ser., Vol. 81, 1985, pp. 17- 27.
- A. I. Kalinitchev, E. V. Kolotinskaya and T. D. Semenovskaya, “Computerized Analyses of the Diffusion Processes in Complexing Ionites,” Journal of Chromatography, Vol. 243, No. 1, 1982, pp. 17-24. doi:10.1016/S0021-9673(00)88159-5
- Y.-I. Hwang and F. Helfferich, “Generalized Model for Multispecies IEx Kinetics including Fast Chemical Reactions,” Reactive Polymers, Vol. 5, 1987, pp. 237-252.
- D. Petruzelli, F. Helfferich, L. Liberti, J. Millar, and R. Passino, “Kinetics of IEx with Intraparticle Rate Control: Models Accounting for Interaction in the Solid Phase,” Reactive Polymers, Vol. 7, 1987, pp. 1-13.
- A. Kalinitchev, “Investigation of Intraparticle IEx Kinetics in Selective Systems,” In: J. Marinsky and Y. Marcus, Eds., IEx & Solv. Extr., Vol. 12, Marcel Dekker, New York, 1995, pp. 149-196.
- F. Helfferich, “Ion Exchange Kinetics,” In: J. I. Marinsky, Ed., Ion Exchange (A Series of Adv.), Vol. 1, St. University of New York at Buffalo, New York, 1966.
- R. Haase, “Thermodynamics of Irreversible Processes,” 1967.
- F. Helfferich, “Ion Exchange,” Chapter 6, Mc.Graw-Hill., New York, 1962.
- F. Helfferich, “Ion Exchange Kinetics-Evolution of a Theory,” In: L. Liberti and F. Helfferich, Eds. Mass Transfer & Kinetics of IEx, Sijthoff and Nordhoff, The Hague, 1983, pp. 157-179. doi:10.1007/978-94-009-6899-8_6
- F. Helfferich and G. Klein, “Multicomponent Chromatography. Theory of Interference,” M. Dekker Inc., New York, 1970.
- F. H. Festschrift, “Industrial & Engineering Chemistry Research,” Journal of the American Chemical Society, Vol. 34, No. 8, 1995, pp. 2551-2922.
- D. Tondeur and M. Bailly, “Unifying Concept in NonLinear Unsteady Processes. PII. Multicomponent Waves, Competition and Diffusion,” Chemical Engineering and Process, Vol. 22, No. 2, 1987, pp. 91-105. doi:10.1016/0255-2701(87)80035-1
- D. Tondeur, “Paradigms and Paradoxes in Modeling Adsorption and Chromatographic Separations,” Industrial & Engineering Chemistry Research, Vol. 34, No. 8, 1995, pp. 2782-2788. doi:10.1021/ie00047a029
- Y. L. Hwang, “Wave Propagation in Mass Transfer Processes: From Chromatography to Distillation,” Industrial & Engineering Chemistry Research, Vol. 34, No. 8, 1995, pp. 2849-2864. doi:10.1021/ie00047a039
- A. E. Rodrigues and D. Tondeur, “Percolation Process: Theory and Applications,” Sijthoff & Nordhoff, The Hague, 1981. doi:10.1007/978-94-009-8579-7
- A. Kalinitchev, “Nonlinear Theory of Multicomponent Sorption Dynamics and Chromatography,” Russian Chemical Reviews, Vol. 65, No. 2, 1996, pp. 95-115. doi:10.1070/RC1996v065n02ABEH000201
- W. Hoell and A. Kalinitchev, “The Theory of Formation of Surface Complexes and Its Application to the Description of Multicomponent Dynamic Sorption Systems,” Russian Chemical Reviews, Vol. 73, No. 4, 2004, pp. 351-370. doi:10.1070/RC2004v073n04ABEH000768
- R. Courant and K. Friedrichs, “Supersonic flow and Shock Waves,” Springer-Verlag, Berlin, 1999.
- I. Prigogine and R. Herman, “Kinetic Theory of Vehicular Traffic,” Elsevier, New York, 1971.
- G. Whitham, “Linear and Nonlinear waves,” Wiley, New York, 1974.
- A. Kalinitchev and W. Hoell, “Multicomponent Ion Exchange Dynamics with the Equilibria Described by Surface Complexation Theory,” In: M. Cox, Ed. IEX 2004, Ion Exchange Technology for Today and Tomorrow, Soc. Chem. Ind., London, 2004, pp. 53-58.
- A. Kalinitchev and W. Hoell, “Theoretical Principles of Multicomponent Frontal and Displacement Elution Chromatography on the Basis of Surface Complexation Theory,” In: M. Cox, Ed., IEX 2008, Recent Advances in IEx Theory & Practice, Soc. Chem. Ind., London, 2008, pp. 85-93.
- G. Korn and T. Korn, “Mathematical Handbook,” McGraw-Hill, New York, 1968.
Nomenclature


