Journal of Applied Mathematics and Physics
Vol.03 No.11(2015), Article ID:61567,8 pages
10.4236/jamp.2015.311178
Capacitance of Vertical Parallel Junction Silicon Solar Cell under Monochromatic Modulated Illumination
Gokhan Sahin, Moustapha Dieng, Mohamed Abderrahim Ould El Moujtaba, Moussa Ibra Ngom, Amary Thiam, Grégoire Sissoko
Physics Department, Faculty of Sciences and Techniques, University of Cheikh Anta Diop, Dakar, Senegal

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 30 September 2015; accepted 27 November 2015; published 30 November 2015

ABSTRACT
The aim of this study is to show the influence of the wavelength on the electrical parameters of vertical parallel junction silicon solar cell by use of impedance spectroscopy technique. The Bode diagrams of the diffusion capacitance are shown for different wavelengths while the solar cell operates under both open circuit and short circuit conditions. The Nyquist diagram of the diffusion capacitance has shown the extension of the space charge region for various wavelengths.
Keywords:
Vertical Parallel Junction, Wavelength, Capacitance, Bode and Nyquist Diagrams

1. Introduction
The space charge region of a solar cell can be considered as a plane capacitor named transition capacitance [1] . The illumination of the solar cell causes a diffusion of excess minority carriers. These carriers, characterized by a lifetime in the base and to the emitter, are the source of the photocurrent. They create a diffusion capacitance whose thickness depends on the junction recombination velocity [1] -[3] , which defines the operating point of the solar cell. The capacitance of the solar cell may be studied under static regime in order to determine the doping rate. Under transient state [4] -[7] , capacitance versus time makes possible the determination of the extended space charge zone and the minority carriers’ lifetime. In frequency dynamic regime [8] [9] , the well known impedance spectroscopy method is used for the determination of electrical parameters. For this work, we use Bode and Nyquist diagrams [10] [11] to show the effect of the wavelength and the junction recombination velocity on the diffusion capacitance of a vertical parallel junction silicon solar cell characterized by the lateral collection.
2. Theory
We present on Figure 1 a unit cell of a vertical junction’s silicon solar cell [12] [13] under various wavelengths. H is the base width.
Given that the contribution of the base to the photocurrent is larger than that of the emitter [14] our analysis will only be developed in the base region.
Taking into account the generation, recombination and diffusion phenomena in the base, the equation governing the variation of the minority carriers density δ(x, t) under modulation frequency [14] [15] is:
 (1)
(1)
D(ω) and τ are respectively, the excess minority carrier diffusion constant and lifetime.
The excess minority carriers’ density can be written as:
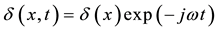 (2)
(2)
Carrier generation rate G(z, t) is given by:
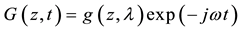 (3)
(3)
Where
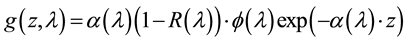 (4)
(4)
x is the base depth along x axis, ω is the angular frequency, z the base depth according to the vertical axis; and λ the wavelength.
If we replace Equation (2) into Equation (1), the temporary part is eliminated and we obtain:
 (5)
(5)
The solution of this equation is:
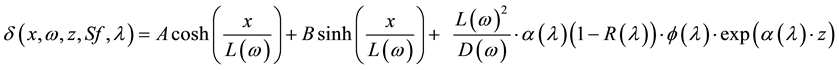 (6)
(6)
Coefficients A and B are determined through the following boundary conditions [16] [17] :
- at the junction (x = 0):
Figure 1. Vertical parallel junction silicon solar cell.
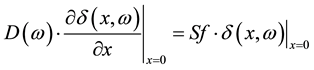 (7)
(7)
Sf is the excess minority carriers recombination velocity at the junction.
- at the middle of the base (x = H/2):
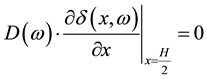 (8)
(8)
The excess minority carriers in the base will flow to the two junctions by diffusion; the photocurrent density is given by the following expression:
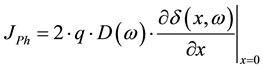 (9)
(9)
where q is the elementary charge.
From the excess minority carriers’ density, we can deduce the photovoltage across the junction, according to the Boltzmann’s relation as follow:
 (10)
(10)
with VT the thermal voltage, Nb the base doping density, ni the intrinsic carriers’ density.
The charge variation in the base leads to a corresponding photovoltage variation across the junction; this gives rise to an associated capacitance. This capacitance is mainly due to the fixed ionized charge (dark capacitance) at the junction boundaries and the diffusion process (diffusion capacitance) [18] [19] . The solar cell’s capacitance can be defined by:
 With
With 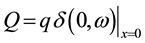 (11)
(11)
Given the photovoltage expression (eq.10), the capacitance can be rewritten as:
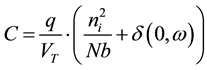 (12)
(12)
3. Results and Discussions
We present in this section the Nyquist and Bode diagrams [20] , to show the effect of the wavelength and the junction recombination velocity on the diffusion capacitance a silicon solar cell in parallel vertical junction.
3.1. Bode and Nyquist Diagrams Capacitance
3.1.1. Bode Diagram Capacitance of the Solar Cell under Open Circuit Condition: Effect of the Wavelength
The profiles of the module and its phase of capacitance versus the logarithm of the frequency for different wavelengths (short and long wavelength), are shown in Figures 2(a)-(c).
In Figure 2(a) and Figure 2(b), we get the same paces of the capacitance module with the logarithm of the modulation frequency. We found that in the wavelength interval (short wavelength) [0.44 μm; 0.50 μm], the magnitude of the capacitance increases, and that in the wavelength interval (long wavelength) [0.58 μm; 0.7 μm], this amplitude decreases as the base is more or less transparent in this wavelength range and phase in a situation of open circuit, very little with the angular frequency to a certain frequency called the cut-off frequency ωc = 2π/τ [21] .
Beyond this cut-off frequency, the capacitance of the solar cell and its phase decreases very rapidly with the angular frequency. In fact, when the frequency is inside the cut-off, the solar cell operates in quasi-static regime and remains insensitive to frequency. For frequencies above the cut-off frequency, the stress of the material


Figure 2. (a) Capacitance versus logarithmic of frequency for different wavelengths. Sf = 2 × 102 cm/s, H = 0.03 cm, Lo = 0.02 cm, Do = 26 cm2/s, z = 0.0001 cm, 1: l = 0.44 μm; 2: l = 0.46 μm; l = 0.48 μm; l = 0.50 μm; Short wavelength; (b) Capacitance versus logarithmic of frequency for different wavelengths. Sf = 2 × 102 cm/s, H = 0.03 cm, Lo = 0.02 cm, Do = 26 cm2/s, z = 0.0001 cm, 1: l = 0.58 μm; 2: l = 0.62 μm; l = 0.66 μm; l = 0.70 μm; Long wavelength; (c) Capacitance phase versus logarithm of the frequency for different wavelengths, Sf = 2 × 102 cm/s, H = 0.03 cm, Lo = 0.02 cm, Do = 26 cm2/s, z = 0.0001 cm.
becomes important to the point that photo generated minority carriers are poorly stored in the vicinity of the junction: this leads to a very low capacitance.
3.1.2. Bode Diagram Capacitance of the Solar Cell in Short-Circuit Operating: Effect of the Wavelength
In Figure 3(a) and Figure 3(b), are shown the profiles of the module and its phase of capacitance (Figure 3(c)), versus the logarithm of the frequency for different wavelengths.
In Figure 3(a) and Figure 3(b), we get the same profile of the capacitance-frequency. In the wavelength interval [0.44 μm; 0.50 μm], the magnitude of the capacitance increases, but in the wavelength interval [0.58 μm; 0.7 μm], the amplitude decreases.
In terms of ac electrical analogy, our study reveals that the behavior of the capacitance- frequency is similar to that observed in the electronic filter low-pass type.


Figure 3. (a) Capacitance versus logarithmic of frequency for different wavelengths. Sf = 6 × 106 cm/s, H = 0.03 cm, Lo = 0.02 cm, Do = 26 cm2/s, z = 0.0001 cm. 1: l = 0.44 μm; 2: l = 0.46 μm; l = 0.48 μm; l = 0.50 μm; Short wavelength; (b) Capacitance versus logarithmic of frequency for different wavelengths. Sf = 6 × 106 cm/s, H = 0.03 cm, Lo = 0.02 cm, Do = 26 cm2/s, z = 0.0001 cm. 1: l = 0.58 μm; 2: l = 0.62 μm; l = 0.66 μm; l = 0.70 μm. Long wavelength; (c) capacitance phase versus frequency for different wavelengths Sf = 6 × 106 cm/s, H = 0.03 cm, Lo = 0.02 cm, Do = 26 cm2/s, z = 0.0001 cm.
3.2. Nyquist Diagram
The Nyquist diagram is the representation of the imaginary part as a function of the real part of a complex quantity [20] [21] .
3.2.1. Nyquist Diagram of the Solar Cell Capacitance in Open Circuit Operating: Effect of the Wavelength
The imaginary part versus real part of the capacitance, for different wavelengths λ, is shown in Figure 4(a) and Figure 4(b).
In Figure 4(a) and Figure 4(b), the curves representing the imaginary part as a function of the real part of the capacitance for different wavelengths are different diameter of semicircles.
In the wavelength interval [0.44 μm; 0.50 μm], the diameter of the semicircles increases because the number of minority carriers stored in the vicinity of the junction also increases. It is noted that in the wavelength interval [0.58 μm; 0.7 μm], the diameter of the semicircles decreases in this case.
When the angular frequency tends to zero, the imaginary part of the capacitance is zero while its real part is equal to its open circuit value in quasi-static regime: it will have one large storage of minority carriers in the


Figure 4. (a) Im(Coc) versus Re(Coc) for open circuit condition Sf = 2 × 102 cm/s, H = 0.03 cm, Lo = 0.02 cm, Do = 26 cm2/s, z = 0.0001 cm. 1: l = 0.44 μm; 2: l = 0.46 μm; l = 0.48 μm; l = 0.50 μm; Short wavelength (b) Im (Coc) versus Re (Coc). for open circuit condition Sf = 2 × 102 cm/s, H = 0.03 cm, Lo = 0.02 cm, Do = 26 cm2/s, z = 0.0001 cm, 1: l = 0.58 μm; 2: l = 0.62 μm; l = 0.66 μm; l = 0.70 μm Long wavelength.
vicinity of the junction. By cons, when the angular frequency approaches infinity, the imaginary and real parts are almost zero: there is no more storage therefore photo generated minority carriers at the junction. By this, we match the capacitance of the solar cell to the diameter of a semicircle obtained for a given depth z between the two angular frequency range (zero to infinity). When the depth z increases, the curves are semicircles at decreasing diameters since there’s a decrease in the number of minority carriers photo generated in the base of the solar cell and stored in the vicinity of the junction
3.2.2. Nyquist Diagram of the Solar Cell Capacitance in Short-Circuit Operating: Effect of the Wavelength
The imaginary part versus real part of the capacitance t for different wavelengths, is shown in Figure 5(a) and Figure 5(b).
In Figure 5(a) and Figure 5(b), the curves representing the imaginary part versus real part of the capacitance for different wavelengths are different diameter of semicircles in the short-circuit situation. In the wavelength interval [0.44 μm; 0.50 μm], the “pseudo-diameters” related to the capacitance of the solar cell under short circuit condition, for a given wavelength, increases, while it decreases in the wave length range [0.58 μm; 0.7 μm]. The resulting curve has two different parts:


Figure 5. (a) Im(Csc) versus Re(Csc) for short circuit condition Sf = 6 × 106 cm/s, H = 0.03 cm, Lo = 0.02 cm, Do = 26 cm2/s, z = 0.0001 cm. 1: l = 0.44 μm; 2: l = 0.46 μm; l = 0.48 μm; l = 0.50 μm; Short wavelength (b) Im (Csc) versus Re(Csc) for short circuit condition Sf = 6 × 106 cm/s, H = 0.03 cm, Lo = 0.02 cm, Do = 26 cm2/s, z = 0.0001 cm. 1: l = 0.58 μm; 2: l = 0.62 μm; l = 0.66 μm; l = 0.70 μm Long wavelength.
i) the range of angular frequency [0; ωc], corresponds to a quart circle;
ii) the imaginary part as a function of the real part is a straight line in the interval [ωc; ¥].
When the depth z increases, the curves that shrink because the amplitudes of the imaginary and real parts of the capacitance decreases: this can be explained by a weak generation of minority carriers in a non relaxed solar cell under high frequency excitation.
4. Conclusion
In this paper, we have developed a mathematical/physical model which enables us to simulate the behavior of the vertical parallel junction solar cell from the frequency-dependence of the capacitance. The capacitance of the space charge region was studied using Bode and Nyquist diagrams while the solar cell remained either under open circuit or short circuit condition and illuminated with different wavelengths. For given operating point, the absorption coefficient influences the region where the carriers are photogenerated and then leads to different diameter of the C-ω curves. Indeed, for a given wavelength the diameter obtained under short circuit is larger than that calculated for the solar cell under open circuit condition, according to the extended space charge region theory.
Cite this paper
GokhanSahin,MoustaphaDieng,Mohamed Abderrahim Ould ElMoujtaba,Moussa IbraNgom,AmaryThiam,GrégoireSissoko, (2015) Capacitance of Vertical Parallel Junction Silicon Solar Cell under Monochromatic Modulated Illumination. Journal of Applied Mathematics and Physics,03,1536-1543. doi: 10.4236/jamp.2015.311178
References
- 1. Chawla, G.B.R. and Gummel, H.K. (1971) Transition Region Capacitance of Diffusion p-n Junction. IEEE Transactions on Electron Devices, 18, 178-195.
http://dx.doi.org/10.1109/T-ED.1971.17172 - 2. Yaron, G. and Frohman-Bentchkowsky, D. (1980) Capacitance Voltage Characterization of Poly Si-SiO2-Si Structures. Solid-State Electronics, 23, 433-439.
http://dx.doi.org/10.1016/0038-1101(80)90078-7 - 3. Jakubowski, A. (1981) Graphic Method of Substrate Doping Determination from C-V Characteristics of MIS Capacitors. Solid-State Electronics, 24, 985-987.
http://dx.doi.org/10.1016/0038-1101(81)90123-4 - 4. Sissoko, G., Dieng, B., Corréa, A., Adj, M. and Azilinon, D. (1998) Silicon Solar Cell Space Charge Region Width Determination by a Study in Modelling. Proceeding of the World Renewable Energy Conference and Exhibition, 3, 1852-1855.
- 5. Bayhan, H. and Kavasglu, A.S. (2003) Admittance and Impedance Spectroscopy on Cu(In,Ga)Se2 Solar Cells. Turkish Journal of Physics, 27, 529-535.
- 6. Diallo, H.L., Wereme, A., Maiga, A.S. and Sissoko, G. (2008) New Approach of Both Junction and Back Surface Recombination Velocities in a 3D Modelling Study of a Polycrystalline Silicon Solar Cell. The European Physical Journal Applied Physics, 42, 203-211.
http://dx.doi.org/10.1051/epjap:2008085 - 7. Ly Diallo, H., Dieng, B., Ly, I., Dione, M.M., Ndiaye, M., Lemrabott, O.H., Bako, Z.N., Wereme, A. and Sissoko, G. (2012) Determination of the Recombination and Electrical Parameters of a Vertical Multijunction Silicon Solar Cell. Research Journal of Applied Sciences, Engineering and Technology, 4, 2626-2631.
- 8. Mbodji, S., Mbow, B., Barro, F.I. and Sissoko, G. (2011) A 3D Model for Thickness and Diffusion Capacitance of Emitter-Base Junction Determination in a Bifacial Polycrystalline Solar Cell under Real Operating Condition. Turkish Journal of Physics, 35, 281-291.
- 9. Sow, E., Mbodji, S., Zouma, B., Zoungrana, M., Zerbo, I., Sere, A. and Sissoko, G. (2012) Determination in 3D Modeling Study of the Width Emitter Extension Region of the Solar Cell Operating in Open Circuit Condition by the Gauss’s Law. International Journal of Science, Environment and Technology (IJSET), 1, 230-246.
- 10. Diao, A., Thiam, N., Zoungrana, M., Ndiaye, M., Sahin, G. and Sissoko, G. (2014) Diffusion Coefficient in Silicon Solar Cell with Applied Magnetic Field and under Frequency: Electric Equivalent Circuits. World Journal of Condensed Matter Physics, 4, 84-92.
http://dx.doi.org/10.4236/wjcmp.2014.42013 - 11. Dieng, A., Zerbo, I., Wade, M., Maiga, A.S. and Sissoko, G. (2011) Three-Dimensional Study of a Polycrystalline Silicon Solar Cell: The Influence of the Applied Magnetic Field on the Electrical Parameters. Semiconductor Science and Technology, 26, 095023.
- 12. Dione, M.M., Mbodji, S., Samb, M.L., Dieng, M., Thiame, M., Ndoye, S., Barro, F.I. and Sissoko, G. (2009) Vertical Junction under Constant Multispectral Light: Determination of Recombination Parameters. Proceedings of the 24th European Photovoltaic Solar Energy Conference, 465-469.
- 13. Arora, J.D., Singh, S.N. and Mathur, P.C. (1981) Surface Recombination Effects on the Performance of n+-p Step and Diffused Junction Silicon Solar Cells. Solid State Electronics, 24, 739-747.
http://dx.doi.org/10.1016/0038-1101(81)90055-1 - 14. Honma, N., Munakata, C. and Shimizu, H. (1988) Calibration of Minority Carrier Lifetime Measured with an ac Photovoltaic Method. Japanese Journal of Applied Physics, 24, 1322-1326.
http://dx.doi.org/10.1143/JJAP.27.1322 - 15. Mandelis, A. (1989) Coupled ac Photocurrent and Photothermal Reflectance Response Theory of Semiconducting p-n Junctions. Journal of Applied Physics, 66, 5572-5583.
http://dx.doi.org/10.1063/1.343662 - 16. Sissoko, G., Museruka, C., Corréa, A., Gaye, I. and Ndiaye, A.L. (1996) Light Spectral Effect on Recombination Parameters of Silicon Solar Cell. World Renewable Energy Congress, Part III, 1487-1490.
- 17. Gôkan, S., Thiam, N., Ndiaye, M., Diao, A., Mbow, B. and Sissoko, G. (2014) Influence of Illumination Wavelength on the Electrical Parameters of a Vertical Junction Silicon Solar Cell in Frequency Modulation. IPASJ International Journal of Electrical Engineering (IIJEE), 2, 23-28.
- 18. Hu, C.C. (2010) Modern Semiconductor Devices for Integrated Circuits. Pearson/Prentice Hall, New Jersey.
- 19. Boer, K.W. (2010) Introduction to Space Charge Effects in Semiconductor. Springer-Verlag.
http://dx.doi.org/10.1007/978-3-642-02236-4 - 20. Pannalal, L.B. (1973-1974) Signals, Systems and Controls. Intext Educational, New York.
- 21. Kosyachenko, L.A. (2011) Solar Cells—Dye-Sensitized Devices; InTech, Rijeka, Croatia.
http://dx.doi.org/10.5772/1757




