Journal of Applied Mathematics and Physics
Vol.03 No.05(2015), Article ID:56789,14 pages
10.4236/jamp.2015.35073
Probing Nucleon Structure in Deep Inelastic Scattering
Mohammed Sultan Al-Buriahi, Mohammed Tarek Hussein, Mohammed Tawfik Ghoneim
Faculty of Science, Cairo University, Cairo, Egypt
Email: moh_soultan@yahoo.com, Tarek@Sci.cu.edu.eg, ghoneim@sci.cu.edu.eg
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 March 2015; accepted 26 May 2015; published 29 May 2015
ABSTRACT
The comparison between the muon and the neutrino as probes of the nucleon structure is presented. The prediction of the structure functions, quark distributions, leptonic currents, and cross section led us to obtain some of the features of the electro-weak interactions in the deep inelastic scattering. A perturbation technique is used to evaluate the leptonic current that is assumed to be a complex quantity. The imaginary part of which represents the rate of absorption. On the other hand, the quarks wave functions forming the nucleon are extracted from experimental data for neutrino-nucleon and muon-nucleon collisions. A numerical technique is applied to analyze the data of the experiments CERN-NA-2 and CERN-WA25, to evaluate the quark functions and hence to calculate the hadronic current. It is found that the quark distribution functions predicted by the muon as a probe is slightly shifted up compared with that of the neutrino. Finally, the differential cross section is calculated in terms of leptonic and hadronic currents.
Keywords:
Lepton-Nucleon Interactions, Deep Inelastic Structure Function, Quark Functions

1. Introduction
Electroweak measurements are a very important part of the physics program targeting the measurement of electroweak precision observables [1] .
The study of structure functions of the nucleon offers a unique window on the internal quark structure of stable baryons. This provides insight into the two defining features of QCD. From measurements of structure functions, we can deduce the fraction of the nucleon momentum and spin carried by quarks.
During more than three decades of measurements at many accelerator facilities worldwide, appreciable amount of data has been collected, covering several orders of magnitude in both kinematic variables (x, the fraction of the nucleon momentum carried by the struck quark, and the momentum transfer squared, Q2).
Although a large body of structure function data exists over a wide range of x and Q2, the region x > 0.6 is not well explored. For x ≥ 0.4 the contributions from the
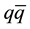 sea are negligible [2] [3] , and the structure functions are dominated by the valence quarks. Knowledge of the valence quark distributions of the nucleon at large x is vital for many reasons [4] [5] . The simplest symmetric quark model predicts that the ratio of d to u quark distributions in the proton is 1/2 [6] [7] . However, the breaking of this symmetry in nature leads to a much smaller ratio. Various mechanisms have been used to explain why the d distribution is softer than u.
sea are negligible [2] [3] , and the structure functions are dominated by the valence quarks. Knowledge of the valence quark distributions of the nucleon at large x is vital for many reasons [4] [5] . The simplest symmetric quark model predicts that the ratio of d to u quark distributions in the proton is 1/2 [6] [7] . However, the breaking of this symmetry in nature leads to a much smaller ratio. Various mechanisms have been used to explain why the d distribution is softer than u.
If the interaction between quarks that are spectators to the deep inelastic collision is dominated by one-gluon exchange [8] [9] , the d quark distribution will be suppressed, and the d/u ratio will tend to zero in the limit x→1.
Determining d/u experimentally would lead to important insights into the mechanisms responsible for spin- flavor symmetry breaking. In addition, quark distributions at large x are a crucial input for estimating backgrounds in searches for new physics beyond the Standard Model at high energy colliders.
From this point of view, we are looking forward to use the data of muon (as electroweak particle) and neutrino (as weak particle) to probe the structure of the nucleon.
The electroweak theory is the unified description of both electromagnetic force and weak force. Although the weak force is 106 weaker than the electromagnetic force at low energies, they would merge into a single electroweak force at energies of the order of 100 GeV.
The W and Z bosons are the mediators of the weak interaction, as in the case of the photon, which is mediator of the electromagnetic interaction. There are several papers [10] -[13] which studied the electroweak force and provided models and theories for the development of this topic. In this work, we highlighted the features of the electromagnetic force and the weak force through our study for muon-nucleon interaction and neutrino-nucleon interaction respectively, and we have been able to realize when both of them become one force in what is called electroweak force.
The paper is organized as follows: After this introduction, Section 2 discusses the general features of neutrino-nucleon and muon-nucleon interactions. In Section 3, a prediction of the quark functions is presented. Section 4 looks to the Simple model for calculation of the DIS. Finally concluding Remarks are given in Section 5.
2. Neutrino and Muon as Probes of Nucleon Structure
2.1. Neutrino-Nucleon Interaction
We use the data of the experiment CERN-WA25 [14] for finding the parametric forms of structure functions F2 and F3 in the variables, Bjorken scale x, and the square of momentum transfer Q2. We carry out the Exponential fitting by MATHEMATICA9.0 to parameterize the function F2 and F3 for neutrino-proton and neutrino-neutron interactions in the form
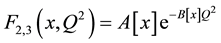 (1.a)
(1.a)
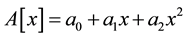 (1.b)
(1.b)
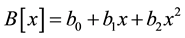 (1.c)
(1.c)
The data in Figure 1(a) and Figure 1(b) are extracted from the deep inelastic neutrino-proton and neutrino-neutron collisions. The solid lines are the prediction of the parametric Equation (1.a). The difference in the values of the parameters (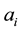 ,
,
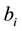 , i = 1, 2, 3) in the two cases which are shown in the Tables 1-3 is due to the difference in the internal structure of the proton (uud) and the neutron (ddu). The two figures show that Equation (1) give fair description to the family of data representing
, i = 1, 2, 3) in the two cases which are shown in the Tables 1-3 is due to the difference in the internal structure of the proton (uud) and the neutron (ddu). The two figures show that Equation (1) give fair description to the family of data representing
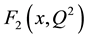 for all values of x and all range of Q2. The figures show also that
for all values of x and all range of Q2. The figures show also that
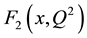 scales with Q2 and increases rapidly toward the DIS (x®0).
scales with Q2 and increases rapidly toward the DIS (x®0).
2.2. Muon-Nucleon Interaction
We used the data of the experiment CERN-NA-2 [15] [16] for finding the parametric forms of structure function F2(x, Q2) for muon-proton and muon-neutron interactions using the previous technique.
2.3. Comparison between Structure Function Deduced by Neutrino and Muon
From Figure 1(a), Figure 1(b) and Figure 2(a), Figure 2(b), we can obtain the general features of the structure


Figure 1. (a) The structure function F2(x, Q2) of the proton and neutron as a function of Q2 at fixed values of x which is extracted from the data of deep inelastic neutrino scattering; (b) The structure function F2(x, Q2) of the proton and neutron as a function of Q2 at fixed values of x which is extracted from the data of deep inelastic muon scattering.
functions of the nucleon F2 in both cases of muon and neutrino interactions. In each value of x, F2 fluctuates about a certain value showing scaling behavior with Q2. F2 increases with x that fits the deep inelastic behavior of the reaction.
Figure 3(a) and Figure 3(b) show the behavior of function F2 in both cases of neutrino and muon with the proton as a target, at two scales Q2 = 2 (Gev/c)2 and Q2 = 40 (Gev/c)2 as a function of x.
Apart from the small changes, F2 is approximately independent of Q2 and independent of any length scale. Such scaling proves that the nucleon is composed of point-like constituents.
The difference between the distributions of neutrino and muon at very DIS (small values of x) is large. As x increases, both come close. i.e. at large x the features of both weak and electromagnetic interaction disappear. In addition, as Q2 increases, the structure function of neutrino increases quickly at very low x, while the structure function of muon increases very slowly with energy.
3. Prediction of the Quark Functions
3.1. Quark Distributions Deduced by a Neutrino as a Probe
In this section, we will apply an empirical method to determine the quark functions for (u & d) and their anti-


Figure 2. (a) The structure function F2(x, Q2) of the proton and neutron as a function of Q2 at fixed values of x which is extracted from the data of deep inelastic muon scattering; (b) The structure function F2(x, Q2) of the proton and neutron as a function of Q2 at fixed values of x which is extracted from the data of deep inelastic muon scattering.
quarks in terms of the structure functions F2(x) and xF3(x) that were extracted from the neutrino deep inelastic scattering experiments. Assumption (SU (2) Isospin); neutron is just proton with u⇔d: Proton = uud; Neutron = ddu. Making the approximation that sets the Cabibbo angle to zero, we obtain the following correspondence relations;
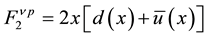 (2.a)
(2.a)
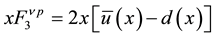 (2.b)
(2.b)
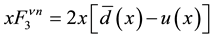 (2.c)
(2.c)
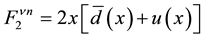 (2.d)
(2.d)
where



Figure 3. (a) The structure function F2 of the proton deduced by the muon (dashed line) and by the neutrino (solid line), at Q2 = 2 (Gev/c)2; (b) The structure function F2 of the proton deduced by the muon (dashed line) and by the neutrino (solid line), at Q2 = 40 (Gev/c)2.
Table 1. The structure functions F2 for proton and neutron expressed by the parameters in Equation (1.a) for ν-nucleon interaction.
interactions respectively. By solving last equations algebraically, we get for the quark and anti-quark functions as;

Table 2. The structure functions F3 for proton and neutron expressed by the parameters in Equation (1.a) for ν-nucleon interaction.
Table 3. The structure functions F2 for proton and neutron expressed by the parameters in Equation (1.a) for muon-nucleon interaction.



Figure 4, represents the quark and anti-quark distributions that were probed by neutrino. They are falling with the value of x and vanish at x→1. In addition, the quark, anti-quark distributions are close to each other in this case, neutrino as a probe. The general feature of the results seems comparable to those produced by NNPDF collaboration [5] , CTEQ4 collaboration [17] and MRS collaboration [18] at adjacent energy values.
3.2. Quark Distributions Deduced by a Muon as a Probe
We shall use the features of the structure functions F2(x) that extracted from the deep inelastic scattering experiments of muon-nucleon collision. Assumption (SU (2) Isospin): neutron is just proton with u⇔d: Proton = uud; Neutron = ddu. Making the approximation that sets the Cabibbo angle to zero, we obtain the correspondent euations;


where



Figure 4. The quark and anti-quark wave functions in the case of neutrino-nucleon scattering.

and for anti-quarks we can use the correspondence


which lead to the anti-quark functions as


Figure 5, represents the Equations (5.a), (5.b), (7.a) and (7.b) which show the quark and anti-quark distributions as found by muon-nucleon DIS.
3.3. Comparison between Quark Functions Deduced by Neutrino and Muon
First judge in Figure 4 and Figure 5, one notices that there is no substantial difference in the general behavior of the quark and anti-quark distributions in both cases of neutrino and muon as probes of the nucleon. They are falling with the value of x and vanish at x ≈ 1. In addition, the quark, anti-quark distributions are close to each other in the case of neutrino as a probe. The general feature of the results seems comparable to those produced by NNPDF collaboration [5] , CTEQ4 collaboration [17] and MRS collaboration [18] at adjacent energy values.
The quark and anti-quark wave functions deduced by neutrino and muon are displayed in Figure 6.
Figure 6, is the close scrutiny of the Figure 4 and Figure 5, it shows that the quark functions that deduced by the muon are slightly shifted up compared to that deduced by the neutrino. This may be due to the influence of the electro-magnetic and the weak fields acting in the two cases.
4. A Simple Model for Calculation of DIS
In this section, the goal is to use the quark functions, deduced by neutrino and muon, in Section 3, into a simple
Figure 5. The quark and anti-quark wave functions in the case of muon-nucleon scattering.
Figure 6. The quark wave functions deduced by neutrino (the black line) and muon (the blue line) as probes in deep inelastic scattering: (a) for up quark; (b) for down quark; (c) for antidown-quark; and (d) for antiup quark.
model for calculating the hadronic current and consequently the deep inelastic differential cross section in both cases. For this aim, we study the lepton current and quark current. In the leptonic current, we view a neutrino as weak particle and a muon as electromagnetic particle.
In this model we assume that the lepton interacts with nucleons via the intermediate vector boson (IVB) as shown in Figure 7.
It is assumed that the interactions go through electromagnetic field mediated by a virtual photon or weak field mediated by Z0 or W± bosons. Our strategy for studying these interactions is to use Feynman diagram of two vertices. The first is related to the field of the lepton and can be either electromagnetic interaction in the case of muon as probe, or weak interaction for the case of neutrino. The second vertex is a strong interaction which excites the nucleon that decays producing many hadrons in the final state.
In the presence of currents, the total interaction matrix element is
4.1. Leptonic Current
The leptonic current describes the transition of leptons from initial to final state during the scattering by the field and is defined as;

where



The 4-component matrix u describes neutrino or muon with spin 1/2 is;

Since the neutrino is massless and the muon has small mass relative to the incident energy, so we can neglect it. Considering the projectile is initially moving in the z-direction, then,

On the other hand, we used the perturbation technique to get the scattered wave function of the lepton as;
Figure 7. Feynman representation for lepton-nucleon interaction in DIS.


The sum runs over the possible orders of perturbation. And r is the distance from the scattering center,


4.1.1. Neutrino-Nucleon Interaction
Feynman representation of the neutrino-nucleon scattering is shown in Figure 8. The neutrino interacts with nucleons through the intermediate vector boson W± or Z0 with effective mass about 80 GeV.
In this case the scattering is due to weak field, then it is sufficient to consider only one term in the perturbation series (where gw is the weak coupling constant)

Then the first component of the leptonic current Jx corresponding to µ = 1 in Equation (8), is given by

The integrals in Equation (13) are regarded as the average of the current allowed in the available space inside the nucleon of radius R. This leads to an analytical form of the current Jx as

Similarly, for the y and z components, corresponding to µ = 2, 3 respectively, we get;


4.1.2. Muon-Nucleon Interaction
Feynman representation of the muon-nucleon scattering is shown in Figure 9. The muon interacts with nucleons through the photon propagator. The interaction may go through the exchange of one or multi photons. Consequently, we shall consider more than one term in the perturbation series.
(17)
where gEM is the electromagnetic coupling constant. Table 4 shows that the scattering probability falls off quickly with the increase number of photons. Hence, it will be reasonable to considerate two terms only in the perturbation series.
Figure 8. Feynman representation for neutrino-nucleon interaction in DIS.
Figure 9. Feynman representation for muon-nucleon interaction in DIS.
Table 4. The probability of exchange one or multi photons.
Then the first component of the leptonic current Jx corresponding to µ = 1 in Equation (8), is given by

The integrals in Equation (18) are regarded as the average of the current allowed in the available space inside the nucleon of radius R. this leads to an analytical form of the current Jx as

Similarly, Jy and Jz corresponding to µ = 2, 3 respectively, are found to be


4.1.3. Comparison the Leptonic Currents for Neutrino and Muon Interactions
The leptonic current density for the both cases is a complex function of the momentum transfer q. The imaginary part measures the absorption rate. The absolute values of the current components Jx and Jy are equal due to the azimuthal symmetry of the problem (Figure 10). The equations of the current components (14, 15, 16), in the case of neutrino, and (19, 20, 21), for the muon, show that the leptonic current density which is deduced by neu-
Figure 10. The absolute value of the leptonic current of the muon (red line) and neutrino × 1017 (black line) as seen in the azimuthal plane (Jx, Jy) (a) the normal component Jz (b) and (c) for the total leptonic current.
trino is proportional inversely with the square of the mass of the IVB as well as with q4, while in the case of muon the leptonic current density is proportional directly with the factor
4.2. Hadronic Current Calculation
The results of the quark and anti-quark functions are used in calculating the quark currents as,

Figure 11 shows that the total quark current decreases rapidly with x. It has the same behavior in both of neutrino and muon interaction, but with lower magnitude in the case of using the neutrino as a probe.
4.3. Matrix Element and Differential Cross-Section
As mentioned above at the beginning of Section 4, the matrix element associated with the propagator of the field as well as with the leptonic current and hadronic (quark) current, then the matrix element

no interaction that is associated with the propagator


And, the matrix element (Mµ) for the muon interaction that is associated with the propagator

Figure 11. The total quark current in the neutrino and in the muon (line that shift up).

Figure 12 and Figure 13 show the differential cross section in both cases of neutrino-nucleon and muon- nucleon interactions respectively.
The differential cross section decreases with x. It has the same behavior for neutrino but with lower magnitude.
5. Concluding Remarks
In this analysis we studied the deep inelastic scattering using neutrino and muon as probes.
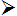 The structure function F2 of the neutrino and muon diverges at very DIS (small-x). As x increases, the two come close i.e. at large x the features of both weak and electromagnetic interaction disappear.
The structure function F2 of the neutrino and muon diverges at very DIS (small-x). As x increases, the two come close i.e. at large x the features of both weak and electromagnetic interaction disappear.
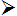 By increasing q2, although the structure function of neutrino increases quickly at very low x, however, the structure function of muon increases very slowly with energy.
By increasing q2, although the structure function of neutrino increases quickly at very low x, however, the structure function of muon increases very slowly with energy.
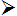 The leptonic current density which is deduced by neutrino is inversely proportional with square of the mass of the IVB as well as with q4, while in the case of muon the leptonic current density is proportional directly with the factor
The leptonic current density which is deduced by neutrino is inversely proportional with square of the mass of the IVB as well as with q4, while in the case of muon the leptonic current density is proportional directly with the factor
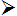
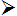
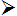
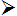

Z with a propagator of the form
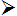
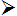 The scattered wave function of the incident lepton is calculated with perturbation technique.
The scattered wave function of the incident lepton is calculated with perturbation technique.
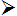 The quark functions are determined by empirical method and extracted from the nucleon structure functions. The hadronic current depends mainly on the Bjorken variable x, and slightly depends on q2.
The quark functions are determined by empirical method and extracted from the nucleon structure functions. The hadronic current depends mainly on the Bjorken variable x, and slightly depends on q2.
Figure 12. The differential cross section for neutrino-nucleon deep inelastic interaction.
Figure 13. The differential cross section for muon-nucleon deep inelastic interaction.
References
- Abazov, V., Abbott, B., Abdesselam, A., Abolins, M., Abramov, V., Acharya, B. and Affolder, T. (2004) Combination of CDF and D0 Results on the W Boson Mass and Width. Physical Review D, 70, Article ID: 092008. http://dx.doi.org/10.1103/PhysRevD.70.092008
- Duan, C.-G., Song, L.-H., Wang, S.-H. and Li, G.-L. (2005) Nuclear Parton Distribution Functions and Energy-Loss Effect in the Drell-Yan Reaction off Nuclei. The European Physical Journal C-Particles and Fields, 39, 179-184. http://dx.doi.org/10.1140/epjc/s2004-02074-1
- Hirai, M., Kumano, S. and Miyama, M. (2001) Determination of Nuclear Parton Distributions. Physical Review D, 64, Article ID: 034003. http://dx.doi.org/10.1103/PhysRevD.64.034003
- Martin, A.D., Roberts, R., Stirling, W. and Thorne, R. (2000) Parton Distributions and the LHC: W and Z Production. The European Physical Journal C-Particles and Fields, 14, 133-145. http://dx.doi.org/10.1007/s100520000324
- Ball, R.D., Bertone, V., Carrazza, S., Deans, C.S., Del Debbio, L., Forte, S. and Rojo, J. (2013) Parton Distributions with LHC Data. Nuclear Physics B, 867, 244-289. http://dx.doi.org/10.1016/j.nuclphysb.2012.10.003
- Allen, P., Grässler, H., Lanske, D., Schulte, R., Böckmann, K., Geich-Gimbel, C. and Saarikko, H. (1981) Determination of the Quark Density Ratio d(x) u (x) in the Proton. Physics Letters B, 103, 71-74. http://dx.doi.org/10.1016/0370-2693(81)90196-9
- Mirjalili, A., Dehghani, M. and Yazdanpanah, M.M. (2013) Parton Densities with the Quark Linear Potential in the Statistical Approach. International Journal of Modern Physics A, 28. http://dx.doi.org/10.1142/s0217751x13500899
- Arkhipov, A. (2014) Quark-Quark Forces in Quantum Chromodynamics. arXiv Preprint arXiv:1410.0271.
- Modarres, M. and Mohamadnejad, A. (2013) The Thermodynamic Properties of Weakly Interacting Quark-Gluon Plasma via the One-Gluon Exchange Interaction. Physics of Particles and Nuclei Letters, 10, 99-104. http://dx.doi.org/10.1134/S1547477113020106
- James, E. (2007) Precision Electroweak Physics at the Tevatron. arXiv preprint hep-ex/0701003.
- Diaconu, C. (2006) Electroweak Measurements. International Journal of Modern Physics A, 21, 1604-1616. http://dx.doi.org/10.1142/S0217751X06032617
- Kopeliovich, B.Z., Morfín, J.G. and Schmidt, I. (2013) Nuclear Shadowing in Electro-Weak Interactions. Progress in Particle and Nuclear Physics, 68, 314-372. http://dx.doi.org/10.1016/j.ppnp.2012.09.004
- Baur, U., Keller, S. and Wackeroth, D. (1998) Electroweak Radiative Corrections to W Boson Production in Hadronic Collisions. Physical Review D, 59, Article ID: 013002. http://dx.doi.org/10.1103/PhysRevD.59.013002
- Allasia, D., Angelini, C., Baldini, A., Bertanza, L., Bigi, A., Bisi, V. and Calimani, E. (1985) Q2 Dependence of the Proton and Neutron Structure Functions from Neutrino and Antineutrino Scattering in Deuterium. Zeitschrift für Physik C Particles and Fields, 28, 321-333. http://dx.doi.org/10.1007/BF01413595
- Benvenuti, A.C., Bollini, D., Bruni, G., Navarria, F., Argento, A., Lohmann, W. and Baranov, S. (1990) A High Statistics Measurement of the Deuteron Structure Functions F2 (x, Q2) and R from Deep Inelastic Muon Scattering at High Q2. Physics Letters B, 237, 592-598. http://dx.doi.org/10.1016/0370-2693(90)91231-Y
- Aubert, J.-J., Bassompierre, G., Becks, K., Best, C., Böhm, E., de Bouard, X. and Carr, J. (1985) A Detailed Study of the Proton Structure Functions in Deep Inelastic Muon-Proton Scattering. Nuclear Physics B, 259, 189-265. http://dx.doi.org/10.1016/0550-3213(85)90635-2
- Martin, A.D., Stirling, W. and Roberts, R.G. (1993) Parton Distributions Updated. Physics Letters B, 306, 145-150. http://dx.doi.org/10.1016/0370-2693(93)91152-D
- Pumplin, J., Stump, D.R., Huston, J., Lai, H.-L., Nadolsky, P. and Tung, W.-K. (2002) New Generation of Parton Distributions with Uncertainties from Global QCD Analysis. Journal of High Energy Physics, 7, 12. http://dx.doi.org/10.1088/1126-6708/2002/07/012















