Theoretical Economics Letters
Vol.07 No.03(2017), Article ID:75459,15 pages
10.4236/tel.2017.73038
Measuring the Technical Efficiency for the Shipping Banks
―An Approach Using Data Envelopment Analysis
Marina Maniati, Evangelos Sambracos
Department of Economics, University of Piraeus, Piraeus, Greece

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 1, 2017; Accepted: April 15, 2017; Published: April 18, 2017
ABSTRACT
The international transportation industry involves various sectors, shipping being one with particular characteristics which differentiates it from others especially as relevant capital risk is concerned. Within this scope, shipping banks are required to assess a number of factors in order to limit the risk from loans, considering the investment capital required. The efficiency of shipping banks is particularly important as it may affect the borrowing level and consequently the financial situation and investment activity in shipping market. This paper examines the Technical Efficiency (TE) of 71 banks operating world- wide in the maritime sector from 2005 to 2010, which is the period that the shipping industry reached its peak and one of its lowest point, making extremely difficult to secure debt finance in shipping, by using Data Envelopment Analysis (DEA) and presents the factors which may affect their technical efficiency, through the application of Regression Analysis. Based on the paper results, most banks during the study period are technically inefficient, whereas TE is proved to be higher under the assumption of variable returns to scale (VRS DEA model) when comparing to constant returns (CRS DEA model). Statistically significant variables are total deposits and total assets for both TE- CRS and TE-VRS and ROE (Return On Equity) for TE-VRS, providing significant information regarding factors on which management should further focus, in order to maintain and reinforce technical efficiency with respect to their strategy for financing shipping sector.
Keywords:
Technical Efficiency, Shipping Banks, DEA, Shipping Finance, Profitability

1. Introduction
Shipping sector bears special characteristics that render it considerably different from all other international transport industries, forming a particularly dynamic environment with equally high risks of investment capital losses. In this context, the commercial banks, as the primary source of financing a market characterized by high capital and operating costs, play a leading role. At the same time, they are required to evaluate a broad range of different factors in order to limit the relevant risk and finally reach an efficient risk-yield balance. This becomes even more important when seen in the context of the latest international developments following the implementation of the Rules of Basel ΙΙΙ in combination with the capital lost due to one of the most prolonged downturns in the shipping market.
Considering the aforementioned, the level of ship finance available remains low while the banks seek ways to shrink their balance sheets, as a result of both regulatory and commercial restraints. Thus, the shipping banks, i.e. commercial banks that provide loans to shipping sector, have become more selective and tighter with the relevant lending volumes and terms, whereas leverage has become shorter with respect to efficiency. Efficiency of commercial banks involved in the shipping industry is crucial for their sustainability, which in turn depends on funding and effective management of operating costs. Thus, bank efficiency plays a significant role in the shipping industry, affecting financial growth or causing systematic risks.
The purpose of this paper is to assess the technical efficiency of banks involved in the shipping industry and to test independent variables that affect shipping banks’ TE for the time period from 2005 to 2010, which is the period that the shipping industry reached its peak and one of its lowest point, making extremely difficult to secure debt finance in shipping. Data Envelopment Analysis is used in order to extract efficiency scores for shipping banks worldwide. The model applied is based on the intermediate approach of banking operation with orientation in outputs (output oriented), while models are executed both with constant and variable returns to scale (CRS and VRS approaches) in order to detect any differences in banks’ TE in terms of technology. Furthermore, Regression Analysis is used, in order to test independent variables that affect shipping banks’ TE.For the purpose of this paper, technical efficiency measures the ability of a bank to produce optimal output from a given set of inputs.
This paper reveals for the first time the most important factors arising from shipping bank’s internal environment based on DEA and implicitly contributes to the development of a specific methodological tool for measuring technical efficiency with respect to bank ability to produce optimal output from a given set of inputs. Essentially, it might be considered as a decision support tool, taking into account certain bank specific factors from its internal operational environment, in order to define the level of its efficiency in the market as a whole.
The paper is structured as follows; Section 2 sets a literature review of DEA approaches for estimating bank efficiency. Section 3 presents the methodology applied, while Section 4 presents the empirical analysis and relevant results. Section 5 concludes the paper along with implications for further research.
2. Literature Review
Bank efficiency has been an important issue for analysts [1] [2] [3] , practitioners and policymakers being expressed as a function of bank-specific, i.e. operating expenses, management, asset quality, bank size and non-interest income and operating environment factors, i.e. interest rate, economic growth, regulatory requirements. In order to model bank efficiency properly, two basic approaches are usually used; the intermediation and the production approach. While in production approach a bank’s resources produce services to customers, under intermediation approach, banks are viewed as mediators between depositors and borrowers, accepting deposits from customers and transforming them into loans to clients [1] [4] . Moreover, estimating bank efficiency involves both parametric and non-parametric methods. The most frequently used non-parametric method is Data Envelopment Analysis (DEA), rooted in the work of Farell [5] and first introduced by Charnes et al. [6] , who applied mathematical programming in order to locate a frontier used to evaluate efficiency of Decision Making Units (DMUs. DEA is become substantially popular in estimating efficiency of the banking industry. In addition, Charnes et al. [6] suggest a constant returns to scale (CRS) approach while Banker et al. [7] a variable returns to scale (VRS) approach, which splits overall technical efficiency into two products, i.e. pure technical efficiency and scale efficiency.
Both approaches are used in previous literature, since some researchers estimate bank efficiency by CRS approach [8] [9] [10] while others use both CRS and VRS approach [11] [12] . Most DEA models regarding bank efficiency are input-oriented, mainly due to the general belief that bank managers are in control mostly of their inputs in relation to the outputs, although there are several studies using DEA models that are output-oriented [13] [14] or both output- and input-oriented [12] [15] . It should be noted, though, that input-oriented or output-oriented DEA models under CRS approach do not show different results in terms of technical efficiency [16] [17] .
DEA models for estimating bank efficiency have been widely used in previous years for several banking industries [4] [18] [19] [20] [21] [22] , based on different approaches and input-output variables. Siems [23] uses as input variables the number of employees, fixed assets, interest expenses, other non-interest expenses and the number of loans, and as output variables deposits and interest income. Miller & Noulas [24] , examining technical efficiency of US banks, use both CRS and VRS output-oriented DEA method, using as inputs total transactions deposits, total non-transactions deposits, total interest expense and total non-interest, and as outputs total interest income, total non-interest income and loans. Casu & Molyneux [12] use a VRS output-oriented approach of DEA, including as outputs total loans and other earning assets and as inputs total costs and total deposits. Ataulla & Le [14] apply a VRS DEA method both input- and output-oriented, consisting of interest expenses and operating expenses as inputs and loans, advances and investments as outputs. Roberta et al. [25] apply an input-oriented DEA method using staff costs, capital (operating expenses excluding staff costs), funds and interest expenses as input variables, and deposits, loans and investments as output variables. Tyrone et al. [26] use the number of employees, interest expenses, deposits and current amount of deposits as input variables, and loans, interest income, operating income and earnings as output ones. Suffian [27] applies an input-oriented VRS DEA approach, with deposits, wages, interest expenses and non-interest expenses as inputs, while Shiang-Tai Liu [28] uses a CRS output-oriented DEA method, including demand deposits short-term loans and medium-term loans as outputs. In addition, Akhtar et al. [29] applies an input-oriented CRS approach, with operating expense, advances and capital as inputs, whereas Varias and Sofianopoulou [30] applied an input oriented model to estimate technical efficiency of 19 biggest Greek commercial banks by using interest expenses/deposits, other overhead expenses/fixed assets and personnel expenses/total assets as inputs. Rahim et al. [31] examined the technical efficiency of Islamic banks by applying DEA method based in the intermediation approach, proving that the main source of technical efficiency was the scale of operation. Nandkumar and Singh [32] used DEA approach to estimate the technical efficiency of commercial banks in India over the years 2006-2010 by applying CCR DEA model, showing that major factors resulting in the poor performance of banks is their huge amount of deposits and operating expenses, as well as the excess number of employees.
Either CRS or VRS DEA methods for estimating bank efficiency aim to detect the most and least efficient banks, but questions often arise about the identification of those ways that improve technical efficiency. In this frame, it is essential to identify those factors that impact overall bank efficiency.
3. Methodology
DEA method is selected as the most suitable for the measurement of technical efficiency of a group of banks, as can process models with many inputs and outputs in different measures, enables comparisons, allows the use of input and output vectors and requires lesser degrees of freedom. Application of DEA in the banking sector refers to the estimation of the relative efficiency of each bank in a current sample in comparison with the relative efficiency of the rest of the banks comprising the total sample [33] . This is achieved by maximizing the ratio of the weighted sum of outputs to the weighted sum of inputs for each DMU (bank) as follows [6] :
(1)
where h0 = the relative efficiency of bank o, o = the bank assessed by banks of the sample, j = the number of banks of the sample, r = the number of outputs, i = the number of inputs, = the amount of output r of bank j ( ), = the amount of input i of bank j ( ), and , = the coefficients of input i and output r, respectively, which maximize the objective function of the bank examined each time.
This linear fractional programming model described above is easily converted in a linear programming model as follows [7] :
(2)
In conclusion, the model is applied once for each bank in the sample looking for the combination of inputs and outputs (ur, vi) that gives the higher degree of the bank’s efficiency (h0), without leading to a input-output ratio greater than 1 (100%) when applied to other banks in the sample. For each bank, the relative efficiency is estimated as follows:
1) h0 = 1, indicating that the bank is relatively efficient, or
2) h0 < 1, indicating that the bank is relatively inefficient.
DEA can be applied assuming either constant returns to scale (CRS) or variable returns to scale (VRS). Consequently, most researchers after having applied DEA methods to estimate technical efficiency, they estimate its determinants, assessing in the same time the degree and the nature (positive or negative) of their impacts on technical efficiency through multiple regression [34] [35] . Formally,
(3)
where, TE = Technical Efficiency, = are the independent variables affecting TE, = their coefficients and = error term. This model is estimated either by Time Series Ordinary Least Squares―OLS or by Panel Data Models. The regression model applied for estimating the factors affecting shipping banks’ efficiency is as follows:
(4)
where te = the technical efficiency of bank, ROA = Return On Assets, ROE = Return On Equity, LLP_TL = Total Loan Loss Provision/Total Loans, LNTTDEP = the natural logarithm of Total Deposits, LNS_TA = Total Loans/Total Assets, and LNTA = the natural logarithm of Total Assets.
4. Empirical Approach and Data
The sample of present analysis consists of seventy-one (71) banks worldwide involved in shipping finance for the time period of 2005-2010, which is the period that the shipping industry reached its peak and one of its lowest point, making extremely difficult to secure debt finance in shipping. All banks (Table 1) are numbered consequently ( ) and 60.5% of selected banks are
Table 1. List of banks.
located in Europe and mostly Germany, 36.61% in Asia and 2.8% in USA. All data were derived from Bloomberg professional data base and Bank scope data base provided by Bureau van Dijk.
Shipping banks’ TE is estimated by the non-parametric DEA method, both in terms of CRS and VRS, in order to test if results are verified by different production and technology circumstances, taking into account the fact that CRS models usually refer to long-term period while VRS models to short-term (Siriopoulos & Tziogkidis, 2009). Additionally, DEA method is consistent with the intermediary approach, according to Berger & Humphrey (1997) belief that this approach is best suited for the estimation of efficiency in the banking sector, since it includes interest expenses which usually are of to of total bank expenses. Moreover, both CRS and VRS DEA methods applied are output-oriented. Regarding input and output variables, total expenses excluding staff cost, staff cost and deposits are used as inputs, while net shipping loans are used as the only output, since it best reflects banks’ profitability. In the subsequent stage of this analysis, A regression model is used in order to test for potential variables that affect technical efficiency.
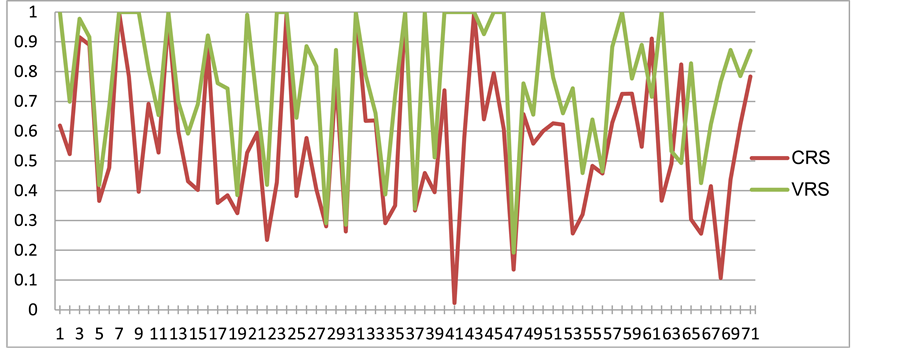
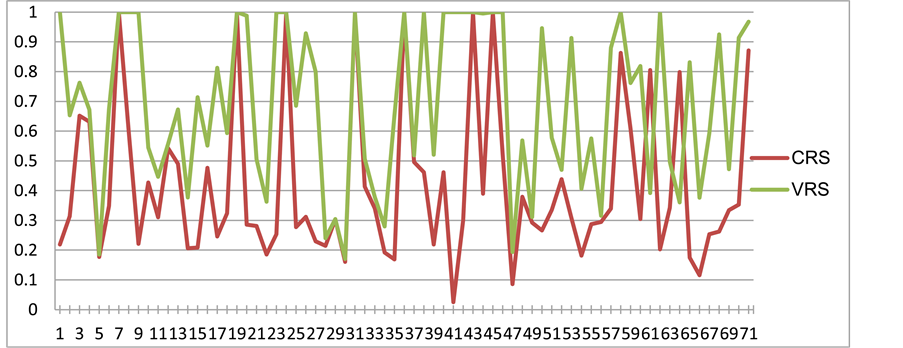
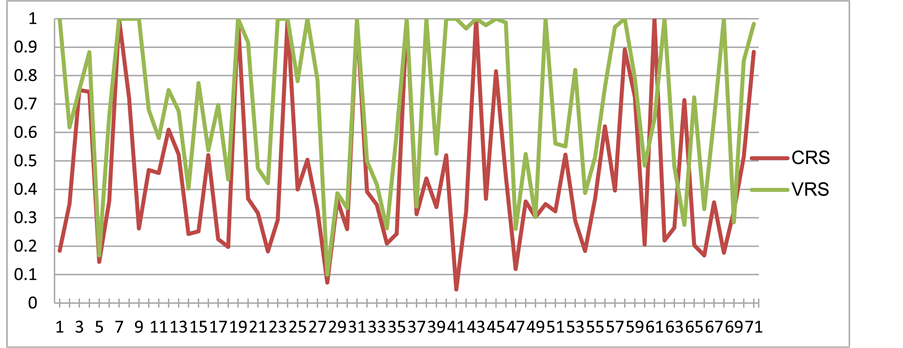
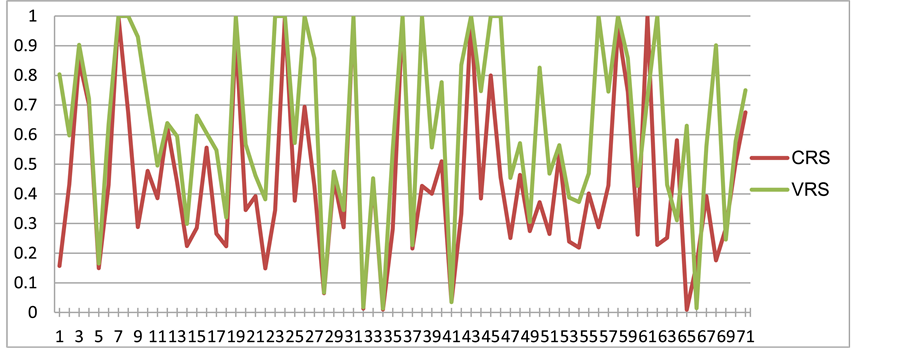
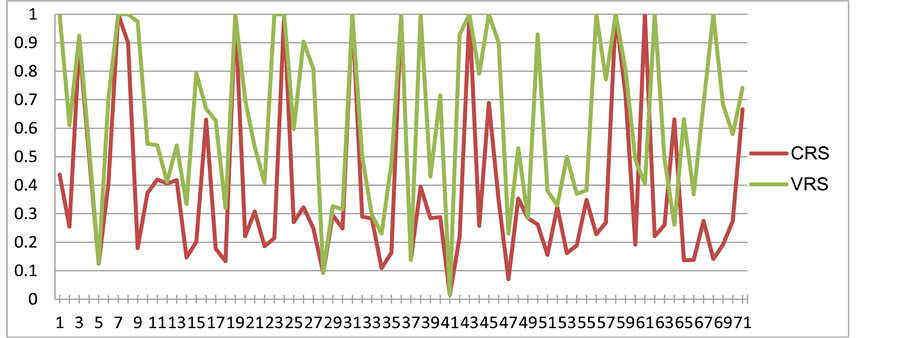
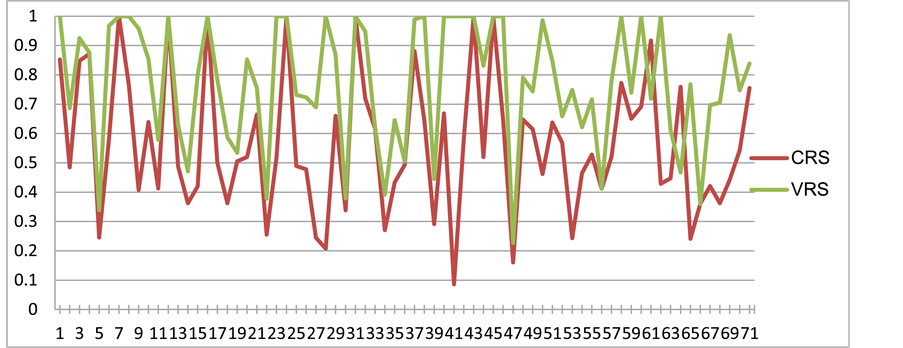
In Figures 1-6, TE of all 71 shipping banks is presented using both CRS and
Figure 1. TE of all 71 banks (CRS-VRS comparison, 2005).
Figure 2. TE of all 71 banks (CRS-VRS comparison, 2006).
Figure 3. TE of all 71 banks (CRS-VRS comparison, 2007).
Figure 4. TE of all 71 banks (CRS-VRS comparison, 2008).
Figure 5. TE of all 71 banks (CRS-VRS comparison, 2009).
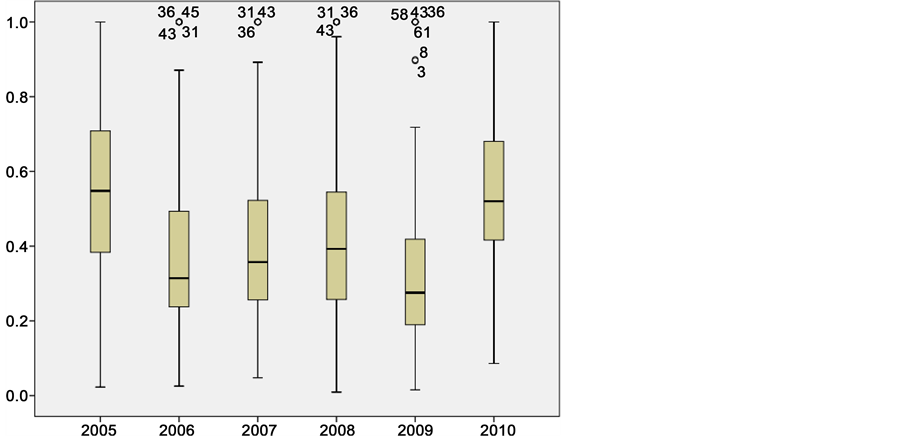
VRS DEA methods, respectively. Firstly, it is proved that TE assessed under VRS hypothesis seems to be more effective in relation to CRS assumption. This is also evidenced through the box plots (Figure 7 & Figure 8), where the mean of TE determined by VRS is higher compared to TE determined by CRS. Additionally TE of shipping banks is observed to show a significantly high degree of variabil-
Figure 6. TE of all 71 banks (CRS-VRS comparison, 2010).
Figure 7. CRS-TE box plots (2006-2010).
Figure 8. VRS-TE box plots (2006-2010).
ity, especially in the case of CRS. Summarized results of TE under the CRS and VRS approaches are presented in Table 2, including the number and percentage of banks having TE for all years. The vast majority of banks are technical inefficient over the years, although the VRS approach gives a higher number of technical efficient banks when compared to CRS approach, denoting probably that VRS approach is influenced by the bank size.
By presenting the descriptive statistics of the data (Table 3) to summarize the central tendency and spread characteristics of banks, it is observed that the mean of ROA(Return on Assets)is equal to 0.816 suggesting that net income of banks is on average slightly lower than the total assets and demonstrating high ability in investment activities of banks. The aforementioned is confirmed by the highmean value of ROE (Return on Equity, 8.341), showing high profitability for the banks by comparing their net income to their average shareholders’ equity. At the same time, the mean of LLP_TL (Loan Loss Provision to Total Loans) shows the very low ratio of total loan loss provision compared to total loans, while the means of the variables LNTTDEP (Natural Logarithm Total Deposits), LNS_TA (Loans to Total Assets) and LNTA (Natural Logarithm Total Assets) are relatively high and equal to 16.895/50.518 and 17.957 respectively.
Table 4 presents the summary results the best model results under CRS and VRS approaches, where statistically significant variables are total deposits and total assets for both TE-CRS and TE-VRS and ROE) for TE-VRS.
The regression models applied or estimating the factors affecting shipping banks’ efficiency based on CRS and VRS approach are respectively as follows:
Table 2. Summarized results of TE banks under CRS and VRS approach.
Table 3. Descriptive statistics for independent variables used in regression models.
Table 4. Best model summarized results under CRS and VRS approach.
(5)
and
(6)
LNTTLDEP (Total Deposits) is positively correlated to TE under CRS and VRS approaches, meaning that more efficient banks have higher market shares. Specifically, a 1% increase in Total Deposits drives to 0.018% and 0.052% increase of technical efficiency score under CRS and VRS approach respectively. Total Assets (LN_TA) is also positively correlated with TE under both CRS and VRS approaches with the technical efficiency score to increase by 0.005% and 0.002% respectively, when Total Assets increase by 1% and vice versa, as confirmed by Hauner [36] , who suggests that the bank size has a positive impact on its efficiency. Larger banks are expected to pay less for their inputs and simultaneously they may face increased returns to scale which increases the relevant efficiency. ROE is negatively correlated with TE only under VRS approach, with an increase in ROE affecting negatively but slightly the technical efficiency scores. TE is not affected by LNS_TA (Total Loans/Total Assets), ROA and LLP/TL (Total Loans Provision/Total Loans), ROA seems to be positively correlated with TE, whereas LLP/TL seems to be negatively correlated with TE, as shown by previous research [37] [38] [39] , where banks facing difficulties in collecting loans are usually driven to bankruptcy [40] [41] [42] .
5. Conclusions
According to results, banks during the study period are technically inefficient, suggesting that market factors may influence the operation of shipping banks. Additionally, TE is proved to be higher under the assumption of variable returns to scale (VRS DEA model) when comparing to constant returns (CRS DEA model). Results obtained by the application of CRS and VRS models, respectively, seem to differ significantly, mainly due to the choices and combinations of inputs and outputs and because of the substantially high levels of TE detected in banks under review. Regarding the factors that affect TE under both CRS and VRS approach, ROA, statistically significant variables are total deposits and total assets for both te-CRS, te-VRS and ROE (Return On Equity) for te-VRS. Total Assets and Total Deposits are positively correlated with TE, denoting that pro- fitability and market power, reflected on the bank’s size, are favorable for obtaining higher levels of TE in the banking sector. In contrast and as expected, ROE is negatively correlated with TE.
Overall, the results of this research indicate banks involved in shipping fi- nance are not technical efficient over the time period examined. Additionally, regression models applied provided useful information to be considered by management regarding factors that affect TE. However, the research focused on shipping market as a whole, whereas the study period was specific. It would be of interest regarding future research to apply the proposed methodology in order to examine if the certain sub sector to be financed, i.e. dry bulk, tankers, container shipping, or the country of origin, the period to be examined, or even ownership structure of shipping banks affect their TE. It would be also interesting to define the internal factors of the operational environment of banks in combination with the external factors associated with shipping market that may affect the amount of loans for the shipping industry based on previous years’ experience. In general, the existence of non-technical efficiency in shipping banks raises questions about their decision to continue financing such a risky and heterogeneous market, despite the regulations set by the Basel Convention.
Acknowledgements
The publication of this paper has been partly supported by the University of Piraeus Research Center.
Cite this paper
Maniati, M. and Sambracos, E. (2017) Measuring the Technical Efficiency for the Shipping Banks. Theo- retical Economics Letters, 7, 502-516. https://doi.org/10.4236/tel.2017.73038
References
- 1. Berger, A.N. and Humphrey, D.B. (1992) Measurement and Efficiency Issues in Commercial Banking. In: Griliches, Z., Ed., Output Measurement in the Service Sectors, National Bureau of Economic Research, Studies in Income and Wealth, Vol. 56, University of Chicago Press, Chicago, 24-79.
- 2. Bergendahl, G. (1998) DEA and Benchmarks—An Application to Nordic Banks. Annals of Operations Research, 82, 233-249. https://doi.org/10.1023/A:1018910719517
- 3. Meryem, F.D. and Pasiouras, F. (2010) Assessing Bank Efficiency and Performance with Operational Research and Artificial Intelligence Techniques: A Survey. European Journal of Operational Research, 204, 189-198.
- 4. Berg, S.A., Forsund, F.R., Hjalmarsson, L. and Suominen, M. (1993) Banking Efficiency in the Nordic Countries. Journal of Banking and Finance, 17, 371-388.
- 5. Farell, M.J. (1957) The Measurement of Productive Efficiency. Journal of the Royal Statistical Society, 120, 253-281. https://doi.org/10.2307/2343100
- 6. Charnes, A., Cooper, W.W. and Rhodes, E. (1978) Measuring the Efficiency of Decision Making Units. European Journal of Operational Research, 2, 312-329.
- 7. Banker, R.D., Charnes, A. and Cooper, W.W. (1984) Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Management Science, 30, 1078-1092. https://doi.org/10.1287/mnsc.30.9.1078
- 8. Noulas, A.G. (1997) Productivity Growth in the Hellenic Banking Industry: State versus Private Banks. Applied Financial Economics, 7, 223-228. https://doi.org/10.1080/096031097333574
- 9. Avkiran, N.K. (1999) The Evidence on Efficiency Gains: The Role of Mergers and the Benefits to the Public. Journal of Banking and Finance, 23, 991-1013.
- 10. Soteriou, A.C. and Zenios, S.A. (1999) Using Data Envelopment Analysis for Costing Bank Products. European Journal of Operational Research, 114, 234-244.
- 11. Canhoto, A. and Dermine, J. (2003) A Note on Banking Efficiency in Portugal, New vs. Old Banks. Journal of Banking and Finance, 27, 2087-2098.
- 12. Casu, B. and Molyneux, P. (2003) A Comparative Study of Efficiency in European Banking. Applied Economics, 35, 1865-1876. https://doi.org/10.1080/0003684032000158109
- 13. Ataullah, A. and Le, H. (2004) Financial Repression and Liability of Foreignness in Developing Countries. Applied Economics Letters, 11, 545-549. https://doi.org/10.1080/1350485042000263034
- 14. Ataullah, A. and Le, H. (2006) Economic Reforms and Bank Efficiency in Developing Countries: The Case of the Indian Banking Industry. Applied Financial Economics, 16, 653-663. https://doi.org/10.1080/09603100500407440
- 15. Beccalli, E., Casu, B. and Girardone, C. (2006) Efficiency and Stock Performance in European Banking. Journal of Business Finance and Accounting, 33, 245-262. https://doi.org/10.1111/j.1468-5957.2006.01362.x
- 16. Coelli, T.J., Prasada-Rao, D.S., O’Donnell, C.J. and Battese, G.E. (2005) An Introduction to Efficiency and Productivity Analysis. 2nd Edition, Springer, Berlin. http://facweb.knowlton.ohio-state.edu/pviton/courses/crp394/coelli_Intro_effic.pdf
- 17. Coelli, T.J. and Perelman, S. (1996) Efficiency Measurement, Multi-Output Technologies and Distance Functions: With Application to European Railways. CreppWp 96/05. Centre de Recherche en Economie Publique Et Economie de la Population, Université de Liège, Liège.http://orbi.ulg.be/bitstream/2268/35665/1/105.%20CREPP%209605%20Coelli-Perelman.pdf
- 18. Sherman, H.D. and Gold, F. (1985) Bank Branch Operating Efficiency. Evaluation with Data Envelopment Analysis. Journal of Banking and Finance, 9, 297-315.
- 19. Ferrier, G.D. and Lovell, C.A.K. (1990) Measuring Cost Efficiency in Banking: Econometric and Linear Programming Evidence. Journal of Econometrics, 46, 229-245.
- 20. Aly, H.Y., Grabowski, R., Pasurka, C. and Rangan, N. (1990) Technical, Scale, and Allocative Efficiencies in U.S. Banking: An Empirical Investigation. Review of Economics and Statistics, 72, 211-218. https://doi.org/10.2307/2109710
- 21. Elayasiani, E. and Mehdian, S.M. (1990) A Nonparametric Approach to Measurement of Efficiency and Technological Change: The Case of Large U.S. Commercial Banks. Journal of Financial Services Research, 4, 157-168. https://doi.org/10.1007/BF00352569
- 22. Brockett, P.L., Charnes, A., Cooper, W.W., Huang, Z.M. and Sun, D.B. (1997) Data Transformations in DEA Cone-Ratio Envelopment Approaches for Monitoring Bank Performances. European Journal of Operational Research, 98, 251-269.
- 23. Siems, T.F. (1991) An Envelopment-Analysis Approach to Measuring Management Quality and Predicting Failure of Banks. PhD Dissertation, Southern Methodist University, Dallas.http://www.worldcat.org/title/envelopment-analysis-approach-to-measuring-management-quality-and-predicting-failure-of-banks/oclc/24006166
- 24. Miller, S.M. and Noulas, A.G. (1996) The Technical Efficiency of Large Bank Production. Journal of Banking & Finance, 20, 495-509.
- 25. Roberta, B., Staub, G., da Silva, G., Souza, B.M. and Tabak, L. (2009) Evolution of Bank Efficiency in Brazil: A DEA Approach. European Journal of Operational Research, 32, 56-71.
- 26. Tyrone, T.L., Chia-Chi, L. and Tsui-Fen, C. (2009) Application of DEA in Analyzing a Bank’s Operating Performance. Research in International Business and Finance, 36, 8883-8891.
- 27. Sufian, F. (2009) Determinants of Bank Efficiency during Unstable Macroeconomic Environment: Empirical Evidence from Malaysia. Research in International Business and Finance, 23, 54-77.
- 28. Shiang-Tai, L. (2010) Measuring and Categorizing Technical Efficiency and Productivity Change of Commercial Banks in Taiwan. Expert Systems with Applications, 37, 2783-2789.
- 29. Akhtar, M.F., Ali, K. and Sadaqat, S. (2011) Performance Efficiency of Commercial Banks of Pakistan: Nonparametric Technique Data Envelopment Analysis (DEA). Asian Journal of Business and Management Sciences, 1, 150-156.
- 30. Varias, A.D. and Sofianopoulou, S. (2012) Efficiency Evaluation of Greek Commercial Banks Using DEA. Journal of Applied Operational Research, 4, 183-193.
- 31. Rahim, A., Rahman, A. and Rosman, R. (2013) Efficiency of Islamic Banks: A Comparative Analysis of MENA and Asian Countries. Journal of Economic Cooperation and Development, 34, 63-92.
- 32. Nandkumar and Singh, A. (2014) A Study of Technical Efficiency of Banks in India Using Dea. IOSR Journal of Business and Management, 16, 37-43. https://doi.org/10.9790/487X-16913743
- 33. Ray, C.S. (2004) Data Envelopment Analysis Theory and Techniques for Economics and Operations Research. Cambridge University Press, New York.http://content.schweitzer-online.de/static/catalog_manager/live/media_files/representation/zd_std_orig__zd_schw_orig/002/204/843/9780521802567_content_pdf_1.pdf https://doi.org/10.1017/CBO9780511606731
- 34. Siriopoulos, C. and Tziogkidis, P. (2009) How Do Greek Banking Institutions React after Significant Events? A DEA Approach. European Journal of Operational Research, 23, 17-25.
- 35. Berger, A.N. and Humphrey, D.B. (1997) Efficiency of Financial Institutions: International Survey and Directions for Future Research. European Journal of Operational Research, 98, 175-212.
- 36. Hauner, D. (2005) Explaining Efficiency Differences among Large German and Austrian Banks. Applied Economics, 37, 969-980.
- 37. Kwan, S.H. and Eisenbeis, R. (1995) An Analysis of Inefficiencies in Banking. Journal of Banking & Finance, 19, 733-734.
- 38. Resti, A. (1997) Evaluating the Cost Efficiency of the Italian Banking System: What Can Be Learned from the Joint Application of Parametric and Non-Parametric Techniques. Journal of Banking & Finance, 21, 221-250.
- 39. Barr, R.S., Killgo, K.A., Siems, T.F. and Zimmel, S.A. (2002) Evaluating the Productive Efficiency and Performance of U.S. Commercial Banks. Managerial Finance, 28, 3-25.
- 40. Dermiguc-Kunt, A. (1989) Deposit Institutions Failure: A Review of the Empirical Literature. Economic Review, Federal Reserve Bank of Cleveland, 25, 2-18.
- 41. Whalen, G. (1991) A Proportional Hazards Model of Bank Failure: An Examination of Its Usefulness as an Early Warning Tool. Economic Review, Federal Reserve Bank of Cleveland, 27, 21-31.
- 42. Barr, R. and Siems, T. (1994) Predicting Bank Failure Using DEA to Quantify Management Quality. Working Paper, Federal Reserve Bank of Dallas, Dallas, 1-31.