Journal of Mathematical Finance
Vol.08 No.01(2018), Article ID:82782,13 pages
10.4236/jmf.2018.81016

Measuring Black Swans in Financial Markets

J. T. Manhire

School of Innovation, Texas A&M University, College Station, Texas, USA

Copyright © 2018 by author and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

Received: November 27, 2017; Accepted: February 25, 2018; Published: February 28, 2018

ABSTRACT

There exists a well-developed statistical theory predicting extreme price values for financial markets known as extreme value theory (EVT). This approach relies on the seemingly obvious, but rarely analyzed, assumption that price displacement extremes actually exist for various markets. This paper attempts to describe the behavior of financial markets as a set of functions in terms of the dynamic variables price and time based on the net difference between ask and bid volumes over a unit period, thereby offering evidence to support the assumption that price extremes exist. Yet, it’s not meaningful to show merely that extremes exist. If the extreme negative price displacement simply represents a complete market collapse then the assumption becomes trivial. Accordingly, the paper also introduces a method to determine whether price displacements are constrained by non-trivial extremes. This description might have implications for EVT and market risk management in approximating the magnitude of “Black Swan” events. The paper also shows that if one can closely approximate the magnitude of such a rare event, one cannot also predict when the event will occur with any meaningful degree of certainty.

Keywords:

Extreme Value Theory, Stock Valuation, Risk Management, Black Swans, Uncertainty

1. Introduction

A “Black Swan” refers to a highly improbable event that lies significantly outside of normal expectations.1 For financial markets, such events typically manifest themselves as extreme price variations.

There exists a well-developed theory predicting these extreme price variations called Extreme Value Theory (EVT) [1] [2] [3] [4] [5] . Different EVT approaches use statistical methods in an attempt to determine the probability of Black Swan-type events occurring [6] [7] . EVT relies on the seemingly obvious, but rarely analyzed, assumption that price displacement extremes actually exist for various markets. This paper attempts to describe the behavior of financial markets as a set of functions in terms of the dynamic variables price and time based on the net difference between ask and bid volumes over a unit period, thereby offering evidence to support the EVT assumption that price extremes exist.

Yet, merely demonstrating that extreme values exist is not enough. In the context of financial markets, the extreme measure that investors and market risk managers care about most is usually a negative price displacement. If the extreme negative price displacement―measured as a percent decrease in prices over a defined period―is simply unity (i.e., a complete market collapse to zero) then the assumption that price displacement extremes exist becomes trivial. This paper introduces a heuristic method to determine whether negative price displacements over a defined period are constrained by extremes that are non-trivial.

There are two reasons to focus on price reductions instead of price increases. The first is the reason just mentioned; it is the focus of most market risk managers. The second is that price increases are theoretically infinite while price decreases are limited to the displacement between the current price and zero. Although we use an extreme price increase variable as part of our mathematical formalism, this paper is careful to only claim a method for approximating price reductions.

Further, this method is only potentially useful for markets that are robust and actively traded, and where the mean value of the price displacement ratio is close to zero. This last requirement implies a form of mean reversion, which remains controversial in the literature [8] [9] [10] [11] .

Lastly, this heuristic is based on an uniformitarian-like assumption that, to some extent, historical data can be used to predict extreme price displacements. There is significant disagreement in the literature over whether this postulate holds [12] [13] [14] [15] . Consequently, this underlying assumption might be a significant limitation of the method.

Although EVT deals with extreme deviations from a probability distribution median, this paper does not use a statistical approach in arguing that extreme prices exist. The paper does employ some basic probability methods in §3, but these are transitional in arriving at a conclusion of non-triviality. Even though these are not the standard probability methods of EVT, the paper’s conclusions offer an approximation of the magnitude of a price displacement extreme, which is a consistent element in traditional EVT analysis [16] [17] [18] . In this way, the paper might make some substantive contribution to the EVT literature and market risk management [19] in addition to supporting the veracity of EVT’s underlying assumption [20] [21] [22] [23] .

The paper is divided into five sections. The first is this brief introduction. The second defines a financial market as a system dependent entirely upon the interactions of generalized buyers and sellers and then offers an inductive argument that suggests the existence of price extremes. The third section offers a way to calculate these price extremes to determine if they are non-trivial. The fourth provides predictive limitations of the heuristic as to the timing of extreme events in the form of an uncertainty principle and other limitations generally. The fifth section offers a brief summary.

2. Do Extreme Prices Exist?

We begin by defining the time and price variables of a financial market and then examine the different perspectives from which one can view these variables as coordinates. We will then derive a general equation of market dynamics based on these perspectives and show that the solution suggests the existence of negative price extremes.

Define a unit period as 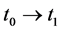with the quantity 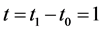unit of elapsed time. The asset of a financial market has a price configuration space.2

An asset also has a set of possible price displacement configurations as functions of elapsed time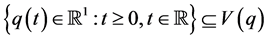. The dynamics of a financial market are time-dependent since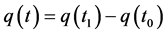. Thus, a market’s price displacement configuration space is a vector field defined by price coordinates 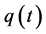that have the time derivatives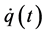, , 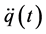etc.

Define as the price displacement ratio for the unit period t and 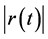as the modulus of the ratio, where 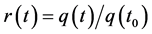Although the price displacement is properly defined as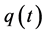, we’ll use “price displacement” and “price displacement ratio” synonymously throughout the remainder of this paper to refer to, and 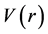for the price displacement ratio vector field.

Because we are primarily concerned with the net price displacement for a unit period, we can imagine a normalized price-time coordinate system K such that, , 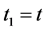and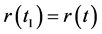. Let’s arbitrarily, but intuitively, designate an increase in price as positive (+) and a decrease in price as negative (−) in K. We’ll first consider an asset moving up or down the stationary one-dimensional vector field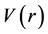. Let’s call this first frame of reference.

In an active market, traders with the desire to buy an asset place bid orders and traders wishing to sell place ask orders. Yet, desire is not enough to directly affect a change in the price of an asset. There must also exist an interaction with another trader to turn a bid or ask order into a transaction. We’ll call transactions associated with bids “bid volume.” This becomes the scalar quantity B representing the number of bid transactions for a unit period. “Ask volume” is similarly the scalar quantity A representing the number of ask transactions for a unit period.

Analysis of historical data from active markets suggests B has the potential to reduce prices while A has the potential to increase prices. The bid price is defined as the highest current price at which a trader is willing to buy. The ask price is defined as the lowest current price at which a trader is willing to sell. Therefore, as bid transactions transpire, the once highest bid price vanishes and the next highest (but lower than before) price becomes the highest current price. As ask transactions transpire, the once lowest ask price vanishes and the next lowest (but higher than before) price becomes the lowest current price. Thus, B is selling volume and A is buying volume [24] .

When a financial market experiences more buying volume than selling volume, there are more traders buying at the ask price. This “pushes” the asset up in price. When a market is experiencing more selling volume than buying volume, there are more traders selling at the bid price, which “pushes” the asset down in price. Thus, the effect of bid volume on price displacement in is the product of B and since we arbitrarily defined price reductions as negative. Likewise, the effect of ask volume is the product of A and.

From this we see that the net effect of all bid volume for a unit period changes the state of the asset along the stationary price dimension in the negative direction from to. This negatively-directed result is proportional to the effect of bid volume on the price displacement attributable to it, or. Similarly, we see that the net effect of all ask volume for a unit period changes the state of the asset along the price dimension in the positive direction from to, or that.

Historical data analysis indicates that not all markets given identical ask and bid volumes have the same ask and bid volume effects with respect to positive and negative price displacement ratios. As a result, we can assume that each market additionally has some specific inertial property―let’s call it n―that constrains the asset in its positive or negative movement away from in K for a specific unit of time. Essentially, n is some number specific to a particular market that is inversely proportionate to the price displacement. The lower the number, the more likely the asset is to move farther from, and vice versa. Therefore, n is minimized when the modulus is maximized, and n is maximized in the limit as. As a result, we can express the price effects of bid and ask volumes as ratios specific to each market. We’ll call these specific ask volumes and specific bid volumes, respectively, expressed as

Of course, this description is incomplete. Ask and bid volumes do not exist in isolation. In an active market, there is always a superposition of specific ask and specific bid volumes over any unit period where the asset is pushed in the positive direction when the ask volume dominates and pushed in the negative direction when the bid volume dominates. This specific net volume gives us

The net effect of the specific net volume―which we’ll call―is then equal to the result experienced by the asset and the direction is determined by whether the ask or bid volume dominates for a unit period:

(1)

Again, this is the equation for an asset moving through the stationary dimension of price resulting from the net effect of the specific ask and specific bid volumes for a unit period. It is, in fact, market mechanics as described from the perspective of the vector field.

Now let’s look at this behavior from a second frame of reference,. This new perspective is identical to in all respects except one: Instead of the price dimension being stationary and the asset moving along it, in the asset is fixed and moves up and down relative to the stationary asset. This becomes price displacement as described from the perspective of the asset. The specific ask and bid volumes remain the cause of any change in just as in. The only difference between and is what we consider to be stationary and what we consider to be changing. Each produces indistinguishable data regarding price displacement magnitudes.

After imagining this behavior from the perspective, we can conclude that to get the same effect as observed in this new frame of reference must experience oppositely-directed changes in. Therefore, every price displacement of the asset resulting from the net effect of ask and bid volumes in is the same as a change in the price dimension in. This means

(2)

where the prime denotes a price derivative just as the dot denotes a time derivative. Combining Equations (1) and (2) gives us the dynamics of a market in terms of both changes in time and price:

But what does comprise? Recall that in K, which we’ll now express as simply for concision. A review of historical data from active, robustly-traded markets reveals that the mean price displacement for a unit period tends to be relatively close to zero in K, the specific frame of reference notwithstanding. Therefore, we can approximate the price displacement vector field with the following Maclaurin series:

(3)

(N.B.: For markets where the mean price displacement for a unit period is not relatively close to zero in K, this assumption cannot hold.)

The first two terms in Equation (3) give us no new information about. Thus, the first meaningful term in this series is. Because changes in the price derivative of the vector field are uniform for all price displacement values, we see that is some mean constant of the vector field for that particular unit period. Let’s call this mean constant h. Therefore, from Equation (3) we get

(4)

Yet, as we just discussed, the only meaningful mean constant for any given unit period is the net (ask and bid) volume for that period since we know from Equations (1) and (2) that

where H is the specific net volume. Therefore,.

From Equation (4), we see that. Consequently, the price displacement dynamics for any unit period in K, from both perspectives, can be expressed as the harmonic approximation

(5)

This is consistent with Equation (2).

The general solution to this harmonic approximation is well known:3

(6)

Here, z is a complex number, is its complex conjugate, i is the imaginary unit, and

(7)

is the phase or principal argument of z. The change in the phase for each unit period is the radial frequency, and the square of this time derivative is H.3 Thus, for a unit period,. If is constant, it is clear that one can determine from.

In solving Equation (5) as an initial value problem, we see that . Here we interpret C as the starting point of in K at, or, which is consistent with Equation (7). This means is constant in K so one can determine from. Therefore, we see from Equation (6) that the price displacement ratio is a function of the net ask and bid volumes over a unit period. This is consistent with our initial assumption that any price change is a direct result of the total ask and bid transactions over a unit period. There are no other factors directly affecting.

Additionally, is the complex modulus in Equation (6). We can regard this also as a radius vector on the complex plane. For simplicity, we’ll denote as R. Thus, Equation (6) becomes. The cosine function, by definition, has the property. Multiplying through by the radius vector R gives us. Consequently, the complex modulus (radius vector) is equivalent to the extreme price displacement ratio magnitude. We can conclude, therefore, that for a given unit period there exists a negative extreme price displacement ratio of.

Of course, this does not necessarily mean that a market has or ever will reach −R, only that the negative extreme theoretically exists for any unit period t. In this way, −R is very similar to a “Black Swan” event from a market risk management perspective [25] . We will return to this predictive limitation in §4.

3. Are Extreme Prices Non-Trivial?

Now that we’ve provided evidence that negative price extremes exist, the next step is to decide under what conditions these extremes approach triviality, if any. Define triviality as an extreme price displacement ratio. In other words, even if price extremes exist, they become trivial if all we can say about them is that a market will hit a zero-price floor for some unit period. The conclusion that a market losing all value can be defined as an extreme price movement is self-evident and, therefore, trivial. Hence, the only price displacement extremes that are meaningful to any risk analysis are those that are greater than −1 and, therefore, non-trivial. As previously discussed, the price displacement ratio can exceed unity in the positive direction, but never in the negative direction.

Here we introduce the Lagrangian function, which is a function of the price displacement ratio coordinates, their time derivatives, and time. It contains the same information about the dynamics of a market in K as contained by Equation (5).4 From the time integral of the Lagrangian of Equation (5) we get the following action functional [26] of an asset:

(8)

We see that and since for any unit period. This means that besides the price displacement, the remainder of the action functional can be regarded as essentially a constant due to the inverse square relationship between n and r. As a result, for any given market, where is a probability function.

For the probability that either the positive or negative square root of the action functional is on the interval between the extreme values of the square root of the action functional, we can write

where is the complementary Gauss error function, defined as. Recall that n is a minimum at this extreme.

Because R is an extreme value, this probability must approach certainty since by definition all measures for the positive or negative square root of the action functional must fall between the positive or negative square root of the action functionals containing the positive or negative extreme price displacement

values. Of course, this means that.

We can define the phase as having values on the interval between, where is a maximum radial measure in the complex plane that is consistent with both the generally-accepted range of the principal value of [27] and the fact that cosine is an even function in Equation (6). As with the probability of the square roots of the action functional, we see that, which implies. Therefore,

(9)

This is only an approximation, but we assume the approximation close enough to express the relationship as an equality for practical purposes.

Another way to think about this is to return to the complex plane from §2. If the real price displacement ratio is the median of and, then there are always two complex numbers and two phases for each real price

displacement ratio on K. For example, at of any unit period in

complex vector space, but there is also a phase in the complex conjugate (dual)

vector space where. Similarly, there is a number z in complex space

for every real price displacement ratio as well as a number in the complex conjugate space [28] . Therefore, the probability of any is equivalent to the probability of z and the probability of, i.e.,. It is also equivalent to the probability of and the probability of, i.e.,.

If we take the inverse complementary error function of both sides of Equation (9) we get, which we can express as

(10)

if we define the constant.

Equation (10) still requires knowledge of n for each market to find the value of R. Since n is not a number regularly measured, we should try to approximate R without relying on a known minimized value of n. If we look at the relationship between the absolute value of a specific price displacement ratio (i.e.,) and the probability that other values of in the same market are greater than, we find

(11)

where is the expectation value of. From this observation of historical data, we assume the following:

1) The measure of centrality (expectation value) of is the arithmetic mean of the absolute value of all observed price displacement ratios for some order of;

2) The measure of centrality of the probability that any is greater than a specific is the geometric mean of all possible probabilities; i.e., all real numbers on the interval; and

3) These measures of centrality coincide.

From these three assumptions, we can define as the specific price displacement that maps to the probability of any being greater than the specific absolute price displacement that is equal to the inverse of the base of the natural logarithm, or

since the geometric mean of all real numbers on the interval is. This is a special case of Equation (11) when.

We can next substitute R for in Equation (11) to get

(12)

From this and Equation (9), we see that

(13)

If we define the constant, this equation becomes

(14)

Thus, we find that the magnitude of a market’s extreme price displacement ratio is linearly dependent on the expectation value of its absolute price displacement ratio.

Because both and are constants relating to the radial measure of the phase, we can combine them into a single constant. From Equations (10) and (14), we can then discover each market’s unique minimum inertial constraint at its price extreme with the expression since is calculable from historical data.

4. Uncertainty and Predictive Limitations

The method outlined here is not without limitations. Although §3 allows us to closely approximate, this does not mean that one can predict both the extreme price displacement ratio of a market and the precise time at which the market will experience this extreme. In fact, because we can predict the price with relative precision, it becomes practically impossible to predict the time of the displacement.

It is well known that the time and frequency domains are Fourier transform pairs [29] . It is also well known that the product of the variances of Fourier transform pairs produces a minimum scalar [30] .

Let x be a function in Hilbert space such that, , and, where is the Fourier transform of. Define the expectation values (means) of t and as

Define the uncertainty (standard deviations) of t and as

From these definitions, Weyl [31] has proved that

(15)

generally, and that when x and are normally distributed. Here, the symbol denotes the uncertainty in a variable, not the change in that variable. The uncertainty in is really just the uncertainty in the square root of the difference between specific ask and bid volumes since. Thus, we have

.

From Equation (6), we see that if we know the measure of and can calculate R then we can deduce. This allows us to closely approximate when. Rearranging Equation (6) yields

(16)

This means. Therefore, if then.

Because knowing the price displacement ratio with arbitrary precision means that we know the time derivative of the phase with the same precision, the more certain we are about the value of the less certain we are about when will occur [32] . Thus, if we know with relative certainty that, thereby yielding, we see from Equation (15) that equation that. This means a market can experience its negative extreme price displacement ratio in any unit period. If Equation (14) allows us to approximate with a high degree of certainty then we cannot know with any meaningful degree of certainty in which unit period will occur. Likewise, if we want to know the price displacement ratio for a specific unit period, thereby making, we see that, meaning can take any value.

Another significant limitation of this method is that it relies heavily on the sample with which one chooses to calculate since, per Equation (14), the accuracy of one’s approximation of depends wholly on this sample. Therefore, this method cannot claim to approximate fixed extreme price displacement measures since some degree of selection bias in a choice of sample for is unavoidable [33] , the discussion around Equations (11) and (12) notwithstanding. While it is possible to approximate an extreme price displacement given sufficient historical data, any such approximation is only valid up to the time of the analysis itself and the sample period chosen to calculate. The extreme measure may, in fact, vary over time for each market and should not be considered an absolute extreme for all time. The inertial coefficient n, therefore, remains in flux for each market.

Still, this method might improve our understanding of the rules that undergird market mechanics and, therefore, serve as an additional tool for managing market risk when faced with price displacements that deviate significantly from historic expectations. For example, based on historical data prior to the market close of October 16, 1987, Equation (14) would have predicted that Coca-Cola Company stock (KO) would have had a daily price displacement ratio extreme of for trading day. During the next trading day, October 19, 1987, KO reached an intraday low ratio of −0.2846, but closed at. The prediction of would have been an assurance for KO’s risk managers (and a potential buying opportunity for traders) at. More recently, there were similar assurances/opportunities for Automated Data Processing, Inc. (ADP) on May 6, 2010, and Bitcoin (BTC/USD) on August 1, 2014, among many others.

5. Summary

By regarding market mechanics in terms of time and price from two separate perspectives, we have presented theoretical evidence that financial markets have extreme price displacements. These extremes appear non-trivial except in the limits as or as. Historical data analysis can illumine whether such non-triviality is common in active markets. While the magnitude of Black Swan events appears calculable to a first approximation, the uncertainty principle outlined herein makes knowing exactly when Black Swans will occur a practical impossibility.

Acknowledgements

I wish to express my gratitude to Christopher L. Culp, Nuno Garoupa, Joseph R. Hanley, James McGrath, Ann M. Manhire, Andrew P. Morriss, Lisa A. Rich, and Saurabh Vishnubhakat for their valuable suggestions. All errors are mine alone and I promise to do better next time.

Cite this paper

Manhire, J.T. (2018) Measuring Black Swans in Financial Markets. Journal of Mathematical Finance, 8, 227-239. https://doi.org/10.4236/jmf.2018.81016

References

  1. 1. Fisher, R.A. and Tippett, L.H.C. (1928) Limiting Forms of the Frequency Distribution of the Largest and Smallest Member of a Sample. Proceedings of the Cambridge Philosophical Society, 24, 180-190. https://doi.org/10.1017/S0305004100015681

  2. 2. Gumbel, E.J. (1935) Les valeurs extrêmes des distributions statistiques. Annales de l’Institut Henri Poincaré, 5, 115-158.

  3. 3. Gnedenko, B.V. (1943) Sur la distribution limite du terme maximum d’une serie aleatoire. Annals of Mathematics, 44, 423-453. https://doi.org/10.2307/1968974

  4. 4. Broussard, J.P. and Booth, G.G. (1998) The Behavior of Extreme Values in Germany’s Stock Index Futures: An Application to Intradaily Margin Setting. European Journal of Operational Research, 104, 393-402. https://doi.org/10.1016/S0377-2217(97)00014-3

  5. 5. Davis, R. and Resnick, S. (1984) Tail Estimates Motivated by Extreme Value Theory. Annals of Statistics, 12, 1467-1487. https://doi.org/10.1214/aos/1176346804

  6. 6. Marohn, F. (1998) Testing the Gumbel Hypothesis via the Pot-Method. Extremes, 1, 191-213. https://doi.org/10.1023/A:1009910806693

  7. 7. Tiku, M.L. and Singh, M. (1981) Testing the Two Parameter Weibull Distribution. Communication in Statistics—Theory and Methods, 10, 907-918. https://doi.org/10.1080/03610928108828082

  8. 8. Poterba, J.M. and Summers, L.H. (1988) Mean Reversion in Stock Prices: Evidence and Implications. Journal of Financial Economics, 22, 27-59. https://doi.org/10.1016/0304-405X(88)90021-9

  9. 9. Kim, M.J., Nelson, C.R. and Startz, R. (1991) Mean Reversion in Stock Prices? A Reappraisal of the Empirical Evidence. Review of Economic Studies, 58, 515-528. https://doi.org/10.2307/2298009

  10. 10. Balvers, R., Wu, Y. and Gilliland, E. (2000) Mean Reversion across National Stock Markets and Parametric Contrarian Investment Strategies. Journal of Finance, 55, 745-772. https://doi.org/10.1111/0022-1082.00225

  11. 11. Akarim, Y.D. and Sevim, S. (2013) The Impact of Mean Reversion Model on Portfolio Investment Strategies: Empirical Evidence from Emerging Markets. Economic Modelling, 31, 453-459. https://doi.org/10.1016/j.econmod.2012.11.028

  12. 12. Caldararo, N. (2009) Primitive and Modern Economics: Derivatives, Liquidity, Value, Panic and Crises: A Uniformitarian View. Forum for Social Economics, 38, 31-51. https://doi.org/10.1007/s12143-008-9029-2

  13. 13. Kohara, K., Ishikawa, T., Fukuhara, Y. and Nakamura, Y. (1997) Stock Price Prediction Using Prior Knowledge and Neural Networks. Intelligent Systems in Accounting Finance & Management, 6, 11-22.

  14. 14. Jeon, S., Hong, B. and Chang, V. (2018) Pattern Graph Tracking-Based Stock Price Prediction Using Big Data. Future Generation Computer Systems, 80, 171-187. https://doi.org/10.1016/j.future.2017.02.010

  15. 15. Nair, B.B., Saravana Kumar, P.K., Sakthivel, N.R. and Vipin, U. (2017) Clustering Stock Price Time Series Data to Generate Stock Trading Recommendations: An Empirical Study. Expert Systems with Applications, 70, 20-36. https://doi.org/10.1016/j.eswa.2016.11.002

  16. 16. de Haan, L. (1976) Sample Extremes: An Elementary Introduction. Statistica Neerlandica, 30, 161-172. https://doi.org/10.1111/j.1467-9574.1976.tb00275.x

  17. 17. Weissman, I. (1978) Estimation of Parameters and Large Quantiles Based on the k Largest Observations. Journal of the American Statistical Association, 73, 812-815.

  18. 18. Naveau, P., Guillou, A., Cooley, D. and Diebolt, J. (2009) Modelling Pairwise Dependence of Maxima in Space. Biometrika, 96, 1-17. https://doi.org/10.1093/biomet/asp001

  19. 19. Culp, C.L. (2012) The “At-Risk” Metrics and Measures. In: Lane, M., Ed., Alternative (Re)Insurance Strategies, 2nd Edition, Risk Books, London, 359.

  20. 20. Embrechts, P., Resnick, S.I. and Samorodnitsky, G. (1999) Extreme Value Theory as a Risk Management Tool. North American Actuarial Journal, 3, 30-41. https://doi.org/10.1080/10920277.1999.10595797

  21. 21. Gilli, M. and Kellezi, E. (2006) An Application of Extreme Value Theory for Measuring Financial Risk. Computational Economics, 27, 207-228. https://doi.org/10.1007/s10614-006-9025-7

  22. 22. Singh, A.K., Allen, D.E. and Robert, P.J. (2013) Extreme Market Risk and Extreme Value Theory. Mathematics and Computers in Simulation, 94, 310-328. https://doi.org/10.1016/j.matcom.2012.05.010

  23. 23. Omari, C., Mwita, P. and Waititu, A. (2017) Using Conditional Extreme Value Theory to Estimate Value-at-Risk for Daily Currency Exchange Rates. Journal of Mathematical Finance, 7, 846-870. https://doi.org/10.4236/jmf.2017.74045

  24. 24. Bauwens, L. and Giot, P. (2001) Econometric Modelling of Stock Market Intraday Activity. Springer, Boston, 46-47.

  25. 25. Paté-Cornell, E. (2012) On “Black Swans” and “Perfect Storms”: Risk Analysis and Management When Statistics Are Not Enough. Risk Analysis, 32, 1823-1833. https://doi.org/10.1111/j.1539-6924.2011.01787.x

  26. 26. Hamilton, W.R. (1834) On a General Method in Dynamics. Philosophical Transactions of the Royal Society, Part II, 247-308.

  27. 27. Schmüdgen, K. (1990) Unbounded Operator Algebras and Representation Theory. Birkhäuser, Basel, 16.

  28. 28. Kasana, H.S. (2005) Complex Variables: Theory and Applications. 2nd Edition, Prentice Hall-India, New Delhi, 14.

  29. 29. Mann, S. and Haykin, S. (1995) The Chirplet Transform: Physical Considerations. IEEE Transactions on Signal Processing, 43, 2745-2761. https://doi.org/10.1109/78.482123

  30. 30. Kennard, E.H. (1927) Zur Quantenmechanik einfacher Bewegungstypen. Zeitschrift für Physik, 44, 326-352. (In German)

  31. 31. Weyl, H. (1928) Gruppentheorie und Quantenmechanik, Leipzig: Hirzel. Transl. by Robertson, H.P. (1931) The Theory of Groups and Quantum Mechanics. Dover.

  32. 32. Stein, E. and Shakarchi, R. (2003) Fourier Analysis: An Introduction. Princeton University Press, Princeton, 158.

  33. 33. Taylor, A.M. (2001) Potential Pitfalls for the Purchasing-Power-Parity Puzzle? Sampling and Specification Biases in Mean-Reversion Tests of the Law of One Price. Econometrica, 69, 473-498. https://doi.org/10.1111/1468-0262.00199

NOTES

1This phrase finds its roots in David Hume’s criticism of reasoning from experience alone, although Hume makes no mention of the water fowl. Hume, D. (1748) An Enquiry into Human Understanding. The black swan metaphor was specifically employed by John Stuart Mill almost one hundred years later and recently popularized in the financial context by Nassim Nicholas Taleb. Mill, J. S. (1843) A System of Logic, Ratiocinative and Inductive; Taleb, N. N. (2007) The Black Swan: The Impact of the Highly Improbable, Random House, New York.

2Actually, , but this then reduces back to, as we shall see at the end of §2. Therefore, it suffices for our purpose generally to define as having real and not complex coordinates, although aspects of this heuristic will rely heavily on complex attributes of the price displacement. The “asset,” as used here, can be thought of as an abstract point particle.

3Equation (5) asks us for a solution to the second-order linear ordinary differential equation. Assume the solution is proportional to where is a constant. This gives us For a finite,. This leaves the roots of the polynomial, which are and. This yields where and are arbitrary constants and is the initial condition of in. Because is the projection of both and on the real axis, we hold that. Given that we get Equation (6).

4The Lagrangian of a market actually precedes its equation of motion; i.e., we construct Equation (5) from the Lagrangian in Equation (8).

Journal Menu>>