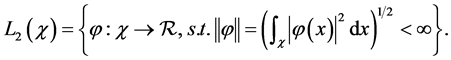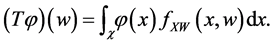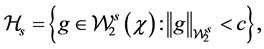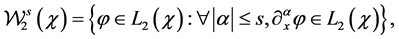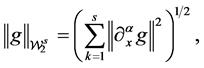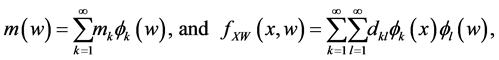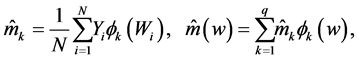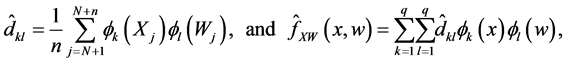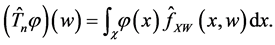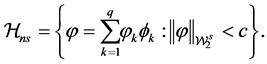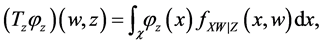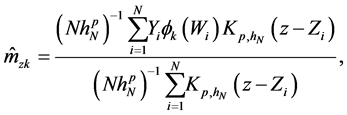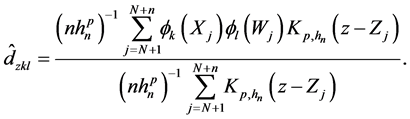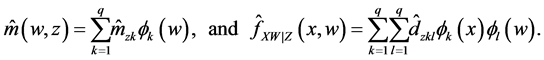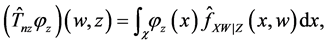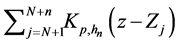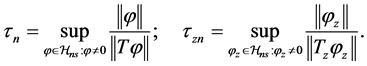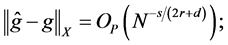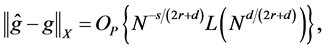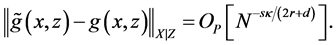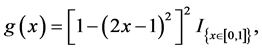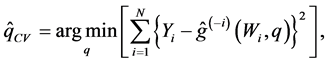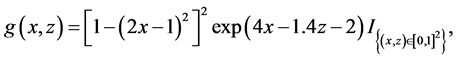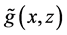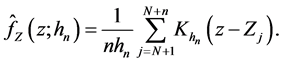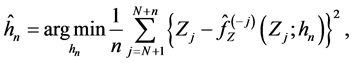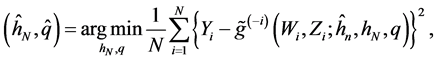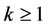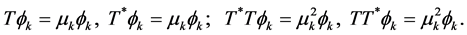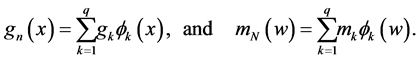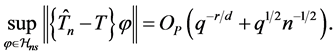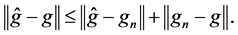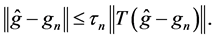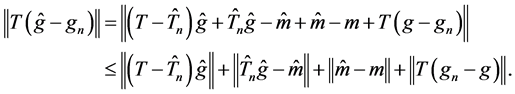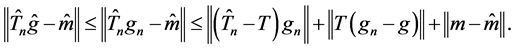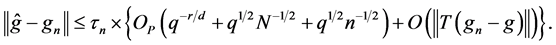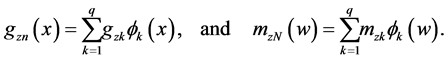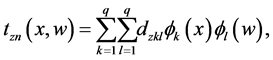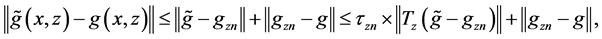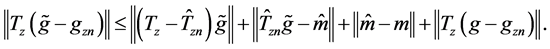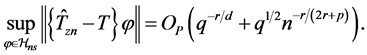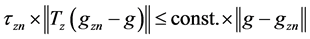Open Journal of Statistics
Vol.05 No.07(2015), Article ID:62410,12 pages
10.4236/ojs.2015.57080
Estimation of Nonparametric Multiple Regression Measurement Error Models with Validation Data
Zanhua Yin, Fang Liu
College of Mathematics and Computer Science, Gannan Normal University, Ganzhou, China

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 November 2015; accepted 27 December 2015; published 30 December 2015
ABSTRACT
In this article, we develop estimation approaches for nonparametric multiple regression measurement error models when both independent validation data on covariables and primary data on the response variable and surrogate covariables are available. An estimator which integrates Fourier series estimation and truncated series approximation methods is derived without any error model structure assumption between the true covariables and surrogate variables. Most importantly, our proposed methodology can be readily extended to the case that only some of covariates are measured with errors with the assistance of validation data. Under mild conditions, we derive the convergence rates of the proposed estimators. The finite-sample properties of the estimators are investigated through simulation studies.
Keywords:
Ill-Posed Inverse Problem, Linear Operator, Measurement Errors, Nonparametric Regression, Validation Data

1. Introduction
We can consider the following nonparametric regression model of a scaler response Y on an explanatory variable X
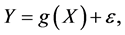 (1)
(1)
where 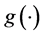 is assumed to be a smooth, continuous but unknown nonparametric regression function and
is assumed to be a smooth, continuous but unknown nonparametric regression function and 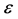 is a noise variable with
is a noise variable with 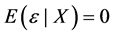 and
and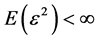 . It is not uncommon that the explanatory variable X is measured with error and instead only its surrogate variable W can be observed. In this case, one observes independent replicates
. It is not uncommon that the explanatory variable X is measured with error and instead only its surrogate variable W can be observed. In this case, one observes independent replicates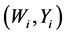 ,
, 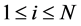 , of
, of 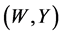 rather than
rather than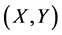 , where the relationship between
, where the relationship between 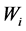 and
and 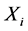 may or may not be specified. If not, the missing information for the statistical inference will be taken from a sample
may or may not be specified. If not, the missing information for the statistical inference will be taken from a sample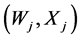 ,
, 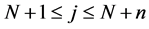 , of so-call validation data independent of the primary (surrogate) sample. The objective of this manuscript is to estimate the unknown function
, of so-call validation data independent of the primary (surrogate) sample. The objective of this manuscript is to estimate the unknown function 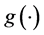 via the surrogate data
via the surrogate data
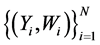 and the validation data
and the validation data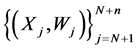
A wide number of problems of similar type have attracted considerable attention in research literature over the past two decades (see, [1] -[6] ). For instance, a quasi-likelihood method is intensively studied by [7] . A regression calibration approach is developed by [8] [9] and [10] [11] propose a method based on simulation- extrapolation (SIMEX) estimation. Other related methods include Bayesian approaches (see, [12] ), semi-parametric method (see, [13] [14] ), empirical likelihood method (see, [15] ) and the instrumental variable method (see, [16] ). Unfortunately, all these work mostly assume some parametric relationships between covariates and responses. Recently, nonparametric estimators of g have been developed by [17] and [18] . [17] develops a kernel-based approach for nonparametric regression function estimation with surrogate data and validation sampling. However, his method is not applicable for model (1) since it assumes that the response but not the covariable is measured with error. [18] proposes a nonparametric estimator which integrates local linear regression and Fourier transformation method when both explanatory and surrogate variable are scalars. Nonetheless, their method cannot be extended to multidimensional problems in which the explanatory variable vectors can consist of variables being measured with or/and without errors. For additional references and relevant topics for nonparametric regression models with measurement errors, ones may consult [19] and the references therein.
In practice, nonparametric estimation of g may not be an easy task since, as explained in Section 2, the relation that identifies g is a Fredholm equation of the first kind, i.e.
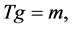
which may lead to an ill-posed inverse problem. Ill-posed inverse problem related to nonparametric regression model has received considerable attention recently. [20] [21] consider kernel-based estimators while [22] and [23] develop series or sieve estimators. However, their methods require an instrumental variable, and assume that the explanatory variable X is directly observable without errors. In this article, we propose a nonparametric estimation approach which consists of two major steps. First, we propose estimators of generalized Fourier coefficients of T and m based on surrogate and validation data. Second, we replace the infinite-dimensional operator T by the finite-dimensional approximation to avoid higher-order coefficient estimation, and hence it develops an estimator of g. Furthermore, we extend this method to the case that only some of covariates are measured with errors. Under mild conditions, the consistencies of the resulting estimators are established and the convergence rates are also derived.
This article is arranged as follows. In Section 2, we first describe our estimation approach for the case that the covariates are all measured with errors. Extension to the case that only some of covariates are measured with errors will be discussed as well. We derive the convergence rates of our estimators under some regularity conditions in Section 3. Section 4 presents some numerical results from simulation studies. A brief discussion will be given in Section 5. Proofs of the theorems are presented in Appendix.
2. Methodology
We first describe our estimation approach for the case that the covariates are all measured with errors. In addi-
tion to the independent and identically distributed (i.i.d.) primary observations 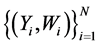
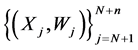
d-dimensional random vectors. Without loss of generality, let the supports of X and W both be contained in 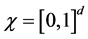
In the following we let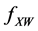
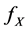
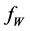
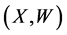
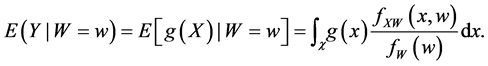
According to Equation (3), g is actually the solution to an integral equation called Fredholm equation of the first kind. Let 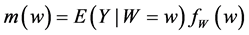
Define the operator 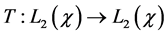
Hence, Equation (3) is equivalent to the operator equation
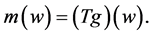
For the unknown smooth function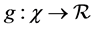
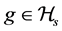
where c is a positive and finite constant. 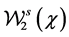
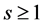
where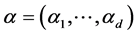
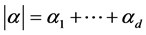
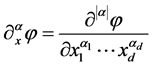
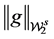
here 
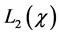
An estimator of g can then be obtained by replacing T and m by their series estimators based on surrogate data and validation data, and solving the resultant empirical version of (4). As before, let 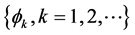
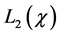
where 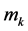
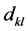
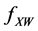
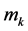
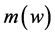
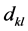
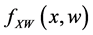
respectively, where the integer q is a truncation point which is the main smoothing parameter in the approximating Fourier series. The operator T can then be consistently estimated by
Define the subset of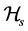
The estimator of 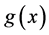
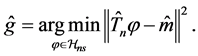
Remark 1. Let 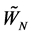
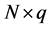
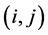
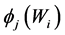
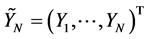
observed vector of Y based on the surrogate data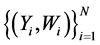
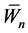
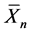
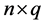
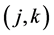
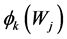
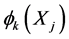
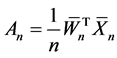

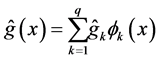
where 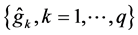
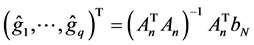
Next, we extend the estimator in (5) to nonparametric regression measurement error models with multi-covariates, that is
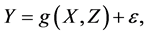
where X is measured with error and W being its observed surrogate variable, and Z is measured without error. Let 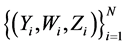
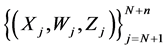
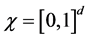
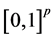
Let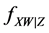
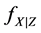
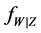
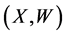
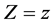
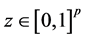
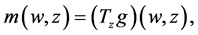
where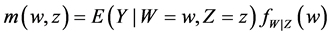
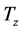
where 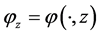
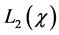
To obtain the estimator of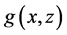
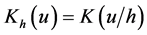
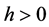
bandwidth. Let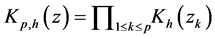
and
Then we have
Define the operator 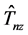
for any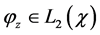
Then, for any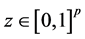
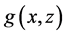
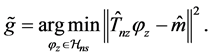
Remark 2. Denote 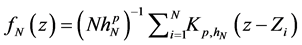
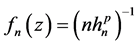
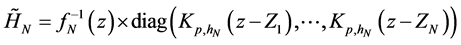
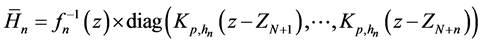
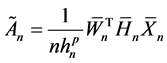
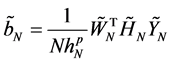
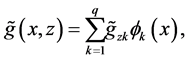
where 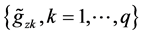
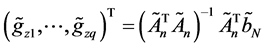
Remark 3. If Z is discretely distributed with finite support, then 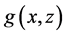
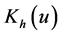
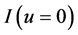
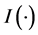
3. Theoretical Properties
In this section, we study the asymptotic properties of the estimators proposed in Section 2. We define 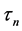
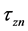
First, we investigate the large-sample properties of the estimator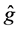
A1. (i) The support of 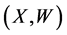
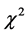
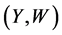
A2. For each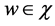
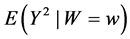
A3. (i) 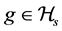
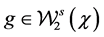
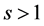
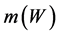
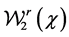
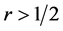
A4. The set of functions 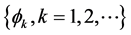
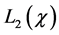
A5. (i) 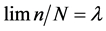
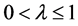
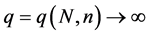
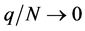
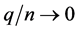
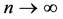
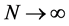
Theorem 1. Under conditions A1 - A5, as 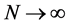
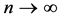
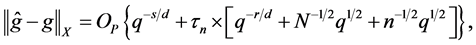
where 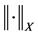
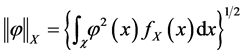
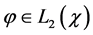
In (11), the term 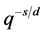
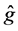
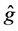
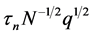
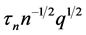
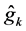
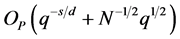
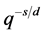
deviation part blows up from 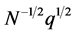
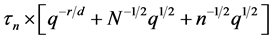
A more precise behaviour of the estimator can be obtained but depends on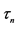
Corollary 1. Suppose the assumptions of Theorem 1 are satisfied.
(i) Let 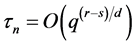
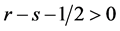
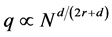
(ii) Let 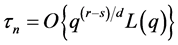
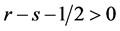
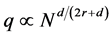
where the function 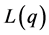
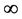
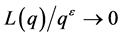
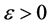
Remark 4. According to Corollary 1(i), the convergence rate becomes 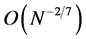
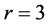
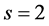
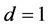
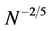
Next, we study the large-sample properties of the estimator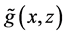
B1. (i) The support of 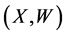
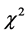
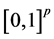
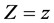
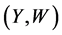
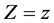
B2. For each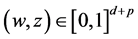
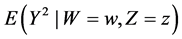
B3. (i) For each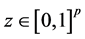
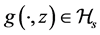
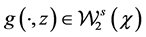
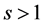
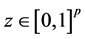
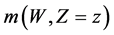
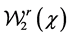
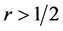
B4. (i) The set of functions 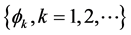
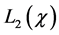
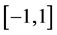
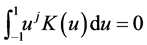
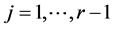
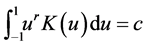
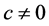
B5. (i) N, n, 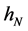
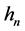
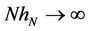
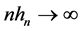
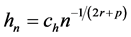
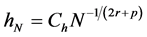
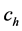
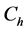
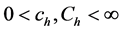
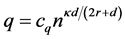
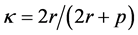
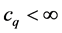
B6. (i) 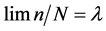
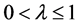
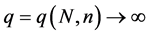
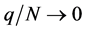
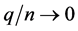
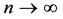
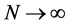
Theorem 2. Suppose assumptions B1 - B6 are satisfied. For each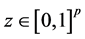
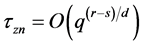
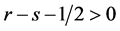
The proofs of all the theorems are reported in Appendix.
4. Numerical Properties
In this subsection, we conducted a simulation study of the finite-sample performance of the proposed estimators. First, we choose the cosine sequence with 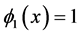
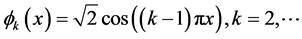
orthonormal basis for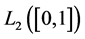
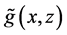
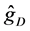
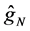
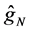
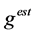
(MISE)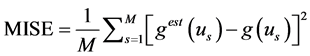
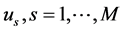
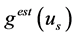
Example 1: We considered model (1) with the regression function being
and 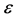
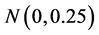
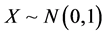
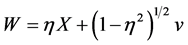
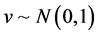
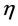
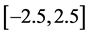
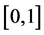
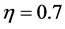
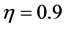
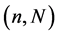
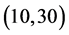
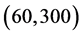
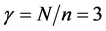
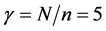
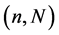
It is interesting to compare our estimator 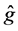
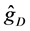
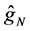
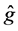
where the subscript 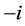
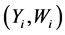
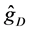
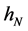
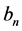
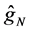
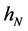
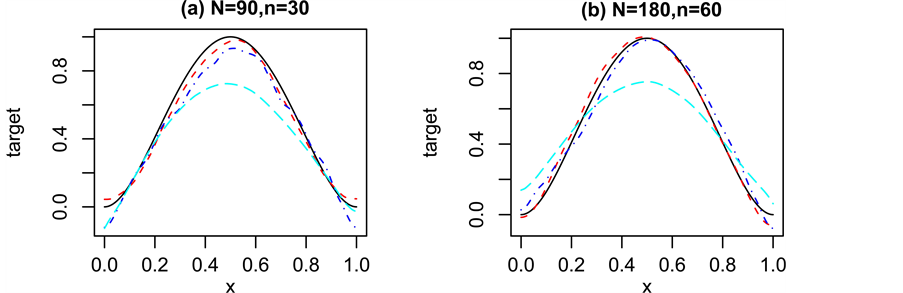
Figure 1 shows the regression function curve
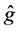
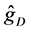
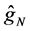
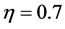
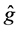
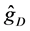
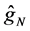
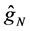
Table 1 compares, for various sample sizes, the results obtained for estimating curve 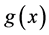
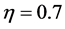
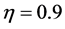
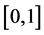
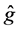
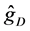
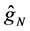
Figure 1. Curves for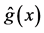
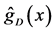
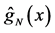
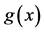
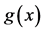
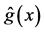
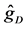
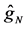
Table 1. The estimated MISE (
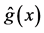
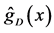
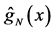
estimator generally performs better than the estimator proposed by [18] for the resultant MISEs of 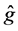
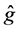
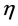
Example 2: We considered model (7) with the regression function being
and 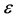
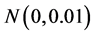
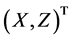
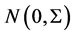
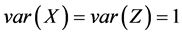
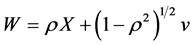
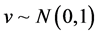
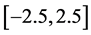
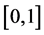
Results for 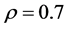
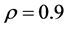
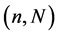
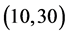
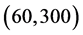
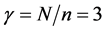
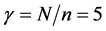
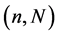
Here, we only compared our estimator 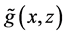
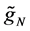
nel regression estimator based on the primary dataset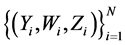
multivariate cases. Here, we used the Epanechnikov kernel function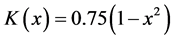
and used an product kernel 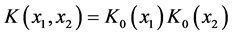
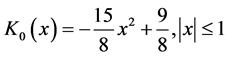
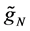
naive estimator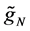
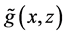
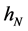
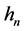
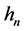
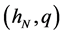
Define
Here, we adopt the cross-validation (CV) approach to estimate 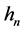
where the subscript 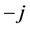
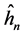
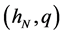
where the subscript 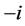
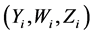
We compute MISE at 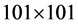
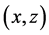
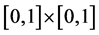
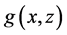
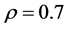
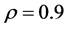
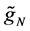
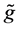
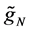
5. Discussion
In this paper, we propose a new method for estimating non-parametric regression measurement error models using surrogate data and validation sampling. The covariates are measured with errors while we do not assume any error model structure between the true covariates and the surrogate variable. Most importantly, our proposed method can be readily extended to the multi-covariates model, say, 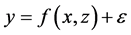
Table 2. The estimated MISE (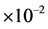
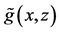
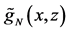
recting the bias arising from the errors-in-variables. It generally preforms better than the approach proposed by [18] .
Acknowledgements
This work was supported by NSFC11301245, NSFC11501126 and Natural Science Foundation of Jiangxi Province of China under grant number 20142BAB211018.
Cite this paper
ZanhuaYin,FangLiu, (2015) Estimation of Nonparametric Multiple Regression Measurement Error Models with Validation Data. Open Journal of Statistics,05,808-819. doi: 10.4236/ojs.2015.57080
References
- 1. Pepe, M.S. and Fleming, T.R. (1991) A General Nonparametric Method for Dealing with Errors in Missing or Surrogate Covaraite Data. Journal of the American Statistical Association, 86, 108-113.
http://dx.doi.org/10.1080/01621459.1991.10475009 - 2. Pepe, M.S. (1992) Inference Using Surrogate Outcome Data and a Validation Sample. Biometrika, 79, 355-365.
http://dx.doi.org/10.1093/biomet/79.2.355 - 3. Lee, L.F. and Sepanski, J. (1995) Estimation of Linear and Nonlinear Errors-in-Variables Models Using Validation Data. Journal of the American Statistical Association, 90, 130-140.
http://dx.doi.org/10.1080/01621459.1995.10476495 - 4. Wang, Q. and Rao, J.N.K. (2002) Empirical Likelihood-Based Inference in Linear Errors-in-Covariables Models with Validation Data. Biometrika, 89, 345-358.
http://dx.doi.org/10.1093/biomet/89.2.345 - 5. Zhang, Y. (2015) Estimation of Partially Linear Regression for Errors-in-Variables Models with Validation Data. Springer International Publishing, 322, 733-742.
http://dx.doi.org/10.1007/978-3-319-08991-1_76 - 6. Xu, W. and Zhu, L. (2015) Nonparametric Check for Partial Linear Errors-in-Covariables Models with Validation Data. Annals of the Institute of Statistical Mathematics, 67, 793-815.
http://dx.doi.org/10.1007/s10463-014-0476-7 - 7. Carroll, R.J. and Stefanski, L.A. (1990) Approximate Quasi-Likelihood Estimation in Models with Surrogate Predictors. Journal of the American Statistical Association, 85, 652-663.
http://dx.doi.org/10.1080/01621459.1990.10474925 - 8. Carroll, R.J. and Wand, M.P. (1991) Semiparametric Estimation in Logistic Measurement Error Models. Journal of the Royal Statistical Society: Series B, 53, 573-585.
- 9. Sepanski, J.H. and Lee, L.F. (1995) Semiparametric Estimation of Nonlinear Errors-in-Variables Models with Validation Study. Journal of Nonparametric Statistics, 4, 365-394.
http://dx.doi.org/10.1080/10485259508832627 - 10. Stute, W., Xue, L. and Zhu, L. (2007) Empirical Likelihood Inference in Nonlinear Errors-in-Covariables Models with Validation Data. Journal of the American Statistical Association, 102, 332-346.
http://dx.doi.org/10.1198/016214506000000816 - 11. Cook, J.R. and Stefanski, L.A. (1994) Simulation-Extrapolation Estimation in Parametric Measurement Error Models. Journal of the American Statistical Association, 89, 1314-1328.
http://dx.doi.org/10.1080/01621459.1994.10476871 - 12. Carroll, R.J., Gail, M.H. and Lubin, J.H. (1993) Case-Control Studied with Errors in Covariables. Journal of the American Statistical Association, 88, 185-199.
- 13. Lü, Y.-Z., Zhang, R.-Q. and Huang, Z.-S. (2013) Estimation of Semi-Varying Coefficient Model with Surrogate Data and Validation Sampling. Acta Mathematicae Applicatae Sinica, English Series, 29, 645-660.
http://dx.doi.org/10.1007/s10255-013-0241-3 - 14. Xiao, Y. and Tian, Z. (2014) Dimension Reduction Estimation in Nonlinear Semiparametric Error-in-Response Models with Validation Data. Mathematica Applicata, 27, 730-737.
- 15. Yu, S.H. and Wang, D.H. (2014) Empirical Likelihood for First-Order Autoregressive Error-in-Variable of Models with Validation Data. Communications in Statistics Theory Methods, 43, 1800-1823.
http://dx.doi.org/10.1080/03610926.2012.679763 - 16. Stefanski, L.A. and Buzas, J.S. (1995) Instrumental Variable Estimation in Binary Regression Measurement Error Models. Journal of the American Statistical Association, 90, 541-550.
http://dx.doi.org/10.1080/01621459.1995.10476546 - 17. Wang, Q. (2006) Nonparametric Regression Function Estimation with Surrogate Data and Validation sampling. Journal of Multivariate Analysis, 97, 1142-1161.
http://dx.doi.org/10.1016/j.jmva.2005.05.008 - 18. Du, L., Zou, C. and Wang, Z. (2011) Nonparametric Regression Function Estimation for Error-in-Variable Models with Validation Data. Statistica Sinica, 21, 1093-1113.
http://dx.doi.org/10.5705/ss.2009.047 - 19. Carroll, R.J., Ruppert, D., Stefanski, L.A. and Crainiceanu, C.M. (2006) Measurement Error in Nonlinear Models. Second Edition, Chapman and Hall CRC Press, Boca Raton.
http://dx.doi.org/10.1201/9781420010138 - 20. Hall, P. and Horowitz, J.L. (2005) Nonparametric Methods for Inference in the Presence of Instrumental Variables. Annals of Statistics, 33, 2904-2929.
http://dx.doi.org/10.1214/009053605000000714 - 21. Darolles, S., Florens, J.P. and Renault, E. (2006) Nonparametric Instrumental Regression. Working Paper, GREMAQ, University of Social Science, Toulouse.
- 22. Newey, W.K. and Powell, J.L. (2003) Instrumental Variable Estimation of Nonparametric Models. Econometrica, 71, 1565-1578.
http://dx.doi.org/10.1111/1468-0262.00459 - 23. Blundell, R., Chen, X. and Kristensen, D. (2007) Semi-Nonparametric IV Estimation of Shape-Invariant Engel Curves. Econometrica, 75, 1613-1669.
http://dx.doi.org/10.1111/j.1468-0262.2007.00808.x - 24. Newey, W.K. (1997) Convergence Rates and Asymptotic Normality for Series Estimators. Journal of Econometrics, 79, 147-168.
http://dx.doi.org/10.1016/S0304-4076(97)00011-0 - 25. Schimek, M.G. (2012) Variance Estimation and Bandwidth Selection for Kernel Regression. John Wiley & Sons, Inc., New York, 71-107.
- 26. Timan, A. (1963) Theory of Approximation of Functions of a Real Variable. McMillan, New York.
Appendix
Proof of Theorem 1
Let 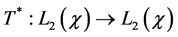
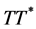
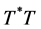
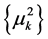
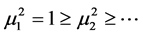
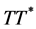
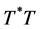
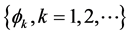
Define
Let 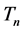
then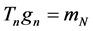
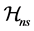
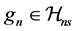
Lemma 1. Under conditions A1 and A3(i) and the sieve space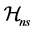
1)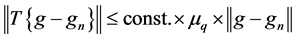
2)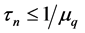
Lemma 2. Under conditions A1, A3(ii) and A4, we have
By some modifications of the proof of Theorem 2 in [23] and applying the Theorem 7 in [24] , the proofs of Lemma 1 and Lemma 2 are straightforward and are omitted.
Proof of Theorem 1. By the triangle inequality, we have
By the definition of 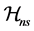
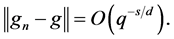
see e.g. [26] for Fourier series.
Next, by the definition of 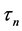
We now analyze the term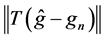
By conditions A2, A4 and central limit theorem, we can show that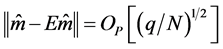
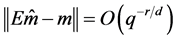
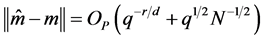
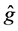
These and Lemma 2 imply
This and Lemma 1 imply
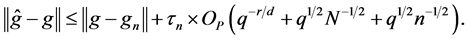
The theorem follows immediately from (12)-(13).
Proof of Theorem 2
Lemma 3. For each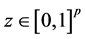
Let 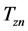
then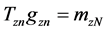
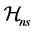
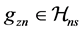
Proof of Theorem 2. For each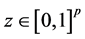
By assumption B3(i), it is easy to show that
Similar to the proof of Theorem 1, we have
According to assumptions B2, B3(ii), B4, and B5(i), we can show that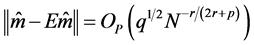
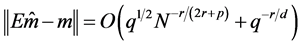
For the term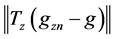
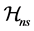
Combining all these results, we complete the proof. W