American Journal of Computational Mathematics
Vol.05 No.02(2015), Article ID:57668,14 pages
10.4236/ajcm.2015.52019
Analytic Solution for Fluid Flow over an Exponentially Stretching Porous Sheet with Surface Heat Flux in Porous Medium by Means of Homotopy Analysis Method
Azhar Ali1*, H. Zaman1, M. Z. Abidin2, Naeemullah1, S. I. A. Shah1
1Faculty of Numerical Science, Islamia College University, Peshawar, Pakistan
2Faculty of Mechanical Engineering, CECOS University of IT and Emerging Science, Peshawar, Pakistan
Email: *azhar_ali017@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 April 2015; accepted 27 June 2015; published 30 June 2015
ABSTRACT
In this paper, the analytical solution of a viscous and incompressible fluid towards an exponentially stretching porous sheet with surface heat flux in porous medium, for the boundary layer and heat transfer flow, is presented. The equations of continuity, momentum and the energy are transformed into non-linear ordinary differential by using similarity transformation. The solutions of these highly non-linear ordinary differential equations are found analytically by means of Homotopy Analysis Method (HAM). The result obtained by HAM is compared with numerical results presented in the literature. The accuracy of the HAM is indicated by close agreement of the two sets of results. By this method, an expression is obtained which is admissible for all values of effective parameters. This method has the ability to control the convergence of the solution.
Keywords:
Exponentially Stretching Sheet, Suction/Blowing, Variable Surface Heat Flux, Porous Medium, Analytical Solution, Homotopy Analysis Method

1. Introduction
In fluid mechanics and heat transfer many engineering problems are basically nonlinear. The majority of these problems do not have analytical solutions. Using numerical techniques, some of them can be solved and some can be solved analytically. Stability and convergence should be considered so that the divergence can be avoided in results obtained by numerical method. To find the analytic solution of these non linear equations, we need other methods such as perturbation method [1] . But in perturbation method, a small parameter is needed that is to be inserted in the equation. The main deficiency of perturbation method is to find that small parameter which is exerted it into the equation.
1992 [2] [3] , Liao introduced the homotopy analysis method (HAM) which doesn’t need such small/large parameter and then he further improved and developed this method. The most significant feature of this method is that region of convergence can be controlled and adjusted, in comparison to other methods. It should be necessary to mention that the Homotopy Perturbation Method (HPM) brought forth in 1998, is only a particular case of HAM [4] [5] .
HAM based on introduction of homotopy in topology combined with the traditional perturbation method for the solution of non linear equations, but contrary to the traditional perturbation methods, HAM doesn’t need a small perturbation parameter in the equation. A homotopy is constructed with an embedding parameter p. Values are given to p from zero to one. The problem under consideration takes a convenient simple form which presents a closed form of analytical solution as p = 0. Similarly if the value of p increases, that finally takes the value one. Then at this stage, the solution of the original problem is obtained. The reliability of HAM also depends on two other auxiliary parameters, first is the parameter 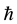 and the other one is function. The choice of that function is to be practiced with in order to find out the optimal solution. With the help of
and the other one is function. The choice of that function is to be practiced with in order to find out the optimal solution. With the help of 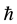 -curve, the convergence of the analytic solution is ensured. HAM is a novel technique [6] [7] , which has been used by many researchers for solving non linear ordinary differential equation. Recently, HAM has applied by many researchers to find the solution of different problems in science and engineering. Ayub [8] has considered the problem of steady, third grade fluid flowing past an infinite porous plate and for exact analytical solution of the governing non-linear differential equation, he uses HAM. On the basis of HAM, Wang and Pop [9] also proposed exact analytic solutions for flow within a non-Newtonian fluid film whose motion is caused solely by the unsteady stretching of a horizontal elastic surface. Wang [10] applied HAM to find out the explicit analytic solution of the Volterra equation. The comparison of HAM and HPM through a linear partial differential equation has been made by Liang and Jeffrey [11] . To numerically approximate the Eigen values of the fractional Sturm-Liouvile problems, Abbasbandy and Shirzadi [12] used HAM. The application of HAM was considered by Nassar [13] , as he suggested that by using HAM the solution of the nonlinear Poisson-Boltzmann equation for semiconductor devices was extremely good analytical approximations. Zaman [14] studied the series solution of stagnation point flow with mass transfer along an accelerated vertical porous plate with suction by means of HAM and he found out an exact analytical solution. Also Zaman, H. [15] proposed exact analytic series solution for heat transfer from a continuous surface in a parallel free stream of viscoelastic fluid. The above discussion shows that HAM is more flexible, valid and effective for the solution of non linear ordinary differential equations arises in science and engineering.
-curve, the convergence of the analytic solution is ensured. HAM is a novel technique [6] [7] , which has been used by many researchers for solving non linear ordinary differential equation. Recently, HAM has applied by many researchers to find the solution of different problems in science and engineering. Ayub [8] has considered the problem of steady, third grade fluid flowing past an infinite porous plate and for exact analytical solution of the governing non-linear differential equation, he uses HAM. On the basis of HAM, Wang and Pop [9] also proposed exact analytic solutions for flow within a non-Newtonian fluid film whose motion is caused solely by the unsteady stretching of a horizontal elastic surface. Wang [10] applied HAM to find out the explicit analytic solution of the Volterra equation. The comparison of HAM and HPM through a linear partial differential equation has been made by Liang and Jeffrey [11] . To numerically approximate the Eigen values of the fractional Sturm-Liouvile problems, Abbasbandy and Shirzadi [12] used HAM. The application of HAM was considered by Nassar [13] , as he suggested that by using HAM the solution of the nonlinear Poisson-Boltzmann equation for semiconductor devices was extremely good analytical approximations. Zaman [14] studied the series solution of stagnation point flow with mass transfer along an accelerated vertical porous plate with suction by means of HAM and he found out an exact analytical solution. Also Zaman, H. [15] proposed exact analytic series solution for heat transfer from a continuous surface in a parallel free stream of viscoelastic fluid. The above discussion shows that HAM is more flexible, valid and effective for the solution of non linear ordinary differential equations arises in science and engineering.
In the present study, we use the homotopy analysis method for the solution of two non linear ordinary differential equations introduced by Mandal [16] . The distribution of the paper is as follows. In Section 2, the methematical formulation of the problem is presented. The basic idea of HAM and solution by means of HAM is discussed in Section 3. The convergence of the obtained series solutions is carefully analyzed in Section 4. The graphical results, table and discusion are presented in Section 5. The conclution is presented in Section 6.
2. Mathematical Formulation
2.1. Flow Problem
Assume the two-dimensional, steady and incompressible flow of a viscous fluid past a flat sheet coincided by the plane 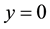 in a porous medium with a non-uniform permeability
in a porous medium with a non-uniform permeability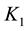 . Mandal [16] considered the flow in the porous medium. The governing equation of the problem is based on Darcy’s law. The Darcy’s law accounts for the drag applied by the porous medium [17] [18] . There is an increase in the form drag [19] due to the significant inertial effects at maximum velocities. The inertial effects and the effects of solid bodies have been ignored. Near the boundary and in a media with high porosity [20] [21] these effects are more important. In addition, the non-linear Forhheimer term is ignored however the linear Darcy term is retained. That Darcy term describes the distributed body force exerts by porous medium. The Reynolds number was assumed to be very small in this study (typically < 10) [20] [22] .
. Mandal [16] considered the flow in the porous medium. The governing equation of the problem is based on Darcy’s law. The Darcy’s law accounts for the drag applied by the porous medium [17] [18] . There is an increase in the form drag [19] due to the significant inertial effects at maximum velocities. The inertial effects and the effects of solid bodies have been ignored. Near the boundary and in a media with high porosity [20] [21] these effects are more important. In addition, the non-linear Forhheimer term is ignored however the linear Darcy term is retained. That Darcy term describes the distributed body force exerts by porous medium. The Reynolds number was assumed to be very small in this study (typically < 10) [20] [22] .
We consider Cartesian coordinates (x; y; z). It is supposed that the sheet is associated to a variable heat flux . The flow is limited to
. The flow is limited to . Two equal and opposite forces are applied along x-axis, as a result the wall is stretched keeping the origin fixed. The effect of these forces causes a symmetric boundary at the centre (the origin as shown in the Figure 1) of the porous medium.
. Two equal and opposite forces are applied along x-axis, as a result the wall is stretched keeping the origin fixed. The effect of these forces causes a symmetric boundary at the centre (the origin as shown in the Figure 1) of the porous medium.
For two-dimensional flow, the velocity field is considered as
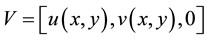 (1)
(1)
where u and v are the velocity components in x and y directions respectively. The governing equations of continuity [23] , momentum [19] [24] and energy [23] [25] are
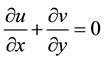 (2)
(2)
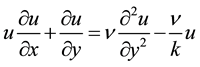 (3)
(3)
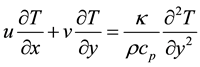 (4)
(4)
where ρ represents the fluid density (assumed constant), 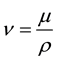 is the kinematic viscosity,
is the kinematic viscosity, 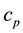 is the specific heat, μ is the coefficient of fluid viscosity,
is the specific heat, μ is the coefficient of fluid viscosity, 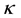 is the thermal conductivity.
is the thermal conductivity.
2.2. Boundary Conditions
The appropriate boundary conditions for the problem are
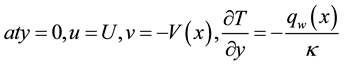 (5)
(5)
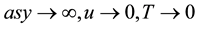 (6)
(6)
Here, 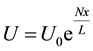 is the stretching velocity [26] ,
is the stretching velocity [26] , 



Figure 1. Geometrical representation of the problem.






However, for the sake of comparison, we shall consider the same case as discuss by Mandal [16] of prescribed surface temperature (PST),
Introducing the similarity variable as




and by substituting (7a)-(7d) in Equations (3) and (4), we obtain


And the boundary conditions become as:


where the prime represents differentiation with respect to



3. Homotopy Analysis Method
3.1. Basic Idea
Assume the following non-linear differential equation in the form of

where 



where 


Then by applying the generalized homotopy method, known as zero-order deformation Equation (12) is

where 






So, as p takes values from 0 to 1, the solution 




and

where 

By defining the vector of

By the definition in Equation (17), the governing equation and the corresponding initial conditions of 


where

And

As we apply inverse operator 

In this way, we can easily solve the Equation (12) to obtained 


By using the initial or boundary conditions we find the constant(s).
As
3.2. The Solution of the Problem by Means of HAM
3.2.1. Zero-Order Deformation Problem
To find the series solution, 




where 
For the problem under discussion, the initial guesses and the auxiliary linear operators has to be chosen as




With


And 
For the probem, the zero-order deformation is







where 















3.2.2. Higher-Order Deformation Problem
The mth-order deformation problem are




where


And

The general soluton of the Equations (45)-(48) is


In which 




thus, it is convenient to find the solution of Equations (44)-(47), continuously in the order m = 1, 2, 3, ∙∙∙ , in particular by using the symbolic computation software Mathematica.
4. Convergence of the Series Solutions
For HAM solution, the rate of convergence of approximation strongly depends on auxiliary parameter ħ, which has big effect on the region of convergence. Due to the region of convergence and rate of convergence of a series are essentially determined by the base functions, its convergence is guaranteed.
We observe that the series solutions (24) and (25) contain the non-zero auxilary parameter 













Figure 2. (a) 





Figure 3. (a) Skin-friction coeficient 



for Figure 3(a) and Figure 3(b) and compared with results obtained by Mandal [16] , which shows that the best value for 


finding the suitable value of



5. Table, Graphical Results and Discussion
In this paper, we consider the same study as discussed by Mandal [16] . Solution of Equations (8) and (9) with the boundary conditions (10) and (11) are find out by means of HAM. For the varification of accuracy of the results obtained by HAM a comparison is made with the results, obtained by Mandal [16] , Magyari and Keller [26] , Bidin and Nazar [23] , El-Aziz [29] and Ishak [25] , for prescribed surface temperature (PST) instead of variable surface heat flux. For this comparison, we also consider the boundary conditions for temprature as follows:
At 


At last, the boundary conditions take the given form:
At 

A comparison is made for the obtained results for precribed surface temprature (PST) coresponding to the values of heat transfer coefficient 



The analytical solution obtained by HAM has a high order of accuracy with a few iterations.
In order to analyze the effect of various parameters on the flow and temperature profile, analytical computations have been carried out for variable surface heat flux(VHF) using the HAM consider the same case as described by Mandal [16] . To see the effect of different parameters of interest on the velocity and tempprature profile, we have plotted the Figures 3(b)-7.
Let us first discuus with the existence of suction at the wall the effect of exponential parameter N on velocity and temprature profile.


Figure 4. (a) Variation of velocity 







Figure 5. (a) Variation of velocity 









Figure 6. (a) Variation of velocity 










Figure 7. Variation of temprature 


Table 1. Comparison of the present analytical results with available numerical results for 
We consider the same case as discussed by Mandal [16] . Figure 4(a) and Figure 4(b) present the effect of exponential parameter N with variable surface heat flux on velocity and temprature profile. Both velocity and temprature decreases with increasing in N due to decreasing behaviour of the momentum and thermal boundary layer thickness. From these figures, it is intresting to mention that the wall temprature decreses for positive value of Nthroughout in the boundary layer.
for exponentially streaching sheet, to see the effect of suction/blowing parameter S on velocity and temprature profile are presented in Figure 5(a) and Figure 5(b) respectively. It is noticed that by increasing suction velocity dereases significantly whereas with increse in blowing fluid velocity is found to increase (Figure 5(a)). It is notice that for the wall suction (S > 0) the boundary layer thikness decreases and the velocity field is reduced. The case of non-porous sretching sheet is represent by S = 0. Noted opposite behaviour for blowing (S < 0). If stronger blowing is consideredthe heated fluid is pushed far from the wall where the flow is accelerated due to less influence of the viscosity. This behaviour increases maximum velocity in the boundary layer. In case of suction the same rule is working but in opposite direction. Figure 5(b) represents the temprature profile for variable suction/blowing parameter S with surface heat flux. By increasing suction it is observerd that decreases whereas temprature increases due to blowing (Figure 5(b)). Actually, the effect of suction more uniform within the boundary layer. At the surface, imposition of fluid suction has the tendency to reduce both the thermal thickness and hydrodynamic of the boundary layer where viscous effect domminate. Due to this effect both the fluid velocity and temnprature are reduced. Alternatively, with injection the thermal boundary layer thickness increase due to which rate of heat transfer decreases.
For the case S = 0, the influence of permeabikity parameter 
In the presence of suction, Figure 4(c) and Figure 4(d) show the effect of the permiability parameter on the velocity and temprature profiles respectivelly. In the presnce of suction, fluid velocity is suppressed a bit more (compare to S = 0 case) with increasing permiiability parameter 
Figure 7 presents the effect of prandtl number Pr on the temprature profile. In presence of variable heat flux, the temprature decreases with the Pr. The thermal bundary layer thicness is reduced due to increase in Pr. In heat transfer problem, the relative thickneing of the momentum and thermul boundary layeris controlled by the prandtl number Pr. With a small Prandtl number Pr, heat diffuses fastly compared to the velocity ( momentum), that is for liquid metals, the thickness of the boundary layer is much bigger than momentum boundary layer. That fluids whichhave higher thermal conductivity with lower Prandtl number (and thicker thermal boundary layer structures) can diffuse from the sheet faster as compared to that fluid which have higher Pr fluids (thinner htermal boundary layers). Thus, Prandtl increases the rate of cooling in conducting flows [20] .
Figure 6(a) shows the behaviour of skin-friction coefficient with exponential parameter N for three different values of suction/blowing parameter S. It is observed that skin-friction coefficient 
It is observed from = Figure 3(a) that at the wall stress is negative, negative sign of 
Figure 3(b) diplays against the permeability parameter 

lity parameter 

6. Conclusion
In this paper, the homotopy analysis method is used to obtain the analytical solutions of a non linear Ordinary differential equations related to the boundary layer flow and heat transfer flow of a viscous and incompressible fluid towards an exponentially stretching porous sheet with surface heat flux in porous medium. The convergence of the HAM solution is discussed in detail. Definitely, the HAM gives us a simple way to control the convergence of series. That is the fundamental difference between the HAM and other analytical methods. The effect of the emerging parameters is discussed and the results are presented graphically. The results obtained by HAM are compared with the numerical results as discussed in the literature and with other stated available results. The comparision shows acceptable agreement between analytical and numerical solutions.
References
- He, J.-H. (2003) Homotopy Perturbation Method: A New Nonlinear Analytical Technique. Applied Mathematics and Computation, 135, 73-79. http://dx.doi.org/10.1016/S0096-3003(01)00312-5
- Liao, S.J. (2003) Beyond Perturbation: Introduction to the Homotopy Analysis Method. CRC Press, Boca Raton. http://dx.doi.org/10.1201/9780203491164
- Liao, S.J. (1992) The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai.
- Sajid, M., Hayat, T. and Asghar, S. (2007) Comparison between the HAM and HPM Solutions of Thin Film Flows of Non-Newtonian Fluids on a Moving Belt. Nonlinear Dynamics, 50, 27-35. http://dx.doi.org/10.1007/s11071-006-9140-y
- Liao, S.J. (2005) Comparison between the Homotopy Analysis Method and Homotopy Perturbation Method. Applied Mathematics and Computation, 169, 1186-1194. http://dx.doi.org/10.1016/j.amc.2004.10.058
- Liao, S.J. (2009) Notes on the Homotopy Analysis Method: Some Definitions and Theorems. Communications in Nonlinear Science and Numerical Simulation, 14, 983-997. http://dx.doi.org/10.1016/j.cnsns.2008.04.013
- Liao, S.J. (2012) Homotopy Analysis Method in Nonlinear Differential Equations. Springer, Berlin and Beijing. http://dx.doi.org/10.1007/978-3-642-25132-0
- Ayub, M., Rasheed, A. and Hayat, T. (2003) Exact Flow of a Third Grade Fluid Past a Porous Plate Using Homotopy Analysis Method. International Journal of Engineering Science, 41, 2091-2103. http://dx.doi.org/10.1016/S0020-7225(03)00207-6
- Wang, C. and Pop, I. (2006) Analysis of the Flow of a Power-Law Fluid Film on an Unsteady Stretching Surface by Means of Homotopy Analysis Method. Journal of Non-Newtonian Fluid Mechanics, 138, 161-172. http://dx.doi.org/10.1016/j.jnnfm.2006.05.011
- Wang, Z., Zou, L. and Zhang, H. (2007) Applying Homotopy Analysis Method for Solving Differential-Difference Equation. Physics Letters A, 369, 77-84. http://dx.doi.org/10.1016/j.physleta.2007.04.070
- Liang, S. and Jeffrey, D.J. (2009) Comparison of Homotopy Analysis Method and Homotopy Perturbation Method through an Evolution Equation. Communications in Nonlinear Science and Numerical Simulation, 14, 4057-4064. http://dx.doi.org/10.1016/j.cnsns.2009.02.016
- Abbasbandy, S. and Shirzadi, A. (2010) Homotopy Analysis Method for Multiple Solutions of the Fractional Sturm- Liouville Problems. Numerical Algorithms, 54, 521-532. http://dx.doi.org/10.1007/s11075-009-9351-7
- Nassar, C.J., Revelli, J.F. and Bowman, R.J. (2011) Application of the Homotopy Analysis Method to the Poisson- Boltzmann Equation for Semiconductor Devices. Communications in Nonlinear Science and Numerical Simulation, 16, 2501-2512. http://dx.doi.org/10.1016/j.cnsns.2010.09.015
- Zaman, H. and Ayub, M. (2010) Series Solution of Unsteady Free Convection Flow with Mass Transfer along an Accelerated Vertical Porous Plate with Suction. Central European Journal of Physics, 8, 931-939.
- Zaman, H., Hayat, T., Ayub, M. and Gorla, R.S.R. (2011) Series Solution for Heat Transfer from a Continuous Surface in a Parallel Free Stream of Viscoelastic Fluid. Numerical Methods for Partial Differential Equations, 27, 1511-1524. http://dx.doi.org/10.1002/num.20593
- Mandal, I.C. and Mukhopadhyay, S. (2013) Heat Transfer Analysis for Fluid Flow over an Exponentially Stretching Porous Sheet with Surface Heat Flux in Porous Medium. Ain Shams Engineering Journal, 4, 103-110. http://dx.doi.org/10.1016/j.asej.2012.06.004
- Pal, D. and Hiremath, P.S. (2010) Computational Modeling of Heat Transfer over an Unsteady Stretching Surface Embedded in a Porous Medium. Meccanica, 45, 415-424.
- Joseph, D.D., Nield, D.A. and Papanicolaou, G. (1982) Nonlinear Equation Governing Flow in a Saturated Porous Medium. Water Resources Research, 18, 1049-1052. http://dx.doi.org/10.1029/WR018i004p01049
- Brinkman, H.C. (1949) A Calculation of the Viscous Force Exerted by a Flowing Fluid on a Dense Swarm of Particles. Applied Scientific Research, 1, 27-34. http://dx.doi.org/10.1007/BF02120313
- Mukhopadhyay, S. and Layek, G.C. (2012) Effects of Variable Fluid Viscosity on Flow past a Heated Stretching Sheet Embedded in a Porous Medium in Presence of Heat Source/Sink. Meccanica, 47, 863-876. http://dx.doi.org/10.1007/s11012-011-9457-6
- Vafai, K. and Tien, C.L. (1981) Boundary and Inertia Effects on Flow and Heat Transfer in Porous Media. International Journal of Heat and Mass Transfer, 24, 195-203. http://dx.doi.org/10.1016/0017-9310(81)90027-2
- Beg, O.A., Bhargava, R., Rawat, S., Takhar, H.S. and Beg, T.A. (2007) Finite Element Modeling of Laminar Flow of a Third Grade Fluid in a Darcy-Forcheimmer Porous Medium with Suction Effects. International Journal of Applied Mechanics and Engineering, 12, 215-233.
- Biliana, B. and Nazar, R. (2009) Numerical Solution of the Boundary Layer Flow over an Exponentially Stretching Sheet with Thermal Radiation. European Journal of Scientific Research, 33, 710-717.
- Cortell, R. (2005) Flow and Heat Transfer of a Fluid through a Porous Medium over a Stretching Surface with Internal Heat Generation/Absorption and Suction/Blowing. Fluid Dynamics Research, 37, 231-245. http://dx.doi.org/10.1016/j.fluiddyn.2005.05.001
- Ishak, A. (2011) MHD Boundary Layer Flow Due to an Exponentially Stretching Sheet with Radiation Effect. Sains Malaysiana, 40, 391-395.
- Magyari, E. and Keller, B. (1999) Heat and Mass Transfer in the Boundary Layers on an Exponentially Stretching Continuous Surface. Journal of Physics D: Applied Physics, 32, 577-585. http://dx.doi.org/10.1088/0022-3727/32/5/012
- Nadeem, S., Zaheer, S. and Fang, T. (2011) Effects of Thermal Radiation on the Boundary Layer Flow of a Jeffrey Fluid over an Exponentially Stretching Surface. Numerical Algorithms, 57, 187-205. http://dx.doi.org/10.1007/s11075-010-9423-8
- Bhattacharyya, K. (2011) Boundary Layer Flow and Heat Transfer over an Exponentially Shrinking Sheet. Chinese Physics Letters, 28, Article ID: 074701. http://dx.doi.org/10.1088/0256-307X/28/7/074701
- Abd El-Aziz, M. (2009) Viscous Dissipation Effect on Mixed Convection Flow of a Micropolar Fluid over an Exponentially Stretching Sheet. Canadian Journal of Physics, 87, 359-368. http://dx.doi.org/10.1139/P09-047
NOTES
*Corresponding author.






