American Journal of Operations Research
Vol. 2 No. 2 (2012) , Article ID: 19955 , 4 pages DOI:10.4236/ajor.2012.22032
Interior-Point Methods Applied to the Predispatch Problem of a Hydroelectric System with Scheduled Line Manipulations
University of Campinas, Campinas, Brazil
Email: silvia@densis.fee.unicamp.br, aurelio@ime.unicamp.br
Received March 12, 2012; revised April 13, 2012; accepted April 27, 2012
Keywords: Interior-Point Methods; Scheduled Line Manipulations; Hydroelectric Systems; The Brazilian Power System
ABSTRACT
Transmission line manipulations in a power system are necessary for the execution of preventative or corrective maintenance in a network, thus ensuring the stability of the system. In this study, primal-dual interior-point methods are used to minimize costs and losses in the generation and transmission of the predispatch active power flow in a hydroelectric system with previously scheduled line manipulations for preventative maintenance, over a period of twenty-four hours. The matrix structure of this problem and the modification that it imposes on the system is also broached in this study. From the computational standpoint, the effort required to solve a problem with or without line manipulations is similar, and the reasons for this are also discussed in this study. Computational results sustain our findings.
1. Introduction
In a power system, continual improvements in operational conditions are always sought; however, to achieve such improvements, constant maintenance and improvement work in the network is required, and scheduled shut-downs are sometimes required. Maintenance is necessary to avoid electrical short circuits and overloads. Thus, the objective is to ensure the continual supply of electric power, with the fewest interruptions of the shortest duration possible, thus maintaining the service levels required by the legislation.
For instance, in Brazil the System Operation Center (COS) is responsible for executing, authorizing and supervising scheduled and emergency line manipulations in the power transmission system, as well as for monitoring the system and reestablishing the power grid in the event of isolated or generalized contingencies. These activities, executed in real time, require situational awareness and management of the execution of the necessary line manipulations, with the aim of ensuring the integrity of personnel and installations, whilst guaranteeing the reliability of the system and the continuity and quality of supply.
In this study, the predispatch will be modeled on a twenty-four hour period, representing the dispatch of a single day, and line manipulations will be an input data point; in other words, they will already have been scheduled, and thus the line manipulations considered herein will be of a preventative nature. It is important to emphasize that there are other types of manipulations, such as generator shut downs, tap changing procedures and flexible alternating current transmission system (FACTS) adjustments, but these are not considered in this study.
Furthermore, by making use of the speed and robustness of interior-point methods [1-3], the intention is to obtain more efficient implementations for predispatch by means of exploiting the matrix structure of the resulting system.
2. The Predispatch Problem
Predispatch is a short-term operational problem, in this case, short-term refers to one-week, or even one-day, planning. The intention is to fulfill demands and satisfy the energy targets that have been defined in long-term planning.
Flow restrictions can be divided into blocks that repeat themselves over a certain time interval, representing the power system in these intervals, and thus we obtain an independent formulation of the Kirchhoff laws, where power flows are represented in order to enable a direct consideration of the transmission limits as restrictions and transmission losses as a performance criterion [4].
A predispatch system with m buses, n lines and g generators, where line manipulations are considered, can be modeled in the following manner:
 (1)
(1)
where• 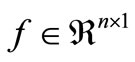 represents the active power flow;
represents the active power flow;
•  represents the active power generation;
represents the active power generation;
• 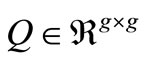 represents the quadratic component of the generation cost;
represents the quadratic component of the generation cost;
• 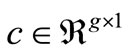 represents the linear component of the generation cost;
represents the linear component of the generation cost;
• 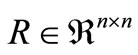 represents the diagonal matrix of line resistance;
represents the diagonal matrix of line resistance;
• 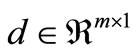 represents the active load;
represents the active load;
• 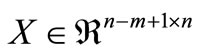 represents the reactance active matrix;
represents the reactance active matrix;
• 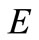 represents a matrix of order m × g, with each column containing exactly one element equal to 1 and all other elements equal to 0;
represents a matrix of order m × g, with each column containing exactly one element equal to 1 and all other elements equal to 0;
• 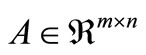 represents the incidence matrix of the transmission network;
represents the incidence matrix of the transmission network;
• 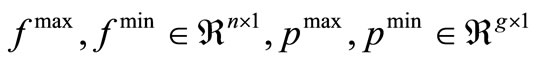 represents the flow and active power generation limits, respectively;
represents the flow and active power generation limits, respectively;
• 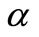 and
and 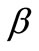 objective function weight constants;
objective function weight constants;
• 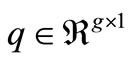 represents the power generation target established in long-term planning.
represents the power generation target established in long-term planning.
For this model, the two objective function components are quadratic with separable variables. The first component represents the value of the transmission losses. The second component characterizes the generation cost of the plants [5].
Problem (1) may be simplified using changes in variables [6] and adding slack variables, thus we get the primal problem in its standard form:
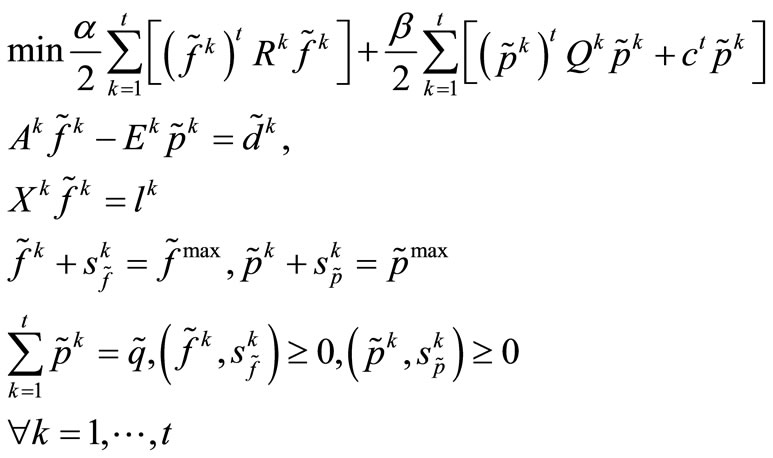
Whose respective dual problem may be expressed as:
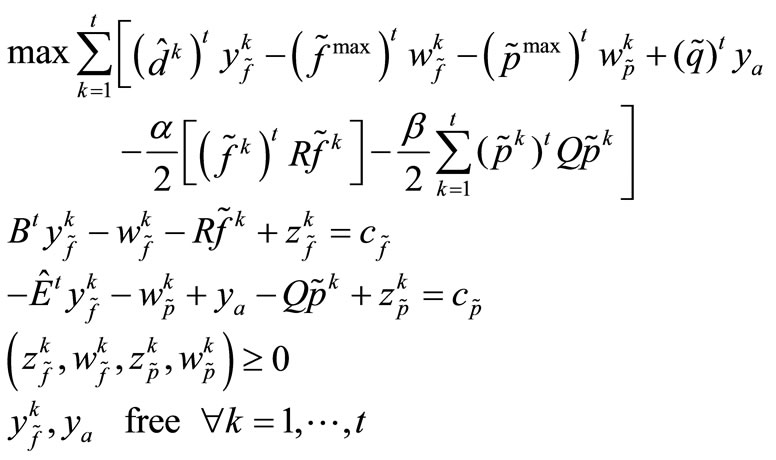 (2)
(2)
Matrix B, formed by the juxtaposed rows of the incidence and reactance matrices, is no longer constant throughout the time intervals t, and may be partioned as:
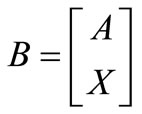
In a more detailed form:
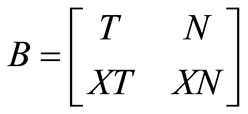
where
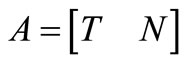
and
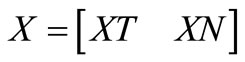
With this partitioning, the columns of incidence matrix A are divided so that T contains the edges of a spanning tree and N is formed by the remaining edges, which belong to the co-tree [7], and the reactance matrix X is partitioned in a similar manner.
Matrices B and E vary in accordance with the time intervals (Bk and Ek), reflecting the modifications to the networks and buses by line manipulations carried out throughout the study window. The reason that these matrices vary according to the time intervals is that the network is no longer constant throughout these t-intervals. Every time a line manipulation occurs, matrix B formed by the juxtaposed rows of the incidence and reactance matrix, and matrix E of order m × g should vary in accordance with the changes imposed on the network.
The primal-dual interior-point methods consist of the application of Newton’s method to the optimality conditions [8]; therefore, the following linear system is obtained:
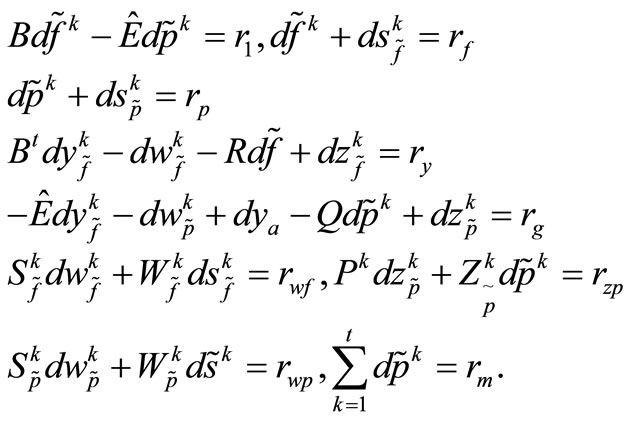 (3)
(3)
when several variable substitutions are made, we get:
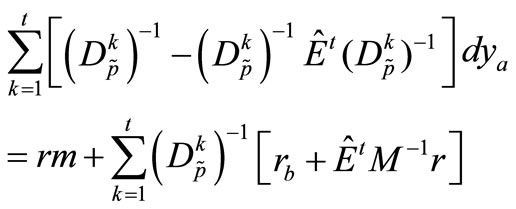 (4)
(4)
whose direct solution requires great computational effortbecause,  has the dimension of the number of rows and dya has the dimension of the number of generators.
has the dimension of the number of rows and dya has the dimension of the number of generators.
3. Scheduled Line Manipulations
Line manipulations are executed with the intention of adapting the transmission network to the load variation (variation of the power demand) throughout the day. In most time intervals, line manipulations are not executed in the Brazilian power system, which means that the transmission network rarely alters from one time interval to another, normally four to six line manipulations are executed per day. The changes considered herein are called preventative line manipulations; in other words, alterations to the network so that maintenance can be carried out and power blackouts avoided.
3.1. Study of the Matrix Structure for the Problem with Line Manipulations
We assume that in this system, i previously scheduled line manipulations take place over t time intervals, where each time interval corresponds to the period of one hour, and i line manipulations are few with the average value ranging from zero to six, which is typical of the Brazilian system.
Matrix B is formed by the juxtaposed rows of the incidence and reactance matrices, and is no longer constant throughout t time intervals, because every time that a line manipulation is executed, we can infer that a row and a column of matrix B are removed (inserted), in the event that more than one line manipulation occurs in the same time interval, more rows and columns of matrix B are removed (inserted). Thus, when we consider a system with line manipulations at different time intervals, we will use the following representation:
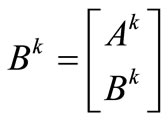
where,
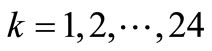
Every time a line manipulation occurs during interval k, matrix B will have its size modified, because it is formed by the incidence matrix, which represents the network topology, and by the reactance matrix. Therefore, if a line is disconnected from the grid at time k, then the incidence matrix should represent the network at that exact instant in time; in other words, a column of A is eliminated, therefore the reactance associated with that row should also be extracted from the matrix.
As the size of matrix B may be modified with each line manipulation, we must adjust the system to these changes; in other words, in order to obtain the product and the sum total with B, the size of some of the matrices involved in the system should also be altered.
The initial objective is to solve the linear system (4), but for this we realize that too much computational effort would be necessary to solve it directly, because in the first equation, we have the following matrix:

whose size is the number of rows at instant t, while the size of vector dya is the number of generators. A more efficient solution follows these steps [6]:
Step 1) Consider a matrix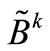 , consisting of matrix Bk and canonical vector ej, thus
, consisting of matrix Bk and canonical vector ej, thus

(note that this matrix is square and nonsingular).
Step 2) A row and a column is added to matrix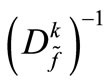 , in order to adjust its size for multiplication of the matrices.
, in order to adjust its size for multiplication of the matrices.
Step 3) In matrix Dk, remove the jth row and the jth column, with j varying from 1, 2, ···, m, where its intersections cannot be zero. Accordingly, we are removing a generation bus from the matrix and its size is not altered, rather only replaced with zero in the removed jth row and column.
Thus 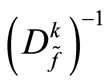
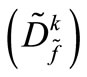 of
of 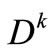
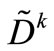 and of, a matrix M becomes
and of, a matrix M becomes 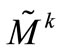 and rewritten as
and rewritten as
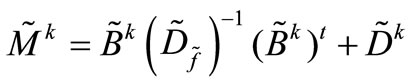
which has the size (n + 1) × (n + 1), and the vector
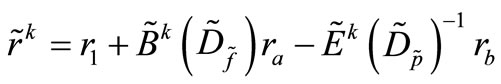
Step 4) We define:
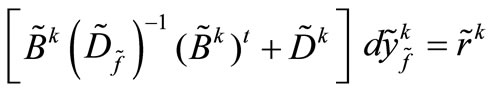 (5)
(5)
this system will be solved in two stages [9]:
We will first solve the following linear system:
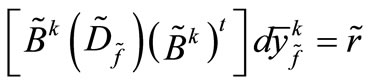
Accordingly, the “inversions” of 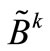 and
and 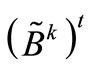 must be calculated. It is important to emphasize that we are supposing that in t time intervals, i-scheduled line manipulations take place; in other words, the matrices
must be calculated. It is important to emphasize that we are supposing that in t time intervals, i-scheduled line manipulations take place; in other words, the matrices 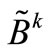 and
and 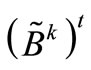 vary throughout the interval, as a function of this number of line manipulations.
vary throughout the interval, as a function of this number of line manipulations.
In order to solve (5), we have  which is found without difficulties, using, for example, the LU factor of which does not vary throughout the iterations. In algerbraic form, we write:
which is found without difficulties, using, for example, the LU factor of which does not vary throughout the iterations. In algerbraic form, we write:
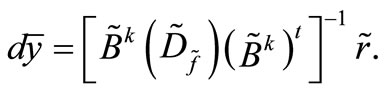
The Sherman-Morrison-Woodbury formula [10] is used to solve the linear system (5), in this case the computation of invertible matrix 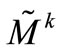
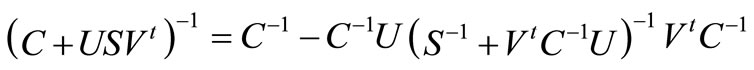
where U and V are matrices of size p × q and S is of size q × q, and therefore suitable for our problem
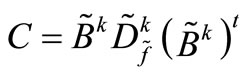
and
• 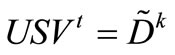
• S is a diagonal matrix of size g × g, whose elements are those that belong to matrix 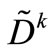
• Matrix U has its columns removed from the identity matrix
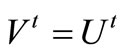
Therefore, 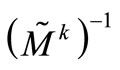 is expressed as:
is expressed as:
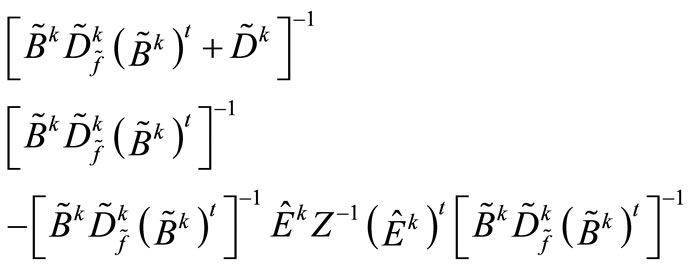
where
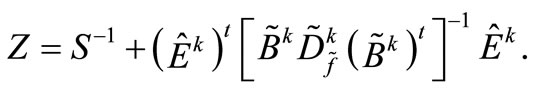
![]() Note that Z is a symmetric positive-definite matrix, with the size of the number of generators. Therefore, the computation of Z is simple, because the matrix enables the application of the Cholesky decomposition [11] and has a relatively small size.
Note that Z is a symmetric positive-definite matrix, with the size of the number of generators. Therefore, the computation of Z is simple, because the matrix enables the application of the Cholesky decomposition [11] and has a relatively small size.
Multiplying the Sherman-Morrison-Woodbury equation, already applied in this context, by we get:
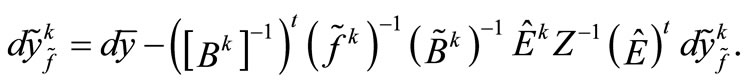
Observe that the matrices 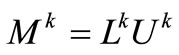 can be decomposed once only before the iterative process, in an identical fashion to what can be done with matrix B, in the case of the problem without line manipulations.
can be decomposed once only before the iterative process, in an identical fashion to what can be done with matrix B, in the case of the problem without line manipulations.
3.2. Implementation Details for the Developed Methods
In order to devinterior-points methods for a system with line manipulations, the network needs to be adapted. With each line manipulation carried out, a row and a column can be inserted (removed) from matrix B.
The spanning tree is represented by matrix T and must not be modified; in other words, only the branches belonging to matrix N, formed by the additional branches of the spanning tree, can be connected (disconnected), thus facilitating implementation and resulting in greater computational efficiency.
It is worth emphasizing that as the spanning tree is not unique and the line manipulations are previously known, any branch may be manipulated, and all this would require is the construction of another spanning tree, as long as the branch to be manipulated did not belong to it.
The tests undertaken in this study use the starting point shown in the Equation (6). This was defined as in [12], which presented satisfactory results in previous experiments.
 (6)
(6)
4. Computational Results
The networks in which the tests were carried out include the IEEE30 bus system, representing the Midwest of the United States of America, and also the Brazilian South-Southeastern-Central-West region with 1732 buses (SSECO1732) and the Brazilian interconnected system, consisting of 1993 buses.
In the computation experiments carried out, the primal-dual interior-point method was used and tests were run with the number of line manipulations varying from zero to six over a 24-hour period, which is what normally happens in practice in the Brazilian power system.
The implementation was developed using Matlab 7.0, with a precision of 10–3, in order to satisfy the optimal conditions of the problem. The computer has an Intel Centrino Core 2 Duo processor, with 4 GB of RAM and a speed of 2.13 GHz.
The branches to be manipulated in the grids were chosen randomly, and we emphasize that several tests were carried out and drastic differences from one test to another were noted, because the number of iterations and the computational time can vary significantly, depending on the branch that is being manipulated. If we were to disconnect a branch where the flow was high, the grid would have to find a new way of fulfilling the demand, thus reflecting on the number of iterations. However, other reasons may be responsible for the increase in the computational effort, because depending on the branches manipulated, the network resulting from these manipulations may not adapt very efficiently.
The first column of the Tables 1, 2 and 3 pertains to the number of manipulations and they are accumulative; for example, in the event of three manipulations, it consists of the branches previously manipulated (1 and 2) plus the new third branch.
Note that in all the tests carried out, the line manipulations represent a greater computational effort, but one that is acceptable due to the amount of support they provide to the grid. The number of iterations necessary for convergence may vary significantly, depending on the branch that is being manipulated. If a branch with a high flow is disconnected, the grid will have to find a new
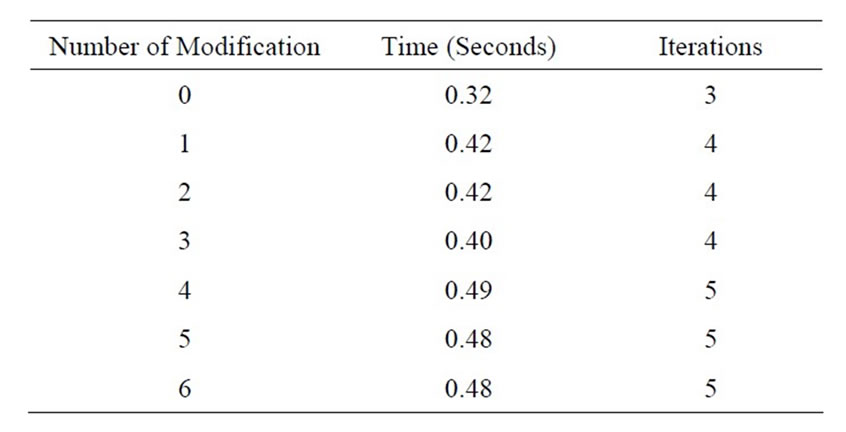
Table 1. IEEE30 system.

Table 2. SSECO1732 system.
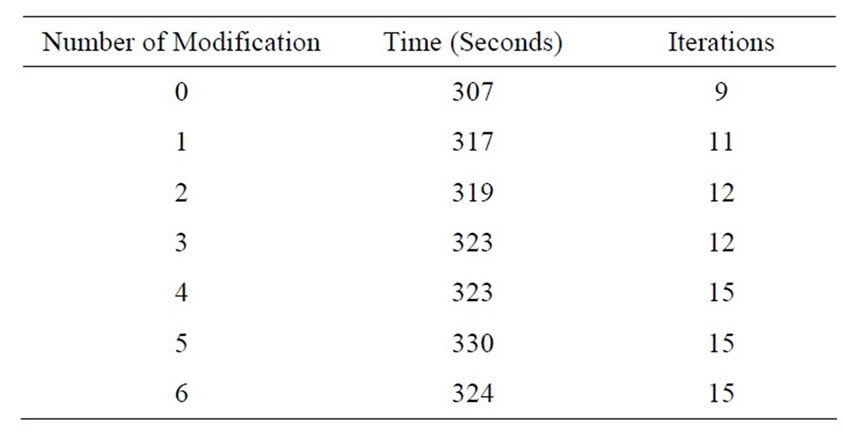
Table 3. Brazil 1993 system.
way through the network to fulfill the demand, reflecting on the number of iterations and, consequently, on the computational time. However, other factors may be responsible for this increase, because depending on the branch that is being manipulated and its resulting network, grid adaptation may not be very efficient.
In Table 1, the fourth manipulation was carried out in the branch with the greatest flow in the grid; note that in this case, the number of iterations and the computational time are greater compared to previous manipulations, therefore manipulating branches with this characteristic becomes a problem that is more challenging to solve. Similar event occurred in Table 3.
5. Conclusions
In this study, interior-point methods are used to solve a predispatch problem in a hydroelectric system. This research contributes to solving this problem with transmission line manipulations. When these manipulations take place, the topology of the network is altered. The characteristics of this problem and its importance to the Brazilian power system have been the drivers behind this research.
In practice, the number of modifications in the network is small, varying from zero to six over a 24-hour period. In this study, it is supposed that all changes in the network are known in advance. Thus, the matrices associated with the problem can be analyzed and decomposed before the interior-point methods are applied. An identical approach has been taken by other authors for a scenario without manipulations.
Line manipulations represent the disconnection and/or return to operational status, of certain transmission lines. For each occurrence of a line manipulation, a column in the incidence matrix and a row in the reactance matrix are removed. The methodology used in the development of this study is the primal-dual interior-point method, because this presents satisfactory results for optimum power flow problems.
From the computational standpoint, the effort to solve a problem with or without modification in network topology is similar. Even with the modifications in the problem matrix, the number of linear systems that need to be solved is still the same, compared to the problem without manipulations. Furthermore, the number of iterations necessary for the convergence of the interior-point method depends on how important the manipulated branches are to the grid.
The new method does not result in greater costs, although it is known that this depends heavily on the branches that are being disconnected, because if the load of a manipulated branch is very high, the grid may not be able to readapt, thus resulting in convergence challenges for the method. The efficiency of the methodology used in this study may be proven not only by means of convergence, but also for non-convergence of some of the tests carried out. Accordingly, it is possible to prove that the implementation actually optimizes the problems covered.
There are other existing approaches that consider scheduled transmission lines manipulation. For instance, line manipulation can be simulated. In this case, there is not network topology modification as oppose of the adopted approach. However, it presents stability difficulties and higher computational cost.
Thus, the solved model gets much closer to the actual problem with an insignificant additional computational effort, and without presenting any issues regarding numerical stability.
6. Acknowledgements
The authors would like to acknowledge the support given to their researches and studies by the Brazilian National Research Council (CNPq), the Brazilian Ministry of Education agency for graduate studies (CAPES) and the Research Foundation of the State of São Paulo (FAPESP).
REFERENCES
- A. Garzillo, M. Innorta and R. Ricci, “The Flexibility of Interior Point Based Power Flow Algorithms Facing Critical Network Situations,” Electrical Power E Energy Systems, Vol. 21, 1999, pp. 579-584.
- J. A. Momoh, M. E. El-Hawary and R. Adapa, “A Review of Selected Optimal Power Flow Literature to 1993, Part II Newton, Linear Programming and Interior Point Methods,” IEEE Transactions on Power Systems, Vol. 14, No. 1, 1999, pp. 105-111. doi:10.1109/59.744495
- V. H. Quintana, G. L. Torres and J. M. Palomo, “Interior Point Methods and Their Applications to Power Systems: A Classification of Publications and Software Codes,” IEEE Transactions on Power Systems, Vol. 15, No. 1, 2000, pp. 170-176. doi:10.1109/59.852117
- T. Ohishi, S. Soares and M. F. Carvalho, “Short Term Hydrothermal Scheduling Approach for Dominantly Hydro Systems,” IEEE Transactions on Power Systems, Vol. 6, No. 2, 1991, pp. 637-643. doi:10.1109/59.76707
- S. Soares and C. T. Salmazo, “Minimum Loss Predispatch Model for Hydroelectric Systems,” IEEE Transactions on Power Systems, Vol. 12, No. 3, 1997, pp. 1220- 1228. doi:10.1109/59.630464
- A. R. L Oliveira, S. Soares and L. Nepomuceno, “Optimal Active Power Dispatch Combining Network Flow and Interior Point Approaches,” IEEE Transactions on Power Systems, Vol. 18, No. 4, 2003, pp. 1235-1240. doi:10.1109/TPWRS.2003.814851
- R. Ahuja, T. Magnanti and J. B. Orlin, “Network Flows,” Prentice Hall, Englewood Cliffs, 1993.
- S. J. Wright, “Primal-Dual Interior Point Methods,” SIAM Publications, Philadelphia, 1996.
- L. M. R. Carvalho and A. R. L. Oliveira, “Primal-Dual Interior Point Method Applied to the Short Term Hydroelectric Scheduling Including a Perturbing Parameter,” IEEE Latin America Transactions, Vol. 7, No. 2, 2009, pp. 533-538. doi:10.1109/TLA.2009.5361190
- I. S. Duff, A. M. Erisman and J. K. Reid, “Direct Methods for Sparse Matrices,” Clarendon Press, Oxford, 1986.
- G. H. Golub and C. F. Van Loan, “Matrix Computations,” 2nd Edition, The Johns Hopkins University Press, Baltimore, 1989.
- A. R. L. Oliveira, S. Soares and L. Nepomuceno, “Short Term Hydroelectric Scheduling Combining Network Flow and Interior Point Approaches,” Electrical Power & Energy Systems, Vol. 27, No. 2, 2005, pp. 91-99.

