Wireless Sensor Network, 2010, 2, 300-308
doi:10.4236/wsn.2010.24041 Published Online April 2010 (http://www.SciRP.org/journal/wsn)
READA: Redundancy Elimination for Accurate Data
Aggregation in Wireless Sensor Networks
Kavi Khedo, Rubeena Doomun, Sonum Aucharuz
Faculty of Engineering, University of Mauritius, Réduit, Mauritius
Received January 14, 2010; revised February 20, 2010; accepted March 4, 2010
Abstract
In monitoring systems, multiple sensor nodes can detect a single target of interest simultaneously and the
data collected are usually highly correlated and redundant. If each node sends data to the base station, energy
will be wasted and thus the network energy will be depleted quickly. Data aggregation is an important para-
digm for compressing data so that the energy of the network is spent efficiently. In this paper, a novel data
aggregation algorithm called Redundancy Elimination for Accurate Data Aggregation (READA) has been
proposed. By exploiting the range of spatial correlations of data in the network, READA applies a grouping
and compression mechanism to remove duplicate data in the aggregated set of data to be sent to the base sta-
tion without largely losing the accuracy of the final aggregated data. One peculiarity of READA is that it
uses a prediction model derived from cached values to confirm whether any outlier is actually an event
which has occurred. From the various simulations conducted, it was observed that in READA the accuracy
of data has been highly preserved taking into consideration the energy dissipated for aggregating the data.
Keywords: Sensor Networks, Data Aggregation, Data Compression, Event Detection, Redundancy Elimination
1. Introduction
Advancement in wireless communication technologies
and low-cost wireless devices for networking has initi-
ated the emergence of a new type of wireless network,
called wireless sensor network (WSN). WSN is a net-
work consisting of a large number of sensor nodes that
are deployed in an ad hoc manner over an area. For ex-
ample, hundreds of sensors are spread out in an external
or internal environment to measure the temperature, light
intensity, humidity, noise level or any other physical
conditions in its locality. The attractive feature of all
these sensor nodes is that they can be self-organised and
interconnected to form a network over which they can do
cooperative processing to accomplish tasks that they
cannot do individually [1].
Wireless sensor networks are being used in many dif-
ferent applications, initially for military networks as well
as in other areas like environment, health, habitat moni-
toring and commercial purposes. With the recent break-
through of “MicroElectroMechanical Systems (MEMS)”
technology [2] whereby sensors are becoming smaller
and more versatile, WSN promises many new applica-
tion areas in the future.
Data aggregation minimizes redundant data which in
turn reduces the number of packets transmitted to the
base station resulting in conservation of energy and
bandwidth. Since data aggregation transmits only the
useful or resultant information to the end point, the
problem of network congestion, traffic implosion and
overlap can be overcome [3]. In classic flooding, nodes
do not modify their activities based on the amount of
energy available to them at a given time. Data aggrega-
tion techniques make the nodes of the network to be “re-
source-aware”, i.e. adapt their communication and com-
putation to the state of their energy resources.
The main goal of data aggregation is to collect and
‘combine’ data in an energy efficient manner so that the
lifespan of the WSN is maximised. The design of an ef-
ficient data aggregation algorithm is a challenging re-
search problem. Several performance measures like net-
work lifetime, data accuracy, false alarm, high data re-
dundancy, latency and scalability need to be considered
concurrently [4,5].
2. Related Works
In this section, some important existing aggregation
techniques are discussed and their underlying assump-

K. KHEDO ET AL.301
tions and drawbacks are considered.
2.1. Greedy Aggregation
In greedy aggregation [5,6], a tree is constructed to indi-
cate the path from each sensor node to the sink. The
shortest path linking a node to the sink is used as an ini-
tialization of the tree. Then, the shortest paths linking the
remaining nodes to the current tree will be incrementally
added to enlarge the tree.
With this technique, the packets will be aggregated as
early as possible and the aggregated packet will be directly
routed back to the sink. However, the efficiency of the
greedy incremental method is entirely determined by the
shortest path. The data transmission is not reliable since
once the path is broken, a large region will be discon-
nected and will not be able to send information to the sink.
2.2. Tiny Aggregation (TAG)
Tiny Aggregation (TAG) by Madden et al. [7,8] is a
generic aggregation service that executes efficiently sim-
ple declarative queries. It is based on aggregation trees.
The principal advantage of TAG is its ability to dramati-
cally decrease the amount of communication required to
compute an aggregate versus a centralized aggregation
approach. TAG can tolerate loss due to information
about queries in partial state records. Lost nodes can re-
connect by listening to other sensor’s state records—not
necessarily intended for them—as they flow up the tree.
Another advantage of the TAG approach is that usu-
ally each sensor is required to transmit only a single
message per epoch, regardless of its depth in the routing
tree. In the centralized (non TAG) case, as data con-
verges towards the root, nodes at the top of the tree are
required to transmit significantly more data than nodes at
the leaves. Thus, their batteries are drained faster and the
lifetime of the network is limited. TAG may be ineffi-
cient for dynamic topologies or link failures. Failures at
intermediate nodes lead to a disconnected sub tree. In
addition, as the topology changes, TAG has to reorganize
the tree structure, which means high costs in terms of
energy consumption and overhead.
2.3. Hybrid Energy Efficient Distributed
Clustering Approach (HEED)
HEED is a protocol proposed by Younis et al. [9,10]. In
this approach, efficient clusters are formed for maximiz-
ing network lifetime. The main assumption in HEED is
the availability of multiple power levels at sensor nodes.
However, HEED does not make assumptions about the
distribution of nodes or about node location-awareness.
Cluster head selection is based on the residual energy of
each node and a secondary parameter which depends on
the node proximity to its neighbors. The cost of a cluster
head is defined as its average minimum reachability
power (AMRP). AMRP is the average of the minimum
power levels required by all nodes within the cluster
range to reach the cluster head. AMRP provides an esti-
mate of the communication cost. At every iteration of
HEED, each node which has not been selected as a clus-
ter head sets its probability PCH of becoming the cluster
head as:
PCH = C * Eresidual / Emax
where C denotes the initial percentage of cluster heads
(specified by the user);
Eresidual is the estimated current residual energy of
the node;
Emax is its initial energy corresponding to a fully
charged battery.
HEED objectives are to prolong network lifetime by
distributing energy consumption. HEED cluster heads
are well distributed regardless of how the nodes are dis-
tributed in the network. This helps in maintaining high
path quality at the inter-cluster level. In HEED, cluster
heads are randomly selected based on their residual en-
ergy. Therefore, HEED cannot guarantee optimal head
selection in terms of energy since it uses the secondary
parameter to resolve conflicts. The cluster head is deter-
mined by repeated iterations. Thus, it requires a complex
algorithm to calculate the number of rounds of iterations.
Also, inter cluster communication has not been consid-
ered in HEED.
3. Problem Statement
Nodes in a WSN sense the environment and send the
collected data to the base station. Many nodes report
similar readings as data in a WSN are correlated. Thus, a
large amount of energy is spent during the transmission
of thousands of redundant data. Furthermore, as nodes
transmit sensed values to the base station by transiting
through intermediate nodes, significant energy is spent in
communication. One technique used to decrease the
number of redundant messages transmitted and thus pro-
long the network lifetime is data aggregation. During
data aggregation, intermediate nodes merge the data re-
ceived from other nodes into a single representative
value. The energy of the network is conserved through a
reduction in the number of messages being exchanged
among nodes. However, in many current data aggrega-
tion techniques, a significant number of redundant mes-
sages still reach the base station. The lifetime of the sen-
sor network is constantly faced by stringent energy con-
sumptions. Other data aggregation techniques have been
able to decrease the number of transmissions but at the

K. KHEDO ET AL. 302
cost of accuracy of final aggregates. Furthermore, if an
uncorrelated (outlier) reading is sensed by a node, most
data aggregation algorithms discard the outlier. The ac-
curacy of the aggregate is again distorted by discarding
such data. So far, no existing technique has been able to
attenuate the limitations of data aggregation, explaining
the wide research undertaken in this field.
4. Proposed Data Aggregation System
For the proposed data aggregation technique, the nodes
will be organised into clusters where one node in each
cluster will act as the clusterhead. Using the advanta-
geous converging features of tree-based approach, inside
each cluster the nodes will be arranged in a tree structure
where the clusterhead will be the root.
This section introduces a new data aggregation tech-
nique called “Redundancy Elimination for Accurate
Data Aggregation” (READA). The first part briefly
describes the system design. The second part explains
how data aggregation is performed in the monitoring
system and in the event detection system. The last part
describes the energy model that has been considered for
designing the technique.
4.1. System Model
A number of sensor nodes (N) are uniformly and ran-
domly distributed in an area as shown schematically in
Figure 1. In the simulation environment, this can be
achieved by randomly assigning an X-coordinate and
Y-coordinate in an area of R × R m2. It is assumed that
all node in the network (as well as the clusterhead) to be
stationary and quasi-stationary. After the sensor nodes
have been uniformly deployed over the sensor network
field, the first stage of the algorithm is to form the clus-
ters. A cluster protocol HEED as discussed in Section 2.3
is used for the cluster formation. The parameter used to
choose a clusterhead (CH) is based on the node’s
Figure 1. Network structure.
residual energy. The node with highest residual energy
among the tentative clusterheads is chosen as clusterhead
(CH). Once selected, the clusterhead advertises its status
to all nodes in the cluster. The clusterhead needs not be
necessarily in the centre of a cluster. The clusterhead can
be positioned anywhere in the cluster, and it is assumed
that all nodes in a cluster have a least a route to reach the
clusterhead. If two or more nodes have the same highest
residual energy, then randomly one of them is selected as
the clusterhead.
The HEED clustering algorithm is run every T unit of
time (or after T number of transmissions), where T gen-
erally depends on the type of application and initial bat-
tery energy of nodes. Each T unit of time is divided into
M rounds. In each round, a clusterhead receives observed
data from nodes within its cluster.
The next stage of READA is to construct a tree within
each cluster. The tree is constructed so that the workload
of aggregating data is shared by every parent node rather
than the clusterhead doing all the jobs. The clusterhead is
chosen as root and sets its level to zero. It then broadcast
a message to its single hop neighbours. Upon receiving
the message, the nodes set their parent ID to that of the
ID of where they received the message, i.e., ID of root
and the level is incremented by 1. Then, they broadcast a
message to their respective single hop neighbours. The
process is repeated until all nodes in the cluster have a
parent.
4.2. Aggregation
Aggregation will be performed for two types of events:
monitoring system and event detection.
Correlation coefficient
Sensor nodes across a network field collect readings
that span over a range of values. The larger the size of
the network, the readings collected from different areas
of the field span over larger ranges. Consider thousands
of sensors deployed over hectares of forest land for fire
detections as shown in Figure 2.
The nodes in the “red region” are spatially correlated,
that is, close nodes detect similar (but not equal) values.
Figure 2. Different ranges of temperature value recorded
over a large forest region.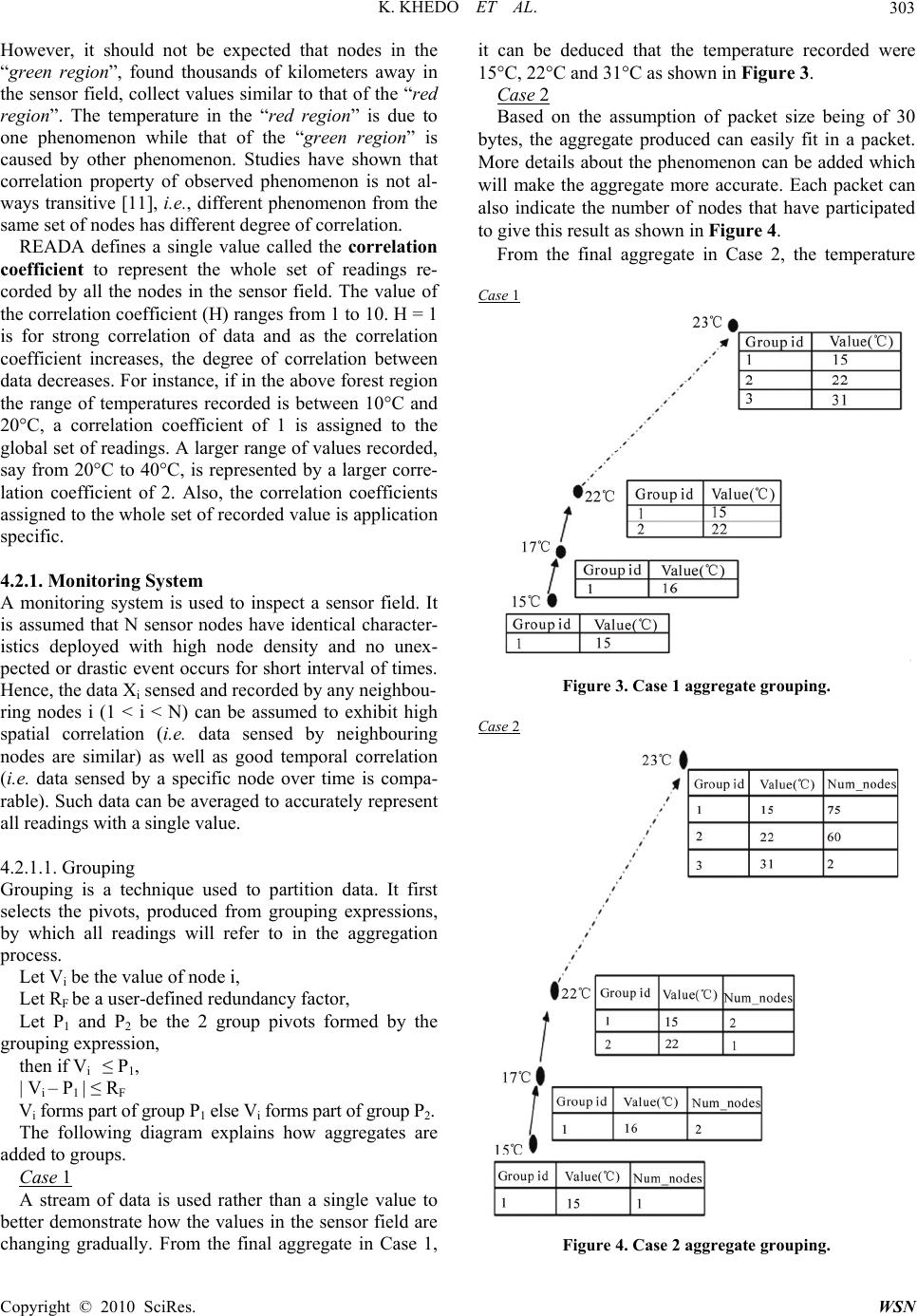

K. KHEDO ET AL.303
However, it should not be expected that nodes in the
“green region”, found thousands of kilometers away in
the sensor field, collect values similar to that of the “red
region”. The temperature in the “red region” is due to
one phenomenon while that of the “green region” is
caused by other phenomenon. Studies have shown that
correlation property of observed phenomenon is not al-
ways transitive [11], i.e., different phenomenon from the
same set of nodes has different degree of correlation.
READA defines a single value called the correlation
coefficient to represent the whole set of readings re-
corded by all the nodes in the sensor field. The value of
the correlation coefficient (H) ranges from 1 to 10. H = 1
is for strong correlation of data and as the correlation
coefficient increases, the degree of correlation between
data decreases. For instance, if in the above forest region
the range of temperatures recorded is between 10°C and
20°C, a correlation coefficient of 1 is assigned to the
global set of readings. A larger range of values recorded,
say from 20°C to 40°C, is represented by a larger corre-
lation coefficient of 2. Also, the correlation coefficients
assigned to the whole set of recorded value is application
specific.
4.2.1. Monitoring System
A monitoring system is used to inspect a sensor field. It
is assumed that N sensor nodes have identical character-
istics deployed with high node density and no unex-
pected or drastic event occurs for short interval of times.
Hence, the data Xi sensed and recorded by any neighbou-
ring nodes i (1 < i < N) can be assumed to exhibit high
spatial correlation (i.e. data sensed by neighbouring
nodes are similar) as well as good temporal correlation
(i.e. data sensed by a specific node over time is compa-
rable). Such data can be averaged to accurately represent
all readings with a single value.
4.2.1.1. Grouping
Grouping is a technique used to partition data. It first
selects the pivots, produced from grouping expressions,
by which all readings will refer to in the aggregation
process.
Let Vi be the value of node i,
Let RF be a user-defined redundancy factor,
Let P1 and P2 be the 2 group pivots formed by the
grouping expression,
then if Vi ≤ P1,
| Vi – P1 | ≤ RF
Vi forms part of group P1 else Vi forms part of group P2.
The following diagram explains how aggregates are
added to groups.
Case 1
A stream of data is used rather than a single value to
better demonstrate how the values in the sensor field are
changing gradually. From the final aggregate in Case 1,
it can be deduced that the temperature recorded were
15°C, 22°C and 31°C as shown in Figure 3.
Case 2
Based on the assumption of packet size being of 30
bytes, the aggregate produced can easily fit in a packet.
More details about the phenomenon can be added which
will make the aggregate more accurate. Each packet can
also indicate the number of nodes that have participated
to give this result as shown in Figure 4.
From the final aggregate in Case 2, the temperature
Case 1
Figure 3. Case 1 aggregate grouping.
Case 2
Figure 4. Case 2 aggregate grouping.

K. KHEDO ET AL. 304
recorded were 15°C, 22°C and 31°C. It can also be seen
that a larger number of nodes detected a reading of 15°C
and 22°C, while a temperature of 31°C was merely pre-
sent among other nodes.
4.2.1.2. Compression
Since the group pivots are known by the base station,
instead of representing the aggregate of each group by
the actual value, it can be represented by a group ID.
Furthermore, data in the group can be compressed in-
stead of sending all data as shown in Figure 5.
Representation of a group:
[group ID | compressed value | Number of nodes
participating]
Consider the following set of data A where pivot 1 is
10 with group ID = 1, pivot 2 is 20 with group ID = 2
and pivot 3 is 30 with group ID = 3.
Knowing that energy utilisation is proportional to
number of bits transmitted, the energy spent in sending
the set A1 is much smaller than the energy spent in send-
ing the set A.
4.2.1.3. Excess Groups
Generally, sensor nodes are deficient in memory capacity,
the amount of data that can be stored and transmitted is
limited. In the design, for simulation purposes, it is as-
sumed that no more than seven data groups can fit in the
sensor node memory. This design assumption does not
impact the simulation as a sensor node will only be re-
quired to communicate with its neighbours and its mem-
ory space will not be overloaded.
Decision Point 1
In order to maintain the accuracy and prevent the loss
of data, information cannot be discarded. The strategy
adopted is to merge groups into a single group while
maintaining the accuracy of the aggregate. The choice of
the groups to be merged is to look at the proximity be-
tween aggregates in neighbouring groups. READA
analyses the groups which are closer to each other and
Figure 5. Compression.
then merges those groups as illustrated in Figure 6 below.
Since the difference in the values of group 0 and group
1 is very small, it is best to merge these 2 groups into 1
group.
Decision Point 2
After the groups to be merged have been identified, it
is necessary to identify which one of the two groups has
to be evicted and which one has to be retained. READA
determines the proximity of the first aggregate from each
group and performs a weighted average. In the above
diagram, since value 9 is closer to group 1, group 1 is
given a weight of 2 and group 0 is given a weight of 1.
Thus, the final aggregate is as shown in Figure 7 be-
low:
4.2.2. Event Detection
READA is basically a monitoring system where nodes
can periodically switch to idle mode. Idle mode enables
energy savings in sensor nodes that are neither transmit-
ting nor receiving packets. However, READA can also
behave as an event detection system where nodes con-
tinuously sense the environment and report if an unusual
behaviour is noted. An event is defined as a different
behaviour, i.e. , which does not exhibit correlation over a
similar region. An abnormal data sensed need not neces-
sarily be an event as it might be a false alarm. In such
situation, READA analyses the cached data of its
neighbouring nodes, extrapolates their values to deter-
mine whether the abnormal data sensed was actually an
event not a false alarm. The event is reported only if the
Figure 6. Merging groups.
Figure 7. Final aggregate.

K. KHEDO ET AL.305
probability of the occurrence of the event passes a user-
defined confidence level.
4.2.2.1. Outlier Detection
Intermediate node analyses the set of results obtained
from its child nodes together with its own to ensure there
is spatial correlation among all the readings. The tech-
nique used is similar to the method used in Lightweight
Temporal Compression (LTC) [12]. Since environmental
data have a nice property that they are usually continuous
in the temporal dimension and at small enough time
windows are approximately linear, all the results can be
continuously mapped onto a line. However, in the pres-
ence of an outlier the point can no longer fit on that line.
The graphs below represent how the points are mapped
onto the same line and how an outlier deviates from the
mapped line of spatially correlated data.
In Case 1, the first point S1 is set as a sample point. A
highline and a lowline are chosen to represent data with a
certain error margin, e, from the point S2 as shown in
Figure 8. The shaded area represents all the possible
values that can fit between the two values. The next point
fits between highline and lowline and thus, the next plot-
ted value shows spatial correlation.
In Case 2, shown in Figure 9, there is the presence of
outliers as the points do not fit in the correlation space.
Hence, they cannot be plotted in the shaded region.
4.2.2.2. Least Square Extrapolation
In order to perform an extrapolation, READA requires
the parent nodes to cache at least two previous values of
their child nodes. A suitable extrapolation technique is
Case 1
Figure 8. Case 1 outlier detection.
Case 2
Figure 9. Case 2 outlier detection.
the Least Square Extrapolation as environmental variable
tends to change linearly over time. The choice of Least
Square is based on its low complexity which makes it
appropriate for low battery power and memory deficient
nodes compared to other extrapolation techniques.
The following formula is used to identify the trend line
through the data:
γ, the trend for a given time period = a + bx
where
22
b()
a =
nxy xy
nx x
yx
b
nn







x refers to the cached time values.
y refers to the cached values .
When an outlier has been detected, the parent node
decides to make an extrapolation based on cached values.
The aim of doing so is to predict the occurrence of an
event. If the extrapolated value corresponds to a certain
degree to the outlier, events can be identified. However,
if the extrapolated value is overestimated or underesti-
mated, the outlier is declared as a false alarm.
5. Experimental Results and Evaluation
In this section, simulations are carried out to demonstrate
the performance of READA. Two other techniques are
compared with READA to show its performance in
terms of energy efficiency, accuracy and outlier detec-
tion. From the several simulation scenarios, the results
are plotted graphically for analysis and evaluation.
READA will be compared with Conventional data
aggregation which allows all unique sensed data to ar-
rive at the base station. All sensor nodes collect data
from the child nodes arranged in a tree like structure,
concatenate the message with their own sensed data and
forward the aggregate up the tree. Conventional data ag-
gregation has been chosen to demonstrate how data ag-
gregation affects the status of sensor networks. READA is
also compared with another algorithm called Tiny Ag-

K. KHEDO ET AL. 306
The values and graphs in Table 1 and Figure 10 show
that READA spends ranging from 23% to 27% less than
Conventional method. This is for the obvious reason that
Conventional method does not perform any aggregation.
Hence READA has saved an average of 25% of energy
in one round of the running of the data aggregation
process.
gregation (TAG). TAG uses a grouping mechanism for
aggregating data.
Correlation Coefficient
During the simulation, the data range is assumed to be
in the set [0…100]. Thus, ranges of data with different
degree of correlation from this set are used. The correla-
tion coefficient is defined as a measure of the spread of the
set of data. For example [0…10], the correlation coeffi-
cient is 1, [0…50] it is 5, [0…100] it is 10 and so on.
The values and graphs in Table 1 and Figure 11 show
that READA spends (~9%) more amount of energy than
TAG when number of nodes is 500 (Run 1). However,
when the number of nodes increases, the amount of en-
ergy dissipated is approximately the same as that of TAG.
As the correlation coefficient increases, data become
more uncorrelated and the energy consumed is higher as
the packet size is greater. This is because both TAG and
READA has a tree structure where they have to route up
the data and this consumed energy because of greater
exchange in number of bits transmissions.
Accuracy
The Mean Average Deviation (MAD) approach is
used to determine accuracy of data. The accuracy in the
simulations is expressed in terms of the average devia-
tion of the estimated mean to the actual mean. A higher
MAD value implies lower data accuracy.
Accuracy ≈
100
|EstimatedMean-ActualMean |
Actual Mean
5.2. Accuracy Comparison
5.1. Energy Comparison
A combined table of values obtained by READA and
TAG is shown in Table 2 to better assess their accuracy
performance.
A combined table of values obtained by READA, TAG
and conventional is shown in Table 1 to better assess
their energy efficiency.
Table 1. Combined energy.
Corr.Coeff = 1 Corr.Coeff = 2 Corr.Coeff = 3 Corr.Coeff = 4 Corr.Coeff = 5
Number
of nodesTAGREADACon.TAG READACon.TAG READACon.TAG READACon.TAG READACon.
500 45.4749.3758.1746.6550.6858.8947.4151.5059.5148.5352.5561.7749.4354.0065.67
1000 90.9294.95119.0193.3396.79121.4394.8798.32123.9497.02100.86129.3198.87102.97133.45
1500 136.38140.63179.58139.87143.35185.09141.99145.47188.20145.87148.65196.05148.06151.98204.88
2000 181.81186.00240.05186.50189.64248.67189.75192.23253.40193.86196.58264.45197.56199.67274.67
2500 227.21231.50300.67233.25236.05311.28237.01238.79319.39242.10243.40331.04246.79248.97348.58
3000 272.68277.12366.93279.85281.86373.57284.59285.71382.45290.79291.49403.12295.99298.40421.30
Table 2. Combined accuracy.
Corr.Coeff = 1 Corr.Coeff = 2 Corr.Coeff = 3 Corr.Coeff = 4 Corr.Coeff = 5
Number
of nodesTAG-1READA-1 TAG-2 READA-2 TAG-3 READA-3 TAG-4 READA-4 TAG-5READA-5
500 178 1.13 1.37 1.07 1.52 0.87 1.58 0.85 1.56 0.24
1000 188 1.30 1.75 1.14 1.55 1.07 1.00 0.64 1.86 0.53
1500 1.57 1.27 1.70 1.14 1.51 1.08 1.06 0.31 2.80 1.61
2000 1.85 1.29 1.73 1.00 1.54 1.00 2.00 0.08 3.02 2.04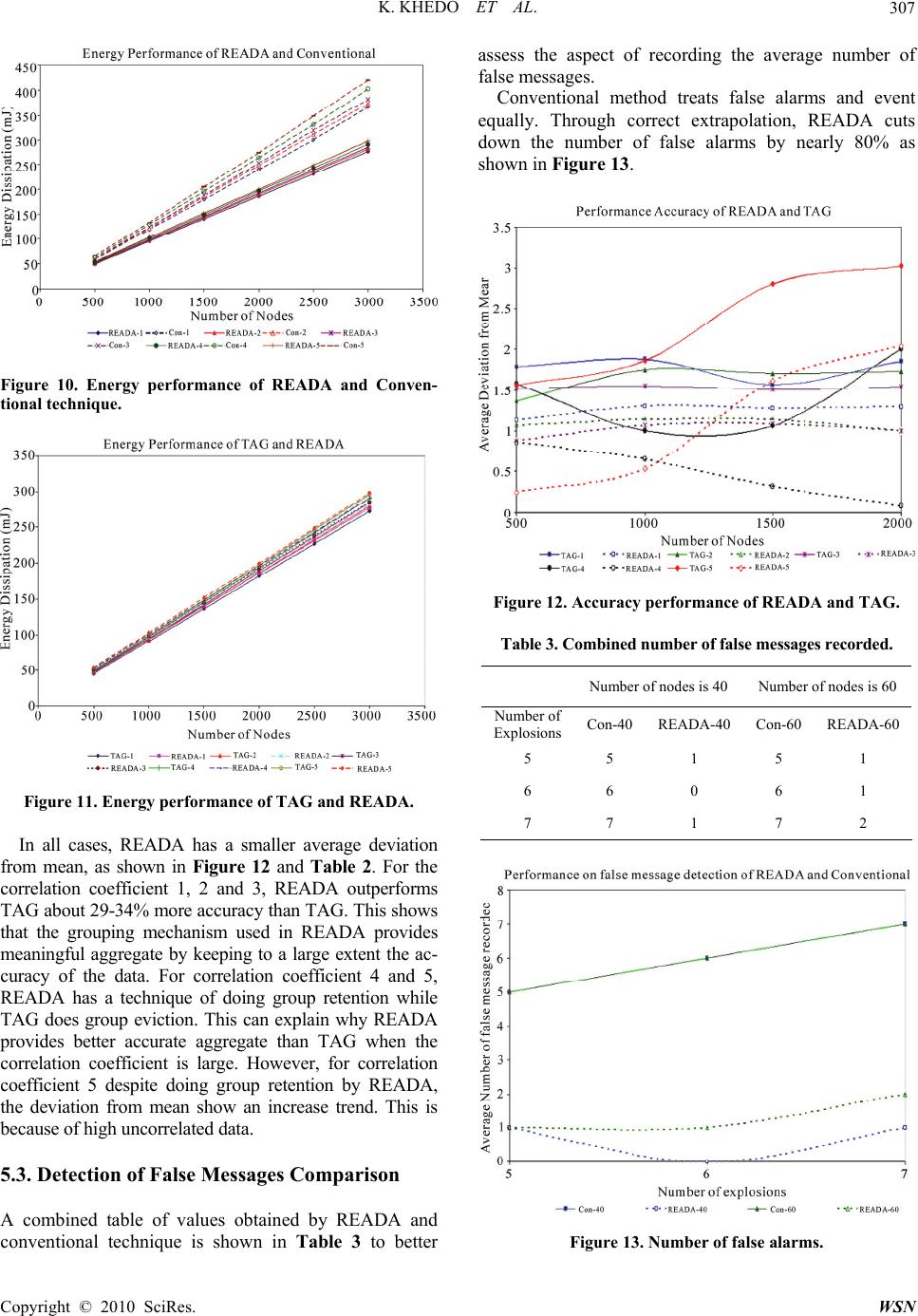

K. KHEDO ET AL. 307
Figure 10. Energy performance of READA and Conven-
tional technique.
Figure 11. Energy performance of TAG and READA.
In all cases, READA has a smaller average deviation
from mean, as shown in Figure 12 and Table 2. For the
correlation coefficient 1, 2 and 3, READA outperforms
TAG about 29-34% more accuracy than TAG. This shows
that the grouping mechanism used in READA provides
meaningful aggregate by keeping to a large extent the ac-
curacy of the data. For correlation coefficient 4 and 5,
READA has a technique of doing group retention while
TAG does group eviction. This can explain why READA
provides better accurate aggregate than TAG when the
correlation coefficient is large. However, for correlation
coefficient 5 despite doing group retention by READA,
the deviation from mean show an increase trend. This is
because of high uncorrelated data.
5.3. Detection of False Messages Comparison
A combined table of values obtained by READA and
conventional technique is shown in Table 3 to better
assess the aspect of recording the average number of
false messages.
Conventional method treats false alarms and event
equally. Through correct extrapolation, READA cuts
down the number of false alarms by nearly 80% as
shown in Figure 13.
Figure 12. Accuracy performance of READA and TAG.
Table 3. Combined number of false messages recorded.
Number of nodes is 40 Number of nodes is 60
Number of
Explosions Con-40READA-40 Con-60READA-60
5 5 1 5 1
6 6 0 6 1
7 7 1 7 2
Figure 13. Number of false alarms.

K. KHEDO ET AL. 308
6. Conclusions
The strategy adopted by READA is a grouping and
compression mechanism to produce a compressed but
accurate aggregate. Since the set of data sensed exhibit
high spatial correlation, READA partitions them into
groups. A group consists of a group id, the compressed
value and the number of nodes participating to give this
compressed value. The group id is the pivot which has
been determined by the base station. Since sensor nodes
are deficient in memory capabilities, when there are an
excess number of groups, the value in the two groups is
merged based on the proximity of the aggregate in the two
groups. The decision of group eviction and group retention
is determined by performing a weighted average.
Another aspect of READA is outlier detection, that is,
data that do not conform to the correlation space. Taking
the advantage of the high degree of spatial correlations
that exist among the sensor readings of the adjacent
nodes in a densely deployed WSN, outliers can be de-
tected if a prediction model is used. READA uses Least
Square Extrapolation based on cached data to determine
whether the outlier is actually an event that has occurred
or a false alarm. From simulation results gathered,
READA offers some 25% in terms of energy saved
compared to conventional data aggregation and READA’s
accuracy was on average 40% more than TAG. It con-
siderably outperforms TAG in terms of accuracy per-
formance and outlier detection. READA can find out
whether an outlier is a false alarm or an event that the
base station needs to be informed about. Nearly 80 % of
false alarms can be filtered.
7. References
[1] I. F. Akyildiz, W. Su, Y. Sankarasubramaniam and E.
Cayirci, “Wireless Sensor Networks: A Survey,” El-
servier Computer Networks, Vol. 38, No. 4, March 2002,
pp. 393-422.
[2] B. Warneke and K. S. J. Pister, “MEMS for Distributed
Wireless Sensor Networks,” 9th International Conference
on Electronics, Circuits and Systems, Dubrovnik, 15-18
September 2002.
[3] J. Kulik, W. R. Heinzelman and H. Balakrishnan, “Nego-
tiation-Based Protocols for Disseminating Information in
Wireless Sensor Networks,” Wireless Networks, Vol. 8,
March 2002, pp. 169-185.
[4] R. Rajagopalan and P. K. Varshney, “Data-Aggregation
Techniques in Sensor Networks: A Survey,” IEEE Com-
munication Surveys and Tutorials, Vol. 8, No. 4, December
2006, pp. 48-63.
[5] X. Li, “A Survey on Data Aggregation in Wireless Sensor
Networks,” Project Report for CMPT 765, Spring 2006.
[6] H. Albert, R. Kravets and I. Gupta, “Building Trees
Based On Aggregation Efficiency in Sensor Networks,”
Ad Hoc Networks, Vol. 5, No. 8, November 2007, pp.
1317-1328.
[7] S. R. Madden, M. J. Franklin, J. M. Hellerstein and W.
Hong, “TAG: Tiny Aggregation Service for Ad-Hoc
Sensor Networks,” Proceedings of the 5th symposium on
Operating Systems Design and Implementation, Boston,
December 2002.
[8] E. Fasolo, M. Rossi, J. Widmer and M. Zorzi,
“In-network Aggregation Techniques for Wireless Sensor
Networks: A Survey,” IEEE Wireless Communications,
Vol. 14, No. 2, April 2007, pp. 70-87.
[9] O. Younis and S. Fahmy, “HEED: A Hybrid, Energy
Efficient, Distributed Clustering Approach for Ad-hoc
Sensor Networks,” Proceedings of IEEE Transactions on
Mobile Computing, Vol. 3, No. 4, October-December
2004, pp. 366-379.
[10] R. Rajagopalan and P. K. Varshney, “Data-Aggregation
Techniques in Sensor Networks: A Survey,” IEEE Com-
munication Surveys and Tutorials, Vol. 8, No. 4, December
2006, pp. 48-63.
[11] S. Tanachaiwiwat and A. Helmy, “Correlation Analysis
for Alleviating Effects of Inserted Data in Wireless Sen-
sor Networks,” Proceedings of the 2nd Annual Interna-
tional Conference on Mobile and Ubiquitous Systems: Net-
working and Services, San Diego, July 2005, pp. 97- 108.
[12] T. Schoellhammer, B. Greenstein, E. Osterweil, M. Wim-
brow and D. Estrin, “Lightweight Temporal Compression
of Microclimate Datasets,” 29th Annual IEEE Interna-
tional Conference on Local Computer Networks, Wash-
ington, DC, November 2004, pp. 516-524.