Engineering, 2010, 2, 166-171
doi:10.4236/eng.2010.23023 lished Online March 2010 (http://www.SciRP.org/journal/eng/)
Pub
Modifications in the Stress Field of a Long Inclined Fault
Caused by the Welded-Contact Boundary Conditions
across the Interface between Two Elastic Half-Spaces
Sunita Rani1, Sarva Jit Singh2
1Department of Mathematics, Guru Jambheshwar University of Science and Technology, Hisar, India
2Department of Mathematics, University of Delhi, New Delhi, India
Received October 6, 2009; revised November 18, 2009; accepted November 22, 2009
Abstract
In welded-contact boundary conditions, some stress components are not required to be continuous across the
boundary between two elastic half-spaces. The purpose of this note is to study the modifications in the stress
field of a long inclined strike-slip, dip-slip or tensile fault caused by the welded-contact boundary conditions
across the interface between two elastic half-spaces. The Poisson’s ratios of the two half-spaces do not ap-
pear in the stress field of a strike-slip fault. In the case of a dip-slip fault, the Poisson’s ratio of the half-space
in which the fault lies, has a significant influence on the stress field across the interface. However, for a ten-
sile fault, the modification in the stress field is significantly affected by the Poisson’s ratios of both the
half-spaces.
Keywords: Dip-Slip Fault, Stress Field, Strike-Slip Fault, Tensile Fault, Two-Dimensional, Welded-Contact
1. Introduction
Elastic dislocation theory has been developed and ap-
plied for the mathematical and physical description of
mechanics of earthquakes [1-4]. Extensive reviews of the
application of the elastic dislocation theory to earthquake
faulting problems have been given by Savage [5] and
Rybicki [6]. Using this theory, stress field around earth-
quake faults can be calculated in a straightforward man-
ner. Both two- and three-dimensional fault models have
been used in the literature. Considering the fact that
some of the faults are sufficiently long, the two-dimen-
sional fault model is found to be adequate in many situa-
tions. Since the Earth is not homogeneous, it is necessary
to consider the effect of internal boundaries on the stress
field generated by earthquake faults. The knowledge of
the modification of the stress field caused by internal
boundaries is useful to study secondary faulting.
Bonafede and Rivalta [7] obtained a plane strain ana-
lytic solution for the displacement and stress fields pro-
duced by a long vertical tensile dislocation in the prox-
imity of the interface between two elastic half-spaces in
welded contact. After detailed numerical computations,
they observed that the welded-contact boundary condi-
tions between a hard half-space and a soft half-space are
responsible for major changes in the stress field. The
stress component, which is not involved in the boundary
conditions, is significantly higher along the hard side of
the interface. In a subsequent paper, Bonafede and Ri-
valta [8] derived the corresponding solution for a long
vertical tensile crack. They noted that the discontinuities
in the elastic parameters across the boundary act as stress
concentrators for the stress component not involved in
the boundary conditions.
Rivalta et al. [9] provided a plane strain analytic solu-
tion for the displacement and stress fields induced by an
edge dislocation in an elastic half-space in welded con-
tact with another elastic half-space. They found unexpec-
ted differences in the normal component of stress parallel
to the interface which is not required to be continuous at
the interface by the boundary conditions. This stress com-
ponent shows wide regions of high stress in the harder
side of the interface. Stress concentration along the interf-
ace is particularly high when the rigidity contrast is high.
In a recent paper, Rybicki and Yamashita [10] derived
formulas for two-dimensional anti-plane and in-plane
problems relating stresses across a plane boundary be-
tween two elastic half-spaces in welded contact, assum-
ing a homogeneous shear stress in one of the two half-
spaces. They concluded that the mechanical conditions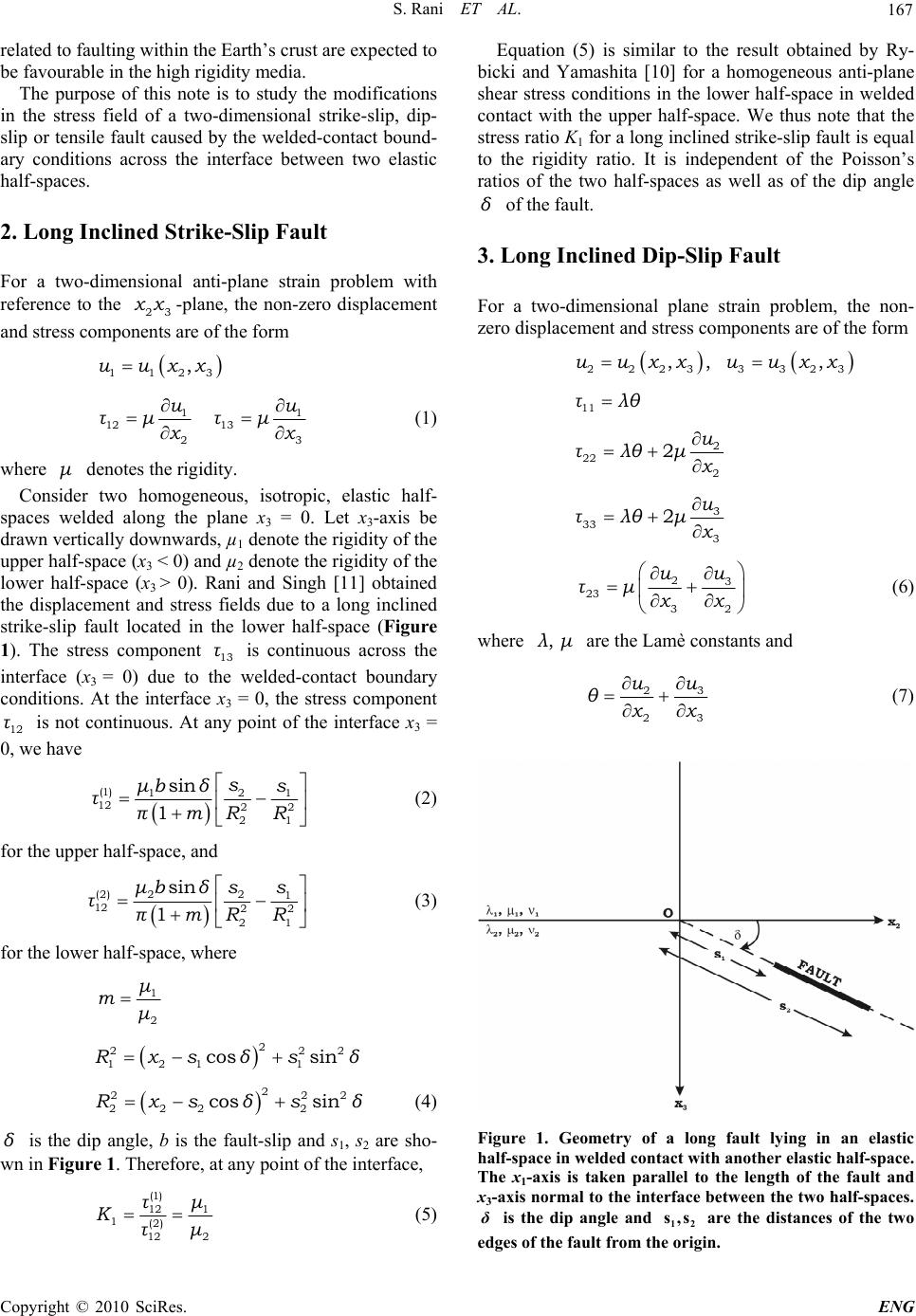

S. Rani ET AL. 167
related to faulting within the Earth’s crust are expected to
be favourable in the high rigidity media.
The purpose of this note is to study the modifications
in the stress field of a two-dimensional strike-slip, dip-
slip or tensile fault caused by the welded-contact bound-
ary conditions across the interface between two elastic
half-spaces.
2. Long Inclined Strike-Slip Fault
For a two-dimensional anti-plane strain problem with
reference to the -plane, the non-zero displacement
and stress components are of the form
23
xx


1123
,uuxx



1
12 13
23
u
τμ τμ
xx

1
u
(1)
where denotes the rigidity.
μ
Consider two homogeneous, isotropic, elastic half-
spaces welded along the plane x3 = 0. Let x3-axis be
drawn vertically downwards, µ1 denote the rigidity of the
upper half-space (x3 < 0) and µ2 denote the rigidity of the
lower half-space (x3 > 0). Rani and Singh [11] obtained
the displacement and stress fields due to a long inclined
strike-slip fault located in the lower half-space (Figure
1). The stress component is continuous across the
interface (x3 = 0) due to the welded-contact boundary
conditions. At the interface x3 = 0, the stress component
is not continuous. At any point of the interface x3 =
0, we have
13
τ
12
τ





(1) 2
1
12 22
21
sin
1
s μbδs
τπmR R 

1
(2)
for the upper half-space, and





(2) 22 1
12 22
21
sin
1
μbδss
τπmR R 

(3)
for the lower half-space, where
1
2
μ
m
μ

 
2
22
121 1
cos sinRxs δsδ
2
2

 
2
22
2222
cos sinRxs δsδ (4)
δ is the dip angle, b is the fault-slip and s1, s2 are sho-
wn in Figure 1. Therefore, at any point of the interface,

(1)
12 1
1(2)
212
τμ
K
μτ (5)
Equation (5) is similar to the result obtained by Ry-
bicki and Yamashita [10] for a homogeneous anti-plane
shear stress conditions in the lower half-space in welded
contact with the upper half-space. We thus note that the
stress ratio K1 for a long inclined strike-slip fault is equal
to the rigidity ratio. It is independent of the Poisson’s
ratios of the two half-spaces as well as of the dip angle
of the fault. δ
3. Long Inclined Dip-Slip Fault
For a two-dimensional plane strain problem, the non-
zero displacement and stress components are of the form



2223 3323
,, ,uu xxuu xx


11
τλθ


2
22
2
2u
τλθμ
x


3
33
3
2u
τλθμ
x






23
23
32
uu
τμ
xx

(6)
where are the Lamè constants and ,λμ





23
23
uu
θxx (7)
Figure 1. Geometry of a long fault lying in an elastic
half-space in welded contact with another elastic half-space.
The x1-axis is taken parallel to the length of the fault and
x3-axis normal to the interface between the two half-spaces.
is the dip angle and are the distances of the two
edges of the fault from the origin.
δ12
s,s
C opyright © 2010 SciRes. ENG

S. Rani ET AL. 168
Rani and Singh [12] derived closed-form analytic ex-
pressions for the displacements and stresses caused by a
long inclined dip-slip fault located in an elastic half-
space in welded contact with another elastic half-space.
The stress components and are continuous
across the interface as required by the welded-contact
boundary conditions. In Figure 1, the origin is taken at
the fault trace, that is at the point where the fault, if ex-
tended, meets the interface x3 = 0. At the origin, the
stress component is given by
23
τ33 τ
22
τ


 


(1) 22
22 2
21
11
1sin2
αμb
τCδ
πss

(8)
for the upper half-space, and


 


(2) 22
22 2
21
11
13 sin2
αμb
τCδ
πss

(9)
for the lower half-space, where


2
2
1
21
αv


2
2
1
12/
m
C
mmα (10)
v2 being the Poisson’s ratio of the lower half-space.
Therefore, at the origin,



 
 
(1)
2
22 2
2(2)
2222
1
11
1
13 11
mv
τCm
K
Cmv m τ2
v
(11)
We observe that the stress ratio K2 for a long inclined
dip-slip fault depends upon the rigidity contrast m =
µ1/µ2 and the Poisson’s ratio v2 of the lower half-space. It
is independent of the Poisson’s ratio v1 of the upper
half-space as well as of the dip angle . From (11), if
, then . This implies that the stress near the
interface generated in the upper half-space is less than
the stress near the interface in the lower half-space in
which the fault lies. On the other hand, if ,
then , implying that the stress generated near the
interface in the upper half-space is more than the stress
near the interface in the lower half-space. For
δ
 1m
K

21K
 2 1 1/mv

21

1
2
mv,
the stress
(
2
)
22
τ at the origin vanishes.
It is interesting to compare (11) with the correspond-
ing result of Rybicki and Yamashita [10] which, in our
notation, is reproduced below:

 
(1)
22
21
(2)
22
1
R
τ
Kmvm
τ
where v1 is the Poisson’s ratio of the upper half-space.
The stress ratio K2R derived by Rybicki and Yamashita
[10] depends upon the rigidity contrast m and the Pois-
son’s ratio of the upper half-space. It is independent of
the Poisson’s ratio of the lower half-space. It may be
noted that while Rybicki and Yamashita [10] considered
a homogeneous shear stress acting on an inclined plane
in the lower medium, we have considered the stress field
of a long inclined dip-slip fault in the lower half-space.
Figure 2 shows the variation of K2 with m for v2 = 0.1,
0.2, 0.3, 0.4. Since K2 is independent of v1, for m = 1, we
have K2 = 1 corresponding to the case when the two
half-spaces have identical elastic parameters. In the
range 0 < m < 1 (Figure 2(a)), we note that K2 < 1 and,
for a given m, K2 decreases as v2 increases. The com-
pressibility is given by



31-2
21+
v
v
μ
. Therefore, in the
range 0 < m < 1, for a given m, K2 increases as the com-
pressibility of the lower half-space increases. In contrast,
in the range 1 < m < 2 (Figure 2(b)), K2 > 1 and, for a
0
0.2
0.4
0.6
0.8
1.0
00.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

2
=0.1

2
=0.2

2
=0.3

2
=0.4
DIP-SLIP FAULT
m
K
2
(a)
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
6.0
1.0 1.11.2 1.3 1.41.5 1.61.7 1.81.9 2.0
2 =0.1
2 =0.2
2 =0.3
2 =0.4
DIP-SLIP FAULT
m
K
2
(b)
Figure 2. Variation of the stress ratio K2 for a long dip-slip
fault with the rigidity ratio 12 m=μ
μ
for four values of
the Poisson’s ratio of the lower half-space for (a)
2
ν

0m1; (b)

12m.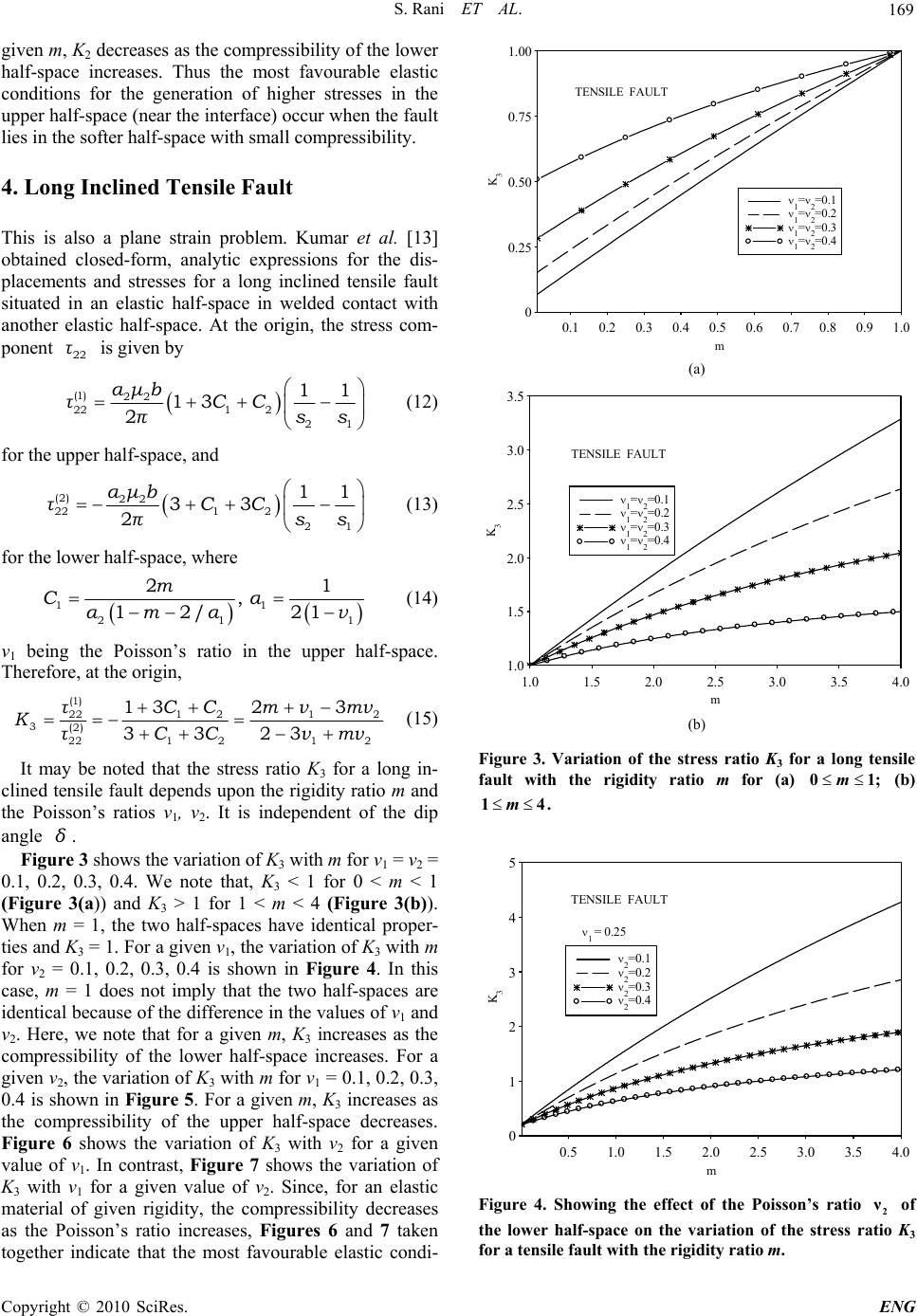

S. Rani ET AL. 169
given m, K2 decreases as the compressibility of the lower
half-space increases. Thus the most favourable elastic
conditions for the generation of higher stresses in the
upper half-space (near the interface) occur when the fault
lies in the softer half-space with small compressibility.
4. Long Inclined Tensile Fault
This is also a plane strain problem. Kumar et al. [13]
obtained closed-form, analytic expressions for the dis-
placements and stresses for a long inclined tensile fault
situated in an elastic half-space in welded contact with
another elastic half-space. At the origin, the stress com-
ponent is given by
22
τ





(1) 22
221 2
21
11
13
2
αμb
τCC
πss

(12)
for the upper half-space, and


 


(2) 22
221 2
21
11
33
2
αμb
τCC
πss

(13)
for the lower half-space, where


 
11
21
21
,
12/ 21
m
Cα
αmαv1
(14)
v1 being the Poisson’s ratio in the upper half-space.
Therefore, at the origin,
 
 
 
(1 )
221 212
3(2)
121 222
132 3
3323
τCC mνmν
K
CC νmντ (15)
It may be noted that the stress ratio K3 for a long in-
clined tensile fault depends upon the rigidity ratio m and
the Poisson’s ratios v1, v2. It is independent of the dip
angle .
δ
Figure 3 shows the variation of K3 with m for v1 = v2 =
0.1, 0.2, 0.3, 0.4. We note that, K3 < 1 for 0 < m < 1
(Figure 3(a)) and K3 > 1 for 1 < m < 4 (Figure 3(b)).
When m = 1, the two half-spaces have identical proper-
ties and K3 = 1. For a given v1, the variation of K3 with m
for v2 = 0.1, 0.2, 0.3, 0.4 is shown in Figure 4. In this
case, m = 1 does not imply that the two half-spaces are
identical because of the difference in the values of v1 and
v2. Here, we note that for a given m, K3 increases as the
compressibility of the lower half-space increases. For a
given v2, the variation of K3 with m for v1 = 0.1, 0.2, 0.3,
0.4 is shown in Figure 5. For a given m, K3 increases as
the compressibility of the upper half-space decreases.
Figure 6 shows the variation of K3 with v2 for a given
value of v1. In contrast, Figure 7 shows the variation of
K3 with v1 for a given value of v2. Since, for an elastic
material of given rigidity, the compressibility decreases
as the Poisson’s ratio increases, Figures 6 and 7 taken
together indicate that the most favourable elastic condi-
0
0.25
0.50
0.75
1.00
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

1
= 
2
=0.1

1
= 
2
=0.2

1
= 
2
=0.3

1
= 
2
=0.4
TENSILE FAULT
m
K
3
(a)
1.0
1.5
2.0
2.5
3.0
3.5
1.0 1.5 2.0 2.5 3.0 3.54.0

1
= 
2
=0.1

1
= 
2
=0.2

1
= 
2
=0.3

1
= 
2
=0.4
TENSILE FAULT
m
K
3
(b)
Figure 3. Variation of the stress ratio K3 for a long tensile
fault with the rigidity ratio m for (a) (b) 0m1;

14m.
0
1
2
3
4
5
0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0

2
=0.1

2
=0.2

2
=0.3

2
=0.4

1
= 0.25
TENSILE FAULT
m
K
3
Figure 4. Showing the effect of the Poisson’s ratio 2
ν
of
the lower half-space on the variation of the stress ratio K3
for a tensile fault with the rigidity ratio m.
C opyright © 2010 SciRes. ENG

S. Rani ET AL. 170
0
0.5
1.0
1.5
2.0
2.5
3.0
0.5 1.0 1.5 2.02.5 3.03.5 4.0

1
=0.1

1
=0.2

1
=0.3

1
=0.4
TENSILE FAULT

2
=0.25
m
K
3
Figure 5. Showing the effect of the Poisson’s ratio 1
ν
of
the upper half-space on the variation of the stress ratio K3
for a tensile fault with the rigidity ratio m.
0
0.5
1.0
1.5
2.0
2.5
3.0
0.10 0.150.20 0.250.300.35 0.4
0
m= 1/2
m=1
m=2
TENSILE FAULT

1
=0.25

2
K
3
Figure 6. Variation of the stress ratio K3 for a tensile fault
with the Poisson’s ratio 2
ν
of the lower half-space.
0
0.5
1.0
1.5
2.0
2.5
0.10 0.150.20 0.25 0.30 0.350.4
0
m=1/2
m=1
m=2

2
= 0.25TENSILE FAULT

1
K
3
Figure 7. Variation of the stress ratio K3 for a tensile fault
with the Poisson’s ratio 1
ν
of the upper half-space.
tions for generation of high stresses in the upper half-
space (near the interface) occur when the tensile fault lies
in the softer half-space, the compressibility of the upper
half is least and the compressibility of the lower half-
space (in which the fault lies) is greatest.
5. Conclusions
In general, when studying the static field in two elastic
half-spaces in contact with source in one of the half-
spaces, it is assumed that the half-spaces are in welded
contact. In welded-contact boundary conditions, the dis-
placement vector and the stress vector across the bound-
ary are assumed to be continuous at the boundary. Con-
sequently, some of the stress components are not re-
quired to be continuous at the boundary. We have stud-
ied the modifications in the stress field of a two-dimen-
sional inclined strike-slip, dip-slip or tensile fault caused
by the welded-contact boundary conditions across the
boundary between the two elastic half-spaces. The re-
sults of the study can be summarised as under. It is as-
sumed that the boundary between the half-spaces is taken
as the x3 = 0 plane and the fault is striking in the x1-di-
rection.
1) In the case of a long inclined strike-slip fault, the
shear stress 
13 is required to be continuous across the
interface by the boundary conditions. However, there is
no restriction on the shear stress 
12. We find that the
ratio of the values of the shear stress 
12 at the interface
when approached from the two half-spaces is equal to the
rigidity ratio. It is independent of the dip angle of the
fault or the Poisson’s ratios of the two half-spaces.
2) In the case of a long inclined dip-slip fault, the
normal stress 
33 and the shear stress

13 are required to
be continuous. There is no restriction on the normal
stresses 
11 and

22. We find that the ratio of the normal
stress 
22 at the interface when approached from the two
half-spaces depends on the rigidity ratio and the Pois-
son’s ratio of the half-space in which the fault lies. It is
independent of the Poisson’s ratio of the other half-space
as well as of the dip angle of the fault. The most favour-
able elastic conditions for generation of large stresses
near the interface in the other half-space occur when the
dip-slip fault lies in the softer half-space with small
compressibility.
3) In the case of a long inclined tensile fault also, 
33
and 
13 are continuous. We find that the ratio of the nor-
mal stress 
22 at the interface depends upon the rigidity
ratio as well as upon the Poisson’s ratios of the two
half-spaces. It is independent of the dip angle. The most
favourable elastic conditions for generation of large
stresses near the interface in the half-space, in which the
fault does not lie, occur when the tensile fault lies in the

S. Rani ET AL. 171
softer half-space, the compressibility of the half-space
with fault is large and the compressibility of the other
half-space is small.
6. Acknowledgment
The authors thank the referee for the improvement of the
paper. SJS thanks the Indian National Science Academy
for financial support under its Senior Scientist Scheme.
7. References
[1] J. A. Steketee, “On Volterra’s disclocations in a semi-
infinite elastic medium,” Canadian Journal of Physics,
Vol. 36, pp. 192-205, 1958.
[2] J. A. Steketee, “Some geophysical applications of the
elasticity theory of dislocation,” Canadian Journal of
Physics, Vol. 36, pp. 1168-1198, 1958.
[3] T. Maruyama, “Statical elastic dislocations in an infinite
and semi-infinite medium,” Bulletin of Earthquake Re-
search Institute, Vol. 42, pp. 289-368, 1964.
[4] T. Maruyama, “On two-dimensional elastic dislocations
in an infinite and semi-infinite medium,” Bulletin of
Earthquake Research Institute, Vol. 44, pp. 811-871,
1966.
[5] J. C. Savage, “Dislocations in seismology,” In: F. R. N.
Nabarro, Ed., Dislocations in Solids, Moving Disloca-
tions, Amsterdam, Vol. 3, pp. 251-339, 1980.
[6] K. Rybicki, “Dislocations and their geophysical applica-
tions,” In: R. Tiesseyre, Ed., Continuum Theories in Solid
Earth Physics, Elsevier, Amsterdam, pp. 18-186, 1986.
[7] M. Bonafede and E. Rivalta, “The tensile dislocation
problem in a layered elastic medium,” Geophysical Jour-
nal International, Vol. 136, pp. 341-356, 1999.
[8] M. Bonafede and E. Rivalta, “On tensile cracks close to
and across the interface between two welded elastic
half-spaces,” Geophysical Journal International, Vol. 138,
pp. 410-434, 1999.
[9] E. Rivalta, W. Mangiavillano and M. Bonafede, “The
edge dislocation problem in a layered elastic medium,”
Geophysical Journal International, Vol. 149, pp. 508-523,
2002.
[10] K. R. Rybicki and T. Yamashita, “Constrains on stresses
in isotropic homogeneous infinite half-spaces being in
welded contact: 2D anti-plane and in-plane cases,” Acta
Geophysica, Vol. 56, pp. 286-292, 2008.
[11] S. Rani and S. J. Singh, “Residual elastic field in two
welded half-spaces caused by a long inclined strike-slip
fault,” Proceedings of the Indian National Science
Academy, Vol. 59, pp. 455-464, 1993.
[12] S. Rani and S. J. Singh, “Static deformation of two
welded half-spaces due to dip-slip faulting,” Proceedings
of the Indian Academy of Sciences (Earth and Planetary
Science), Vol. 101, pp. 269-282, 1992.
[13] A. Kumar, S. J. Singh and J. Singh, “Deformation of two
welded elastic half-spaces due to a long inclined tensile
fault,” Journal of Earth System Science, Vol. 114, pp.
97-103, 2005.