Vol.2, No.3, 145-154 (2010) Natural Science
http://dx.doi.org/10.4236/ns.2010.23024
Signature of chaos in the semi quantum behavior of a
classically regular triple well heterostructure
Tiokeng Olivier Lekeufack1, Serge Bruno Yamgoue2, Timoleon Crepin Kofane1,3
1Laboratory of Mechanics, Department of Physics, Faculty of Science, University of Yaounde I, Yaounde, Cameroon;
2Department of Physics Higher, Teacher’s Training College, Bamenda, Cameroon
3The Abdus Salam International Center for Theoretical Physics, Trieste, Italy
Received 28 December 2009; revised 14 January 2010; accepted 25 January 2010.
ABSTRACT
We analyze the phenomenon of semiquantum
chaos in the classically regular triple well model
from classical to quantum. His dynamics is very
rich because it provides areas of regular be-
havior, chaotic ones and multiple quantum tun-
neling depending on the energy of the system
as the Planck’s constant  varies from 0 to 1.
The Time Dependent Variational Principle TDVP
using generalized Gaussian trial wave function,
which, in many-body theory leads to the Hartree
Fock Approximation TDHF, is added to the tech-
niques of Gaussian effective potentials and both
are used to study the system. The extended
classical system with fluctuation variables non-
linearly coupled to the average variables exhibit
energy dependent transitions between regular
behavior and semi quantum chaos monitored by
bifurcation diagram together with some numerical
indicators.
Keywords: Nonlinear Dynamics; Semi Quantum
Chaos; Effective Potential
1. INTRODUCTION
The quantum computer science, the quantal dynamics of
hetero-structures, the mesoscopic behavior of some sys-
tems, the chaotic entropy production in open quantum
systems, the zero momentum (long wavelength) part of
the problem of pair production of charged scalar parti-
cles by a strong external electric field [1], the quantum
suppression of diffusion (dynamic localization) [2] and
the quantum unique ergodicity in statistical thermody-
namics are good candidates for a wide range of the study
and the application of semiquantum chaos in experi-
mental physics, nuclear physics and quantum chemistry
as well. The definition and observation of chaotic be-
havior in classical systems are familiar and well under-
stood [3,4]. However, the proper definition of chaos for
quantum systems and its experimental manifestations are
still unclear [5-8]. We use the term semiquantum chaos
to refer to the study of the quantum dynamics of systems
whose classical limit is regular (restriction to Hamilto-
nian systems).
Over the last years, different approaches of studying
chaos in classical and quantum systems have attracted
increasing attention. For example, we have the prob-
lem of pair production of particles by strong external
electric field, the two particles interaction through a
biquadratic coupling, i.e., a two-degrees of freedom
system of which one is classical and the other purely
quantum non linearly coupled and which exhibit chaos
[9-11]. In addition, great attention is focused on a sys-
tem of two particles non-linearly coupled, whose clas-
sical limit is chaotic, involving quantum properties.
This is the case for the authors of [9], who studied the
duality wave/particle to take into account the quantum
dynamics, then combined Quantum Theory of Motion
(QTM) with Quantum Fluid Dynamics (QFD) in clas-
sical chaos, and found quantum parameters being cha-
otic. For the full quantum dynamics, only experimental
studies have been done up till date on hetero-structures
undergoing multiple tunneling resonance, and leading
to different approaches of building quantum computers
[12,13]. In addition to all the aforementioned routes of
analyzing non-classical chaos, many theories and for-
malisms are always used. One of the most important of
these routes is the time dependent variational approach,
which, in the many body theory, leads to the TDHF
using a Gaussian trial wave function [14-20]. The ap-
pearance of this wave function has provided great and
interesting results not only in general universe physics
field, but also in nuclear physics and quantum chemis-
try [14,16]. This usage generally integrates the mean
field theory [21-24]. The signature of the Gaussian
Effective potential GEP [1,17,25,26] is also a good
indicator of non-classical chaos. In fact, effective po-
tentials [26] are used to assess the impact of quantum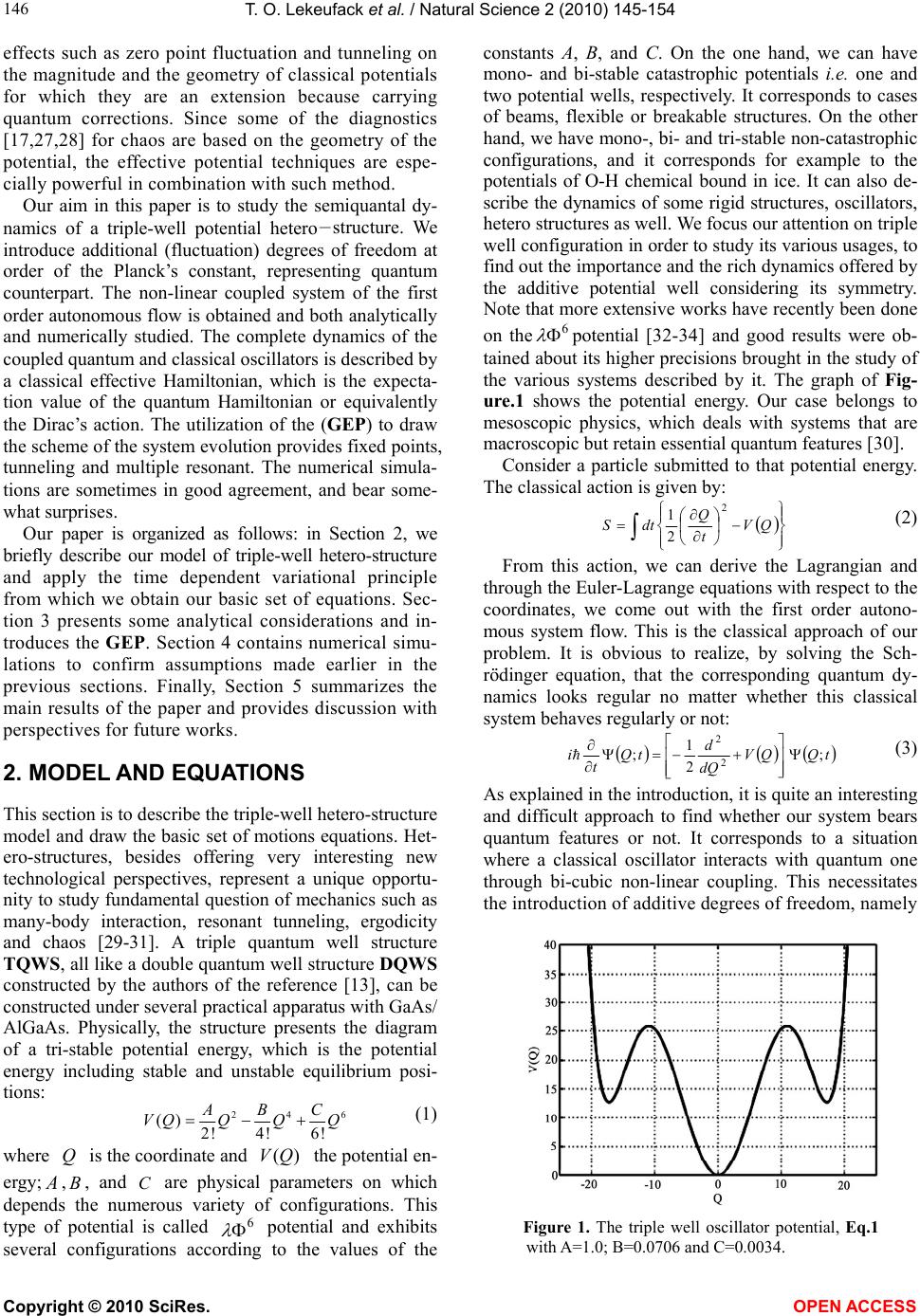

T. O. Lekeufack et al. / Natural Science 2 (2010) 145-154
146
effects such as zero point fluctuation and tunneling on
the magnitude and the geometry of classical potentials
for which they are an extension because carrying
quantum corrections. Since some of the diagnostics
[17,27,28] for chaos are based on the geometry of the
potential, the effective potential techniques are espe-
cially powerful in combination with such method.
Our aim in this paper is to study the semiquantal dy-
namics of a triple-well potential hetero－structure. We
introduce additional (fluctuation) degrees of freedom at
order of the Planck’s constant, representing quantum
counterpart. The non-linear coupled system of the first
order autonomous flow is obtained and both analytically
and numerically studied. The complete dynamics of the
coupled quantum and classical oscillators is described by
a classical effective Hamiltonian, which is the expecta-
tion value of the quantum Hamiltonian or equivalently
the Dirac’s action. The utilization of the (GEP) to draw
the scheme of the system evolution provides fixed points,
tunneling and multiple resonant. The numerical simula-
tions are sometimes in good agreement, and bear some-
what surprises.
Our paper is organized as follows: in Section 2, we
briefly describe our model of triple-well hetero-structure
and apply the time dependent variational principle
from which we obtain our basic set of equations. Sec-
tion 3 presents some analytical considerations and in-
troduces the GEP. Section 4 contains numerical simu-
lations to confirm assumptions made earlier in the
previous sections. Finally, Section 5 summarizes the
main results of the paper and provides discussion with
perspectives for future works.
2. MODEL AND EQUATIONS
This section is to describe the triple-well hetero-structure
model and draw the basic set of motions equations. Het-
ero-structures, besides offering very interesting new
technological perspectives, represent a unique opportu-
nity to study fundamental question of mechanics such as
many-body interaction, resonant tunneling, ergodicity
and chaos [29-31]. A triple quantum well structure
TQWS, all like a double quantum well structure DQWS
constructed by the authors of the reference [13], can be
constructed under several practical apparatus with GaAs/
AlGaAs. Physically, the structure presents the diagram
of a tri-stable potential energy, which is the potential
energy including stable and unstable equilibrium posi-
tions:
246
() 2! 4! 6!
A
BC
VQQQQ
(1)
where Q is the coordinate and ()VQ the potential en-
ergy;
A
,B, and C are physical parameters on which
depends the numerous variety of configurations. This
type of potential is called 6


potential and exhibits
several configurations according to the values of the
constants A, B, and C. On the one hand, we can have
mono- and bi-stable catastrophic potentials i.e. one and
two potential wells, respectively. It corresponds to cases
of beams, flexible or breakable structures. On the other
hand, we have mono-, bi- and tri-stable non-catastrophic
configurations, and it corresponds for example to the
potentials of O-H chemical bound in ice. It can also de-
scribe the dynamics of some rigid structures, oscillators,
hetero structures as well. We focus our attention on triple
well configuration in order to study its various usages, to
find out the importance and the rich dynamics offered by
the additive potential well considering its symmetry.
Note that more extensive works have recently been done
on the6
  potential [32-34] and good results were ob-
tained about its higher precisions brought in the study of
the various systems described by it. The graph of Fig-
ure.1 shows the potential energy. Our case belongs to
mesoscopic physics, which deals with systems that are
macroscopic but retain essential quantum features [30].
Consider a particle submitted to that potential energy.
The classical action is given by:



















QV
t
Q
dtS
2
2
1 (2)
From this action, we can derive the Lagrangian and
through the Euler-Lagrange equations with respect to the
coordinates, we come out with the first order autono-
mous system flow. This is the classical approach of our
problem. It is obvious to realize, by solving the Sch-
rödinger equation, that the corresponding quantum dy-
namics looks regular no matter whether this classical
system behaves regularly or not:
   tQQV
dQ
d
tQ
t
i;
2
1
;2
2











 (3)
As explained in the introduction, it is quite an interesting
and difficult approach to find whether our system bears
quantum features or not. It corresponds to a situation
where a classical oscillator interacts with quantum one
through bi-cubic non-linear coupling. This necessitates
the introduction of additive degrees of freedom, namely
Figure 1. The triple well oscillator potential, Eq.1
with A=1.0; B=0.0706 and C=0.0034.

T. O. Lekeufack et al. / Natural Science 2 (2010) 145-154
147
fluctuation ones. Their quantum nature belongs to the
significance of the Planck’s constant . We introduce
classical and quantum coordinates [18]
  Qtq ; 
22 QQtG (4)
Together with classical and quantum momenta [18]
  Pt;
 


 Q itp  (5)
The < > has the sense of the mean value. We now
consider a trial wave function, particularly the one that
has been successfully introduced by Gauss [15,18,35]
and whose results were in good convenience with the
physics of the considered system
  





 qQP
i
qQNtQ 
2
2
1
exp, (6)
With
 
1
12
2Gt it

  from the authors of [15].
This wave function has to satisfy usual quantum re-
quirements such as the normalization condition and the
Heisenberg uncertainty principle. The normalization
condition gives

4
1
2  GN and the mean values are
easily calculated

Qqt

 ;

ipt
Q

 

;

22
QqGt

; ipqG
t


 




Moreover, the uncertainty principle is obtained:

2
1
2
1
2
1
2
1212222 4
4
1




 GGGPPQQ 
 
2
41
2
2
1
2  G
Q,
P
, G and are variational parameters and
we demand that their variation vanishes at infinity.
We now turn to the derivation of appropriate semi
quantum equations of motion. The TDHF or Gaussian
variational approximation can easily be performed with
the help of Dirac’s variational principle [15]. We require
the effective action
  


tH
t
itdtSeff  (7)
to be stationary against arbitrary variation of a nor-
malized wave function which vanishes at


t
:
0
Seff




for all , with 1. This is equ-
ivalent to the exact time dependent Schrödinger equation.
With this variational principle, one can solve the quan-
tum mechanical time evolution problem approximately
by restricting the variation of the wave function to a sub
space of Hilbert space. The effective action is therefore
given by:














 qVG
G
HqpdtS cleff
22
2
1
2
8











 qV
G
qV
G6
33
4
22
488
 (8)
where
  qV
p
pqHcl  2 ,
2 ;

n
n
n
Q
V
V

 (9)
This contains higher order additive term in 33 G
symbolizing higher quantum correction as compared to
Eq.6 of [18] and Eq.18 of [35]. The appearance of the
additive term may increase the richness of the studied
systems dynamics. The semi quantum variational equa-
tions of motion are therefore derived via the Euler La-
grange equation for the effective action, Eq.9, by inde-
pendent variation with respect to Q,
P
, G and

:




























qV
G
qV
G
qVG
GG
qV
G
qV
G
qVp
pq
6
22
4222
5
22
3
1642
1
2
8
1
4
162






(10)
As compared to Eq.7 of [18] and Eqs.22-25 of [35],
there appear additive non-linear terms. We expect more
corrections on the dynamics of the aforementioned stud-
ied system. The above equations are the TDHF ones
because using the Gaussian wave function in Dirac’s
principle. The validity of this TDHF approximation,
which has been widely tested [11,18] by being applied to
various quantum mechanical problems and drawing
good results, is awaited here. Since the equations are
highly nonlinear, we expect the trajectories to be regular
and irregular providing chaotic behavior. It is important
to note that our equations are coupled, showing the link
between classical and quantum interactions. At 0
classical limit, only the first two equations remain, con-
firming that the fluctuation variables are responsible for
quantum effects. In addition, the Ehrenfest theorem is
then verified to confirm the validity of our system [17].
3. GEP AND THEORETICAL ANALYSIS
The purpose of this section is to derive the Gaussian
Effective Potential (GEP) and to report some analytical
considerations, which may help to better understand the
dynamics of the semiquantum equations of motion.
3.1. The Static GEP
The variety of techniques used to study dynamical sys-
tems comes about because the measures (such as K en-
tropy [36], Lyapunov numbers [36-39]), the diagnostics
(the Melnikov functions [38-40]), and the signatures of
chaos, which generally lie in phase space, are dynamic
and have no direct interpretation in quantum dynamics.
We consider a parallel approach, that of using classical
techniques of analysis by reducing the problem to that of
an effective classical system i.e. looking at Hamiltons’
equations in a modified potential. Effective potentials
are therefore used to assess the impact of quantum ef-

T. O. Lekeufack et al. / Natural Science 2 (2010) 145-154
148
fects such as zero-point fluctuations and tunneling on the
magnitude and the geometry of the classical potentials. It
was introduced by Stevenson [26] and successfully
tested in the Henon Heiles and four leg potentials prob-
lem. Most of the diagnostics for chaos are based on the
geometry of the potential. The effective potential tech-
nique is especially powerful in combination with such
method [17]. The idea of Stevenson is to approximate
the effective potential of a system by using Gaussian
wave function. In general, the effective potential of a
system gives us a picture of how the quantum fluctua-
tions modify the classical potential. Following the con-
served total energy for our non-dissipative model with
its complicated functions of q, p, G and

, we
choose the simplest initial conditions with zero momenta
 000  ttp ; then, evaluating the initial total energy
 


 2
22
2Q
QVE  we have:
 C
G
q
C
B
G
q
C
q
B
A
G
G
qVGqE 482824228 ),(
33
2
22
42  












(11)
At the minima of the classical potential, (i.e. q = 0 or
q = ± 17.2, numerically), we obtain the initial energy for
the correspondent minimum q = 0,
3
3
2
2
48828
)( G
C
G
B
G
A
G
GEq
  (12)
which is a function of the initial value of G: this is the
relevant control parameter for our model. We now derive
the GEP. In analogy to a classical system, we consider
the effective potential which is defined as the total minus
the kinetic energy, from Eq.8, the kinetic part being zero
according to the initial conditions. Thus,
 q
C
q
B
A
G
G
qVGqEGqVeff 24228 ,,42
 






C
G
q
C
B
G
4828
33
2
22  





 (13)
In Figure 2, we present equipotentials for the GEP
corresponding to couples of (q,G) varying through
Figure2. The effective semi-quantum potential (GEP),
Eq.13 restricted in the q-G positive plane.
Eq.10 for the same conservative energy. It shows how
the classical potential is modified.
In the particular case of a potential well, the Heisen-
berg uncertainty principle implies that, if the centroid is
concentrated in a small region ΔQ then the uncertainty
on the conjugate momentum ΔP is very large ΔP ≥
ћ/2ΔQ; there appears a large kinetic contribution in the
total energy. In the triple well, the quantum fluctuations
lower the potential barriers such that a particle with clas-
sical insufficient energy to spray over the barrier finds it
possible: that is quantum tunnel effect [21-24]. The most
interesting features are the valleys in the potential energy
surface that lead to the saddle point regions separating
the three effective potential wells. They are observable at
q = 10.9, corresponding to the maximum of the classical
potential. The GEP, in its analytical expression, shows
the quantum corrections on the classical potential. New
phenomena are expected as shown in Figure 2. In some
situations, this potential is shown to exhibit chaotic be-
havior for some restricted energy ranges [41]. According
to the graph, we expect multiple quantum tunnel effects,
as well as energy (medium value) dependent transitions
between regular and chaotic motion in the GEP; this
needs to be confirmed in the numerical study. Quantum
tunneling must be observable in our system, for energy
range between the potential wells. Since the potential
has symmetric wells, we expect on resonance [18] tun-
neling process to occur. One can also explain this using
the static effective potential

eff
Vq
 that is obtained by
eliminating G in


,
eff
VqG via. From Eq.13:
   q
C
q
B
A
qG
qG
qVqVeff 24228
~42
 








C
qG
q
C
B
qG
4828
33
2
22  







(14)
where G(q) is the solution of the following equation:
0
2
242
8
2
4
2
242
2
324 











 C
Gq
C
q
B
A
C
Gq
C
B
C
G

(15)
Figure 3, we realise that
 qV
eff
~ (Static GEP) changes
from

 qV and

 GqVeff , as if there were a phase transition.
Figure 3. The static effective potential.

T. O. Lekeufack et al. / Natural Science 2 (2010) 145-154
149
3.2. Fix Points and Instabilities
Our potential shows the classical contribution plus the
higher order quantum corrections. Note that the num-
ber of valleys is in increase as compared to the one in
[35]; so does the number of fixed points by two. This
increase was earlier predicted by those authors be-
cause of the higher order term corrections considered
(33G) in the GEP. In the fix points’ theory, a hetero
structure bears additive properties whose importance
is over the aim of this paper. Nevertheless, we focus
on the variety of its usage while considering it. Our
system offers various possibilities and useful aspects
therewith into its rich dynamics (see stationary condi-
tions 0 

 Gqp ). Concavities observed in the pic-
ture are good diagnostics for chaos [30-32]. Really, since
there are various combinations of initial conditions cor-
responding to the same total energy, numerically unob-
servable chaos may exist at all energies. Nevertheless, it
did not happen so; that is why it was difficult to find
energy ranges where chaos occurred. As G increases in
the GEP, three minima appear in the half plane, corre-
sponding to the well minima of the original problem;
two saddle points also emerge, interestingly. In addition,
the
 pq, system, as driven by the
 ,G system, is like
a non-linearly driven Duffing oscillator [17,39] with
back reaction. With these ingredients, added to the
highly non-linearity, it is not surprising that our semi
quantum equations exhibit chaos. On the other hand, the
instabilities are important and their study is based on the
motion equations Eq.10 in the second order form to
show the similarity to coupled oscillators:







0
0
2
2
GG
qq
eff
eff

 
(16)
with
42
22
2
12026
1
82 q
C
qC
G
BC
G
B
G
A
eff 













 

(17)
and
2
2
2422
4212
2G
C
Gq
C
Bq
C
BqA
eff













 (18)
Two coupled parametric oscillators then describe the
dynamic of the system. Both oscillators can become un-
stable due to exponentially growing modes for a finite
range of initial values for q and G. Taking the both ef-
fective mass squared terms to be negative, gives the
conditions
2
1
4
2
1
432
²
²
16
45
8
2
12
²
3
132
²
²
16
45
8
2
12
²
3
1










 A
C
B
C
q
C
B
qGA
C
B
C
q
C
B
q
(19)
with the range
4
1
4
1
²
²2
90
²
²2
90 




















C
B
C
A
q
C
B
C
A (20)
for Eq.17; and
2
1
4
2
1
432
²
²16
3
8
2
12
²
32
²
²16
3
8
2
12
²










 C
A
C
B
q
C
B
qG
C
A
C
B
q
C
B
q
(21)
with the range
4
1
4
1
²
²2
6
²
²2
6




















C B
C
A
q
C
B
C
A (22)
for Eq.18.
The both ranges of q indicate the relationship among
the parameters A, B and C to be satisfied for a given po-
tential in order to present oscillations with possible in-
stabilities:
0
²
²2 
C
B
C
A that is C
B
A2
²
 (23)
For G to remain positive, the previous conditions
give



















2
1
4
2
1
4
32
²
²16
45
8
2
12
²0
32
²
²
16
45
8
2
12
²
3
1
0
C
A
C
B
q
C
B
qG
C
A
B
C
q
C
B
qG
(24)
Hence, the instability zone added to the q range ob-
tained from Eq.17 gives
2
1
432
²
²16
45
8
2
12
²
3
1
0




 C
A
C
B
q
C
B
qG (25)
Note that our parameters satisfy the condition Eq.23
and the q range for instability is 9.10q or 9.10


q,
corresponding to domains containing the two extreme
classical potential wells. We can conclude that the equi-
librium positions q = 17.2 and q =17.2 of our potential
are unstable ones. Nevertheless, note that condition Eq.25
provides the criterion not only for a better choice of ini-
tial G, but also for sensitivity to initial conditions.
4. NUMERICAL STUDIES
In this section, we present the results obtained by direct
numerical integrations of our semi quantum equations of
motion. Numerical integration is necessary for us in or-
der to confirm the estimates of the theoretical predictions
and/or to obtain other results in domains where the GEP,
and the analytical study cannot be successful. In fact, it
is the principal mean that allows knowing about the ex-
act behavior of the solutions for non-trivial nonlinear
ordinary differential (semi quantum) equations Eq.16.
Unfortunately, unlike an analytical relation from which
one can discuss the appearance of chaos for different
initial conditions, the numerical integration has the draw
back of requiring a discrete variation of the control pa-
rameter of the system. Consequently, numerically study-
ing such a semi quantum system for several values of its
control parameter, which may vary within intervals of
relatively long length, will demand a cumbersome quan-
tity of plots. Thus, despite the fact that we focus great

T. O. Lekeufack et al. / Natural Science 2 (2010) 145-154
150
attention only on the influence of the control parameter,
the numerical description involves quite a large number
of plots, where lie the key results of this paper. The
fourth-order Runge - Kutta algorithm is the scheme we
have used. The time step is fixed at Δt = 1e – 3. We al-
ways fixed




000
t
t
p
initially and chose G,
together with various values for q to represent initial
configurations corresponding to varying total energy.
Generally, we did not explore the full set of all initial
conditions at a given energy. This would require much
more extensive numerical calculations which is beyond
the scope of the present paper.
We have used five standard indicators including Bi-
furcation diagrams, phase portraits, frequency spectrum,
Poincare sections displays and computation of maximal
Lyapunov exponent to characterize the long time dy-
namics of our model under slight perturbation of initial
conditions. These indicators complement each other in
the following way: The bifurcation diagram indicates a
range where values can be found to obtain regular or
chaotic behavior; phase portraits are basically used to
appreciate the shape of trajectories in the phase space on
which the system evolves in time. They may be suffi-
cient to state whether the dynamic is regular or not.
Nevertheless, they are not practical when the phase
space is of dimension greater than two. Moreover, we
cannot easily distinguish roughly between chaotic states
and some quasi-periodic ones using only phase portraits.
Poincare surfaces of section are useful to determine in
particular the periodicity of the systems evolution. Strange
attractors correspond to surfaces of section made up of
an infinite number of points that occupy a bounded do-
main of the cross section without forming a smooth
closed curve. They may be chaotic or not. Thus, we need
the maximal Lyapunov exponent to know the nature of
the strange attractor, in this case. The frequency spec-
trum is also useful here to determine, in particular, the
value of the frequency in the case of regular periodic
motion. Regular spacing shows regular motion.
For a system of first order equations of the form

,
X
FXt
, where

12
, ,..........T
n
XXX X, the Lya-
punov exponents are defined as the asymptotic values of
the eigen values of the solution of the matrix differential
equation




F
B
DXt B
, assuming the initial condi-
tions


nn
IB  0, where nn
I
 is the n × n square identity
matrix.
 tXD
F
represents the Jacobean matrix of the
function F evaluated at the solution X(t). The involved
Eigenvalues can be computed using the code stated by
Wolf et al. [37,40].
A chaotic state is the one for which at least one expo-
nent is positive. The bifurcation diagram (see Figure 4)
shows here the increase of chaotic behavior of the sys-
tem when moving from classical (=0) to quantum
(=1). We present here phase portraits and correspond-
ing Poincare sections in the phase space planes of the
two conjugate pairs of variable
 pq, and



,G for
some values of the total energy closer to the minimum of
the classical potential energy. Figure 5 shows some
regularity in the motion of the centroid at low energies.
The first row presents the phase space at E = 4, G =
0.4 together with the corresponding frequency spectrum,
which is regularly spaced; indicating regularity. Indeed,
the value of the Lyapunov exponent is negative -0.0004.
The remaining rows indicate the aspects of the Poincare
sections in the both phase spaces for energies 0.9; 4 and
5, respectively. The motion still looks regular and pre-
Figure 4. Bifurcation diagrams as ћ moves from 0 to 1, for (a):
q = 0.01, G = 0.1, (b): q = 0.01, G = 0.1, (c): q = 5.3, G = 0.09,
(d): q = 17.2, G = 0.09.
Figure 5. Phase portrait and frequency spectrum in the first
line for E = 4, G = 0.4; Poincaré sections in the remaining lines
and from top to bottom for E = 0.9, G = 1.2; E = 4, G=1.2 and E
= 5, G = 4.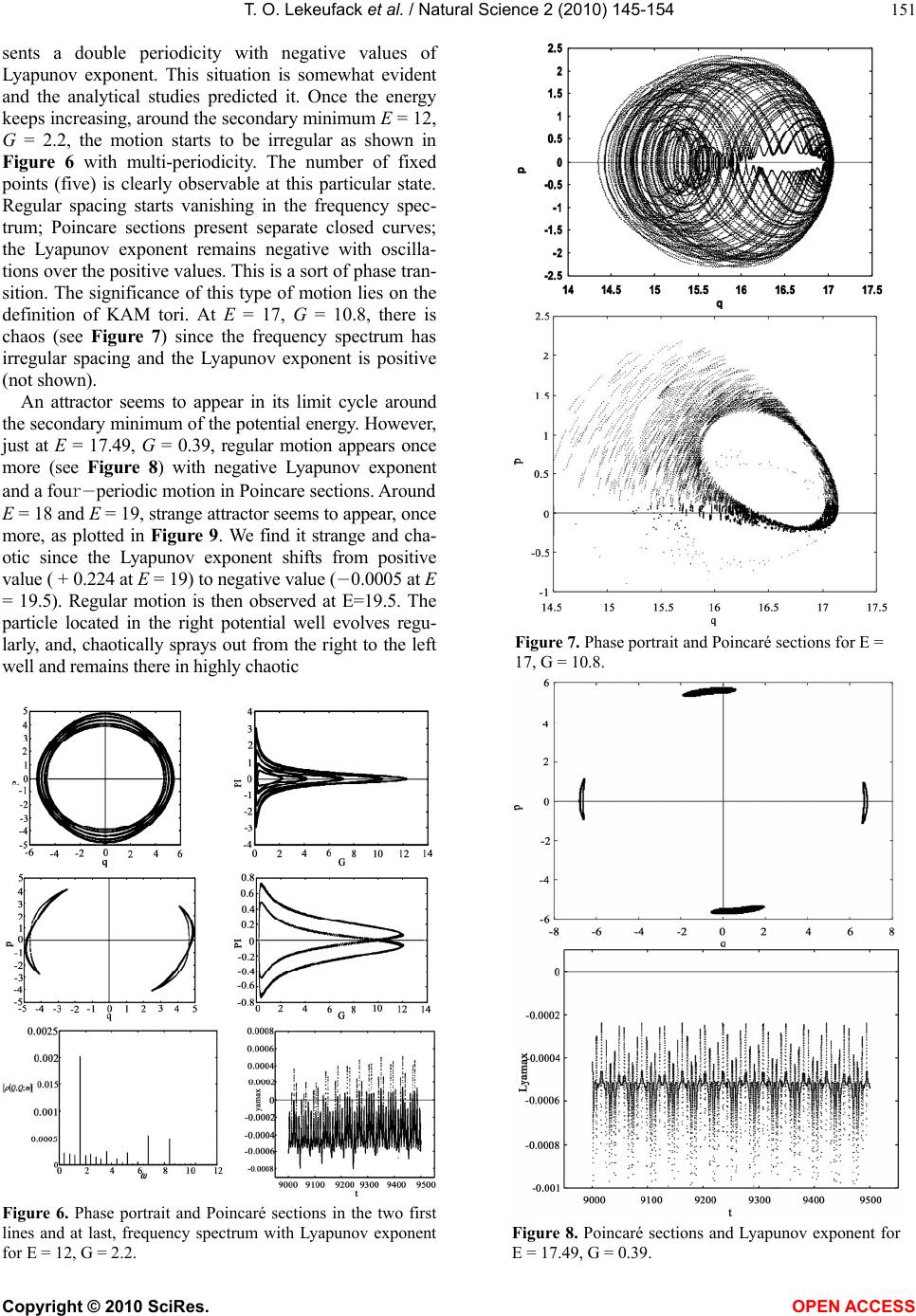

T. O. Lekeufack et al. / Natural Science 2 (2010) 145-154
151
sents a double periodicity with negative values of
Lyapunov exponent. This situation is somewhat evident
and the analytical studies predicted it. Once the energy
keeps increasing, around the secondary minimum E = 12,
G = 2.2, the motion starts to be irregular as shown in
Figure 6 with multi-periodicity. The number of fixed
points (five) is clearly observable at this particular state.
Regular spacing starts vanishing in the frequency spec-
trum; Poincare sections present separate closed curves;
the Lyapunov exponent remains negative with oscilla-
tions over the positive values. This is a sort of phase tran-
sition. The significance of this type of motion lies on the
definition of KAM tori. At E = 17, G = 10.8, there is
chaos (see Figure 7) since the frequency spectrum has
irregular spacing and the Lyapunov exponent is positive
(not shown).
An attractor seems to appear in its limit cycle around
the secondary minimum of the potential energy. However,
just at E = 17.49, G = 0.39, regular motion appears once
more (see Figure 8) with negative Lyapunov exponent
and a four－periodic motion in Poincare sections. Around
E = 18 and E = 19, strange attractor seems to appear, once
more, as plotted in Figure 9. We find it strange and cha-
otic since the Lyapunov exponent shifts from positive
value ( + 0.224 at E = 19) to negative value (－0.0005 at E
= 19.5). Regular motion is then observed at E=19.5. The
particle located in the right potential well evolves regu-
larly, and, chaotically sprays out from the right to the left
well and remains there in highly chaotic
Figure 6. Phase portrait and Poincaré sections in the two first
lines and at last, frequency spectrum with Lyapunov exponent
for E = 12, G = 2.2.
Figure 7. Phase portrait and Poincaré sections for E =
17, G = 10.8.
Figure 8. Poincaré sections and Lyapunov exponent for
E = 17.49, G = 0.39.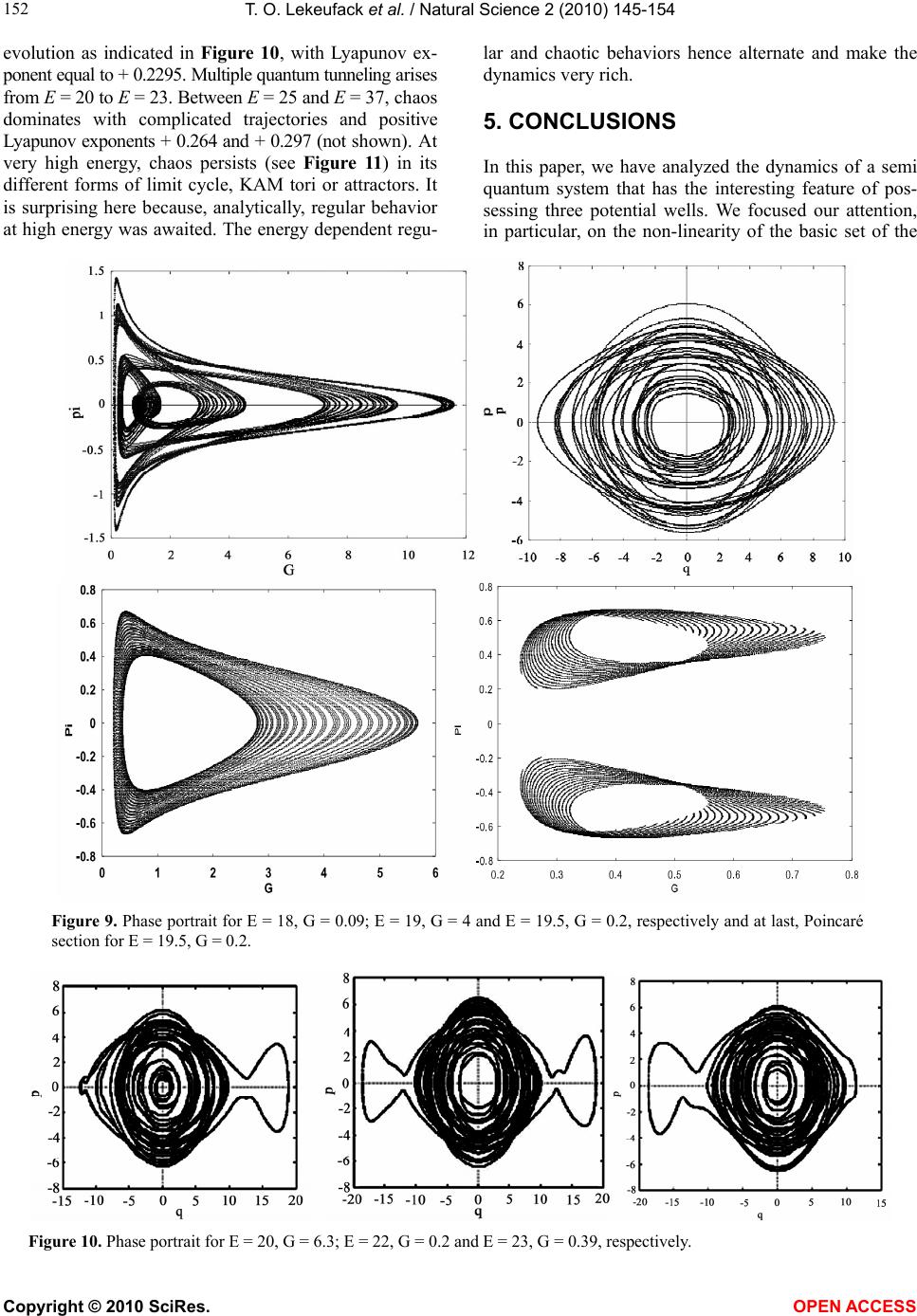

T. O. Lekeufack et al. / Natural Science 2 (2010) 145-154
152
evolution as indicated in Figure 10, with Lyapunov ex-
ponent equal to + 0.2295. Multiple quantum tunneling arises
from E = 20 to E = 23. Between E = 25 and E = 37, chaos
dominates with complicated trajectories and positive
Lyapunov exponents + 0.264 and + 0.297 (not shown). At
very high energy, chaos persists (see Figure 11) in its
different forms of limit cycle, KAM tori or attractors. It
is surprising here because, analytically, regular behavior
at high energy was awaited. The energy dependent regu-
lar and chaotic behaviors hence alternate and make the
dynamics very rich.
5. CONCLUSIONS
In this paper, we have analyzed the dynamics of a semi
quantum system that has the interesting feature of pos-
sessing three potential wells. We focused our attention,
in particular, on the non-linearity of the basic set of the
Figure 9. Phase portrait for E = 18, G = 0.09; E = 19, G = 4 and E = 19.5, G = 0.2, respectively and at last, Poincaré
section for E = 19.5, G = 0.2.
Figure 10. Phase portrait for E = 20, G = 6.3; E = 22, G = 0.2 and E = 23, G = 0.39, respectively.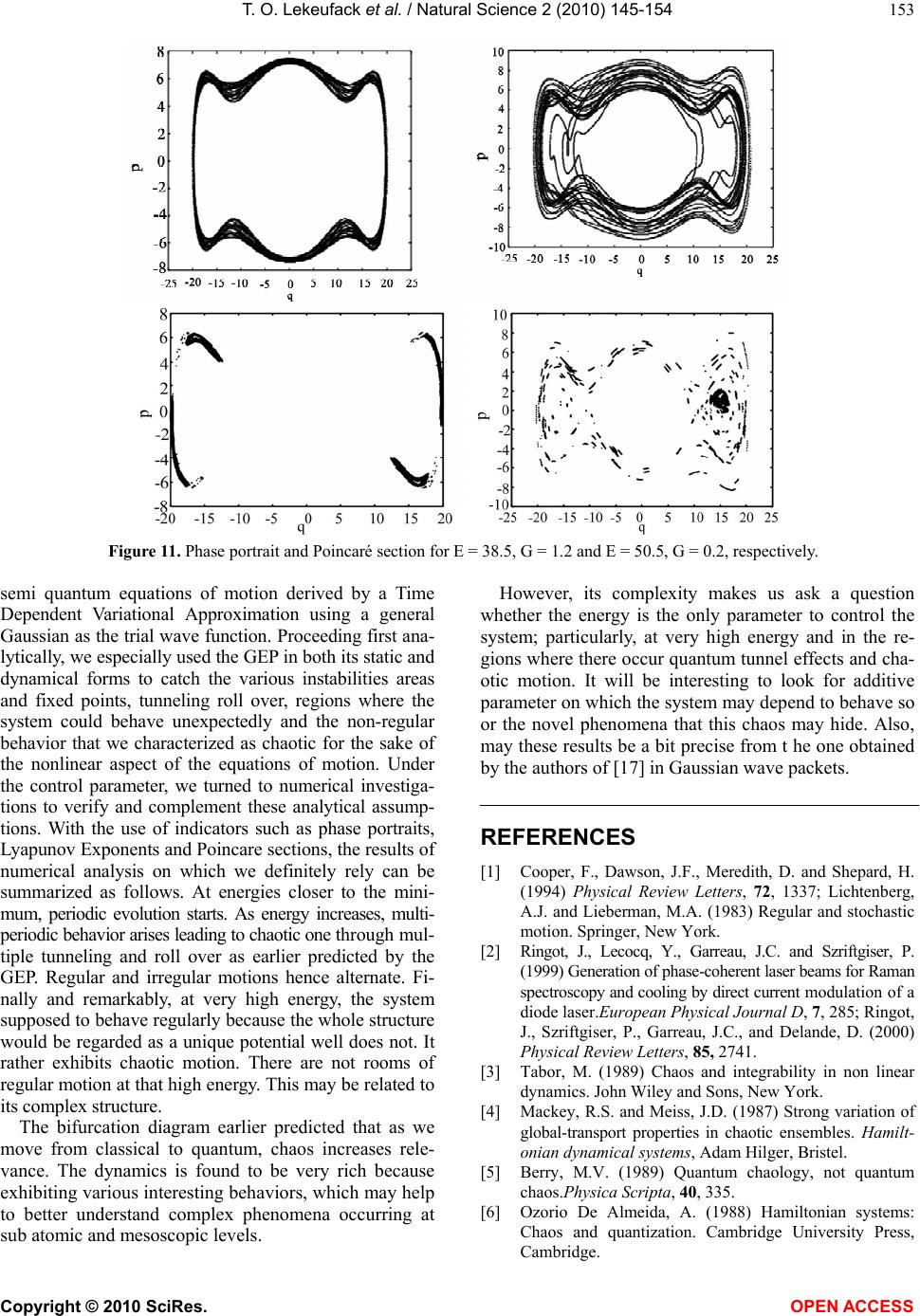

T. O. Lekeufack et al. / Natural Science 2 (2010) 145-154
153
Figure 11. Phase portrait and Poincaré section for E = 38.5, G = 1.2 and E = 50.5, G = 0.2, respectively.
semi quantum equations of motion derived by a Time
Dependent Variational Approximation using a general
Gaussian as the trial wave function. Proceeding first ana-
lytically, we especially used the GEP in both its static and
dynamical forms to catch the various instabilities areas
and fixed points, tunneling roll over, regions where the
system could behave unexpectedly and the non-regular
behavior that we characterized as chaotic for the sake of
the nonlinear aspect of the equations of motion. Under
the control parameter, we turned to numerical investiga-
tions to verify and complement these analytical assump-
tions. With the use of indicators such as phase portraits,
Lyapunov Exponents and Poincare sections, the results of
numerical analysis on which we definitely rely can be
summarized as follows. At energies closer to the mini-
mum, periodic evolution starts. As energy increases, multi-
periodic behavior arises leading to chaotic one through mul-
tiple tunneling and roll over as earlier predicted by the
GEP. Regular and irregular motions hence alternate. Fi-
nally and remarkably, at very high energy, the system
supposed to behave regularly because the whole structure
would be regarded as a unique potential well does not. It
rather exhibits chaotic motion. There are not rooms of
regular motion at that high energy. This may be related to
its complex structure.
The bifurcation diagram earlier predicted that as we
move from classical to quantum, chaos increases rele-
vance. The dynamics is found to be very rich because
exhibiting various interesting behaviors, which may help
to better understand complex phenomena occurring at
sub atomic and mesoscopic levels.
However, its complexity makes us ask a question
whether the energy is the only parameter to control the
system; particularly, at very high energy and in the re-
gions where there occur quantum tunnel effects and cha-
otic motion. It will be interesting to look for additive
parameter on which the system may depend to behave so
or the novel phenomena that this chaos may hide. Also,
may these results be a bit precise from t he one obtained
by the authors of [17] in Gaussian wave packets.
REFERENCES
[1] Cooper, F., Dawson, J.F., Meredith, D. and Shepard, H.
(1994) Physical Review Letters, 72, 1337; Lichtenberg,
A.J. and Lieberman, M.A. (1983) Regular and stochastic
motion. Springer, New York.
[2] Ringot, J., Lecocq, Y., Garreau, J.C. and Szriftgiser, P.
(1999) Generation of phase-coherent laser beams for Raman
spectroscopy and cooling by direct current modulation of a
diode laser.European Physical Journal D, 7, 285; Ringot,
J., Szriftgiser, P., Garreau, J.C., and Delande, D. (2000)
Physical Review Letters, 85, 2741.
[3] Tabor, M. (1989) Chaos and integrability in non linear
dynamics. John Wiley and Sons, New York.
[4] Mackey, R.S. and Meiss, J.D. (1987) Strong variation of
global-transport properties in chaotic ensembles. Hamilt-
onian dynamical systems, Adam Hilger, Bristel.
[5] Berry, M.V. (1989) Quantum chaology, not quantum
chaos.Physica Scripta, 40, 335.
[6] Ozorio De Almeida, A. (1988) Hamiltonian systems:
Chaos and quantization. Cambridge University Press,
Cambridge.

T. O. Lekeufack et al. / Natural Science 2 (2010) 145-154
154
[7] Gutzwiller, M.C. (1990) Chaos in classical and quantum
mechanics. Springer Verlag, New York.
[8] Reichl, L.E. (1992) The transition to chaos in conservative
classical systems: Quantum manifestations. Springer
Verlag, New York.
[9] Sengupta, S. and Chattaraj, P.K. (1996) Physics Letters A,
215, 119.
[10] Kluger, Y., Eisenberg, J.M., Svetisky, B., Cooper, F. and
Mottola, E. (1991) Physical Review Letters, 67, 2427.
[11] Pradhan, T. and Khare, A.V. (1973) American Journal of
Physics, 41, 59.
[12] Jona Lasinio, G., Presilla, C. and Capasso, F. (1992).
Physical Review Letters, 68, 2269.
[13] Leo, K., Shah, J., Gobel, E.O., Damen, T.C., Schmitt S.,
Ring, Schafer, W. and Kholer, K. (1991) Physical
Review Letters, 66, 201.
[14] Elze, H.T. (1995) Quantum decoherence, entropy and
thermalization in strong interactions at high energy.
Nuclear Physics B, 436, 213; Nuclear Physics B, 39, 169.
[15] Jackiw, R. and Kerman, A. (1978) Physics Letters A,
71, 158.
[16] Heller, E.J. (1975) Calculations and mathematical
techniques in atomic and molecular physics. Journal of
Chemical Physics, 62, 1544; Heller, E.J. and Sundberg,
R.L. (1985) Chaotic behavior in quantum systems.
Plenum Press, New York, 255.
[17] Pattanayak, A.K. and Schieve, W.C. (1994) Physical
Review Letters, 72, 2855; (1992) Physical Review Letters,
46, 1821, Proceedings from workshop in honor of
Sundarshan., E.G.G. Gleeson, A.M., Ed., (world scientific,
Singapore, in press).
[18] Cooper, F., Pi, S.Y. and Stancioff, P.N. (1986) Physical
Review D, 34, 3831.
[19] Kovner, A. and Roseinstein, B. (1983) Physical Review
D, 39, 2332.
[20] Littlejohn, R.G. (1988) Physical Review Letters, 61,
2159.
[21] Tannoudji, C.C., Diu, B. and Laloe, F. (1988) Quantum
mechanics, Ed., Masson.
[22] Perez, J.P. and Saint Crieq Chery, N. (1986) Relativity
and Quantisation, University Paul Sabatier, Toulouse,
Ed., Masson.
[23] Gaudaire, M. (1969) Propriete de la matiere: Onde et
Matiere, Colorado Dunod University, Orsay.
[24] Ott, E. (1997) Chaos in dynamical systems. Cambridge
University Press, Cambridge.
[25] Carlson, L. and Schieve, W.C. (1989) Physical Review A,
40, 5896.
[26] Stevenson, P. (1984) Physical Review D, 30, 1712; (1985)
Physical Review D, 32, 1389.
[27] Toda, M. (1974) Instability of trajectories of the lattice
with cubic nonlinearity. Physics Letters A, 48, 335.
[28] Brumer, P. and Duff, J.N. (1976) Journal of Chemical
Physics, 65, 3566.
[29] Capasso, F. and Datta, S. (1990) Bandgap and interface
engineering for advanced electronic and photonic
devices.Physics Today, 43(2), 74.
[30] Kramer, B. (1991) Quantum coherence in mesoscopic
systems. Plenum, New York.
[31] Presilla, C., Jona – Lasinio, G.. and Capasso, F. (1991)
Nonlinear feedback oscillations in resonant tunneling
through double barriers.Physical Review B, 43, 5200
[32] Tchoukuegno, R. and Woafo, P. (2002) Physical D 167,
86; Tchoukuegno, R., Nana, B.R. and Woafo, P. (2002)
Physical Review A, 304, 362; (2003) International
Journal of Non-Linear Mechanics, 38, 531.
[33] Jing, Z.J., Yang, Z.Y. and Jiang, T. (2006) Bifurcation
and chaos in discrete-time predator–prey system.Chaos,
Solitons and Fractals, 27, 722.
[34] Sun, Z.K., Xu, W. and Yang, X.L. (2006) Chaos,
Solitons and Fractals, 27, 778.
[35] Blum, T.C. and Elze, H.T. (1996) Semiquantum chaos in
the double well.Physical Review E, 53, 3123.
[36] Zaslavsky, G.M. (1985) Chaos in dynamic systems.
Harwood Academic, Chur, Switzerland.
[37] Wolf, A., Swift, J. B., Swinney, H.L. and Vastano, J.A.
(1985) Determining Lyapunov exponents from a time
series.Physical Review D, 16, 285.
[38] Melnikov, V.K. (1963) On the stability of a center for
time-periodic perturbations. Transactions of the Moscow
Mathematical Society, 12, 1.
[39] Gucken, H. J. and Holmes, P. (1983) Nonlinear oscillations,
dynamical systems and bifurcations of vector fields.
Springer Verlag, Berlin.
[40] Yamgoue, S.B. and Kofane, T.C. (2002) The subharmonic
Melnikov theory for damped and driven oscillators
revisited .International Journal of Bifurcation and Chaos,
8, 1915; (2003) Chaos, Solitons & Fractals, 17, 155.
[41] Churchill, R.C., Pecelli, G. and Rod, L. (1975) J. Diff.
Eqs. 17, 329; (1977) J. Diff. Eqs. 24, 329; Churchill, R.C.
and Rod, D.L. (1976) Ibid. 21, 39; (1976) Ibid. 21, 66;
(1980) Ibid. 37, 23.