Paper Menu >>
Journal Menu >>
 J. Serv. Sci. & Management, 2008, 1: 206-214 Published Online December 2008 in SciRes (www.SciRP.org/journal/jssm) Copyright © 2008 SciRes JSSM 1 Intertemporal Pricing and Allotment of Sea-cargo Capacity under Reference Effect * Xiangzhi Bu 1 , Lei Xu 2 & Li Su 3 1 School of Business, Shantou University, Shantou, China, 2 School of Business, Shantou University, Shantou, China, 3 English Lan- guage Center, Shantou University, Shantou, China Email: xzpu@stu.edu.cn, lxu3@stu.edu.cn, lisu@stu.edu.cn Received August 16 th , 2008; revised December 8 th , 2008; accepted December 15 th , 2008. ABSTRACT Reference effect influences the shippers’ purchase behavior to some extent, and it makes shippers’ behavior more mys- terious. Furthermore, it leads to complex to coordinate procurement and pricing of forwarder and carrier. Firstly, we introduce the reference effect into the sea-cargo service supply chain composed with carriers and forwarders, and build the game-theoretical model to decide the optimal contract price and order quantity. Considering the situation where the market demand is affected by current price and reference price, we adopt dynamic programming and classical varia- tion method to analyze the dynamic equilibrium of the game under reference effect with symmetric information or not, respectively. Finally, this paper analyzes the reference effect to price, procurement and profit of carrier with digital analysis. Keywords: reference effect, anchoring effect, sea-cargo service chain, dynamic pricing, revenue management 1. Introduction The marine environment has two types of markets gener- ally, the contract market and the spot one in reality [1,2]. In order to lower the risk of capacity allocation and price, carriers often choose to sale advance in contract market that is to sell most capacity to the forwarders and other big shippers. And then, in the second stage, the remaining space is sold by carrier to direct-ship shippers on ad-hoc or free-sale basis. As to the forwarders, in the first stage the forwarders purchase large amount of cargo capacity, which qualifies them for a volume discount. The discount may depend upon the size of allotment as well as the ac- tual volume tendered by the forwarder [3]. In the second stage, the forwarder drums up downstream shippers, for- warders can offer more services and often better prices to downstream shippers in comparison to the carriers’ stan- dard tariff. In this paper, we just focus on coordination between the carrier and the forwarder in the contract market. In the downstream freight market, due to the repeated purchase behavior, shippers will develop reference price, through observing prices of other channels and for- warder’s past prices. Comparing current price and refer- ence price, thereafter, shippers make their capacity pur- chasing decision. This theory is similar to the Prospect Theory of Kahneman and Tversky [4]. During purchasing, they buy less and then turn to other carriers or forwarders if the current price is above reference price, or they do more on site. Throughout the paper, we just analyze shippers’ behavior as a whole, not the individual ship- per’s purchasing behavior. In this way, the downstream shippers’ purchasing decision is not only based on the cost-plus price [1], but the price expectations. In such complex situations, the carrier and the forwarder must take into account the shippers’ price reference effect be- fore they decide the contract price, procurement level and the resale price. And carrier and forwarder could share information and communication to quantity the reference effect to make optimal ordering and pricing decision. In the paper, we adopt the common supply chain con- tract-wholesale contract. In a channel context, we observe in some cases that channel transactions are “governed by simple contracts defined only by a per unit wholesale price” [5]. As noted some time ago by [6], incentive con- tracts in the real world frequently take simpler forms than what theory often predicts. This can also happen because firms have little to lose using a simpler contract [7]. We build a von-Stackelberg model of the carrier and the for- warder where the carrier is the game leader, and the for- warder is the game follower. In which the carrier firstly announces the contract prices according to the ordering quantity of forwarder, and then the forwarder decides the contract quantity. Here, both the carrier and the forwarder act strategically, and the shippers are only sensitive in price. The mathematical representation of the interaction between carrier and forwarder is based on a stylized * T he research is supported in part by the National Science Foundation of China under Grant NO. NSFC 70701022, t he Natural Science Foundation of Guangdong Province under Grant NO. 07301452 and the China Post- doctoral Scienc e Foundation under Grant NO. 2006039084 7 .  Intertemporal Pricing and Allotment of Sea-cargo Capacity under Reference Effect 207 Copyright © 2008 SciRes JSSM model in which certain real-life details have been either omitted or simplified to maintain tractability. The remainder of this paper is organized as follows. In Section 2, we begin with a review of the relevant literatures. In Section 3 we present the problem and also give the defi- nitions of symbols and parameters. We propose a formal price reference model in Section 4. In Section 5, we firstly give an analysis on the decision making process when price reference effect is common knowledge in part 5.1; when price reference effect is asymmetrical information to the carrier, see part 5.2. We then continue in Section 6 with a presentation of our numerical studies and report on various insights that can be drawn from digital simulation. Section 7 concludes our paper. 2. Literature Review Extensive literature has evolved around the coordination between carrier and forwarder, yet relatively attention has been directed to the problem of intertemporal pricing in multi-stages. [1,2] considered a situation where contract market and spot one coexist; asset provider and intermediary can make coordination through option contract, and the overbooking is also considered. Gupta [8] analyzed a flexible contract where carrier has priority to change con- tract parameters later to adjust contract quantity. Then, Amaruchkul, Cooper and Gupta [9] analyzed capacity contracts under asymmetric information, and proposed optimal contract. However, these researches mostly focus on a single-stage problem. In real world, carrier and for- warder coordinate in a multi stages, more. As to the dynamic pricing of finite inventory, the rele- vant literature has mostly ignored the reference effect. Gallego and van Ryzin [10] and Bitran and Mondschein [11] analyze a continous and discrete time pricing schemes, in environment where the distribution of con- sumer valuation does not change over time. Lazer [12] and Aviv and Pazgal [13] discuss dynamic pricing of fashion goods where demand is uncertain. Next, Aviv and Pazgal [14] analyze optimal pricing of seasonal products where the consumer is forwarder- looking (stra- tegic) and distinguish two classes of pricing strategies. For further information on the above body of research, we refer the reader to Popescu and Wu [15]and Bu Xiang-zhi et al. [16]. There are a lot of papers study on the effects of refer- ence price to market demand. Helson’s [17] Adaptation Level Theory pointed that people measures the current result with his past activities as standards; Consumer’s price perception depends on the difference between the interior reference price and exterior reference price. Sor- ger [18] studies local stability of joint dynamic pricing and advertising policies under reference price effects. Fibich [19] investigates the dynamic pricing problem with linear reference effects. The research on dynamic pricing under reference price effects is also in Popescu et al. [15], during which, both consumers of risk neutral and risk preference are concluded. Kapalle et al. [20] bring quality into the reference effect and analyzed the condition under which reference effect of price and quality are both existed. Oliver and Winer [20], Zeithaml [21] consider the reference effect to be the key factor which affects market demand. But all the papers above is in the area of marketing, it doesn’t refer to the coordination between retailers and manufacturers or channel distributor’s problems of produc- tion quantity and inventory in supply chain system. 3. Problem Description The pricing and ordering of repeat-purchase capacity are what we studied in this paper. With the repeated purchase behavior, shippers will develop a reference price r p through observing price of other channels and forwarder’s past prices. Then, comparing the current price and the refer- ence price, shippers would like to purchase less and turn to other channels to procure if the current price is higher than the reference price; otherwise shippers would pur- chase more on site [4]. This price reference effect makes the demand much more complex. Because of the double impact of current price and price reference, the forwarder faces a more complex cargo market. In that case, the price reference effect has to be considered during pricing decision, based on which, for- warder makes the resale prices and quantity at each pe- riod to pursue the maximum profit. And furthermore, the market price also affects the reference price. Thus, both current price and reference price change interactively. Due to the double impact of current price and reference price, it becomes difficult that the coordination between carrier and forwarder, and how the forwarder makes the resale prices as well. In this paper, a finite-period model is involved in a steady economic circumstance, that is to say the contract prices difference and resale prices difference are not at- tributable to economical conditions change, such as cost changes and competition, but strategically pricing. Moreover, cargo that shippers provide lies in the same type, avoiding the prices difference from cargo type dif- ference. And the ordering tactics is not referred specifi- cally. We assume that the carrier sells capacity on the same cargo market in N periods, and the contract be- tween the carrier and the forwarder is the classical dis- count price contract used widely in real economic activi- ties [23]. It means carrier announces a contract price ( ) k t according to forwarder’s books level. We choose the linear rebate through all the paper [24]. And, the unit cost is constant as c [25]. The decision process is as following: Firstly, the carrier announces its discount price con- tract according to forwarder’s future booking decision. Then, the forwarder decides its resale price ( ) p t in pe- riod t , based on the discount price ( ) k t and the ship-  208 Xiangzhi Bu, Lei Xu & Li Su Copyright © 2008 SciRes JSSM pers’ reference price to achieve the dynamic long run maximum profit. And, procure quantity ( ) k t in each single period is determined based on a take-it-or-leave-it basis. During this paper, we mainly study the problems de- scribed as follows: how forwarder determines the resale prices and procurement quantity with the double impact of current price and reference price, and how carrier makes sea-cargo capacity contract under reference effect with symmetric information or not. The mathematical repre- sentation of the interaction between the carrier and the forwarder is based on a stylized model in which certain real-life details have been omitted or simplified to main- tain tractability. Moreover, we assume rational and risk-neutral decision makers. The basic parameters of the model are as follows: γ the memory effect of shippers to past price c the constant unit cost ( ) k t the discount price made by the carrier in period t ( ) d t the procurement (demand) in period t ( ) p t the sales price made by the forwarder in period t ( ) r p t the reference price developed by shippers in period t ( ) b t π the forwarder’s revenue in period t ( ) s t π the carrier’s revenue in period t All the parameters above satisfy ( )( ) p tktc ≥ ≥ , while ( ) k tc = is the situation that the decision is made by the carrier and the forwarder jointly. It is a classical pricing problem of marketing on vertical integration of the car- rier and the forwarder [15,16], we don’t study on it more in the following. 4. Reference Effect Model Recently, many empirical studies had tested the price reference effect and set up the reference effect equations, of which important empirical studies were based on prospect theory. Prospect theory considers that the dif- ference between price and reference price affects market demand, and the effect is asymmetrical. Kahneman and Tversky [4] estimated that when the loss and the gain are almost equal, we often emphasize the loss more, and even two times as much as the gain. As to the same variation, consumers often pay attention to that when price is above reference price [26]. Kalyanaram and Winer [27] tested the strong effect of prospect theory under reference effect. The derivation of mathematic equation is following: Assumption: at period t , the market demand is ( ) d t , as the function of price ( ) p t and reference price ( ) r p t . For simplicity, we adopt the linear demand function [25], as follows: ( )( ){( )( )} r dtabp tmptp t = −+− (1) where, , 0 a b > and are all positive constants, 12 1 2 ,( )( ) {, 0 ,( )( ) r r ptp t mp tpt θθ θ θ > => > >and . The penalty for each unit price above reference price is 2 θ , and the gain for each unit price below reference price is 1 θ . Following the past literatures on the formation of ref- erence prices, we model it as a weighted average of past prices [28], that is: (1)( )( )(1( ))( ) r r pttp ttpt γ γ +=+ − (2) Here, we assume shippers are homogeneous and have the same memory effect γ . Where, γ is shipper’s mem- ory effect to historic price, and the bigger γ is, the stronger the memory effect is. In particular, 1 γ = is ideal state, reference price is equal to the initial reference price 0 ( )( ) r p tp t = . 5. Coordination Between Carrier and Forwarder 5.1. Decision under Symmetric Information Under this situation, carrier and forwarder are attached to different enterprises, and make their decision respectively. Carrier decides the contract prices, and forwarder set re- sale price and order quantity. The Von-Stackelberg game process between carrier and forwarder is: At period t , the decision of carrier is: ( )[( )]( ) s tk tcd t π =− × (3) Based on that, we adopt dynamic programming method to find the general property of carrier’s objective function. Assume (( ),( )) t r Vp tpt is total profit function from period 0 to period t . So, the Bellman equation is [29] 1 (( ),( ))(( ))( )((1),(1)) ..(1)( )( )(1( ))( ) s s t rtr r r Vptptktc dtVp tpt stp ttp ttpt γ γ + = −+++ +=+ − (4) At period t , the decision of forwarder is: ( )[( )()]( ) b tp tk tdt π =− × (5) Then, we adopt dynamic programming method to find the general property of carrier’s objective function. As- suming (( ),( )) t r Vp tpt is total profit function from pe- riod 1 N − to period t .  Intertemporal Pricing and Allotment of Sea-cargo Capacity under Reference Effect 209 Copyright © 2008 SciRes JSSM So, the Bellman equation is [29] 1 (( ),( ))(( ))( )((1),(1)) ..(1)( )( )(1( ))( ) s s t rtr r r Vptptktc dtVp tpt stp ttp ttpt γ γ + = −+++ +=+ − (6) The forwarder’s decision and state are separable, so the long run objective function can be transformed into: [ ] 1 1 0 0 0 ( )(( )( ))( ) (1)( )( )(1( ))( ) . .(0) N N t t r r r r tptktdt p ttp ttpt s tp p π π γ γ − − = = = =− +=+ − = ∑ ∑ (7) Then, the objective function of the forwarder is trans- formed into optimal control problem about single state variable ( ) r p t and single decision variable ( ) p t , which we use maximum principle [30] to solve the dis- crete-time optimal control problem. And based on the analysis of the iterative multi-stage problem, we decom- pose the multi-stage dynamic coordination problem into single-stage coordination problems with classical varia- tion method, and based on that analyze iterative multi-stage problem. Theorem 1: single-stage market price ( ) p t for for- warder is pathwise increasing in the contract price ( ) k t and the reference price ( ) r p t , decreasing in reference effect ( ) t γ . Proof: Constructing Hamilton Function: (( ),(1),( ),) [( )( )][( )(( )( ))] (1)[( )( )(1())( )] r r r Hpttp tt p tktabp tmptp t ttpttp t λ λ γγ + = −− +− +++ − (8) (( ),(1),( ),) 0 ( ) r Hpttp ttp t λ ∂ + = ∂ ( ( )( ) p tktc > > ), then [2()( )( )()( )] (1)(1())0 r abmp tmptbm k t t t λ γ −+++ + + +−= Solving the canonical equations: (1)( )( )(1())( ) r r pttpttp t γ γ +=+− , 0 (0) r r p p = (( ),(1),( ),) ( ) ( ) (( )( ))(1)( ) r r Hpttp tt t p t p tktmtt λ λ λ γ ∂ + =∂ =−+ + , ( )0 N λ = We obtain, ()( )( )(1)(1()) ( )2( ) r abm ktmpttt p tb m λ γ + ++++− =+ By the first order conditions, ( )1 0 2 ( ) p t k t ∂ = > ∂ , ( ) 0 2( ) ( ) r p tmb m p t ∂ = > + ∂ , ( ) (1) 0 ( ) p tt t λ γ ∂ = −+< ∂ . End. Theorem 2: single-stage profit function ( ) s t π for the carrier is concave in the contract price ( ) k t . Proof: Solving the first condition of ( ) s t π to ( ) k t , we ob- tain ( ) ( )() ( ) (1)(1( ))2()( ) s r t a mptb mc k t ttbm kt π λ γ ∂= +++ ∂ − +−−+ The second condition of ( ) s t π to ( ) k t is 2 2 ( ) 2( ) [( )] s t b m k t π ∂ = −+ ∂ . Because of , 0 b m > , we get 2 2 ( ) 2() 0 [( )] s tb m k t π ∂ = −+< ∂ . Then Theorem 2 is proved. According to Theorem 2, then we can get value of ( ) k t when ( ) s t π get the maximum. That is ()( )(1)(1( )) ( )2( ) r abm cmpttt k tb m λ γ + ++−+− =+ . Substituting ( ) k t into ( ) p t , we get 3()3( )(1)(1( )) ( )4( ) r abm cmpttt p tb m λ γ + ++++− =+ . In particular, when ( )0 t γ = , there is no reference ef- fect, the market demand function is ( )( ) dtabp t = − , it is definite, through solving Von Stackelberg model, we obtain ( ) 2 a bc k t b + = , 3 ( )4 a bc p t b + = , 1 ( )() 4 d tabc = − . When ( )1 t γ = , it is complete price reference effect. The demand function is transformed into ( ) d ta = (0)()( ) r mpbmp t − + , and ( )(0) r r p tp= . It is also defi- nite, through solving Von Stackelberg model, we obtain  210 Xiangzhi Bu, Lei Xu & Li Su Copyright © 2008 SciRes JSSM (0) () ( )2( ) r apbmc k tb m ++ + =+ , 33(0) () ( )4( ) r ampbmc p tb m +++ =+ , 1 ( )((0)()) 4 r dtampbmc =+− + . As to the specified coordination problem between car- rier and forwarder, we will give a further analysis in the Section 6.1. 5.2. Decision under Asymmetric Information This section analyzes a two-level supply chain composed with single carrier and single forwarder. Where, the car- rier as the game leader, and the forwarder as the follower in the Von Stackelberg model, the forwarder faces a multi-stage market demand influenced by reference price. Due to near market, the forwarder owns much more market information than the carrier. That is to say, when the reference effect is asymmetric information, the for- warder knows about the exact state. However, because of the asymmetric information about reference effect, the car- rier knows little. Under this condition, constant discount contract can’t maximize the profit of the carrier any longer. Assume ( ) t γ is reference effect, and ( ) t γ satisfies 0( )1 t γ ≤ ≤ . Here, the probability of ( )( ) i t t γ γ = , ( 1,2,..., i n = ) is ( ) i i p p θ θ = = , and it is common knowledge ( except reference effect, cost of the carrier and both profit functions are all common knowledge ). Under this condition, the decision process of the for- warder is: firstly, the forwarder determines the retail price according to the reference effect, then inquires the dis- count price, and determines his ordering quantity. At period t , the decision of the forwarder is: ( )[( )( )]( ) b tp tk tdt π =− × Then, we search for the general property of for- warder’s objective function using dynamic programming method. Assume (( ),( )) t r Vp tpt is the total profits func- tion from period 0 to period t .So, the Bellman equation is [29]: 1 (( ),( ))(( )( ))( ) ( 1,(1),( 1)) ..(1)( )( )(1())( ) b b t rt r r r Vp tptp tktdtV tp tpt stp ttp ttpt γ γ + = −+ + ++ +=+− (9) According to the optimization principle of dynamic programming method, sub strategy of an optimal strategy is optimal. According to the analysis of Section 4.1, at period t , the optimal pricing strategy of forwarder is 3()3( )(1)(1( )) ( )4( ) r abm cmpttt p tb m λ γ + ++++− =+ . The decision process of the carrier is: before forwarder makes the order quantity, the carrier never knows the exact reference effect, only knows about the probability ( ) i i p p θ θ = = . According to Harsanyi transformation principle, we assume that there exist n kinds of for- warders; every forwarder has one kind of reference effect. Thus, the carrier can’t maximize his profit by setting only one discount price. Then, the carrier announces his dis- count contract in early of each period: set ( )( ), i j d tdtij ≤ ≤ , corresponding discount price is ( )() i j k tkt ≥ , and ( )() j i cktk t < ≤ . The carrier maxi- mizes his profit through setting up discount contract. And, the order quantity of the forwarder is continuous, and only the order quantity is equal to or bigger than ( ) i d t , the discount price is equal to ( ) i k t . According to Bayes- ian and Revelation principle, at third stage the forwarder chooses optimal order quantity and discount price ac- cording to his type, for example {( ),( )} i i q tk t , and this signal releases the forwarder’s type. Theorem 3: the combination of discount price and or- der quantity is 1 {[( ),( )],( )} i ii q tqtkt + . Proof: According to the result of Theorem 1, the market re- tailing price ( ) i t γ is corresponding to ()()( )(1)(1( )) ( )2( ) i ri i abm ktmpttt p tb m λ γ + ++++− =+ . And according to Theorem 2, the discount price of the carrier is ()()(1)(1()) ( )2( ) r i abm cmpttt k tb m λ γ + ++−+− =+ . Based on the formula of ( ) i p t and ( ) i k t , we can obtain the order quantity 1 ( )[( )() 4 i r qtamptbm c =× +−+ (1)(1( ))] i t t λ γ − +− at period t when the reference ef- fect is ( ) i t γ ; And correspondingly, when the reference effect is 1 ( ) i t γ + , the order quantity is 1 1 1 ( )[( )()(1)(1())] 4 i ri qtamptbmctt λ γ + + =× +−+−+− . So when the forwarder’s type is ( ) i t γ , the carrier set up the combination of discount price and order quantity is 1 {[( ),( )],( )} i ii q tqtkt + . 5.2.1. Mechanism Design Because the reference effect is not common knowledge to the carrier, we can take the carrier’s decision as a classi- cal mechanism design problem. And based on the revela- tion principle [31], the carrier can make n kinds of combination 1 {[( ),( )],( )} i ii q tqtkt + . Each combination matches along with one type of forwarder. Assuming that ( ) i Q t ( 1 ( )( )( ) ii i qtQtqt + ≤ ≤ ) and ( ) i k t is a combina-  Intertemporal Pricing and Allotment of Sea-cargo Capacity under Reference Effect 211 Copyright © 2008 SciRes JSSM tion of discount price and order quantity to type i for- warder, so the expected profit of the carrier is (10): 1 , (( ),( ))(( ))( ) (( 1),( 1)) ..max(( ),( ))0,1,2,...,,...() (( ),())(( ),( )), 1,2,..., ,,...() () 0,()0,1,2,..., s ti ii s t i iii i iiijj i j i i Vktp tpktcdt Vktp t s tQtktinIR Qt ktQt kti n jiIC Q tktin π π π + = − ++ + ≥ = ≥ = ≠ ≥≥ = (10) Where, the first item is Individual Rational constraint ( ) i IR which ensures the forwarder to accept the dis- count contract; the second item is Incentive Compatibility constraint , ( ) i j IC which shows type i forwarder chooses the combination {discount price, order quantity} corresponding his type. 5.2.2. Analysis of Mechanism Design According to the maximum principle, the forwarder chooses the optimal order quantity, and in the third stage, the forwarder releases his type to the carrier through sig- nal about the forwarder’s type. The segmentation of order quantity that the carrier makes is corresponding to the forwarder’s type, that is: 1 ( )[( )()(1)(1( ))] 4 i ri qtamptbmctt λ γ =+− +−+− . Theorem 4: the optimal order quantity of the for- warder is the initial quantity ( ) i q t in the interval 1 [(),( )] i i q tqt + . That is: 1 ( )[( )()(1)(1( ))] 4 i ri qta mptb mctt λ γ =× +−+−+− Proof: according to Theorem 1 and the principle of Mecha- nism Design in section 4.2.1, Theorem 4 can be proved simply. Based on Theorem 4, we transform formula (10) into (11): 1 , (( ),( ))(( ))( )((1),(1)) ..max(( ),( ))0,1,2,...,,...() ((),())(( ),( )), 1,2,...,,,...() ( )0,( )0,1,2,..., s s ti iit i iii i iiijj i j i i Vktp tpktc dtVktp t s tqtktinIR q tk tqtkti n jiIC q tk tin π π π + =−++ + ≥ = ≥ = ≠ ≥≥ = (11) Theorem 5: 1) the sufficient and necessary condi- tion to solve problem 5.2.2 is: for the given combina- tion {( ),( )} i i q tk t , problem 5.2.2 must satisfy Indi- vidual Rational Constraint i IR ; the feasible solution to , 1 , 2,3,..., i i IC in − = and , 1 , i i IC i + = 1,2,..., 1 n − is equal. 2) The sufficient condition to solve problem 5.2.2 is: for the given condition {( ),( )} i i q tk t , there must exist fea- sible solution of 5.2.2 satisfies ( )(( )) ii i q tQ k t = , and satisfies Individual Rational Constraint i IR , Incentive Compatibility Constraint , 1 , 2,3,..., i i IC in − = and , 1 , 1,2,...,1 i i IC in + = − . As to the proof of Theorem 5, [31,32] have given com- plete proof. 6. Case Simulation and Discussion 6.1. Digital Simulation under Symmetric Information The above sections give the property of single-period profit function. However, as to multi-period problem we can’t give the pricing trajectory of both the carrier and the forwarder directly. Based on the analysis of Section 5.1, we discuss the optimal pricing trajectory of multi-period discount contract, and the pricing decision of the carrier through case simulaiton. We take the fol- lowing parameters for example: ( )0 t γ = , ( )0.2 t γ = , ( )0.4 t γ = , ( )0.6 t γ = , ( )0.8 t γ = , ( )1 t γ = , 30 a = , 2 b = , 1 2 3( 4,2) m θ θ = == , 4 c = , (0) 5 r p = . Be- cause shipper goods, in particular the brand commodities have different procurement frequency. We choose 22 periods as rolling horizon windows. The trajectory of discount price, retailing price and profit under reference effect is following: (Notes: the Lagrange multipliers are different to dif- ferent time windows, and then the results of data analysis are different.) Figure 1 gives the forwarder’s optimal pricing trajec- tory about six kinds of reference effect. When the refer- ence effect ( )1 t γ = , the forwarder chooses the lowest price and holds on for the whole time windows. When the reference effect ( )0 t γ = , the forwarder makes the highest price and also holds on. Under other reference 6 7 8 9 10 11 12 13 t0t1 t2t3 t4 t5t6t7 t8t9t10t11t12t13t14t15t16t17t18t19t20 0 0.2 0.40.6 0.8 1 Figure 1. The forwarder’s resale pricing trajectory curve 13 12 11 10 9 8 7 6 0 0.2 0.4 0.6 0.8 t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11 t12 t13 t14 t15 t16 t17 t18 t19 t20 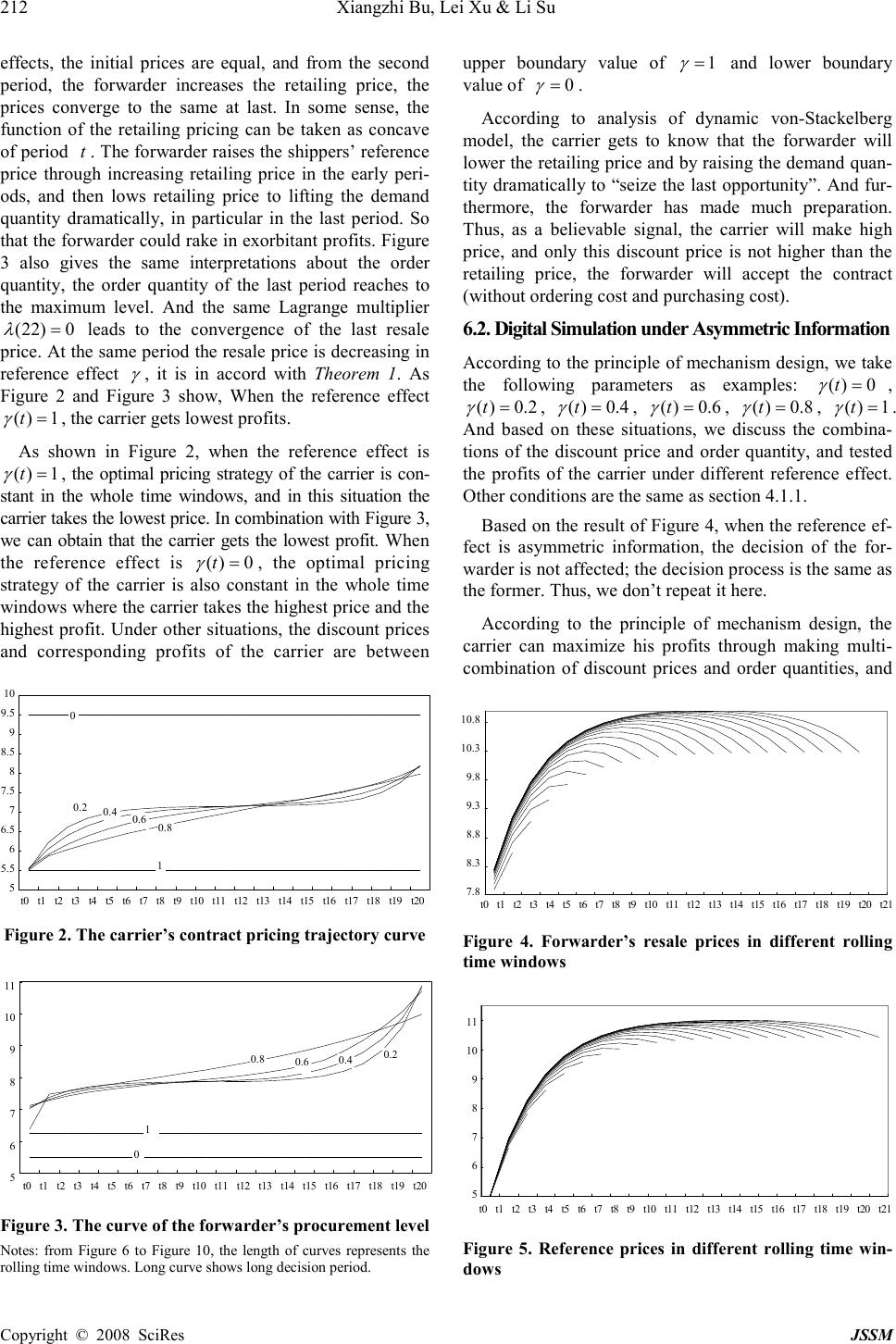 212 Xiangzhi Bu, Lei Xu & Li Su Copyright © 2008 SciRes JSSM effects, the initial prices are equal, and from the second period, the forwarder increases the retailing price, the prices converge to the same at last. In some sense, the function of the retailing pricing can be taken as concave of period t . The forwarder raises the shippers’ reference price through increasing retailing price in the early peri- ods, and then lows retailing price to lifting the demand quantity dramatically, in particular in the last period. So that the forwarder could rake in exorbitant profits. Figure 3 also gives the same interpretations about the order quantity, the order quantity of the last period reaches to the maximum level. And the same Lagrange multiplier (22) 0 λ = leads to the convergence of the last resale price. At the same period the resale price is decreasing in reference effect γ , it is in accord with Theorem 1. As Figure 2 and Figure 3 show, When the reference effect ( )1 t γ = , the carrier gets lowest profits. As shown in Figure 2, when the reference effect is ( )1 t γ = , the optimal pricing strategy of the carrier is con- stant in the whole time windows, and in this situation the carrier takes the lowest price. In combination with Figure 3, we can obtain that the carrier gets the lowest profit. When the reference effect is ( )0 t γ = , the optimal pricing strategy of the carrier is also constant in the whole time windows where the carrier takes the highest price and the highest profit. Under other situations, the discount prices and corresponding profits of the carrier are between Figure 2. The carrier’s contract pricing trajectory curve Figure 3. The curve of the forwarder’s procurement level Notes: from Figure 6 to Figure 10, the length of curves represents the rolling time windows. Long curve shows long decision period. upper boundary value of 1 γ = and lower boundary value of 0 γ = . According to analysis of dynamic von-Stackelberg model, the carrier gets to know that the forwarder will lower the retailing price and by raising the demand quan- tity dramatically to “seize the last opportunity”. And fur- thermore, the forwarder has made much preparation. Thus, as a believable signal, the carrier will make high price, and only this discount price is not higher than the retailing price, the forwarder will accept the contract (without ordering cost and purchasing cost). 6.2. Digital Simulation under Asymmetric Information According to the principle of mechanism design, we take the following parameters as examples: ( )0 t γ = , ( )0.2 t γ = , ( )0.4 t γ = , ( )0.6 t γ = , ( )0.8 t γ = , ( )1 t γ = . And based on these situations, we discuss the combina- tions of the discount price and order quantity, and tested the profits of the carrier under different reference effect. Other conditions are the same as section 4.1.1. Based on the result of Figure 4, when the reference ef- fect is asymmetric information, the decision of the for- warder is not affected; the decision process is the same as the former. Thus, we don’t repeat it here. According to the principle of mechanism design, the carrier can maximize his profits through making multi- combination of discount prices and order quantities, and Figure 4. Forwarder’s resale prices in different rolling time windows Figure 5. Reference prices in different rolling time win- dows 5 5.5 6 6.5 7 7.5 8 8.5 9 9.5 10 t0 t1 t2 t3 t4 t5 t6 t7 t8 t9t10t11t12t13t14t15t16t17t18t19t20 0 0.2 0.4 0.6 0.8 1 10 9.5 9 8.5 8 7.5 7 6.5 6 5.5 5 0 0.2 0.4 0.6 0.8 t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11 t12 t13 t14 t15 t16 t17 t18 t19 t20 1 5 6 7 8 9 10 11 t0t1t2t3t4t5t6t7t8t9t10 t11 t12 t13 t14 t15 t16 t17 t18 t19 t20 1 0.80.6 0.4 0.2 0 11 10 9 8 7 6 5 1 0.2 0.4 0.6 0.8 t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11 t12 t13 t14 t15 t16 t17 t18 t19 t20 0 7.8 8.3 8.8 9.3 9.8 10.3 10.8 t0t1t2t3t4t5t6t7t8t9t10t11t12 t13 t14t15t16 t17 t18 t19 t20 t21 10.8 10.3 9.8 9.3 8.8 8.3 7.8t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11 t12 t13 t14 t15 t16 t17 t18 t19 t20 t21 5 6 7 8 9 10 11 t0 t1 t2 t3 t4 t5 t6 t7 t8 t9t10t11t12t13t14t15t16t17t18t19t20t21 11 10 9 8 7 6 5 t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11 t12 t13 t14 t15 t16 t17 t18 t19 t20 t21  Intertemporal Pricing and Allotment of Sea-cargo Capacity under Reference Effect 213 Copyright © 2008 SciRes JSSM with the help of the mechanism, the carrier will know the forwarder’s type. That is when the forwarder chooses the relevant combination; he releases real reference effect unconsciously. Thus, the carrier can realize the same profit as the situation where the reference effect is sym- metrical information. 6.3. Different Rolling Time Windows Analysis For the maximum profit, the forwarder decides the opti- mal resale prices and the optimal procurement quantity; Moreover, he must take into account the price reference effect of its downward market. Due to Theorem 1, sin- gle-stage resale price ( ) p t is pathwise increasing in the reference price ( ) r p t , and decreasing in reference effect ( ) t γ . However, it’s only a single-period optimal decision. As a multi-period decision problem, we should show some managerial suggestions about a long-run pricing decision, in additionally, under price reference effect. As the simulation result of Figure 4, it shows that the multi-period resale prices are concave in t . It is different from the result of Popescu and Wu [20], which proved that optimal pricing policies induce a perception of monotonic prices. In our paper, we analyze the resale pricing policies, but also the optimal procurement deci- sion. Theoretically, so long as the forwarder knows about his decision period or about approximate one, he can make the optimal resale prices to maximize his long-run profit. Figure 6. Carrier’s contract prices in different rolling time windows Figure 7. Forwarder’s procurement level in different rolling time windows The reference price ( ) r p t is exponential smoothing in resale price ( ) p t . And the exponent represents the reference effect of the shippers. We take ( )0.4 t γ = for example. Based on Figure 4 and Figure 5, it shows the long-run relation between resale price and reference price. As Winer [28] tested, (1)( )( )(1( ))( ) r r pttp ttpt γ γ +=+ − Based on the decision of the forwarder, the carrier de- cides the contract prices to maximize his profit. As Fig- ure 6 and Figure 7 show, the carrier’s optimal contract prices curve and the forwarder’s procurement curve are the kinked S-shaped. 7. Conclusions and Future Study We propose a stylized model of dynamic pricing for car- rier that sells a finite quantity of units of capacity, to price reference shippers, using dynamic programming method and classical variation method. In the sea-cargo service supply chain, the carrier applies discount contract under the market demand influenced by current price and reference price. Based on that, the paper considers two situations: the reference effect is symmetric information or not. Under both of situations, how the carrier makes his discount pricing decision and how the forwarder makes his resale price and procurement level are the critical problems in the paper. For the first case, we identify dynamic von- Stackel- berg equilibrium for the game between carrier (pricing strategy) and forwarder (ordering strategy). And we find single-stage market price ( ) p t for forwarder is path- wise increasing in the contract price ( ) k t and the refer- ence price ( ) r p t , decreasing in reference effect ( ) t γ , and single-stage profit function ( ) s t π for the carrier is concave in the contract price ( ) k t . Moreover, an em- pirical study presents the discount pricing is between upper boundary 1 γ = and lower boundary 0 γ = , and the bigger the reference effect is, the lower the discount price is. For the second case, the carrier designs relevant mechanism to make forwarder to show his type about the market demand, and based on that, to maximize his profit through Bayesian game. Reference effect interfaces with the drivers of the benefits of price segmentation. Especially, the iterative reference effect leads to a complex where carrier and forwarder make decisions. Carrier and forwarder must take into account both the past price and the past refer- ence price. In the paper, we assume the shippers strategi- cally purchase, and the shippers know about all the resale prices and their own reference price. There are several directions for future investigations within this line of research. For example, we can consider a situation where the spot market and contract one co- exist at the same time. Facing uncertain demand and 5.5 6 6.5 7 7.5 8 8.5 t0t1t2t3t4t5t6t7t8t9t10 t11 t12 t13 t14t15t16 t17t18 t19t20 t21 t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11 t12 t13 t14 t15 t16 t17 t18 t19 t20 t21 8.5 8 7.5 7 6.5 6 5.5 7 7.5 8 8.5 9 9.5 10 10.5 11 t0t1t2t3t4t5t6t7t8t9t10t11 t12 t13t14 t15t16 t17 t18 t19 t20 t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11 t12 t13 t14 t15 t16 t17 t18 t19 t20 11 10.5 10 9.5 9 8.5 8 7.5 7  214 Xiangzhi Bu, Lei Xu & Li Su Copyright © 2008 SciRes JSSM price of spot market, how carrier should allocate the ca- pacity between spot and contract market, respectively. And in the contract market, what price carrier should announce. We don’t allow players to overbook in the paper. However in practice, overbooking and other varie- ties of rules should be used to prioritize loads when de- mand exceeds total supply. And in the paper, we assume shippers have homogeneous memory effect γ . So a de- tailed investigation of reference effect with both contrac- tual and spot market capacity purchases is another direc- tion worthy of future study. 8. Acknowledgment The authors would like to thank the referees for their helpful suggestions. The authors are grateful to Associate Professor ZHAO Quan-wu of Shantou University for his helpful comments on an earlier draft of the manuscript, and YANG Min, BEI Xiaofen of Shantou University for their valuable discussions. The research is supported in part by the National Science Foundation of China under Grant NO. 70701022, the Natural Science Foundation of Guangdong Province under Grant NO. 07301452, and the China Postdoctoral Science Foundation under Grant NO. 20060390847. REFERENCES [1] H. Rolf, “Capacity option for revenue management: Theory and applications in the air cargo industry,” P. H. D. thesis, Springer, 2006. [2] S. Spinler, “Capacity reservation for capital-intensive technology: A Options Approach,” Springer, Heidelberg, 2003. [3] D. Sigworth, “Contracting: Making the rate case,” Traffic World, 268(17): pp. 32-33, 2004. [4] D. Kahneman and A. Tversky, “Prospect theory: An analysis of decision under risk,” Econometrica, 47(2), pp. 263-291, 1979. [5] M. A. Lariviere and E. L. Porteus, “Selling to the newsvendor: An analysis of price-only contracts,” Manufacturing Service Operation, Management, 3 (4): pp. 293-305, 2001. [6] B. Holmstrom and P. Milgrom, “Aggregation and linearity in the provision of intertemporal incentives,” Econometrica, 55(2), pp. 303-328, 1987. [7] J. S. Raju, V. Srinivasan, “Quota-based compensation plans for multiterritory heterogeneous salesforces,” Management Science, 42(10) , pp. 1454-1463, 1996. [8] D. Gupta, “Carrier-Forwarder Contracts in the Air Cargo Industry,” Department of Mechanical Engineering, Uni- versity of Minnesota, Working Paper, 2006. [9] K. Amaruchkul, W. L. Cooper, and D. Gupta, “Air-Cargo capacity contracts under asymmetric information,” Work- ing Paper, 2007. [10] G. Gallego and G. van Ryzin, “Optimal dynamic pricing of inventories with stochastic demand over finite hori- zons,” Management Science, 40 (8), pp. 999-1020. 1994. [11] R. G. Bitran and S. V. Mondschein. “Periodic pricing of seasonal products in retailing,” Management Science, 43 (1), 1997, pp. 64-79. [12] E. P. Lazer, “Retail pricing and clearance sales,” The America Economic Review 76(1) pp. 14-32, 1986. [13] Y. Aviv and A. Pazgal, “A partially observed markov decision process for dynamic pricing,” Management Science, 51 (9), pp.1400-1416, 2005. [14] Y. Aviv and A. Pazgal, “Optimal pricing of seasonal products in the presence of forwarder-looking customers,” Working Paper, 2005. [15] I. Popescu and Y. Z. Wu, “Dynamic pricing strategies with reference effects,” Operations Research, 55(3), pp. 413-429, 2007. [16] X. Z. Bu and X. lei, “Integration operation for production and pricing of dynamic supply chain under reference effect,” working paper, pp. 10, 2007. [17] M. Helson, “Adaptation level theory,” Harper and Row, New York, 1964. [18] G. Sorger, “Reference price formation and optimal mar- keting strategies,” Optimal Control Theory and Economic Analysis, 3, pp. 97-120, 1988. [19] G. Fibich, A. Gavious, and O. Lowengrart, “Explicit solu- tions of optimization models and differential games with nonsmooth (asymmetric) reference-price effect,” Operations Research, 51(5), pp. 721-734, 2003. [20] K. P. Kopalle, A. G. Rao, and J. L. Assuncao, “Asymmetric reference price effects and dynamic pricing polices,” Marketing Science, 15(1), pp. 60-85, 1994. [21] Oliver, L. Richard, and S. Russell Winer, “A framework for the formation and structure of consumer expectations: Review and propositions,” Journal of Economic Psychol- ogy, 469-499, December 1987. [22] V. A. Zeithaml, “Consumer Perceptions of price, quality and value: a means-end model and synthesis of evidence,” journal of marketing, 52(7), pp. 2-22, 1988. [23] A. Burnetas, S. M. Gilbert, and C. Smith, “Quantity dis- counts in single period supply contracts with asymmetric demand information,” Working paper, 2005. [24] T. Taylor, “Supply chain coordination under channel re- bates with sales effect,” Management Science, 48(8), pp. 992-1007, 2002. [25] H. Varian, “Microeconomic Analysis,” New York: Norton, 1992. [26] G. Kalyanaram and R. S. Winer, “Empirical generalizations from reference price and asymmetric price response re- search,” Marketing Science, 14(3), pp. 161-169, 1995. [27] D. Putler, “Incorporating reference price effects into a theory of shipper choice,” Marketing Science (summer), pp. 287-309, 1992. [28] Winer and S. Russell, “A reference price model of brand choice for frequently purchased products,” Journal of Shipper Research 13 (September), pp. 250-256, 1986. [29] N. L. Stokey, R. E. Lucas, and E.C. Prescott, “Recursive method in economic dynamics,” Harvard University Press. 1989. [30] R. F. Hartl and S. P. Sethi , “Optimal control problems with differential inclusions: Sufficiency conditions and an appli- cation to a production inventory model,” Optimal Control Applications and Methods 5 (1984), pp. 289–307. [31] D. Fudenberg and J. Tirole, “Game Theory,” China people publisher, 10 (in Chinese) 2002. [32] W. Y. Zhang, “Game theory and information economics,” Shanghai people publisher, 8 (in Chinese), 1996. |

