Wireless Sensor Network, 2010, 2, 243-249
doi:10.4236/wsn.2010.23033 Published Online March 2010 (http://www.scirp.org/journal/wsn)
QPSK DS-CDMA System over Rayleigh Channel with a
Randomly-Varying Frequency Narrow-Band
Interference: Frequency Tracking Analysis
Aloys N. Mvuma
School of Informatics, University of Dodoma, Dodoma, Tanzania
Received August 25, 2009; revised September 7, 2009; accepted September 21, 2009
Abstract
This paper analyses frequency tracking characteristics of a complex-coefficient adaptive infinite-impulse
response (IIR) notch filter used for suppression of narrow-band interference (NBI) with a randomly-varying
frequency in a quadriphase shift keying (QPSK) modulated direct-sequence code-division multiple-access
(DS-CDMA) communication system. The QPSK DS-CDMA signals are transmitted over a frequency
non-selective Rayleigh fading channel. The analysis is based on a first-order real-coefficient difference equa-
tion with respect to steady-state instantaneous frequency tracking error from which a closed-form expression
that relates frequency tracking mean square error (MSE) with number of DS-CDMA active users and NBI
power is obtained. Closed-form expressions for optimum notch bandwidth coefficient and step size constant
that minimize the frequency tracking MSE are also derived. Computer simulations are included to substanti-
ate the accuracy of the analyses.
Keywords: Code-Division Multiple Access (CDMA), Quadriphase Shift Keying (QPSK), Complex Adaptive
IIR Notch Filter, Narrow-Band Interference (NBI), Frequency Tracking MSE
1. Introduction
Direct-sequence code-division multiple-access (DS-CDMA)
is a preferred multiplexing technique in cellular tele-
communications services as it exhibits desired features
that are not inherently found in other multiple access
techniques, i.e., time-division multiple-access (TDMA)
and frequency-division multiple-access (FDMA). Some
of superior DS-CDMA features include robustness in
multipath fading environment, flexibility in allocation of
channels and increased spectral efficiency due to its ca-
pability of sharing bandwidth with narrow-band commu-
nication systems [1–3]. The bandwidth sharing capability
is made possible by the inherent narrow-band interfer-
ence (NBI) suppression capacity of DS-CDMA due to
the processing gain of spread spectrum systems. How-
ever, for high levels of NBI power, the NBI suppression
capacity of DS-CDMA system can be enhanced by
means of signal processing techniques at the receiver.
Several methods with varying complexities have been
proposed for suppression of NBI in DS-CDMA commu-
nication systems [4–9].
In [10], a complex coefficient adaptive notch filter
implemented as a constrained infinite-impulse response
(IIR) filter with a complex Gauss-Newton adaptation
algorithm was proposed. Its application in the suppres-
sion of NBI in quadriphase shift keying (QPSK) di-
rect-sequence spread-spectrum (DSSS) communication
system was shown to result in a better signal-to-noise
ratio (SNR) improvement factor than that achieved by
finite-impulse response (FIR) adaptive prediction filter.
In [11] a complex coefficient adaptive IIR notch filter
with a simplified gradient-based algorithm that does not
require any matrix inversion was presented. Analyses of
its convergence, steady-state and tracking characteristics
were presented in [12–15], respectively. Its application in
suppression of NBI in QPSK-DSSS system with fixed
unknown frequency was introduced in [13].
This paper investigates frequency tracking characteris-
tics of the complex-coefficient adaptive IIR notch filter
in [11] that is used for suppression of NBI with ran-
domly-varying frequency in a synchronous QPSK DS-
CDMA communication system communicating over a
frequency non-selective Rayleigh fading channel. The
analysis is based on the derived first-order real-coeff-

A. N. Mvuma 244


i
s
t

I
itb

I
i
ct

cos 2c Pft





I
i
s
t


wt


it
icient difference equation with respect to steady-state
instantaneous frequency tracking error from which a
closed-form expression for frequency tracking mean
square error (MSE) is obtained. In addition, closed-form
expressions for optimum notch bandwidth coefficient
and step size constant are also derived. Computer simu-
lations are included to substantiate accuracy of the
analyses.
This paper is organized as follows. Section 2 presents
the system model. Complex coefficient adaptive IIR not-
ch filter is presented in Section 3 whereas frequency trac-
king is analyzed in Section 4. In Section 5 simulations are
presented and discussed before a conclusion in Section 6.
2. System Model
We consider a synchronous DS-CDMA system over
frequency-nonselective Rayleigh fading channel using
QPSK modulation, quaternary pseudo-noise (PN) spr-
eading m-sequences and the rectangular chip waveform.
It is assumed that there are K simultaneously transmit-
ting users. Referring to Figure 1, the transmitted signal
for the i-th user

1
K
ii
st  is expressed as
 
 
cos
sin
II
iiic
QQ
ii c
stPb tctt
Pbt ctt






 (1)
where:
P is the power of the transmitted signal.


I
i
bt
and


Q
i
bt
are in-phase and quadrature-phase
binary data signals, respectively.


I
i
ct and


Q
i
ctare in-phase and quadrature-phase
PN spectrum spreading signals, respectively.
c

and

are the modulator carrier frequency and
phase, respectively.
We define the rectangular pulse with duration
as

T
pt
T

1, 0
0, elsewhere
T
tT
pt 


 (2)
Therefore the in-phase and quadrature-phase data and
spectrum spreading signals are expressed as
 
,,
s
II
iijT
j
btbp t jT



s
(3)


rt

Q
i
bt



Q
i
ct

sin2c Pft





Q
i
s
t

1sin2c
c
ft
T

 

1cos 2c
c
ft
T

 

Q
ic
Tck

I
ckT
ic
1


rt


c
x
kT

I
c
x
kT

Q
c
x
kT


c
ekT
Figure 1. QPSK DS-CDMA communications system model. (a) Transmitter; (b) Receiver.


ht
(
a
)
1
0
L
l



Complex
Adaptive
IIR
Notch
Filter

(1)
.
c
c
kT
kT
dt





Re c ekT
To decision

(1)
.
c
c
kT
kT
dt

1
0
L
l







Im c ekT
(
b
)

A. N. Mvuma245
s

c
c

 

 
,s
QQ
iijT
j
bt bptjT



 (4)
 
,,
c
II
iijT
j
ctcpt jT



 (5)
 
,c
QQ
iijT
j
ct cptjT



 (6)
where

,1, 1
I
ij
b  and are identically and
independently distributed (IID) random j-th data bits
of the i-th user for the in-phase and quadrature-phase
components.

,1, 1
Q
ij
b 

,1, 1
I
ij
c  and


,1, 1
Q
ij
c  are IID random
j-th chips for the i-th user for the in-phase and quad-
rature-phase components, respectively.
c
T and
s
T are the chip duration and the symbol du-
ration, respectively, where is the number
of chips per symbol or processing gain.
/
sc
TT L
The QPSK DS-CDMA signal comprising of signals
for all K active users is transmitted over a frequency
non-selective Rayleigh fading channel with impulse re-
sponse given by


 
exphtj t

   (7)
where

is the phase shift with uniform PDF over

0, 2


,

is the time delay which is uniformly dis-
tributed over
 
0,
s
T and

is the Rayleigh distrib-
uted attenuation having a probability density function
(PDF) expressed as

2
exp, 0,
2
0, 0.
A
f










(8)
The transmitted signal is corrupted with a zero-mean
additive white Gaussian noise (AWGN)


wt
0/2N
with
two-sided power spectral density (PSD) and a
NBI modeled as
  
2cos c

I
tJ tt   (9)
where
J
is the power of the interference and


t

is
the instantaneous phase deviation.
The received signal at the input of the correla-
tor bank in Figure 1 is expressed as

rt
 
1
K
i
i
rts twtIt 


 (10)
At time kTc the samples

I
c
()() () ()
IIII
x
ksknk kz=++ (11)
()() () ()
QQQQ
x
ksknkkz=++ (12)

,,
1
4
K
I
II
ikik
i
P
s
kb 

c
(13)

,,
1
4
K
Q
ik ik
i
PQ
Q
s
kb 

c (14)
where


,1, 1
I
ik
b

 and

,1, 1
Q
ik
b


 are the values of
data signals at the k-th sampling instant of the i-th user
for the in-phase and quadrature-phase components.


,1, 1
I
ik
c

 and

,1, 1
Q
ik
c


 are the values of
the spectrum spreading signals at the k-th sampling
instant for the i-th user for the in-phase and quadra-
ture-phase components, respectively.


I
nk
and


Q
nk
are independent and uncorrelated
random processes with zero mean and variance
2
4
N
 0
c
T.
Assuming


t

to be varying slowly such that it is
constant over one chip interval, then NBI components


Ik
 and


Qk
 in (11) and (12) are expressed as
 
cos
2
IJ
k
 k  (15)
 
sin
2
QJ
k
 k  (16)
It can easily be shown that

I
s
k and


Q
s
k are
zero-mean uncorrelated random processes each with
variance 22
4
s
P
EK 

 .
3. Complex Coefficient Adaptive IIR Notch
Filter
Using complex notation, a complex input signal to a
complex coefficient adaptive IIR notch filter in Figure 1
is of the form


() (),
x
kskknk    (17)
where




IQ

s
kskjsk (18)
  
exp
2
J
kj  

x
kT and


Q
c
x
kT
c
T
in
Figure 1 can be written as (for simplicity, is nor-
malized to unity)

k  (19)
()(1)(),kk k



 (20)

A. N. Mvuma 246
() ()().
IQ
nkn kjnk (21)
()k

is the instantaneous frequency that follows a
random walk model and is expressed as
0
()(1)(), (0)kk k

   (22)
where is a zero-mean white noise with variance

k 
2
v

,

is the scaling factor for the frequency drift and
is assumed to be small, i.e., 1

 and 0

is the ini-
tial frequency.
Transfer function of first-order complex coefficient
IIR notch filter for suppression of the NBI in (17) is
given by [11].
1
1
() 1
0
() 1
0
11
() 21
jk
jk
ez
Hz ez







 (23)
where 0

is the notch bandwidth coefficient and 1

is
the notch frequency coefficient. Adaptation algorithm
used here to estimate the instantaneous frequency of the
NBI is expressed as [11].
*
11
(1)()Re()()kkek 

 . k


(24)
Re[.] denotes real number and * denotes complex conju-
gate. Here

is the step size constant, is the
complex notch filter output and

ek
()k

is the gradient
signal. Referring to (23), the instantaneous frequency can
be estimated by where

ˆk

1
ˆ() ().kk

  (25)
Transfer function from the input ()
x
k to the gradient
signal ()k

in (24) is given by [11].
1
1
() 1
0
() 1
0
1
() .
21
jk
jk
je z
Gz ez







 (26)
4. Frequency Tracking Error Analysis
In this section, frequency tracking error of the algorithm
in (24) is analyzed. We define steady-state tracking error
of instantaneous frequency ()k

as [14], [15].
ˆ
()() ().kkk

  (27)
Referring to the coefficient adaptation algorithm in
(24), it follows from (27) that [15]:
*
(1)()()Re[() ()],kkkek   k (28)
A first-order difference equation with respect to ()k

is
and
obtained by using approximations for steady-state signals
()ek ()k

ved in [14], and is expressed by deri
0
2
0
1
(1)1()(),
21 4
J
kkk





k  is



 
 
 
 (29)
where the input to the difference equation
given by

(())(()
*
22
1
() ()()
jk jk
J
knkenke



 )
**
24
1( )
()()()()
2
ee
ee
k
nknknknk











(30)
Here


e
nk and


nk

are the output of


H
z and


Gz , respectively, due to




s
knk. Byg to
function
referrin
r (29), t-ordercoefficient transfea firs real


F
z between the input


k 
and the output


k 
is given by
1
1
2
()
11
24
z
Fz Jz









. (31)
4.1. Square of Tracking Error Due to Frequency
Drift
ro the frequency drift is found to be given by
By referring to (29), (30) and (31), square of tracking
r due toer
2222
22 11
1
2
12
() ().
2
v
vFzFzzdz
jJ


 




 (32)
(32) is obtained by assuming that 2 4
2
J

 w
means the step-size parameter is sufficiently small.
um
hich
4.2. Frequency Tracking Mean Square Error
Frequency tracking mean square error (MSE) is the s
f 2 o1

in (32) and frequency error variance 2
2

due to
()
e
nk and ()nk

. 2
2

is obtained by [12,14].
223
0
0
(1 )
22
c
N JP
K
T


 

2
22
00
2
16(1) (1)(1)
E 



, (33)
2
11
24
J 


,
The following observations are made f
1) Frequency tracking error varia
(34)
rom (33) and (34):
nce is directly pro-
portional to the NBI power .
J
2) For small AWGN PSD 0 N frequency tracking
error variance is directly o the signal
transmit power P and num
proportional t
ber of active users .
K
3) Frequency tracking error variance can be reduced
by expanding the notch bandwidth, i.e., reducing the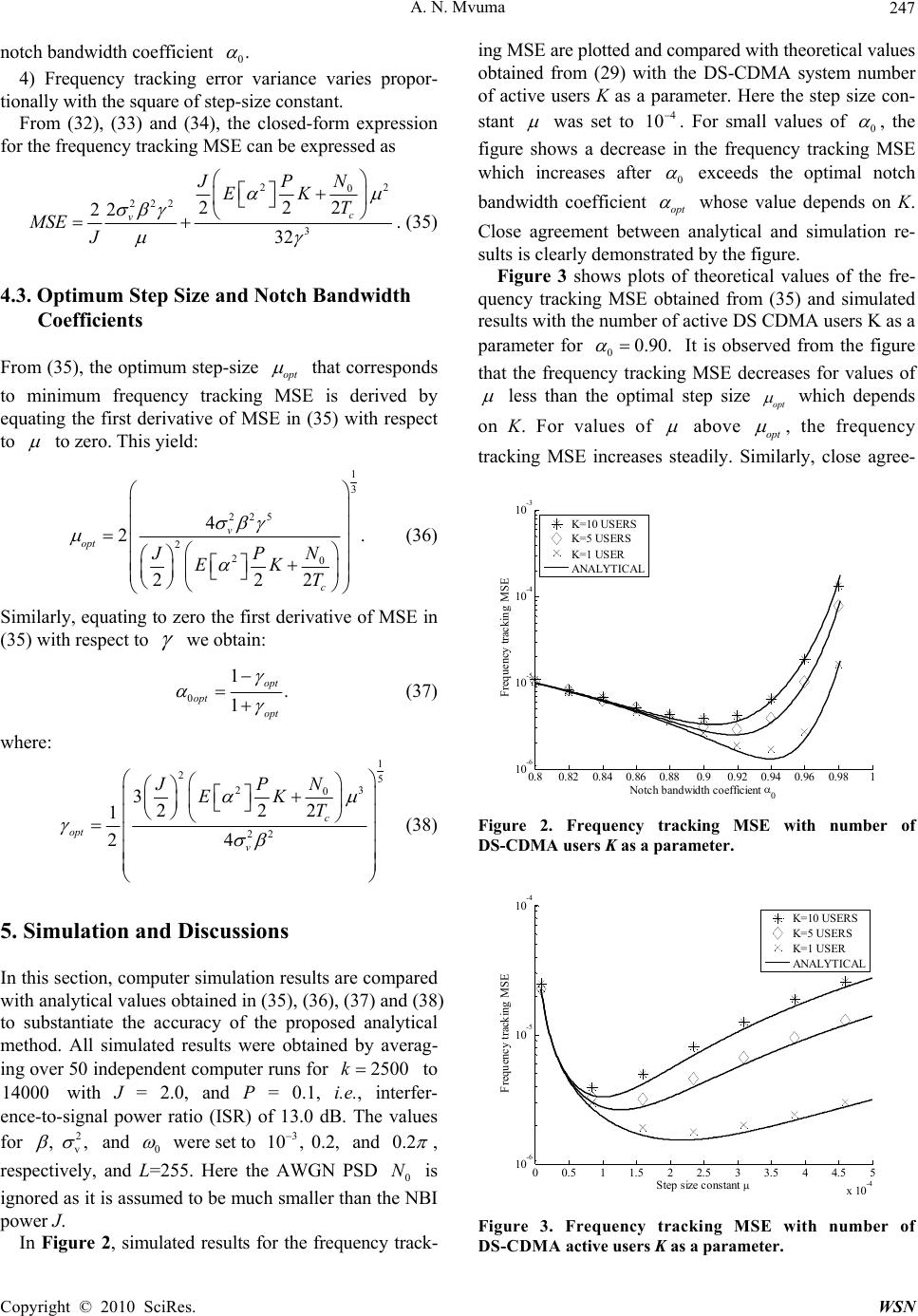

A. N. Mvuma247
notch bandwidth coefficient 0.

4) Frequency tracking error variance varies propor-
tionally with the square of step-size constant.
From (32), (33) and (34), the closed-form expression
for the frequency tracking MSE can be expressed as
22
0
222 222
2 2c
v
N
P
EK
T
MSE 3
32 J
J



 






. (35)
4.3. Optimum Step Size and Notch Bandwidth
Coefficients
From (35), the optimum step-size opt

that corresponds
by
ct
to
to minimum frequency tracking MSE is derived
equating the first derivative of MSE in (35) with respe

to zero. This yield:
1
3
225
2
4
2.
v
opt N
J
E









 

(36)
20
22
2
c
P
K
T


 
 



Similarly, equating to zero the first derivative of MSE in
(35) with respect to

we obtain:
0
1.
1
opt
opt
opt




 (37)
where:
1
25
23
0
22
3222
c
T

(38)
1
24
opt
v
N
JP
EK 



 


 






5. Simulation and Discussions
In this section, computer simulation results are compared
with analytical values obtained in (35), (36), (37) and (38)
substantiate the accuracy of the proposed analytical
tained by averag-
or to
to
method. All simulated results were ob
g over 50 independent computer runs fin2500k
14000 with J = 2.0, and P = 0.1, i.e., interfer-
ence-to-signal power ratio (ISR) of 13.0 dB. The values
for 2
v
, ,


and 0

were set to 3 10, 0.2,
 and 0.2

,
respectively, and L=255. Here the AWGN PSD N is
ignored as it is assumed to be much smaller than the NBI
power J.
In Figure 2, simulated results for the frequency track-
ing MSE are plotted and compared retical vs
obtained from (29) with the DS-CDMA system nber
of active users K as a parameter. Here the step size con-
stant
0
with theo alue
um

was set to 4 10

. For small values of 0

, the
figure shows a decrease in the frequency tracking MSE
which increases after 0

exceeds the optimal notch
bandwidth coefficient opt

whose value depends on K.
Close agreement between analytical and simulation re-
sults is clearly demonstrated by the figure.
Figure 3 shows plots of theoretical values of the fre-
quency tracking MSE obined from (35) and simulated
results with the numberactive DS CDMA users K as a
parameter for 00.90.
ta
of


It is observed from the figure
that the frequency tracking MSE decreases for values of

less than the optimal step size opt

which depends
on K. For values of

above opt

, the frequency
tracking MSE increases steadily. Similarly, close agree-
0.80.820.84 0.86 0.880.90.92 0.940.960.981
10
-6
10
-5
10
-4
10
-3
Notch bandwidth coefficient

0
Frequency tracking MSE
K=10 USERS
K=5 USERS
K=1 USER
ANALYTICAL
Figure 2. Frequency tracking MSE with number of
DS-CDMA users K as a parameter.
00.5 11.5 22.5 33.5 44.5 5
x 10
-4
10
-6
10
-5
10
-4
Step size constant

Frequency trackin
K=10 USERS
K=5 USERS
g MSE
K=1 USER
ANALYTICAL
Figure 3. Frequency tracking MSE with number of
DS-CDMA active users K as a parameter.

A. N. Mvuma 248
ment between analytical values and simulation results is
clearly shown by the figure.
Figure 4 shows simulated results and theoretical val-
ues for the optimum notch bandwidth coefficient opt
0

s K
ease in
plotted against the number of DS-CDMA active user
for Similarly, the figure shows a decr
4
10 . 


opt
0

with the increase in K as predicted by (37
(38). There is a close agreement between simulated re-
sults and theoretical values as validated by the figure.
Simulated results and theoretical values obtained from
(36) for the optimum step-size constant
) and
opt

versus
number of active DS-CDMA users K are Fig-
ure 5 with
plotted in
00.9

. The figure shows ain decrease
opt

with the increase in K as anticipated by (30). Close
agreement between simulated results and theoretical
values is clearly demonstrated by the figure.
Figure 4. Optimum step-size constant versus number of
ctive users K.
igure 5. Optimum notch bandwidth coefficient versus the
number of DS-CDMA active users K.
6. Conclusions
Frequency tracking characteristics of the complex-coe-
fficient adaptive IIR notch filter for suppression of NBI
with randomly-varying frequency in a DS-CDMA com-
munication system over a Rayleigh fading channel were
investigated in this paper. Derived closed-form expres-
sions for frequency tracking MSE and optimum step size
and notch bandwidth coefficient have revealed a need for
proper setting of adaptation algorithm and IIR notch fil-
ter parameters to minimize frequency tracking MSE.
Moreover, computer simulation results have demon-
strated the accuracy of the analytical approach. In the
future, probability of bit error of the DS-CDMA system
with NBI suppression complex adaptive IIR notch filter
will be investigated.
“Adaptive LMS filters for
overlay situations,” IEEE Journal on Se-
Communications, Vol. 14, pp. 1548–1559,
October 1996.
a
F
7. References
[1] W. C. Y. Lee, “Overview of cellular CDMA,” IEEE
Transactions on Vehicular Technology, Vol. 40, pp. 291–
301, May 1991.
[2] R. L. Pickholtz, D. L. Schilling, and L. B. Milstein,
“Theory of spread spectrum communications: A tutorial,”
IEEE Transactions on Communications, Vol. COMM-30,
pp. 855–884, May 1982.
[3] L. B. Milstein, et al., “On the feasibility of a CDMA
overlay for personal communications networks,” IEEE
Journal on Selected Areas in Communications, Vol. 10,
pp. 655–668, May 1992.
[4] H. V. Poor and L. A. Rusch, “Narrowband interference
suppression in spread spectrum CDMA,” IEEE Commu-
nications Magazine, Vol. 1, pp. 14–27, August 1994.
] J. Wang and L. N. Miltein,[5
cellular CDMA
lected Areas in
[6] M. Lops, G. Ricci, and A. M. Tulino, “Narrowband in-
terference suppression in multiuser CDMA systems,”
IEEE Transactions on Communications, Vol. 46, pp.
1163–1175, September 1998.
[7] S. Buzzi, M. Lops, and A. M. Tulino, “Time-varying
narrow-band interference rejection in asynchronous mul-
tiuser DS/CDMA systems over frequency-selective fad-
ing channels,” IEEE Transactions on Communications,
Vol. 47, pp. 1523–1535, October 1999.
[8] W. S. Hou, L. M. Chen and B. S. Chen, “Adaptive nar-
rowband interference rejection in DS-CDMA systems: A
scheme of parallel interference cancellers,” IEEE Journal
on Selected Areas in Communications, Vol. 19, pp.
1103–1114, June 2001.
[9] V. Krishnamurthy, G. Yin, and S. Singh, “Adaptive
step-size algorithms for blind interference suppression in
DS/CDMA systems,” IEEE Transactions on Signal Proc-
essing, Vol. 49, pp. 190–201, January 2001.
1 23 45 67 891
0
1
1. 2
1. 4
1. 6
1. 8
2
2. 2
2.4 x 10
-
4
Number of users
Analytical
Simulation
Optimum step size constant

opt

A. N. Mvuma 249
amoto, “Conver-
o. 5, pp.
, pp. 1526–1529, June 2009.
[10] S. C. Pei and C. C. Tseng, “Complex adaptive IIR notch
filter algorithm and its applications,” IEEE Transactions
on Circuits and Systems, Vol. CAS-41, No. 2, pp. 158–
163, February 1994.
[11] S. Nishimura and H. Y. Jiang, “Simplified realization of
cascaded adaptive notch filters with complex coeffi-
cients,” Proceedings of International Symposium on Cir-
cuits and Systems, Vol. 5, pp. 269–272, 1998.
[12] H. Y. Jiang, S. Nishimura, and T. Hin
gence analysis of complex adaptive IIR notch filters for
the detection of single sinusoid,” IEICE Transactions
Fundamentals, Vol. E82-A, No. 6, pp. 912–915, June
1999.
[13] H. Y. Jiang, S. Nishimura, and T. Hinamoto, “Steady-
state analysis of complex adaptive IIR notch filter and its
application to QPSK communication systems,” IEICE
Transactions Fundamentals, Vol. E85-A, N
1088–1085, May 2002.
[14] A. Mvuma, S. Nishimura, and T. Hinamoto, “Tracking
analysis of complex adaptive IIR notch filter for a linear
chirp signal,” IEICE Transactions Fundamentals, Vol.
E92-A
[15] A. Mvuma, S. Nishimura, and T. Hinamoto, “Complex
coefficient adaptive IIR notch filter tracking characteris-
tics,” Proceedings of Midwest Symposium on Circuits
and Systems, pp. 640–643, August 2009.