Wireless Sensor Network, 2010, 2, 218-226
doi:10.4236/wsn.2010.23029 Published Online March 2010 (http://www.scirp.org/journal/wsn)
Performance Analysis of Multi-Parametric Call Admission
Control Strategies in Un-Buffered Multi-Service Cellular
Wireless Networks
Jang Hyun Baek1, Che Soong Kim2, Agassi Melikov3, Mehriban Fattakhova3
1Department of Industrial and Information Systems Engineering, Chonbuk National University, Jeonju, Republic of Korea
2Department of Industrial Engineering, Sangji University, Wonju, Republic of Korea
3Department of Aerospace Information Technologies & Control Systems, National Aviation Academy, Azerbaijan
Received December 28, 2009; revised January 12, 2010; accepted January 15, 2010
Abstract
In this paper model of integrated voice/data cellular wireless networks (CWN) are investigated. The unified
approximate approach to calculate the desired Quality of Service (QoS) metrics in an isolated cell of such
networks under two multi-parametric call admission control (CAC) strategies is developed. One of them is
based on the guard channels scheme while the second is based on a threshold scheme. Results of the nu-
merical experiments are given and a comparison of QoS metrics under different CAC strategies is carried
out.
Keywords: Cellular Networks, Call Admission Control, Quality of Service, Calculation Algorithm
1. Introduction
A cellular wireless network (CWN) consists of radio
access points, called base stations (BS), each covering a
certain geographic area. With distance, the power of ra-
dio signals fade away (fading or attenuation of signal
occurs) which makes it possible to use the same frequen-
cies over several cells, but in order to avoid interference,
this process must be carefully planned. For better use of
frequency resources, existing carrier frequencies are
grouped, and the number of cells, in which this group of
frequencies is used, defines the so called, frequency re-
use factor. Therefore, in densely populated areas with a
large number of mobile subscribers (MS), small dimen-
sioned cells (micro-cells and pico-cells) are to be used.
In connection with the limitation of transmission spec-
trum in a CWN, problems of allocation of common spec-
trum among cells are very important. A unit of the wire-
less spectrum, necessary for serving a single user is
called a channel (for instance, time slots in TDMA are
considered as channels). There are three solutions for the
channels allocation problem: Fixed Channel Allocation
(FCA), Dynamic Channel Allocation (DCA) and Hybrid
Channel Allocation (HCA). Advantages and disadvan-
tage of each of these are well known [1–3]. At the same
time, owing to realization simplicity, the FCA scheme is
widely used in existing cellular networks. In this paper
models with FCA schemes are considered.
Quality of service (QoS) in the certain cell with the
FCA scheme could be improved if appropriate call
ad-mission control (CAC) strategies for the heterogene-
ous traffic are provided. The use of such an access strat-
egy doesn’t require many resources, therefore this me-
thod could be considered operative and more effective in
view of problems relating to resource shortages.
Apart from original (or new) calls (o-calls) flows, ad-
ditional classes of calls that require a special approach
also exist in wireless cellular networks. These are so-
called handover calls (h-calls). This is specific only for
wireless cellular networks. The essence of this phe-
nomenon is that a moving MS, that already established
connection with a network, passes boundaries between
cells and gets served by a new cell. From the new cell’s
point of view this is an h-call, and since the connection
with the MS has already been established, the handling
of the transfer to a new cell must be transparent for the
user. In other words, in wireless networks the call may
occupy channels from different cells, several times dur-
ing the duration of the call. This means that the channel
occupation period is not the same as the call duration.
Mathematical models of call handling processes in
multi-service CWN can be developed adequately enough

J. H. Baek ET AL.219
based on a queuing theory of networks with different
types of calls and random topology. Such models are
researched poorly in literature [4–6]. This is explained by
the fact, that despite the elegance of those models, in
practice they are useful only for small dimensional net-
works and with some limiting simplifying assumptions
that are contrary to fact in real functioning wireless net-
works. In connection with that, in the majority of the
research work models of an isolated cell are analyzed.
In the overwhelming majority of available work,
one-dimensional queuing models of call handling proc-
esses in an isolated cell of mono-service CWN are pro-
posed. However these models cannot describe the study-
ing processes in multi-service CWN since in such
net-works calls of heterogeneous traffic differ signifi-
cantly with respect to their bandwidth requirement and
arrival rate and channel occupancy time. In connection
with that in the given paper new two-dimensional (2-D)
queuing models of multi-service networks are developed.
In order to be specific we consider integrated voice/data
CWN. In such networks voice calls (v-calls) are more
susceptible to possible losses and delays than data (orig-
inal or handover) call (d-calls). That is why a number of
different CAC strategies for prioritization of v-calls are
suggested in various works, mostly implying the use of
guard channels (cutoff strategy) for high priority calls
[7–8] and/or threshold strategies [9] which restrict the
number of low priority calls in channels.
In this paper we introduce a unified approach to ap-
proximate performance analysis of two multi-parametric
CAC in a single cell of un-buffered integrated voice/data
CWN which differs from known works in this area. Our
approach is based on the principles of theory of phase
merging of stochastic systems [10].
The proposed approach allows overcoming an as-
sumption made in almost all of the known papers about
equality of handling intensities of heterogeneous calls.
Due to this assumption the functioning of the CWN is
described with one-dimensional Markov chain (1-D MC)
and authors managed simple formulas for calculating the
QoS metrics of the system. However as it was mentioned
in [11] the assumption of the same mean channel occu-
pancy time even for both original and handover calls of
the same class is unrealistic. The presented models are
more general in terms of handling intensities and the
equality is no longer required.
This paper is organized as follows. In Section 2, we
provide a simple algorithm to calculate approximate
values of desired QoS metrics of the model of integrated
voice/data networks under CAC based on the guard
channels strategy. A similar algorithm is suggested in
Section 3 for the same model under CAC based on a
threshold strategy. In Section 4, we give results of nu-
merical experiments which indicate high accuracy of the
proposed approximate algorithms as well as a compari-
son of QoS metrics in different CAC strategies. In Sec-
tion 5 we provide some conclusion remarks in conclu-
sion.
2. The CAC Based on Guard Channels
Strategy
It is well-known that in an integrating voice/data CWN
voice calls of any type (original or handover) have a high
priority over data calls and within each, flow handover
calls have high priority over original calls.
As a means of assigning priorities to handover v-calls
(hv-call) in such networks a back-up scheme that in-
volves reserving a particular number of guard channels
of a cell, expressly for calls of this type, is often utilized.
According to this scheme any hv-call is accepted if there
exists at least one free channel, while calls of the re-
maining kind are accepted only when the number of busy
channels does not exceed some class-dependent thresh-
old value.
We consider a model of an isolated cell in an inte-
grated voice/data CWN without queues. This cell con-
tains N channels, 1 < N < . These channels are used by
Poisson flows of hv-calls, original v-calls (ov-calls),
handover d-calls (hd-calls) and original d-calls (od-calls).
Intensity of x-calls is

x, xov,hv,od,hd. As in almost
all cited works the values of handover intensities are
considered known hereinafter, although it is apparent
that definition of their values depending on the intensity
of original calls, shape of a cell, mobility of an MS and
etc. is rather challenging and complex. However, if we
consider the case of a uniform traffic distribution and at
most one handover per call, the average handover inten-
sity can be given by the ratio of the average call holding
time to the average cell sojourn time [12].
To handle any narrow-band v-call (either original or
handover) only one free channel is required, while one
wide-band d-call (either original or handover) requires
simultaneously b  1 channels. Here it is assumed that
wide-band d-calls are inelastic, i.e. all b channels are
occupied and released simultaneously (though can be
investigated as can models with elastic d-calls).
Note that the channels’ occupancy time considers both
components of occupancy time: the measure of calls du-
ration, and their mobility. Distribution functions of
channel occupancy time of heterogeneous calls are as-
sumed to be independent and exponential, but their pa-
rameters are different, namely the intensity of handling
of voice (data) calls equals

v (

d), and generally speak-
ing 
v
 
d. If during call handling the handover proce-
dure is initiated, the remaining handling time of this call
in a new cell (yet as an h-call) is also exponentially dis-
tributed with the same mean due to the memory-free
property of exponential distribution.
In a given CAC the procedure by which the channels
are engaged by calls of different types is realized in the

J. H. Baek ET AL. 220

.
S
1
2
,:()( ,)
hvd v
S
PpnnN 



n
n (3)
following way. As was mentioned before, if upon arrival
of an hv-call, there is at least one free channel, this call
seizes one of any free channels; otherwise this call is
blocked. With the purpose of defining the proposed CAC
for calls of other types, three parameters N1, N2 and N3
(where 1  N1  N2  N3  N) are introduced. It is assumed
that N1 and N2 are multiples of b.
3
:()( )
ovd v
S
PpInnN

,

n
n (4)
2
:()( )
hdd v
S
PpInnN

,

n
n (5)
1
:()( )
odd v
S
PpInnN

,

n
n (6)
Arrived ov-call is accepted if the number of busy
channels is less than N3, otherwise it is blocked. Arrived
od-call (respectively, hd-call) is accepted only in the case
at most N1-b (respectively, N2-b) busy channels, other-
wise it is blocked.
where I(A) denoted the indicator function of event А and
 (i, j) represents Kronecker’s symbols.
The mean number of busy channels is also calcu-
lated via stationary distribution as follows:
N

Consider the problem of finding the major QoS met-
rics of the given multi-parametric CAC strategy – block-
ing (loss) probabilities of calls of each type and overall
channels utilization. For simplicity of intermediate
mathematical transformations first we shall assume that
b=1. The case b > 1 is straightforward (see below).

1
:
N
k
Nkpk


, (7)
where






,, 1,
dv
S
pkpnn kkN 

 ,

n
n are mar-
ginal probability mass functions.
By adopting an assumption for the type of distribution
laws governing the incoming traffics and their holding
times it becomes possible to describe the operation of an
isolated cell by means of a two-dimensional Markov
chain (2-D MC), i.e. in a stationary regime the state of
the cell at an arbitrary moment of time is described by a
2-D vector n=(nd, nv), where nd (respectively, nv) is the
number of data (respectively, voice) calls in the channels.
Then the state space of the corresponding Markov chain
describing this call handling scheme is defined as
follows:

2
::0,1,,, 0,1,,,
dvdv
SnNnNnnN  n(1)
Elements of generating matrix of this MC
are determined from the following
relations:
(),qn,n' n,n'

11
12
32
3
1
2
if 1,,
if 1,,
if 1,,
if 1,,
if ,
if ,
0in other cases,
ddv
hdd v
vdv
hvd v
dd
vv
nnN
Nnn N
nnN
qNnnN
n
n






  


 


 

  






nne
nne
nne
n,n nne
nne
nne
(2)
Stationary distribution is determined as a result of the
solution of an appropriate SGBE of the given 2-D MC.
However, to solve the last problem one requires labori-
ous computation efforts for large values of N since the
corresponding SGBE has no explicit solution. Very often
the solution of such problems is evident if the corre-
sponding 2-D MC has reversibility property [15] and
hence there exists stationary distribution in a multiplica-
tive form. Given the SGBE has a multiplicative solution
only in a special case when N1
= N2 = N3 = N (even in this
case there are known computational difficulties). How-
ever, by applying Kolmogorov criteria [15] it is easily
verified that the given 2-D MC is not reversible. Indeed,
according to the mentioned criteria the necessary re-
versibility condition of 2-D MC consists in the fact that
if the transition from state (i,j) into state (i
 ,j  ) exists, then
there must also be the reverse transition from state (i
 ,j  )
to state (i,j). However, for MC considered this condition
is not fulfilled. So by the relations (2) in the given MC
the transition (nd,nv)(nd -1,nv) exists with intensity nd

d
where nd + nv  N2, but the inverse transition not existing.
In [13], a recursive technique has been proposed as the
solution to the above-mentioned SGBE. It requires mul-
tiple inversion calculations of certain matrices of suffi-
ciently large dimensions that in itself is a complex cal-
culating procedure. To overcome the mentioned difficul-
ties, a new, efficient and refined approximate method for
the calculation of the stationary distribution of the given
model is suggested below. The proposed method, due to
right selection of state space splitting of corresponding
2-D MC allows one to reduce the solution of the problem
considered to calculation by explicit formulae which
contain the known (even tabulated) stationary distribu-
tions of classical queuing models.
where

d:=

od +

hd ,

v :=

ov +

hv, e1 = (1,0), e2 = (0,1).
State diagram of the model and the system of global
balance equations (SGBE) for the steady state probabili-
ties p(n), nS are shown in [13]. Existence of stationary
regime is proved by the fact that all states of finite-di-
mensional state space S are communicating.
Desired QoS metrics are determined via stationary
distribution of the initial model. Let Px denote the blo-
cking probability of the x-calls, xhv,ov,hd,od. Then
by using the PASTA theorem [14] we obtain:

J. H. Baek ET AL.221

k
k
For correct application of phase merging algorithms
(PMA) it is assumed below thatv 
d and

v

d.
This assumption is not extraordinary for an integrating
voice/data CWN, since this is a regime that commonly
occurs in multimedia networks, in which wideband
d-calls have both longer holding times and significantly
smaller arrival rates than narrowband v-calls, e.g. see [16,
17]. Moreover, it is more important to note, that the final
results as shown below, are independent of traffic pa-
rameters, and are determined from their ratio, i.e. the
developed approach can provide a refined approximation
even when parameters of heterogeneous traffic are only
moderately distinctive.
The following splitting of state space (1) is examined:
2
'
0
, , '
N
kkk
k
SSSS k


 , (8)
where .

::
kd
SSn n
Further state classes Sk combine into separate merged
states <k> and the following merging function in state
space S is introduced:
2
() if , 0,.
k
Uk SkN nn (9)
Function (9) determines the merged model which is a
one-dimensional Markov chain (1-D MC) with the state
space

2
:: 0,SkkN 


. Then, according to PMA,
the stationary distribution of the initial model approxi-
mately equals:


2
(,)()(), ,, 0,,
kk
pkiikkiSkN   (10)
where is stationary distribution of a
split model with state space Sk and
  
:,
k
ikiS  

k



:kkS  

is stationary distribution of a merged model, respec-
tively.
By using (2) we conclude that the elements of gener-
ating matrix of this 1-D birth-death processes (BDP)
qk(i,j) are obtained as follows:

3
3
if 1,1,
if ,1,
,if 1,
0in other cases.
v
hv
k
v
iN kji
NkiNji
qij iji



 



 





So, stationary distribution within class Sk is the same
as that M/M/N k/N k queuing system where the ser-
vice rate of each channel is constant,

v and arrival rates
are variable quantities. Hence
 


3
3
3
0if 1,
!
()
0if 1
!
i
v
k
Nk
ki
vhv
k
hv
iN k
i
i
Nk iNk
i

where
3
3
3
1
01
(0) ,
!!
:/,: /.
Nk
ii Nk Nk
vv hv
k
iiNk
hv
vvvhv hvv
ii
 

 














Then, from (2) and (11) by means of PMA elements of
generating matrix of a merged model


,'qk k ,
S ,'kk

  are found:

 

12
1
2
11
01
1
1
0
12
if 01,1,
,' if 1,1,
if 1,
0
in other cases.
NkN k
dkhd k
iiN
Nk
hd k
i
d
ii
kNk k
i
qk kNkN kk
k
kk
 


 







 






 










(12)
The latter formula allows determining the stationary
distribution of a merged model. It coincides with an ap-
propriate distribution of state probabilities of a 1-D BDP,
for which transition intensities are determined in accor-
dance with (12). Consequently, stationary distribution of
a merged model is determined as



2
1
0
()1, ,1,
!
k
k
i
d
kqkkk
k,N





 

(13)
where,

2
1
11
1
(0) 11,
!
Nk
k
ki
d
qk k
k




 



Then by using (11) and (13) from (10) stationary dis-
tribution of the initial 2-D MC can be found. So, summa-
rizing the above given and omitting the complex alge-
braic transformations the following approximate formu-
lae for the calculation of QoS metrics (3)–(7) can be
suggested:

2
0
;
N
hv k
k
PkN 

k

 
 (14)
 
2
3
0
;
NNk
ov k
kiNk
Pk 




i
i 
(15)

2
2
0
();
NNk
hd k
kiNk
Pk 




(16)
,





 



 



(11)
 
12
11
1
0
() ;
NN
Nk
od k
kiNkkN
Pkik 



 
 (17)




2
10
N
fi
N
k
ik
Nik ik 



 

. (18)

J. H. Baek ET AL. 222






22
:()(,) ,
hdddvd
SnS
PpnRpnnNInR 

,


n
nn
(22)
Hereinafter

if 1,
if .
k
x
xk
fx kkiN




Now we can develop the algorithm to calculate the
QoS metrics of the investigated multi-parametric CAC
for the similar model with wide-band d-calls (due to the
limited volume of work this algorithm does not present
here).
 


11
:()( ),
oddd vd
SnS
PpInRpnnNInR 

 .


n
nn
(23)
Unlike the CAC based on the guard channel strategy,
it is easy to see that under this one there is no circulation
flow in the state diagram of the underlying 2-D MC, i.e.,
reversible [15]. In other words, there is a general solution
to the system of local balance equations (SLBE) in this
chain. Therefore, by choosing any path between these
states in the state diagram, we can express any state
probability p(nd,nv) using the state probability p(0,0). So,
in case R2+R3  N we get the following multiplicative
solution for stationary distribution of the underlying 2-D
MC:
3. The CAC Based on Threshold Strategy
Now we consider an alternative CAC in the integrated
voice/data networks which is based on a threshold strat-
egy. A more detailed description of the given CAC, fol-
lows. As in the CAC based on guard channels, we as-
sume that an arrived hv-call is accepted as long as at
least one free channel is available; otherwise it is blocked.
For the purpose of definition of CAC based on a thresh-
old strategy for calls of other types, three parameters R1,
R2 and R3, where 1
 R
1
 R
2
 R
3
 N are introduced.
Then the proposed CAC defines the following rules for
admission of heterogeneous calls: an od-call (respec-
tively, hd-call and ov-call) is accepted only if the number
of calls of the given type in progress is less than R1 (re-
spectively, R2 and R3) and a free channel is available;
otherwise it is blocked.
For the sake of simplicity we shall assume that b=1.
The case b > 1 is straightforward (see Section 2). The
state of the system under the given CAC at any time is
also described by 2-D vector n = (nd, nv), where nd (re-
spectively, nv) is the number of data (respectively, voice)
calls in the channels. Then state space of appropriate 2-D
MC is given by:

2
:: 0,,0,;
dvdv
SnRnNnnN n





3
1
13
13
13
123
0, 0,
!!
if ,,
0, 0,
!!
if ,,
,
0, 0,
!!
if ,,
0, 0,
!!
dv
dv
dv
dv
nn
dv
dv
dv
R
nn
dhvv
dvhv
dv
dv R
nn
hd vd
dv hd
dv
RR
nn
hd hvdv
d vhdhv
p
nn
nRnR
p
nn
nRRnN
pn n
p
nn
RnRn R
p
nn

 

 

 












 

 


123
if ,,
dv
RnRRn N



















 

(24)
.
1
,
(19)
where p(0,0) is determined from normalizing condition,
The elements of generating matrix of the appropriate
2-D MC in this case is determined as follows:

11
12
32
32
1
2
if 1,,
if 1,,
if 1,,
if 1,,
if ,
if ,
0in other cases.
dd
hd d
vv
hv v
dd
vv
nR
Rn R
nR
qRnN
n
n







 


 


 


 






nne
nne
nne
n,n nne
nne
nne
(20)
31
12
1
32
1
3
(0,0) !! !!
!!
dv dv
dv dv
!
R
R
nn nn
dvvdhv d
nS nS
dv hvdvhd
RR
nn nn
hd vdvhd hv
nT nS
dvhdhvd v
pnn nn
nn nn
 

 




 

 
 
 



 





Here we use the following notations:

d: =

d/

d,

hd:
= 
hd/

d;





2
113
213
31 3
4123
::,,
::,1 ,
::1 ,,
::1 ,1
dv
dv
dv
dv
SSnRnR
SSnRRnN
SSRnRnR
SSRnRRn
 
 
 
 
n
n
n
n
Blocking probability of hv-calls and the mean number
of busy channels are defined similarly to (3) and (7),
respectively. The other QoS metrics are defined as the
following marginal distributions of initial chain: .N
In the case R2 + R3 > N stationary distribution has the
following form:
3
:()( )
ov v
S
PpInR



n
n (21)

J. H. Baek ET AL.223




2
3
13
12
33
0, 0,
!!
if 0,0,
0, 0,
!!
,
if 1,0,
0, 0,
!!
if 01,1,
dv
dv
dv
nn
dv
dv
dv
R
nn
hd vd
dv hd
dv
dvd
R
nn
dhv v
dv hv
dv
p
nn
nR nR
p
nn
pn n
RnRnNn
p
nn
nNR RnN

 

 




 


 


 


 


 

(25)
where

13
12
3
1
0, 0!! !!
;
!
dv dv
dv
R
R
nn nn
dv dhdvv
nT nT
dvhddvhv
nn
dhv
nT dv
pnn nn
nn
  





 


 
 








11
::0 ,0
dv
TSnRn n

3
R
,
d
N
k
k


212
::1 ,0
dv
TSRnRnNnn

333
::0 1,1
dv
TSnNRRn n
The exact method to determine the steady state
probabilities, in terms of a multiplicative representation
(25) (or (26)) for large values of N, encounters numerical
problems such as imprecision and overflow. These are
related to the fact that with such a method the entire state
space has to be generated, and large factorials and
powers, close to zero, of the quantities (for low loads) or
large values (for high loads) have to be calculated, i.e.
there arises the problem of exponent overflow or
underflow. Hence we can use a developed approximate
method to determine the QoS metrics of the model,
under the use of the proposed CAC based on threshold
strategy, even when state space (19) is large.
As in Section 2, we assume that 
v

d and

v

d
and examine the following splitting of the state space
2
'
0
, , '
R
kkk
k
SSSSk


 ,
where .

::
kd
SSn n
Next classes of states Sk are combined into individual
merged states <k> and in (19) the merged function with
range which is similar to
(27) is introduced. As in the exact algorithm, in order to
find the stationary distribution within splitting classes Sk
we will distinguish two cases: 1) R2+R3  N and 2) R2+R3
> N. In the first case, the elements of the generating
matrix, of appropriate 1-D BDP, are the same for all
splitting models, i.e.

2
:: 0,1,,Skk R 


3
3
if 1,1,
if 1,1,
,if 1,
0in other cases.
v
hv
k
v
iR ji
RiN ji
qij iji



 

 





From the last formula we conclude that the stationary
distribution within class Sk is the same as that of the
M/M/N

k/N

k queuing system with state-dependent
arrival rates and constant service rate of each channel, i.e.


3
3
3
0if 1,
!
()
0if 1
!
i
v
k
R
ki
vhv
k
hv
iR
i
i
RiN
i








 


,k
(26)
where
3
3
3
1
01
(0) .
!!
R
ii
RNk
vv hv
k
iiR
hv
ii
 













So, from (20) and (26) we conclude that elements of
the generating matrix, of the merged model, are




 
1
12
1
if 01,1,
1
if 1,1,
,'
if 1,
0
in other cases.
dk
hd k
d
Nk
kRk k
Nk
RkR kk
qkk
k
kk






 




 
 







(27)
Distribution of the merged model is calculated by us-
ing (27) and has the following form:


2
1
0
()1, ,1,
!
k
k
i
d
kqkkk
k




 
,R
(28)
where,

2
1
11
1
(0) 11,
!
Rk
k
ki
d
qk k
k







.
Finally the following approximate formulae to
calculate the desired QoS metrics, under the use of the
proposed CAC based on the threshold strategy, are
obtained:

2
0
;
R
hv k
k
PkN 

 
k
i

k
(29)
 
2
3
0
;
RNk
ov k
kiR
Pk 




(30)
 
21
2
0
;
R
hd k
k
PR kN 



 (31)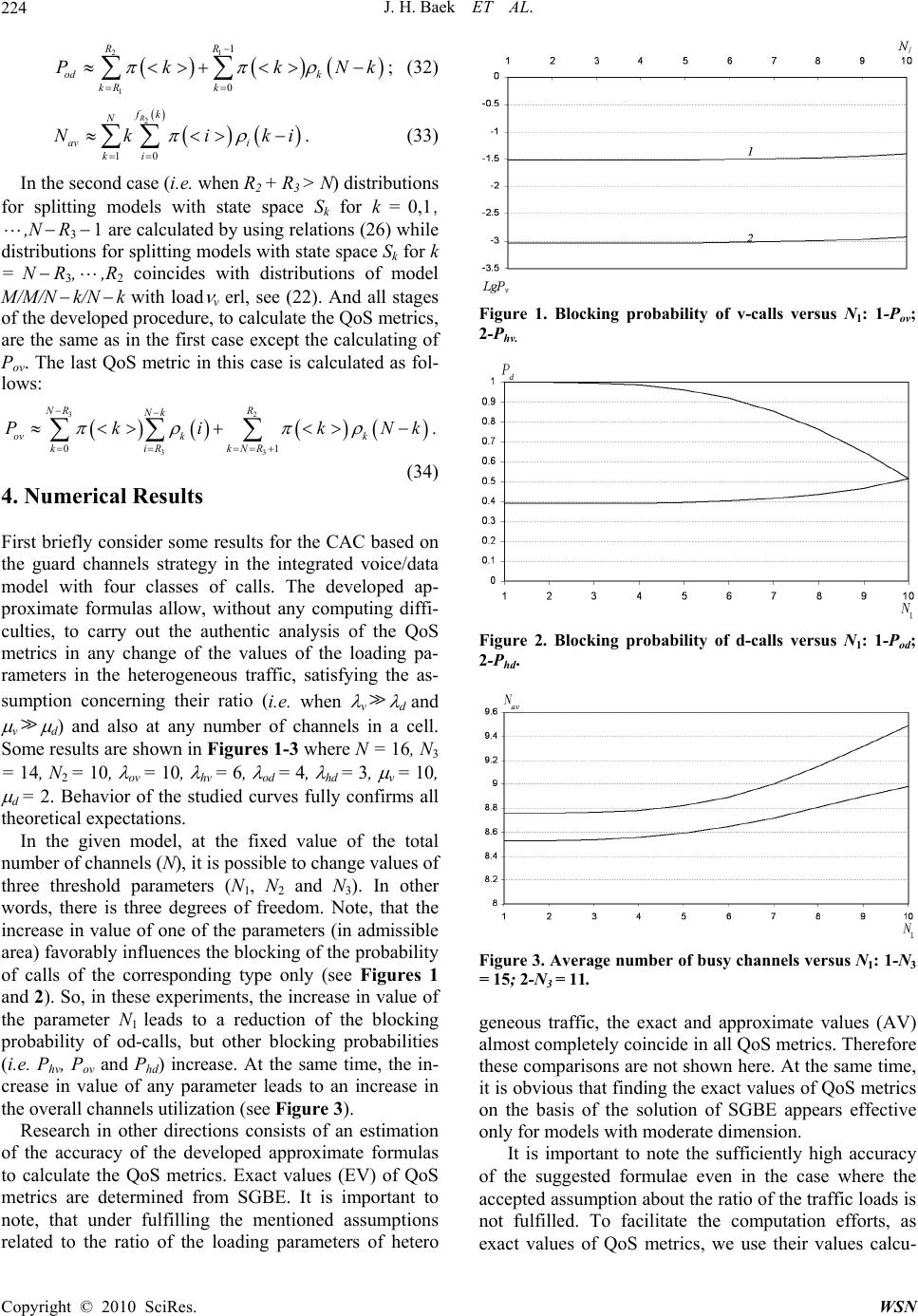

J. H. Baek ET AL. 224
k
 
21
1
1
0
;
RR
od k
kR k
Pk kN 



 (32)



2
10
.
R
fk
N
av i
ki
Nk ik 


 i

k
(33)
In the second case (i.e. when R2 + R3 > N) distributions
for splitting models with state space Sk for k = 0,1,
,N R31 are calculated by using relations (26) while
distributions for splitting models with state space Sk for k
= N R3,,R2 coincides with distributions of model
M/M/N k/N k with load 
v erl, see (22). And all stages
of the developed procedure, to calculate the QoS metrics,
are the same as in the first case except the calculating of
Pov. The last QoS metric in this case is calculated as fol-
lows:




 
 
32
33
01
.
NR R
Nk
ov kk
kiRkNR
PkikN  


 

(34)
4. Numerical Results
First briefly consider some results for the CAC based on
the guard channels strategy in the integrated voice/data
model with four classes of calls. The developed ap-
proximate formulas allow, without any computing diffi-
culties, to carry out the authentic analysis of the QoS
metrics in any change of the values of the loading pa-
rameters in the heterogeneous traffic, satisfying the as-
sumption concerning their ratio (i.e. when 
v

d and

v

d) and also at any number of channels in a cell.
Some results are shown in Figures 1-3 where N = 16, N3
= 14, N2 = 10, 
ov = 10 ,

hv = 6,

od = 4,

hd = 3,

v = 10,

d = 2. Behavior of the studied curves fully confirms all
theoretical expectations.

In the given model, at the fixed value of the total
number of channels (N), it is possible to change values of
three threshold parameters (N1, N
2 and N3). In other
words, there is three degrees of freedom. Note, that the
increase in value of one of the parameters (in admissible
area) favorably influences the blocking of the probability
of calls of the corresponding type only (see Figures 1
and 2). So, in these experiments, the increase in value of
the parameter N1 leads to a reduction of the blocking
probability of od-calls, but other blocking probabilities
(i.e. Phv, Pov and Phd) increase. At the same time, the in-
crease in value of any parameter leads to an increase in
the overall channels utilization (see Figure 3).
Research in other directions consists of an estimation
of the accuracy of the developed approximate formulas
to calculate the QoS metrics. Exact values (EV) of QoS
metrics are determined from SGBE. It is important to
note, that under fulfilling the mentioned assumptions
related to the ratio of the loading parameters of hetero
Figure 1. Blocking probability of v-calls versus N1: 1-Pov;
2-Phv.
Figure 2. Blocking probability of d-calls versus N1: 1-Pod;
2-Phd.
Figure 3. Average number of busy channels versus N1: 1-N3
= 15; 2-N3 = 11.
geneous traffic, the exact and approximate values (AV)
almost completely coincide in all QoS metrics. Therefore
these comparisons are not shown here. At the same time,
it is obvious that finding the exact values of QoS metrics
on the basis of the solution of SGBE appears effective
only for models with moderate dimension.
It is important to note the sufficiently high accuracy
of the suggested formulae even in the case where the
accepted assumption about the ratio of the traffic loads is
not fulfilled. To facilitate the computation efforts, as
exact values of QoS metrics, we use their values calcu-

J. H. Baek ET AL.225
lated from explicit formulas, see [21]. In mentioned work,
appropriate results are obtained in the special case b = 1
and 
v =

d. Let's note, that condition

v =

d contradicts
our assumption 
v

d. Highest accuracy of the devel-
oped approximate formulas is observed at the calculation
of the QoS metric for v-calls, since the maximal differ-
ence between exact and approximate values does not
exceed 0.001. Small deviations take place in the calcula-
tion of the QoS metrics for d-calls, but also thus in the
worst case scenario the absolute error of the proposed
formulas does not exceed 0.09, that are quite compre-
hensible in an engineering practice. Similar results are
observed for an average number of occupied channels of
a cell. It is important to note, that numerous numerical
experiments have shown, that at all admissible loads, the
accuracy of the proposed approximate formulas grows
with the increase in the value of the total number of
channels. It is clear that in terms of simplicity and effi-
ciency, the proposed approach is emphatically superior
to the approach based on the use of balance equations to
calculate the QoS metrics of the given CAC in the model
with a non-identical channel occupancy time.

Also note, that high accuracy in the calculation of the
QoS metrics for v-calls is observed even at those load-
ings which do not satisfy any of the accepted assump-
tions above concerning the ratio of intensities of hetero-
geneous traffic. So, for example, at the same values of
number of channels and parameters of strategy, at 
ov = 4,

hv = 3,

od = 10,

hd = 6,

v =

d = 2 (i.e. when assump-
tions 
v

d,

v

d are not fulfilled) the absolute error
for the mentioned QoS metric does not exceed 0.002.
Similar results are observed for an average number of
occupied channels of a cell. However, the proposed ap-
proximate formulas show low accuracy for d-calls since
for them the maximal absolute error exceeds 0.2.
 
Numerical experiments with the CAC based on the
threshold strategy are carried out also. Due to the limited
volume of work these results are not presented here. As
in CAC based on guard channels, the increase in value of
one of the parameters (in admissible area), favorably
affect the blocking probability of calls of the corre-
sponding type only. So, the increase in value of parame-
ter R1 leads to a reduction of the blocking probability of
od-calls but other blocking probabilities (i.e. Phv, Pov and
Phd) increase. At the same time, the increase in the value
of any parameter leads to an increase in the overall
channels utilization.
At the end of this section we conducted research on
comparative analysis of QoS metrics of two schemes:
CAC based on the guard channels scheme and the CAC
based on the threshold strategy. Comparison was done in
the broad range of the number of channels and load pa-
rameters. In each access strategy the total number of
channels is fixed and controllable parameters are N1, N2,
N3 (for CAC based on the guard channels scheme) and R1,
R2, R
3 (for CAC based on the threshold strategy). As
mentioned above, the behavior of the QoS metrics, with
respect to the indicated controllable parameters, in dif-
ferent CAC, are the same.
It is important to note that with the given number of
channels, loads and QoS requirements in either of the
CAC strategies may or may not meet the requirements.
For instance, in the model of mono-service CWN for the
given values of N = 100, 
o = 50 erl,

h = 35 erl follow-
ing requirements Po  0.1, Ph  0.007 and80N
~
are not
met with CAC based on guard channels irrespective of
the value of the parameter g (number of guard channels),
whereas CAC based on individual pool only for h-calls
(i.e. ro = 0) meets the requirements at rh = 40. However,
for the same given initial data, requirements Po  0.3, Ph
 0.0001 andare only met by CAC based on the
guard channel scheme at g = 20, and never met by CAC
based on the individual pool strategy irrespective of the
value of its parameter rh. Thus it is possible to find the
optimal strategy (in a given context) at the given loads
without changing the number of channels.
60
~N
Apparently, both strategies have the same implemen-
tation complexity. That is why the selection of either of
them, at each particular case, must be based on the an-
swer to the following question: does it meet the given
QoS requirements? These issues are a subject to a sepa-
rate investigation.
5. Conclusions
In this paper, an effective and refined approximate
approach to the performance analysis of the un-buffered
integrated voice/data CWN, under different multi-
parametric CAC, has been proposed. Note that many
well-known results related to the mono-service CWN are
special cases of such proposed ones. In almost all of the
available work on devoted mono-service CWN, the
queuing model is investigated with assumption that both
handover and original calls are identical in terms of
channel occupancy time. This assumption is rather li-
miting and unrealistic. Here, models of the un-buffered
integrated voice/data CWN are explored with more
general parameter requirements. Performed numerical
results demonstrate high accuracy of the developed
approximate method.
It is important to note that the proposed approach may
facilitate the solution of problems related to the selection
of the optimal (in given sense) values of parameters in
the investigated multi-parametric CAC. These problems
are subjects to separate investigation.
6. Acknowledgements
This research has been supported by Sangji University
Research Fund 2009.

J. H. Baek ET AL. 226
7. References
[1] S. Tekinay and B. Jabbari, “Handover policies and chan-
nel assignment strategies in mobile cellular networks,”
IEEE Communication Magazine, Vol. 29, No. 11, pp.
42–46, 1991.
[2] I. Katzela and M. Naghshineh, “Channel assignment sch-
emes for cellular mobile telecommunication systems,”
IEEE Personal Communications, pp. 10–31, June 1996.
[3] S. DasBit and S. Mitra, “Challenges of computing in
mobile cellular environment—a survey,” Computer Com-
munications, Vol. 26, pp. 2090–2105, 2003.
[4] R. J. Boucherie and M. Mandjes, “Estimation of per-
formance measures for product form cellular mobile
communications networks,” Telecommunication Systems,
Vol. 10, pp. 321–354, 1998.
[5] R. J. Boucherie and N. M. Van Dijk, “On a queuing net-
work model for cellular mobile telecommunications net-
works,” Operation Research, Vol. 48, No. 1, pp. 38–49,
2000.
[6] W. Li and X. Chao, “Modeling and performance evalua-
tion of cellular mobile networks,” IEEE/ACM Transac-
tions on Networking, Vol. 12, No. 1, pp. 131–145, 2004.
[7] D. Hong and S. S. Rapoport, “Traffic model and per-
formance analysis of cellular mobile radio telephones
systems with prioritized and non-prioritized handoff pro-
cedures,” IEEE Transactions on Vehicular Technology,
Vol. 35, No. 3, pp. 77–92, 1986.
[8] G. Haring, R. Marie, R. Puigjaner, and K. Trivedi, “Loss
formulas and their application to optimization for cellular
networks,” IEEE Transactions on Vehicular Technology,
Vol. 50, No. 3, pp. 664–673, 2001.
[9] B. Gavish and S. Sridhar, “Threshold priority policy for
channel assignment in cellular networks,” IEEE Transac-
tions on Computers, Vol. 46, No. 3, pp. 367–370, 1997.
[10] V. S. Korolyuk and V. V. Korolyuk, “Stochastic model of
systems,” Kluwer Academic Publishers, Boston, 1999.
[11] W. Yue and Y. Matsumoto, “Performance analysis of
multi-channel and multi-traffic on wireless communica-
tion networks,” Kluwer Academic Publishers, Boston,
2002.
[12] S. Nanda, “Teletraffic models for urban and suburban
microcells: Cell sizes and hand-off rates,” IEEE Transac-
tions on Vehicular Technology, Vol. 42, No. 4, pp. 673–
682, 1993.
[13] S. E. Ogbonmwan and L. Wei, “Multi-threshold band-
width reservation scheme of an integrated voice/data
wireless network,” Computer Communications, Vol. 29,
No. 9, pp. 1504–1515, 2006.
[14] R. W. Wolff, “Poisson arrivals see time averages,” Op-
erations Research, Vol. 30, No. 2, pp. 223–231, 1992.
[15] F. P. Kelly, “Reversibility and stochastic networks,” John
Wiley & Sons, New York, 1979.
[16] V. Casares-Giner, “Integration of dispatch and intercon-
nect traffic in a land mobile trunking system. Waiting
time distributions,” Telecommunication Systems, Vol. 16,
No. 3–4, pp. 539–554, 2001.
[17] A. G. Greenberg, R. Srikant, and W. Whitt, “Resource
sharing for book-ahead and instantaneous-request calls,”
IEEE/ACM Transactions on Networking, Vol. 7, No. 1,
pp. 10–22, 1999.
[18] A. Z. Melikov and A. T. Babayev, “Refined approxima-
tions for performance analysis and optimization of queu-
ing model with guard channels for handovers in cellular
networks,” Computer Communications, Vol. 29, No. 9,
pp. 1386–1392, 2006.
[19] R. L. Freeman, “Reference manual for telecommunica-
tions engineering,” John Wiley & Sons, New York, 1994.
[20] A. Z. Melikov, M. I. Fattakhova, and A. T. Babayev,
“Investigation of cellular communication networks with
private channels for service of handover calls,” Auto-
matic Control and Computer Sciences, Vol. 39, No. 3, pp.
61– 69, 2005.
[21] H. Chen, L. Huang, S. Kumar, an d C. C. Kuo, “Radio
resource management for multimedia QoS supports in
wireless networks,” Kluwer Academic Publishers, Boston,
2004.