Wireless Sensor Network, 2010, 2, 199-205
doi:10.4236/wsn.2010.23026 Published Online March 2010 (http://www.scirp.org/journal/wsn)
A General Algorithm for Biorthogonal Functions and
Performance Analysis of Biorthogonal Scramble
Modulation System
Yueyun Chen1,2, Zhenhui Tan1
1State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing, China
2Beijing Science and Technology University, Beijing, China
Received August 26, 2009; revised September 7, 2009; accepted November 6, 2009
Abstract
Applying the theorems of Mobius inverse and Dirichlet inverse, a general algorithm to obtain biorthogonal
functions based on generalized Fourier series analysis is introduced. In the algorithm, the orthogonal func-
tion can be not only Fourier or Legendre series, but also can be any one of all orthogonal function systems.
These kinds of biorthogonal function sets are used as scramble signals to construct biorthogonal scramble
modulation (BOSM) wireless transmission systems. In a BOSM system, the transmitted signal has signifi-
cant security performance. Several different BOSM and orthogonal systems are compared on aspects of BER
performance and spectrum efficiency, simulation results show that the BOSM systems based on Chebyshev
polynomial and Legendre polynomial are better than BOSM system based on Fourier series, also better than
orthogonal MCM and OFDM systems.
Keywords: Biorthogonal Functions, Biorthogonal Scramble Modulation, Generalized, Fourier Series, Mobius
Inverse, Wireless Transmission
1. Introduction
In wireless transmission systems, orthogonal signals are
often used for transmission information. In order to re-
duce the complexity of receivers in orthogonal transmis-
sion system and improve the bandwidth efficiency, a
kind of special biorthogonal modulation was adopted.
The biorthogonal signals are consisted of two groups of
orthogonal signals [1,2]. In group one, the M/2 functions
are directly obtained from orthogonal function system;
the M/2 functions in the other group are the inverse func-
tions of group one’s. Therefore, only half of the band-
width and half correlators were required compared with
M orthogonal functions modulation system. Biorthogo-
nal CDMA is also helpful to improve spectrum effi-
ciency, reduce multiple-access interference and com-
plexity in receiver [3,4]. However, these systems also
belong to orthogonal systems because all the biorthogo-
nal signals are also orthogonal.
In fact, security is difficult to be guaranteed in or-
thogonal systems, because the signals used in modulation
and de-modulation are same in transmitter and receiver
(sometimes except the symbol “+” or “–”). Recently, a
kind of biorthogonal functions which are no-orthogonal
was discussed. In paper [5,6], Wei Yuchuan and Chen
Nianxian analyzed several periodic waves based on Fou-
rier series expansions with the theorem of Möbius in-
verse and the extended Möbius inverse theorem proposed
by Chen Nanxian [7], pointed out that a periodic signal is
able to be represented as the a superposition of some
easily generated periodic functions (such as sawtooth
wave and triangular wave) with different frequencies,
and gave an algorithm to obtain the biorthogonal func-
tions based on Fourier series analysis. The kind of bior-
thogonal functions is not orthogonal. However, the con-
dition above is that the Fourier coefficients of the period
functions are completely multiplicative. Subsequently,
Su Wuxun in paper [8] gave similarly the inverse trans-
form of some often-used symmetrical periodic wave-
forms based on Fourier series analysis, and suggested a
digital communication system architecture using bior-
thogonal functions as multi-carriers in paper [9]. How-
ever, the condition of completely multiplicative Fourier
coefficients limited the space of biorthogonal functions.
In paper [10], we introduced an algorithm to obtain
biorthogonal functions based on Fourier-Legendre series

Y. Y. Chen ET AL. 200
analysis, and proposed a wireless transmission system of
biorthogonal scramble modulation (BOSM) based on
such kind of biorthogonal function sets. It was pointed
out that in flat fading channel, the BOSM systems based
on Fourier series analysis have the close BER perform-
ance, and spectrum efficiency is similar to MCM system;
but the system based on Fourier-Legendre series analysis
has higher spectrum efficiency better BER performance
than other systems.
In this paper, we introduce a universal algorithm to
obtain biorthogonal functions based on General Fourier
series analysis. The algorithm doesn’t need the condition
that the series coefficients are completely multiplicative.
In the meantime, the orthogonal function can be not only
Fourier or Legendre series, but also can be any one of all
orthogonal function systems. Then we propose a BOSM
(biorthogonal scramble modulation) system using some
of these new biorthogonal functions. On the condition of
flat fading channel, we analyze and compare the BER
performance and spectrum efficiency of different BOSM
and orthogonal systems. The simulating results show that
the BOSM based on General Fourier series analysis not
only has better BER performance, but also has higher
spectrum efficiency than the BOSM system based on
Fourier series analysis.
2. The Fundamental Theorems of Möbius
Inverse Transform and Dirichlet Inverse
Möbius inverse transform and Dirichlet inversion are
helpful theorems. The related theorems are briefly intro-
duced in this section.
A basic Möbius inverse formula is described as fol-
lows. If ()
f
n is a number-theoretic function and
|
() ()
dn
F
nfd (1)
then, for all positive integers n, there exists
|
()() ()
dn
n
fn dFd
  (2)
Inversely, if Equation (2) exists, then Equation (1) can
be yielded. In above equation, ()n

is a Mobiu s func-
tion defined as
1, 1
()(1)if all the primes ofare different
0,has a squared factor
r
n
n
if n








n
If f(n) and ()
g
n are number-theoretic functions, then
their Dirichlet multiplication is also a number-
theoretic functions [11]
()hn

|
() ()1,2,3,
dn
n
hnf ngn
d





and it can be written as
()() ()hnf ngn

 (4)
If (1) 0f

, there exists a unique number-theoretic
function 1()
f
n
 satisfying
11
1
()()() ()n fn f nf n fn




where 1n


is Kroneche ’s delta symbol and
1()
f
n

is
called Dirichlet inverse of
1
(). ()
f
nf n

can be calcu-
lated by recurrence formula as following
11
() (1) fn
f
 (n =
1) (5)

11
|
<
1
()() > 1
(1) dn
dn
n
fnffd n
fd






(6)
Specially, if ()
f
x is complete multiplicative, then




1


f
nnfn (7)
Following is a useful Mobius inverse formula. It is
expressed as follows [8,12]
  
1
11





nn
Gx rngnxgx rnGnx(8)
where


Gx and


g
x are two functions defined in


-,

 and


rd
1 is Dirichlet inverse of


rd.
3. Fourier Series Analysis
Function ()
f
x belongs to function space


2-,

 L
with period 2

. It has a unique Fourier series expressed as
 
1
0cossin


 





n
f
taanntbn nt (9)
where,


0a,


an and are the Fourier series
coefficients of

bn


f
t.
Supposing that


ut and


vt are respectively an
even and odd functions with period of 2

, their Fourier
series is expressed respectively as
 
1
cos




n
utAnn t
 
1
sin




n
vtBnn t
By the theorem of Möbius inverse [12], Equation (9)
can be rewritten as the following form

(3)

Y. Y. Chen ET AL.201
  
   
 
11
11 11
11
1| 1|
11
0
0
0
 

 
 







 


 
 
 
 

 
 

nm nm
kdk kdk
kk
f
taanAmumntbnBm vmnt
kk
aadAuktbdBvkt
dd
ackuktdkvkt
(10)
where
 

 
1
|
1
|
1cos( )
dk
dk
k
k
ckadAd
k
ftdt dtAd
ftgtdt




















(11)
 

 
1
|
1
|
1sin( )
dk
dk
k
k
dkbdB d
k
ftdtdtB d
fth tdt




















(12)
Equation (10) shows that a quadratically integrabel
function can be decomposed as the superposition of even
function


ut and


vt and odd function


vt with
different frequencies. In Equation (11) and Equation (12),

k
g
t and is given respectively by

t
k
h

1
|
1cos





k
dk
k
g
tA
ddt (13)

1
|
1sin





k
dk
k
ht Bdt
d (14)
It can be proved that





n
umtg tdtnm (15)





n
vmth tdtnm (16)
namely,

k
g
t and are
biorthogonal functions, the same are
 
1
cos



n
umtAn mnt


k
ht

nt
and
. In Equation (10),
 
sinvmt m

1



n
Bn


ut and
are called the basic function of biorthogonal func-
tions. In fact, the proof of Equation (15) and Equation
(16) do not need the condition that Fourier coefficients

vt

A
n

or of or are completely
multiplicative. When

Bn

ut

vt


A
n or


Bn
 
are not com-
pletely multiplicative, i.e.,


1


A
nnAn or






1

Bn nBn, the conclusion of Equation (15)
and Equation (16) can also be obtained.
4. General Fourier Series Analysis
Supposing


n
Px is an infinite orthogonal series with
weight function


hx in the orthogonal interval


,ab,
namely

b
ahx
P x
 
0,
1




mn
mn
P xdxmn (17)
where weight function


hx is nonnegative and inte-
grable in the interval


,ab [13]. If

f
x is a function
defined in interval


,ab and satisfies

2<

b
ahxf xdx,
then it can be decomposed to generalized Fourier series as

0


n
n
f
xanPx (18)
The coefficient of generalized Fourier series


an is
defined by

an
 
b
n
ahxfxP xdx (19)
Then, a more universal algorithm to obtain biorthogo-
nal functions is introduced by following proposition.
Proposition 1. Supposing is orthogonal series
with weighted function in orthogonal interval

n
Px

hx


,ab. If


f
x is a function defined in interval


,ab
and satisfies the relation of

2<

b
ahxf xdx (i.e.


f
x belongs to


,;




xabh ). Then, the two group
functions
 
1
,




 mnm
n
F
xanPxnmK (20)
and
  
1
|



n


dk
n
F
xahxPdx
d (21)
is a biorthogonal function set, namely
 



mn
Fxdx
b
aFx mn
(22)
where


an is the coefficient of generalized Fourier
series of


f
x,


is its Dirichlet inverse, a
K is the order of biorthogonal function set
1
an nd
.
Proof.

Y. Y. Chen ET AL. 202
 

1
1|
1
,
1|
1
|
|
1
|
|
/
/









 






 
 
 
 

 
 






bb
mn im
aa
idn
im d
idn
dn
mn
mn
dn
mn
n
F
xFxdxaiP xahxPdxdx
d
n
aia d
dn
aa
md
dnm
aa
mdm
The proof is completed.
In Proposition 1, represents any a kind of or-
thogonal series expanded in orthogonal function system
. With the difference of , can be
different orthogonal polynomials series, such as Legen-
dre polynomials, Chabyshev polynomials, Hermite
polynomials, Laguarre polynomials, etc. The particular
case is Fourier series when and

n
Px
 
n
Px
 
hx

1hx

n
Px


Px
n is
trigonometric function. Therefore, the algorithm given
by Equation (20) and Equation (21) is a general algo-
rithm to obtain biorthogonal functions. In fact, the proc-
ess of biorthogonalizing corresponds to rotate the or-
thogonal polynomials coordinate axis, thus one function
in bi-orthogonal function set has projection on one or
more axis.
There is a fast algorithm for biorthogonal functions.
Functions (20) and (21) can be rewritten as matrix forms as










   

 









1234
1
2
3
4
123456
010203
00 1002
000 100
00000 1
 
 











 





 

T
K
K
F FxFxFxFxFx
aaaaa aaKPx
aa aP
aa
aP
aPx
AP x

















x
P




x
x
1
(23)
  


 
 
 


 





 
1234
1
11
1
11
2
11 1
3
1
4
111
1
100 00
2100 0
30 100
420 10
500 00
6320 0
0
1



 



   




































  










T
K
K
F FxFxFxFxFx
a



P
x
aa
P
x aa
P
x aa a
hx
P
x
a
aaa
P
x
aK a
hxBPx
(24)
where
K
is called the order of biorthogonal function
set. If matrix
A
and is normalized individually by
B


1a and


11 
a, Equation (23) and Equation (24) are
rewritten as


F
AP x (25)





F
hxBPx (26)
where


1/


A
Aa , . Then, matrix

1
/1



BBa
A
and are sparse triangular matrixes and they are
transposes each other (regardless the upper-mark “-1”).
Therefore, the calculation speed of the algorithm method
is improved rapidly.
B
Following takes Chabyshev polynomials as an exam-
ple. Chabyshev polynomials is defined in orthogonal
interval [-1,1] with weight function

2
1/ 1hxx .
The series can be expressed as



 
arccos0,1, 2,
nnx ncosTx
 
(27)
If
 
1
1
1n11n 22





n
n
n
f
xx Tx
n, then
 
1
21, 1,

 
nn nan and can be calcu-
lated by Equation (6) and Equation (7). Let

1
an
6

K, then
the biorthogonal functions can be directly obtained as
follows














1
2
3
4
5
6
1
2
3
4
5
6
11213141516
010 120 14
0010012
00 01 0 0
00 00 1 0
00 00 01

 































F
xPx
F
xPx
F
xPx
F
xPx
F
xPx
F
xPx
(28)














1 1
2
3
4
5
6
2
3
24
5
6
100000
121000 0
13010 0 0
1
121201 0 0
1
15000 1 0
1613 12001

















 





 










 






Px
Px
Px
Px
x
Px
Px






Fx
Fx
Fx
Fx
Fx
Fx
(29)
It can be proved that functions

 
m

F
x and





m
F
x are biorthogonal, and the functions in one
group are not orthogonal. So, this is a kind of more gen-
eral biorthogonal functions.
5. Transmission System of BOSM
The biorthogonal function sets discussed above have a
magnetic feature that the functions in same one group are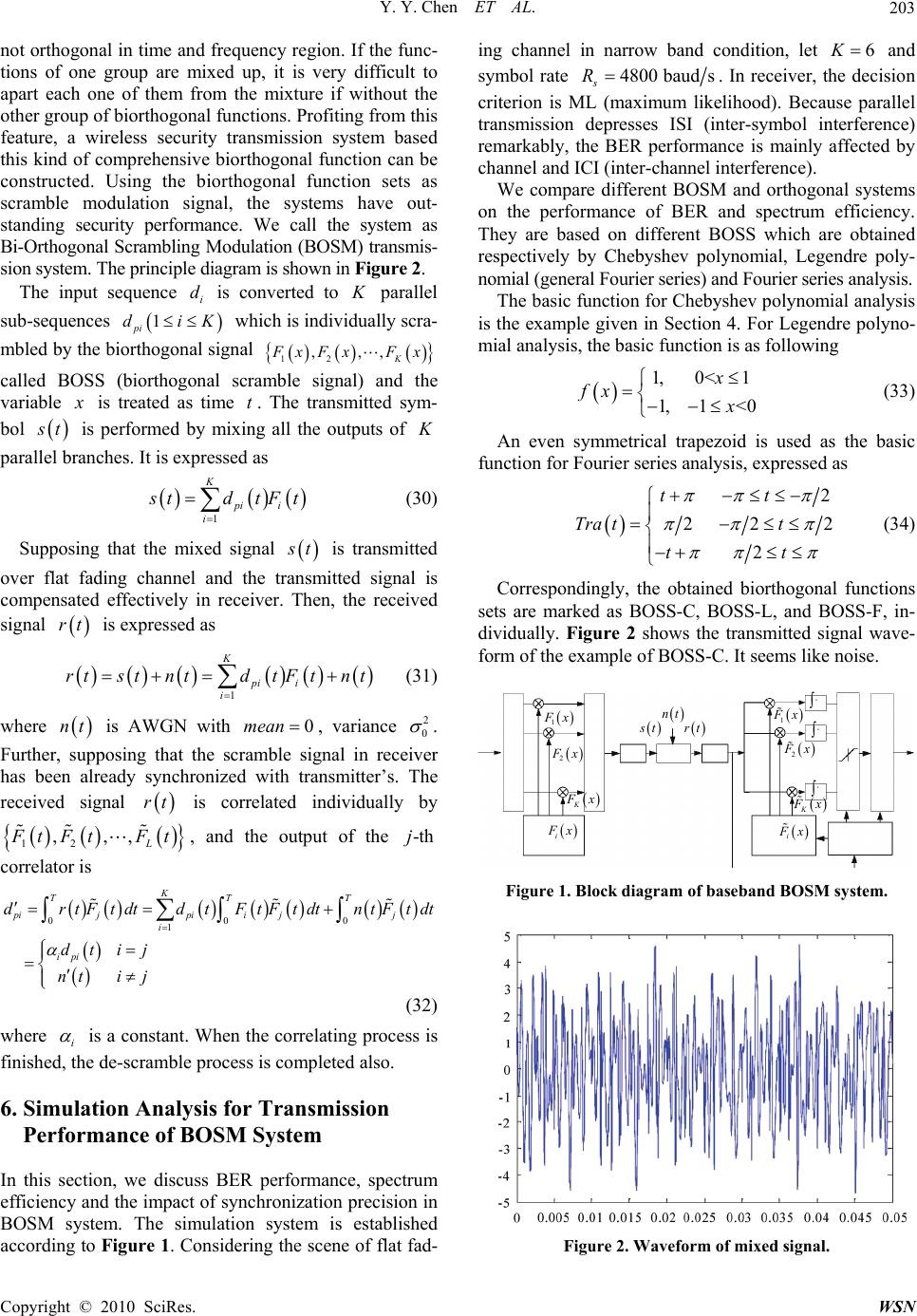

Y. Y. Chen ET AL.203
not orthogonal in time and frequency region. If the func-
tions of one group are mixed up, it is very difficult to
apart each one of them from the mixture if without the
other group of biorthogonal functions. Profiting from this
feature, a wireless security transmission system based
this kind of comprehensive biorthogonal function can be
constructed. Using the biorthogonal function sets as
scramble modulation signal, the systems have out-
standing security performance. We call the system as
Bi-Orthogonal Scrambling Modulation (BOSM) transmis-
sion system. The principle diagram is shown in Figure 2.
The input sequence is converted to parallel
sub-sequences
i
dK


1
pi
diK which is individually scra-
mbled by the biorthogonal signal








12 , K
,,
F
xFF xx
called BOSS (biorthogonal scramble signal) and the
variable
x
is treated as time . The transmitted sym-
bol
t

s
t is performed by mixing all the outputs of
K
parallel branches. It is expressed as
 
1

K
pi i
i
s
tdtFt (30)
Supposing that the mixed signal


s
t is transmitted
over flat fading channel and the transmitted signal is
compensated effectively in receiver. Then, the received
signal is expressed as

rt

1
 

K
pi i
i
rtstntdtFtnt (31)
where is AWGN with , variance

nt 0mean 2
0

.
Further, supposing that the scramble signal in receiver
has been already synchronized with transmitter’s. The
received signal is correlated individually by

rt

,

L

,,


12


F
tFtFt , and the output of the
correlator is
-thj
   


000
1


 








K
TTT
pijpii jj
i
ipi
drtFtdtdtFtFt dtntFt dt
dt ij
nti j

(32)
where

i is a constant. When the correlating process is
finished, the de-scramble process is completed also.
6. Simulation Analysis for Transmission
Performance of BOSM System
In this section, we discuss BER performance, spectrum
efficiency and the impact of synchronization precision in
BOSM system. The simulation system is established
according to Figure 1. Considering the scene of flat fad-
ing channel in narrow band condition, let 6

K and
symbol rate 4800 bauds
s
R

. In receiver, the decision
criterion is ML (maximum likelihood). Because parallel
transmission depresses ISI (inter-symbol interference)
remarkably, the BER performance is mainly affected by
channel and ICI (inter-channel interference).
We compare different BOSM and orthogonal systems
on the performance of BER and spectrum efficiency.
They are based on different BOSS which are obtained
respectively by Chebyshev polynomial, Legendre poly-
nomial (general Fourier series) and Fourier series analysis.
The basic function for Chebyshev polynomial analysis
is the example given in Section 4. For Legendre polyno-
mial analysis, the basic function is as following

1,0< 1
1,1<0




x
fx
x
(33)
An even symmetrical trapezoid is used as the basic
function for Fourier series analysis, expressed as

2
22
2
2











 

tt
Tra tt
tt
(34)
Correspondingly, the obtained biorthogonal functions
sets are marked as BOSS-C, BOSS-L, and BOSS-F, in-
dividually. Figure 2 shows the transmitted signal wave-
form of the example of BOSS-C. It seems like noise.




nt

1

Fx


1
Fx




rt
s
t


2

Fx


2
Fx




K
Fx


K
Fx


i
Fx


i
Fx
Figure 1. Block diagram of baseband BOSM system.
Figure 2. Waveform of mixed signal.

Y. Y. Chen ET AL. 204
6.1. Spectrum Efficiency
In BOSS-F, the bandwidth of mixed signal is 14

BkHz
(see Figure 3), the spectrum efficiency is 0.34 baud/Hz
approximately, and equal to orthogonal MCM (Multiple
Carriers Modulation) system regardless the guard band.
In BOSS-C and BOSS-L, the PSD (power spectrum
density) of mixed signal is shown respectively in Figures
4(a) and 4(b). The energy of mixed signal is mainly con-
centrated in interval of 0~3.2kHz and 0~4.8kHz, and the
Figure 3. Spectrum of mixed signal for BOSS-F.
(a)
(b)
Figure 4. Single-side PSD of mixed signal. (a)
BOSS-C; (b) BOSS-L.
spectrum efficiency approximately is 1 baud/Hz and 1.5
baud/Hz respectively. In fact, the PSD of mixed signals
are changed a bit with the change of basic function


f
t.
In OFDM system, the spectrum efficiency is improved
approaching 1 times than orthogonal MCM system.
Compared with OFDM system, the BOSM system based
on 10 Legendre polynomial analyses has similar per-
formance of spectrum efficiency. Therefore, the BOSM
systems based on general Fourier series analysis, includ-
ing Chebyshev series and Legendre series analysis, have
higher spectrum efficiency.
6.2. BER Performance
In paper [10], we had given a conclusion that the BOSM
systems based on Fourier series with different basic
functions have close BER performance. Supposing syn-
chronization is exactly established. The BER perform-
ance of different systems is shown in Figure 5. It reveals
that, in flat fading channel, the BER performance of
BOSS-L and BOSS-C systems are the best, and BOSS-F
and orthogonal-M systems (or OFDM system) have the
close BER performance. Therefore, the BER perform-
ance of the BOSM systems based on general Fourier
series analysis is satisfying.
6.3. Synchronization Property
Synchronization error of biorthogonal signals between
transmitter and receiver leads to ICI. Supposing the error is

, then, the output of correlator is (-t hj


nt is omitted)
 
 
 
0
1
0
111
0
111
















KT
pipii j
i
KKK
T
piik ijlj
ikl
KKKT
piik jlij
ikl
ddtFtFtdt
dtAP BPtdt
dtAB PtPtdt
(35)
Figure 5. Spectrum of mixed signal.

Y. Y. Chen ET AL. 205
In above expression, the output is impacted by all
other K-1 channels, because the biorthogonal feature is
damaged in different degree with different

. When
using the example of BOSS-C, Figure 6 shows the im-
pact of synchronization error to BER performance. The
BER curve is changed periodically with the synchroniza-
tion error, and the period is the length of interval [a,b]
(sample number 40 represents the interval length).
Therefore, synchronization precision needed to be guar-
antied in BOSM system, just same as OFDM systems.
error probability will be deteriorate when the energy in a
symbol interval is significantly weaker than the considered
noise level. Therefore, the order
K
should be not too big.
To properly choose the basic function can change the
PDF and PAPR of transmitted signal. In order to make
BOSM systems with better performance, how to con-
struct a proper basic function in an orthogonal function
system to obtain the biorthogonal functions, it is still a
challenge.
8. References
7. Conclusions
[1] R. B. Blizard, “Comparison of biorthogonal and bisim-
plex codes,” IEEE Transactions on Communications
Technology, Vol. 15, No. 4, pp. 657–658, August 1967.
The biorthogonal functions were introduced into ordi-
nary orthogonal function systems, and pointed out that
the condition of complete multiplication is not needed. In
the meantime, a more general algorithm for biorthogonal
functions called general Fourier series analysis was pro-
posed. Because the obtained biorthogonal functions are
not orthogonal each other, the BOSS that the obtained
biorthogonal functions were used as scramble signal to
be modulated by transmitted symbols has outstanding
security performance, especially when the order is
enough big. This is very different from orthogonal sys-
tem and traditional biorthogonal modulation system. By
simulation analysis, in flat fading channel, the BOSM
systems based on general Fourier series analysis, such as
Chebyshev polynomial and Legendre polynomial analy-
sis, have better BER performance and spectrum effi-
ciency than the BOSM system based on Fourier series
analysis, orthogonal MCM system or OFDM system.
[2] M. Kim and S. Tretter, “Performance of sequential de-
coding with biorthogonal modulation and Q-level quan-
tization,” IEEE Transactions on Communications, Vol.
19, pp. 88–92, February 1971.
[3] S.-H. Hong and J.-S. No, “Performance analysis of
CDMA systems by using biorthogonal codes,” IEEE 45th
Conference on Vehicular Technology, Vol. 2, pp. 694–
698, July 1995.
[4] S.-J. Kang, D.-K. Hong, et al., “Constant-amplitude mul-
ticode-biorthogonal modulation,” IEEE Transactions on
Communications, Vol. 55, No. 1, pp. 69–75, January
2007.
[5] Y. Wei and N. Chen, “Square wave analysis,” Journal of
Mathematical Physics, Vol. 39, No. 8, pp. 4226–4245,
August 1998.
[6] Y. Wei, “Dirichlet multiplication and easily-generated
function analysis,” Computers & Mathematical with Ap-
plications, Vol. 39, pp. 173–199, 2000.
However, the demand of high synchronization preci-
sion and having high PAPR (peak average power rate) in
BOSM systems are two primary problems, just as OFDM
or multi-carriers systems, and the degree of PAPR rises
with increasing of the order of BOSS. Because smaller
amplitude of polynomial coefficients in biorthogonal
functions appears with the increasing of the order of
biorthogonal function set, the performance of demodulation
[7] N. Chen, “Modified Möbius inverse formula and its ap-
plications in physics,” Physics Review Letters, Vol. 64,
No. 11, pp. 1193–l195, 1990.
[8] W. Su, W. Zhang, and J. Wang, “The evaluations of the
inverse transform of eight often-used waveforms by
Möbius transform—The inverse transform of their Fou-
rier series,” Chinese of Journal Electronics, Vol. 14, No.
3, pp. 513–518, July 2005.
[9] C. Ling, F. Chen, and W. Su, “The Chen-mobius
multi-carriers digital communication system and its
simulation,” IEEE International Workshop on Anti-Coun-
terfeiting, Security and Identification, pp. 16–18, April
2007.
[10] Y. Chen, J. Zhang, and Z. Tan, “A kind of biorthogonal
functions based on Fourier-Legendre series and its appli-
cation in wireless transmission system,” IEEE 9th Inter-
national Conference on Signal Processing, 2008.
[11] K. H. Rosen, “Elementary number theory and its applica-
tion,” 5th edition, Pearson Education Inc. Press, 2005.
[12] M. R. Schroeder, “Number theory in science and com-
munication,” 4th edition, Springer-Verlag Press, New
York, 2006.
[13] Z. Liu, “Orthogonal function and its application,” Na-
tional Defense Industry Publisher, Beijing, 1982.
Figure 6. Impact on BER by synchronization error.