J. Biomedical Science and Engineering, 2010, 3, 274-284
doi:10.4236/jbise.2010.33037 Published Online March 2010 (http://www.SciRP.org/journal/jbise/
JBiSE
).
Published Online March 2010 in SciRes. http://www.scirp.org/journal/jbise
Mathematical model for the ubiquitin activating enzyme E1
Francisco Javier López-Cánovas1, Francisca Cánovas2, María Antonia Günther Sillero1, Antonio Sillero1
1Departamento de Bioquímica, Instituto de Investigaciones Biomédicas Alberto Sols UAM/CSIC, Facultad de Medicina, Madrid,
Spain;
2Departamento de Matemáticas e Informática, Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos, Universidad
Politécnica de Madrid, Madrid, Spain.
Received 21 December 2009; revised 4 January 2010; accepted 8 January 2010.
ABSTRACT
The ubiquitin-activating enzyme E1 (EC 6.3.2.19)
represents the first step in the degradation of proteins
by the ubiquitin proteasome pathway. E1 transfers
ubiquitin from the ubiquitinated E1 to the ubiquitin
carrier proteins (E2), ubiquitin-protein ligases (E3)
and proteins. This process is rather complex, and
known from the work of Haas, Ciechanover, Hershko,
Rose and others. The occurrence of 19 hypothetical
intermediate enzyme forms (EFs) and 22 different
reactions were considered in the presence of ubiq-
uitin (Ub), ATP, adenosine 5’-tetraphosphate (p4A),
pyrophosphate (P2), and tripolyphosphate (P3) as
substrates, and iodoacetamide (IAA) and dithioth-
reitol (DTT) as inhibitors. Inspired by the work of
Cha (Cha (1968) J. Biol. Chem., 243, 820-825) we
have treated these reactions in two complementary
ways: in rapid equilibrium and in steady state. The
kinetics of both types of reactions were simulated and
solved with a system of ordinary differential equa-
tions using the Mathematica Program. The ubiquiti-
nation of E1 has been also theoretically coupled to
the ubiquitination of E2, E3 and proteins. This makes
the model useful to predict the theoretical influence
of inhibitors (or of changes in some parameters of the
reaction) on the ubiquitination of proteins. The Pro-
gram responds to changes in the concentration of
ATP or ubiquitin and has predictive properties as
shown by the influence of AMP on the synthesis of
p4A, calculated theoretically and confirmed experi-
mentally.
Keywords: Dinucleoside Polyphosphates; Adenosine
Tetraphosphate; Tripolyphosphate; Proteasome;
Mathematical Model
1. INTRODUCTION
The work here presented deals with the development of
a mathematical model for the ubiquitin activating en-
zyme E1 (EC 6.3.2.19) and is based on the following
grounds, A, B, C, D:
1) Ligases catalyze the synthesis of diadenosine
tetraphosphate (Ap4A) and other (di)nucleoside poly-
phosphates through the general reactions a) and b),
where X is a co-substrate of a ligase [1]
a) E + X + ATP <-----> E-X-AMP + P2
b) E-X-AMP + ATP -----> Ap4A + X + E
As reaction a) is reversible, the synthesis of Ap4A is
greatly favored in the presence of pyrophosphatase
(PPase). In our experience, reaction b) is rather unspecific
and the AMP residue of the E-X-AMP complex may
react with the terminal phosphate of almost any mole-
cule containing an intact terminal pyrophosphate, such
as ATP, GTP, adenosine tetra phosphate (p4A), tri, tetra,
penta phosphate (P3, P4, P5) [2].
2) The ubiquitin-activating enzyme E1 is a particular
ligase using ubiquitin (Ub) and ATP (reaction c), or p4A
(reaction d) as substrates for the synthesis of the AMP
derivative of the enzyme and, by the same token, uses P2
or P3 in the reverse reactions; p4A and P3 act as analogs
of ATP and P2, respectively [3].
c) E + Ub + ATP <-----> E-Ub-AMP + P2
d) E + Ub + p4A <-----> E-Ub-AMP + P3
The reactions of E1 with ubiquitin and ATP as sub-
strates and iodoacetamide (IAA), dithiothreitol (DTT)
and pyrophosphatase as modifiers of the reaction consti-
tute a complex metabolic pathway thoroughly explored
by the groups of Ciechanover, Hershko, Rose and others
[4,5,6,7]. The knowledge developed by these authors on
this system is the cornerstone of the work shown below.
We have recently approached the reactions catalyzed by
E1 using ATP, P3 and p4A as substrates and io-
doacetamide and dithiothreitol as inhibitors of the reac-
tion [3].
3) Two main processes can be considered in the ubiq-
uitin proteasome system for degradation of proteins: a)
ubiquitination of proteins and b) proteolytic cleavage of
the tagged proteins by the 26 S proteasome complex. In
the initial conjugative phase the ubiquitin activating en-

F. J. López-Cánovas et al. / J. Biomedical Science and Engineering 3 (2010) 274-284
275
JBiSE
zyme E1 catalyzes the formation of a high-energy thio-
ester bond between the C-terminal of ubiquitin and a
cysteine residue of E1; one of the several E2 enzymes
(ubiquitin-carriers or ubiquitin conjugating enzymes)
transfers the activated ubiquitin moiety from E1, via an
additional high energy thioester intermediate, to the sub-
strate that is specifically bound to a member of the ubiq-
uitin-protein ligase family E3. The ubiquitinated protein
is degraded by the proteasome with liberation of pep-
tides and ubiquitin monomers [7,8,9,10,11].
4) Finally, as shown below, we have applied our pre-
vious experience in the mathematical modeling of
metabolic pathways of glucose [12], and purine nucleo-
tide metabolism in rat brain [13] and Saccharomyces
cerevisiae [14] to the ubiquitin proteasome system.
On the above bases, we have tried to develop a
mathematical model of the reactions catalyzed by E1 in
order to get new insights into the proteasome system in
general, and on the role of E1 in this system. The de-
scription of the reactions catalyzed by E1 are presented
(Figure 1) in a way that facilitates their mathematical
writing with the powerful Mathematica Program [15].
The theoretical and experimental results can be com-
pared, so that the analysis of some physiological aspects
of E1, difficult to be explored in vivo or in vitro, can be
attempted with the mathematical approach. In our view,
the mathematical method here described may serve as a
guide to explore other complex metabolic situations,
changes in the concentration of intermediate enzyme
forms of E1 (Figure 1), as well as to approach the
mechanism of action of potential inhibitors of the en-
zyme. As an example of its predictive properties, the ef-
fect of AMP on the synthesis of p4A by E1 was studied
theoretically and confronted with the experimental results.
2. EXPERIMENTAL PROCEDURES
2.1. Nomenclature
Ubiquitin (abbreviated as Ub, U, u or u) is a small 76-
residue polypeptide containing a C-terminal glycine, to
which an adenylated residue can be covalently bound.
The ubiquitin-activating enzyme will be named as E1, E
or HSE. The two functional regions or areas of this en-
zyme will be written at the left and at the right side of
the letter E. The area at the left, corresponding to the U
region (acronym of ubiquitin), may contain a molecule
of ubiquitin covalently bound, by a thioester bond, to a
cysteine residue of the enzyme (UbSE); this area is also
called the ubiquitin donating area, as this ubiquitin can
be donated to E2. The area at the right of E1 corresponds
to the region named as A-u (acronym of AMP and ubiq-
uitin), where the ubiquityl-adenylate (AMP-Ub) com-
plex is tightly, but not covalently, bound to E1. The
AMP-Ub complex is formed by the reaction between
Figure 1. Scheme of the reactions considered for the ubiquitin
activating enzyme E1. The following reactants were involved:
ATP, adenosine 5’-tetraphosphate (p4A), pyrophosphate (P2),
tripolyphosphate (P3), ubiquitin (Ub), iodoacetamide (IAA),
dithiothreitol (DTT), ubiquitin carrier-proteins (E2), ubiquitin
protein-ligases (E3) and proteins to be ubiquitinated (E2 + E3
+ proteins = Blot in the Figure). The enzyme forms (EFs) of E1
with the potential reactants are also indicated with a number in
bold face and between brackets. The reactions between two
EFs have been indicated in regular face numbers from 1 to 22.
Three Boxes were contemplated: X, Y and Z. The reactions
within each one of these Boxes are considered: in rapid equi-
librium, reversible and indicated with two opposing arrow
heads. The reactions between boxes are considered in steady
state. For more details on nomenclature see the text.
one OH-residue of the phosphate moiety of AMP and the
C-terminal of ubiquitin. The ubiquitin moiety of this
complex is in an activated state, but it will not be donated
to E2; the A-u area is also called the ubiquitin activating
area. The different forms of the enzyme will be named as
EF followed by a number in bold face. The reactions be-
tween two different EFs are designated with numbers
from 1 to 22. The dissociation constants are named with
two to five letters. The letters x, y or z indicate that the
reaction belongs to Box X, Y or Z, respectively (see below,
Subsection 3.1.1); the other letters of the constant name
indicate the substrate involved, as indicated between
brackets: a (ATP); A (p4A); u, U or u (ubiquitin); p (P2); P
(P3); e (AMP); d (DTT); B (Blot or the sum of E2 + E3
+ Protein). The order of those letters indicates, in general,
the sequence in which the reactants are bound to the en-
zyme complex. Forward reactions (Table 1, Appendix B)
refer to those in the direction of the synthesis of EF 11,
the enzyme form donating ubiquitin to E2; they have
kinetic constants sub-indexed with uneven numbers; the
contrary applies to the reverse reactions.

276 F. J. López-Cánovas et al. / J. Biomedical Science and Engineering 3 (2010) 274-284
2.2. Computation
The solving of the equations and the plotting of the solu-
tions have been carried with a personal laptop computer
Intel® Pentium® M processor 1.70 GHz with the help of
the Mathematica 5.0 Program [15].
3. RESULTS AND DISCUSSION
3.1. The System
The complete set of reactions catalyzed by E1, using
ATP, p4A, P2, P3, AMP, ubiquitin, and E2 as substrates
and IAA and DTT as inhibitors are presented in Tables 1
and 2 and schematically shown in Figure 1. The reac-
tions have been numbered from 1 to 22. Those reactions
identified with two opposing arrow heads indicate bind-
ing of substrates to E1 or rearrangement of substrates
within the enzyme complex; they are considered in rapid
equilibrium, following Michaelis-Menten postulates.
The reactions noted with a simple arrow head, involving
transformation of the bound substrate(s), are considered
rate-limiting reactions and treated as being in steady
state. The dissociation constants and the equilibrium
constant (yue) are indicated in Table 1. The enzyme
forms (EF) are expressed with the potential reactants or
simply with a number in bold face, between brackets. As
noted in Experimental procedures, the parts at the left
and right side of E1 correspond to the U (acronym of
ubiquitin) and to the A-u (acronym of AMP and ubiquitin)
areas, respectively. The U area of E1 is the ubiquitin donat-
ing area to E2. The reactions depicted in Figure 1 can be
dissected into two parts.
The one at the right side of Figure 1 represents the
classical reactions previously described [7] using ATP, P2
and ubiquitin as substrates. In summary, ATP and ubiq-
uitin are joined to E1 (reactions 1 and 2); the bound ATP
is split into AMP + P2 (reaction 5), the bound P2 is liber-
ated (reaction 8) and ubiquitin is displaced from the A-u
to the U region of the enzyme, with concomitant libera-
tion of AMP (reactions 9 and 10). Once ubiquitin is co-
valently joined to the U region of E1, another moiety of
ubiquitin is bound to the A-u area of the enzyme (using
ATP as co-substrate) through a sequence of reactions
(reactions 11, 12, 18, 20) similar to those previously
described (reactions 1, 2, 5, 8). The enzyme form (EF 11)
is already prepared to serve as donor of ubiquitin from
the U area of E1 to E2 (named as “Blot” in Figure 1).
The EF 9 generated in this step is ready to repeat the
cycle, catalyzed by reactions 9-12, 18, and 20 and to
afford the ubiquitin molecules needed for the processing
of the proteins by the proteasome.
The part at the left side of Figure 1 shows similar re-
actions to those just described with the exception that
p4A serves as a source of energy instead of ATP (com-
pare reactions 1 and 11 with reactions 3, 14, respec-
tively), and a molecule of P3, instead of P2, is involved in
Table 1. Reactions in rapid equilibrium inside boxes X, Y, and
Z. (Figure 1). The number, substrates and product of the reac-
tions are as indicated in the Table and in Figure 1. The disso-
ciation (equilibrium) constants were named according to the
following rules: the binding of a reactant to the A-u area of E1
is represented with a letter between brackets: P2 (p), P3 (P), ATP
(a), p4A (A), Ub (u), AMP (e), DTT (d) or Blot (B); x, y or z
indicates their location in boxes X, Y or Z; u represents the
oscillation of ubiquitin from the A-u to the U area of E1; U
represents ubiquitin bound to a –SH group of the U area of E1.
For more details on the nomenclature of the constants see Ex-
perimental procedures. Dissociation constants are defined as
the product of the concentration of the substrates divided by
the concentration of the bound complex (product EF); for ex-
ample, constant xa= HSE x ATP/HSEAT P . The equilibrium con-
stant yue is defined as UbSEAMP/HSEAMPUb. Numeric values for
these constants have either been taken from the literature or
tuned (#) to reflect available experimental data. To facilitate
location of the reactions in Figure 1, EFs are also indicated by
their assigned numbers (in bold characters between brackets).
Table 2. Rate constant values (simplified procedure) of the
steady state reactions. The constants with uneven or even
numbers indicate forward or reverse direction, respectively,
towards formation of UbSEAMPUb (EF 11, the enzyme complex
donating Ub to the ubiquitin carrier proteins E2).
Constants Reactions Value (s-1) References
k1=k3 Vp; VP 0.75 x k5 [4]
k2=k4 Vp; VP 0.75 x k6 [4]
k5=k7 VUp; VUP 0.13 Tuned
k6=k8 VUp; VUP 6.25 x k5 [4]
k10 Ve 0.57 Tuned
k12 VB 3.3 Tuned
the process (compare reactions 8 and 20 with reactions
13 and 21, respectively). Treatment of this part of Figure 1
is based on previous publications from our laboratory [3],

F. J. López-Cánovas et al. / J. Biomedical Science and Engineering 3 (2010) 274-284
277
JBiSE
with the assumption that the binding of p4A and P3, be-
have similarly to the binding of ATP and P2, respectively.
3.1.1. Kinetics Considerations
The kinetic treatment followed here is based on the gen-
eral consensus on how to handle rapid equilibrium and
steady state reactions of uni-reactant enzymes [16] and
on the simplifications introduced by Cha [17]. He
showed that the calculation of rates of equations of com-
plex enzyme systems could be simplified by treating all
the enzyme forms, implying binding of a substrate to an
enzyme within a rapid equilibrium segment, as a single
entity. On the contrary, reactions involving transforma-
tion of the previously bound substrates are considered
rate-limiting reactions and treated as being in a steady state.
Following these criteria three set of reactions, consid-
ered in rapid equilibrium among themselves, were ar-
ranged in Boxes X, Y and Z. Reactions 1-4, in which
binding of ATP, p4A, or Ub, to E1 take place, were
grouped in Box X; Reactions 8-12 and 14-15, implying
the binding of P2, P3, AMP, ATP, p4A and ubiquitin to E1,
were grouped in Box Y. Reactions 20-22, catalyzing
binding of P2, or P3 to E1 and transfer of ubiquitin from
E1 to E2 were grouped in Box Z.
The reactions considered as being in steady state were
those implying cleavage of ATP (reactions 5 and 18) or
of p4A (reactions 6 and 19) (Figure 1). These reactions
interconnect Boxes X-Y and Boxes Y-Z).
3.1.2. Reactions in the Presence of Added
Dithiothreitol (DTT), Iodoacetamide (IAA),
Blot or Pyrophosphatase
As shown by Haas [6], DTT does not split the ubiquityl
adenylate complex if it is tightly bound to the A-u area
of E1 (as in EF 5). However, DTT breaks the thioester
bond between Ub and a cysteine of E1 (Figure 1, EF 6),
with formation of DTT-Ub. This last complex is rather
unstable due either to the ability of ubiquitin itself to
monitor its own C-terminal for the occurrence of thio-
ester bond or to a possible contaminant thiolesterase
present in the sample of E1 [6]. Iodoacetamide (IAA)
binds covalently to -SH group(s) here indicated (sche-
matically) at the left side of all the EFs (Figure 1). Par-
ticularly important, in the context of this work, is the
reaction between IAA and the -SH residue of EF 5, to
which ubiquitin is linked prior to its transference to E2.
The effect of IAA (as it blocks reaction 9) results in a
displacement of all the enzyme forms (EFs) of Figure 1
towards those above EF 5, with the subsequent disap-
pearance of EFs 6-11 and 15-17.
With respect to the effect of E2 on E1, E1 can also be
viewed as the first enzymatic step for the ubiquitination
of proteins and further degradation by the proteasome.
To simulate the whole ubiquitination process a hypo-
thetical reactant named Blot (from Blotting of ubiquitin)
has been introduced. Blot is the sum of ubiquitin carrier
proteins (E2), ubiquitin protein ligases (E3) and pro-
tein(s) to be ubiquitinated, and represents the destiny for
all the ubiquitin molecules activated by E1. To simulate
physiological conditions, Blot is supposed to be in large
excess over E1. The reaction between EF 11 and the
entity Blot has been named 22 and was considered in
rapid equilibrium (Figure 1).
Finally, the effect of the addition of PPase to the sys-
tem has been easily simulated by the following reaction,
assumed to have Michaelis-Menten kinetics:
PPase + P2 <———> PPaseP2 ———>PPase + 2 Pi
Thus, PPase hydrolyzing the P2 liberated in reaction 8
(between EFs 4-5) and 20 (between EFs 10-11) displaces the
equilibrium towards EF 5 and EF 11, respectively (Figure 1).
3.2. Mathematical Model
The mathematical model, a symbolic expression of the
enzyme reactions assumed above (Figure 1 and Tables 1
and 2), was developed with the help of the Mathematica
Program according to the following steps:
3.2.1. Application to the Rapid Equilibrium
Reactions Inside Boxes X, Y and Z
(Supplemental Data, Appendix A)
The concentrations of the enzyme forms in rapid equi-
librium were calculated following a similar procedure in
each one of the Boxes: 1) each dissociation constant was
equalled to its corresponding value according to the sub-
strates and products involved; 2) the sum of the EFs
contained in Boxes X, Y and Z were equalled to X, Y
and Z, respectively; 3) the values of the 19 EFs to be
calculated (5 in Box X; 10 in Box Y and 4 in Box Z)
were requested with the command “Solve” of the
Mathematica Program (Supplemental data, Appendix A).
The rather cumbersome resulting equations, were disen-
tangled with the command “Simplify” and used in the
following step.
3.2.2. Steady State Reactions between Boxes X-Y and
Y-Z (Supplemental Data, Appendix B)
The resulting equations for the 10 EFs involved in the
steady state reactions were used to determine the actual
net velocities: Vp (between EFs 3 and 4); VP (between
EFs 13 and 14); VUp (between EFs 9 and 10); VUP
(between EFs 16 and 17); Ve (between EF 18 and 1) and
VB (between EFs 19 and 5). The velocities Ve and VB
were also included to cope with situations described
below, where the presence of dithiothreitol and E2 are
contemplated. Those six velocities (Vp, VP, VUp, VUP,
Ve and VB), were calculated as functions of the concen-
trations of EFs (as determined in Appendix A), the rate
constants (k1-k8, k10, k12), and taking into account the
forward (towards the synthesis of EF 11) and the reverse
reactions (Supplemental data, Appendix B, a). In part b
of Appendix B, the values of the 19 enzyme forms cal-

278 F. J. López-Cánovas et al. / J. Biomedical Science and Engineering 3 (2010) 274-284
culated in Appendix A are presented; note that these
values are grouped into two sections: 1) comprising
those values directly involved in the steady state situa-
tion, and 2) the values implicit in the anterior formulas
and needed for their solutions. In part c of Appendix B
the statements needed for the solution of the equations
are given: the total enzyme is defined as the sum of the
amount of enzyme in Boxes X, Y and Z; by application
of the steady state treatment suggested by Cha to the
diagram of reactions (Figure 1), the net flux between
boxes X and Y (VP + Vp-Ve) and between boxes Y and
Z (VUP + VUp-VB) is set equal to zero and, finally, the
unknowns to be solved are listed.
3.2.3. Ordinary Differential Equations System
(Supplemental Data, Appendix C)
The changes in the concentration of reactants (or even of
EFs) with the incubation time can be calculated with a
system of differential equations performed with the
Command “NDSolve” of the Mathematica Program,
once the expression of the velocities are known. The
syntax for this procedure admits many variants depend-
ing on the entity to be clarified. As an example, changes
in the concentrations of ATP, p4A, P3, P2, AMP, Blot or
BlotUb are presented in Supplemental data, Appendix C.
The Program admits other requested variants. The pa-
rameter values, initial assay conditions, and time of the
reaction must also be included. Concerning the parame-
ter values, two Procedures have been employed: Com-
prehensive and Simplified. The Comprehensive Proce-
dure allows the theoretical calculation of all the variables
of the system (19 EFs) as a function of: a) the total
amount of E1, b) the value of the 15 dissociation con-
stants and of the equilibrium constant yue, c) the value
of the 10 rate constants, and d) the concentration of the
reactants. This can be contemplated as an ideal scenery,
helpful for example, to handle reactions that can not be
performed experimentally, to investigate the role of each
constant on the system and to calculate the concentra-
tions of EFs and of the reactants under different experi-
mental conditions, etc. However, given the scarcity of
available experimental data, we considered it more con-
venient to introduce the Simplified Procedure (Table 2)
with the following assumptions: the dissociation con-
stant values for the binding of ATP, p4A, P2, P3, Ub,
AMP to any EF were set equal for each substrate, irre-
spective of the enzyme form (EFs) to which they bind
(Figure 1, Tables 1 and 2); the values of the dissociation
constants were taken from the literature, calculated as
the average of different reported values (when this was
the case) or tuned to fit the experimental results when no
data on a particular constant had been reported (Tables 1
and 2); the constant UzueB (dissociation constant be-
tween EF 11 and EF 19 (Figure 1) was chosen arbitrar-
ily as equal to 33 mM, since Blot is an hypothetical sub-
strate that represents the sum of E2 + E3 + proteins
(theoretically considered in large excess over E1); ii) the
rate constants of each one of the pairs (k1, k3), (k2, k4),
(k5, k7) and (k6, k8) were given the same value, as they
correspond to similar catalyzed reactions (Table 2); from
some experimental data [3,4] it can be deduced that the
values of (k1, k3) and (k2, k4) are 75% of those of (k5,
k7) and (k6, k8), respectively (Table 1 and 2) (Figure 1);
finally, a previous study [4] specifically calculated that
k7/k8 = 0.16; rate constant k5 was tuned to 0.13 s-1; rate
constant k12 was arbitrarily made equal to 3.3 s-1, as we
only wanted to compare the effect of different assay
conditions in the ubiquitination rate of Blot. All these
data are sufficient to fix one of the eight rate constants,
allowing the rest of the seven constants to be calculated
automatically by the program
3.3. Experimental Test of the Mathematical
Model
Once the mathematical model was established and sim-
plified, it was critical to confront it with the experimen-
tal results. As the mathematical scanning of the plethora
of experimental results available on E1 would be beyond
the scope of the present study, only the reactions taking
place in the presence of ubiquitin, ATP, p4A and P3 and
the influence of DTT, IAA, pyrophosphatase and Blot
(E2 + E3 + proteins) on these reactions are considered.
The advantage of P3 over P2 concerning the evaluation
of the experimental results should be stressed. Whereas
in the presence of ATP (±P2) synthesis or degradation of
ATP is observed [5] (i.e. no new compound is synthe-
sized and the reaction could be studied mainly using
radioactive substrates), in the presence of ATP (±P3) the
rate of synthesis of a new compound (p4A) can be used
as a tool to follow the course of the reaction.
3.3.1. Effect of Dithiothreitol (DTT)
According to the experimental findings reported by Haas
[6], the effect of DTT has been here mathematically re-
produced through the rapid equilibrium binding of DTT
to EF 6, consequent breakage of the thioester bond be-
tween Ub and a cysteine located in the U region of the
enzyme, formation of EF 1 and final liberation of AMP,
DTT and Ub to the medium (Figure 1). The effect of
DTT is theoretically clear: the synthesis of AMP from
ATP is produced and AMP is liberated irreversibly to the
reaction medium with displacement of the reactions to-
ward the enzyme forms located above EF 6 in the
scheme shown in Figure 1; the synthesis of p4A takes
place both through reaction 3, between EF 12 and EF 1
(Box X), and through reaction 14, between EF 15 and
EF 7 (Box Y). As a consequence of the disappearance of
the enzyme forms located below EF 6 by the effect of
DTT, changes in the rate of synthesis of p4A in the pres-
ence of DTT would be indicative of the relative rate of
synthesis of p4A by reaction 6 (between Boxes X-Y)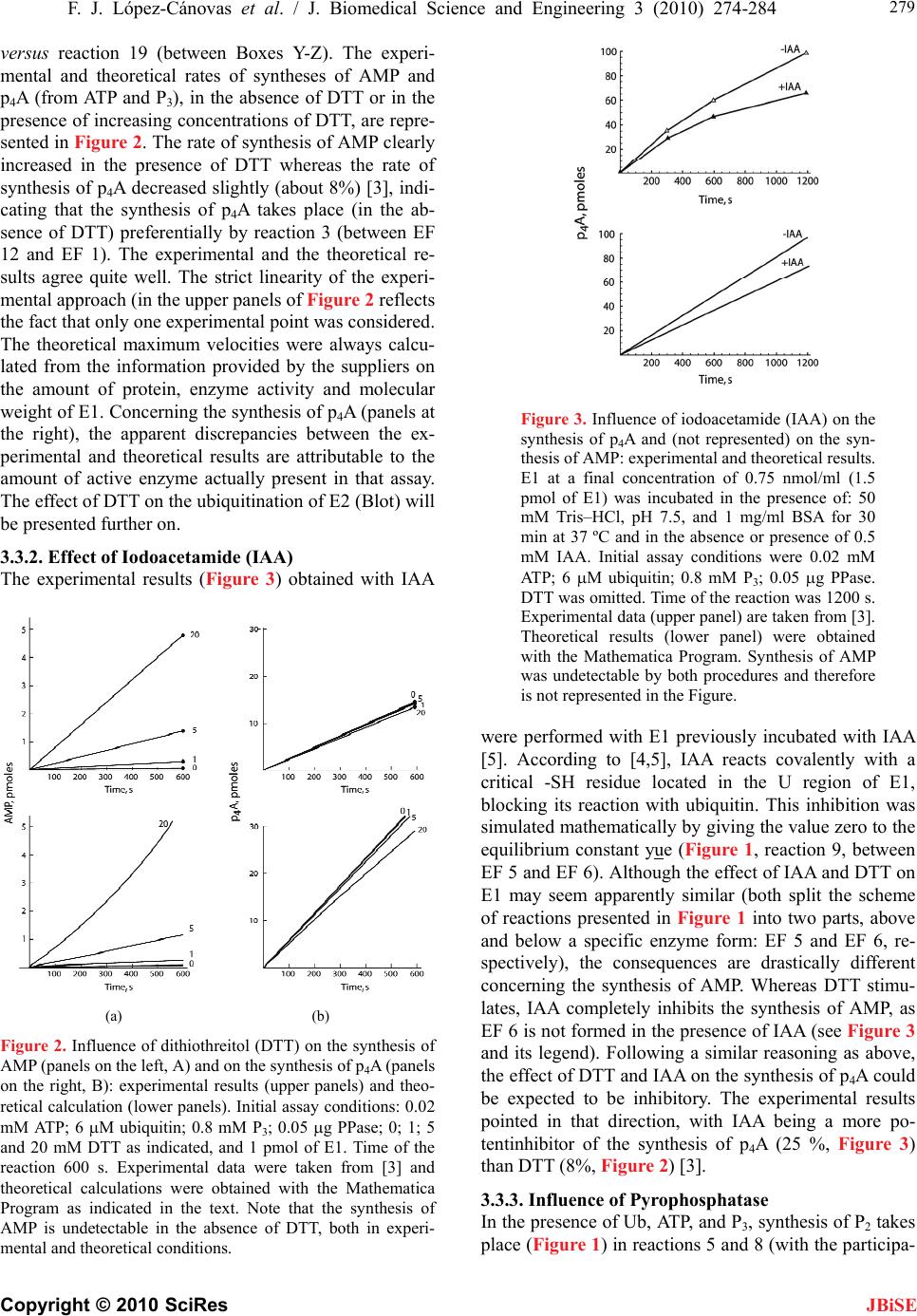

F. J. López-Cánovas et al. / J. Biomedical Science and Engineering 3 (2010) 274-284
279
JBiSE
versus reaction 19 (between Boxes Y-Z). The experi-
mental and theoretical rates of syntheses of AMP and
p4A (from ATP and P3), in the absence of DTT or in the
presence of increasing concentrations of DTT, are repre-
sented in Figure 2. The rate of synthesis of AMP clearly
increased in the presence of DTT whereas the rate of
synthesis of p4A decreased slightly (about 8%) [3], indi-
cating that the synthesis of p4A takes place (in the ab-
sence of DTT) preferentially by reaction 3 (between EF
12 and EF 1). The experimental and the theoretical re-
sults agree quite well. The strict linearity of the experi-
mental approach (in the upper panels of Figure 2 reflects
the fact that only one experimental point was considered.
The theoretical maximum velocities were always calcu-
lated from the information provided by the suppliers on
the amount of protein, enzyme activity and molecular
weight of E1. Concerning the synthesis of p4A (panels at
the right), the apparent discrepancies between the ex-
perimental and theoretical results are attributable to the
amount of active enzyme actually present in that assay.
The effect of DTT on the ubiquitination of E2 (Blot) will
be presented further on.
3.3.2. Effect of Iodoacetamide (IAA)
The experimental results (Figure 3) obtained with IAA
(a) (b)
Figure 2. Influynthesis of
mental and theoretical conditions.
ence of dithiothreitol (DTT) on the s
AMP (panels on the left, A) and on the synthesis of p4A (panels
on the right, B): experimental results (upper panels) and theo-
retical calculation (lower panels). Initial assay conditions: 0.02
mM ATP; 6 M ubiquitin; 0.8 mM P3; 0.05 g PPase; 0; 1; 5
and 20 mM DTT as indicated, and 1 pmol of E1. Time of the
reaction 600 s. Experimental data were taken from [3] and
theoretical calculations were obtained with the Mathematica
Program as indicated in the text. Note that the synthesis of
AMP is undetectable in the absence of DTT, both in experi-
Figure 3. Influence of iodoacetamide (IAA) on the
synthesis of p4A and (not represented) on yn-
wereincubated with IAA
the s
thesis of AMP: experimental and theoretical results.
E1 at a final concentration of 0.75 nmol/ml (1.5
pmol of E1) was incubated in the presence of: 50
mM Tris–HCl, pH 7.5, and 1 mg/ml BSA for 30
min at 37 ºC and in the absence or presence of 0.5
mM IAA. Initial assay conditions were 0.02 mM
ATP; 6 M ubiquitin; 0.8 mM P3; 0.05 g PPase.
DTT was omitted. Time of the reaction was 1200 s.
Experimental data (upper panel) are taken from [3].
Theoretical results (lower panel) were obtained
with the Mathematica Program. Synthesis of AMP
was undetectable by both procedures and therefore
is not represented in the Figure.
performed with E1 previously
[5]. According to [4,5], IAA reacts covalently with a
critical -SH residue located in the U region of E1,
blocking its reaction with ubiquitin. This inhibition was
simulated mathematically by giving the value zero to the
equilibrium constant yue (Figure 1, reaction 9, between
EF 5 and EF 6). Although the effect of IAA and DTT on
E1 may seem apparently similar (both split the scheme
of reactions presented in Figure 1 into two parts, above
and below a specific enzyme form: EF 5 and EF 6, re-
spectively), the consequences are drastically different
concerning the synthesis of AMP. Whereas DTT stimu-
lates, IAA completely inhibits the synthesis of AMP, as
EF 6 is not formed in the presence of IAA (see Figure 3
and its legend). Following a similar reasoning as above,
the effect of DTT and IAA on the synthesis of p4A could
be expected to be inhibitory. The experimental results
pointed in that direction, with IAA being a more po-
tentinhibitor of the synthesis of p4A (25 %, Figure 3)
than DTT (8%, Figure 2) [3].
3.3.3. Influence of Pyrophosphatase
In the presence of Ub, ATP, and P, synthesis of P2 takes
ith the participa-
3
place (Figure 1) in reactions 5 and 8 (w

280 F. J. López-Cánovas et al. / J. Biomedical Science and Engineering 3 (2010) 274-284
rformed by allowing a complete
d [a-32P]p4A in
ce of only ATP and ubiquitin, the enzyme
teady state situation where only
action 22 between EF 11
an
JBiSE
tion of EFs 3-5) and in reactions 18 and 20 (with par-
ticipation of EFs 9-11); P2 is a substrate for the synthesis
of ATP in the same reactions as above, acting in the re-
verse direction. In the presence of PPase, P2 is degraded
and reactions 8 and 20 cannot proceed in the reverse
direction (Figure 4). Consequently, in the presence of
PPase and P3 the synthesis of p4A is favored, by displace-
ment of the E1 cycle towards the left part of Figure 1,
i.e. toward the synthesis of p4A. Previous results from
this laboratory [3] had shown that the addition of PPase
to a reaction mixture containing P3, almost doubled the
rate of synthesis of p4A and slightly inhibited the synthe-
sis of AMP. The theoretical and experimental results on
the influence of PPase on the synthesis of AMP and p4A
are shown in Figure 4.
3.3.4. p4A as Substrate of the Reaction
This experiment was pe
transformation of [a-32P]ATP into labele
the presence of Ub, P3 and PPase [3]. Further incubation
of this reaction mixture converted gradually the synthe-
sized p4A into AMP thanks to the effect of DTT. The ex-
perimental and theoretical results are shown in Figure 5,
demonstrating that p4A is a substrate for the synthesis of
AMP through EFs 12-14, 5, 6, 18 and 1. In this way,
when the final equilibrium is reached, AMP is the only
destiny for all the ATP initially present in the assay mix-
ture. The small differences between the experimental
and theoretical results might be related to the inactiva-
tion of the enzyme after prolonged times of incubation
(Figure 5).
3.3.5. Influence of E2
In the presen
catalyzes a rapid pre-s
two equivalents of ATP per equivalent of enzyme are
hydrolyzed [4]. The hydrolysis of ATP can be stimulated
by the addition of P3 (as in previous sections) or by the
addition of an ubiquitin acceptor (Figure 1). This last
situation is here simulated by the addition of Blot, a
mixture of E2 + E3 + proteins, representing a sink for
the activated ubiquitin. The main reaction in the pres-
ence of Blot is represented by:
UbSEAMPUb (EF 11) + Blot <—> UbSEAMPUbBlot (EF 19)
—> HSEAMPUb (EF 5)+ BlotUb
These steps have been simulated by one reversible re-
action in rapid equilibrium (re
d EF 19) and one reaction in steady state (VB). This
last reaction (17) is considered irreversible because of
the physiological large excess of (E2 + E3 + proteins)
over E1 (Figure 1). The complete cycle for the hydroly-
sis of ATP in the presence of Blot is composed of reac-
tions 22, 17, 9-12, 18, 20 (Figure 1). The influence of
Blot (at 0, 0.5, 1, 2, 5, 15 mM) on the reaction catalyzed
(a) (b)
Figure 4. Influence of PPase on the synthesis of AMP
(left-hand panels A) and pA ight-hand panels, B): experi-
mental and titions: 0.02
4
heoretical results. Initial assay cond
(r
mM ATP; 6 M Ub; 0.8 mM P3; 20 mM DTT; 1.5 pmol E1 and,
when indicated, 0.05 g PPase. Reaction time: 900 s. Experi-
mental data were taken from [3] and represented in the upper
part of both panels. The theoretical results are represented in
the lower panels.
(a) (b)
Figure 5. Adenosine 5’-tetraphosphate (p4A) as substrate for
the synthesis of AMP: experental and theoretical results.
Initial assay conditions: 0.04 m ATP; 12 M Ub; 0.8 mM P3;
0.05 μg PPaseaction time
earance of ATP in-
with increasing concentrations of Blot, with an
apparent activation constant of about 1.5 mM for Blot in
im
M
e; 2 mM DTT and 4 pmol E1. The r
was increased to 7200 s (2 hours) in order to consume all the
ATP in the assay. In this way, the synthesis and posterior deg-
radation of p4A towards formation of AMP can be observed, as
a function of incubation time. Experimental data were taken
from [3] and represented in the upper part of both panels.
Theoretical results obtained for the synthesis of AMP and p4A
are represented in the lower panels.
by E1 is represented in Figure 6 panels a and b. In the
absence of Blot changes in the concentration of ATP, or
synthesis of AMP (not represented) are undetectable
gure 6 (a)); the rate of disapp(Fi
creased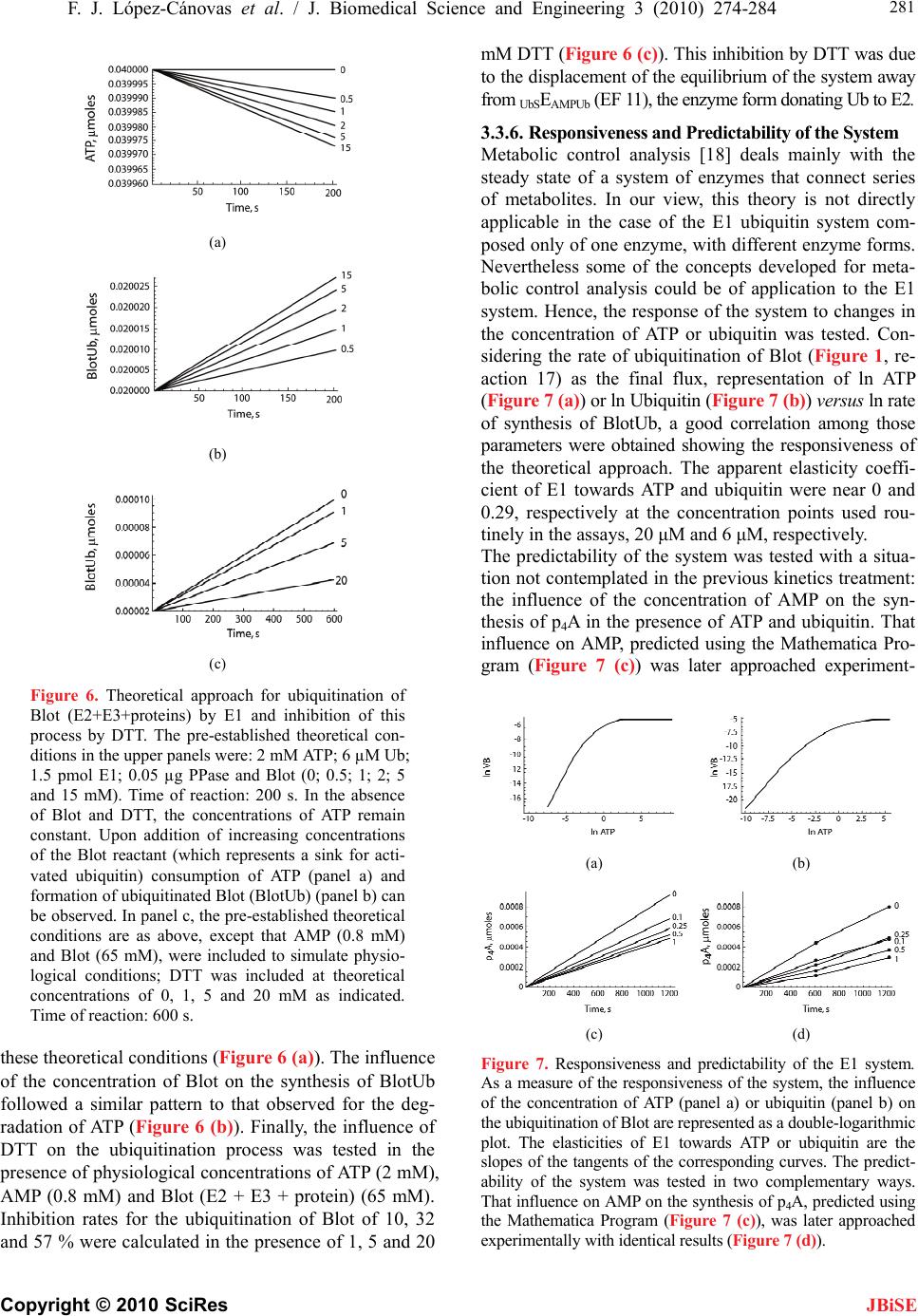

F. J. López-Cánovas et al. / J. Biomedical Science and Engineering 3 (2010) 274-284
281
JBiSE
(a)
(b)
(c)
Figure 6. Theoretical approach for ubiquitination of
Blot (E2+E3+proteins) by E1 and inhibition of this
process by DTT. The pre-established theoretical con-
ditions in the upper panels were: 2 mM ATP; 6 µM Ub;
1.5 pmol E1; 0.05 µg PPase and Blot (0; 0.5; 2; 5
and 15 mM). Time of ren: 200 s. In the absence
thes ce
of tUb
foll g-
rad of
DTn process was tested in the
-
; 1
actio
of Blot and DTT, the concentrations of ATP remain
constant. Upon addition of increasing concentrations
of the Blot reactant (which represents a sink for acti-
vated ubiquitin) consumption of ATP (panel a) and
formation of ubiquitinated Blot (BlotUb) (panel b) can
be observed. In panel c, the pre-established theoretical
conditions are as above, except that AMP (0.8 mM)
and Blot (65 mM), were included to simulate physio-
logical conditions; DTT was included at theoretical
concentrations of 0, 1, 5 and 20 mM as indicated.
Time of reaction: 600 s.
e theoretical conditions (Figure 6 (a)). The influen
he concentration of Blot on the synthesis of Blot
owed a similar pattern to that observed for the de
ation of ATP (Figure 6 (b)). Finally, the influence
T on the ubiquitinatio
presence of physiological concentrations of ATP (2 mM),
AMP (0.8 mM) and Blot (E2 + E3 + protein) (65 mM).
Inhibition rates for the ubiquitination of Blot of 10, 32
and 57 % were calculated in the presence of 1, 5 and 20
mM DTT (Figure 6 (c)). This inhibition by DTT was due
to the displacement of the equilibrium of the system away
from UbSEAMPUb (EF 11), the enzyme form donating Ub to E2.
3.3.6. Responsiveness and Predictability of the System
Metabolic control analysis [18] deals mainly with the
steady state of a system of enzymes that connect series
of metabolites. In our view, this theory is not directly
applicable in the case of the E1 ubiquitin system com-
posed only of one enzyme, with different enzyme forms.
Nevertheless some of the concepts developed for meta
bolic control analysis could be of application to the E1
system. Hence, the response of the system to changes in
the concentration of ATP or ubiquitin was tested. Con-
sidering the rate of ubiquitination of Blot (Figure 1, re-
action 17) as the final flux, representation of ln ATP
(Figure 7 (a)) or ln Ubiquitin (Figure 7 (b)) versus ln rate
of synthesis of BlotUb, a good correlation among those
parameters were obtained showing the responsiveness of
the theoretical approach. The apparent elasticity coeffi-
cient of E1 towards ATP and ubiquitin were near 0 and
0.29, respectively at the concentration points used rou-
tinely in the assays, 20 μM and 6 μM, respectively.
The predictability of the system was tested with a situa-
tion not contemplated in the previous kinetics treatment:
the influence of the concentration of AMP on the syn-
thesis of p4A in the presence of ATP and ubiquitin. That
influence on AMP, predicted using the Mathematica Pro-
gram (Figure 7 (c)) was later approached experiment-
(a) (b)
(c) (d)
Figure 7. Responsiveness and predictability of the E1 system.
As a measure of the responsiveness of the system, the influence
of the concentration of ATP (panel a) or ubiquitin (panel b) on
the ubiquitination of Blot are represented as a double-logarithmic
plot. The elasticities of E1 towards ATP or ubiquitin are the
slopes of the tangents of the corresponding curves. The predict-
ability of the system was teste in two complementary ways.
That influence on AMP on the nthesis of pA, predicted using
the Mathematic er approached
experimentally with identical results (Figure 7 (d)).
d
sy 4
a Program (Figure 7 (c)), was lat

282 F. J. López-Cánovas et al. / J. Biomedical Science and Engineering 3 (2010) 274-284
he simplifications in-
eneral comment
these methods
rent as-
pe
-
bo
te
strate of the enzyme has greatly helped to follow the
JBiSE
tally with identical results (Figure 7 (d)). In both cases
AMP accelerated the rate of synthesis of p4A. The
physiological implications of this finding will be ex-
plored elsewhere in another study.
4. CONCLUDING REMARKS
The above results may be considered from different per-
spectives. The ubiquitin activating enzyme E1 has been
treated as a complex enzyme system comprising 8 reac-
tants, 2 inhibitors/effectors, and 19 enzyme forms (EFs)
(Figure 1). Calculation of the rate equations of this type
of reactions has been approached with the King and
Altman method [19] and/or with t
troduced in [20,21] and in [17]. For a g
on these procedures, see [22]. Although
may appear mathematically simple they present great
difficulties due to the potential errors introduced during
the process of manual operations. Fortunately, with the
introduction of computer methods of calculation, per-
formed here with the Mathematica Program [15], treat-
ment of the concerned equations has been greatly sim-
plified. The only difficulty is how to feed the computer
with the appropriate information. The simplifications
introduced by Cha [17] have been of great help for the
mathematical treatment of the postulated reactions cata-
lyzed by the ubiquitin activating enzyme, a system that
seemed to be particularly appropriated for this mathe-
matical treatment. Cha [17] postulated that when an en-
zyme-catalyzed reaction consists of more than one step,
and one or more portions of the whole reaction are sig-
nificantly faster than the over-all reaction, the partial
reactions in such segments have almost reached equilib-
rium when the over-all reaction reaches a steady state.
As shown in Figure 1, clusters of reactions of the E1
system involving binding of substrates were considered
in rapid equilibrium, were grouped in boxes X, Y and Z,
and treated as three single entities; another group of re-
actions involving modification of the bound substrates
were treated as in a steady state situation. Altogether, the
panorama is similar to the one presented by Cha to de-
velop his methodology [17]. In our view, other complex
enzyme situations can be approached in the same way,
and the kinetics treatment of E1, here shown, can be
taken as an example. Presently we are applying Cha’s
approach to the mathematical treatment of the signal
transductions involved in glycogen metabolism.
Although P3 and p4A are here exclusively considered
as a kinetic tool to unravel the set of reactions catalyzed
by E1, they also have physiological significance by
themselves. Inorganic polyphosphates are probably pre-
sent in every cell [23,24,25] and are particularly abun-
dant in yeast extracts where P3 and P4 have been de-
scribed at mM concentrations [23]. As previously
pointed out [3,26], the potential effects exerted by poly-
phosphates can be considered under two diffe
cts: Either caused by their presence at high concentra-
tion and frequently condensed in organelles or caused by
their occurrence at low concentration in different cellular
compartments. Although their role in the last case is not
clear, there is a widespread concern about the possibility
of polyphosphates playing more general and universal
functions in biology [23,24]. In the case of E1, it is dif-
ficult for us to envisage the physiological role of P3,
considering its high apparent Km value in the reactions
here described [3]. The occurrence of p4A has been de-
scribed in chromaffin granules of the adrenal medulla
[27], in skeletal and cardiac muscle [28,29], in the
aqueous humor of rabbits [30] and in yeast [31]. p4A has
been involved in yeast sporulation [31] and as a modu-
lator of cardiac vascular tone [29]. p4A could also indi-
rectly modulate the levels of Ap4A and Ap4N (nucleo-
tides with apparently elusive physiological roles [32,
33]), by inhibiting (Ki, nM) the activity of the (assymet-
rical) dinucleoside tetraphoshatase (EC 3.6.1.17) [34].
The present study can also be viewed as pertinent to
the so-called System Biology aiming to understand gen-
eral principles of the complexity of living cells [35,36,
37]. This complexity is so astonishing that restricted
approaches to simple networks could pave the way for
the uncovering of some general principles governing
higher organisms. Examples are the study of signal
transductions, gene expression, evolution and selfor-
ganization, understanding the cell cycle, fluxes in meta
lic pathways, neural networks, modeling of biological
processes, etc. Study of metabolic processes is one of the
main topics of modern System Biology and the work
presented here can be considered as an example on how
the conjugation of a theoretical and an experimental ap-
proach to a particular topic, may help to jump from a
mere reductionism to a more global vision of that problem.
The present study has to be considered as an example
rather than a framework for the mathematical treatment
of complex biological systems. This work may be im-
portant to understand the ubiquitin proteasome system
itself. This system is the center of a vast arrangement of
cellular processes including: cell cycle, transcription
control, regulation of enzyme levels, antigen presenta-
tion, rate for disposing of unfolded or damaged proteins
and controlling life span of regulatory proteins, etc. Al-
ration of the ubiquitin proteasome system is also re-
sponsible for the genesis of malignant diseases and neu-
rodegenerative disorders.
In summary, as shown above this work deals only
with the ubiquitin activating enzyme (E1). The reactions
catalyzed by E1 are well known from studies developed
by Haas, Ciechanover, Hersko, Rose and others [4,5,6],
mainly in crude extracts. The present report, greatly in-
spired by their work, has been carried out with purified,
and commercially available E1. The use of P3 as sub-

F. J. López-Cánovas et al. / J. Biomedical Science and Engineering 3 (2010) 274-284
283
been used for that purpose:
C
and th
e forms approached with a
JBiSE
steps of the intermediary reactions (see above). Two
mathematical methods have
omprehensive and Simplified methods. Some of the
kinetic constants involved in these reactions, implicit in
the Comprehensive Method, are not yet known and have
been tuned; in addition, a simplification of the Compre-
hensive method has been introduced. The corner-stone
of the mathematical treatment of any of these systems is
that the experimental and the theoretical results must be
consistent. When this is so, the theoretical approach can
be used with more confidence and new questions can be
theoretically proposed and contrasted with experimental
results. In this regard, the effect of potential drugs acting
on E1 [38] can be explored in the presence of ATP, P3
and ubiquitin, and the experimental results contrasted
with the theoretical approach developed here aiming to
pinpoint their precise mode of drug action.
5. CONCLUSSIONS
The aim of this work was to investigate the reactions
catalyzed by the ubiquitin activating enzyme (E1) using
ubiquitin, ATP, adenosine tetraphosphate (p4A), pyro-
phosphate, tripolyphosphate, and ubiquitin activating
enzyme (E2) as substrates and iodoacetamide dithio-
threitol, as inhibitors of the reaction. A total of 19 dif-
ferent hypothetical enzyme forms (EF) of E1 and 22
different enzyme reactions were establishede
equations relating the enzym
system of ordinary differential equations and solved with
the help of the Mathematica Program. This study can be
view a) as a way to treat a complex biological system, b)
as a possibility to follow the steps of the intermediate
reactions and the theoretical concentrations of the inter-
mediate enzyme forms; c) as a method to study the ef-
fects of possible inhibitors on E1 and by extrapolation
on the proteasome system itself. Note: the Supplemental
Data is available on request from Antonio Sillero at:
6. ACKNOWLEDGEMENTS
This investigation was supported by grants from Dirección General de
Investigación Científica y Técnica (BFU 2008-00666 and BFU2009-
08977). We thank Anabel de Diego, Antonio Fernández and Javier
Pérez for very capable technical assistance and Professor José Gon-
zalez Castaño and Dr. Gabriela Morreale de Escobar for helpful sug-
gestions and critical reading of the manuscript.
REFERENCES
[1] Sillero, A. and Günther Sillero, M.A. (2000) Synthesis of
by firefly lucif
tics, 87,
Specific synthesis of adenosine(5’)tetraphospho(5’)
Silles, E. and Sillero,
vating enzyme E1. FEBS Letter, 579,
Portland Press, MiamiBrookfield.
erasdinucleoside polyphosphates catalyzed
and several ligases. Pharmacology and Therapeu
e
equations for enzyme-catalyzed reactions under the rapid
equilibrium assumption or combined assumptions of
equilibrium and steady state. Journal of Biological
Chemistry, 243, 820-825.
[18] Fell, D. (1997) Understanding the control of metabolism,
91-102.
[2] Ortiz, B., Sillero, A. and Günther Sillero, M.A. (1993)
nucleoside and adenosine(5’)oligophospho(5’)adenosine
(n > 4) catalyzed by firefly luciferase. European Journal
of Biochemistry, 212, 263-270.
3] Günther Sillero, M.A., de Diego, A., [
A. (2005) Synthesis of (d
the ubiquitin acti
i)nucleoside polyphosphates by
6223-6229.
[4] Haas, A.L. and Rose, I.A. (1982) The mechanism of
ubiquitin activating enzyme. A kinetic and equilibrium
analysis. Journal of Biological Chemistry, 257, 10329-
10337.
[5] Haas, A.L., Warms, J.V., Hershko, A. and Rose, I.A.
(1982) Ubiquitin-activating enzyme. Mechanism and role
in protein-ubiquitin conjugation. Journal of Biological
Chemistry, 257, 2543-2548.
Haas, A.L., Warms, J.V. and Ro[6] se, I.A. (1983) Ubiquitin
adenylate: Structure and role in ubiquitin activation. Bio-
chemistry, 22, 4388-4394.
[7] Hershko, A. and Ciechanover, A. (1998) The ubiquitin
system. Annual review of biochemistry, 67, 425-479.
[8] Baumeister, W., Walz, J., Zuhl, F. and Seemuller, E.
(1998) The proteasome: Paradigm of a self-compart-
mentalizing protease. Cell, 92, 367-380.
Ciechan[9] over, A., Orian, A. and Schwartz, A.L. (2000)
The ubiquitin-mediated proteolytic pathway: Mode of
action and clinical implications. Journal of Cell Bio-
chemistry Supply, 34, 40-51.
Glickman, M.H. and Ciechanov[10] er, A. (2002) The ubiq-
uitin-proteasome proteolytic pathway: Destruction for the
sake of construction. Physiological reviews, 82, 373–428.
Lee, I. and Schindelin, H. ([11] 2008) Structural insights into
E1-catalyzed ubiquitin activation and transfer to conju-
gating enzymes. Cell, 134, 268-278.
[12] Selivanov, V.A., Puigjaner, J., Sillero, A., Centelles, J.J.,
Ramos-Montoy ante, M. (2004) a, A., Lee, P.W. and Casc
An optimized algorithm for flux estimation from iso-
topomer distribution in glucose metabolites. Bioinfor-
matics, 20, 3387-3397.
[13] Torrecilla, A., Marques, A.F., Buscalioni, R.D., Oliveira,
J.M., Teixeira, N.A., Atencia, E.A., Günther Sillero, M.A.
and Sillero, A. (2001) Metabolic fate of AMP, IMP, GMP
and XMP in the cytosol of rat brain: An experimental and
theoretical analysis. Journal of Neurochemistry, 76,
1291-1307.
[14] Osorio, H., Carvalho, E., del Valle, M., Günther Sillero,
M.A., Moradas-Ferreira, P. and Sillero, A. (2003) H2O2,
but not menadione, provokes a decrease in the ATP and
an increase in the inosine levels in Saccharomyces cere-
visiae. An experimental and theoretical approach. Euro-
pean Journal of Biochemistry, 270, 1578-1589.
[15] Wolfram, S. (1996) The Mathematica Book. Cambridge
University Press, Cambridge.
[16] Segel, I.H. (1975) Enzyme kinetics: Behavior and analy-
sis of rapid equilibrium and steady state enzyme systems.
Wiley, New York.
[17] Cha, S. (1968) A simple method for derivation of rate

284 F. J. López-Cánovas et al. / J. Biomedical Science and Engineering 3 (2010) 274-284
eactions.
962) Kinetic formulations
and Goldstein, B.N. (1966) Allosteric
, V.M. (1983) Polyphosphate
by poly(A)
te (ApA), ATP and catechola-
nd Cooper, C. (1966) Studies on the occur-
d characteri-
normotensive rabbit eyes. Journal
revisiae is accompanied by synthesis of
e? Pharmacology and Therapeutics, 87, 73-89.
[34]
sinetetraphosphatase from rat liver:
-
hein.
ibitors of ubiquitin-activating
JBiSE
[19] King, E.L. and Altman, C. (1956) A schematic method
for deriving the rate laws for enzyme-catalyzed r
The Journal of Physical Chemistry, 60, 1357-1378.
[20] Wong, J.T. and Hanes, C.S. (1
for enzymic reactions involving two substrates. Canadian
journal of biochemistry and Physiology, 40, 763-804.
[21] Volkenstein, M.V.
enzyme models and their analysis by the theory of graphs.
Biochimica et Biophysica Acta, 115, 471-477.
[22] Cornish-Bowden, A. (1995) Fundamental of enzyme kinet-
ics. Portland Press, London.
[23] Kulaev, I.S. and Vagabov
metabolism in micro-organisms. Advances in Microbial
Physiology, 24, 83-171.
[24] Wood, H.G. and Clark. J.E. (1988) Biological aspects of
inorganic polyphosphates. Annual Review of Biochemistry,
57, 235-260.
[25] Kornberg, A., Rao, N.N. and Ault-Riche, D. (1999) Inor-
ganic polyphosphate: A molecule of many functions.
Annual Review of Biochemistry, 68, 89-125.
[26] Günther Sillero, M.A., de Diego, A., Silles, E., Osorio, H.
and Sillero, A. (2003) Polyphosphates strongly inhibit the
tRNA dependent synthesis of poly(A) catalyzed
istr
polymerase from Saccharomyces cerevisiae. FEBS Letter,
550, 41-45.
[27] Günther Sillero, M.A., Del Valle, M., Zaera, E., Mich-
elena, P., Garcia, A.G. and Sillero, A. (1994) Diadenosine
5’,5’’-P1,P4-tetraphospha 4
mine content in bovine adrenal medulla, chromaffin
granules and chromaffin cells. Biochimie, 76, 404-409.
[28] Small, G.D. a
rence and biosynthesis of adenosine tetraphosphate. Bio-
chemistry, 5, 26-33.
[29] Westhoff, T., et al. (2003) Identification an
zation of adenosine 5’-tetraphosphate in human myocar-
dial tissue. The Journal of Biological Chemistry, 278,
17735-17740.
[30] Pintor, J., Pelaez, T. and Peral, A. (2004) Adenosine
tetraphosphate, Ap4, a physiological regulator of in-
traocular pressure in
of Pharmacology and Experimental Therapeutics, 308,
468-473.
[31] Jakubowski, H. (1986) Sporulation of the yeast Sac-
charomyces ce
adenosine 5’-tetraphosphate and adenosine 5’-pentapho-
sphate. Proceedings of the National Academy of Sciences,
83, 2378-2382.
[32] McLennan, A.G. (2000) Dinucleoside polyphosphates-
friend or fo
[33] Mc Lennan, A.G., et al. (2001) Recent progress in the
study of the intracellular functions of diadenosine poly-
phosphates. Drug Development Research, 52, 249-259.
Lobatón, C.D., Vallejo, C.G., Sillero, A. and Sillero, M.A.
(1975) Diguano
Acitivity on diadenosine tetraphosphate and inhibition by
adenosine tetraphosphate. European journal of Biochem
y, 50, 495-501.
[35] Alon, U. (2006) An introduction to system biology. De-
sign principles of biological circuits. CRC Press, Taylor
& Francis Group, London.
[36] Klipp, E., Herwig, R., Kowald, A., Wierling, C. and Le-
hrach, H. (2005) System biology in practice. Concepts,
implementation and application, Wiley-VCH Verlag
GmbH & Co., Wein
[37] Fell, D. (1997) Undersatnding the control of metabolism,
Portland Press, London.
[38] Yang, Y., et al. (2007) Inh
enzyme (E1), a new class of potential cancer therapeutics.
Cancer Research, 67, 9472-9481.