J. Biomedical Science and Engineering, 2010, 3, 253-261
doi:10.4236/jbise.2010.33034 Published Online March 2010 (http://www.SciRP.org/journal/jbise/
JBiSE
).
Published Online March 2010 in SciRes. http://www.scirp.org/journal/jbise
Extracting a seizure intensity index from one-channel EEG
signal using bispectral and detrended fluctuation analysis
Pegah Tayaranian Hosseini1*, Reza Shalbaf 2*, Ali Motie Nasrabadi3
1Biomedical Engineering Department, Amirkabir University of Technology, Tehran, Iran;
2Electrical Engineering Department, Iran University of Science and Technology, Tehran, Iran;
3Biomedical Engineering Department, Faculty of Engineering, Shahed University, Tehran, Iran.
Received 7 December 2009; revised 20 December 2009; accepted 28 December 2009.
ABSTRACT
Epilepsy is a medical condition that produces seizures
affecting a variety of mental and physical functions.
Seizures can last from a few seconds to a few minutes.
They can have many symptoms, from convulsions
and loss of consciousness to blank staring, lip
smacking, or jerking movements of arms and legs. If
early warning signals of an upcoming seizure (diag-
nosis of preictal period) are detected, proper treat-
ment can be applied to the patient to help prevent the
seizure. In this research, an epileptic disorder has
been divided into three subsets: Normal, Preictal
(just before the seizure), and Ictal (during seizure).
By using Detrended Fluctuation Analysis (DFA), Bis-
pectral Analysis (BIS), and Standard Deviation (SD)
three features from single-channel EEG signals have
been derived in the foresaid groups. A fuzzy classifier
is used to separate the three groups which can suc-
cessfully separate them with a separation degree of
100% and further a fuzzy inference engine is used to
extract a Seizure Intensity Index (SII) from the Elec-
troencephalogram (EEG) signals of the three differ-
ent states. One can apparently see the distinction of
SII amounts between the three states. It is more im-
portant when one remembers that these results are
just from single-channel EEG signal.
Keywords: Epilepsy; Fuzzy Inference Engine;
Bispectrum; Detrended Fluctuation Analysis
1. INTRODUCTION
Epilepsy is a brain disorder in which clusters of nerve
cells or neurons in the brain, sometimes, signal abnor-
mally. In epilepsy, the normal pattern of neuronal activity
becomes disturbed, causing strange sensations, emotions,
and behavior or sometimes convulsions, muscle spasms,
and loss of consciousness. Epilepsy is a disorder with
many possible causes. Epilepsy may develop because of
an abnormality in brain wiring, an imbalance of nerve
signaling chemicals called neurotransmitters, or some
combination of these factors. EEGs and brain scans are
common diagnostic tests for epilepsy.
Once epilepsy is diagnosed, it is important to begin
treatment as soon as possible. For about 80 percent of
those diagnosed with epilepsy, seizures can be controlled
with modern medicines and surgical techniques. Some
antiepileptic drugs can interfere with the effectiveness of
oral contraceptives. Scientists are studying potential an-
tiepileptic drugs with the goal of enhancing treatment for
epilepsy. Once a seizure is predicted, antiepileptic drugs
could be injected to prevent the seizure.
In this research, the brain situation of an epileptic pa-
tient has been divided into 3 states: Normal (normal
brain state), Preictal (just before the seizure), and Ictal
(during seizure). Here, a technique to calculate a two
digit index that can distinctly separate these three states
during patient monitoring is seeked: a two digit index
that can represent the brain state of the patient.
Bispectral (BIS) analysis is an advanced signal proc-
essing technique that quantifies quadratic nonlinearities
(phase-coupling) among the components of a signal.
There are only a few reports concerning the bispectrum
of electroencephalogram (EEG). Barnett et al. first re-
ported the bispectral analysis of EEG in 1971. Sigl and
Chamoun introduced the detailed principle and concept
of bispectral analysis in 1994. Ning and Bronzino re-
ported the changes of bispectrum of the rat EEG during
various vigilance states. Muthuswamy et al. reported the
bispectral analysis of burst patterns in EEG. This infor-
mation is represented in [1]. In [2] bispectrum is used to
predict epileptic seizures. Tallach et al. tried to monitor
seizures using bispectral index in [3] and Ye et al. repre-
sented an anesthesia index using bispectral analysis in
[4]. There are, therefore, not many researches concern-
ing bispectrum for seizure detection. This analysis has
been introduced in this article and it has been used to
extract a BIS feature. One can further see the application
*The two authors contributed equally to this work.

254 P. T. Hosseini et al. / J. Biomedical Science and Engineering 3 (2010) 253-261
of this feature in Seizure Intensity Index (SII) calculation.
Nonlinear dynamical analysis has emerged as a novel
method for the study of complex systems in the past few
decades. Besides BIS, a nonlinear technique called De-
trended Fluctuation Analysis (DFA) is introduced and
this method is used to derive another feature from sin-
gle-channel EEG for SII computation process. DFA was
invented by Peng [5] and established as an important
tool for the detection of long-range (auto-) correlations
in time series with non-stationarities. In [6] DFA is used
to extract a depth of anesthesia index. It is also used in
[7] to measure the depth of anesthesia. One of DFA’s
most important recent applications is in anesthesia index
detection while there is no significant record showing its
application in epileptic seizure detection or prediction.
These two features (BIS and DFA) are used separately
along with Standard Deviation (SD) to classify the three
mentioned groups in this research. A fuzzy classifier
with distinct characteristics is utilized to well classify the
three states. A fuzzy inference engine is further used to
produce a Seizure Intensity Index (SII).
Using the database of Andrzejak [8] and a leave-
Bone-out technique, we came to 100% separation be-
tween the three classes for SD and DFA combination and
98% for SD and BIS combination. We further extract the
mentioned index that can well represent the different
states of the brain especially in case of SD and DFA
combination. These results become more considerable
when we remember that the dataset includes single-
channel EEG signals. This means that monitoring of
seizure situation can be easily performed with a two-
electrode EEG recorder.
The outline of the paper is as follows: in the next sec-
tion, the complete information of the used database is
presented. Section 3 describes the algorithms applied on
the mentioned database. The results and a conclusion of
the whole article are represented in Sections 4 and 5,
respectively.
2. DATABASE
In this research, the data described in [8] is used, which
is publicly available. In this section, we restrict ourselves
to only a short description and refer to [8] for further
details. The complete dataset consists of five sets (de-
noted A-E), each containing 100 single-channels EEG
signals of 23.6s with sample frequency of 173.6Hz.
Sets A and B have been taken from surface EEG re-
cordings of five healthy volunteers with eyes open and
closed, respectively. Signals in two sets have been
measured in seizure-free intervals from five patients in
the epileptogenic zone (D) and from the hippocampal
formation of the opposite hemisphere of the brain (C).
Set E contains seizure activity, selected from all re-
cording sites exhibiting ictal activity. Sets A and B have
been recorded extra cranially whereas sets C, D, and E
have been recorded intra cranially.
In the present study, the three datasets (A, C, E) of the
complete database are classified.
3. PROPOSED ALGORITHMS
The major algorithms which are utilized in this study are
described in the following subsections. The explanations
are represented along with our specified amounts of the
parameters in the whole research.
3.1. Detrended Fluctuation Analysis
In the analysis of EEG data, different chaotic measures
such as correlation dimension, Lyapunov exponent and
entropy have been used in recent years. These method-
ologies have been under question for several reasons. In
general, the brain as a complex system is not expected to
produce an activity which can be described by a low
dimensional dynamic. Furthermore, if the existence of a
sufficiently low-dimensional attractor is assumed, for a
reliable estimation of the fractal dimension, a time series
must satisfy the requirements such as stationarity, a suf-
ficiently large number of data points, and a reasonable
signal-to-noise ratio. It is very improbable that these
necessities are simultaneously met in the case of the
EEG signal.
However, as the statistical characteristics of biological
signals often change with time, and are typically highly
irregular and non-stationary, analyses of such systems
are complicated. To overcome these limitations we have
focused on the long-range power-law correlations, which
have been discovered in a wide variety of systems, in-
cluding those that are physiological. The quantification
of power-law correlations, with a critical exponent, may
give useful information on understanding the properties
of the nonlinear dynamic systems. In this paper, we have
proposed an optimal nonlinear analysis algorithm for
processing the EEG signals without being concerned
about the non-stationarity and finite length of the signal.
The fractal-scaling exponents that quantify the power-
law correlations are computed by DFA which is known
for its robustness against nonstationarity in [6].
According to [6] and [9], the stepwise algorithm of
DFA is as follows:
1) n is set to 3.
2) 10s epoch of EEG signal x is considered. Its size N
is 10×173.6 samples.
3) The average of the epoch is subtracted from each
sample of the epoch.
4) An integral of the signal is calculated using (1):
 


j
i
ixjy
1
(1)

P. T. Hosseini et al. / J. Biomedical Science and Engineering 3 (2010) 253-261
255
JBiSE
5) y is divided into n-sample epochs without overlap-
ping. So y is divided into K=N/n epochs and each epoch
is named as yk.
6) The linear trend of yk (k = 1,…,K) is calculated and
named as yfit.
7) yfit is subtracted from yk and the variance of the re-
sulted amounts is calculated as (2):
  
 
n
ikiyiy
n
kF
1
2
fit
21
 (2)
8) The fluctuations of n is computed as the average of
variances using (3):
 
21
1
2
1






K
k
kF
k
nF (3)
9) n is increased one unit and the steps from 5 to 8 are
repeated till n = 30.
10) The curve of lg(F(n)) via lg(n) is plotted and the
slope of this curve is considered as the DFA feature of
the 10s epoch.
11) The next 10s epoch is extracted without overlap-
ping and the steps 3 to 10 are repeated till we get to the
end of EEG signal.
The steps explained above are shown consecutively in
Figure 1 and Figure 2. Figure 1(a) represents the origi-
nal signals, Figure 1(b) shows the integral of original
signals using (1), and Figure 1(c) displays the signals in
1(b) along with their linear trends (yk and yfit) for 50-
point epochs. Figure 2 represents the curves of Fn via n.
These slopes of these curves are the DFA features.
This should be noted that, in each 10s epoch, for dif-
ferent amounts of n, if the last epoch has fewer samples
than n, this epoch is eliminated and is not considered in
future calculations.
3.2. Bispectral Analysis
Bispectral (BIS) analysis is an advanced signal process-
ing technique that quantifies quadratic nonlinearities
(phase-coupling) among the components of a signal.
There are only a few reports concerning the bispectrum
of electroencephalogram (EEG) [1]. The number of arti-
cles concerning the bispectrum of EEG in seizure analy-
sis is rare [2,3]. In this paper, the BIS analysis is used to
derive a feature from single-channel EEG signal. This
feature is further used to produce an index for seizure
situation in epileptic patients.
Each bispectrum value is calculated as follows:

21
*
2121..,ffXfXfXffTP jjjj 


(4)
 


jjffTPffB 2121,, (5)
Complex numbers, X(f1), X(f2), and X(f1+f2) are power
spectrum components by FFT. X*(f) is the conjugate of
X(f). TPj is called triple product. The summation in (5) is
the heart of the bispectral analysis [1].
(a)
(b)
(c)
Figure 1. (a) Original EEG signals; (b) Integral of signals in
1(a); (c) the signals in 1(b) along with their linear trends for
50-point epochs.
For each group of signals (Normal, Preictal, and Ictal)
the bispectrum scheme was similar for different signals.
It means the coordinates of higher peaks were approxi-
mately in the same position for different signals in one
group.
Inspiring from [4], for each signal, the 10 higher
peaks are selected. Among these 10 peaks, the peaks that
have an amount more than 15% of the highest peak are
chosen. The Euclidean distances of the chosen peaks

256 P. T. Hosseini et al. / J. Biomedical Science and Engineering 3 (2010) 253-261
Figure 2. The Fn curves of the EEG signals of Figure 1(a) for
different n’s. Their slopes are the final DFA features.
from zero are calculated and summed together. The final
amount is considered as the BIS feature of that signal.
3.3. Fuzzy Inference Engine
In this section, we briefly describe the fuzzy classifica-
tion method based on fuzzy if-then rules proposed in
[10,11,12,13].
Designing membership functions (MF’s) is the fun-
damental stage in constructing a fuzzy classifier. MF’s
should partition the input space efficiently such that the
different subsets of training patterns can be well learned
by the classifier [13]. In the present study, input mem-
bership functions are designed with respect to the data
distribution pattern over each dimension (the box plots
of the obtained features are represented in Section 4).
Figure 3 shows the membership functions that were
used for BIS, DFA, and SD inputs. As described later,
the proposed fuzzy procedure has 2 inputs. Once the
inputs are DFA and SD and the other time they are BIS
and SD.
The proposed fuzzy rule-based classification system
consists of N fuzzy if-then rules each of which has a
form as in (6):
,,...,2,1 ,
... : 11
NjCFwithCisclassthenA
isxandandAisxIfRRule
jjjn
njj
 (6)
where Rj is the label of the j-th fuzzy if-then rule, Aj1,…,
Ajn are antecedent fuzzy sets on the input range, Cj is the
consequent class (i.e. one of the M given classes), and
CFj is the grade of certainty of the fuzzy if-then rule Rj .
There are two steps in the generation of fuzzy if-then
rules: specification of antecedent part and determination
of consequent class Cj and the grade of certainty CFj.
The antecedent part of fuzzy if-then rules is specified
manually. Then the consequent part (i.e. consequent
class and the grade of certainty) is determined from the
given training patterns [12].
Let us assume that m training patterns xp= (xp1, …,
xpn), p=1 ,…, m, are given for an n-dimensional C-class
pattern classification problem. It is also assumed that a
weight wp, p=1, …, m, is assigned to each training pat-
tern a priori. The consequent class Cj and the grade of
certainty CFj of the if-then rule are determined in the
following manner:
Step 1: Calculate

Class h(j) for Class h

as (7):






hClassxppjh
p
wxj
Class.


(7)
where,






pnjnpjpj xxx





...
11 (8)
and 
jn is the membership function of the fuzzy set Ajn.
In this paper, the fuzzy sets are used as in Figure 3.
Step 2: Find the Class h that has the maximum value
of

Class h(j):

 jj k
Mk
h Class
1
ˆ
Classmax





(9)
This should be noted that this fuzzy rule generation
method can also be applied to the standard pattern clas-
sification problem where there are no pattern weights. In
this case, the class and the grade of certainty are deter-
mined from training patterns by specifying a pattern
weight as wp=1 for p=1,…, m.
If two or more classes take the maximum value,
the consequent class Cj of the rule Rj cannot be deter-
mined uniquely. In this case, specify Cj as Cj=

. If a
single class h

takes the maximum value, let Cj be class
h

. The grade of certainty CFj is determined as (10):





hh
h
jj
j
CF
Class
ˆ
Class


(10)
with:




hh
hj
cˆ Class 1
1
 (11)
After both the consequent class Cj and the grade of
certainty CFj are determined for all N rules, a new pat-
tern x=(x1 ,…, xn) can be classified by the following pro-
cedure. Calculate

J (x) for j =1,…, N, as:




jjjJ CCFxx.max
  (12)
in which J is the number of winner rule. The class of the
new pattern would be the CJ i.e. the class that has been
assigned to rule number J.
If two or more classes take the maximum value, then
the classification of x is rejected (i.e. x is left as an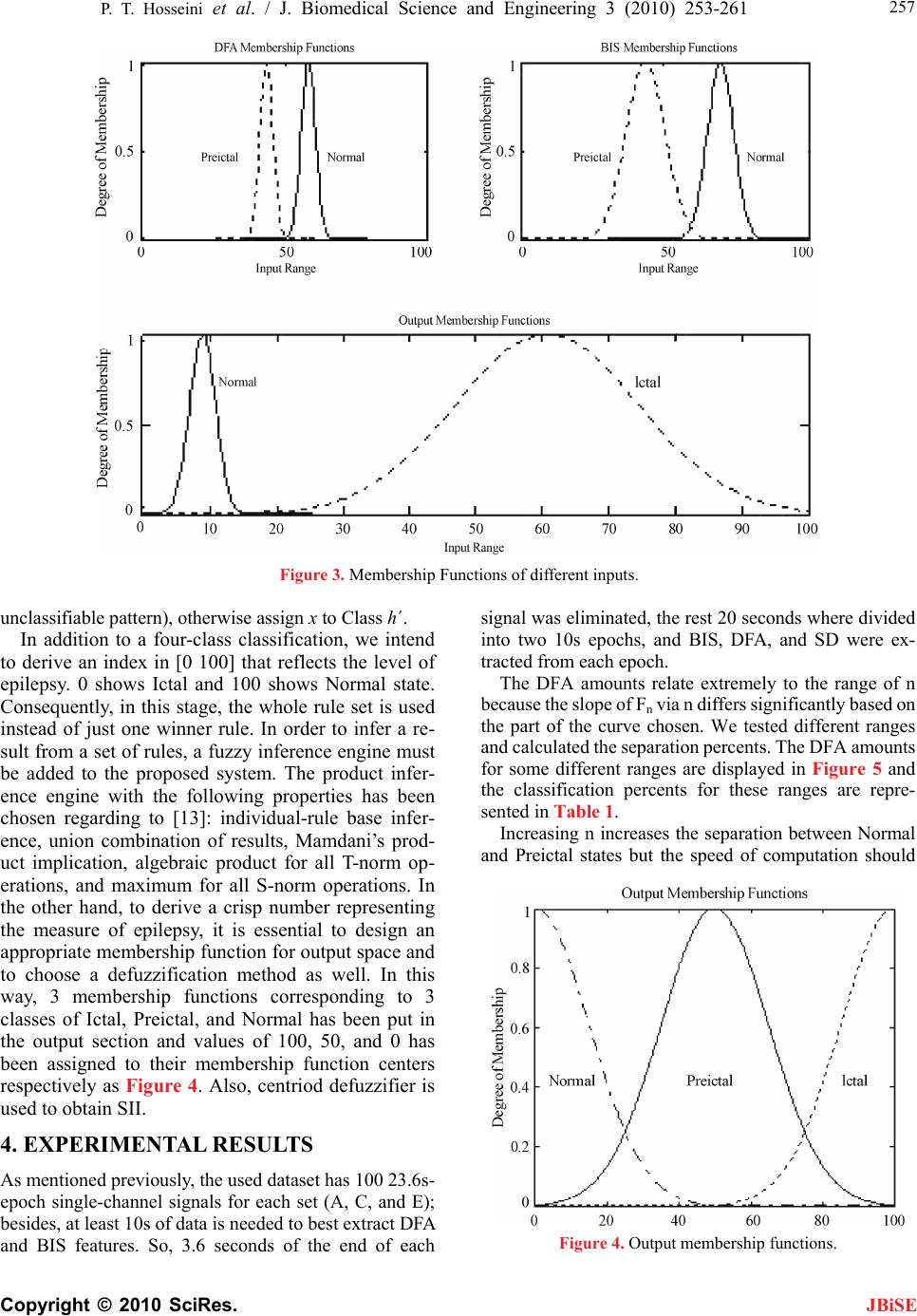

P. T. Hosseini et al. / J. Biomedical Science and Engineering 3 (2010) 253-261
257
Figure 3. Membership Functions of different inputs.
unclassifiable pattern), otherwise assign x to Class h´.
In addition to a four-class classification, we intend
to derive an index in [0 100] that reflects the level of
epilepsy. 0 shows Ictal and 100 shows Normal state.
Consequently, in this stage, the whole rule set is used
instead of just one winner rule. In order to infer a re-
sult from a set of rules, a fuzzy inference engine must
be added to the proposed system. The product infer-
ence engine with the following properties has been
chosen regarding to [13]: individual-rule base infer-
ence, union combination of results, Mamdani’s prod-
uct implication, algebraic product for all T-norm op-
erations, and maximum for all S-norm operations. In
the other hand, to derive a crisp number representing
the measure of epilepsy, it is essential to design an
appropriate membership function for output space and
to choose a defuzzification method as well. In this
way, 3 membership functions corresponding to 3
classes of Ictal, Preictal, and Normal has been put in
the output section and values of 100, 50, and 0 has
been assigned to their membership function centers
respectively as Figure 4. Also, centriod defuzzifier is
used to obtain SII.
JBiSE
4. EXPERIMENTAL RESULTS
As mentioned previously, the used dataset has 100 23.6s-
epoch single-channel signals for each set (A, C, and E);
besides, at least 10s of data is needed to best extract DFA
and BIS features. So, 3.6 seconds of the end of each
signal was eliminated, the rest 20 seconds where divided
into two 10s epochs, and BIS, DFA, and SD were ex-
tracted from each epoch.
The DFA amounts relate extremely to the range of n
because the slope of Fn via n differs significantly based on
the part of the curve chosen. We tested different ranges
and calculated the separation percents. The DFA amounts
for some different ranges are displayed in Figure 5 and
the classification percents for these ranges are repre-
sented in Table 1.
Increasing n increases the separation between Normal
and Preictal states but the speed of computation should
Figure 4. Output membership functions.

258 P. T. Hosseini et al. / J. Biomedical Science and Engineering 3 (2010) 253-261
Table 1. Classification percents of three states using DFA and
SD changes with different ranges of n.
Range of n Classification Percent
3 < n < 10 97.23
3 < n < 15 99.13
3 < n < 30 100
3 < n < 50 100
also be considered especially when we speak of using
this method in patient monitoring and index calculation.
After lots of observations, the best range for n is chosen
to be [3,30].
After computation of DFA with the best range, an 8-
point moving average is applied on each feature of each
set, so the first 7 features of each group are omitted. In
the end, there are 193 3-feature vectors for each group
(A, C, and E). The BIS, DFA, and SD features of these
193 vectors are represented separately for each set of
data along with their box plots in Figure 6.
From Figure 6, it is obvious that SD along with
just one of the other features is enough to make a
good separation between three states. As mentioned in
Section 3.3, a fuzzy classifier with membership func-
tions of Figure 3 is used to separate the three sets A,
C, and E.
The p-values of each pair of DFA, BIS, and SD fea-
tures are represented separately in tables 2 to 4. P < 0.05
means that the two groups have similar amounts for that
specific feature and cannot be separated easily using that
feature. The represented values are relevant to the results
in Figure 6.
A leave-one-out technique is applied to the data in
classification process. It means that the classification
performed 193 × 3 times. Each time, one of the samples
is used as a test and the whole other samples are used as
train. At the end, an average of all classification percents
of these 193 × 3 tries is declared as the classification
percent of the whole system. The classification percent
for SD and BIS is 99.82% and for SD and DFA is 100%.
Table 5 is a comparison of the proposed method with
previous works on the same data.
The important part of this study is the index extraction.
Along with SD feature, DFA and BIS can separately well
classify the three states, so they are used separately as
the inputs of the fuzzy inference engine. The used infer-
ence engine is the product engine and the input and out-
put membership functions are as displayed in Figures 3
and 4. A centroid defuzzifier is applied to the output to
compute the final index which is called SII. The index is
programmed to be between 0 and 100. Zero means the
patient is in Normal situation and 100 means he is in
Ictal situation. Convenient ranges for these amounts are
specified to better interpret the medical situation of the
patient. Table 6 is exposed to suggest a range for differ-
ent states.
Figure 5. Different Ranges for n produces different DFAs.

P. T. Hosseini et al. / J. Biomedical Science and Engineering 3 (2010) 253-261
259
JBiSE
Figure 6. (a) DFA; (b) BIS; (c) SD features of 3 sets and their box plots.
Table 2. P-values of different DFA vectors.
DFA p-values Normal Preictal Ictal
Normal 0 0.3476 0.1198
Preictal 0.34762 0 0.0049
Ictal 0.11982 0.0049 0
Table 3. P-values of different BIS vectors.
BIS p-values Normal Preictal Ictal
Normal 0 0.8421 0.0019
Preictal 0.8421 0 0.8019
Ictal 0.0019 0.8019 0
Table 4. P-values of different SD vectors.
SD p-values Normal Preictal Ictal
Normal 0 3.4814e-005 0.62488
Preictal 3.4814e-005 0 0.12001
Ictal 0.62488 0.12001 0
First, the inputs of the engine are SD and BIS and then
the inputs are SD and DFA. The output of both systems is
the desired index SII. There are 193 values for each feature
in each set. We feed all 579 values of each feature to each
system and come to the results shown in Figure 7. The
vertical lines separate the samples of each set (A, C, and E).
One can obviously see the well separation in index
amounts for different states of both DFA and BIS.
Both of these methods are fast and their algorithms are
not complex although DFA is faster and less complex.
Though, the proposed methods can easily be used in pa-
tient monitoring of epileptic patients. As the output index is
a two digit number, the system can be manufactured com-
pletely user friendly and the interpretation of the results is
so easy for the physicians. The important point is that just
one channel of EEG signal has been used.
5. CONCLUSIONS
Epilepsy is a brain disorder in which clusters of nerve
cells, or neurons, in the brain sometimes signal abnor-
mally. In epilepsy, the normal pattern of neuronal activity
becomes disturbed, causing strange sensations, emotions,
and behavior or sometimes convulsions, muscle spasms,
and loss of consciousness. Though, once epilepsy is di-
agnosed, it is important to begin treatment as soon as
possible. Scientists are studying potential antiepileptic
drugs with the goal of enhancing treatment for epilepsy.
Once a seizure is predicted, antiepileptic drugs can be
injected to prevent the seizure.
We have divided the brain situation of an epileptic pa-
tient into 3 states: Normal (normal brain state), Preictal
(just before the seizure), and Ictal (during seizure). In this
research, we are seeking a technique to calculate an index
that can distinctly separate these three states.
The dataset used is a public dataset which is described
thoroughly in the text. This database includes 5 sets in
every which there are 100 single-channel EEG signals of
a specific state of epileptic patients’ brains (A to E).
In this paper, three features are extracted from single-

260 P. T. Hosseini et al. / J. Biomedical Science and Engineering 3 (2010) 253-261
Table 5. Proposed method and previous works.
Features Classifiers Used datasets
Classification Percents
(%)
Spectral and embedding entropies [14] ANFIS A and E 92
Lyapunov Exponent [15] Neural Network A,D, and E 96.79
Wavelet [16] Neural Network A and E 95
Chaotic features [17] Neural Network A, C, and E 96.7
FFT [18] Decision Tree A and E 98.72
Welch (FFT) and PCA [19] AIRS with fuzzy A and E 100
BIS and SD (Proposed Method) Fuzzy A, C, and E 99.82
DFA and SD (Proposed Method) Fuzzy A, C, and E 100
Table 6. The appropriate ranges for differnt states.
State Range
Normal 0 < SII < 30
Preictal 30 < SII < 70
Ictal 70 < SII < 100
(a) Number of Samples
(b) Number of Samples
Figure 7. SII index using. (a) BIS and SD; (b) DFA and SD.
channel EEG signals: BIS (Bispectral feature), DFA
(Detrended Fluctuation Analysis feature), and SD (Stan-
dard Deviation). The first and second features are dis-
cussed completely in the paper. For classification and
index extraction, fuzzy classifier and fuzzy inference
engine are used.
In classification process, first, BIS and SD are used and
the three states can be separated with 99.82% accuracy.
Then, using DFA and SD, Normal, Preictal, and Ictal are
separated with 100% classification percent. In compari-
son with previous works which are discussed in the paper,
our results are much higher.
Using the product engine as the fuzzy inference engine,
a Seizure Intensity Index (SII) is calculated once with BIS
and SD and once with DFA and SD as the inputs. In both
cases, the index is completely separable for the three sets
(A, C, and E). The index stands between 0 and 100. Zero
means the patient is in the Normal situation and 100
means he is experiencing seizure. We can specify a range
for the index. If the index is between 30 and 70, the pa-
tient is in the preictal period and the antiepileptic drugs
should be injected.
The proposed methods are fast and simple and may
easily run a user friendly system. Our research can be
used vastly in medical care sections because it works with
single-channel EEG signal and it can significantly help
the physicians understand the situation of an epileptic
patient and apply an appropriate treatment based on the
patient situation.
REFERENCES
[1] Hagihira, S., Takashina, M., Mori, T., Mashimo, T. and
Yoshiya, I. (2001) Practical issues in bispectral analysis
of electroencephalographic signals. Journal of Anesthesia
Analgesia, 93, 966-970.
[2] Huang, L., Sun, Q., Cheng, J. and Huang, Y. (2003) Pre-
diction of epileptic seizures using bispectrum analysis of
electroencephalograms and artificial neural network.
Proceedings of 25th Annual International Conference of
the IEEE Engineering in Medicine and Biology Society, 3,
2947-2949.
[3] Tallach, R., Ball, D. and Jefferson, P. (2004) Monitoring
seizures with the bispectral index. Journal of Anesthesia,
59, 1033-1034.
[4] Ye, S., Park, J., Kim, J., Jung, J., Jeon, A., Kim, I., Son, J.,
Nam, K., Baik, S., Ro, J. and Jeon G. (2009) Develop-
ment for the Evaluation Index of an Anesthesia Depth
using the Bispectrum Analysis. International Journal of

P. T. Hosseini et al. / J. Biomedical Science and Engineering 3 (2010) 253-261
261
JBiSE
Biological and Medical Sciences, 4, 67-70.
[5] Peng, C., Buldyrev, S., Havlin, S., Simons, M., Stanley,
H. and Goldberger, A. (1994) Mosaic organization of
DNA nucleotides. Journal of Physical Review E, 49,
1685-1689.
[6] Gifani, P., Rabiee, H., Hashemi, M., Taslimi, P. and
Ghanbari, M. (2007) Optimal fractal-scaling analysis of
human EEG dynamic for depth of anesthesia quantifica-
tion. Journal of the Franklin Institute, 344, 212-229.
[7] Jospin, M., Caminal, P., Jensen, E., Litvan, H., Vallverdu,
M., Struys, M., Vereecke, H. and Kaplan, D. (2007) De-
trended fluctuation analysis of EEG as a measure of
depth of anesthesia. IEEE Transactions on Biomedical
Engineering, 54, 840-846.
[8] Andrzejak, R., Lehnertz, K., Rieke, C., Mormann, F.,
David, P. and Elger, C. (2001) Indications of nonlinear
deterministic and finite dimensional structures in time
series of brain electrical activity: Dependence on re-
cording region and brain state. Journal of Physical Re-
view E, 64, 061907.
[9] Kantelhardta, J., Bundea, E., Regoa, H., Havlinb, S. and
Bundea, A. (2001) Detecting long-range correlations
with detrended Fluctuation analysis. Journal of Physica
A, 295, 441-444.
[10] Ishibuchi, H., Nozaki, K., Yamamoto, N. and Tanaka, H.
(1995) Selecting fuzzy if-then rules for classification
problems using genetic algorithms. IEEE Transactions
on Fuzzy Systems, 3, 260-270.
[11] Ishibuchi, H. and Nakashima, T. (2001) Effect of rule
weights in fuzzy rule-based classification systems. IEEE
Transactions on Fuzzy Systems, 9, 506-515.
[12] Nakashima, T., Yokota, Y. and Ishibuchi, H. (2005)
Learning fuzzy if-then rules for pattern classification
with weighted training patterns. Proceedings of 4th Con-
ference of the European Society for Fuzzy Logic and
Technology and 11th Rencontres Francophones sur la
Logique Floue et ses Applications, 1064-1069.
[13] Esmaeili, V., Assareh, A., Shamsollahi, M., Moradi, M.
and Arefian, N. (2008) Estimating the depth of anesthesia
using fuzzy soft computation applied to EEG features.
Journal of Intelligent Data Analysis, 12, 393-407.
[14] Kannathal, N., Choo, M., Acharya, U. and Sadasivan, P.
(2005) Entropies for detection of epilepsy in EEG. Jour-
nal of Computer Methods and Programs in Biomedicine,
80, 187-194.
[15] Guler, N., Ubeyli, E. and Guler, I. (2005) Recurrent neu-
ral networks employing Lyapunov exponents for EEG
signals classification. Journal of Expert Systems with
Applications, 29, 506-514.
[16] Subasi, A. (2007) EEG signal classification using wave-
let feature extraction and a mixture of expert model. Jour-
nal of Expert Systems with Applications, 32, 1084- 1093.
[17] Dastidar, S., Adeli, H. and Dadmehr, N. (2007) Mixed-
band wavelet-chaos-neural network methodology for
epilepsy and epileptic seizure detection. IEEE Transac-
tions on Biomedical Engineering, 54, 1545-1551.
[18] Polat, K. and Gunes, S. (2007) Classification of epilepti-
form EEG using a hybrid system based on decision tree
classifier and fast Fourier transform. Journal of Applied
Mathematics and Computation, 187, 1017-1026.
[19] Polat, K. and Gunes, S. (2008) Artificial immune recog-
nition system with fuzzy resource allocation mechanism
classifier, principal component analysis and FFT method
based new hybrid automated identification system for
classification of EEG signals. Journal of Expert Systems
with Applications, 34, 2039-2048.