J. Software Engineering & Applications, 2008, 1: 76-82
Published Online December 2008 in SciRes (www.SciRP.org/journal/jsea)
An Algorithm for Generation of Attack Signatures
Based on Sequences Alignment
Nan Li, Chunhe Xia, Yi Yang, Hai-Quan Wang
State Key Laboratory of Virtual Reality Technology, Key Laboratory of Beijing Network Technology, School of Computer Science
and Engineering, Beihang University, Beijing, China
Received November 11
th
; 2008; revised November 19
th
, 2008; accepted November 24
th
, 2008
ABSTRACT
This paper presents a new algorithm for generation of attack signatures based on sequence alignment. The algorithm is
composed of two parts: a local alignment algorithm-GASBSLA (Generation of Attack Signatures Based on Sequence
Local Alignment) and a multi-sequence alignment algorithm-TGMSA (Tri-stage Gradual Multi-Sequence Alignment).
With the inspiration of sequence alignment used in Bioinformatics, GASBSLA replaces global alignment and constant
weight penalty model by local alignment and affine penalty model to improve the generality of attack signatures.
TGMSA presents a new pruning policy to make the algorithm more insensitive to noises in the generation of attack
signatures. In this paper, GASBSLA and TGMSA are described in detail and validated by experiments.
Keywords: Attack Signatures Generation, Sequence Local Alignment, Affine Penalty, Intrusion Detection, Pruning Policy
1. Introduction
Network worms, viruses and malicious codes are still the
top threat against the current Internet and enterprise
security, and they cause a loss of hundreds of millions
dollars every year [1].Intrusion detection based on attack
signatures is the most effective solution of this issue
currently, but the continuous emergence of new types of
attacks and polymorphic engines such as PHolyP [2] are
great challenges to the existing intrusion detection
technologies. To solve this problem, automatic
generation of attack signatures has been concerned by
more and more researchers and has become a new
hotspot in intrusion detection since 2003 [3].
Algorithms for generation of attack signatures can be
divided into two categories: one is based on string mode
and the other is based on semantics. However, the latter
relies on prior semantic analysis of a certain type of
attacks, so it is incompetent for generating signatures of
unknown attacks automatically. Currently the research on
algorithms for generation of attack signatures is mainly
based on string mode, including the following categories:
algorithms based on the LCS (longest common substring),
algorithms based on the Token (the strings appearing
frequently in suspicious datum and containing more than
one character) [4], algorithms based on sequence
alignment, algorithms based on finite automaton and
algorithms based on protocol field and length [5].
The algorithms for generation of attack signatures
based on Token is considered as the most effective and
approbatory method currently. But in [3], the authors
point out that signatures generated by this kind of
algorithm are not precise and give out an algorithm based
on sequence alignment. In this paper, we present a new
algorithm for generation of attack signatures based on
sequence alignment through analyzing the algorithms
presented by [3] and referring to the idea of sequence
alignment used in Bioinformatics. The algorithm is
composed of two parts: GASBSLA algorithm and
TGMSA algorithm. With the inspiration of sequence
alignment used in Bioinformatics, GASBSLA replaces
global alignment and constant weight penalty model by
local alignment and affine penalty model to improve the
generality of attack signatures. TGMSA presents a new
pruning policy to make the algorithm more insensitive to
noises in the generation of attack signatures.
The rest of the paper is organized as follows. Section 2
refers to related research, which describes the algorithms
for generating attack signatures in [3] and analyzes its
weakness. Section 3 presents the design of GASBSLA
algorithm and TGMSA algorithm, and details their
relative analysis. Section 4 presents the experiments on
the effectiveness and the anti-noise ability of the
algorithms. Section 5 concludes the paper and mentions
of some future work.
This work was supported by three projects: the National 863 Project-
Research on high level descripti
on of network survivability model and
its validation simulation platform under Grant No.2007 AA01Z407,
The Co-Funding Project of Beijing Municipal E
ducation Commission
under Grant No.JD100060630 and National Foundation Research
Project.

An Algorithm for Generation of Attack Signatures Based on Sequences Alignment 77
2. Related Research
Sequence alignment is divided into pair-wise alignment and
multi-sequence alignment, and most of multi- sequence
alignment is based on pair-wise alignment. Firstly, this
section introduces and analyzes a pair-wise sequence alignment
algorithm CMENW (Contiguous- Matches Encouraging
Needleman-Wunsch) and a multi-sequence alignment algorithm
HMSA (Hierarchical Multi-Sequence Alignment) [3].
They are the most representative algorithms applied to
the generation of attack signatures based on sequence
alignment, and they are also the foundation of this paper.
Then we introduce the most representative pair-wise local
alignment algorithm-Smith-Waterman algorithm [6].
2.1 CMENW Algorithm
CMENW algorithm is a pair-wise alignment algorithm
based on global alignment. It is improved on Needleman-
Wunsch algorithm [7], which is the typical pair-wise
alignment algorithm. The main difference between the
two algorithms is: Needleman-Wunsch algorithm easily
leads to fragments. In order to reduce the influence of
fragments in the process of alignment, CMENW
algorithm introduces contiguous-matches encouraging
function
( )
enc x
(
x
is the number of contiguous bytes
in the alignment), which is used to encourage contiguous
bytes to be aligned together. The score function of
CMENW algorithm is as follows:
12 3
( ,)()
S x ykmkdkencs
δ δδ δ =×+× +× + =×+× +× +=×+× +× + =×+×+×+∑
∑∑
∑
(1)
m
is the score of bytes matched,
d
is the score of
bytes unmatched,
δ
δδ
δ
is the score of empty penalty,
1
k
is the number of bytes matched in the result of alignment,
2
k
is the number of bytes unmatched,
3
k
is the number
of gaps,
s
is contiguous bytes.
Attack signatures generated by CMENW algorithm are
not effective enough while facing to polymorphic attack
because of the insufficient generality. It can be improved
by using multi-sequence alignment, but the number of
samples is difficult to meet the requirement in real world
situation.
2.2 HMSA Algorithm
HMSA algorithm is a type of hierarchical multi-sequence
alignment algorithm based on pair-wise alignment
CMENW algorithm, which is suitable for attack
signatures generation. This algorithm has three main
features [3]: (1) hierarchical pair-wise alignment; (2)
supporting wildcard characters; (3) with a pruning
function.
HMSA algorithm possesses the function of pruning,
which accelerates its convergence and enhances the noise
resisting ability. However, the effectiveness of pruning
function is based on two assumptions: (1) the alignment
result of any two noise will be pruned because of trivial
solution; (2) the alignment result of any two samples will
not be pruned and get a precise attack signature. However,
in reality, it is possible that the alignment result of any
two noises is not pruned, because input sequences of
signatures generation algorithm are often processed by
clustering algorithms. Thus the alignment results of noise
that not pruned and the alignment results of sample will
be easily prone to trivial solution and be pruned, and
finally there is no result returned.
2.3 Smith-Waterman Algorithm
Smith-Waterman algorithm is a pair-wise local alignment
algorithm put forward by Smith and Waterman in 1981,
which is used to find and compare the similarity in local
regions in an overall view. Even today it is still a
common basic algorithm in bioinformatics. Given
sequence
x
and
y
as inputs, Smith-Waterman algorithm
outputs a local alignment result which is global optimal.
The similarity value of it is maximal according to
formula (2). And the meanings of the bytes in this
formula are the same as those in the formula (1) in
Section 2.1.
12 3
( ,) S x ykmkdk
δ δδ δ
=×+× +× =×+× +×=×+× +× =×+× +×
(2)
Smith-Waterman algorithm is used to find the biggest
similarity value and the best alignment based on the
principle of dynamic programming, and its process
includes two major steps:
1. Calculate the similarity values of two given sequences,
and get a similarity matrix;
2. Get the best results of sequence alignment through
dynamic programming and backtracking algorithm,
according to the similarity matrix got in step 1.
Smith-Waterman algorithm improves Needleman- Wunsch
algorithm. The main difference between them is:
Smith-Waterman algorithm uses 0 to replace all the
negatives in the similarity matrix; if the similarity values
no longer increases when the length of alignment result
increases, this algorithm will finish backtracking and
output the result. According to the differences between
the two algorithms, the idea of Smith-Waterman
algorithm is helpful for CMENW algorithms to overcome
the problem of insufficient generalization.
3. GASBSLA Algorithm and TGMSA Algorithm
Through the analysis of CMENW algorithm and HMSA
algorithm, we present a new algorithm for generation of
attack signatures based on sequence alignment. The
algorithm is composed of two parts: a local alignment
algorithm—GASBSLA (Generation of Attack Signatures
Based on Sequence Local Alignment) and a multi-
sequence alignment algorithm—TGMSA (Tri-stage Gradual
Multi-Sequence Alignment).
3.1 GASBSLA Algorithm
In Bioinformatics, local alignment has more practical
significance than global alignment because two sequences
are often with very high similarity just in some local
regions [8]. For example, two long DNA sequences often

78 An Algorithm for Generation of Attack Signatures Based on Sequences Alignment
have relation with each other only in seldom areas
(password districts); proteins belonging to different
families often have some regions in the same on the
structure and function. The situation in generating of
attack signatures is very similar with that of
Bioinformatics, so GASBSLA algorithm replaces global
alignment by local alignment to improve the generality
and precision of attack signature under the conditions of a
small sample. In addition, to further reduce the number of
fragments, GASBSLA algorithm replaces constant
weight penalty model by affine penalty model [9].
The differences between affine penalty model and
constant weight penalty model are: the penalty for each
gap is independent in constant weight penalty model.
That is, in any case, the penalty for one gap is
d
, and
the penalty for
n
gaps is
nd
; but in affine penalty
model, the penalty for
n
gaps which attached together
is 1
( )
q nr
+− × +− ×+− × +− ×
. Where
q
is the penalty for the first
one of
n
gaps attached together,
r
is the penalty for
the other gaps, and r « «« « q. We can learn from descriptions
above that in affine penalty model, the penalty for the
first gap is more than the other ones which means the
reduction of single gaps and fragments in the attack
signatures.
The general idea of GASBSLA algorithm based on
Dynamic Programming is: First, calculating the similarity
values of two sequences and keeping them in a matrix
(named similarity matrix or DP matrix); second,
according to the dynamic programming backtracking
algorithm, finding the optimal alignment sequence on the
basis of the DP matrix. Both the time complexity and the
space complexity of GASBSLA algorithm are
( )
O mn
,
where
m
and
n
are the lengths of the two sequences.
( ,)
x y
σ
σσ
σ
is the similarity value of the alignment of
x
and
y
, where
x
and
y
are any two characters.
Algorithm 1. GASBSLA algorithm
Input: sequence
a
and
b
Output: the similarity value and optimal sequence
alignment of
a
and
b
Initialization:
a.
0 00
( ,) T
=
==
=
b. 1 2
, ,,
L
ForeachiM
=
==
=
0 0
( ,) F i
=
==
=
，
0 0
( ,)T i
=
==
=
c. 1 2
, ,,
L
For eachjN
=
==
=
0 0
( ,)F j
=
==
=
，
0 0
( ,)T j
=
==
=
Main iteration:
1 2
, ,,
L
ForeachiM
= == =
1 2
, ,,
L
For eachjN
=
==
=
1 1
0
( ,),
( ,),
T ijifab
i j
T ij
ifa b
i j
  
  
  
  
  
− −=
− −=− −=
− −=
=
==
=
≠
≠≠
≠
0
1
1 1
2
1
3
1
4
( ,)max
[ ]
(,)(,)(( ,))
[ ]
(, )(,)
[ ]
( ,)(,)
[ ]
i j
i
j
F ij
case
Fijabenc Tijcase
F ijacase
F ijbcase
σ σσ σ
σ
σσ
σ
σ
σσ
σ









  



  



= == =
−− ++ −− ++−− ++ −− ++
− +−
− +−− +−
− +−
− +− − +−− +− − +−
1
2
3
4
[ ]
[ ]
( ,)
[ ]
[ ]
STOP case
DIAG case
Ptr ijLEFT case
UP case
  
  
  
  



  



= == =
3.2 TGMSA Algorithm
TGMSA algorithm presents a new pruning policy to
avoid the situation of no output caused by not being
pruned in the alignment process of two noises. The
general idea is modifying pruning policy in the nth (n>1)
layer alignment according to alignment similarity value.
If the alignment similarity value is less than the threshold
(that the alignment similarity value is out of confidence
interval), the alignment result will not be pruned, but the
two sequences will be laid aside then align respectively
with the signature sequence result, which is the alignment
result of other sequences. If the alignment result does not
accord with pruning conditions, it will replace the
original signature sequence, otherwise it will be deserted.
Algorithm 2. TGMSA algorithm
Input: sequence set S
Output: multi-sequence alignment result
Initialization:
R S
←
←←
←
{}
W
←
←←
←
{}
T
←
←←
←
Iteration of the first stage:
while
1
R
≥
≥≥
≥
, do
if
1
R
=
==
=
(denote the sequence by
i
s
)
then
i
s W
→ →→ →
else
take out two sequences
i
s
and
j
s
orderly from
R
align
i
s
with
j
s
using pair-wise alignment algorithm,
the alignment result is denoted by
,
i j
S S
Ali
(including
the similarity value and optimal sequence alignment)
pruning
if the number of fragments in
,
i j
S S
Ali
≥ 3 and there
exists at least two fragments whose length ≥ 3
,
i j
S S
Ali T
→ →→ →
Iteration of the second stage:
do
{}
V
←
←←
←
while
1
T
≥
≥≥
≥
, do

An Algorithm for Generation of Attack Signatures Based on Sequences Alignment 79
if
1
T
= == =
(denote the sequence by
i
s
)
then
i
s V
→ →→ →
else
take out two sequences
i
s
and
j
s
randomly from
R
align
i
s
with
j
s
using pair-wise alignment
algorithm, the alignment result is denoted by
,
i j
S S
Ali
pruning
if the similarity value of
,
i j
S S
Ali
falls in confidence
interval(the calculation of similarity value confidence
interval will be specified in Section 3.3.)
,
i j
S S
Ali V
→ →→ →
else
,
i j
S S
Ali W
→ →→ →
T V
← ←← ←
until
1
V
≤ ≤≤ ≤
Iteration of the third stage:
if
1
V
= == =
while
0
W
≠ ≠≠ ≠
take out single sequence from
W
orderly, then align
it with the alignment result
Ali
in the second stage
respectively to generate a new alignment result
'
Ali
if
the number of fragments in
'
Ali
≥ 3[10] and there exists
at least two fragments whose length ≥ 3 [11,12]
then
Ali
=
'
Ali
else Ali
= Φ
= Φ= Φ
= Φ
3.3 The Selection of Alignment Similarity
Confidence Interval
Central limit theorem holds that regardless of the
statistics population on the subject obeying whatever
distribution, the distribution of sample mean is close to a
normal distribution, the mean of normal distribution
equals that of population distribution, and the variance
equals that of population distribution divided by the
Sample size. Therefore, we can estimate the average
signature alignment similarity based on a certain attack
by the average of the similarity value samples. We use all
the alignment similarity values calculated in the first
stage as a sample to calculate the similarity value
confidence interval which is the judgement condition of
pruning in the second stage.
Assume
1 2
( ,,,)
LL
n
F FF
is a sample of the
alignment similarity value population
F
, so the sample
mean and sample standard variance are as follows:
1
1
1
1
i
n
n
F
i
F
n
+ ++ +
+
++
+
∑
∑∑
∑
=
==
=
= == =
+
++
+
(3)
( (( ( ) )) )
(
((
( )
))
)
1
1
12
1
1
1
2
121
1
n i
i n
n
SF F
ni
nFn F
ni
+ ++ +
+ ++ +
      
      
      
 
  
 
 
  
 
 
  
 
+ ++ +
= − = −= − = −
∑ ∑∑ ∑
=
==
=
+ ++ +
=− +
=− +=− +
=− +
∑
∑∑
∑
= == =
(4)
According to the small probability event theory of normal
distribution: the most datum of normal population (99.7%)
falls in the range of
3
µ σ
±
, and those cases out of the
range are called small probability events. Statistics holds
that small probability events occur almost impossibly,
and they can be ignored. The confidence interval of
alignment similarity value is as follows:
1 1
1 1
3 3
1 1
,
n n
n n
S S
F F
n n
+ + + ++ + + +
+ + + ++ + + +
 
  
 
 
  
 
 
  
 
− +
− +− +
− +
+ + + ++ + + +
(5)
That is:
( (( ( ) )) )
( (( ( ) )) )
( (( ( ) )) )
( (( ( ) )) )
1 1
1 1
1 1
2 2
2 2
1 1
1 1
1 1
3 3
1 1
1 1
,
i ni n i i
n n
n n
Fn FFn F
F F
i i
i i
n n
n nn n
+ + + ++ + + +
      
      
      
      
      
      
      
+ +
+ ++ +
+ +
+ + + ++ + + +
− +− + − +− +− +− + − +− +
∑ ∑ ∑ ∑∑ ∑ ∑ ∑
∑ ∑ ∑ ∑∑ ∑ ∑ ∑
= = = == = = =
= = = == = = =
− + − +− + − +
+ +
+ ++ +
+ +
+ + + ++ + + +
(6)
4. Experimental Results
In this section we verify the effectiveness and the noise
resisting ability by practical results. In our experiments,
CMENW algorithm and HMSA algorithm are
implemented to verify pertinently the effectiveness of
improvement gave out in GASBSLA algorithm and
TGMSA algorithm.
4.1 Experiments Environment
Hardware environment: Dawning Server (Intel® Xeon®
CPU, 4G internal storage);
Software environment: Linux Red Hat 9.0 Operating
System(the version of kernel is 2.4.20-8).
4.2 Algorithm Validity Verification
For the purpose of comparison, we selected the same
experimental method as [3]. We generate signatures for
polymorphic versions of four real-world exploits:
Apache-Knacker [13], CodeRed Ⅱ [14], IISPrinter [15]
and TSIG [16]. The Apache-Knacker exploit, the
CodeRed Ⅱ exploit and the IISPrinter exploit use the
text-based HTTP protocol. The TSIG exploit uses the
binary-based DNS protocol. We use polymorphic engine
to generate 150 samples for each exploit attack include
50 samples used to generate signatures and 100 samples
used to detect false negatives. In order to simulate an
ideal polymorphic engine, we fill wildcard and code
bytes for each exploit with values chosen uniformly at
random. In addition, we select 10,000 data samples
without attacks from the MIT Lincoln Laboratory
intrusion detection system test set — DARPA99 (the third
week data sets) [17] to detect False positives.
In our experiments, we set the matching score
1
m
=
==
=
,
the mismatching score
0 2
.
d
= −
= −= −
= −
, the penalty for the first
gap
1
δ
δδ
δ
= −
= −= −
= −
, the penalty for the other gaps
0 05
'
.
δ
δδ
δ = −
= −= −
= − .
The Contiguous-Matches encouragement function is set
as:

80 An Algorithm for Generation of Attack Signatures Based on Sequences Alignment
1153
33053
(). ,
( )(). ,
x x
enc xxx






  
− ×≤ − ×≤− ×≤ − ×≤
= == =
+−×> +−×>+−×> +−×>
(7)
Table 1 and Table 2 show the signatures of the four
exploit attacks introduced above which are generated by
CMENW algorithm and HMSA algorithm and by
GASBSLA algorithm and TGMSA algorithm. The two
tables also give out the rate of false positives and false
negatives of the detection experiment using the
signatures. It can be discovered from the comparison of
Table 1 and Table 2, the signatures generated by
GASBSLA algorithm and TGMSA algorithm have
better generality and effect when they are used to detect
polymorphic attacks. We take TSIG for example to
analyze the reason: signatures generated by CMENW
algorithm and HMSA algorithm include exact position
relation, but in fact polymorphic attacks are effective
attack codes through processed by polymorphic
mechanism(some methods to add useless codes into
effective attack codes), and the lengths of useless codes
is alterable, which leads to false negatives when
signatures generated by CMENW algorithm and HMSA
algorithm are used to detect polymorphic attacks. For
Apache-Knacker exploit, the effective attack codes
contain distance restriction, so the false negatives of
CMENW algorithm and HMSA algorithm is zero, while
the false positives of GASBSLA algorithm and TGMSA
algorithm is 0.08. Nowadays, but, most of the
polymorphic attacks contain no distance restriction in
their effective attack codes.
4.3 Noise Resisting Ability Verification
We selected the same experimental method with HMSA
algorithm: testing the noise resisting ability using
CodeRed exploit and IISPrinter exploit as attack Ⅱ
samples and comparing it with HMSA algorithm. The
sample set contains 20 samples for each attack, and the
number of noises included in the sample set is increased
gradually to observe the numbers of generating signatures
and generating precise signatures using HMSA algorithm
and TGMSA algorithm. Generating precise signatures
means both false negatives and false positives generated
from the sample set are zero.
It can be found from the results as showed in Figure 1
and Figure 2 that: when SNR below or equal to one, both
HMSA algorithm and TGMSA algorithm possess strong
noise immunity; but when SNR is more than one, the
noise resisting ability of TGMSA algorithm is better than
that of HMSA algorithm. The reason is that: when SNR
is more than one, there must be the situation that two
noise align with each other. HMSA algorithm assume
that any alignment of two noise will de pruned, but in
fact the assumption usually cannot to met which leads to
no result or no precise result when the alignment of
noises aligns with the alignment of sample. Aiming at
this fact TGMSA algorithm improves the pruning policy,
and the experimental results prove that our improvement
enhance the noise resisting ability of the algorithm.
Table 1. Attack signatures generated by CMENW algorithm and HMSA algorithm
Table 2. Attack signatures generated by GASBSLA algorithm and TGMSA algorithm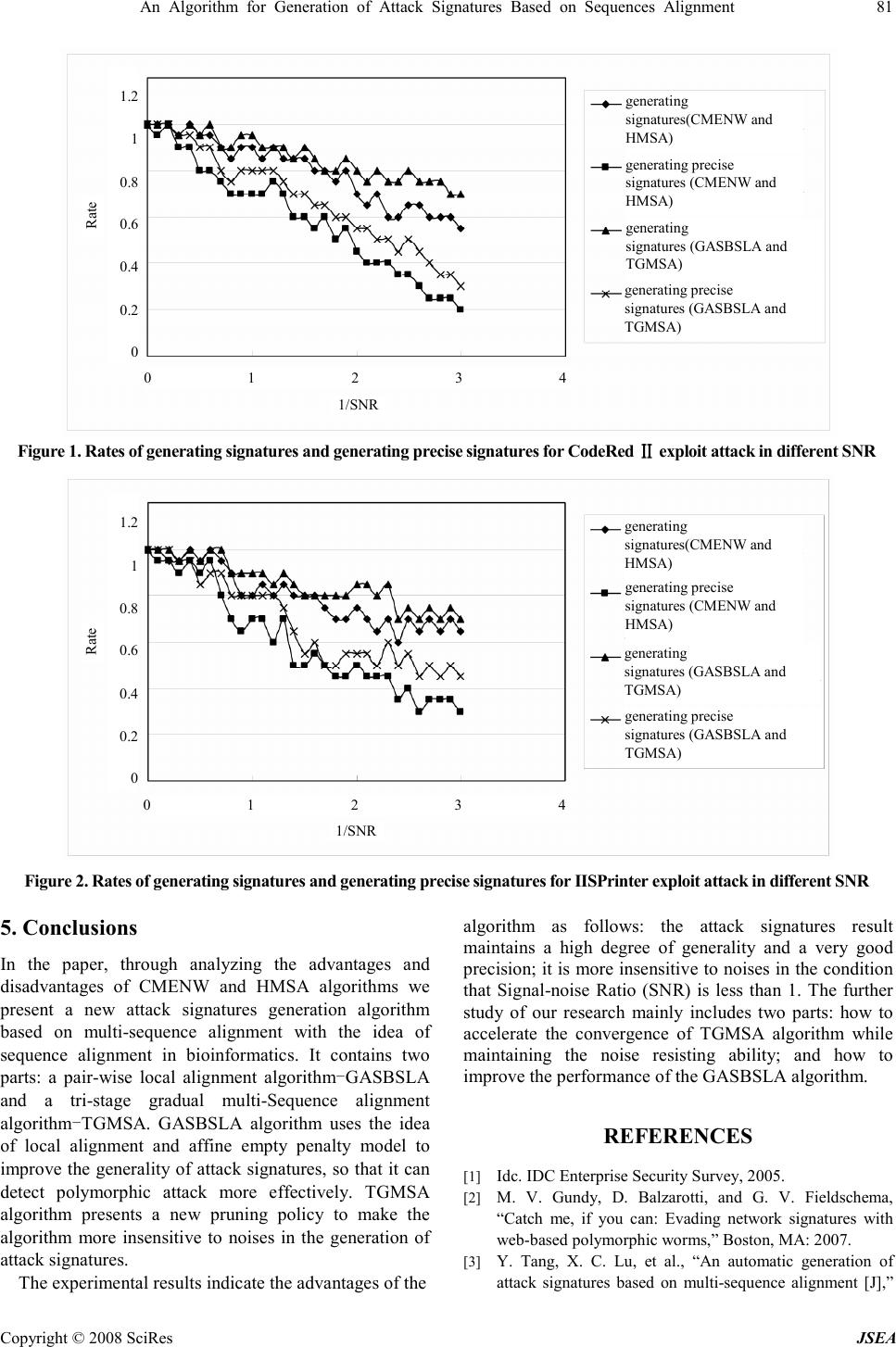

An Algorithm for Generation of Attack Signatures Based on Sequences Alignment 81
Figure 1. Rates of generating signatures and generating precise signatures for CodeRed exploit attack in different SNRⅡ ⅡⅡ Ⅱ
Figure 2. Rates of generating signatures and generating precise signatures for IISPrinter exploit attack in different SNR
5. Conclusions
In the paper, through analyzing the advantages and
disadvantages of CMENW and HMSA algorithms we
present a new attack signatures generation algorithm
based on multi-sequence alignment with the idea of
sequence alignment in bioinformatics. It contains two
parts: a pair-wise local alignment algorithm - GASBSLA
and a tri-stage gradual multi-Sequence alignment
algorithm - TGMSA. GASBSLA algorithm uses the idea
of local alignment and affine empty penalty model to
improve the generality of attack signatures, so that it can
detect polymorphic attack more effectively. TGMSA
algorithm presents a new pruning policy to make the
algorithm more insensitive to noises in the generation of
attack signatures.
The experimental results indicate the advantages of the
algorithm as follows: the attack signatures result
maintains a high degree of generality and a very good
precision; it is more insensitive to noises in the condition
that Signal-noise Ratio (SNR) is less than 1. The further
study of our research mainly includes two parts: how to
accelerate the convergence of TGMSA algorithm while
maintaining the noise resisting ability; and how to
improve the performance of the GASBSLA algorithm.
REFERENCES
[1] Idc. IDC Enterprise Security Survey, 2005.
[2] M. V. Gundy, D. Balzarotti, and G. V. Fieldschema,
“Catch me, if you can: Evading network signatures with
web-based polymorphic worms,” Boston, MA: 2007.
[3] Y. Tang, X. C. Lu, et al., “An automatic generation of
attack signatures based on multi-sequence alignment [J],”
1.2
1
0.8
0.6
0.4
0.2
0
Rate
0 1 2 3 4
1/SNR
generating
signatures(CMENW and
HMSA)
generating precise
signatures (CMENW and
HMSA)
generating
signatures (GASBSLA and
TGMSA)
generating precise
signatures (GASBSLA and
TGMSA)
1/SNR
0 1 2 3 4
1.2
1
0.8
0.6
0.4
0.2
0
Rate
generating
signatures(CMENW and
HMSA)
generating precise
signatures (CMENW and
HMSA)
generating
signatures (GASBSLA and
TGMSA)
generating precise
signatures (GASBSLA and
TGMSA)

82 An Algorithm for Generation of Attack Signatures Based on Sequences Alignment
Chinese Journal of Computers, 2006, 29 (9): 153321541.
[4] J. Newsome, B. Karp, and D. Song, “Polygraph:
Automatically generating signatures for polymorphic
worms,” in: Proceedings of the IEEE S &P 2005, Oakland,
California, pp. 226-241, 2005.
[5] Z. Li, M. Sanghi, Y. Chen, et al., “Network-based and
attack-resilient length signature generation for zero-day
polymorphic worms[C],” 2007.
[6] T. Smith and M. Waterman, “Identification of common
molecular subsequences,” Journal of Molecular Biology,
147 (1): pp. 195-197, 1981.
[7] S. B. Needleman and C. D. Wunsch, “A general method
applicable to the search for similarities in the amino acid
sequence of two proteins,” Journal of Molecular Biology,
48(3): pp. 443-453, 1970.
[8] P. K. Murphy, “Biological sequence comparison: An
overview of techniques,” Technical Report, University of
Arizona, Department of Computer Science, 1994.
[9] S. Uliel, A. Fliess, A. Amir, and R. Unger., “A simple
algorithm for detecting circular permutations in proteins,”
Bioinformatics, Vol. 15, No. 11: pp. 930-936, 1999.
[10] J . R. Crandall, S. F. Wu, and F. T. Chong, “Experiences
using Minos as a tool for capturing and analyzing novel
worms for unknown vulnerabilities,” in: Proceedings of the
GI SIG SIDAR Conference on Detection of Intrusions and
Malware and Vulnerability Assessment, Vienna, pp. 32-50, 2005.
[11] J. R. Crandall, Su Zhen Dong, S. F. Wu, and F. T. Chong,
“On deriving unknown vulnerabilities from Zero Day
polymorphic and metamorphic worm exploits,” in:
Proceedings of the ACM CCS 2005, Alexandria, Virginia,
pp. 235-248, 2005.
[12] J. Xu, P. Ning, C. Kil, Y. Zhai, and C. Bookholt,
“Automatic diagnosis and response to memory corruption
vulnerabilities,” in: Proceedings of the ACM CCS 2005,
Alexandria, Virginia, pp. 223-234, 2005.
[13] Symantec Security Response: CodeRed Worm. http://www.
sarc.com/avcenter/venc/data/codered.worm.html.
[14] C. CAN-2003-0245. Apache apr-psprintf memory corruption
vulnerability.
http://www.securityfocus.com/bi-d/7723/ discussion/.
[15] Viruslist.com: Net-Worm. Linux. Adm.
http://www.viruslist.com/en/viruses/encyclopedia?virusid
=23854.
[16] SANS Institute: Lion worm.
http://www.sans.o-rg/y2k/ lion.htm.
[17] R. P. Lippmann, D. J. Fried, I. Graf, et al., “Evaluating
intrusion detection systems: The 1998 DARPA offline
intrusion detection evaluation,” in: Proceedings of the
2000 DARPA Information Survivability Conference and
Exposition, Hilton Head, SC, 2: pp. 1012-1035, 2000.