Paper Menu >>
Journal Menu >>
 I. J. Communications, Network and System Sciences. 2008; 1: 1-103 Published Online February 2008 in SciRes (http://www.SRPublishing.org/journal/ijcns/). Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 Abstract Energy efficiency and enhanced backbone capacity is obtained by exploiting the geometric orientation of cooperative nodes in wireless sensor network. The cooperative communication in wireless sensor networks (WSN) gives us leverage to get the inherent advantages of its random node’s locations and the direction of the data flow. Depending on the channel conditions and the transmission distance, the number of cooperative nodes is selected, that participate in an energy efficient transmission/reception. Simulation results show that increasing the cooperative receive diversity, decreases the energy consumption per bit in cooperative communications. It has also been shown that the network backbone capacity can be increased by controlled displacement of antennas at base station at the expense of energy per bit. Keywords: Cooperative Communication, Energy Efficiency, Capacity, Receive Diversity Sensor Network. 1. Introduction Wireless sensor network consists of hundred or thousand of small, inexpensive wireless nodes responsible for monitoring a physical activity and reporting to the base station (BS), where end user can access the reported data. Cooperative communication has gain an obdurate place in wireless networks. It has been shown [1] that multiple-input multiple-output (MIMO) systems require less transmission energy than the single-input single-output systems. It’s still intricate to build multiple antennas on low-cost, small-sized sensor nodes; therefore MIMO techniques cannot be applied directly on wireless sensor networks. However it is possible to implement MIMO techniques in WSN without physically having multiple antennas at the sensor nodes via cooperative communication techniques [2][3], such distributed MIMO techniques can offer considerable energy saving even after allowing some extra circuit power, communication and training overheads. The use of cooperative communications in wireless sensor networks allows for energy savings through spatial diversity gains [2]. Traditional MIMO utilizes fixed antenna arrays in transmitter/receiver. These arrays are of definite geometric shapes, e.g., one dimensional array, circular array, rectangular array etc, but in cooperative MIMO communications there is no pre-defined array of antennas, the cooperative nodes cooperate with each other at run time to send/receive data. There is already a lot of works related to cluster formation [4-7], capacity improvement [8] and energy efficient cooperative communication [2][3][9] in WSN, but little attention has been given to cooperative nodes selection on the basis of their location in clusters to improve the energy efficiency and reliability. Most of the recent research work in wireless sensor networks, modeled the wireless channel with rich scattered or Rayleigh fading channel model [2][3][10], which is suitable channel model for wireless communications in urban areas where dense and large man made buildings act as rich scatterers. Sensor networks are usually deployed in the areas far away from human population, e.g., in plain desert areas for surveillance, on volcano hills for early alerts and near sea-shore for storm alerts etc. In all these situations, Ricean fading channel model works well, because it contains both non line-of-sight (NLOS) and line-of-sight (LOS) components. In this paper, we have divided the WSN into two functional model parts, i) whole sensor network except the backbone link is modeled with Ricean fading channel and ii) the backbone link (the link between base station and the Exploiting Geometric Advantages of Cooperative Communications for Energy Efficient Wireless Sensor Networks Irfan AHMED1, Mugen PENG2, Wenbo WANG2 Wireless Signal Processing and Network Lab Beijing University of Posts and Telecommunications, Beijing, P.R.China E-mail: 1irfanahmed44@gmail.com, 2{pmg, wbwang}@bupt.edu.cn  56 I. AHMED ET AL. Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 cooperative nodes near the base station) is modeled by pure deterministic channel. Remainder of this paper is organized as follows. System model is presented in section 2. Section 3 exploits the inherent advantages of wireless sensor network. Performance analysis in terms of energy efficiency and capacity of sensor network is presented in section 4. We show simulation results in Section 5, and conclude in Section 6. 2. System Model The system model shown in figure 1, it consists of a cluster based sensor network. Sensor nodes are grouped for cooperative communications. The selection of group nodes is described in next section. In typical wireless sensor network scenarios as narrated above, large number of nodes are randomly deployed in an unattended area. Due to the presence of scatterers as well as line-of-sight component in those areas, Ricean fading channel model has been used to modeled the WSN, Ricean fading channel has both LOS and NLOS components [1] () () /1 1/1H= HHw KK K++ + (1) where () /1 HKK+ is LOS or deterministic component of the channel, () 1/ 1Hw K+ is NLOS or scattered component Figure 1. System Model of the channel and K is the Ricean factor, it is the ratio of the LOS power to the scattered power. 0K = in the presence of rich scattered or pure Rayleigh fading, and K→∞ in case of non-fading channel. We restrict our analysis to the case of frequency-flat fading. The elements of Hw are zero-mean circularly symmetric complex Gaussian (ZMCSCG) random variable with unit variance [1]. We have assumed binary phase shift keying (BPSK) modulation with Alamouti scheme [11] for cooperative MIMO communications. We have furthermore assumed that the channel is unknown to the transmit nodes and is perfectly known to the nodes at receive side. 3. Advantages of Cooperative Communications in WSN 3.1. Exploiting the WSN Architecture 1) WSN is deployed with hundred or thousand of structural or randomly placed nodes making it ideal for cooperative communications. Selections of nodes in a cooperative group which are approximately at same distance from the intended receive nodes, results in equal energy consumption per bit in cooperative communications. 2) By selecting closest nodes within a cooperative group, we can decrease energy consumption per bit in intra-cooperative node communications. 3) In WSN the data flow direction is from sensor network to BS i.e., most of the time BS act as a receiver (neglecting small amount of signaling data from BS to network). By increasing the number of antennas at BS, we can take advantages of receive diversity at BS, because BS has no energy constraint. 4) Usually the base station is located at some height in order to get reliable communication with the network, which results in a dominant LOS component. By exploiting this LOS communications we try to get maximum capacity in this backbone link. 3.2. Selection of Cooperative Nodes in a Network Cooperative communications in WSN can be more beneficial if transmit cooperative nodes are at equal distance from the intended receive nodes. This strategy evenly distributes the transmission energy in LOS component because in LOS component the power loss is inversely proportional to the square of the distance between the transmitter and receiver. In addition to this the cooperative nodes should be at minimum distance from each other to save energy in local communication within the cooperative nodes group. These measures reduce the required bit energy for desired BER. How these measures can be taken? 3.2.1. Algorithm After the cluster formation [5] and selection of cluster-heads in each cluster, following steps ensure the energy efficient selection of cooperative nodes: Step I: BS broadcasts RSSI (Receive Signal Strength Indication) beacon signal to neighbor cluster nodes.  EXPLOITING GEOMETRIC ADVANTAGES OF COOPERATIVE COMMUNICATIONS FOR ENERGY 57 EFFICIENT WIRELESS SENSOR NETW Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 Step II: Each node () i χ measures receive signal strength, calculate ( ) di χ and send back an ACK beacon signal to BS, where () di χ is the distance between node () i χ and BS. Step III: Upon receiving the ACK beacons from all nodes, BS calculates their distances from itself ( ) BS di . Final estimate () _BS di χ is obtained by averaging () di χ and () BS di. Please note that () diis not an actual physical distance, it is equal-power-distance. Step IV: Based on these estimates BS allocates an equal-power group identity to those nodes which lies within a certain range () () _ min BS di χ +ℵ∆Ξ, where ℵ is an integer and ∆Ξ is small distance depends upon () () _ min BS di χ and () () _ max BS di χ . Step V: Each node in equal-power group P multicasts a RSSI beacon signal within its group. It will know its distance from other nodes in the group with the help of ACK receives. Finally the cooperative communications group , CC P ⊆ . Nodes selection preference order in C is Proximity > Residual node energy Node within a cooperative communication group with highest residual energy becomes the cooperative-group-head, it responsible for data aggregation and the communication within the cooperative group. In the same way cooperative-group-head plays the role of BS for neighbor clusters and follows from Step I to V. 4. Performance Analysis 4.1. Network Performance in Ricean Fading Channel We have modeled the sensor network with Ricean fading channel model. In the particular arrangement of cooperative nodes shown in figure 1, where all nodes (antennas) are at same distance from the intended receivers, we use following equation [2] for total energy required per bit per hop, ()() 2 __ 02 4 1tx electrx elect bitl fTR bbtr PP d E NMNn n RR GG π αρ λ =++ + (2) where α is depends upon the drain efficiency of power amplifier in transmitter circuitry, ρ is the signal power (from nT transmit nodes) to noise ratio at each of the receive node, 0 N is AWGN power spectral density, dis the distance between transmitter and receiver, λ is the carrier wavelength, , tr GG are antenna gains of transmitter and receiver respectively, l M is the link margin compensating hardware process variations and other noise or interference, f N is the receiver noise figure,b Ris transmission rate and _tx elect P,_rx elect P are power dissipated in transmitter and receiver circuits, respectively. The system parameters related to above equation are taken from [2, Table I], and the power consumption values of transmitter and receiver circuits (_tx elect P=38mW, _rx elect P=41mW) are of TelosB mote1 [12]. Expression for BER as a function of SNR in Ricean fading channel is given as [1] 22 min 2 min 4 14 2 min 1 1/4 HF T TR TR T dK n nn nn d Kn b T K Pe Kd n ρ ρ ρ ⎛⎞ ⎜⎟ ⎜⎟ −×⎜⎟ ×⎜⎟ ++ ⎜⎟ ⎝⎠ ⎛⎞ + ≤⎜⎟ ++ ⎝⎠ (3) where min d is the minimum distance of separation of underlying scalar constellation and H F is the Frobenius norm of channel matrix H. Using upper bound in above expression, we obtain table I, which has been used for evaluation of energy per bit in equation (2). 4.1.1. Discussion From equation (2) and (3), we can see that the transmission energy per bit for a desired BER is functions of the number of transmit/receive nodes, underlying constellation size and the channel condition. Table I shows the values of ρ for different combinations of transmit and receive nodes at 3 10 b P− =. It can be seen that required SNR at receiver nodes decreases with increasing number of cooperative nodes for a fixed BER. 4.2. Backbone Link Performance in Deterministic or LOS Channel 4.2.1. Energy Consumption The backbone link is modeled by LOS channel, for which the total energy required per bit is given by equation (2). The SNR ( ρ ) per receive node in equation (2) is given as [1, equation 5.60] ( ) 2 exp 4/H bT F Pn ρ =− (4) then the equation (2) becomes 1 With very low power TelosB mote and power loss exponent of two, we can neglect the inter-node cooperation overhead [14].  58 I. AHMED ET AL. Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 () () 2 0 22 __ ln 1/4 1 4H b T bitl f tr F tx electrx elect TR bb nPN d E MN GG PP nn RR π αλ =+ ++ (5) 4.2.2. Capacity The instantaneous capacity (in bps/Hz) for T n transmit and R n receive cooperative nodes under an average transmit power constraint is given by [1] 2 logdetIHH R H n T Cn ρ ⎡⎤ ⎛⎞ =+ ⎢⎥ ⎜⎟ ⎢⎥ ⎝⎠ ⎣⎦ (6) where I R nis R R nn× identity matrix, His R T nn× channel matrix and H H is the Hermitian transpose of H. For LOS propagation, and a narrow-band channel at fixed carrier frequency/ c f c λ =, ray tracing from transmitter to receiver gives following channel matrix H with complex scalar entries () ,, ,, exp 2/ nodejnode k jk nodejnode k jT R HTR π λ −− =− (7) where ,,nodejnode k TR− is the distance between jth transmit node and kth receive node. Let RT nnn== be the number of nodes participating in cooperative communication on either side. With , rt ddd in figure 2, the path lengths between any pair of transmit and receive nodes are approximately the same to within the array size i.e.,,,nodejnodek dT R≈− , and the complex scalars j k H all have same magnitude but different phases j k θ . Mathematical example of this particular type of normalized His given as [13] ( ) exp jk jk Hj θ = (8) where ()( ) 2 00jk ii kk n π θ =−−− ⎡⎤ ⎣⎦ , 00 ,ik are arbitrary integers. Consider the case of 2n=and 00 ,0ik=, the small path length difference ,1 ,1,1,2/4 node nodenode node TR TR δ λ =−−− = (9) guaranteed that the channel matrix is orthogonal and of full rank, 2 in this case. Practically this can be realized by the slight movement of antennas at base station. Since base station is mostly act as a receiver in the wireless sensor network, positioning of antennas based on received RSSI at base station can be easily achieved. With these values orthogonal channel matrix become 1 1 Horthognal j j ⎛⎞ =⎜⎟ ⎝⎠ (10) and the capacity from equation (6) [ ] 2 log 1Cn ρ = + (11) Advantage of cooperative MIMO in terms of capacity can be obtained if the channel matrix H is orthogonal. 4.2.3. Discussion Interestingly, from equation (5) we see that the distance dependant part of above equation is inversely proportional to the square of Frobenius norm of channel matrix, and, it linearly dependent on the number of transmit nodes. Therefore the receive diversity techniques provide more energy efficient communication. In clear LOS environment, capacity of wireless channel depends upon the rank of channel matrixHas depicted by equation (6). Capacity becomes maximum, when the channel matrix is of full rank (or orthogonal). 5. Simulation Results We determine the impact of the selection of cooperative nodes and the physical orientation of antennas of BS on the total energy required per bit transmission in WSN and the capacity of the backbone link. The simulations are performed using MATLAB® by The MathWorks. Figure 3 shows an amount of extra energy consumption per bit compared to our selection algorithm. The transmission distance ratio along x-axis is the ratio of the distance of intra cooperative group nodes without our node selection algorithm and with our algorithm. Since intra cooperative group communication is non-cooperative 1 to 1 communication, therefore more energy consumption per bit is observed in the case of severe fading, K=1, it rises with square of the distance and consumes 33% more energy when the nodes separation is 3.5 time to that of closest nodes of our algorithm. With increasing values of K (i.e., less fading) the slope of extra energy consumption decreases. Therefore in fading channels our algorithm saves a sufficient amount of energy. In figure 4 we have total energy consumption per bit as a function of long-hual distance in a rich scattering environment i.e., K=1. Among different combinations of transmit and receive cooperative nodes, the largest receive diversity combination (1, 4 TR nn = =) gives lower energy consumption per bit in a wide range of transmission distance (from 60m to onwards). Figure 5 shows an improvement in all energy curves as compared to the energy curves in figure 4, this is due to  EXPLOITING GEOMETRIC ADVANTAGES OF COOPERATIVE COMMUNICATIONS FOR ENERGY 59 EFFICIENT WIRELESS SENSOR NETW Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 less severe fading environment, K=2. When the deterministic or LOS component is dominant K=10, (i.e., the channel is more close to AWGN channel) as shown in figure 6 the lowest energy consumption per bit is given by the case when there is one transmit node and two receive cooperative nodes, it remains with lowest energy per bit up to the transmission range of 100m., after that (1,4 TR nn==) combination becomes the lowest energy. This confirms the effectiveness of large receive diversity in long haul transmissions because at large distances the 1st term (which depends upon d, nT, and nR) in equation (2) becomes more dominant than 2nd and 3rd terms. In pure deterministic or LOS communications with BS, we have neglected the receive circuit energy consumption in the BS, because BS has no energy constraint. Figure 7, shows that the receive diversity case (1,4 TR nn==) renders the least energy consumption per bit in the entire transmission range. Due to the LOS BS antennas orientation the energy consumption per bit is smallest among all other Ricean cases. But the cost we have given for this, is the degradation in spectral efficiency (bps/Hz). Figure 8 shows a comparison of LOS orthogonal channel capacity (2,2 TR nn==) with (1, 4 TR nn==). We can see that there is a trade off between energy consumed per bit and the capacity. In most of the cases capacity is not the main issue, and we are more concerned about the energy consumption. Finally, figure 9 shows how cooperative energy consumption depends on the constellation sizebfor various cooperative MIMO schemes. It is clear from Figure 9 that there is an optimal constellation size for each cooperative MIMO scheme for which the total transmission energy per bit is minimized. It again strengthens our argument that receive diversity give more energy efficient cooperative communication. We have used following approx. expression to obtain relation between BER and SER in (3) for K=1, 2 ,2 log b M b P PM M ≈= (12) Table 1. 6. Conclusion Geometric orientation based selection of cooperative nodes and the specific placement of antennas at BS, greatly impact the total transmission energy consumption per bit and the capacity of the backbone link. Simulation results show that, using the geometric advantages in selecting the cooperative nodes, we come across an energy efficient transmission for different transmission ranges. Since the sensor network is data centric and most of the time there is unidirectional data flow (from network to BS), therefore cooperative communication with minimum number of transmit nodes and maximum optimal number of receive nodes result in low energy per bit transmission. An optimal constellation size for various cooperative schemes also reveals that receive cooperative diversity is near optimal. A trade off exists between energy consumption per bit and the capacity. Since sensor networks are usually a low data rate networks, therefore we usually opt low energy cooperative communication. 7. Acknowledgement This work was supported by National advanced technologies researching and developing programs. (China 863 programming, NO.: 2006AA01Z257). Figure 2. nT transmit and nR receive cooperative nodes LOS channel model 11.5 22.5 33.5 4 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4x 10-7 Transmission distance ratio Extra energy consumption per bit (J) Extra Energy Consumption compared to our Algorithm K=1 K=2 K=10 K->infinity Figure 3. Energy consumption as compared to our algorithm 3 10 b P− = ρ 2, 1 T R n n = = 1, 2 T R n n = = 2, 2 T R n n = = 1, 4 T R n n = = 2, 4 T R n n = = K=1 16.6 13.6 8.8 5.8 4 K=2 14.7 11.7 7.9 4.9 3.5 K=10 9.9 6.9 6 3 2.7 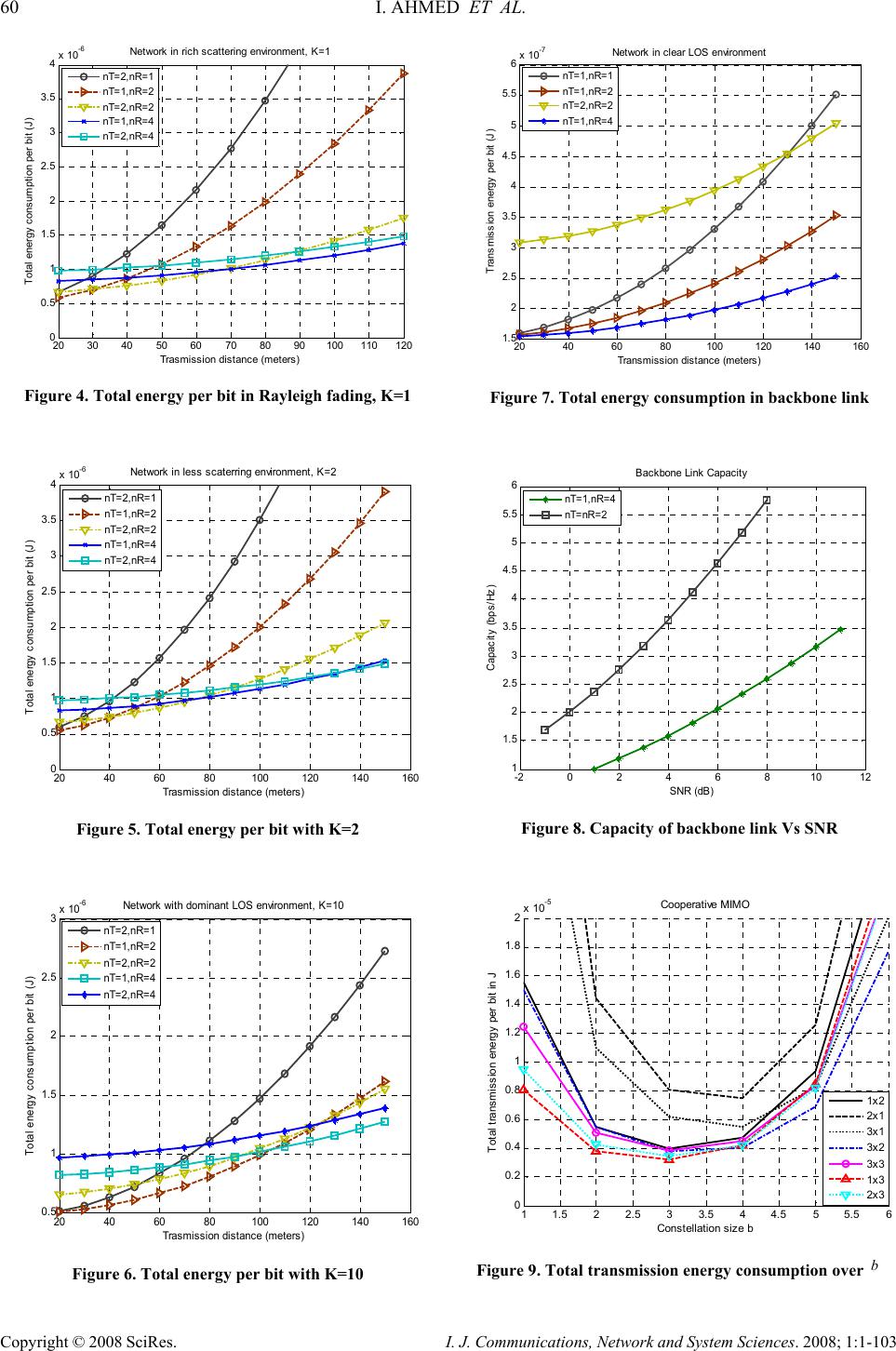 60 I. AHMED ET AL. Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 20 30 4050 6070 80 90100110120 0 0.5 1 1.5 2 2.5 3 3.5 4x 10 -6 Trasmission distance (meters) Total energy consumption per bit (J) Network in rich scattering environment, K=1 nT=2,nR=1 nT=1,nR=2 nT=2,nR=2 nT=1,nR=4 nT=2,nR=4 Figure 4. Total energy per bit in Rayleigh fading, K=1 20 40 60 80100 120 140 160 0 0. 5 1 1. 5 2 2. 5 3 3. 5 4x 10 -6 Trasmission distance (meters) Total energy consumption per bit (J) Network in less scaterring environment, K=2 nT=2,nR= 1 nT=1,nR= 2 nT=2,nR= 2 nT=1,nR= 4 nT=2,nR= 4 Figure 5. Total energy per bit with K=2 20 40 6080100120 140 160 0. 5 1 1. 5 2 2. 5 3x 10 -6 Trasmission distance (meters) Total energy consumption per bit (J) Network with dominant LOS environment, K=10 nT=2,nR= 1 nT=1,nR= 2 nT=2,nR= 2 nT=1,nR= 4 nT=2,nR= 4 Figure 6. Total energy per bit with K=10 20 40 6080100120 140 160 1. 5 2 2. 5 3 3. 5 4 4. 5 5 5. 5 6x 10 -7 Transmission distance (meters) Transmission energy per bit (J) Network in clear LOS environment nT=1,nR=1 nT=1,nR=2 nT=2,nR=2 nT=1,nR=4 Figure 7. Total energy consumption in backbone link -2 0246810 12 1 1. 5 2 2. 5 3 3. 5 4 4. 5 5 5. 5 6 SNR (dB) Capacity (bps/Hz) Backbone Link Capacity nT=1,nR=4 nT=nR=2 Figure 8. Capacity of backbone link Vs SNR 11.5 22.5 33.5 44.5 55.5 6 0 0. 2 0. 4 0. 6 0. 8 1 1. 2 1. 4 1. 6 1. 8 2x 10-5 Constellation size b Total transmission energy per bit in J Cooperative MIMO 1x2 2x1 3x1 3x2 3x3 1x3 2x3 Figure 9. Total transmission energy consumption over b  EXPLOITING GEOMETRIC ADVANTAGES OF COOPERATIVE COMMUNICATIONS FOR ENERGY 61 EFFICIENT WIRELESS SENSOR NETW Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 8. References [1] A. Paulraj, R. Nabar, and D. Gore, Introduction to Space-Time Wireless Communications, Cambridge Univ. Press, 2003. [2] C. Shuguang and A. Goldsmith, “Energy-efficiency of MIMO and cooperative MIMO techniques in sensor networks,” IEEE J. Select. Areas in Comm., vol. 22, no. 6, pp. 1089–1098, Aug.2004. [3] Wenyu Liu Xiaohua Li Mo Chen, “Energy efficiency of MIMO transmissions in wireless sensor networks with diversity and multiplexing gains,” Acoustics, Speech, and Signal Processing, 2005. Proc. (ICASSP’05). IEEE International Conference, Vol.: 4, On page(s): iv/897- iv/900 Vol. 4 March 2005 [4] Wenfeng Li; Weike Chen; Xinzhu Ming, “A Local-centralized Adaptive Clustering Algorithm for Wireless Sensor Networks,” Proc. -15th Int’l Conf. on Computer Comm. and Networks, Oct. 2006 Page(s):149 – 154 [5] SangHak Lee; JuneJae Yoo; TaeChoong Chung; “Distance based energy efficient clustering for wireless sensor networks,” 29th Annual IEEE International Conference on Local Computer Networks, 2004, 16-18 Nov. 2004 Page(s):567 – 568 [6] O. Younis and S. Fahmy, “Distributed Clustering in Adhoc Sensor Networks: A Hybrid, Energy-Efficient Approach”, IEEE INFOCOM 2004, Mar. 2004. [7] Y. Xu, J. Heidemann, and D. Estrin, “Geography-Informed Energy Conservation for Ad Hoc Routing,” MOBICOM 2000, Rome, Italy, July 2001, pp. 70-84. [8] Sankaranarayanan, L.; Kramer, G.; Mandayam, N.B.; “Hierarchical sensor networks: capacity bounds and cooperative strategies using the multiple-access relay channel model,” First Annual IEEE Comm. Society Conference on Sensor and Ad Hoc Comm. and Networks 2004. [9] J. N. Laneman, D. N. C. Tse, and G. W. Wornell, “Cooperative diversity in wireless networks: Efficient protocols and outage behavior,” IEEE Trans. on Information Theory, vol. 22, no. 12, pp. 3062–3080, Dec 2004. [10] Yong Yuan, Min Chen, Tackyong, “A Novel Cluster-based Cooperative MIMO Scheme for Multihop Wireless Sensor Networks”, EURASIP Journal on Wireless and Networking, Vol 2006, Article ID 72493, page 1-9. [11] S. Alamouti, “A simple transmit diversity technique for wireless communications,” IEEE J. Select. Areas Commun., vol. 16, pp. 1451–1458, Oct. 1998. [12] Joseph Polastre, Robert Szewczyk, and David Culler, “Telos: Enabling Ultra-Low Power Wireless Research,” Proceedings of the 4th Int’l symposium on Information processing in sensor networks, Los Angeles, California, Apr.2005 [13] P.F. Driessen, G.J. Foschini, “On the capacity of multiple- input multiple-output wireless channels: a geometric interpretation,” IEEE Trans. Commun., vol. 47, No.2, pp.173-176, Feb. 1999. [14] S. K. Jayaweera, “Virtual MIMO-based cooperative communications for energy-constraint wireless sensor networks”, IEEE Trans. on wireless comm., Vol. 5, No. 5, May 2006 |

