Engineering
Vol. 3 No. 7 (2011) , Article ID: 6155 , 8 pages DOI:10.4236/eng.2011.37094
Suiting Dynamic Models of Fixed-Bed Catalytic Reactors for Computer-Based Applications
1Petrobras, Paulínia Refinery (Replan), Paulínia, Brazil
2Laboratory of Optimization, Design and Advanced Control, School of Chemical Engineering, University of Campinas, Campinas, Brazil
3Institute of Mathematics, Statistics, and Scientific Computation, University of Campinas, Campinas, Brazil
E-mail: eduardo.coselli@petrobras.com.br
Received March 11, 2011; revised May 31, 2011; accepted June 10, 2011
Keywords: Dynamic Models, Inverse Response, Fixed-Bed, Catalytic Reactors, Simulation
ABSTRACT
This work investigated the applicability of heterogeneous and pseudo-homogeneous models to predict the dynamic behavior of a fixed-bed catalytic reactor. Some issues concerning the dynamic behavior of the system were discussed, such as the prediction of the inverse response phenomenon. The proposed models (Heterogeneous I and II and Pseudo-homogeneous) were able to predict with qualitative similarity the main characte-ristics of the dynamic behavior of a fixed-bed catalytic reactor, including the inverse response. The computational time demanded for the solution of the heterogeneous models was 10% to 50% longer than in the case of the pseudo-homogeneous model, making the use of the former suitable for applications where computational time is not the major restriction (off-line applications). On the other hand, when on-line applications are requi-red, the simplified model (Pseudo-homogeneous model) showed to be a good alternative because this model was able to predict (qualitatively) the dynamics of the reactor using a faster and easier numerical solution.
1. Introduction
Nowadays, the economic feasibility of many commodity production processes characterized by large throughputs relies on computer-based operations, in which a good process model is not only important, but necessary. This is especially true for fixed-bed catalytic reactors, whose nonlinear and complex behavior makes it difficult to obtain their best performance (high conversion). The interest in this class of reactors lies on their recognized importance in the chemical and petrochemical industries, so much for the volume of products generated as well as for the economical amount of such products.
Generally, dynamic models reveal more information about the reactor performance, and they can also be used for simulating steady-state operation. The need for a dynamic model is especially strong when process start-up, shut down, or transients during process disturbances are simulated, but also in safety studies [1,2]. A comprehensive mathematical model of a fixed-bed catalytic reactor usually has a complex formulation and some features associated with its behavior can only be revealed through transient analysis. When running exothermic reactions, these reactors are dynamically unstable in the sense that they tend to amplify transient perturbations of input temperature, rather than attenuating them. This dynamic, thermal instability results from the inherently different rates of matter and heat flow through the reactor bed, together with the positive thermal feedback inherent in exothermic reaction [3]. These non-linear distributed features give rise to phenomena such as the inverse response, hot spots and, ultimately, catastrophic instabilities such as the temperature runaway [4,5]. Furthermore, the location of regions with unstable behavior can change in space and time and is dependent on input disturbances and control actions. For these reasons, the detailed formulation of the model considering the equations in dynamic mode is necessary to ensure the reliability of such complex predictions.
The construction of a reliable model depends mainly on identifying how the physic-chemical mechanisms and external factors affect the overall performance of the system. Particularly when on-line applications are required, simplified models that reproduce the essential characteristics of the system are preferred because computational time is a major restriction in these cases. Bearing this in mind, the object of the present studies was the development of dynamic models of fixed-bed catalytic reactors based on the heterogeneous and pseudo-homogeneous approaches. The models show different degrees of details and the analyses of the dynamic behavior of a fixed-bed catalytic reactor that promotes the oxidation of ethanol into acetaldehyde allowed to identify the differences in the predictions generated by each model as well as to determine which model is more adequate for a specific application, either offor on-line.
2. Mathematical Models
Based on mathematical models available in the literature [6-12], three deterministic mathematical models designed to represent the dynamic behavior of a fixed-bed catalytic reactor (Figure 1) were developed according to the following considerations and assumptions: 1) variation of physical-chemical properties and mass and heat transfer coefficients along the reactor length; 2) plug flow profile of velocity; 3) mass and thermal axial dispersion was neglected. These models include aspects whose combination is not usually found in the literature such as consideration 1), variations of coolant fluid temperature and reactor pressure, and temporal dimension.
The partial differential equations were solved by discretization (radial and axial coordinates) through the method of lines in conjunction with orthogonal collocation, originating a system of ordinary differential equations. The resulting equations were integrated over time using the LSODAR algorithm in Fortran 90, which is suitable for stiff systems.
Next, the models are presented in decreasing order of complexity according to the heterogeneous and pseudohomogeneous approaches, which differ in relation how the fluid and solid phases are considered in the formulation. Continuity equation, coolant fluid equation, and momentum balance are the same for all models and, for this reason, they are presented only once in the formulation of the first model.
2.1. Heterogeneous Model I
This model consists of mass and heat balance equations for the catalyst particles as well as for the gas-phase, including the resistances to mass and heat transfer at the
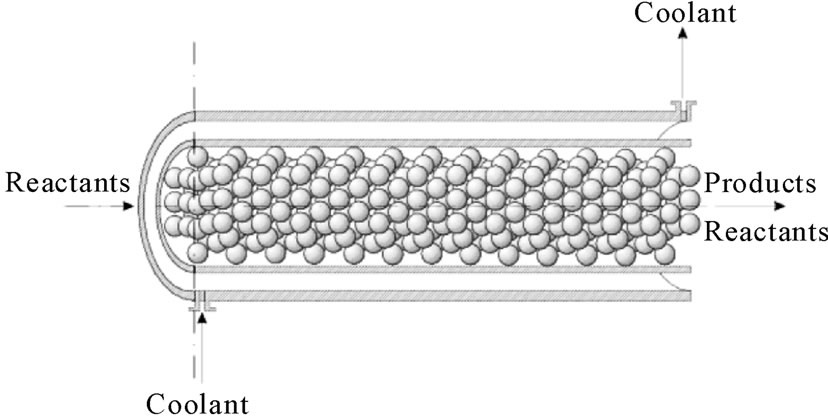
Figure 1. Scheme of a fixed-bed catalytic reactor.
gas-solid interface and also consider the resistances inside the catalyst particle (radial dimension) [9-11].
Reactant Fluid Mass Balance:
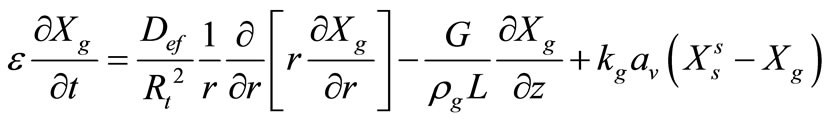 (1)
(1)
Reactant Fluid Energy Balance:
 (2)
(2)
Catalyst Particle Mass Balance:
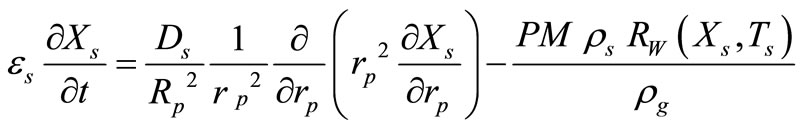 (3)
(3)
Catalyst Particle Energy Balance:
 (4)
(4)
Continuity Equation:
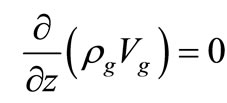 (5)
(5)
Coolant Fluid Equation:
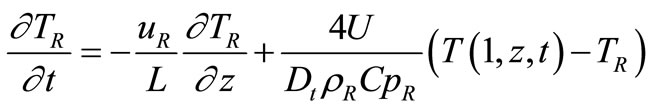 (6)
(6)
Momentum Balance:
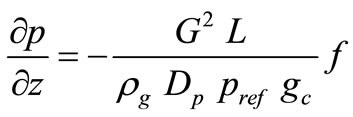 (7)
(7)
with the following boundary conditions:
 (symmetry)(8)
(symmetry)(8)
 (symmetry)(9)
(symmetry)(9)
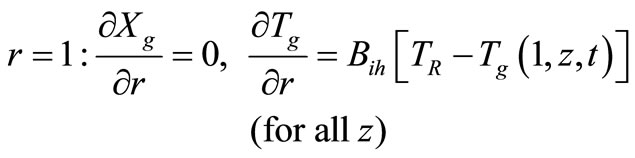 (10)
(10)
 (11)
(11)
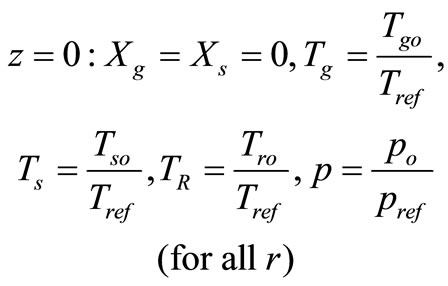 (12)
(12)
2.2. Heterogeneous Model II
This model is a simplification of the Heterogeneous model I. In this case the resistances inside the catalyst particle (radial dimension) are not considered. Temperature and conversion inside the particle are mean values (Tsm and Xsm, respectively).
Reactant Fluid Mass Balance:
 (13)
(13)
Reactant Fluid Energy Balance:
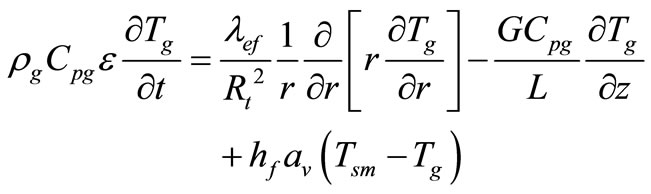 (14)
(14)
Catalyst Particle Mass Balance:
 (15)
(15)
Catalyst Particle Energy Balance:
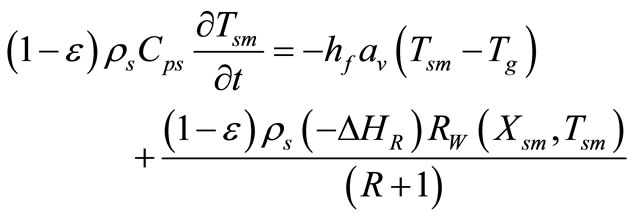 (16)
(16)
with the following boundary conditions:
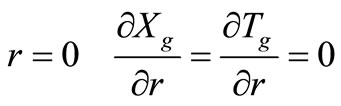 (symmetry) (17)
(symmetry) (17)
 (18)
(18)
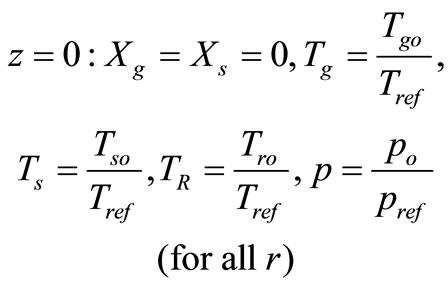 (12)
(12)
2.3. Pseudo-Homogeneous Model
The pseudo-homogeneous model was developed based on the approach that incorporates in the formulation the thermal capacities of the fluid and solid [6,8]. In this manner, the presence of the solid is considered implicitly and the reactor is described as having only one single phase.
Mass Balance:
 (19)
(19)
Energy Balance:
 (20)
(20)
where

with the following boundary conditions:
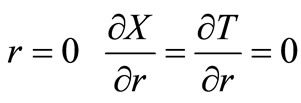 (symmetry)(24)
(symmetry)(24)
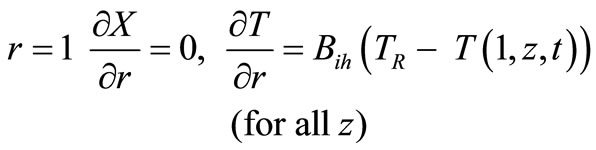 (25)
(25)
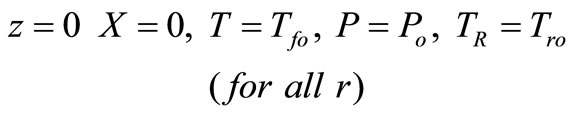 (26)
(26)
3. Case Study
The catalytic oxidation of ethanol into acetaldehyde over Fe-Mo catalyst was considered as case study. This is a very exothermic reaction, and is representative of an important class of industrial catalytic processes. The following reaction rate equation describes the conversion of ethanol into acetaldehyde [13]:
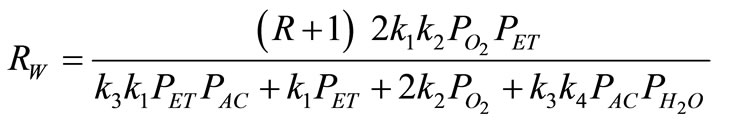 (27)
(27)
4. Results and Discussion
In fixed-bed catalytic reactors, conversion is indirectly regulated by controlling the temperature in the reactor. Thus, the characterization of the thermal behavior of the reactor is essential for the design and operation of the reactor. Bearing this in mind, the feed temperature of the reactant (Tgo) was perturbed by +5% (step perturbation) and the dynamics of the reactor (temperature and conversion) were evaluated (Figure 2). Both heterogeneous and pseudo-homogeneous models were able to predict with qualitative similarity that a perturbation in Tgo causes an inverse response (a temporary behavior contrary to that expected) of the reactor temperature at points located next to the reactor entrance (at z = 0.03 m and 0.13 m; L = 1 m). The inverse response is a typical characteristic of fixed-bed catalytic reactors observed in practice and arises from the presence of different heat capacities of the fluid and solid as well as the bulk flow of fluid, causing interactions between heat and mass transfer phases. This causes differential rates of propagation of heat and mass transfer, which influence the heat generation through reaction on the solid catalyst.
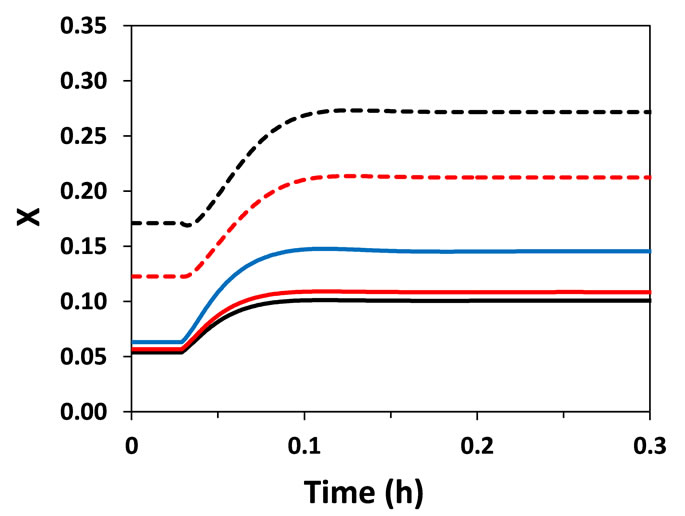 (a)
(a)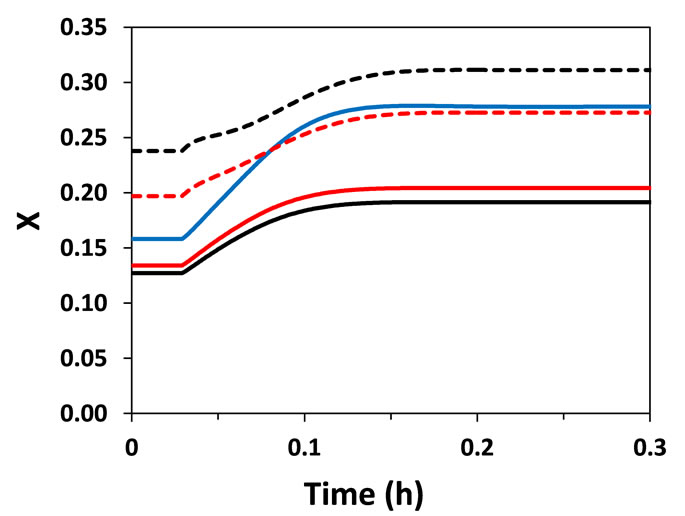 (b)
(b)
Figure 2. Temperature (T) and conversion (X) responses to a step perturbation (+5%) in reactor feed temperature. (a) Near the entrance of the reactor (z = 0.03 m); (b) At z = 0.13 m.
The identification of the inverse response is very important in the elaboration of safe and efficient control strategies. This is a useful piece of information during the choice of pairs of manipulated and controlled variables as well as of axial positions where the control of the system must be placed. For instance, after a step perturbation in the coolant fluid feed temperature (Tro), the inverse response was not observed in the reactor temperature profile (Figure 3). Moreover, Tro had a greater effect on the axial thermal profile of the reactor. This may indicate that the manipulation of Tro is more adequate to control the reactor temperature. However, it is important to have in mind two points: 1) this conclusion cannot be generalized for all operating and design conditions and 2) if necessary, large changes on coolant feed temperature can be difficult due to the high heat capacity of thermal fluids. Figure 4 allows a better understanding of the effects of the step perturbations in Tgo and Tro on reactor temperature throughout reactor length. As mentioned above, inverse response, when observed, took place only in the first portion of the reactor.
Interestingly, temperature and conversion profiles in the catalytic particles determined by Hetero-geneous model II using mean radial values (particle radial dimension was not considered) were very similar to those generated by Heterogeneous model I (Figures 2 and 3). Therefore, the consideration of the internal resistance to mass and energy transfers (in Heterogeneous model I) did not have significant effect on the dynamic behavior of the reactor under the considered operating conditions
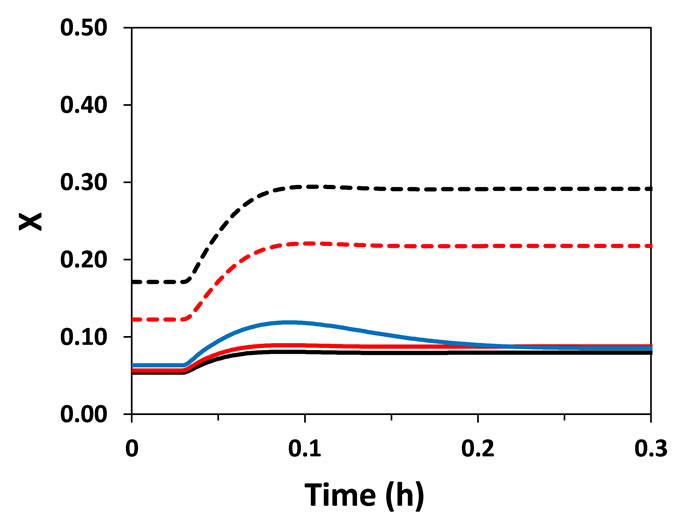 (a)
(a)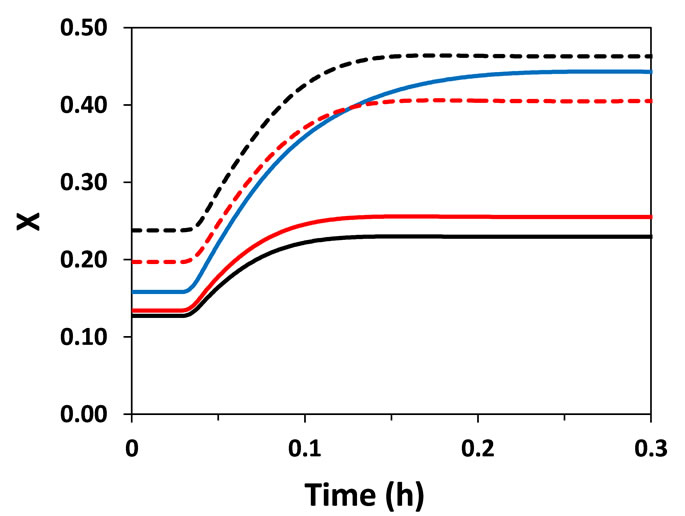 (b)
(b)
Figure 3. Temperature (T) and conversion (X) responses to a step perturbation (+4%) in coolant fluid feed temperature. (a) Near the entrance of the reactor (z = 0.03 m); (b) At z = 0.13 m.
 (a)
(a)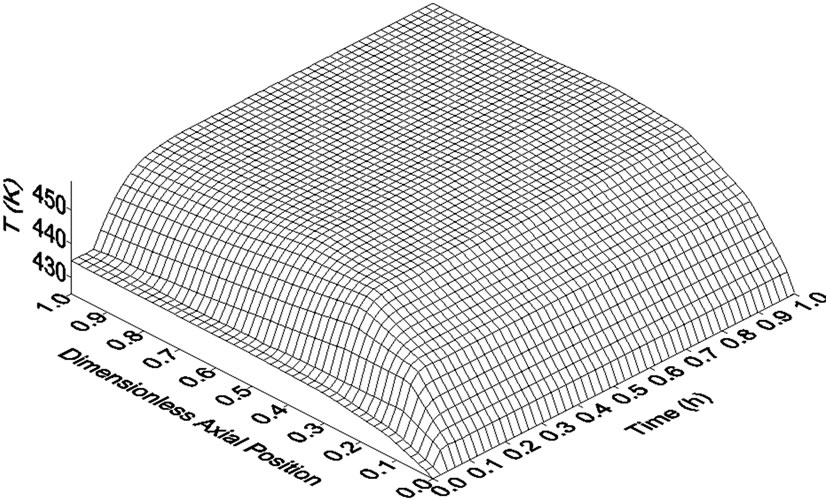 (b)
(b)
Figure 4. Temperature responses along reactor length to step perturbations in (a) reactor feed temperature (+5%) and in (b) coolant fluid feed temperature (+4%). Data generated by Heterogeneous Model I.
and design specifications. The good agreement between the heterogeneous models is especially important in cases that trustful correlations for the determination of heat and mass transfer parameters (those exclusive to model I) are not available. On the other hand, profiles of temperature and conversion determined by the Pseudohomogeneous model were quantitatively different from those obtained with the heterogeneous models.
The choice of which model is more suitable for a particular purpose (either offor on-line applications) should primarily depend on qualitative aspects such as the capability of the model to predict the main features of the dynamics of the reactor. In cases where either industrial or experimental data are not available, such as the case study presented here, the results generated by the most detailed model can be taken as reference for an accuracy comparison (quantitative aspect). Rigorous models generally present good accuracy because they feature a more detailed representation of the physic-chemical phenomena that takes place in the system [7,9,11]. Another important aspect is the computational time, which is the major restriction for on-line optimization and control purposes. Given that the computational time to simulate the Pseudo-homogeneous model was about 10% - 50% lower than that of the Heterogeneous models I and II and also considering that the Pseudo-homogeneous was able to predict the dynamics of the reactor, the proposed formulation for this model showed to be adequate for on-line applications. On the other hand, if quantitative accuracy of the results is demanded, computational time is not a restriction, and detailed physical-chemical data for reactants and catalyst are available, the heterogeneous models should be preferred. Examples of applications for the rigorous model would include design, and planning of start-ups, shutdowns and emergency procedure.
It is important to highlight that the performance of the models can be different for other operating conditions and design specifications, as well as for other reacting systems. Perturbations with different intensities can also have effects on the performance of the models. Therefore, for any of these scenarios, the quality of the predictions generated by the models should be reanalyzed in order to determine the best application for each model.
5. Conclusions
The proposed models (Heterogeneous I and II and Pseudo-homogeneous) were able to predict with qualitative similarity the main characteristics of the dynamic behavior of a fixed-bed catalytic reactor, including the inverse response phenomenon. This knowledge is essential for the design and operation of fixed-bed catalytic reactors. The computational time demanded for the solution of the heterogeneous models was 10% to 50% longer than in the case of the pseudo-homogeneous model, making the use of the former suitable for applications where computational time is not the major restriction (off-line applications). On the other hand, when on-line applications are required, the simplified model (Pseudohomogeneous model) showed to be a good alternative because this model was able to predict (qualitatively) the dynamics of the reactor using a faster and easier numerical solution.
6. REFERENCES
- H. H. Lou, J. Chandrasekaran and R. A. Smith, “LargeScale Dynamic Simulation for Security Assessment of an Ethylene Oxide Manufacturing Process,” Computers & Chemical Engineering, Vol. 30, No. 6, 2006, pp. 1102- 1118. doi:10.1016/j.compchemeng.2006.02.011
- V. Alopaeus, H. Laavi and J. Aittamaa, “A Dynamic Model for Plug Flow Reactor State Profiles,” Computers & Chemical Engineering, Vol. 32, No. 7, 2008, pp. 1494- 1506. doi:10.1016/j.compchemeng.2007.06.025
- A. Jaree, B. Boonsomlanjit and J. Limtrakul, “On the Dynamical Instability of Packed-Bed Reactors in the Presence of Catalyst Deactivation,” Computers & Chemical Engineering, Vol. 32, No. 12, 2008, pp. 2897-2902. doi:10.1016/j.compchemeng.2008.02.004
- A. Jaree, R. R. Hudgins, H. Budman, R. L. Silveston, V. Yakhnin and M. Menzinger, “Amplification of Inlet Temperature Disturbances in a Packed-Bed Reactor for CO Oxidation over Pt/Al2O3,” Chemical Engineering Science, Vol. 58, No. 3-6, 2003, pp. 833-839. doi:10.1016/S0009-2509(02)00614-0
- C. McGreavy and R. M. Filho, “Dynamic Behaviour of Fixed Bed Catalytic Reactors,” In: IFAC Dynamics and Control of Chemical Reactors, Maastricht, the Netherlands, 1989.
- A. Jutan, J. P. Tremblay, J. F. McGregor and J. D. Wright, “Multivariable Computer Control of a Butane Hydrogenolysis Reactor: Part I. State Space Reactor Modelling,” AIChE Journal, Vol. 23, No. 5, 1977, pp. 732-742. doi:10.1002/aic.690230516
- O. M. Martinez, S. J. Pereira Duarte and N. O. Lemcoff, “Modeling of Fixed Bed Catalytic Reactors,” Computers & Chemical Engineering, Vol. 9, No. 5, 1985, pp. 535- 545. doi:10.1016/0098-1354(85)80028-4
- R. Maciel Filho, “Modelling and Control of Multitubular Reactors,” Ph.D. Dissertation, University of Leeds, Leeds, 1989.
- L. Pellegrini, G. Biardi and E. Ranzi, “Dynamic Model of Packed-Bed Tubular Reactors,” Computers Chemical Engineering, Vol. 13, No. 4-5, 1989, pp. 511-518. doi:10.1016/0098-1354(89)85033-1
- G. H. Froment and K. B. Bischoff, “Chemical Reactor Analysis and Design,” 2nd Edition, John Wiley & Sons, New York, 1990.
- S. S. E. H. Elnashaie and S. S. Elshishini, “Modelling, Simulation and Optimization of Industrial Fixed Bed Catalytic Reactors,” Topics in Chemical Engineering, Vol. 7, 1st Edition, Gordon and Breach Science Publishers, Yverdon, Switzerland, 1993.
- E. C. V. de Toledo, “Modelling, Simulation and Control of the Fixed Bed Catalytic Reactors,” Ph.D. Dissertation, University of Campinas, São Paulo, 1999.
- R. Maciel Filho, “Oxidação Catalítica de Etanol a Acetaldeído sobre Catalisador de Óxido de Ferro-Molibdênio,” Msc. Thesis, University of Campinas, São Paulo, 1985.
Nomenclature
am catalyst heat transfer area, m2/kgcatalyst
av catalyst surface area per unit catalyst volume, m–1
Bih Biot Number
Cp calorific capacity, kcal/kg·K
D radial effective diffusivity, m/h
Dp particle diameter, m
f friction factor
G mass flow velocity, kg/m2·h
gc conversion factor
hf particle to fluid heat transfer coefficient, kcal/ m2·h·K
hW convective heat transfer coefficient in the wall, kcal/m2·h·K
kg particle to fluid mass transfer coefficient, m/s
ki kinetic constants in Arrhenius Equation
L reactor length, m
p reactor pressure, atm
PAC partial pressure of acetaldehyde
PET partial pressure of ethanol
 partial pressure of water
partial pressure of water
PM mean molecular weight, kg/kmol
 partial pressure of oxygen
partial pressure of oxygen
r reactor dimensionless radial distance
R air to ethanol ratio
rp particle dimensionless radial distance
Rp particle radius, m
Rt reactor radius, m
RW rate of oxidation, kmolreactant/h.kgcatalyst
T temperature, K
Tsm mean radial temperature of the solid phase, K
t time, h
T(1, z, t) wall temperature of the reagent fluid, K
u velocity, m/h
U global heat transfer coefficient, kcal/m2·h·K
V velocity, m/h
X conversion
Xsm mean radial conversion of the solid phase
z dimensionless axial distance
Greek Letters
λ conductivity, kcal/m·h·K
ρ density, kg/m3
ε porosity
ρB catalyst density, kgcat/m3
ΔHR molar reaction enthalpy, kcal/kmol
ρs catalyst density, kgcat/m3
Subscripts
ef` effective
f fluid
g gas
i interstitial
o feed
R refrigerant (coolant)
ref reference
s solid
Superscript
s condition at external surface

