Received 3 May 2016; accepted 15 May 2016; published 16 August 2016

ABSTRACT

The booming electronics itself carries an impact on power quality. Superconducting Magnetic Energy Storage (SMES) is proposed to enhance power quality in three-phase systems under various loads. This paper aimed to compensate the voltage sags under various faults in the grid systems. The SMES is selected as an energy storage unit to improve the capability of voltage sag compensation. Optimized Dual Fuzzy Flow (ODFF) logic controller is designed to prevent the voltage sag time during excessive phase voltage variation. Hence the proposed controller strategy reduces the total harmonic distortion during various fault conditions. To regulate the contribution of active power, the least possible value is improved using ODFF. The depth of voltage sags compensation is achieved by the over modulation and an iterative loop is designed in the control block. While protecting sensitive loads from voltage disturbances, and sags initiated by the power system, the proposed configuration is advantageous for an industrial implementation. It is found that the proposed method can result in more than 50% additional sag support time when compared with the previous methods such as PI and PSO. Utilizing MATLAB Simulink, compensation of sag and minimization of THD is established, and the simulation tests are performed to evaluate the performance of the proposed control method.

Keywords:

Optimized Dual Fuzzy Flow (ODFF), Superconducting Magnetic Energy Storage (SMES), Total Harmonic Distortion (THD), Voltage Sag Compensation, Voltage Sag Depth

1. Introduction

In industrial distribution systems, the grid voltage disturbances (voltage sags, swells, flicker, and harmonics) are the most common power quality problems. Sag, being the most frequent voltage disturbance, is typically caused by a fault at the remote bus and is always accompanied by a phase angle jump. The phase jump in the voltage can initiate transient current in the capacitors, transformers, and motors [1] .

Harmonics and non-linear loads lead to major power quality issues. The Dynamic Voltage Restorer (DVR) in [2] , nevertheless uniquely compensates on sag, it limits itself for certain percentage and thus the quality problem is not suppressed completely. The sag compensation factor is directly proportional to the rate of sag depth in a grid system. The Dynamic Voltage Restorer with other controlling techniques gives positive result on quality enhancement with its advantage of less computational efforts and low cost [3] .

The Superconducting Magnetic Energy Storage (SMES) [4] is expected to contribute to high power quality due to its characteristics of swift response and energy storage. The system voltage wavering can be compensated by the SMES. The parallel connection of SMES controls the system voltage indirectly by regulating the injecting current of SMES. The SMES can be expressed as

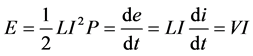(1)

The capability of compensation is inclined by short circuit capacity of the system and SMES location. The power factor is another crucial factor to be noted for analyses.

The DVR based SMES leads to better compensation than individual performance of DVR. The series injected voltage of the DVR can be written as

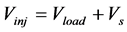(2)

Voltage sag is a momentary decrease in RMS AC voltage 0.1 - 0.9 p.u of the nominal voltage at the power frequency derived in [5] . Voltage swell or sag (dips) is caused by faults occurring in the customers’ installations on the public distribution systems. The power quality problems become major concerns of industries due to massive loss of time and cost. Reduction of voltage sags, harmonic distortion and interruptions solves the issues in power quality problems. The number of methods available to overcome the voltage sags such as DVR is one of the best methods to compensate voltage sag. DVR is an electronic device that is able to compensate the voltage sag on critical loads dynamically. Thus the compensation of sag is done by fuzzy logic and BFO fuzzy logic function which takes two inputs: error (e) and error rate and gives one output.

In this paper, section 2 describes the brief survey on the related work and section 3 presents the proposed methodology and Optimized Dual Fuzzy Flow (ODFF) logic controller circuits are briefed in section 4 and section 5. The simulation test outputs are discussed in section 6 and finally concluded in section 7.

2. Previous Research

Numerous related research works are already existed in literature which based on power quality control, THD and Voltage sag compensation system. Some of them are reviewed here.

The emphasis is on either reducing the voltage rating of DVR by aligning the injected voltage with the source voltage (i.e., in-phase compensation) or minimizing the dc storage capacity by using the reactive power compensation/energy-optimized approach presented in [6] . All of these methods, however, cannot correct the phase jump and thus can result in premature tripping of sensitive loads discussed in [7] .

Kumar and Mishra discussed about the first category are series active filters (SeAFs), including hybrid- type ones [8] . They were developed to eliminate current harmonics produced by nonlinear load from the power system. SeAFs are less scattered than the shunt type of active filters presented in [9] . The advantage of the SeAF compared to these hunt type is the inferior rating of the compensator versus the load nominal rating. However, the complexity of the configuration and necessity of an isolation series transformer had decelerated their industrial application in the distribution system are briefed in [10] .

The concept of AC voltage sags and swells compensator based on three-phase hybrid transformer with buck? boost matrix-reactance chopper. Commonly known as DVR, they have a similar configuration as the SeAF [11] . These two categories are different from each other in their control principle. This difference relies on the purpose of their application in the system. Hybrid Series Active Filter design eliminates the voltage distortions and power distortions at the point of common coupling (PCC). Hypothetically, they are capable of compensating current harmonics, ensuring a Power Factor (PF) correction at the PCC [12] . The concept of Decoupled State Feedback Control for Current Source Power Conditioning is presented in [13] .The idea of compensating voltage fluctuations using SMES based Dynamic Voltage Restorer for long term where the simulation result illustrates the superconducting magnets increases the compensation when compared to the capacitor banks [14] .

The fuzzy system has proved the better minimization of the THD than using PI controllers. The output depicts that the THD is minimized after the BFO optimization. DVR based different controllers are designed to improve power quality regarding sag and swell characteristics under different load conditions [15] . M. Manikandan and A. Mahabub Basha proposed their work on the improvement of power quality and three phase or single phase fault leading to sag compensation by SMES combined with Fuzzy logic control [16] .

The basic concept of fuzzy control strategy and problem-solving methods are discussed with clear key points [17] . The application of fuzzy logic to knowledge representation relating to the industrial computational system is presented in [18] . The concept of uncertainty and imprecision in the context of knowledge, meaning, and inference is discussed.

3. Proposed Topology

The schematic diagram of the proposed topology with detailed phase sag supporter is shown in Figure 1. The voltage sag supporter is provided between the PCC and the load. When a voltage sag occurs at the PCC of any of the phases, the corresponding sag supporter injects appropriate voltage in series with the supply voltage to maintain the desired load voltage.

To account for phase Skip compensation, this topology incorporates the merits of the inter phase ac?ac topology, by having a sag supporter with two choppers and isolation transformers in each phase. The secondary’s of the isolation transformers are connected such that they add the output voltages of the choppers and inject them. Deriving the injected voltage from two voltage sources facilitates the realization of the desired reference voltage with phase shift. In this scheme, compensation of fundamental quantities has been considered. In case of harmonics; fundamental components are extracted and compensated by the scheme.

3.1. Proposed Phase Skip Scheme for Voltage Sag Compensation

The work presented in this paper proposes an enhanced voltage sag compensation method to extend the SMES based DVR compensation time. It optimizes the gradient of the dc link voltage (dvdc/dt) by regulating the amount of active power injected by SMES based DVR. In the proposed method, the controller restores both phase and amplitude of the load voltage to the presag value and then initiates a transition toward the Low active power (LAP) mode. The overall operation sequence and implementation of the proposed compensation method is discussed in the following subsections.

3.1.1. Phase Skip Detection and Presag Restoration

For detecting the phase Skip, two PLLs are employed (one over the load voltage and another over the source voltage), giving θ_VL and θ_Vg, respectively. As soon as the sag is detected, the first step is to determine the SMES based DVR initial injection angle that avoids the phase Skip at the load side. This is done by freezing the load voltage PLL that gives the presag angle (θ_VLp). On the other hand, the unrestricted grid voltage PLL gives the grid voltage phase (θ_Vg). The difference between these two angles gives the initial angle of injection Note that, in the steady state, both angles will be identical, and thus, the difference will be zero. For sag detection, the absolute difference between the reference load voltage (1 p.u.) and the actual grid voltage (p.u.) in synchronous reference frame is calculated as follows:

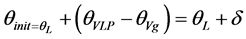(3)

For sag detection, the absolute difference between the reference load voltage (1 p.u.) and the actual grid voltage (p.u.) in synchronous reference frame is calculated as follows

(4)

3.1.2. Controlled Transition toward the LAP Mode

Once the presag voltage is successfully restored, after one cycle, a smooth transition toward the LAP mode is initiated and completed over the next one to two cycles. The final injection angle of SMES based DVR (θ_fin) is given as

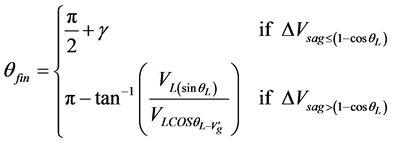(5)

The first part of Equation (5) represents the self-supporting mode of operation in which the SMES based DVR absorbs active power (relatively very small amount) from the grid to overcome the system losses and thus maintains a constant voltage across the dc link capacitor. The term γ indicates the reduction in θ_fin due to loss component and it is determined by the dc link (PI) controller. The second part of Equation (5) represents a case where the self-supported dc link. To ensure a smooth changeover, a transition ramp is defined between the initial and final operating points, as given in the following:

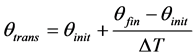(6)

3.1.3. Iterative Decrement in Injection Angle

In self-supporting mode, the SMES based DVR can compensate the sag for an indefinitely long time. However, for deeper sag depths, there is certain nonzero active power injected by SMES based DVR. This causes a reduction in the energy stored in the dc link capacitor, and consequently, its voltage reduces (gradually). To maintain the required voltage at the inverter output side, the controller increases the modulation index mi until it reaches mi-max. This is the limiting case as explained by Equation (7), beyond which the controller goes into over modulation and cannot maintain the rated load voltage. To avoid this over modulation condition, an iterative control loop is used, which constantly monitors the dc link voltage and decreases θ_fin in Equation (6) to keep V_dc > V_dc−min and is given as

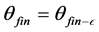(7)

3.1.4. Operation Sequence

Figures 2(a)-(c) depict the overall operation sequence of the proposed phase Skip compensation scheme. The transition from high active power mode (presag) to LAP mode is shown in three steps. The illustration is for the case where the sag depth is more than the limit in (5) and there is a positive phase Skip associated with the sag. As discussed previously and shown in Figure 2(a), SMES based DVR initiates the compensation by supplying high active power to the load (V_r1 _ V_x1) and restores both magnitude and phase of the load voltage to presag values. After one cycle, the transition toward the LAP mode is initiated, and SMES BASED DVR gradually increases the contribution of reactive power. As seen from Figure 2(b) and Figure 2(c), the injected voltage magnitude and its phase angle are gradually increasing until V_L reaches V_L−opt. Note that at the final operating point V_r1 _ V_x1. The aforementioned SMES based DVR operation can be viewed as an equivalent variable impedance Z_v where the operation begins with dominant resistive impedance Z_v = R (high active power) and completes as dominant capacitive impedance Z_ν ≈ XC (high reactive power).

4. SMES Based DVR ODFF Switching Logic

Selection of switching logic for the proposed topology to compensate voltage sags are elucidate in this section. To obtain the reference load voltage, the control system is divided into two sub modules: 1) phase Skip detection plus SMES based DVR injection angle calculation and 2) LAP injection.

To achieve a decoupled active and reactive power control, the phase of the line current is considered as the reference and is obtained by the PLL. The phase Skip detection block computes the SMES based DVR initial (presag injection) angle and final (LAP injection) angle. As shown in Figure 3, the obtained SMES based DVR reference voltage V_dvr is compared with the actual voltage in the stationary reference frame. A proportional-resonant (PR) controller with a large gain at the grid fundamental frequency is used for accurate tracking of V_dvr. To compensate for SMES based DVR system losses, V_dvr is added as a feed forward signal to the output of the PR controller. The dc link voltage is constantly monitored in an iterative control loop to regulate the injected voltage angle, thus avoiding over modulation. Note that this block is only required when the sag depth is close to the system design limit.

4.1. Proposed ODFF Optimized Dual Fuzzy Flow Algorithm

The proposed ODFF flow is represented in Figure 4. The proposed system is designed to consider Fault distur-

bances of the DVR. Initially, Continuous Wavelet Transform is applied to extract the features of Power system dataset block. The difference in generated and converter voltage is identified. The proposed Fuzzy uses two models. The first model is called the plant, which describes a virtual Machine model. The second type of model is known as a system model, which shows the load voltage regulatory system in a SMES based DVR model. The Proposed model is used to specify the AC load assessment whenever sags are generated, and LAP mode is injected subcutaneously. And also this model finds a suitable way of directing voltage injections.

(8)

where x and y are the input variables, A and B represents fuzzy sets in the antecedent part, and the consequent part (output) is 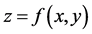which is a crisp function, e.g.. This equation represents first-order polynomial function, but it can also be any function that describes the output within the fuzzy region mentioned by the antecedence of the rule. There are two unknowns design parameters: p₀ and p₁, the value for these parameters are identified through a linear system of algebraic equations (Figure 5).

The degree the input matches i^th rule is typically computed using min operator:

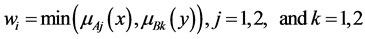(9)

Each specified fuzzy rule has a crisp output. The Overall output is attained through weighted average (reduce computation time of defuzzification required in a Mamdani model)

(10)

where is matching degree of rule R_i (result of the if … part evaluation), i = 1, 2. The solution for the coefficients of the consequent in TSK Systems

There are two unknowns: p₀ and p₁. So we need two simultaneous equations for two values of x, say x₁ and x₂, and two values of y ? y₁ and y₂

In order to determine the values of the parameters p in the consequents, one solves the LINEAR system of algebraic equations and tries to minimize the difference between the ACTUAL output of the system (Y) and the simulation [X]^T[P]:

4.1.1. Algorithm Flow of ODFF

・ FUZZUFICATION: The values of the membership functions for the two values x₁ = 12 & x₂ = 5 shown in Table 1.

・ INFERENCE & CONSEQUENCE: The Sample System Rules are shown in Table 2.

・ AGGREGATION:

Using a Centre of Area computation for y we get:

4.1.2. Optimization of ODFF Parameter Tuning

The simulation of system is based on the intensity of pheromone and the path length. The probability with which an ant ‘a’ selects the path from i to j is defined in Equation,

(11)

where and are the intensity of pheromone and the length of the path between features j and i, respectively. and are the control parameters for defining the weight of the trail intensity and the length of the path, respectively. is the set of neighbors of feature i for the d^th ant. After selecting the next path of features, the trail intensity of pheromone is updated and defined in Equation (12).

(12)

is the phenomenon trial evaporation rate. is the amount of pheromone trail added to by ants. d is a constant parameter. Lr is the length of the global best tour.

Table 3 expresses rules like:

Rule 1: If e(k) is PL AND De(k) is N then Du(k) = α₁e + β₁De + δ₁

Rule 2: If e(k) is PL AND De(k) is Z then Du(k) = α₂e + β₂De + δ₂ ・・・ etc …

Rule 21: If e(k) is NB AND De(k) is P then Du(k) = α₂₁e + β₂₁De + δ₂₁

α, β and δ are design parameters whose values are determined by the fuzzy system developer, based on relating the behaviour of the errors and change in errors over a fixed range of changes in control. There are 2N a total of design parameters for rules. These TSK parameters are selected by the trial and error method.

5. Results and Discussions

The specifications of the fault occurring system is specified with all the fundamental parameters in Table 4. The values of real power and reactive power at the generation side during fault condition in Table 5.

The SMES based Dynamic Voltage Restorer circuit in the distribution system is shown below in Figure 6.

The control block of chopper circuit is shown in Figure 7 which eliminates the harmonic contents in the phase voltage. This SMES based DVR gets the input from the PWM inverter that which gives the control signal for compensation. The control block shown above receives the parameters by conversion process of abc/dq transform during fault condition and compares with the reference value that which is fed to the SMES based DVR block. The error is filtered not just by comparing the dq values but with the defalut value set to the error comparator block.

The Mamdani for fuzzy logic Error and controller is shown above in Figure 8 that which gives the comparative output of the membership functions. The error and the error rate ranges from −1 to +1 and the output voltage

ranges from −0.5 to +0.5.

The real and reactive power of the three phase distribution line under fault condition whose duration is from 0.1 sec to 0.45 sec without any control techniques is shown in Figure 9. Figure 10 shows the input and output current and voltage waveform during current and voltage waveform at fault without SMES based DVR. In the same manner Figure 11 shows the real and reactive power of the three phase distribution line under fault condition using ODFF control techniques is shown in Figure 12. Shows the input and output current and Voltage waveform during current and voltage waveform at fault using SMES based DVR.

Figure 13 shows the total harmonic distortion value at fault condition before SMES based DVR control the value reaches for about 1.00% for 50 Hz while in the case of using proposed control technique produces very less Distortion value of 0.12% for 50 HZ shown in Figure 14. THD is the summation of all harmonic components of the voltage or current waveform compared against the fundamental component of the voltage current wave. THD can exceed 1 and generally expressed as a percentage. THD calculated as

(13)

The Total Harmonic Distortion THD value after fault compensation primarily sag compensation is shown above in Figure 14 where the range has reduced to 0.12% for 50 Hz.

The cosine of angle between the voltage and current is known as power factor (pf)

(14)

The power factor for the 3 phase system with the ODFF controller for the sag compensation has been obtained as 0.94.

Figure 15 and Figure 16 show the comparative results of with and without using SMES based DVR-ODFF controller in terms of THD, Power factor. Finally, the proposed SMES based DVR using ODFF controller achieves low distortion compared to previous optimization methods. The THD comparative results of different

controller are shown in Figure 17.

6. Conclusion

The compensation on sag in three phase system at distribution end, when eliminated, enhances the stability of

the supply power and also the sustained of the power factor without variation as it is tightly coupled to THD where the results imply the betterment on THD value reduction when compared with the SMES based DVR control without the combination of SMES coil and dual fuzzy logic control.

Cite this paper

M. Manikandan,A. Mahabub Basha, (2016) ODFF: Optimized Dual Fuzzy Flow Controller Based Voltage Sag Compensation for SMES-Based DVR in Power Quality Applications. Circuits and Systems,07,2959-2974. doi: 10.4236/cs.2016.710254

References