ABSTRACT

This work briefly reviews and extends the author’s three previous works (2015), Journal of Modern Physics, 6, 78-87, and 1360-1370; (2016), 7, 1829- 1844 that propose as an alternative to the accelerating ΛCDM universe, the decelerating Einstein de Sitter (EdS) universe, in which dark energy is a different phase of dark matter located only in intergalactic space (IGS), and that instead of a negative pressure, it has an index of refraction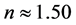, and hence a reduced speed of light c / n through it. This allows the EdS universe to expand the extra distance necessary to obtain the diminished brightness of the Type Ia supernovae. In view of the recent suggestion that the universe is not accelerating, but possibly expanding uniformly, a table is given comparing both the accelerating and uniformly expanding universes with the EdS universe supplemented by the reduced speed of light. It is shown that fitting the uniformly expanding universe leads to a smaller value of n, and hence too short an age for the EdS universe, unlike the case with fitting the accelerating universe. The main result is that the proposed reduced speed of light in the IGS predicts discordant redshifts. It is shown that the current explanation of “accidental superposition,” is most likely insufficient to explain the number of observations, and that the present proposal could make up the difference. It can be tested astronomically, as illustrated in a figure.

Keywords:

Dark Energy, Speed of Light, Expansion Comparisons, Discordant Redshifts

1. Introduction

Recently the author has published three papers [1] [2] [3] that describe a possible alternative to the accelerating universe that emerged from the Type Ia supernovae (SNe Ia) studies of Riess, et al. [4] , Schmidt, et al. [5] , and Perlmutter, et al. [6] . In the proposed alternative model, the dark energy instead of having a negative pressure, has rather an index of refraction n, so that the speed of light through it is reduced to c / n. Moreover, in the model it is assumed that the dark energy is only in the intergalactic space (IGS), so that within the galaxies themselves, the speed of light is c. Since galaxies do not have sharp boundaries, there will obviously be a transitional behavior of the speed of light in the halos. In Section 2, the relation of dark energy to dark matter in the model is given, in which it is proposed that dark energy is a different phase of dark matter, rather than a different substance. Also, expressions for increased apparent magnitude and distance, derived in [1] as a function of redshift and n, are given, and briefly discussed. In Section 3, the two different approaches to determining n are described: one, based on a least squares analysis, and the other, on an assumption about the expression for n in electromagnetic theory. In Section 4, in view of the recent work of Nielsen, et al. [7] , who suggest, on the basis of a statistical analysis of a larger number of SNe Ia than were used previously, that the universe seems to be expanding uniformly, rather than accelerating, a smaller least squares value, n = 1.26,was found when fitting this model, and it was used to make a comparison with the decelerating model in Table 1 which also includes two examples of the earlier comparison of the accelerating universe with the EdS universe. It is also shown from the field equations that unphysical behavior of the energy-stress tensor is found for this model. In Section 5, some predictions of the decelerating EdS model for the age of the universe are presented, where it is also shown that the smaller value of n leads to too short an age for the EdS universe. Significantly, an astronomical test of the proposed model based on discordant galactic red shifts is proposed, since a numerical analysis indicates that the current explanation underestimates the number of cases observed. A simplified description of the test is presented in Figure 1. In Section 6, there are concluding remarks.

2. Dark Energy, Reduced Speed of Light, Dark Matter

As mentioned, dark energy in this model does not have a negative pressure, or indeed any pressure at the level of approximation used here, but instead, has an index of refraction n that reduces the speed of light through it to c / n. Because of this reduction, it obviously takes longer for light to reach the Earth from the SNe Ia than it would if the speed of light remained c. This in turn gives the decelerating, but still expanding, EdS universe the additional time needed to further expand, so as to result in there being a greater distance to the SNe Ia, and hence a greater diminution in brightness, than if light traveled with speed c. This additional distance also shows up in the verification of the ΛCDM model by Anderson, et al. [8] [9] through their determination of increased distances (angular distance D_A, and luminosity distance D_L, as discussed in [1] )) to the “standard ruler” of the baryon acoustic oscillations (BAO). Also, the additional distance shows up in other Large Scale Structure (LSS) studies which, for brevity, will not be examined here.

On the other hand, since the speed of light within the galaxies is taken to be c, the model effectively assumes that the speed of light reduction is only occurring within the intergalactic space (IGS), and therefore that dark energy is only in the IGS. Since it was noted by Riess, et al. [10] that for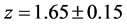, the apparent magnitude of a supernova Ia indicated that at that epoch the universe was not accelerating, hence, in the alternative model proposed here, this can only mean that the dark energy started to appear at that epoch, and that before that time there was only dark matter in the IGS, since extra-galactic baryonic matter, cosmic microwave background radiation (CMBR), neutrinos, the Higgs field, axions, gravitational radiation, and other possible constituents of the IGS are all ignored in this preliminary model. Consequently, in this model, one is led to the idea that dark energy is another phase of dark matter, and that this phase change started to take place at the above value of z, call it z*. The cause of this phase change is attributed to the expansion cooling of the dark matter in the IGS, since in the expanding universe it is the IGS that expands, and not the galaxies themselves. Clearly, there will be a transition from the central regions of the galaxies, where the speed of light is c, to the ill-defined edges of the galaxies, with their widely varying morphologies, where the speed of light would become c/n. 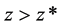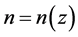Also, there will be a variation of n with z, with n = 1, for, and for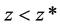, although the transition at 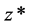need not be sharp. For simplicity, it is assumed that for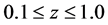, 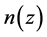is a constant, and it is left to future work to determine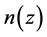, although in Section 5, the consequence of restricting the constancy of n to 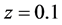to 0.6 is briefly discussed. Since no dispersion was observed, no frequency dependence for n is assumed. Under these assumptions it was shown in [1] that the increase in apparent magnitude 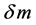is given by

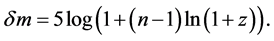(1)

However, for some purposes, it is more convenient to convenient to work with the logarithmic measure of the fractional distance increase given by

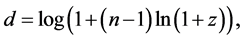
(2)

which will be done here. The above corrections do not depend on the kind of universe that is being compared with the accelerated universe; all that is required, in addition to the independence of n on z, is that the expansion parameter satisfies

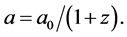(3)

Thus, as was shown in [3] , one can carry out a comparison of the universe with a closed universe. Also, it need not be an accelerating universe that is being compared with the EdS universe, one could have instead, a uniformly expanding universe, as suggested in [7] , that will be studied below in Section 4.

3. Two Ways of Determining n

In [1] n was determined by a least squares approach, in which the difference of apparent magnitude between the universe and the EdS universe was obtained by differencing the curves in Tonry et al. [11] , and then comparing with 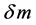given in Equation (1) for. Thus, for each of the ten values of z, a value for n_i, for i = 0.1 to 1.0, was obtained that made from (1) agree with the difference of the curves in [11] . The least squares value of n was then given by the average value:. The cosmological density parameters were taken to have the fiducial values. It was found from the least squares analysis that. For the BAO comparison, distances were involved rather than apparent magnitude, and the logarithmic distance differences between the universe and the EdS universe was obtained analytically, and compared with d given in Equation (2). The percentages of disagreement, as a function of z, were identical with that obtained for apparent magnitude disagreement when round-off errors were taken into account.

In [1] it was also assumed that n was not of electromagnetic origin, but it was found subsequently that there are difficulties with this assumption, and hence in [2] , upon assuming that dark energy is a medium that is linear, isotropic and non-dispersive, one is led to the following standard relation, , where K is the dielectric constant, and is the relative permeability. Under the further assumption that

(4)

one has finally that

(5)

Calculations were made in [2] and [3] for various values of in the model, where, with given by the Planck collaboration findings in Abe, et al. [12] that find, which compares favorably with the more recent finding of the BOSS collaboration of Shadab, et al. [13] based on examination of the BAO, that find for a flat ΛCDM universe. One sets, since for flat FLRW universes, and empirically it is very close to unity, since the finding in [12] is that a possible curvature contribution is given by, and this is believed to be due to measurement limitations. (In [3] it was mistakenly given as) It should be noted that since the dark energy in the alternative model has negligible pressure, its sole contribution to EdS is to, so that. It therefore has to be assumed that the gravitational interaction of the dark energy with the galaxies behaves in such a way that its overall effect on their peculiar velocities is of higher order, and that it can be neglected in this preliminary model. This assumption is necessary to insure agreement with the fact that studies of large scale structure have indicated such as from the 2dFGalaxy Red shift survey, see e.g. Verde, et al. [14] , and Hawkins, et al. [15] .

In [2] it was found that for, that n (least squares) = 1.47, and that n(square root) = 1.46. In [3] , with, , , and; and finally, also in [3] , with , , , and. Averaging these results, one has, and.

4. Comparison of EdS with Accelerating and Uniformly Expanding Universes

Although much of the following analysis is standard, it is necessary to present it here so as to make clear the meaning of the terms in Table 1. The FLRW flat space-time line element, provides the metric to obtain the Einstein field equation for the energy density for the model, with and, where is the CDM mass density, composed of dark matter and baryonic matter, so that the energy density equation becomes

(6)

Upon introducing the Hubble parameter, and the Hubble constant, Equation (6) can be written

(7)

Since the CDM obeys the conservation law, in the absence of pressure in the source tensor, and since, one has. Hence, from the definitions:, , , , one has. After intro-

ducing the standard definition:, it follows that (7) can be written as Since in the model, as well as the EdS model (without the correction for refraction by dark energy), light travels along the null geodesic of the flat FRLW line element, , and hence

(8)

Upon making use of from (3), integrating, and simplifying, one has

(9)

Now for the model, with, one obtains a value from Equation (9) for which will be denoted by. Likewise, for the EdS model, with, in which, one obtains . One can then form the ratio in which the distance cancels. It is therefore convenient to define a dimensionless quantity that is independent of given by

(10)

Thus the above ratio becomes The basic idea of the alternative model is that Hence upon taking logarithms, since in comparing apparent magnitudes logarithms are used, one has

(11)

For the universe one has

(12)

which has to be evaluated numerically. For the EdS universe, for, one has

(13)

In [1] , the integral in Equation (12) was evaluated for, with the range to 1.0 with steps, and this led to the least squares value n = 1.49. Here, the Planck collaboration values for the Ω’s that were used in [3] are used, but only for the one case:. These values yielded the least squares value. The results of the comparison of with d for n = 1.48 are given in Table 1, the first four columns of which are taken from Table 1 in [3] . In the fifth column just the percentage disagreement is given for the square root value n = 1.50, also from Table 1 in [3] . In the last four columns, comparison will be made with a uniformly expanding universe suggested in [7] . The assumptions about energy density and pressure that uniform expansion entails in Einstein’s field equations will be discussed below Table 1.

Under the uniform expansion scenario suggested in [7] , one has

(14)

where u is some constant speed of expansion whose value is left open, since it will drop out. Then it follows that

(15)

Where, since the universe is expanding, the positive root has been chosen. Then, from, Equation (15) becomes. Since, it follows that, and since one has finally that. By the same analysis as that above, one has

(16)

Once again, will cancel upon taking the ratio, so that the ratios reduce to with

(17)

and hence.

To compare with , it is necessary to determine n by a least squares analysis. It was found that, with negligible sigma. In Table 1 it is seen that, apart from several exceptions, the fit from to 1.0 is clearly better for the uniformly expanding universe than for the accelerating universe for either or n = 1.50. Hence it would seem that for the alternative, decelerating model with reduced speed of light, the refractive index, n = 1.26, should be chosen over n = 1.48 or n = 1.50. However, as will be shown below Table 1, from the general relativity field equations, the energy density and pressure for the uniformly expanding universe is unphysical, and also it will be shown in the next section that would lead to too short an age for the decelerating universe.

It will now be shown what (14) entails about the energy density and pressure for the uniformly expanding universe, from the standpoint of the field equations. Upon rewriting the line element as

, one has

(18)

and, and from symmetry. Eliminating the term, it follows that

(19)

Since for uniform expansion, one has. Also, because of the signature of the metric, , where p is the pressure, so that. Thus, analogous to the accelerating universe, the uniformly expanding universe has a negative pressure, albeit one-third the fraction of the energy density in magnitude. Returning to (14), one has from (18), , and hence, so that the energy density falls off as, whereas empirically, the matter energy density falls off as, and the radiation energy density falls off as, thus a re-examination of the larger SNe Ia data set is possibly indicated.

5. Some Predictions of the Alternative EdS Model

Although it is clear from Table 1 that the proposed EdS model can provide an alternative to the accelerating universe to within several percent over the range to, it is desirable that the model make other predictions. As shown in [2] , because of the reduced speed of light, the model leads to a modification of the age of the EdS universe from the usual expression of (2/3) to. This comes about as follows: the Hubble constant can be obtained from the first order Doppler shift as, where is the proper distance to the galaxy experiencing the Hubble flow. However, the light coming from that galaxy traveled mainly through the dark energy in the IGS, hence, ignoring the small correction for the time spent traveling through the Galaxy to the observer, it traveled with speed , and consequently, from the expression for the first order Doppler shift, the above expression for the Hubble constant should be corrected to. Thus one should distinguish between and, with. Denoting the age of the universe by, then it follows that the age of the EdS universe is

(20)

with, and [12] . (Note that Cheng and Huang [16] , based on BAO studies, obtain, , while the BOSS collaboration [13] , likewise from BAO studies, find for a flat ΛCDM universe; both findings are in excellent agreement with [12] which will be used here. On the other hand, Riess, et al. [17] find which is in conflict with the above values, and leads to too short an age for the EdS universe as discussed in [3] . It follows from (20) that the EdS universe is ~0.4 Gyr older than the accelerating universe of, as given in [12] . If stars should be found with ages close to or greater than that of the accelerating universe, but less than that from (20), that would tend to support the proposed model. At this writing, a star that comes close to meeting this requirement is the subgiant HD140283 whose age, when all uncertainties have been taken into account, is given by Bond et al. [18] as. However, because of the large uncertainty, no definite conclusion can be drawn as to whether its age is in agreement or disagreement with that of the accelerating universe. Nevertheless, if more such very old stars should be found, it may become possible to decide on the issue.

In contrast to the above results, based on the value of n derived from the fit to the accelerating universe, if one uses n = 1.26 that was found in fitting the uniformly expanding universe, one finds for the age of the EdS universe . This age is inconsistent with the finding in [3] that the age of the EdS has to be greater than that of the accelerating universe in order to acquire the extra distance needed to explain the diminished brightness of the SNe Ia. In addition, such an age is too small to accommodate HD 140283, and also it is too small to accommodate the ages of the oldest globular clusters as found, e.g. in Gratton, et al. [19] , who give the age of the oldest globular clusters in the Galaxy as. See also the discussion in Krauss and Chaboyer [20] . In contrast, for the uniformly expanding universe, , and; hence the age, , is given by. Thus the EdS universe with reduced speed of light is not a possible alternative to the uniformly expanding universe, although it is a possible alternative to the accelerating universe. On the other hand, interestingly, for both alternatives to the accelerating universe predict exactly the same age of the universe.

Although the least squares fit yielded for, in contrast with the fact that for these values of the density parameters. It should be noted that the least squares value was based on the redshift range to. If instead, in obtaining, one had restricted the redshift range to being from to, on the grounds that for, is no longer a constant, and is starting to diminish, one would have found that. Hence, to three places, there would have been perfect agreement between the two different ways of obtaining n. If it should turn out from future astronomical observation that indeed, then it would follow that n exactly cancels the 2/3 factor in the age of the EdS universe, and since, as shown in [3] , such a factor is also present in the approximation for the age of the closed universe, this would suggest, on the basis of an as yet unknown theory, that n is either the reciprocal of this 2/3 factor, or very close to it. This in turn would mean that one could predict the increase in apparent magnitude of the SNe Ia with the aid of given in (1), as well as the increased distances to the BAO with the aid of d given in (2). Also, importantly, one could also predict the ratio, since. Furthermore, according to the assumption in (4) that, it is possible such a theory would take one closer to a unification of gravitation with electromagnetism, as long sought for by Einstein. But one needs confirmation of this possibility from astronomy, as discussed below.

In [2] there are also predictions concerning cosmic rays, but in view of space limitations, they will be omitted here, and instead, a new astronomical prediction will be discussed, that goes beyond that given in [2] , that would give a direct test of the proposed reduction of the speed of light in the IGS, and moreover, it may have already been observed, but not recognized as such. For simplicity, imagine galaxies are spheres with sharp boundaries. Then a ray of light, impinging on a galaxy from the IGS, where the speed of light is c/n, at an angle to the normal, and hence the radius of the sphere to that entry point, will be bent away from the normal, then travel through the galaxy, and upon exiting, will be bent towards the normal, and then travel to the observer that is in the plane defined by the more distant galaxy G, the point of entry R, and the center of the more nearby galaxy F Assume further that the light that came originally from G is well off to the side of F, so that G is directly observable. This situation is described in Figure 1 that is analogous to that in [2] , but in contrast, the gravitational deflection of light from G by F has been included. On the other hand, as in [2] , the refraction of the light entering our Galaxy on its way to the observer at E has been omitted. In [2] it was imagined that F and G were sufficiently nearby so that cosmological expansion could be ignored, but here it will be assumed that this is not the case. Then F will have a smaller redshift than G, and the image of G that one would see within F would provide an example of a discordant galactic redshift, a source of controversy earlier, since some investigators, particularly Arp [21] , (for a later work see Arp [22] ) mistakenly believed that discordant redshifts were an indication that greater z did not necessarily mean greater distance from the observer. Within the framework of standard Big Bang cosmology, in the absence of the herein proposed alternative model, the only admissible interpretation is that there is a galaxy behind F, but at a greater distance, and hence with a greater redshift, as shown in Figure 1 as, and described below as “accidental superposition.” In contrast, the proposed model suggests a second possibility, also consistent with greater redshift meaning greater distance, as shown in Figure 1, and further described in the caption.

Thus, as a test of the proposed alternative model, since the location of the discordant redshift galaxies are known, astronomers should undertake to see whether there are any higher redshift galaxies that are suitably located off to the side of the lower redshift galaxies with the same morphology and spectral signature that could alternatively be responsible for the discordant redshift images. The failure to find any appropriate candidates, would rule out the proposed model, since the probability for this scenario would seem to be about the same as for the case when there is an actual galaxy at, although since galaxies are not spheres with sharp edges, it is difficult to assess the relative probabilities. However, what one can say is that if the proposed model is correct, there should be more examples of discordant redshifts than predicted by the accidental superposition of higher redshift galaxies in the background appearing to be in the close neighborhood of lower redshift galaxies.

In regard to this issue, Bahcall [23] made a very helpful estimate of the probable number of such accidental superpositions that suggest physical connection, as Arp [21] thought was the case. He lets be the probable number of accidental configurations that suggest physical connection. As an example, he takes N to be the number of spiral galaxies in which there would be accidental superposition of the more distant higher redshift galaxies with the more nearby lower redshift galaxies that would give rise to discordant redshifts, as, e.g., NGC7603 and its companion in Arp’s Atlas [21] . (See the photographs in Arp’s more recent work [22] .) To determine N, Bahcall set

(21)

where is the total number of galaxies whose vicinity has been searched for a faint companion. A denotes the area in square degrees in which an object must fall to be considered a “close companion,” and hence an example of a discordant redshift. B denotes the number of objects per square degree. Finally, O is described by Bahcall as a “catch all” parameter which he estimates as being 1/6, since the order of one-sixth of the total area surrounding NGC7603 contains “interesting protuberances.” He goes on to set, the number of galaxies listed in the catalogue compiled by de Vaucouleurs and de Vaucoulers [24] . He sets where is the mean separation size of physical association. In other words, it is the mean angular distance between the center of the lower redshift galaxy, which is rather uncertain, and that of the higher redshift companion, that is likewise uncertain, hence the designation, “suggestive.” He indicates that for the special case of NGC7603 and its companion, the minimum value of is 1 arc minute. This leads to a lower limit on A to be square degrees which he rounds off to 10^-3 sq. degrees. He sets objects/sq. degrees, based on the number of galaxies brighter than 19^th magnitude, as determined in the Lick survey [25] . He then inserts these values, while also rounding C to galaxies, into (21) and obtains. He emphasizes that although the number is “highly uncertain,” it is in satisfactory agreement with the 64 cases of such association listed by Arp [21] . He concludes the section by saying that it is possible to explain all of the close companions in Arp’s catalogue on the basis of accidental superposition. Given the absence of the present proposal at the time when Bahcall said that, his conclusion was certainly the only reasonable one that was consistent with the standard interpretation of the Hubble expansion. However, since the model proposed here describes in Figure 1 an alternative way to obtain the discordant redshifts, and, importantly in a way that is consistent with the standard interpretation of the redshift, it seemed desirable to recalculate without rounding up and A. One then has

(22)

This smaller, but still highly uncertain, value for N suggests that about one- half of the 64 cases listed by Arp are due to something other than accidental superposition, and could instead be due to the reduced speed of light in the IGS, and the refraction scenario proposed in the highly simplified Figure 1. However, in keeping with the scientific method, only astronomical observation can settle this issue.

6. Concluding Remarks

The decelerating EdS universe, supplemented by the proposed reduction of the speed of light by the dark energy, can fit the increased distances to the SNe Ia, and hence their diminished brightness predicted by the accelerating universe to within several percent for, as reported earlier. It can also fit the findings of the BAO studies that support the flat universe. No assumptions are made about the particle nature of the dark matter or dark energy, although the latter is assumed to be a different phase of the dark matter located solely in the IGS, in the simplified model used here that ignores a transition region in the halos. However, the challenging problem as to how the extremely low density dark energy could have such a large index of refraction, , and not show any dispersion as well, is left unsolved; although a possible explanation for that hints at a possible unification of gravitation and electromagnetism as sought by Einstein is briefly described. The decelerating model can also fit the recently proposed uniformly expanding universe with better overall percentage agreement for. However, the uniformly expanding universe has problems with the physical dimensionality of its energy density, as determined from the general relativistic field equations. Moreover, the smaller value of n leads to too short an age for the EdS universe. This latter problem does not arise in conjunction with fitting the accelerating universe, i.e., all the values of n that were found led to satisfactory ages of the universe. Thus while the proposed model is a possible alternative to the accelerating universe, it is not a possible alternative to the uniformly expanding universe. Nevertheless, and somewhat paradoxically, for, both the EdS with reduced speed of light, and the uniformly expanding universe, predict the same age for the universe. Finally, it is shown that the assumption that there is a reduced speed of light in the IGS, in the above redshift range, is capable of falsification astronomically by examining the field of higher redshift galaxies surrounding galaxies with discordant redshifts, to see whether they could be responsible for some of them. The proposal could also be falsified by finding galaxies without discordant redshifts that when surrounded by galaxies at higher redshifts and suitable relative orientation, should have produced such discordant redshifts.

Cite this paper

Tangherlini, F.R. (2017) A Possible Alternative to the Accelerating Universe IV. Journal of Modern Physics, 8, 622-635. https://doi.org/10.4236/jmp.2017.84042

References