ABSTRACT

The observed correlation of the angular momenta 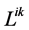and magnetic moments of celestial bodies (the Sun, planets and stars) was discussed by many authors but without any explanation. In this paper, a possible explanation of this phenomenon is suggested. It is shown that the function 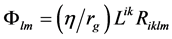satisfies Maxwell equations and can be considered as a function which determines the electro-magnetic properties of rotating heavy bodies. The 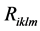is the Riemann tensor, which determines the gravitational field of the body, is the gravitational radius of the body, and is the constant which has to be determined by observations. The field 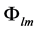describes the observed correlation. It explains the stability of magnetic field of white dwarfs and neutron stars despite the ohmic dissipation. The function 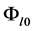describes the electric field created by rotating heavy bodies. The presented theory does not contradict any existed experiments and observations.

Keywords:

Electromagnetic Field, Rotating Celestial Bodies, Gravitation

1. The Observed Dependence of the Magnetic Moments on the Angular Momenta of Celestial Bodies

The common accepted theory on the origin of the magnetic field of stars and planets is based on the assumption that the field is maintained by hydro-magnetic dynamo. Indeed, it is possible to select the appropriate motions inside the celestial bodies which can support the dynamo action. The assumed motions do not contradict the existing models of stars and planets. The numerical calculations of the magnetic field confirm the dynamo model. Unfortunately, there are no certain evidences on motions inside the bodies and the theory is based on more or less true assumption on these motions. Ne- vertheless, it seems that the general approach to the problem is true, through some important data remain unexplained. Some problems are connected with the existing correlation of the angular momenta of the rotation and magnetic moments of celestial bodies.

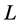P. M. Blackett [1] in 1947, based on the data on Earth, Sun and one other star, speculated that there exists an unknown universal physical law: for all astrophysical objects. Here is amagnetic moment, is anangular momentum and 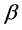is number of the order of unity. Blackett did not specify what the origin of this law might be. This result was never generally accepted and by 1950 even Blackett refuted this idea.

However, recent observations show that the 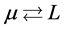correlation exists for planets and for other celestial bodies (Russell, Dolginov, Arge et al., Cain et al.) [2] [3] [4] [5] [6] . In this paper we suggest a possible explanation of this phenomenon.

The motions of matter inside different bodies have to be very different. However, observations show the similar connection of magnetic moments and angular momenta for absolutely different bodies. The observed dependence of the logarithm 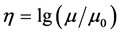on 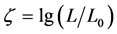is presented in Figure 1 below (Dolginov, 1988) [4] [5] .

Here 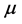is used for the magnetic moments of planets and for the average magnetic momenta of groups of stars, mentioned in this figure, 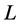is the angular momentum. The magnetic moment of the Earth is, the angular momentum of the Earthis. The spread of these values is very large and is the reason why the logarithmic scale is used here. There are marked: My―Mercury, E―Earth, Ms―Mars, J―Jupiter, S―Saturn, U―Uranus, N―Neptune, S―Sun. The classes of ordinary stars, used in astronomy, are: (A, O, F, K, G, M). White dwarfs (WD). Neutron Stars (NS). We present here the average values of and, for stars belonging to each class. The spread of

the observed values, within groups of stars of the corresponding class, reaches two orders of magnitude, but almost linear dependence of the mean values extends to twenty orders of magnitude and much more if the galaxy as a whole is included.

The correlation has been investigated in more detail (Arge et al. 1995) [6] for 727 astrophysical objects divided into seven groups (solar system, cool stars, hot stars, isolated white dwarfs, cataclysmic variables, isolated pulsars, binary pulsars). In Table 1 presented below the simplified expression for angular momentum was used:, where is the rotation period, , and is the polar field in Gauss. For the Sun: Gauss, is the radius of a body. It is derived:. Below in Table 1 is the standard deviation in the slope, and is in the intercept. The C.C is the correlation coefficient.

The plotted points span a range of some 20 orders of magnitude in both and. It was shown that the center of distribution for all these sub-samples, excluding binary pulsars and cataclysmic variable, are located close to the same line:

with the correlation coefficient: 0.941.

We will consider below only the case of single stars. The case of binary stars needs a separate investigation. Our result also describes approximately the correlation for most planets in the solar system. However, this correlation needs a special investigation for such bodies as the Moon, since the rotation of these bodies is strongly connected with their orbital motion. More detailed investigation of the correlation for binary and multibody systems is necessary to decide how their magnetic field is determined by gravitation, by the spin and by the orbital angular momentum of the body.

2. Possible Explanation of Correlation

To explain the correlation, we assume: 1) the existence of an electromagnetic field which is created by rotation of a body, 2) this field has to be described by Maxwell equation, 3) this field has to be linearly dependent on the body angular momentum, 4) this field is significant only for very heavy bodies such as stars and planets. To this

purpose consider the anti-symmetric second rank tensor:

(1)

Here is the Riemann tensor which determine the gravitational field of the body, is the gravitational radius of the body and is the constant which has to be determined by observations.

(2)

Here is the vacuum part of the Riemann tensor and is the Weyl tensor.

Angular momentum depends on the body characteristics, but not on the space- time coordinates and:

(3)

Using Bianchi identities and contracted Bianchi identities:

(4)

where is the Ricci tensor and is the covariant derivative of, we obtain Maxwell equations for:

(5)

(6)

where determine the effective current, created by the body rotation. This current is divergence free.

(7)

The result (7) is not identical to the four dimensional divergence law for the energy-momentum tensor:. It was proved (Pagels, 1961) [7] that. This is an additional condition that follows from the Einstein equation.

The so called “electromagnetic components of the Riemann tensor” were considered in many papers (see, for example, the paper of B. Mashhoom and references there) [8] but without any connection to problems of correlation for astrophysical objects. The main assumption of our paper is the assumption that the field, which is described by is a real electromagnetic field which interacts with electrical charges. This assumption does not contradict observations because the effect of this field can be observed only for very heavy objects, such as stars and planets. The gravitation was never considered in connection with the problem of correlation.

Let us consider the simplest case of a heavy spherical body having the mass, radius and constant mass density. The metric of the body gravitational field is determined from:

(8)

We will consider the case of a weak field and use the linear approximation. Inside the body:. In this case the nonzero are:

(9)

The metric of rotating bodies depends on angular momentum (the Kerr metric, for example). However, the dependence of the metric on the potential is much stronger than on. Using the obtained values and choosing the axis Z along the angular momentum, i.e. taking where is the moment of inertia and is the angular velocity, we obtain the field inside the body that is approximately constant. Gravitational potential outside the body is:. In this case:

(10)

Using (1) and (8) we can see that outside the body the represents a dipole field:

(11)

We can see from (5)-(11) that there exists an antisymmetric tensor that satisfy Maxwell equations and is determined by the divergent free current. Can the function describe the interaction of charged particles? In other words: can the be considered as the tensor of the electromagnetic field, created by rotation of heavy bodies? This possibility does not follow from the definition, but there are no arguments to exclude it. This possibility can be proved or denied only by experiment or astrophysical observations.

The estimate value of the is of the order of that is approximately equivalent to.

Astrophysical objects have both poloidal and toroidal magnetic fields. The toroidal field is easily created from poloidal field by differential rotation of the convective matter inside the body. Such rotation inside the body is common for most astrophysical objects, but the creation of the poloidal field needs complicated cyclonic motions.

The magnetic energy of the body is quadratic with respect to, and, therefore, the magnetic energy does not depend on the direction of angular momentum. In other words, we have degenerated state. In such a case, some perturbations may change the magnetic field direction with respect to the direction of the angular momentum. The change of the field polarity may be due to some irregular or regular changes of motions inside the body. The change of the field direction took place several times in the Earth history.

3. Electrical Field of Rotating Bodies

The electric field created by the body rotation is determined, according to the expression (1), as:

(12)

The stationary electric field is created in the system if the metric of the system contains terms with, where. If the interval is determined by (8) then the electric field of a body is not zero if the gravitational potential depends on time. For example, time dependent are tidal forces. However, a simple estimation show that such field is much less than the observed electric field of the Earth and can be considered only as a seed field. The Earth surface has the positive charge of 1800 amperes, 400,000 volts-a power of 700 megawatts (Feynman 1957) [9] . The total electric current reaching the Earth surface at any time is approximately constant. What maintains this field? There are many attempts to describe this field as due to ionization of the atmosphere by cosmic rays, by solar wind etc., but there is no commonly accepted explanation. Regarding other celestial bodies, there are no observations related to their global electric field. This problem needs a special investigation.

4. White Dwarfs and Neutron Stars

The field of white dwarfs and neutron stars is usually explained as a relict field conversed during the star contraction. If the initial surface field of a star with radius was, then the field after contraction to the radius will be. In this paper we did not take into account that some fraction of mass is lost in the process of the star contraction and the conductivity could be significantly changed. The conductivity of compact objects is provided by electron transfer, whereas in non-compact parent star it was provided by turbulent plasma motions. It seems that there is no a priory reason to think that the centers of distribution of compact objects in the plot should have any relation to the centers of distribution of non-compact objects. However, the analysis (see Arge et al. 1995, and Dolginov 1989) [5] [6] demonstrates that the centers of the distribution for white dwarfs and neutron stars are located on the same curve as for all other stars and planets. It can be explained if there exist some kind of universal connection also for these stars. The possible explanation of these observations is the existence of the field. The difference of white drafts and neutron stars from other stars may be connected with the white dwarfs and neutron stars internal structure. The table of presented above do not include any data related to the inner structures of astrophysical objects. In reality these structures are very complicated, including differential rotation of different layers, convective motions etc. These motions are considered in the dynamo theory, which is the most accepted theory of the magnetic field generation in stars and planets.

Motions inside the bodies could be important not only for dynamo actions but also for the correlation.

Unfortunately, there are no direct evidences on the internal structures of celestial bodies, although some qualitative estimations are apparently true. The Earth solid inner core, the mantle and the liquid core are rotating with slightly different angular velocities, and have the axis of rotation slightly inclined towards each other. Interiors of white dwarfs and neutron stars is much more inhomogeneous than the Earth interior. In particular, the shift of the point for isolated white dwarfs in the table presented above, could be due to the different rotation of the different internal layers which was not taken into account in the presented table. The internal structures of massive white dwarfs and neutron stars contain superfluid layers which provide different rotation of different internal regions. These layers can rotate independently of the matter on the star surface. It is possible that the magnetic field of neutron stars is determined mostly by the rotation of the star interior, which is much heavier than the surface layers and could rotate opposite to the surface layers. This may explain the negative sign of the coefficient in Table 1 presented above.

The existence of the motions inside celestial bodies which create the dynamo action does not contradict to the possibility of the universal field created by the body rotation.

It was shown by L. Ferarro, et al. (2015) [10] that: “There is no evidence that fields of highly magnetic white dwarfs decay over time, which is considered, with the estimated ohmic decay time scales of 10¹¹ years.” The similar result was obtained by Y. Sang and G. Chanmugam (1987) [11] . These results can be explained taking into account that the ohmic decay do not destroy the field created by the body rotation.

5. Conclusion

Astronomical data show that there exists correlation of the magnetic moments and angular momenta for all celestial bodies. It is impossible that the correlation of such a mechanical property, as the angular momentum and the electromagnetic property, characterized by magnetic moment, can appear accidentally for all celestial bodies in the interval more than twenty orders of magnitude in and, (and much more if we include the Galaxy as a whole) with scattering about two orders of magnitude. We assume that the rotation of heavy bodies create electromagnetic field: . The is the solution of Maxwell equations. It explains the observed correlation. It does not contradict to the possible changing the direction of the field polarity. It explains why the magnetic field of white dwarfs and neutron stars do not decay in the time predicted in the case of ohmic dissipation. The component describes, at least, the part of electric field of the rotating body. The presented theory: 1) does not contradict any existing experiments and observations; 2) it does not contradict conclusions following from Maxwell and Einstein equations; and 3) it explains observations which were not explained up to now. The satisfied these criteria. The obtained results do not contradict the possibility of the dynamo action inside astrophysical objects.

Cite this paper

Dolginov, A. (2016) Electromagnetic Field Created by Rotation of Celestial Bodies. Journal of Modern Phy- sics, 7, 2418-2425. http://dx.doi.org/10.4236/jmp.2016.716208

References