Journal of Modern Physics
Vol.07 No.13(2016), Article ID:71085,10 pages
10.4236/jmp.2016.713160
Fundamental Harmonic Power Laws Relating the Frequency Equivalents of the Electron, Bohr Radius, Rydberg Constant with the Fine Structure, Planck’s Constant, 2 and π
Donald William Chakeres
Department of Radiology, The Ohio State University, Columbus, OH, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 3, 2016; Accepted: September 27, 2016; Published: September 30, 2016
ABSTRACT
We evaluate three of the quantum constants of hydrogen, the electron, e−, the Bohr radius, a0, and the Rydberg constants, R∞, as natural unit frequency equivalents, v. This is equivalent to Planck’s constant, h, the speed of light, c, and the electron charge, e, all scaled to 1 similar in concept to the Hartree atomic, and Planck units. These frequency ratios are analyzed as fundamental coupling constants. We recognize that the ratio of the product of 8π2, the ve− times the vR divided by va0 squared equals 1. This is a power law defining Planck’s constant in a dimensionless domain as 1. We also find that all of the possible dimensionless and dimensioned ratios correspond to other constants or classic relationships, and are systematically inter-related by multiple power laws to the fine structure constant, α; and the geometric factors 2, and π. One is related to an angular momentum scaled by Planck’s constant, and another is the kinetic energy law. There are harmonic sinusoidal relationships based on 2π circle geometry. In the dimensionless domain, α is equivalent to the free space constant of permeability, and its reciprocal to permittivity. If any two quanta are known, all of the others can be derived within power laws. This demonstrates that 8π2 represents the logical geometric conversion factor that links the Euclid geometric factors/three dimensional space, and the quantum domain. We conclude that the relative scale and organization of many of the fundamental constants even beyond hydrogen are related to a unified power law system defined by only three physical quanta of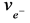 ,
, 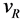 , and
, and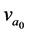 .
.
Keywords:
Fundamental Physical Constants, Unification Models, Hydrogen, Electron, Bohr Radius, Rydberg Constant, Fine Structure Constant

1. Introduction
The quantum properties characterizing hydrogen are fundamental constants important in many divergent areas of physics [1] . We focus on the electron, e−, Bohr radius, a0, and the Rydberg constant, R∞, within hydrogen as a unified physical and mathematical system. These constants represent a mass, a distance, and a frequency (1/time) so they span the physical units. These constants are all known to be inter-related through power laws with the geometric factors of 2, π, the fine structure constant, α, the speed of light, c, and Planck’s constant, h. In fact, each one of the hydrogen quantum constants is defined utilizing α, c, h in its derived unit value. None of them are experimentally directly measurable. This system is associated with all of the elements through Mosley’s law. These quanta are related to the kinetic energy equation through Sommerfeld’s original physical interpretation of α as a velocity divided by c, a dimensionless β. For the hydrogen system, the product of the rest mass of the electron times the speed of light times α both squared divided by 2 equals the hydrogen ionization energy. Through α and these constants, broad segments of physics are directly mathematically and conceptually inter-related within systematic power laws [2] [3] .
Our goal is to evaluate these three quantum values as frequency equivalents: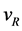 ,
, 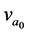 , and
, and  in the simplest fundamental manner, ratios, which are independent of any arbitrary physical unit system. We evaluate these three quantum constants all as natural unit frequency equivalents, v Hz similar to Planck’s time, and the Hartree atomic units [4] - [6] . This unit transformation is equivalent to Planck’s constant, h, the speed of light, c, the electron charge, e, all scaled to 1. By definition when h equals 1, its angular momentum is dimensionless. Their SI unit values can be reconstructed by multiplying the dimensionless calculation times the SI units. The final results are identical. We are searching for power law and harmonic sinusoidal patterns since these quanta are associated with quantum oscillators that have wave properties, and these constants are inter-related by many different power laws utilizing their SI units. Any other physical units such as mass, energy, or distance would result in the identical coupling constants, and not change the conclusions or dimensionless calculations. We conceptually choose frequency as our physical unit of choice since we are searching for wave properties.
in the simplest fundamental manner, ratios, which are independent of any arbitrary physical unit system. We evaluate these three quantum constants all as natural unit frequency equivalents, v Hz similar to Planck’s time, and the Hartree atomic units [4] - [6] . This unit transformation is equivalent to Planck’s constant, h, the speed of light, c, the electron charge, e, all scaled to 1. By definition when h equals 1, its angular momentum is dimensionless. Their SI unit values can be reconstructed by multiplying the dimensionless calculation times the SI units. The final results are identical. We are searching for power law and harmonic sinusoidal patterns since these quanta are associated with quantum oscillators that have wave properties, and these constants are inter-related by many different power laws utilizing their SI units. Any other physical units such as mass, energy, or distance would result in the identical coupling constants, and not change the conclusions or dimensionless calculations. We conceptually choose frequency as our physical unit of choice since we are searching for wave properties.
We find that these three quantum ratios and α represents an integrated power law system broader than presently recognized. They are fundamentally related to the geometric factors of 2 and π as a composite in 8π2 [7] . It is possible to define any of these quantum values as a power law of any other quantum value utilizing these geometric factors. We also find that many other fundamental constants can be simply defined in terms of these three quanta in this dimensionless domain simplifying and unifying the unit system greatly.
2. Methods
All data for the constants’ transformations to frequency equivalents were obtained from the websites: http://physics.nist.gov/cuu/Constants/, and http://physics.nist.gov/cuu/Constants/energy.html The NIST site has an online physical unit converter that can be used for these types of calculations. The respective frequency equivalents are: the Rydberg constant, 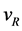 , 3.28984196(17) × 1015 Hz, Bohr radius,
, 3.28984196(17) × 1015 Hz, Bohr radius, 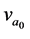 , 5.66525639(28) × 1018 Hz, and the electron,
, 5.66525639(28) × 1018 Hz, and the electron, 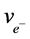 , 1.23558996(05) × 1020 Hz. The reciprocal of α is 137.0359999(78). The relative precision of the calculations is 5 × 10−8, and limited by the uncertainty of h.
, 1.23558996(05) × 1020 Hz. The reciprocal of α is 137.0359999(78). The relative precision of the calculations is 5 × 10−8, and limited by the uncertainty of h.
The italic number 1 is utilized after the standard constant’s symbol to notate that is it scaled in the units of 1 for h, c, and e rather than SI units, or in the dimensionless domain. Two examples are ε01, and h1. Many of the possible dimensionless and dimensional ratios of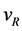 ,
, 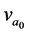 , and
, and 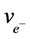 define fundamental integer power laws, and harmonic circle sinusoidal relationships.
define fundamental integer power laws, and harmonic circle sinusoidal relationships.
We use a specialized notation to abbreviate the power law ratio relationships. These all represent fundamental constants. The notation allows for complicated ratios and powers to be expressed as text. Fundamental constants are commonly associated with super and subscript notations characterizing them. Capital A is chosen to represent ratios. The superscript are the symbols for the frequencies of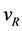 ,
, 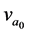 ,
, 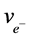 or α of the numerator. The subscript is for the denominator. The powers of
or α of the numerator. The subscript is for the denominator. The powers of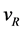 ,
, 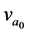 ,
, 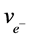 or α are within parentheses to their right. These represent power laws so different points along a single power line are all inter-related. For example,
or α are within parentheses to their right. These represent power laws so different points along a single power line are all inter-related. For example, 




Equation (1a) demonstrates a pure geometric factor. 1/8π2 equals the ratio of the product of 




Equations (2a), (2b), (3a, 3b), (4a), (4b), (4c) are all of the possible dimensionless frequency ratios of 


















The derivation of the dimensionless values for permittivity, ε01 and permeability, μ01, are shown in Equations (5)-(11). Here ε01 equals 1/α, 137.0359999(78), and permeability, μ01 equals α, 7.29735256(36) × 10−3. Equation (5) demonstrates the relationship between α, electron charge, e, ε0, 2, 4π, h, ħ, and c used in the derivation. Equation (6) derives the ionization energy of the electron in hydrogen. Equation (7) transforms the ionization energy from joules to frequency in Hz by dividing by h. In Equation (7) the a0 is converted to a frequency equivalent utilizing a ratio with c. Equation (8) transforms the relationship to the dimensionless coupling constant of 





Coulomb’s dimensionless unit 1 constant, ke1, must equal α/4π, 5.80704866(29) × 10−4. Equations (8) and (9) derive the dimensionless ε01 constant from ke1. Here, ε01 must equal 1/α, 137.0359999(78).

The dimensionless relationship of ε01, μ01, and c1 is shown in Equation (10). μ01 equals α, 7.29735256(36) × 10−3.

The following is an example a power law derivation of one hydrogen quantum value from another utilizing a different, but parallel method. This example derives 









For these two hydrogen constants, the 






Table 1. Power law ratio matrix.
Table 1 is a power ratio matrix of 


The ratio relationships in Equations (2)-(4) are solved for any hydrogen quantum value, and are raised to the ninth power which is closest to a scalar value of 1, for this example




In Equation (14) 



Equation (15) is another power law variation of this relationship deriving 



Equation (16) is another example that derives 



3. Results
Equation (1) is related to Planck’s constant in the dimensionless domain, and equals 1, Equations (17a), (17b). This is logical since h1 is intentionally scaled as 1 in this system since energy and frequency are scaled identically in a pure frequency domain. This ratio is equivalent to an angular momentum since the ratio represents the product of a mass, a frequency, a distance squared, (kg∙m2/s) in the SI dimensional domain. Since this ratio is in the frequency domain, a distance is related to the reciprocal of the frequency equivalent. This relationship is related to the annihilation energy of a mass. Equation (17b) demonstrates that the reduced Planck’s constant, ħ, equals 1/2 in the dimensionless domain, ħ1.


Equations (18a) and (18b) demonstrate that this same relationship is valid in the standard SI unit equations of h and ħ.


Equation (4c) is equivalent to the prototype kinetic energy equation where the product of a mass times the velocity divided by c, β squared divided by 2.
Equation (2) demonstrates that the α derivation from 

The dimensionless constants that define ε01, μ01, and ke1 are all very simple values related to α and geometric factors, Equations (8)-(10). ke1 logically is related to α/(4π) since the energy is proportional to the distance frequency equivalent. This is a universal relationship for any distance as a frequency equivalent. Here, 

Equations (12)-(16) demonstrate that if any two of the quantum values, including an A factor, are known then all of the constants can be derived.
The A factors do not represent errors, but are fundamental essential constants incorporating the geometric factors that are imbedded within the quantum domain scalar values. These geometric factors represent conversion factors that bridge between Euclid geometry; and the power laws of


4. Discussion
The existing physical unit system of SI units is an arbitrary system of mass, time, distance, and energy units. They were chosen for measurement convenience, and their previous utilization/standardization. In quantum physics integer quantum numbers are associated with natural quantum units, such as the Rydberg constant. Planck’s time is a classic time natural unit. Quantum spin is associated with h as a natural unit. This method has a long history, and is a valid approach in physics [4] - [6] . Natural units are not arbitrary, and essential if the system is to be evaluated from a quantum number perspective. The ratio of two natural units of a single physical unit represents a fundamental dimensionless scaling ratio. The Standard Model is not helpful in most scaling relationships between particles. The Higgs boson could not be predicted with accuracy within the Standard Model. The Buckingham Pi theory of dimensionless analysis of physical systems is well established, and states that physical systems can be analyzed in a dimensionless domain. These reasons are the rationale for the methods utilized to search for the most fundamental quantum relationships.
This paper demonstrates that many of the fundamental constants in this hydrogen system demonstrate very simple, and integrate definitions as ratios of three hydrogen quanta and geometric factors. It is logical that all of these ratios should be related to fundamental constants and relationships. These are truly the only three constants in this global power law system. This is not the typical concept of these individual constants. Though they are inter-related they are not thought of as being only ratio or product projections of just three quanta. Equations (1), (17a), (17b) demonstrate that Planck’s constant is related to the dimensionless ratio of the frequencies defining an angular momentum scaled to the number 1. This is anticipated in a natural unit system. Planck’s reduced, ħ1, constant is scaled to 1/2. This is logical since Planck’s constant times one Hz represents at minimum unit of energy per cycle. This equates the annihilation energy of a mass to an equivalent frequency. The h1 is directly related to a spin of 1 since it refers to 1 Hz times a dimensionless value associated with the energy of a wave with a frequency of 1 Hz. Photons have a spin of 1. The reduced Planck’s constant ħ1 is 1/2, and associated with a spin of 1/2 of a fermion, in this case the electron. The 8π2 geometric factor is the composite of 2π squared, 4π2; and 2. The 2π squared scales the circumference distance an electron orbiting the proton. The 2 is related to the fact this angular momentum refers to the process of mass annihilation to photons, not to a kinetic energy. 
Multiple different ratios of






This work demonstrates that there are a myriad of power law relationships where any constant can derived if any two are known including an A value, Equations (12)-(16). There are many power laws of these constants in the SI unit domain, but since their scaling relationships are not apparent these types of derivations starting with only three quanta are not possible. We present only a few of the possible power laws. In the SI unit system there are many different constants that appear to be unique values, but based on this analysis they actually represent only a product or ratio combination of the same three hydrogen quanta. Equation (5) is a standard unit equation and inter-relates five different physical constants. In this dimensionless unified domain three of the constants drop out from the scaling of the calculations as 1’s. The other two are inter-related by a geometric factor. Two of the constants are both related to the same natural unit value, α. There is really only one essential quantum constant that inter-relates all five of the SI values.
These power law relationships are not felt to coincidental or mathematically contrived, but rather fundamental. The ratio of the 

5. Conclusion
This paper describes the fundamental scaling relationships between the unified physical system of the electron, Bohr radius, and Rydberg constant of hydrogen within a natural unit dimensionless or dimensional system. It is found that classic geometric factors are embedded within the scaling of these quanta. This system bridges from the quantum wave domain to three dimensional space domains. When the relationships of these three constants are analyzed, their simple ratios and products project out to a wide array of other fundamental constants and relationships. There are also a myriad of power laws, and A values, some known and some new, inter-relating these constants so that they can all be derived from the knowledge of just two. These finding demonstrate that the fundamental constants of hydrogen represent a highly integrated logical harmonic power law system that extends beyond hydrogen. This represents a new perspective on the Standard Model within a parallel power law system.
Acknowledgements
I would like to thank Richard White M. D., Vola Andrianarijaon PhD, Keshab Sapkota PhD, and Richard Vento MS for their help.
Cite this paper
Chakeres, D.W. (2016) Fundamental Harmonic Power Laws Relating the Frequency Equivalents of the Electron, Bohr Radius, Rydberg Constant with the Fine Structure, Planck’s Constant, 2 and π. Journal of Modern Physics, 7, 1801-1810. http://dx.doi.org/10.4236/jmp.2016.713160
References
- 1. Zhao P., Lichten, W. and Zhou, Z. (1989) Physical Review A, 29, 2888.
http://dx.doi.org/10.1103/PhysRevA.39.2888 - 2. Saichev, A., Malevergne, Y. and Sornette, D. (2009) Lecture Notes in Economics and Mathematical Systems, 632.
- 3. Katznelson, Y. (2004) An Introduction to Harmonic Analysis. 3rd Edition, Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9781139165372 - 4. Mills, J. (1932) The Journal of Physical Chemistry, 36, 1089-1107.
http://dx.doi.org/10.1021/j150334a001 - 5. Karshenboima, S. (2008) The European Physical Journal Special Topics, 163, 141.
- 6. Flowers, J. and Petley, B. (2001) Reports on Progress in Physics, 64, 1191.
http://dx.doi.org/10.1088/0034-4885/64/10/201 - 7. Chakeres, D. (2011) Particle Physics Insights, 4, 33.
http://dx.doi.org/10.4137/PPI.S8269 - 8. Friedmann, T. and Hagen, C. (2015) Journal of Mathematical Physics, 56, 112101.
http://dx.doi.org/10.1063/1.4930800


